1 Introduction

Recently, sub-wavelength localization of an atom have attracted lots of attention of many researchers in coherent media due to its important role in laser cooling and trapping of neutral atoms (Metcalf and Van der Straten 1994), Bose–Einstein condensation (Wu and Cˆot´e 2002) and so on. Different techniques to measure the position of the atom passing through a standing-wave field have developed in recent years. As one of pioneering works, Storey et al. (1993) have discussed sub-wavelength atom localization using the measurement of the phase shift after the passage of the atom through an off-resonant standing-wave field. In addition, two schemes for position measurement were performed, using absorption light masks (Abfalterer et al. 1997; Johnson et al. 1998), in which the precision of measurement achieved was nearly tens of nanometers.

Also, a number of quantum optical phenomena based on quantum coherence and quantum interference have studied (Harris 1989; Wu and Yang 2005; Wu et al. 2004; Li et al. 2011; Wang and Yu 2012; Hamedi 2014; Wu and Yang 2007; Wu 2005; Hamedi et al. 2014; Bai et al. 2010; Wang et al. 2013; Hamedi 2015; Wu and Yang 2004; Hamedi et al. 2013; Hamedi 2014; Ou et al. 2009; Han et al. 2011; Yang et al. 2008; Ding et al. 2010; Zhang et al. 2013; Wu and Yang 2007; Wu et al. 1999; Wang et al. 2012; Yang et al. 2009; Li et al. 2006, 2008; Li 2007; Zhang et al. 2012; Cheng et al. 2004). There exist various one dimensional (1D) and two dimensional (2D) schemes for atom and electron localization properties of media by monitoring spontaneous emission spectrum and by monitoring absorption of a weak probe field (Sahrai et al. 2005; Kapale and Zubairy 2006; Xu et al. 2008; Li et al. 2011; Ding et al. 2011; Wang and Yu 2014; Ding et al. 2011a, b; Zhang et al. 2014; Hamedi 2014; Wang et al. 2013). For instance, Xu et al. (2008) investigated the possibility to 1D localization of a two-level atom in a half-wavelength region by using a trichromatic field to drive the atom. Ding et al. (2011) considered a five-level M-type atomic system interacting with two orthogonal standing wave laser fields and the vacuum of the radiation field. They showed that the interaction of the atom with space-dependent standing-wave fields can provide information about the position of the atom passing through, thus leading to two-dimensional atom localization. They also found that the localization in their model is significantly improved due to the interference effect between the spontaneous decay channels and the dynamically induced quantum interference generated by the two standing-wave fields. Wang and his colleague (Wang and Yu 2014) proposed a four level tripod type atomic system for high precision two-dimensional atom localization via measurement of the excited state population. Recently, the efficient two-dimensional atom localization via phase-sensitive absorption and gain spectra in a cycle-configuration four-level atomic system is also explored with Zhang et al. (2014). All these researches indicate that it is possible to control 2D atom localization via the measurement of the upper state population or any ground state population, interacting double dark resonances, controlled spontaneous emission, or the probe absorption spectrum.

The localization behavior of an asymmetric coupled quantum well (CQW) driven by two orthogonal standing-wave lasers based on intersubband transitions is recently investigated (Hamedi 2014).

In this paper, we investigate the 2D atom localization based on the measurement of absorption of a weak probe field in a four-level Λ-type system interacting with two orthogonal standing wave laser fields and one microwave field. It is found that through proper tuning of system parameters, the absorption profile manifests various localization patterns. The possibility to obtain high resolution and precision atom localization is then explored. It should be mentioned that this system has been previously used to realize the possible giant Kerr nonlinearity (Hamedi et al. 2013), optical bistability (Xiao and Kim 2010), as well as absorption and dispersion properties (Sahrai et al. 2010).

2 Model and equations

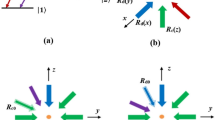
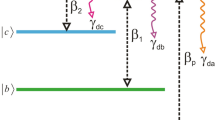
Figure 1 illustrates a four-level Λ-type system with twofold lower-levels based on Refs. (Hamedi et al. 2013; Sahrai et al. 2010). The atom moves in the z direction and interacts with two standing-wave fields in the x–y plane. In this system under consideration, upper level \(\left| b \right\rangle\) is coupled to ground level \(\left| a \right\rangle\) with a weak tunable probe field of Rabi-frequency \( \Omega_{p} = \frac{{\vec {\epsilon}_{p} .\vec {\wp }_{ba} }}{\hbar } \), while it is coupled to two closely lying lower levels \(\left| c \right\rangle\) and \(\left| d \right\rangle\) by two orthogonal standing-wave laser fields, which are respectively aligned along the x and y axes. The corresponding Rabi frequencies are dependent on the position and can be as Ω c (x) = Ω c  sin(k x x) and Ω d (y) = Ω d  sin (k y y), where \( \Omega_{c} = \frac{{\vec {\epsilon}_{c} \cdot\vec {\wp }_{bc} }}{\hbar } \) and \( \Omega_{d} = \frac{{\vec{\epsilon}_{d} \cdot\vec {\wp }_{bd} }}{\hbar } \) respectively, and k x , k y are the corresponding wave vectors. Level \(\left| c \right\rangle\) and \(\left| d \right\rangle\) are coupled by a microwave field of Rabi-frequency \( \Omega_{m} = \frac{{\vec {\epsilon}_{m} \cdot\vec {\wp }_{cd} }}{\hbar } \). Here, \( \vec {\epsilon}_{p} ,\vec{\epsilon}_{c} ,\vec{\epsilon}_{d} ,\vec{\epsilon}_{m} \) are the amplitude of probe, coupling and microwave fields, respectively. Moreover, \( \vec{\wp }_{ij} \) are the corresponding atomic dipole moments.

Fig. 1
figure 1

Configuration of four level atomic system with twofold lower-levels

Full size image

The Hamiltonian of this system is given by H = H 0 + H I , where H 0 is the free energy component and H I is the Hamiltonian of the interaction picture.

$$ \begin{aligned} H_{0} & = \hbar \omega_{a} \left| a \right\rangle \left\langle a \right| + \hbar \omega_{b} \left| b \right\rangle \left\langle b \right| + \hbar \omega_{c} \left| c \right\rangle \left\langle c \right| + \hbar \omega_{d} \left| d \right\rangle \left\langle d \right|, \\ H_{I} & = - \hbar \Omega_{p} \exp ( - i\upsilon_{p} t)\left| b \right\rangle \left\langle a \right| - \hbar \Omega_{c} (x)\exp ( - i\upsilon_{c} t)\left| b \right\rangle \left\langle c \right| \\ & \quad - \hbar \Omega_{m} \exp ( - i\upsilon_{m} t)\left| c \right\rangle \left\langle d \right| - \hbar \Omega_{d} (y)\exp ( - i\upsilon_{d} t)\left| b \right\rangle \left\langle d \right| + H.C. \\ \end{aligned} $$
(1)

where ℏω i and υ i are the energy of state \(\left| i \right\rangle\), as well as the angular frequencies of the optical fields, respectively.

Using the rotating-wave and the electric dipole approximations and in the interaction picture, the density matrix equations of motion of this Λ-type system can be written as:

$$ \begin{aligned} \dot{\tilde{\rho }}_{ba} & = - (\gamma_{ba} + i\Delta_{p} )\tilde{\rho }_{ba} + i\Omega _{c} (x)\tilde{\rho }_{ca} + i\Omega_{p} (\tilde{\rho }_{aa} - \tilde{\rho }_{bb} ) + i\Omega_{d} (y)\tilde{\rho }_{da} , \\ \dot{\tilde{\rho }}_{ca} & = - (\gamma_{ca} + i(\Delta_{p} - \Delta_{c} ))\tilde{\rho }_{ca} + i\Omega_{c} (x)\tilde{\rho }_{ba} - i\Omega_{p} \tilde{\rho }_{cb} + i\Omega_{m} e^{i\phi } \tilde{\rho }_{da} , \\ \dot{\tilde{\rho }}_{da} & = - (\gamma_{da} + i(\Delta_{p} - \Delta_{c} - \Delta_{m} ))\tilde{\rho }_{da} - i\Omega_{p} \tilde{\rho }_{db} + i\Omega_{m} e^{ - i\phi } \tilde{\rho }_{ca} + i\Omega_{d} (y)\tilde{\rho }_{ba} , \\ \dot{\tilde{\rho }}_{bc} & = - (\gamma_{bc} + i\Delta_{2} )\tilde{\rho }_{bc} - i\Omega_{c} (x)(\tilde{\rho }_{bb} - \tilde{\rho }_{cc} ) + i\Omega_{p} \tilde{\rho }_{ac} - i\Omega_{m} e^{ - i\phi } \tilde{\rho }_{bd} + i\Omega_{d} (y)\tilde{\rho }_{dc} , \\ \dot{\tilde{\rho }}_{bd} & = - (\gamma_{bd} + i(\Delta_{2} + \Delta_{3} ))\tilde{\rho }_{bd} + i\Omega_{c} (x)\tilde{\rho }_{cd} + i\Omega_{p} \tilde{\rho }_{ad} - i\Omega_{m} e^{i\phi } \tilde{\rho }_{bc} + i\Omega {}_{d}(y)(\tilde{\rho }_{dd} - \tilde{\rho }_{bb} ), \\ \dot{\tilde{\rho }}_{cd} & = - (\gamma_{cd} + i\Delta_{3} )\tilde{\rho }_{cd} + i\Omega_{c} (x)\tilde{\rho }_{bd} + i\Omega_{m} e^{i\phi } (\tilde{\rho }_{dd} - \tilde{\rho }_{cc} ) - i\Omega_{d} (y)\tilde{\rho }_{cb} , \\ \dot{\tilde{\rho }}_{aa} & = \gamma_{a} \tilde{\rho }_{bb} + i\Omega_{p} (\tilde{\rho }_{ab} - \tilde{\rho }_{ba} ), \\ \dot{\tilde{\rho }}_{bb} & = - (\gamma_{a} + \gamma_{c} + \gamma_{d} )\tilde{\rho }_{bb} + i\Omega_{p} (\tilde{\rho }_{ab} - \tilde{\rho }_{ba} ) - i\Omega_{c} (x)(\tilde{\rho }_{bc} - \tilde{\rho }_{cb} ) - i\Omega_{d} (y)(\tilde{\rho }_{bd} - \tilde{\rho }_{db} ), \\ \dot{\tilde{\rho }}_{cc} & = - i\Omega_{m} (\tilde{\rho }_{cd} e^{ - i\phi } - \tilde{\rho }_{dc} e^{i\phi } ) + i\Omega_{c} (x)(\tilde{\rho }_{bc} - \tilde{\rho }_{cb} ) + \gamma_{c} \tilde{\rho }_{bb} , \\ \dot{\tilde{\rho }}_{dd} & = \gamma_{d} \tilde{\rho }_{bb} - i\Omega_{d} (y)(\tilde{\rho }_{db} - \tilde{\rho }_{bd} ) + i\Omega {}_{m}(\tilde{\rho }_{cd} e^{ - i\phi } - \tilde{\rho }_{dc} e^{i\phi } ) \\ \end{aligned} $$
(2)

where the detuning parameters are \( \Delta_{p} = \omega_{ba} - \upsilon_{p} \), Δ c  = ω bc  − υ c , Δ m  = ω cd  − υ m , corresponding to the frequency detuning of the probe, control and microwave fields. Also, for convenience we define Δ = Δ1 − Δ2. Also, ϕ = φ p  + φ c  − φ d  − φ m represents the relative phase of applied fields. As one knows, the optical properties of a closed-loop structure are very sensitive to the relative phase of the applied fields. If all the fields have phase dependence, only the collective phase would be important and no individual phase-dependent terms would appear. In fact, the phase dependence in a closed-loop four-level atomic system can be imparted to any one of the applied fields. Here, we keep the initial phases of the weak probe field as well as standing waves fixed and modulate the initial phase of the microwave field. Here, γ j (j = a, c, d) is the decay rate of the atomic population from upper level \(\left| b \right\rangle\) to level \(\left| j \right\rangle\). The relaxation rate of the respective coherences are denoted by γ ik (i, k = a, b, c, d).

Evidently, the level configuration of the four-level system is a Λ-type system, where one lower state had a structure of twofold closely spaced levels. Thus, the probe pulse propagation through a system exhibits interacting dark resonances.

The possible experimental candidate for this theoretical study is 87 Rb atoms (Li 2007 and Steck) using the D 2 line structure. We can choose the designated states as: \(\left| a \right\rangle\) = |5S 1/2, F = 2, m F  = 2〉, \(\left| b \right\rangle\) = |5P 3/2, F = 2, m F  = 1〉, \(\left| c \right\rangle\) = |5S 1/2, F = 1, m F  = 0〉, \(\left| d \right\rangle\) = |5S 1/2, F = 2, m F  = 0〉. Thus, for this system, the spontaneous decay rates of the state \(\left| b \right\rangle\) = |5P 3/2, F = 2, m F  = 1〉 is 6 MHz. It should be mentioned that in practical experiments the transition between the states 5S 1/2 and 5P 3/2 is driven by standing wave or traveling wave laser fields at a wavelength of 780.2 nm. The hyperfine transition \(\left| c \right\rangle\) = |5S 1/2, F = 1, m F  = 0〉 ↔ \(\left| d \right\rangle\) = |5S 1/2, F = 2, m F  = 0〉 is resonantly coupled by a microwave field of frequency around 6.8 GHz, which may lead to a great enhancement of the localization precision. We note that these fields can be obtained from the external cavity diode lasers (Vanier et al. 1998). So, with a good approximation, the coupled Rb system can be regarded as equivalent to a generic four-level scheme as shown in Fig. 1. Several researches support the validity of such a simplification (Li et al. 2011; Li 2007; Wang et al. 2012).

The aim of the present paper is to obtain the information about the atomic position from the susceptibility of the system at the probe frequency. The absorption is determined by term \( \tilde{\rho }_{ba}^{(1)} \). Under weak probe field approximation, the atom is predominantly populated in the initial ground state \(\left| a \right\rangle\), and the perturbation approach which is introduced as the perturbation expansion \( \rho_{ij} = \rho_{ij}^{0} + \rho_{ij}^{1} + \rho_{ij}^{2} + \rho_{ij}^{3} + \ldots \), can be applied to the density matrix Eq. (2). In this limit, we have \( \tilde{\rho }_{aa}^{(0)} = 1 \) and others such as \( \tilde{\rho }_{ij}^{(0)} = 1,\,(i,j = a,b,c,d) \) for the zero-order density-matrix elements. Here, the terms up to the first order in the density-matrix equations are needed. When the field is sufficiently weak, only the first-order term is important. Therefore, since the driving fields are strong fields compared to the probe field, we only keep the first order in the probe field and hold all of the orders of the driving fields.

Thus, by these assumptions, the equations of motion for the first-order density-matrix element \( \tilde{\rho }_{ij}^{(1)} \) can be written as

$$ \begin{aligned} \dot{\tilde{\rho }}_{ba}^{(1)} & = - (\gamma_{ba} + i\Delta_{p} )\tilde{\rho }_{ba}^{(1)} + i\Omega_{c} (x)\tilde{\rho }_{ca}^{(1)} + i\Omega_{d} (y)\tilde{\rho }_{da}^{(1)} + i\Omega_{p} , \\ \dot{\tilde{\rho }}_{ca}^{(1)} & = - (\gamma_{ca} + i(\Delta_{p} - \Delta_{c} ))\tilde{\rho }_{ca}^{(1)} + i\Omega_{c} (x)\tilde{\rho }_{ba}^{(1)} + i\Omega_{m} e^{i\phi } \tilde{\rho }_{da}^{(1)} , \\ \dot{\tilde{\rho }}_{da} & = - (\gamma_{da} + i(\Delta_{p} - \Delta_{c} - \Delta_{m} ))\tilde{\rho }_{da}^{(1)} + i\Omega_{m} e^{ - i\phi } \tilde{\rho }_{ca}^{(1)} + i\Omega_{d} (y)\tilde{\rho }_{ba}^{(1)} . \\ \end{aligned} $$
(3)

The set of Eq. (3) can be written in the form of one deferential matrix equation:

$$ \dot{R}(t) = - MR + A, $$
(4)

with

$$ M = \left[ {\begin{array}{*{20}c} {\gamma_{ba} + i\Delta_{p} } & { - i\Omega_{c} (x)} & { - i\Omega_{d} (y)} \\ { - i\Omega_{c} (x)} & {\gamma_{ca} + i(\Delta_{p} - \Delta_{c} )} & { - i\Omega_{m} e^{i\phi } } \\ { - i\Omega_{d} (y)} & { - i\Omega_{m} e^{ - i\phi } } & {\gamma_{da} + i(\Delta_{p} - \Delta_{c} - \Delta_{m} )} \\ \end{array} } \right], $$
(5)
$$ R = \left[ {\begin{array}{*{20}c} {\tilde{\rho }_{ba}^{(1)} } \\ {\tilde{\rho }_{ca}^{(1)} } \\ {\tilde{\rho }_{da}^{(1)} } \\ \end{array} } \right], $$
(6)
$$ A = \left[ {\begin{array}{*{20}c} {i\Omega_{p} } \\ 0 \\ 0 \\ \end{array} } \right], $$
(7)

where M is the matrix of coefficients, while R and A are column vectors.

The formal solution of such an equation is given by

$$ R(t) = \int_{ - \infty }^{t} {e^{{ - M(t - t^{\prime})}} \,C\,dt^{\prime} = M^{ - 1} \,A} , $$
(8)

We now calculate a simple analytical expression of \( \tilde{\rho }_{ba}^{(1)} \) corresponding to the probe field as

$$ \tilde{\rho }_{ba}^{(1)} = i\Omega_{p} \frac{{(bc + \Omega_{m}^{2} )}}{W}, $$
(9)

Optical response of the medium is determined by the linear susceptibility χ = χ′ + iχ″ of the probe field,

$$ \chi = \frac{2N}{{\varepsilon_{0} \hbar \Omega_{p} }}\left( {\wp_{ba}^{2} \tilde{\rho }_{ba}^{(1)} } \right) $$
(10)

where, N is the atomic number density of the medium. As well known, the imaginary part of susceptibility which is proportional to the coherence term ρ ba denotes probe absorption. Thus, according to the above equation, the normalized probe absorption reads

$$ \chi^{\prime\prime} = \text{Im} \chi = \frac{{iN\wp_{ba}^{2} }}{{\varepsilon_{0} \hbar }}\left[\frac{{(bc + \Omega_{m}^{2} )W^{*} + (b^{*} c^{*} + \Omega_{m}^{2} )W}}{{WW^{*} }}\right], $$
(11)

where

$$ \begin{aligned} W & = [a\,\Omega_{m}^{2} + b\,\Omega_{d}^{2} (y) + c\,\Omega_{c}^{2} (x) - 2i\Omega_{c} (x)\Omega_{d} (y)\Omega_{m} \,\cos \phi ], \\ a & = \gamma_{ba} + i\Delta_{p} , \\ b & = \gamma_{ca} + i(\Delta_{p} - \Delta_{c} ), \\ c & = \gamma_{da} + i(\Delta_{p} - \Delta_{c} - \Delta_{m} ). \\ \end{aligned} $$
(12)

Equation (11) shows that the conditional position probability distribution depends on the controllable parameters of the system like the intensity and detuning of the standing and microwave fields, probe and driving field detunings, and relative phase of applied fields. As a result, it makes feasible to obtain the position information of the atom by monitoring the probe absorption through proper tuning of system parameters.

3 Results and discussion

In the following, we discuss the probe absorption which can directly reflect the conditional position probability distribution through plotting 2D localization patterns. Before beginning it should be pointed out that the peak position of the probe absorption denotes where the atom is localized, and the peak number of the probe absorption in one period of the standing-wave fields means the conditional position probability. Also, the width of peak shows the localization precision.

For the linear susceptibility we plot all the curves in the units of \( \frac{{2N\wp_{ba}^{2} }}{{\varepsilon_{0} \hbar }} \). We set the parameters as γ ba  = γ ca  = γ da  = (γ a  + γ c  + γ d )/2 = γ, γ a  = γ c  = 0.7γ, γ d  = 0.6γ, and γ cd  = γ bd  = γ bc  = 0.5γ, when all the parameters are reduced to dimensionless units through scaling by γ. The numerical results are displayed in Figs. (2, 3, 4, 5, 6, 7). Figure 2 shows the probe absorption versus positions (k x x, k y y) for Ω c  = Ω d  = Ω m  = 30γ, Δ c  = Δ d  = 10γ, Δ = 0, and ϕ = 0, which shows two ‘∞’-like patterns in second and forth quadrants. In fact, Fig. 2 plays the role of a template which we will compare our results with respect to that. Here, it should be mentioned that with respect to the scale in Fig. 2, the brighter parts in absorption profile represents the better resolution and the higher localization precision, while the darker parts correspond to the poor spatial resolution. First of all, we explore the effect of the intensities of the two standing-wave fields Ω c and Ω d on the spatial distributions of the probe absorption, separately in Figs. 3 and 4. The plot of probe absorption in the x–y plane for different values of stand wave Ω c is displayed in Fig. 3. As one can see, for Ω c  = γ the peaks of the probe absorption are distributed in all four quadrants but mainly in first and third quadrants of the x–y plane (Fig. 3a). For the case Ω c  = 15γ the conditional position probability has two double-spot structures distributed in quadrants II and IV as shown in Figs. 3b. With the increase of the standing wave Ω c to further higher value i.e., Ω c  = 30γ the localization pattern changes to our template displayed in Fig. 2 and form a ‘∞’-like pattern. More increasing the value of Ω c to 40γ, the edges of the localization peaks of Fig. 2 get farther to each other as can be seen in Fig. 3c. Now, we turn to illustrate the influences of the standing wave Ω d on 2D atom localization. Figure 4 shows the impact of Ω d on the spatial distribution of probe absorption. From Fig. 4a it is obvious that for Ω d  = γ the peaks of atom localization are aligned along y axis and the peak maxima of \( \text{Im} (\chi ) \) are mainly localized in second and fourth quadrants. Also, high-precision localization is destroyed in this case. However, poor and sharp ‘∞’-like patterns can be obtained by increasing the intensity of Ω d to 15γ and 30γ, as can be observed in Figs. 4b and 2 (template), respectively. When the intensity of standing wave Ω d reached to the large value 40γ, two pairs of deltoid-like patterns appear in quadrants II and IV. Our objective is to enhance the spatial resolution to achieve a high-precision atom localization pattern in x–y plane. In order to explore this possibility, we investigate the influence of standing wave detunings on localization behavior of the system. Starting again from our template (Fig. 2), and increasing the frequency detuning of both standing waves to larger values, ‘∞’-like (Fig. 5a), elliptic-like (Fig. 5b, c) and spot-like (Fig. 5d) patterns can be observed. It can be seen that by increasing the combination of Δ c , Δ d , the larger diameter of elliptic-like pattern in Fig. 5b, c reduces smoothly so that it convert to two spot-like structure located in second and fourth quadrants. In this situation (Fig. 5d), high precision and high spatial resolution 2D atom localization can be achieved, and the probability of finding an atom within one period is 50 %. Thus, the uncertainty of conditional position probability is reduced correspondingly. Now, let us investigate the conditional position probability distribution by varying the probe field detuning Δ in Fig. 6. Reminding our template (Fig. 2) illustrated for zero probe field detuning, we start to increase the value of Δ. It can be seen that obtained pattern for the condition Δ = 5γ shown in Fig. 6a is very similar to Fig. 3b. However, for the case Δ = 15γ, the peaks of the probe absorption are distributed again in all four quadrants but in contrast with Fig. 3a) mainly in second and fourth quadrants of the x–y plane as shown in Fig. 6b. When detuning parameter Δ increases to 25γ, the atom localization exhibits curvature-like patterns distributed in all four quadrants (Fig. 6c). With further increase of the probe detuning parameter, as can be seen in the rest of figures, the localization peaks in quadrants II and IV completely vanishes which can be due to the destructive quantum interference occurred in this four-level configuration. In this case the probe absorption shows the circular-like pattern (Fig. 6d) which leads to the localization of atom at the circular edges of the peak maxima. By more increasing the value of Δ the caliber of every circular-like pattern becomes smaller and smaller (Fig. 6e) and finally, two spot-like patterns appear (Fig. 6f). Thus, another approach is presented to obtain high precision and high spatial resolution 2D atom localization in another set of quadrants (I and III), and the probability of finding a atom within one period is again 1/2. Based on above results, there is strong correlation between the probe detuning and probe absorption. Finally, the influence of the relative phase on spatial distribution of probe absorption is discussed in Fig. 7. As one can observe, the atom localization is very sensitive to the phase ϕ. It is obvious that depending on the value of ϕ various localization patterns with different resolutions can be obtained in two—or all four quadrants.

Fig. 2
figure 2

Display plot of probe absorption in the x–y plane. The selected parameters are γ ba  = γ ca  = γ da  = (γ a  + γ c  + γ d )/2 = γ, γ a  = γ c  = 0.7γ, γ d  = 0.6γ, γ cd  = γ bd  = γ bc  = 0.5γ, and Ω c  = Ω d  = Ω m  = 30γ, Δ c  = Δ d  = 10γ, Δ = 0, ϕ = 0

Full size image
Fig. 3
figure 3

Display plot of probe absorption in the x–y plane. The selected parameters are: Ω c  = γ (a) Ω c  = 15γ (b), Ω c  = 40γ (c). The other parameters are as the same as Fig. 2

Full size image
Fig. 4
figure 4

Display plot of probe absorption in the x–y plane. The selected parameters are: Ω d  = γ (a), Ω d  = 15γ (b), Ω d  = 40γ (c). The other parameters are as the same as Fig. 2

Full size image
Fig. 5
figure 5

Display plot of probe absorption in the x–y plane. The selected parameters are: Δ c  = Δ d  = 20γ (a), Δ c  = Δ d  = 30γ (b), Δ c  = Δ d  = 40γ (c), and Δ c  = Δ d  = 50γ (d), and the other parameters are as the same as Fig. 2

Full size image
Fig. 6
figure 6

Display plot of probe absorption in the x–y plane. The selected parameters are: Δ = 5γ (a), Δ = 15γ (b), Δ = 25γ (c), Δ = 30γ (d), Δ = 35γ (e), Δ = 40γ (f), and the other parameters are as the same as Fig. 2

Full size image
Fig. 7
figure 7

Display plot of probe absorption in the x–y plane. The selected parameters are: \( \phi = \frac{\pi }{4} \) (a), \( \phi = \frac{\pi }{2} \) (b), \( \phi = \frac{3\pi }{4} \) (c), and ϕ = π (d), and the other parameters are as the same as Fig. 2

Full size image

As it is mentioned, enhancing the spatial resolution to achieve a high-precision atom localization pattern in x–y plane is the objective of this study. However, we showed that through such atom-standing wave interaction described above, the maximal probability of finding the atom in one period of the standing-waves reaches 1/2. In order to obtain a 100 % detecting probability of the atom, we consider another type of atom-standing wave interaction in which the transition \(\left| c \right\rangle\) ↔ \(\left| b \right\rangle\) is coupled with the combination of two orthogonal standing-waves with the same frequency (Ω c (x, y) = Ω c ( sin (kx) + sin (ky))), while \(\left| d \right\rangle\) ↔ \(\left| b \right\rangle\) is coupled with a traveling-wave field. Under this condition, we investigate the effect of microwave field Ω m on spatial absorption profile as shown in Fig. 8. In fact, the microwave source is more readily available and easier to control than an extra laser field. It can be seen from Fig. 8(a) that for Ω m  = γ the spatial probe-absorption maxima is distributed in all four quadrants which determines a very weak atom localization. Increasing Ω m to 6γ one spot-like pattern in first quadrant and one circular-like pattern in third quadrant are observed (Fig. 8b). The spot-like pattern in first quadrant is vanished for Ω m  = 10γ and only the circular-like pattern on third quadrant is left as can be seen in Fig. 8c). Finally, a spot-like atom localization pattern located completely in third quadrant is obtained by increasing Ω m to 20γ. In this case, the atom can be localized at a particular position and the maximal probability of detecting the atom in one period of the standing-wave fields increases to unity. Thus, we could achieve a high-precision and high-resolution atom localization for this four-level scheme, through the effect of microwave field.

Fig. 8
figure 8

Display plot of probe absorption in the x–y plane. The selected parameters are: Ω m  = γ (a), Ω m  = 6γ (b), Ω m  = 10γ (c), and Ω m  = 20γ (d). Here, Ω c  = Ω d  = 5γ and the other parameters are as the same as Fig. 2

Full size image

Physically, the probe absorption for the weak probe field coupled to the transition \(\left| a \right\rangle\) ↔ \(\left| b \right\rangle\) is directly proportional to the imaginary part of the susceptibility, which as it was shown in Eq. 11 strongly depends on the position of the atom passing through the standing-wave fields. Therefore by measuring the probe absorption, one can directly obtain information from the position of the atom when it passes through the standing-wave fields. Indeed, the origin of the localization peaks can be understood in the dressed-state picture of the standing wave fields and microwave field. In an appropriate dressed representation, the bare-state levels \(\left| b \right\rangle\), \(\left| c \right\rangle\) and \(\left| d \right\rangle\) can be replaced by three dressed states (for instance \(\left| {\lambda}_{1} \right\rangle\), \(\left| {\lambda}_{2} \right\rangle\) and \(\left| {\lambda}_{3} \right\rangle\)) which are not shown here. Different localization patterns and precision of an atom stems from the different contribution of three bare-state levels to the dressed states as well as the different quantum interference effects between three transition channels from the ground level to the dressed levels (see “Appendix”).

Before ending this paper, it should be pointed out that the physical basis of the system considered in this paper is different from that of proposed in Ref. (Zhang et al. 2014). The scheme of Ref. (Li 2007) includes an excited level, two intermediate levels, as well as one ground level, which form a closed-loop four-level diamond-shape scheme. In our proposal, the physical basis of the proposed four-level system is based on the Lambda-type three-level system in which the second transition is replaced by three laser fields Ω c , Ω d and Ω m which form a closed-loop structure. As a result, the optical response of the schemes considered here and in Ref. (Zhang et al. 2014) to the applied fields are different.

4 Conclusions

In conclusion, we theoretically investigated the 2D atom localization in a four-level Λ-type system with twofold lower levels by monitoring the probe absorption spectra. The effect of different system parameters on 2D atom localization behavior of the medium is discussed. It is shown that different localization patterns can be obtained by properly changing the controlling parameters of system. We found that as a result of space-dependent atom–field interaction, the resolution and precision of 2D atom localization can be greatly improved. Our scheme may be helpful in laser cooling or the atom nano-lithography via 2D atom localization.