1 Introduction

Studying the function of thermodynamics in information theory has provided a good insight into the quantum mechanics [1,2,3,4]. A focus on features of quantum correlations and entanglement conducted remarkably to the progress in our realization of the thermodynamics of quantum systems [2, 5, 6]. Up to now, the role and significance of thermodynamics in quantum information processing have fascinated the attention of many people [7, 8]. Moreover, the recognition of critical temperature in spin models is identified through different techniques [9].

The main objective of quantum mechanics is considered the quantum correlations, which not only contains a deeper understanding of the principles of quantum mechanics, but can also reveal an essential function of quantum information [10, 11] and enables the facility of quantum cryptographic protocol [12], quantum teleportation [13], quantum dense coding [14], and so forth. For example, in dense coding which is considered as an intriguing nonclassical implication, the sender can communicate two bits of classical information to the receiver by forwarding a single qubit if they mix a two-qubit maximally entangled state. Dense coding has been investigated not only theoretically [15,16,17,18,19] but also experimentally [20]. Along this line, much research has been devoted to study the quantum information and quantum correlation [21, 22] in various many-body systems [23].

To address the fundamental limitations inflicted by thermodynamics on the growth of correlations and entanglement in bipartite and multipartite settings, some systems have been inspected [24, 25]. In Ref. [25], the authors have studied the energy cost of the created correlations between the uncorrelated thermal quantum systems via performing such global unitary operations such as quantum discord and local quantum uncertainty. Therefore, anyone can ask whether other quantum correlations such as quantum Fisher information and spin squeezing can show a correlation in present thermodynamic limitations. Recently, it has been represented that quantum Fisher information provides a tool for understanding the phase sensitivity that systems can prepare for the imperfection of quantum measurement devices [26,27,28]. As a document of multipartite entanglement, it is asserted that it specifies topological states [29] and non-Gaussian many-body entangled states [30]. Quantum Fisher information can be widely explored in some intent such as the connection between quantum coherence and quantum phase transition [31,32,33], quantum metrology [34], and quantum speedup limit time [35]. Recently, it is attractive to find that spin squeezing is connected to quantum entanglement and one can use spin squeezing to characterize entanglement. It is found that spin squeezing relates to the minimum spin fluctuation in the plane perpendicular to the mean spin direction [36,37,38].

We know that correlated states play a significant role in dense coding. For this purpose, we present a straightforward calculation of how quantum Fisher information and also spin squeezing of states can occur the fundamental limitations coming from the initial temperature of two initially uncorrelated thermal quantum systems for building quantum correlations. The problem can be interested: how we can distinguish the connection between the dynamic properties of energy cost and dense coding capacity? Our results suggest that valid dense coding can be detected using the dynamic energy cost in thermodynamic effects.

The road map of this paper is formed as follows. In Sect. 2, we compute the density matrix for two initially uncorrelated two-dimensional thermal quantum systems, and then, we give out the analytical expression to the quantum Fisher information and spin squeezing and demonstrate how creating quantum correlations can be confined by the thermodynamics of the system. In Sect. 3, the super dense coding is discussed. We finish the paper with our main results and outlook in Sect. 4.

2 Creating quantum correlation between two thermal qubits

Let us take a global system can be included by two basic separable d-dimensional quantum systems A and B. And they link with a hot heat bath at temperature T, the Hamiltonian of each of which may be expressed as \(H= \sum ^{d-1}_{i=0}E_{i} | \psi _i \rangle \langle \psi _i |\), in which \(E_{i}\) and \(| \psi _i \rangle \) are eigenvalues and eigenstates, respectively. The thermal state of this system at a temperature T is given by [7]

$$\begin{aligned} \begin{array}{cc} \rho _T = \rho \otimes \rho , \end{array} \end{aligned}$$
(1)

where \(\rho = \frac{\text {e}^{-\beta H} }{\text {Tr}(\text {e}^{-\beta H})} \), \(\beta = 1/k T (k=1)\), and k is the Boltzmann constant. In the following of discussion, we will stand for energy of the ground and excited state by \(E_0 = 0\) and \(E_1 = E\), respectively. Also, the initial thermal state of a qubit can be given as \(\rho = p |0 \rangle \langle 0| +(1-p) |1\rangle \langle 1|\). The coefficient p sets the ground populations that can be written

$$\begin{aligned} \begin{array}{cc} p=\frac{1}{1+ \text {e}^{- \beta E}}. \end{array} \end{aligned}$$
(2)

As in Ref. [39] was showed the maximal entanglement of two-qubit arises by optimal global unitary operations. The global unitary operator U which is made in this protocol can be easily represented as two unitary operators \((U = V_2V_1)\), so we can obtain the final state as\(\rho _f = V_2V_1 \rho _i V_1^{\dagger } V_2^{\dagger }\), where

$$\begin{aligned} \begin{array}{cc} V_1=|00\rangle \langle 00| +|01\rangle \langle 01|+|11\rangle \langle 10|+|10\rangle \langle 11| \end{array} \end{aligned}$$
(3)

is the action of the CNOT gate and

$$\begin{aligned} \begin{array}{cc} V_2=|\varphi _ {00} \rangle \langle 00| +|01\rangle \langle 01|+|10\rangle \langle 10|+|\varphi _ {11}\rangle \langle 11| \end{array} \end{aligned}$$
(4)

is a rotation in the subspace spanned by \(|00\rangle , |11\rangle \) to maximally entangled states which are \(|\varphi _ {00} \rangle =\frac{1}{\sqrt{2}}({|00\rangle +|11\rangle })\) and \(|\varphi _ {11} \rangle = \frac{1}{\sqrt{2}}({|00\rangle -|11\rangle })\). Hence, the density matrix of the final state in the basis \(| 00\rangle , | 10\rangle , | 01\rangle ,| 11\rangle \) can be easily obtained by the following forms:

$$\begin{aligned} \begin{array}{cc} \rho _ f=\left( \begin{array}{cccc} \frac{p}{2} &{} 0&{} 0 &{} p^{2}- \frac{p}{2} \\ 0 &{} p (1-p) &{} 0 &{} 0 \\ 0 &{} 0 &{} (1-p)^2 &{} 0 \\ p^{2}- \frac{p}{2} &{} 0 &{} 0 &{} \frac{p}{2}\\ \end{array} \right) . \end{array} \end{aligned}$$
(5)

In the following, for obtaining quantum correlation, we focus on the quantum Fisher information and spin squeezing.

Fig. 1
figure 1

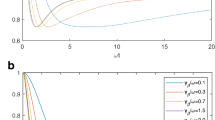
a \(\textit{QF}\) and the evolution of the first derivative of the \(\textit{QF}\) versus \(T \) for various values of \(E \) (\(E = 1\) (red , solid line), \(E = 2\) (blue, dotted line), \(E = 3\) (black, dashed line)). b \(\textit{QF}\) and the evolution of the first derivative of the \(\textit{QF}\) versus \(E \) for various values of \(T \) (\(T = 0.1\) (red , solid line), \(T = 0.3\) (blue, dotted line), \(T = 0.5\) (black, dashed line))

Full size image

2.1 Fisher information between two thermal qubits

The quantum Fisher information (QF) is a widespread tool for explaining optimal validity in parameter estimation protocols [40,41,42]. An active area of research dedicated to evaluating the evolution of QF to determine the relation between quantum entanglement and quantum metrology [43, 44]. It has been illustrated that in the unitary evolution, quantum entanglement leads to a remarkable promotion in precision of parameter estimation. For an arbitrary parametric state \(\rho _{\theta }\) that depends on \(\theta \), the \(\textit{QF}\) is characterized as follows:

$$\begin{aligned} \begin{array}{cc} \textit{F} ^{2}(\rho _{\theta })= \frac{1}{4} \text {tr} (\rho _{\theta } L^{2}_{\theta }), \end{array} \end{aligned}$$
(6)

where \(L_{\theta }\) is the symmetric logarithmic derivative operator. \(L_{\theta }\) is defined as the solution of the equation

$$\begin{aligned} \begin{array}{cc} \frac{\partial { \rho _{\theta }}}{\partial \theta }=\frac{1}{2}( L_{\theta } \rho _{\theta } +\rho _{\theta } L_{\theta }). \end{array} \end{aligned}$$
(7)

The effect of the unitary evolution \(U_\theta = \text {e}^ {- \textit{i} H \theta }\) on \(\rho \), \(\rho _{\theta } = U^{}_\theta \rho U_\theta \), can be lead to parametric state \(\rho _{\theta }\). For a defined quantum state \(\rho = \sum _{l} | \uplambda _{l} \rangle \langle \uplambda _{l}|\) with \(\uplambda _{l} \geqslant 0\), \( \sum _{l} \uplambda _{l}= 1 \). Here, we stand for \(\textit{F} ^{2}(\rho _{\theta })\) with \( \textit{F} ^{2}(\rho , \textit{H})\), which can also be expressed by [45]

$$\begin{aligned} \begin{array}{cc} \textit{F}(\rho _f , \textit{H})= \frac{1}{2}\sum _{l \ne n} \frac{(\uplambda _{l}-\uplambda _{n})^2}{\uplambda _{l}+\uplambda _{n}} |\langle l | \textit{H} | n \rangle |^2. \end{array} \end{aligned}$$
(8)

According to Eq. (5), \(\textit{QFI}\) can easily obtain as follows:

$$\begin{aligned} \begin{array}{cc} \textit{F}(\rho _f , \textit{H})= \frac{(1- \text {e}^{- \beta E})^2}{2}\lbrace \frac{1}{(1- \text {e}^{\beta E})^3} - \frac{1}{1+ \text {e}^{2 \beta E}} \rbrace . \end{array} \end{aligned}$$
(9)

Obviously, if \(T \rightarrow \infty \), \(\textit{F}(\rho _f , \textit{H})\) is equal to zero. Also, the maximal amount of the \(\textit{QF}\) can be obtained in the limit \(T \rightarrow 0\), which is equal to 0.5. In Fig. 1a, we plot the \(\textit{QF}\) which has given in Eq. (9) to study the quantum correlations behavior with respect to initial temperature of the system. It is seen that the quantum correlations vanish completely after a threshold temperature for any specific energy. As can be observed for any specific energy E due to thermal fluctuations, QF is decreased by increasing temperature. Also, we see that by enhancing the energy value of excited states E, the threshold temperature is raised and, therefore, the QF can exist in a vast limit of temperature. It should be noted that the maximal value of the QF is equal to 0.5 which is obtained at \(T = 0\). To further investigate the critical behavior of QF, we have plotted the first derivation of Fisher information with respect to initial temperature of the system for various values of E in Fig. 1a. It appears that the \(\frac{\text {d}QF}{\text {d} T}\) have sharp dips in the thermal evolution for any specific energy E. A more detailed analysis shows that the position of the dips located at a critical temperature \(T_c\). In fact, these sharp dips originate from the non-analytical property of QF at the critical temperature, which further demonstrates that the QF can detect the critical temperature for two initially uncorrelated thermal quantum systems. Now, we analyze the correspondence between the singularity of the threshold energy and the phase diagram for different temperatures. We have plotted \(\textit{QF}\) and evolution of the first derivative \(\textit{QF}\) with respect to the energy in Fig. 1b. From Fig. 1b, we see that with the increasing of energy for any special temperature, QF enhances to a maximum value. According to Fig. 1b, a threshold energy exists that depends on the temperature value. For a more detailed analysis, we display the evolution of the first derivative of the \(\textit{QF}\) versus \(E \) in Fig. 1b. This graph reveals how the position of critical point energy alters as the temperature of the system increases.

Fig. 2
figure 2

a Spin squeezing and the evolution of the first derivative of the spin squeezing versus \(T \) for various values of \(E \) (\(E = 1\) (red , solid line), \(E = 2\) (blue, dotted line), \(E = 3\) (black, dashed line)) b spin squeezing and the evolution of the first derivative of the spin squeezing versus \(E \) for various values of \(T \) (\(T = 0.1\) (red , solid line), \(T = 0.3\) (blue, dotted line), \(T = 0.5\) (black, dashed line))

Full size image

2.2 Spin squeezing between two thermal qubits

Following Kitagawa and Ueda’s [38] criterion of spin squeezing, we briefly review the definition of the spin squeezing parameter for a collection of N qubits with components \(S^{\alpha }=\sum ^{N} _{i=1} \frac{\sigma ^{\alpha }_{i}}{2} ,(\alpha \in {x,y,z})\) as

$$\begin{aligned} \xi ^2= & {} \frac{2(\Delta S_{\overrightarrow{n}_{\perp }})^2_{\min }}{J} = \frac{4(\Delta S_{\overrightarrow{n}_{\perp }})^2_{\min }}{N}. \end{aligned}$$
(10)

Here, the subscript \({\overrightarrow{n}_{\perp }}\) refers to an axis perpendicular to angular momentum operator. \(S = (S_x , S_y, S_z)\) denotes the angular momentum operator of an ensemble of spin-1/2 particles. Where \((\Delta S_{\overrightarrow{n}_{\perp }})^2_{\min }\) is the minimal spin fluctuation in a plane perpendicular to the mean spin, and \(J=\frac{N}{2}\), and \(S_{\overrightarrow{n}_{\perp }}=\overrightarrow{S}. \overrightarrow{n}_{\perp }\) . The non-correlated limit yields \(\xi ^2 =1\), while the inequality \(\xi ^2 < 1\) indicates that the system is spin squeezed and entangled. In Ref [46] was indicated for the mean spin along the z direction spin squeezing can be written as

$$\begin{aligned} \xi ^2= & {} 1+\frac{N}{2}-\frac{2}{N} [\langle S^{2}_z\rangle + |\langle S^{2}_{+}\rangle |], \end{aligned}$$
(11)

where \(S_{\pm }=S_{x} \pm S_{y}\) are the ladder operators. From Eq. (11), we see that the squeezing parameter is determined by a sum of two expectation values \(\langle S^{2}_z\rangle \) and \(\langle S^{2}_{+}\rangle \); hence, the calculations are greatly simplified. For this density matrix Eq.(5), the associated spin squeezing is given by

$$\begin{aligned} \xi ^2= & {} 1 - \frac{1}{4} \tanh \frac{\beta E}{2}\left( 1+\tanh \frac{\beta E}{2}\right) . \end{aligned}$$
(12)

According to Eq. (12), it is clear that the maximal value of the spin squeezing is equal to 1, which is obtained at \(T \rightarrow \infty \). Also, the minimal amount of the infinity can be obtained in the limit \(T \rightarrow 0\). Variations of spin squeezing are given in Fig. 2a for any specific energy E. We can see the spin squeezing undergoes to value one with increasing temperature of the system for any specific energy. As a physical interpretation, the interaction between the system with its environment at high temperatures can be lead to non-squeezed states. Notably, previous studies [25] have shown that the entanglement vanished completely at a finite critical temperature. It is also known in which all the specific energy is supplied at a low temperature has a spin squeezing efficient. Therefore, low temperature can maintain squeezing. Having this in mind, the first derivative of the spin squeezing is depicted as a function of T in Fig. 2a. The derivative of spin squeezing versus temperature of the system shows a singular behavior at the critical temperature for any specific energy E. As, the spin squeezing constructs a maximum at the critical temperature. In generally, It can be seen how the temperature of the initial state affects the amount of correlation that we can be created. To confirm the previous discussions, we investigate the behavior of the spin squeezing and the first derivative of the spin squeezing versus energy E for the difference of temperatures in Fig. 2b. We find that spin squeezing exhibits a sudden change at the critical point. This indicates that spin squeezing can be used to detect the phase transition that has happened in initially uncorrelated thermal quantum systems.

Fig. 3
figure 3

a Dense coding capacity and b energy cost of dense coding versus T for various values of E (\(E= 1\) (red , solid line), \(E= 2\) (blue, dotted line), and \(E= 3\) (black, dashed line))

Full size image

3 Superdense coding

Now, we carry out the thermal optimal dense coding in a global system consisting of two initially uncorrelated d-dimensional quantum systems A and B as a quantum channel. For this purpose, the set of mutually orthogonal unitary transformations is necessary to be made. The set of mutually orthogonal unitary transformations for two-qubit are given as follows [47]:

$$\begin{aligned} U_{00} |j \rangle= & {} |j \rangle \nonumber \\ U_{01} |j \rangle= & {} |j +1 (mod 2)\rangle \nonumber \\ U_{10} |j \rangle= & {} e^{\sqrt{-1}(2\pi /2)j} |j \rangle \nonumber \\ U_{11} |j \rangle= & {} \text {e}^{\sqrt{-1}(2\pi /2)j} |j+1 (mod2) \rangle , \end{aligned}$$
(13)

where \(|j \rangle \) is the single qubit computational basis \(( |j \rangle = |0 \rangle , |1 \rangle ) \). The average state of the ensemble of signal states generated by the unitary transformations Eq. (13) is given by

$$\begin{aligned} \overline{\rho ^{*}} = \frac{1}{4} \sum _{i=0}^{3} (U_{i} \otimes I_{2} ) \rho (U^{\dagger }_{i} \otimes I_{2} ), \end{aligned}$$
(14)

where 0 stands for 00, 1 for 01, 2 for 10, 3 for 11, and \(\rho \) is the density matrix of the quantum channel. Equation (13) represents the operations that Alice (sender) performs on the shared entangled state \(\rho \). If the sender does the set of mutually orthogonal unitary transformations, the maximum dense coding capacity \(\chi \) can be obtained by

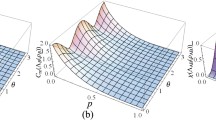
$$\begin{aligned} \chi =S(\overline{\rho ^{*}})- S(\rho ), \end{aligned}$$
(15)

where \(S(\overline{\rho ^{*}})\) is a von Neumann entropy for the average state of an ensemble of signal states \(\overline{\rho ^{*}}\), and \(S(\rho )\) is the von Neumann entropy of the quantum channel. If \(\chi > 1\) dense coding is valid, and for optimal dense coding \(\chi \) must be the maximum, i.e., \(\chi _{\max }=2\). We are now ready to discuss the validity of the generated quantum correlation a global system consisted of two initially uncorrelated d-dimensional quantum systems A and B in contact with a heat bath at temperature T as a quantum channel to study the optimal dense coding. By considering the density matrix Eq. (5), we first focus on the thermal dense coding capacity. By numerical calculation, we can plot dense coding capacity as a function T for different specific energy values. In Fig. 3a, we observe valid dense coding for any specific energy in low temperatures. It is reduced from the maximum to zero in a short interval of temperature and disappears for the large amounts of T. The increase in the energy value of excited states helps dense coding capacity can be alive in a broad range of temperature.

Now, we start to explore a work cost W to the optimal dense coding. Thermodynamic cost of dense coding W is given by [7, 48, 49]

$$\begin{aligned} W = {{\,\mathrm{Tr}\,}}(H_{tot} \rho ^{*})- {{\,\mathrm{Tr}\,}}(H_{tot} \rho _f), \end{aligned}$$
(16)

where \(\rho ^{*}\) is the final state Eq. (14) as follows:

$$\begin{aligned} \begin{array}{cc} \rho ^{*}=\left( \begin{array}{cccc} \frac{p^2 - \frac{3 p}{2}+1}{2} &{} 0&{} 0 &{} 0 \\ 0 &{} \frac{p (3-2p)}{4} &{} 0 &{} 0 \\ 0 &{} 0 &{} \frac{p (3-2p) }{4} &{} 0 \\ 0&{} 0 &{} 0 &{} \frac{ p^2 - \frac{3 p}{2}+1}{2} \\ \end{array} \right) , \end{array} \end{aligned}$$
(17)

and \(H_{tot} = \sum _i H^{(i)}\) is the total Hamiltonian as

$$\begin{aligned} H_{tot}=H \otimes I_2 + I_2 \otimes H = \left( \begin{array}{cccc} 0 &{} 0&{} 0 &{} 0 \\ 0 &{} E &{} 0 &{} 0 \\ 0 &{} 0 &{} E &{} 0 \\ 0 &{} 0 &{} 0 &{} 2 E\\ \end{array} \right) . \end{aligned}$$
(18)

By substituting Eqs. (5), (18) and (17) into Eq. (16), work cost can be obtained as

$$\begin{aligned} W=\frac{\text {e}^{ \beta E} -1}{2(\text {e}^{\beta E}+1)^2} E. \end{aligned}$$
(19)

We find that the energy cost is dependent on temperature and specific energy. According to Eq. (19), it is easy to prove that value of the energy cost can be maximal in the critical temperature \(T_c =0.91E\) which the dense coding is not valid, i.e., \( \chi < 1\) (see Fig.  3a). In Fig. 3b, the energy cost of dense coding is plotted as a function of temperature for any specific energy. It can be seen when the temperature is smaller than \( T_c\), the energy cost increases until its maximum value with raising the temperature. However, it for \( T > T_c\) specific energy exhibits a collapse as temperature increases. Moreover, the range of T for energy cost is also broadened as specific energy increases in this interval. Notably, the height of peaks energy cost changes manifestly. It approaches the higher peak by increasing specific energy. Comparing dynamic energy cost Fig.  3b and dense coding capacity Fig.  3a leads to an interesting outcome, there is no optimal dense coding when energy cost is decreasing, i.e., after the phase transition \(T> T_c\). We notice that when \(T < T_c\), until the energy cost reaches its maximum value, we can obtain optimal dense coding. With these results at hand, one can detect optimal dense coding via the behavior of energy cost. Therefore, it is helpful to investigate the energy cost as indicators of valid dense coding in every system.

4 Conclusion

In conclusion, we have prospected the number of quantum correlations that can be made between two initially uncorrelated thermal quantum systems via an optimal protocol that maximizes the quantum correlation. We inspected the thermal evolution of quantum correlations such as quantum Fisher information and spin squeezing in this system. It is illustrated that increasing the initial equilibrium temperature leads to diminishing the amount of quantum correlations that can be caused between two thermal states. Quantum correlations undergo an abrupt death at the critical temperature. Moreover, we have investigated the quantum dense coding for this model. We have found appealing results as the existence of a relationship between dense coding and energy cost that will certainly lead to a better comprehension of the non-equilibrium systems. Our analyses have indicated by enhancing the value of temperature, the value of energy cost tends to its maximum. Interestingly, after crossing the critical temperature, when no optimal dense coding exists in the system, the energy cost of dense coding becomes spoiled. We offer these features as a tool to detect optimal dense coding.