Singular value decomposition compressed ghost imaging

Abstract

Compressed ghost imaging method can effectively reduce the number of measurements required for ghost imaging reconstruction. The non-negative characteristics of measurement matrix in compressed ghost imaging method is inconsistent with the requirements of the measurement matrix in traditional compressed sensing theory, leading to low quality reconstruction. Aiming at the point, this paper proposes a singular value decomposition compressed ghost imaging method to improve the reconstruction quality of ghost imaging. First, the singular value decomposition is performed on the measurement matrix, and then the optimized measurement matrix and measurements are obtained, finally the reconstruction of the image is completed by the reconstruction algorithm. Numerical simulation experiments verify the superiority of our proposed singular value decomposition compressed ghost imaging method.

1 Introduction

In recent years, ghost imaging (GI) [1,2,3,4,5,6] has been one of the frontiers and hot spots in the field of quantum optics. Compared to traditional imaging techniques, GI is a novel imaging technology, which enables detecting and imaging as separate parts. GI takes the advantages of anti-turbulence perturbation and lensless imaging, which has wide application in the fields of earth observation [7, 8], radar imaging [9], life science [10], optical computing [11, 12] and secure communication [13] and so on. However, the drawback of GI is that the imaging quality is still very poor.

In 2010, Ferry et al. [14] proposed differential ghost imaging (DGI), which adds a new differential bucket detector to record a reference light, and performs differential calculation on measurements, which can dramatically enhance the signal-to-noise ratio (SNR) and improve the image reconstruction quality. In 2012, Sun et al. [15, 16] proposed normalized ghost imaging (NGI). Compared to DGI, NGI made some improvements which normalizes each individual measurement of the bucket detector, such as running the average, according to the speckle field detected by the reference arm, which can achieve higher quality imaging by eliminating the noise caused by laser power fluctuations.

In 2009, Katz et al. [17,18,19,20] proposed compressed ghost imaging (CGI) based on compressed sensing theory, which can achieve better reconstruction using measurements much lower than Nyquist rate. In 2014, pseudo-inverse ghost imaging (PGI) [21, 22] was proposed, which reconstruction by pseudo-inverse of the measurement matrix, which achieve simpler, faster and better performance. In 2018, singular value decomposition ghost imaging (SVDGI) [23] was proposed. Different from PGI, SVDGI firstly performs singular value decomposition (SVD) on the random measurement matrix to make the non-zero elements of singular value matrix to be equal to 1.0, and then the measurement matrix is obtained by the inverse singular value decomposition, finally a better reconstruction can be achieved by multiplying the transposition of the measurement matrix.

To further improve the reconstruction quality of GI, this paper proposes a method of compressed ghost imaging based on singular value decomposition (SVDCGI). The nonnegative characteristic of measurement matrix and measurements are simultaneously optimized using singular value decomposition, and the original image is then reconstructed via the optimized measurement matrix and the measurements. A theoretically guarantees for optimized measurement matrix via singular value decomposition is also presented. By combining SVD with CS, the proposed method is superior to the state-of-the-art method, as demonstrated through numerical simulation experiments.

2 Overview of non-iterative reconstruction algorithms for ghost imaging

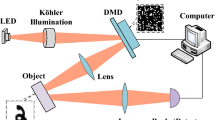
Figure 1 depicts an optical step of GI system. First, the pesudo-thermal light is divided into two beams. One beam is “object arm”, in which an unknown object is illuminated and then collected by a bucket detector. The other beam named “reference arm”, which is detected by a pixelated sensor. The $i{\text{ - th}}$ measurement is recorded as $I_{i} (x,y)$. At the object arm, the bucket detector measures the intensity from the object, and each measurement is recorded as $B_{i}$, the reference light $R_{i}$ is extracted by adding the second bucket detector.

Fig. 1

Schematics of Ghost imaging system

After $M$ pairs of measurements $\left\{ {I_{i} } \right\}_{i = 1}^{M}$ and $\left\{ {B_{i} } \right\}_{i = 1}^{M}$ are sequentially recorded, respectively, we can obtain the following imaging model for ghost imaging:

$$\left( {\begin{array}{*{20}c} {B_{1} } \\ {B_{2} } \\ \vdots \\ {B_{M} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {I_{1} (1,1)} & {I_{1} (1,2)} & \cdots & {I_{1} (P,P)} \\ {I_{2} (1,1)} & {I_{2} (1,2)} & \cdots & {I_{2} (P,P)} \\ \vdots & \vdots & \ddots & \vdots \\ {I_{M} (1,1)} & {I_{M} (1,2)} & \cdots & {I_{M} (P,P)} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {T(1,1)} \\ {T(1,2)} \\ \vdots \\ {T(P,P)} \\ \end{array} } \right)$$

(1)

which can be expressed in matrix–vector form

$$B = \Phi \cdot {\text{vec }}(T)$$

(2)

where $\text{vec}( \cdot )$ transforms a two-dimensional (2D) image in terms of a vector by the lexicographical order. Note that as the measurements $\Phi$ and $B$ are recorded by the CCD and bucket detectors, all the entries in both of them are nonnegative, i.e. $B \ge 0$ and $\Phi \ge 0$.

The aim of ghost imaging is to find the solution to following optimization problem with $B$ and $\Phi$ are known

$$\begin{gathered} {\text{find }}T \hfill \\ {\text{s.t.}}\;\text{ }B = \Phi \cdot {\text{vec}}(T) \hfill \\ \end{gathered}$$

(3)

Based on the basic principles of traditional ghost imaging (TGI), traditional non-iterative ghost imaging methods such as pseudo-inverse ghost imaging (PGI), normalized ghost imaging (NGI), differential ghost imaging (DGI) and singular value decomposition ghost imaging (SVDGI) are proposed. Table 1 presents the definition of variables in five traditional non-iterative ghost imaging methods, and the reconstruction process of five different methods can be expressed in the Table 2.

Table 1 Variable definition

Table 2 Reconstruction process of five traditional non-iterative methods

3 Singular value decomposition compressed ghost imaging

3.1 Compressed sensing

Classical Nyquist sampling theory leads to a large amount of data acquisition redundancy and waste of sensor resources. In 2006, Donoho and Candès firstly proposed compressed sensing (CS), CS theory shows that if a signal is sparse or compressible on some basis, accurate recovery of the original signal with a small number of incoherent projections far below the Nyquist sampling rate. And the CS theoretical framework is shown in Fig. 2.

Fig. 2

CS theoretical framework

In Fig. 2, $\alpha$ is a coefficient vector with size $N \times 1$, $\Psi$ is a sparse basis of size $N \times N$, and $f$ is a one-dimensional vectorized signal of size $N \times 1$. $g$ is the measurements, $\Phi$ is the measurement matrix.

3.2 Compressed ghost imaging

One of the main disadvantages of traditional ghost imaging is that the measurements required for image recovery with a high quality. In 2009, Katz et al. Proposed an advanced reconstruction algorithm for GI based on compressed sensing termed as compressed ghost imaging (CGI), which can reduce significantly the required acquisition times by an order of magnitude. CGI enables accurate recovery of a high-resolution image from few linear measurements.

In the case of $M < N$, the imaging model of GI in Eq. (1) can be expressed into matrix–vector form under the framework of compressed sensing by exploit:

$$B = \Phi \cdot {\text{vec}}(T) = \Phi \Psi \alpha$$

(4)

Note that the significant difference is that our measurement matrix is restricted to nonnegative constraints, which is rarely handled in classical compressed sensing and lack of theoretically guarantees for successful recovery.

The reconstruction process of CGI can be expressed as solving a convex optimization problem by seeking for the image $T(x,y)$ which the minimizes the $\ell_{1}$-norm in the sparse basis as follows:

$$\begin{gathered} \hat{T}_{{{\text{CGI}}}} = \arg \, \min \left\| {\Psi^{ - 1} \left\{ {T_{{{\text{CGI}}}} (x,y)} \right\}} \right\|_{L1} \hfill \\ {\text{s.t.}}\;B = \Phi \cdot {\text{vec}}\left( {T_{{{\text{CGI}}}} } \right) = \Phi \Psi \alpha \hfill \\ \end{gathered}$$

(5)

where $\Psi^{ - 1}$ is the inverse of the sparse basis, the elements in the measurement matrix $\Phi$ are all non-negative, and all the elements in the measurements $B$ are also non-negative.

In 2018, Shi et al. [24] proposed a method named modified compressed ghost imaging (MCGI) to reduce the background caused by randomly distributed detector noise on the signal path. Here, the detector noise is assumed as additive noise and propose the idea that subtracting a constant value ($C$) from the bucket measurements $B$, the MCGI as follows:

$$\begin{gathered} \hat{T}_{{\text{MCGI}}} = \arg \, min\left\| {\Psi^{ - 1} \left\{ {T_{{\text{MCGI}}} (x,y)} \right\}} \right\|_{L1} \hfill \\ \text{s.t.} \, B^{\prime} = \Phi \cdot \text{vec}(T_{{\text{MCGI}}} ) = \Phi \Psi \alpha \hfill \\ \end{gathered}$$

(6)

where the new bucket measurements $B^{\prime} = B - C$, and the statistical mean of noise value $\left\langle {B_{{{\text{noise}}}} } \right\rangle$ is originally used as the constant $C$.

3.3 Singular value decomposition compressed ghost imaging

Assuming that the size of an non-singular matrix is $M \times N$, its singular value decomposition can be expressed as:

$$\Phi = U\Sigma V^{T}$$

(7)

where, the $U$ and $V^{T}$ are orthogonal matrix, and the sizes are $M \times M$, $N \times N$ respectively, and the singular value matrix $\Sigma$, which is a semi-positive diagonal matrix of size is $M \times N$, as follows:

$$\Phi_{{{\text{SVD}}}} = U_{M \times M} \left[ {\Lambda_{M \times M} \, {\mathbf{0}}} \right]_{M \times N} V^{T}_{N \times N}$$

(8)

where, $\Lambda$ is a diagonal matrix of size is $M \times M$, and the size of 0 is $(N - M) \times M$ with all entries 0.

Combining the Eq. (7) with the Eq. (2), we can get:

$$\begin{gathered} B = \Phi {\text{vec}}(T) = U\Sigma V^{T} {\text{vec}}(T) \\ { = }U\underbrace {{\left[ {\begin{array}{*{20}c} {\overbrace {{\Sigma_{1} }}^{M \times M}} & {\overbrace {{\mathbf{0}}}^{M \times (N - M)}} \\ \end{array} } \right]}}_{M \times N}\left[ {\begin{array}{*{20}c} {\underbrace {{V_{1}^{\text{T}} }}_{M \times N}} \\ {\overbrace {{V_{2}^{\text{T}} }}^{(N - M) \times N}} \\ \end{array} } \right]{\text{vec}}(T) \\ = U\Sigma_{1} V_{1}^{\text{T}} {\text{vec}}(T) \\ \end{gathered}$$

(9)

By multiplying the matrix $\Sigma_{1}^{ - 1} U^{T}$ on both sides of Eq. (9), we can get:

$$\Sigma_{1}^{ - 1} U^{T} B = \Sigma_{1}^{ - 1} U^{T} U\Sigma_{1} V_{1}^{T} {\text{vec}}(T) = V_{1}^{T} {\text{vec}}(T)$$

(10)

Then, a new compressed measurement system can be expressed as follows:

$$B_{{{\text{SVDCGI}}}} = \Phi_{{{\text{SVDCGI}}}} {\text{vec}}(T) = \Phi \Psi \alpha$$

(11)

where, $B_{{{\text{SVDCGI}}}} = \Sigma _{1}^{{ - 1}} U^{T} B$ is the new measurements after optimization, $\Phi _{{{\text{SVDCGI}}}} = V_{1}^{T}$.

Finally, Orthogonal Matching Pursuit algorithm (OMP) [25, 26] is used to restore the original image in terms of low implementation cost and high speed of recovery:

$$\begin{gathered} \hat{T}_{{\text{SVDCGI}}} = \arg \, min\left\| {\Psi^{ - 1} \left\{ {T_{{\text{SVDCGI}}} (x,y)} \right\}} \right\|_{L0} \hfill \\ \text{s.t.}\;{\text{ B}}_{{{\text{SVDCGI}}}} = \Phi_{{{\text{SVDCGI}}}} \cdot {\text{vec}}\left( {T_{{\text{SVDCGI}}} } \right) = \Phi_{{{\text{SVDCGI}}}} \Psi \alpha \hfill \\ \end{gathered}$$

(12)

3.4 Theoretical analysis of singular value decomposition compressed ghost imaging

In SVDGI, the singular value decomposition is performed on the measurement matrix to make the non-zero elements of singular value matrix to be equal to 1.0, for high sampling ratio (especially full-sampling), SVDGI can dramatically enhance the reconstruction quality due to the small proportion of ‘0’ element. But under low sub-sampling ratio condition, as the “0” element in the diagonal element of the measurement matrix is excessive, which leads to low quality of GI reconstruction. Different from the SVDGI method, this paper proposes singular value decomposition compressed ghost imaging (SVDCGI) firstly perform SVD on the non-negative measurement matrix in the GI imaging and then an improved compressed measurement system is constructed with the measurement matrix and related measurements are simultaneously optimized.

In the CGI method, as the non-negativity of measurement matrix and the measurements are recorded by the detector, resulting in low quality reconstruction. Compared with the CS reconstruction method, the SVDCGI has different requirements for the measurement matrix, which uses singular value decomposition on non-negative measurement matrix, then $\Phi _{{{\text{SVDCGI}}}}$ can be regarded as picking $M$ rows from a special orthogonal matrix. In other words, after the singular value decomposition, we can obtain new measurement matrix $\Phi _{{{\text{SVDCGI}}}} = V_{1}^{T}$ is general orthogonal measurement matrices.

Lemma 1 (RIP for General Orthogonal Measurement Ensemble)

[27,28,29] Let $F$ be an $N \times N$ orthogonal matrix with $\left| {H_{S} ,j} \right| \le \mu (Q)$.Then picking its $M$ rows to construct a random measurement matrix of size $M \times N$, while the rows of $\sqrt N Q$ uniformly at random. Then it is probability satisfy the RIP with RIC $\delta = 1/4$, if the number of measurement support that:

$$M \ge C_{0} \cdot \left| Q \right| \cdot \mu^{2} \left( H \right) \cdot \log \left( {N/\delta } \right)$$

(13)

where, $C_{0}$ is some constant, each integer $S = 1,2, \ldots$.$F$ is a subset of the signal domain, $\mu$ is the mutual coherence coefficient:

$$\mu = \mathop {\max }\limits_{i \ne j} \left| {\left\langle {\varphi_{i} ,\varphi_{j} } \right\rangle } \right|$$

(14)

$\mu$ can be interpreted as a rough measure of how concentrated the rows of measurement matrix. The smaller $\mu$, i.e. the more incoherent the measurement matrix.

Proof

As the $\Phi_{i}$ and $\Phi_{j}$ are the i-th row and j-th row of $\Phi$, thus we have

$$\Phi_{{{\text{SVDCGI}}}} = \phi_{i} \phi_{j}^{T} = < \phi_{i} ,\phi_{j} > = \left\{ {\begin{array}{*{20}c} 1 & {i = j} \\ 0 & {\text{others}} \\ \end{array} } \right.$$

(15)

Finally, we can find that the rows of the matrix are $\Phi_{{{\text{SVDCGI}}}}$ orthogonalized, thus it's a general orthogonal measurement ensemble. Then through Lemma1, the measurement matrix obtained by our proposed SVDCGI satisfies the RIP condition is concluded.

Therefore, the singular value decomposition is used to decompose the measurement matrix to obtain the optimized measurement matrix and the optimized measurements in SVDCGI. Since the rows of the optimized measurement matrix are orthogonal to each other, the correlation between the measurements is completely eliminated. Compared to other ghost imaging methods, SVDCGI method which not only reduces the number of measurements, but also improves the reconstruction quality.

4 Numerical simulation

In this section, four sets of numerical simulation experiments are presented to verify the effectiveness of our proposed SVDCGI method. The test environment is Matlab 2016b. For comparison, SVDCGI is compared with other eight method (TGI, NGI, DGI, PGI, CGI,MCGI and SVDGI).

4.1 Single reconstruction numerical simulation

In this numerical simulation, some binary images with $64 \times 64$ pixels are selected as the target image, and the reconstruction results with different reconstruction methods are shown in Figs. 3 and 4, respectively. The number of measurements for each method is 2000 in Fig. 3 and 4096 in Fig. 4. For further testing, some complex gray images with size $64 \times 64$ are also chosen as test images, and the number of measurements is 2000 under noiseless condition, the reconstruction results in Fig. 5.

Fig. 3

Comparison results of eight reconstruction method for binary images with 2000 measurements (under-sampling): a original image; b TGI; c PGI; d DGI; e NGI; f CGI; g SVDGI; h our proposed SVDCGI

Fig. 4

Comparison results of eight reconstruction method for binary images with 4096 measurements (full-sampling): a original image; b TGI; c PGI; d DGI; e NGI; f CGI; g SVDGI; h our proposed SVDCGI

Fig. 5

Comparison results of eight reconstruction method for grayscale images with 2000 measurements (under-sampling): a original image; b TGI; c PGI; d DGI; e NGI; f CGI; g SVDGI; h our proposed SVDCGI

To further analyze the reconstruction performance of the eight methods above, peak signal to noise ratio (PSNR) is used to quantify the reconstruction quality. $W$ represents the original image, $W^{^{\prime}}$ represents the reconstructed image, the image size is $64 \times 64$. The definition of PSNR is defined as below:

$${\text{PSNR}} = 10 \times \log_{10} \frac{{255^{2} }}{{{\text{MSE}}}}$$

(16)

where ${\text{MSE}} = \left\| {W - W^{\prime}} \right\|_{2}^{2} /(P \times P)$ is the mean square error.

Also, the correlation coefficient (CC) is also used to indicate the similarity between the reconstruction results and the original image, which is defined as:

$${\text{CC}} = \frac{{{\text{COV}}\left( {W,W^{\prime}} \right)}}{{\sigma_{W} \sigma_{{W^{\prime}}} }}$$

(17)

It can be seen from Fig. 3 that the reconstruction results by TGI, DGI, and NGI are very poor, and the reconstruction results of PGI, CGI, MCGI and SVDGI are relatively improved, but the reconstruction result is far less than our proposed SVDCGI. As can be seen from Fig. 4, the quality of the reconstruction is improved when full sampling and can be almost well reconstructed. From Fig. 5, although the CGI and MCGI method surpass other methods (TGI, PGI, DGI, NGI, SVDGI) substantially, but it is obvious that our proposed SVDCGI also has made a greater progress on reconstruction quality and the original image can be reconstructed when under sampling. As shown in Table 3, SVDCGI has no advantage on the reconstruction time due to the iterative scheme, the same as CGI and MCGI. But in Table 4, SVDCGI has advantage on the reconstruction quality.

Table 3 Reconstruction time of eight different reconstruction methods for binary images with 2000 measurements (under-sampling) 

Table 4 PSNR and CC comparison of eight different reconstruction methods

4.2 Reconstruction under different sparsity

To compare the performance of our proposed SVDCGI method with other six reconstruction methods which under different sparsity level ($K$), the size of test image is $32 \times 32$, i.e. $N = 1024$, picking a random non-negative measurement matrix, the number of measurements $M = 256$, the sparsity level varies from 60 to 200, and the step size is set to 5. Under each set of $(N,M,K)$ parameters, the average CC and PSNR of 1000 times experiments are calculated and depicted in Fig. 6.

Fig. 6

a The relationship between CC and the sparsity level. b The relationship between PSNR and the sparsity level

As shown in Fig. 6, the CC and PSNR of TGI, DGI, NGI are nearly the same, which decreases slowly as the sparsity level increase. The PGI is nearly unchanged as the increase of sparsity, because it’s independent to the change of sparsity level. For CGI and our proposed SVDCGI, as the sparsity level increases, the PSNR and CC are better than other reconstruction methods, and our proposed SVDCGI is best. The reasons are that, after singular value decomposition, in the new compressed measurement system we get, the correlation between different measurements is eliminated, which maximize the efficacy of the measurements, thus our proposed SVDCGI method has made an great progress on enhancing the reconstruction quality.

4.3 Reconstruction under different number of measurements

Considering the relationship of the reconstruction performance and the number of measurements. In this experiment, under different number of measurement, the size of test image is $32 \times 32$, i.e. $N = 1024$ and the sparsity level $K = 60$, the number of measurement varies from 60 to 360, and the step size is set to 10. Under each set of $(N,M,K)$ parameters, the average CC and PSNR of 1000 times experiments are calculated and depicted in Fig. 7.

Fig. 7

a The relationship between CC and the number of measurements. b The relationship between PSNR and the number of measurements

As can be seen from Fig. 7a and b, as the number of measurements increases, the CC and PSNR of TGI, DGI, and NGI increases slowly. The CC and PSNR of PGI, CGI and SVDGI increases as the number of measurements increases, and the CC value of CGI and SVDCGI increases until reaches 1.0. However, the curves of PSNR of SVDCGI increase rapidly than other methods, indicating that the SVDCGI method is much better than other methods.

4.4 Reconstruction under different noises

However, the environmental noise is inevitable in ghost imaging. To analyze the influence of the noise on the eight methods, we add Additive White Gaussian Noise (AWGN) to measurement vector $B$. Under different the value of noise standard deviation, the size of test image is $32 \times 32$, i.e.$N = 1024$ and the sparsity level $K = 60$, the number of measurement $M = 256$ and the value of noise standard deviation varies from 0.01 to 2, the step size is set to 0.08. Under each set of $(N,M,K)$ parameters, the experiment is performed independently for 1000 times. The average of CC and PSNR are shown in Fig. 8.

Fig. 8

a The relationship between CC with noise. b The relationship between PSNR with noise

As we can be seen from Fig. 8a and b that the CC and PSNR of NGI and DGI are almost equal to TGI and approximately linearly decrease with noise standard deviation increase. The CC and PSNR of CGI and SVDCGI decrease as the noise standard deviation increases. Obviously, in the case of noise, the CC and PSNR of our proposed SVDCGI is best. Therefore, the SVDCGI method has a promising prospect in real applications.

4.5 Numerical simulation experimental analysis and summary

For further verification the mutual coherence of measurement matrix under different methods (CGI, SVDCGI). In this experiment, under different number of measurement, the size of test image is $64 \times 64$, i.e. $N = 4096$, the number of measurement varies from 500 to 4000, and the step size is set to 500. The mutual coherence of measurement matrix is shown in Fig. 9.

Fig. 9

Mutual coherence of measurement matrix under different number of measurement

In summary, the singular value decomposition is applied to decompose the measurement matrix, and then the optimized measurement matrix and measurements are obtained. Since the rows of the optimized measurement matrix are orthogonal to each other, the correlation between the measurements is eliminated as shown in Fig. 9. Therefore, the performance of the reconstruction can be greatly improved, and the quality of the reconstructed image is nearly optimal under the same number of measurements.

5 Conclusion

In conclusion, we propose a method of singular value decomposition compressed ghost imaging based on non-negative constraints to reconstruct original image, which can eliminate the correlation between the measurements by performing singular value decomposition on measurement matrix to enhance the reconstruction quality of original images. Also, the numerical simulation experimental demonstrate the feasibility and superiority of our proposed method.