1 Introduction

Laser-based diagnostics in combustion in general, and in combustion-assisted nanomaterial synthesis in particular, yield benchmark experimental data for mechanism validation [1,2,3,4] Among various diagnostic techniques laser-induced fluorescence (LIF) has particularly strong record in revealing quantitative and spatially resolved information on wide variety of combustion intermediates [5,6,7,8]. However, several factors, such as fluorescence quantum yield, fluorescence trapping, detection and collection efficiency, have to be quantified in order to convert LIF signal to absolute species concentrations [9,10,11]. In cases where the light absorption is particularly strong, the attenuation of the excitation laser beam induces LIF signal, whose intensity decays with the propagation of the laser beam through the absorbing medium, providing information about local absorbance and, therefore, absolute concentration. This principle was implemented by Stepowsky [12] to deduce absolute concentration between two successive (close) points of flame-borne OH by bidirectional beam configuration. Similarly, Versluis et al. [13], presented a way to obtain OH quantitative distributions from bidirectional LIF images, where collisional quenching effects cancelled out. Somewhat different approach was undertaken by Hecht et al. [14] who used a weak (with virtually no light attenuation) and a strong transition (noticeably attenuated along the laser sheet propagation direction) originating from the same level of Fe-atom in nanoparticle flame synthesis reactor to deduce absolute Fe(I) concentration. The pixel-by-pixel ratio of the LIF image recorded via the strong spectral transition to the one recorded using weak transition, under identical reaction conditions, yielded the local absorbance values and consequently—the absolute concentration of Fe(I), resolved along the line-of-sight.

Tian et al. [15], who studied LIF of Fe atoms in the ferrocene-doped premixed propene/oxygen/argon flat flame pointed out that bidirectional scheme suggested by Versluis et al. [13] can be reduced to the unidirectional configuration, taking advantage of the axial symmetry of the flame. The use of symmetry for evaluation of absolute OH concentration was implemented also in the early work of Stepowski and Garo [16], where they compared the intensity of the LIF signals in two boundary points of a conical diffusion flame. However, this method was applicable only to the specific situations due to limitations of the equipment available at that time (e.g. two photomultipliers were used instead of CCD detector commonly used nowadays).

The present work reports a detailed analysis of advantages and challenges associated with this approach on the example of Fe-atom imaging in hydrogen/oxygen/argon premixed flame doped with iron pentacarbonyl (IPC, Fe(CO)\(_5\)). This system is widespread in detailed studies of iron oxide nanoparticle flame synthesis (see Ref. [17] and references therein). Taking into consideration the flame reflection symmetry with respect to the plane perpendicular to the laser beam (feature applicable to a wide class of burners), a single laser beam operating at single (strong) spectral transition is sufficient to obtain absolute concentration. A ratio of the LIF images on the two sides of the flame symmetry plane cancels out factors, such as fluorescence quantum yield, collection and detection efficiency, and fluorescence trapping, thus reducing the absolute concentration measurements to local LIF signal attenuation quantification. While being conceptually similar to a traditional absorption experiment, this method retains spatial resolution along the line-of-sight, since the imaging of the laser-induced fluorescence attenuation yields local absorbance values. Furthermore, since only the fluorescence emerging due to the portion of the laser line interacting with the absorber is observable, this approach possesses detection sensitivity superior to a traditional absorption experiment and does not impose upper limit on the laser linewidth. For the case of ideally monochromatic laser, the local absorbance values can be directly converted to the absorber’s absolute concentration, using the known value of absorption cross-section. We show, that for the case of finite laser linewidth, the observed local absorbance can be transformed into absolute concentration, using, in addition to the absorption cross-section, a scaling factor straightforwardly derived based on the knowledge of laser/absorber linewidth ratio.

The Fe-atom concentration field retrieved with this approach was compared to predictions of the current reduced iron flame chemistry models [18]. This comparison reveals that the model strongly overpredicts the conversion of the IPC precursor to atomic iron and that the radial profile of Fe deviates from uniform concentration distribution anticipated for a flat flame burner. These findings hint at the shortcomings in the present picture of early iron cluster formation in flames and suggest that the processes of iron cluster nucleation, iron particle growth and their heterogeneous oxidation should be incorporated in a model aiming at quantitative description of the synthesis process.

2 Experimental

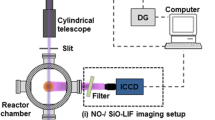
The schematic of the experimental setup is shown in Fig. 1

Fig. 1
figure 1

Schematic of the experimental setup. SHG second harmonic generator, F filter, I iris, M mirror, L lens (f1 = 20 cm, f2 = 10 cm), PD-photodiode. X-laser beam propagation axis (see Sect. 4.1)

Full size image

Premixed downward-firing low-pressure flames were stabilized on a 36 mm-diameter porous water-cooled bronze sinter burner mounted on an automated linear feedthrough (Huntington Mechanical Labs) enabling to control the distance between the LIF laser beam and the burner surface. The burner was situated in a 50 cm-long cylindrical chamber of 27 cm diameter, and the pressure was kept at 30 mbar in all the experiments described in this work. The mass flow rates of the gases forming the reacting flow were regulated by mass flow controllers (MKS Instruments). The parameters of the two flames used in this work, differing only by the IPC load, referred hereafter as flame A and flame B, are listed in Table 1:

Table 1 Parameters of the flames used in this work
Full size table

A collimated, unfocused laser beam (0.6 mm FWHM) near 298.3 nm, generated by frequency doubling of the output of the ND-60 dye laser filled with mixture of Rhodamine 590 and Rhodamine 610 dyes, pumped by the second harmonics of Continuum Surelite Nd:YAG pulsed laser, was used to excite the \(\hbox {a}^5\hbox {D} \leftarrow \hbox {y}^5\hbox {D}^0\) transition of Fe(I) (Einstein coefficient for spontaneous emission \(A=2.79\times 10^7\hbox {s}^{-1}\) [19]). This line is not superimposed with any other spectral line in flame, including the OH radical spectral lines. No signal was observed upon excitation at this wavelength in the undoped hydrogen/oxygen/argon flame. The resulting fluorescence line image was recorded by a gated ICCD camera (Princeton Instruments PI MAX(512 × 512 pixels) using a short (6 ns) gate promptly after the laser pulse. The LIF line images recorded at different distances from the burner (from 0.5 to 40 mm) were stitched together to generate the two-dimensional(2D)-LIF intensity distribution. Laser pulses with less than 0.1 nJ per pulse were used to avoid saturation and ensure linear dependence of the fluorescence signal on the excitation laser intensity.

The temperature profiles, required for conversion of the quantum state-specific Fe(I) concentration to the total concentration of iron atoms, were measured via multi-line OH laser-induced fluorescence (LIF) imaging. The fluorescence signal was detected during 10-ns gate by ICCD camera after excitation of the OH \(A^2\varSigma ^+\leftarrow X^2\varPi _i\) band R-branch centered around 307 nm with a frequency-doubled output of a tunable dye laser (ND 60, Continuum) pumped by the second harmonics of a pulsed Nd:YAG laser (Surelite). The frequency-doubled output of the dye laser was shaped into a sheet using a concave cylindrical lens (f = 10 mm) and convex spherical lens (f = 200 mm). The ICCD camera enables to use a 10-ns detection gate that is short compared to the OH fluorescence lifetime. The detection was started promptly after the excitation laser pulse. Under these conditions, the rotational-level dependence of the fluorescence quantum yield can be neglected, since only negligible quenching occurs at 30 mbar pressure during the short and prompt detection gate [20]. The signal was corrected for variations in the laser pulse intensity. Temperatures were extracted on a pixel-by-pixel basis from Boltzmann plots of the ground-state-energy dependence of the LIF signal intensity, based on the rotational line intensities extracted from the experimental spectra and LIFBASE [21] tabulated Einstein absorption coefficients of individual rovibronic transitions.

3 Modeling of the iron atom formation and consumption

The downward-firing, flat, low-pressure flame was reconstructed for temperature, flow and concentration fields in a quasi 2D simulation of the reacting laminar flow. The simulations were performed using a finite volume approximation for the conservation equations. The chemical kinetics was described using a finite rate model and a conservation equation was solved for every chemical component. We employed the open-source finite volume library OpenFOAM [22], modified for detailed computation of molecular transport properties for each of the gas species. The convective terms of the conservation equations were discretized using a central discretization schemes (CDS) for first and second derivatives. For the convective transport of all scalar quantities, a blended variant of the CDS was used to ensure total variation diminishing. Because of the steady-state nature of the flame, the temporal integration was performed using an implicit Euler-scheme of first-order accuracy. The PISO scheme [23] was used for the pressure-velocity coupling. The pressure at the outlet boundaries of the computational domain was fixed considering the hydrostatic contribution. At the inlet, the pressure gradient was set to zero, while the mass flow rate was prescribed. The inlet boundary condition for the chemical species is modified by a correction velocity [24], which is necessary in laminar flames of gases with highly different diffusion coefficients. For further details we would like to refer to previous reports on simulation of laminar premixed flames [25, 26]. The iron chemistry in 2D simulations was described using a reduced mechanism, recently published by Nanjaiah et al. [18], which consists most probably of the minimal set of reactions required to describe the gas phase kinetics of Fe-combustion in a low-pressure, premixed flame.

The reduced mechanism proposed by Nanjaiah et al. [18] was shown to reproduce well the simulation outputs of the detailed reaction scheme and to reliably predict the temperature, flame speed and relative FeO concentration field. It comprises lumped Fe(CO)\(_5\) pyrolysis [27], simplified scheme describing the formation of iron clusters (up to \(\hbox {Fe}_7\)), their subsequent evaporation in the high-temperature reaction zone, and steps including interaction of Fe-containing species (not including iron clusters) with \(\hbox {H}_2\), \(\hbox {O}_2\), \(\hbox {H}_2\)O, H, O and OH, eventually leading to the formation of \(\hbox {Fe}_2\hbox {O}_3\) monomer [28], suggested to link the gas-phase iron-chemistry to the solid iron oxide nanoparticles. While this model was able to qualitatively describe the formation of condensable matter in the vicinity of the burner surface [26, 29, 30], it does not include steps beyond incipient cluster formation, leading to formation of nanoparticles within several nm-size range. Note that recent studies, e.g. Sellmann et al. [30], reported formation of early particles with diameters up to 4 nm with addition of already 200 ppm of Fe(CO)\(_5\) to the flame—far larger than the presently assumed early formed Fe-clusters (for example, Fe-particle of 4 nm contains already \(\sim\) 2850 iron atoms). It also appears very unlikely that these particles would simply evaporate into Fe-atoms [31, 32], while the ignition temperature of iron powder aerosols was reported to be around 850 K [33].

Therefore, we investigated the role of nucleation and growth of realistic iron particles as a possible sink for Fe-atoms. As a similar study was previously performed in the context of shock-tube experiment by Giesen et al. [34], we employed for the sake of consistency the same models for homogeneous nucleation [35], particle coagulation [36] and surface condensation [34]. The evaporation of these iron particles is not significant in the temperature range characteristic for the preheat zone of the flame and the heterogeneous processes responsible for particle consumption via chemical transport reactions are not well known. Therefore, instead of direct incorporation of the above mentioned particle formation and grow model into the flame simulation, we have performed a parametric study for the range of IPC concentrations, residence time and temperatures, characteristic for the flame conditions in the present work. Further details concerning this simulation are presented in Sect. 4.2

4 Results and discussion

4.1 Measurement concept and data evaluation

The measurement concept of this work allows for evaluation of the absolute concentration from the LIF image along the excitation laser beam propagation axis, provided that the absorption of the laser radiation is sufficiently high, and, therefore, the attenuation of the fluorescence induced by the laser beam is observable. The intensity of the excitation LIF signal, S(x), emerging from a point x along the laser propagation axis for spectral transition 1 \(\rightarrow\) 2 excited by the laser radiation at frequency \(\nu\), having the intensity \(I(x,\nu )\) is given as follows:

$$\begin{aligned} S(x)=\int _{-\infty }^\infty I(x,\nu )g(\nu )\sigma _{12}A(x)d\nu \end{aligned}$$
(1)

defining A(x) as follows:

$$\begin{aligned} A(x)=C(x)\eta (x)N_1(x) \end{aligned}$$
(2)

where \(g(\nu )\) is the area-normalized lineshape function of the absorber, \(\eta (x)\) is the fluorescence quantum yield, \(\sigma _{12}\) is the temperature-independent state-to-state-specific, frequency integrated absorption cross section, \(N_1(x)\) is the number density at level 1, and C(x) is an experimental constant, which depends on the solid angle of light collection, fluorescence trapping, the transmission efficiency of the optics and the photoelectric efficiency of light detection.

Note that A(x) depends on the position along the laser propagation axis, x, and does not depend on the excitation frequency \(\nu\). This is due to the fact that parameters C(x) and \(\eta (x)\) are associated with the fluorescence following the excitation to the upper level 2, which is, in general case, spectrally shifted with respect to the absorption and does not have a “memory” of the excitation frequency. Strictly speaking, the absorber lineshape, \(g(\nu )\), can also include some dependence on the position along the laser propagation axis, x, e.g. in case of Doppler broadening and drastic variation of the temperature along the x axis. However, this is not the case in the most of flat flame experiments, including the current one, therefore we will consider the absorber lineshape \(g(\nu )\) to be independent of x.

For burner configurations, symmetrical with respect to the surface plane perpendicular to the laser beam propagation axis, and furthermore, for burners with cylindrical symmetry, the quantity A(x) is also symmetric, that is \(A(x)=A(-x)\).

Let us consider first a monochromatic laser beam at frequency \(\nu _0\) with intensity I(x) propagating from a point − \(x\) through the origin of coordinate \(x=0\), located at the burner center, to a point x. According to the Beer–Lambert extinction law the intensity of the laser beam is attenuated as follows:

$$\begin{aligned} I(x)=I(-x)\exp \left( -\sigma _{12}g(\nu _0)\int _{-x}^{+x}N_1(\chi )d\chi \right) \end{aligned}$$
(3)

Due to the laser beam extinction, the LIF signal S(x) is attenuated with respect to \(S(-x)\) as follows:

$$\begin{aligned} \frac{S(x)}{S(-x)}= & {} \frac{I(x)\sigma _{12}g(\nu _0)A(x)}{I(-x)\sigma _{12}g(\nu _0)A(-x)} \nonumber \\= & {} \frac{A(x)}{A(-x)}\exp \left( -\sigma _{12}g(\nu _0)\int _{-x}^{+x}N_1(\chi )d\chi \right) \end{aligned}$$
(4)

Since \(A(x)=A(-x)\), we have the following:

$$\begin{aligned} \frac{S(x)}{S(-x)}=\exp \left( -\sigma _{12}g(\nu _0)\int _{-x}^{+x}N_1(\chi )d\chi \right) \nonumber \\ \end{aligned}$$
(5)

The experimentally observable extinction function \(R(x) =- \ln \left[ \frac{S(x)}{S(-x)}\right]\) is given as follows:

$$\begin{aligned} R(x)=\sigma _{12}g(\nu _0)\int _{-x}^{+x}N_1(\chi )d\chi = 2\sigma _{12}g(\nu _0) \int _{0}^{+x}N_1(\chi )d\chi \end{aligned}$$
(6)

The state-specific concentration \(N_1(x)\) can be evaluated by the differentiation of Eq. (6) as follows:

$$\begin{aligned} N_1(x)=\frac{1}{2\sigma _{12}g(\nu _0)}\frac{dR(x)}{dx} \end{aligned}$$
(7)

Therefore, in the case of ideally monochromatic laser excitation, the imaging of the LIF signal attenuation is conceptually similar to traditional absorption experiment, with the advantage of retrieving the information about local absorption along the line-of-sight.

However, in the more realistic situation, where the laser linewidth is finite, the measurement of absorption via the LIF emission attenuation imaging differs in one additional important aspect from a traditional absorption experiment. In the latter the intensity decrease at the center of the absorption contour depends on the transition absorption cross section \(\sigma _{12}\) multiplied by the peak value of the observed line contour, \(f(\nu )\). This line contour is a convolution of the laser, \(l(\nu )\), and the absorption, \(g(\nu )\), lineshapes. The broadening of the laser line leads to the proportional decrease of \(f(\nu )\) peak value and, therefore, to the reduction of the observed absorption. Simply put, when the laser linewidth significantly exceeds the absorption linewidth, most of the laser emission passes through the absorbing medium without any interaction with atoms or molecules, and as a consequence, the attenuation of the total, frequency-integrated laser beam intensity is substantially reduced.

The situation is different when we measure the absorption by comparing the fluorescence intensity at two points along the laser beam propagation axis. In this case, the portion of light which does not interact with the absorber is not observable. Therefore, the attenuation of the fluorescence intensity along the excitation laser beam is readily observable even for laser with virtually infinite linewidth. Let us consider this case.

The intensity of the laser at wavenumber \(\nu\) starting at the point \(x=-\,L\) varies along the x axis according to the Beer–Lambert law as follows:

$$\begin{aligned} I(x,\nu )=I_0(-L)l(\nu )e^{-g(\nu )\sigma _{12}\int _{-L}^{x}N_1(\chi )d\chi } \end{aligned}$$
(8)

The observed fluorescence signal, S(x), carrying the information about the variation of the laser beam intensity, is, therefore, expressed by the following:

$$\begin{aligned} S(x)= & {} A(x)\int _{-\infty }^{\infty }I(x,\nu )g(\nu )\sigma _{12}d\nu \nonumber \\= & {} A(x)\sigma _{12}I_0(-L)\int _{-\infty }^{\infty }l(\nu )g(\nu )e^{-g(\nu )\sigma _{12}\int _{-L}^{x}N_1(\chi )d\chi }d\nu \end{aligned}$$
(9)

Thus, Eq. (6) for the experimentally observable extinction function R(x) transforms into a more elaborate expression as follows:

$$\begin{aligned} R(x)= & {} - \ln \left[ \frac{S(x)}{S(-x)}\right] \nonumber \\= & {} -\ln \left[ \frac{\int _{-\infty }^{\infty }g(\nu )l(\nu )e^{-g(\nu )\sigma _{12}\int _{-L}^{x}N_1(\chi ) d\chi }d\nu }{\int _{-\infty }^{\infty }g(\nu )l(\nu )e^{-g(\nu )\sigma _{12}\int _{-L}^{-x}N_1(\chi ) d\chi }d\nu }\right] \end{aligned}$$
(10)

Following Eq. (7) the experimentally measured R(X) function can be numerically differentiated to yield information concerning \(N_1(x)\) as follows:

$$\begin{aligned} \varDelta R(x)= & {} R(x+\varDelta x)-R(x)\nonumber \\= & {} \ln \left[ \frac{\int _{-\infty }^{\infty }gle^{-g\sigma _{12}F(x)}d\nu }{\int _{-\infty }^{\infty }gle^{-g\sigma _{12}F(-x)}d\nu } \frac{\int _{-\infty }^{\infty }gle^{-g\sigma _{12}[F(-x)-\delta F]}d\nu }{\int _{-\infty }^{\infty }gle^{-g\sigma _{12}[F(x)+\delta F]}d\nu },\right] \end{aligned}$$
(11)

where \(F(x)=\int _{-L}^x N_1(\chi )d\chi\), and \(\delta F=\int _x^{x+\varDelta x}N_1(\chi )d\chi \sim N_1(x)\varDelta x=N_1(-x)\varDelta x\). We also omit \((\nu )\) in the equations for brevity. Since \(\delta F\) is small, the exponential function can be approximated by its first series expansion term as follows:

$$\begin{aligned} \varDelta R(x)=\ln \left[ \frac{\int _{-\infty }^{\infty }gle^{-g\sigma _{12}F(x)}d\nu }{\int _{-\infty }^{\infty }gle^{-g\sigma _{12}F(-x)}d\nu } \frac{(\int _{-\infty }^{\infty }gle^{-g\sigma _{12}F(-x)}d\nu +\delta F\sigma _{12}\int _{-\infty }^{\infty }g^2le^{-g\sigma _{12}F(-x)}d\nu ) }{(\int _{-\infty }^{\infty }gle^{-g\sigma _{12}F(x)}d\nu -\delta F\sigma _{12}\int _{-\infty }^{\infty }g^2le^{-g\sigma _{12}F(x)}d\nu )}\right] \end{aligned}$$
(12)

Equation (12) can be rewritten as follows:

$$\begin{aligned} \varDelta R(x)=\ln \left[ \frac{1+\delta F\sigma _{12}\varPhi (-x)}{1-\delta F\sigma _{12}\varPhi (x)}\right] \sim \delta F\sigma _{12}(\varPhi (x)+\varPhi (-x))=N_1(x)\sigma _{12}(\varPhi (x)+\varPhi (-x))\varDelta x , \end{aligned}$$
(13)

where

$$\begin{aligned} \varPhi (x)=\frac{\int _{-\infty }^{\infty }g^2le^{-g\sigma _{12}F(x)}d\nu }{\int _{-\infty }^{\infty }gle^{-g\sigma _{12}F(x)}d\nu } \end{aligned}$$
(14)

and

$$\begin{aligned} N_1(x)=\frac{1}{(\varPhi (x)+\varPhi (-x))\sigma _{12}}\frac{\varDelta R(x)}{\varDelta x} \end{aligned}$$
(15)

For the case of purely monochromatic laser light, its lineshape can be approximated by Dirac delta function \(l(\nu ) = \delta (\nu -\nu _0)\). In such case \(\varPhi (x)=g(\nu _0)\) and, therefore,

$$\begin{aligned} N_1(x)=\frac{1}{2g(\nu _0)\sigma _{12}}\frac{\varDelta R(x)}{\varDelta x} \end{aligned}$$
(16)

Thus, Eq. (16) is identical to Eq. (7).

The situation with a broadband laser, where l(v) can be treated as a constant over the frequency range of the absorption line \(g(\nu )\), was considered by Stepowski [12]. He demonstrated that \(\varPhi (x)\) is a linear function of F(x) in the case of Doppler broadening of the absorption line \(g(\nu )\), as long as the total absorption \(\sigma _{12} g(\nu _0) F(x)\) is less than 4. The \(\varPhi (x)\) function depends on x through the function F(x); therefore, we can express it as \(\varPhi (\alpha )\), where \(\alpha = \sigma _{12}g(\nu _0)F(x)\) is the total absorption. Note, that for the clarity of presentation we assume that the absorption line-center coincides with the laser centerline frequency \(\nu _0\).

Figure 2 depicts the function \(\varPhi (\alpha )\), normalized by the centerline value of the absorber lineshape, \(g(\nu _0)\), for several laser/absorber linewidth ratios (\(\delta \nu _{\text{laser}}/\delta \nu _{\text{line}}\)), shown by solid lines. We assume Gaussian profiles for both laser and absorber lineshapes. In the case of broadband excitation, corresponding to infinite linewidths of the laser, \(\varPhi (\alpha )/g(\nu _0)\) coincides with Stepowski’s [12] result. Figure 2 also shows the result for laser/absorber linewidth ratio of 2.6 used in this work. The important feature of \(\varPhi (\alpha )\) is that it can be fitted well by a linear function up to \(\alpha \lesssim 4\) (shown by the dashed lines in Fig. 2).

Fig. 2
figure 2

Function \(\varPhi (\alpha )/g(\nu _0)\) —solid lines (see text) at different ratios of laser and absorber linewidths, dashed lines—linear fits of \(\varPhi (\alpha )/g(\nu _0)\) for \(\alpha <4\)

Full size image

Thus, \(\varPhi (x)\) can be expressed by \(\varPhi (x)=A-BF(x)\) and

$$\begin{aligned} \varPhi (x)+\varPhi (-x)=2A-B(F(x) + F(-x))=2A-BF(L) \nonumber \\ \end{aligned}$$
(17)

since \(F(x)+F(-x)=F(L)\) due to the symmetry: \(\int _{-L}^{-x}N_1(\chi )d\chi =\int _{x}^{L}N_1(\chi )d\chi\) The sum \(\varPhi (x)+\varPhi (-x) = A+\varPhi (L)\) does not depend on x as long as the total absorption is not excessively large. Therefore Eq. (15) can be rewritten as follows:

$$\begin{aligned} N_1(x)=\frac{1}{2\sigma _{12}g(\nu _0)f}\frac{dR(x)}{dx} \end{aligned}$$
(18)

Equation (18) is very similar to the Eq. (16), valid for the case of monochromatic light, with exception of normalization by the attenuation factor f, given by the following:

$$\begin{aligned} f=\frac{A+\varPhi (L) }{2g(\nu _0)} \end{aligned}$$
(19)

In addition to the potentially known lineshapes \(l(\nu )\) and \(g(\nu )\), \(\varPhi (L)\) depends on the function \(F(L)= \int ^L_{-L}N_1(x)dx\). In order to find the dependence of this function on the measurable total extinction R(L), Stepowski [12] suggested using a special calibration function. In this work we took a different approach.

The attenuation factor f depends on the lineshapes \(l(\nu )\) and \(g(\nu )\) and on the total extinction R(L) and does not depend on x and the specific shape of \(N_1(x)\). Thus, even applying the “monochromatic case” Eq. (16) to experimentally observed dependence of the fluorescence signal extinction on x, R(x), will yield an accurate radial concentration profile in relative units. This relative concentration profile differs from the absolute one by the attenuation factor f (see Eqs. (7) and (18)).

In order to determine the attenuation factor f, we mimicked the experimentally observable fluorescence signal extinction R(x) using an artificial symmetric function \(N_1(x)\) as an input to Eq. (10). Subsequently, we used Eq. (16) for recovering back the apparent radial concentration profile \(N_1^{\text{app}}(x)\). The apparent radial concentration profile differs from the true concentration profile \(N_1(x)\) only by the attenuation factor f, which, therefore, can be obtained from the ratio between \(N_1^{\text{app}}(x)\) and \(N_1(x)\): \(f=N_1^{\text{app}}(x)/N_1(x)\).

This factor depends on the laser and the absorber linewidths ratio \(\delta \nu _{\text{laser}}/\delta \nu _{\text{line}}\) and on the total extinction R(L). As demonstrated above (see Eq. (16) ) for the case where the laser linewidth is much narrower than that of the absorber, the attenuation factor f is nearly unity and is practically independent on the total absorption. Figure 3 depicts the dependence of the attenuation factor f on the ratio of the laser and absorber linewidths and on the total extinction R(L).

Fig. 3
figure 3

Dependence of the attenuation factor f on the laser/absorber linewidth ratio, \(\delta \nu _{\text{laser}}/\delta \nu _{\text{line}}\) and on the total extinction R(L)

Full size image

The spectral width of Fe(I) \(\hbox {a}^5\)D \(\leftarrow\) \(\hbox {y}^5\hbox {D}^0\) transition at 298.3 nm recorded in 30 mbar flame is dictated predominantly by Doppler broadening which amounts to 0.1 cm−1 (FWHM) at T = 1000 K. The exact collisional broadening parameters of the 298.3 nm line are not reported in the literature. Basing on the measured collisional broadening of the Fe 371.99 nm line [37, 38] we estimated that under our conditions it corresponds to a linewidth \(\delta \nu _{\text{coll}}\) < 0.006 \(\hbox {cm}^{-1}\), and, therefore, the Lorentzian contribution to the lineshape can be neglected. Figure 4 depicts the observed profile of the Fe spectral line fitted by a Gaussian lineshape. It corresponds to the convolution of the absorber lineshape \(g(\nu )\) and the laser lineshape \(l(\nu )\).

Fig. 4
figure 4

The observed spectral profile of the \(\hbox {a}^5\)D \(\rightarrow\) \(\hbox {y}^5\hbox {D}^0\) transition of Fe(I); solid squares—experimental data-points, solid line—Gaussian fit; FWHM = 0.28 \(\hbox {cm}^{-1}\)

Full size image

As mentioned above, \(\delta \nu _{\text{line}}\) = 0.1 \(\hbox {cm}^{-1}\), while the laser linewidths \(\delta \nu _{\text{laser}}\) = 0.26 \(\hbox {cm}^{-1}\) is evaluated from the Gaussian fit of the observed 298.3 nm line spectral profile (see Fig.4), approximating both the absorber and the laser spectral profiles by Gaussian lineshapes:

$$\begin{aligned} \delta \nu _{\text{laser}}=\sqrt{\delta \nu _{\text{observed}}^2-\delta \nu _{\text{line}}^2} \end{aligned}$$
(20)

The observed spectral profile linewidth (0.28 \(\hbox {cm}^{-1}\)) is dictated mainly by the laser linewidth (0.26 \(\hbox {cm}^{-1}\)) and, therefore, the laser linewidth derived from Eq. (20) has little dependence on the absorber broadening. Furthermore, as has been stressed out earlier, due to the independence of the fluorescence trapping on the excitation frequency, it does not contribute to the absorber linewidth in the excitation-LIF spectrum. We did not observe any substantial variation in the observed spectral profile linewidth during fourfold Fe concentration changes. The temperature variation along the laser propagation axis does not exceed 100 K that results in maximum 5% variation of the Doppler linewidth. Thus, our assumption of the independency of the absorber linewidth, \(g(\nu )\), on x is valid.

Figure 5 shows the dependence of the attenuation factor f on the total attenuation R(L) for laser to absorber linewidth ratio \(\delta \nu _{\text{laser}}/\delta \nu _{\text{line}}\)=2.6, characteristic for this work.

Fig. 5
figure 5

Dependence of the attenuation factor f on the total extinction R(L) for \(\delta \nu _{\text{laser}}/\delta \nu _{\text{line}}\) = 2.6, characteristic for this work

Full size image

For this value of laser to absorber linewidth ratio the attenuation factor f can be approximated by the following expression:

$$\begin{aligned} f=0.714-0.0539z-0.016z^2, \end{aligned}$$
(21)

where \(z= R(L)\)

Thus, the concentration profile can be reconstructed by numerical differentiation of the experimentally observed LIF signal S(x) according to Eq. (16) followed by normalization by the attenuation factor f calculated using calibration curve similar to the one depicted in Fig. 5.

The validity of the above described analysis relies on the symmetry of the function A(x) (see Eq. (2)). Indeed, our experimental observations confirm the symmetric distribution of the fluorescence quantum yield, \(\eta (x)\) and the experimental constant C(x) with respect to the burner center. To assess the distribution of the fluorescence quantum yield, we mapped the distribution of the effective fluorescence lifetime of Fe-atoms electronically excited by 298.3 nm laser radiation using the fast-gated ICCD camera. It was found that the distribution of the effective fluorescence lifetime is symmetric with respect to the burner center. The effective lifetime, \(\tau _{\text{eff}}\) is given as follows:

$$\begin{aligned} \tau _{\text{eff}}=\frac{1}{(k_{\text{rad}}+Q)}, \end{aligned}$$
(22)

where \(k_{\text{rad}}=\sum _jA_{jk}\) is the radiative decay rate given by sum of Einstein coefficients for spontaneous emission over all radiative pathways, and Q is collisional quenching. The fluorescence quantum yield, \(\eta\), is given by the following:

$$\begin{aligned} \eta =k_{\text{rad}} \tau _{\text{eff}}=\frac{k_{\text{rad}}}{k_{\text{rad}}+Q} \end{aligned}$$
(23)

Since both \(\tau _{\text{eff}}\) (as was verified experimentally) and \(k_{\text{rad}}\) (which is independent of the local flame conditions) are symmetric with respect to the burner center, the fluorescence quantum yield, \(\eta\), is, therefore, also fulfills the condition \(\eta (x)=\eta (-x)\). The symmetry of the experimental constant C(x) with respect to the burner center was assessed by recording the cumulative image of the light emerging from the opening of integrating sphere excited by the same laser beam used for LIF diagnostics.

The presence of the symmetry with respect to the burner center is also manifested by LIF signal of the OH radical in the flame—see Fig. 6. Due to lower absorption cross section of OH in comparison with that of Fe, the attenuation of the laser beam in the flame is negligible and, therefore, the LIF image appears to be symmetric with respect to the burner center.

Fig. 6
figure 6

Fluorescence signal resulting from planar LIF excitation of the \(\hbox {R}_1\)(4) transition belonging to A-X(0,0) band of OH, recorded in Flame B

Full size image

The validity of our approach relies not only on the existence of the (axial or reflection) symmetry, which is valid for most of the commonly used burner configurations, but also on the accurate determination of the symmetry plane (or axis). For the accurate determination of the symmetry plane position we used the image of the burner or of the flame emission recorded on the CCD for long exposure times without the presence of the laser beam. In the case of the flame emission we compare the integrated intensity on the left- and right-hand sides of the dividing plane; the position of the dividing plane for which the integrated intensities on the left-hand side and the right-hand side are equal corresponds to the symmetry plane. We estimate of the symmetry plane determination to be ± 5 pixels which corresponds to ± 0.5 mm.

Figure 7 demonstrates the uncertainties in the reconstructed Fe radial distribution induced by ± 0.5 mm uncertainty in the determination of the symmetry plane position.

Fig. 7
figure 7

Radial profile of Fe, reconstructed from the line fluorescence image recorded at 6 mm from the burner in Flame B. Note the variations in the reconstructed radial distribution when the position of the symmetry plane is artificially varied within the ± 0.5 mm uncertainty limits

Full size image

Figure 7 also reveals that the radial distribution of Fe-atoms is far from exhibiting a flat radial profile, despite the nominally uniform radial distribution of the gas flow delivered by the porous bronze sinter, designed to yield a flat, quazi-1D flame. Rather, strongly enhanced concentration of Fe is observed at the annular region, close to the edges of the porous sinter. Possible experimental uncertainties in the determination of the accurate position of the symmetry plane can affect the peak concentration magnitude, but obviously cannot account for the unflatness of the observed radial distribution.

4.2 Absolute concentration of iron atom and comparison to model predictions

Figures 8 and 9 depict the observed LIF images and the corresponding reconstructed total concentration maps for flames doped with 50 and 200 ppm of IPC.

Fig. 8
figure 8

a LIF signal normalized to the maximum value and b reconstructed absolute concentration distribution of Fe in the flame doped with 50 ppm of IPC. (Flame A); DFB distance from the burner

Full size image
Fig. 9
figure 9

a LIF signal normalized to the maximum value and b reconstructed absolute concentration distribution of Fe in the flame doped with 200 ppm of IPC. (Flame B); DFB distance from the burner

Full size image

The total Fe-concentration was obtained from the state-specific Fe-concentration (retrieved from the LIF image) with the Boltzmann factors calculated using the temperature distribution measured by OH-LIF thermometry. As expected, the radial asymmetry of the recorded LIF image is more profound in the case with 200 ppm IPC load, reflecting higher concentration of Fe-atoms leading to stronger attenuation of the excitation laser light, compared to the 50 ppm case. From the reconstructed Fe-atom absolute concentration distributions, shown in Figs. 8 and 9, two observations are immediately apparent. First, the Fe radial distribution does not look as one would expect for a flat flame burner, that is, nearly uniform in the radial direction with slightly pronounced maximum at the burner center. Rather, significant enhancement of the Fe-concentration is observed at the annular region of the burner, leading to toroidal, “donut-like” shape. For example, in the flame doped with 200 ppm IPC (see Fig. 9) at distance from the burner DFB) \(\sim\) 7.5 mm the Fe mole fraction at the annular region of the burner (at \(\sim\) 15 mm from the burner center) exceeds by a factor of \(\sim\) 2 the Fe mole fraction at the burner center. Second, the conversion of IPC to Fe-atoms is far from being complete. While the Fe(CO)\(_5\) precursor undergoes a complete decomposition in the preheat zone of the flame it appears that only a fraction of the IPC precursor doped to the flame is channeled into atomic iron. For instance, at the flame doped with 200 ppm of IPC, the mole fraction of Fe (at the annular region of the burner) reaches only \(\sim\) 30 ppm.

The observed radial distribution of Fe-atoms with substantial minimum of Fe-concentration at the burner center is quite surprising, taking into account rather flat temperature [18] and OH profiles (see Fig. 6), with slightly pronounced maxima at the center of the burner. Furthermore, the relative flatness of the temperature distribution, and even more so, its good correspondence to the predictions of two-dimensional computational fluid dynamics (CFD) model [17, 18] indicate that the observed toroidal shape of the Fe-atom distribution cannot be related to possible imperfections of the burner matrix. Note, that the observation of deviations from uniform distribution of the concentration field is not without precedent for flat flame burners. For example, Migliorini et al. [39] found dramatic enhancement of soot volume fraction at annular region of McKenna burner-stabilized ethylene/air flames. This enhancement could be consistently observed by the authors [39] with several techniques including tomographic extinction measurements, scattering and laser-induced incandescence. Similarly, to our case, the annular enhancement was observed despite nearly ideally flat temperature radial profile in the vicinity of the burner.

Previous studies including our own [40] demonstrated that gas-phase intermediate can exhibit radial distribution deviating from uniform flat flame profile: this observation is well documented for \(\hbox {NH}_2\) radical formed in ammonia-doped methane-air flames [40] and morpholine/oxygen/argon flame [41].

Fig. 10
figure 10

Fe-atom concentration in the Flame B—experiment vs. simulation. Note the same scale for the simulated and the experimentally derived Fe-atom concentration. Left panel shows simulation performed without inclusion of early iron cluster formation. Right panel shows simulation accounting for early formation of iron clusters

Full size image

The experimentally observed Fe-atom concentration field was compared to the predictions of 2-D simulation using a reduced mechanism proposed by Nanjaiah et al. [18] (see Sect. 3). The simulation with and without inclusion of early iron cluster formation mechanism was attempted—see Fig. 10, but failed to quantitatively reproduce the experimental observations. For the case where the mechanism neglects the early formation of iron clusters, the simulation predicts nearly full conversion of IPC to atomic gas-phase iron (see Fig. 10—left panel). When the early cluster formation is accounted for in the reduced mechanism [18] (Fig. 10—right panel), the simulation predicts 5 mm shift of the Fe concentration profile peak towards higher DFB and \(\sim\) 10% reduction in the IPC conversion efficiency into atomic iron, compared to the scheme without iron cluster formation, far more modest than nearly 85% reduction observed in the experiment. The observed toroidal shape of the Fe-concentration distribution is also not captured by the model.

We show in the following that this discrepancy is most likely related to the shortcomings in the reduced mechanism [18] that utilizes the mechanism of Wen et al. [32] as a reference in the optimization of the simplified iron cluster formation and destruction scheme. The reduced scheme [18] overpredicts gas phase Fe-atom concentration, since it does not include processes of Fe-atom consumption via surface condensation on nanoparticles in the size range of several nm, playing dominant role in the detailed mechanism of Wen et al. [32] . Furthermore, the early formed iron particles vanishing in the high-temperature, radical-rich reaction zone [26, 29, 30] are unlikely to decompose by evaporation. The fragmentation energies, D(\(\hbox {Fe}_n\)-Fe), were shown to increase with the cluster size and to level off to values above 300 kJ/mol for iron clusters beyond \(\hbox {Fe}_8\) [31], hampering the evaporation of larger clusters. In fact, the model of Wen et al. [32] disregards dissociation for particles larger than \(\hbox {Fe}_8\). Hence, it is conceivable that iron particle consumption proceeds via surface chemical transport reactions leading to oxidation into gas phase Fe-O-H species. Scenario where a solid iron oxide heterogeneously forms as shell on the surface of the iron nanoparticles was also reported [42].

The incorporation of the comprehensive iron cluster and particle formation scheme proposed by Wen et al. [32] into the 2-D simulation cannot be done directly due to the computational cost. Even more fundamental obstacle to the direct incorporation of several nm diameter iron particles into flame model—is the lack of knowledge concerning the mechanistic details of their heterogeneous oxidation and decomposition. Therefore, we restricted ourselves in this case to a parametric study of gas phase Fe consumption for well-defined initial IPC concentrations, using a nucleation model approach, which was demonstrated to be instrumental for description of iron consumption during cluster and particles formation in shock-tube experiments [34] (See Sect. 3). This parametric study does not pretend to yield a fully quantitative prediction of the synthesis flame structure. Rather, it is introduced primarily as illustration, demonstrating how one can rationalize the observed concentrations of atomic iron and the shape of the concentration distribution.

In order to cover a large parameter space, the growth of Fe-particles was simulated for a set of initial IPC concentrations in argon at different (constant) temperatures for fixed values of residence time. The investigated parameter space was prescribed by the thermodynamic state of the pre-heat zone of the flame. The decomposition of IPC begins approximately at 500 K. At temperatures above 750 K the precursor is completely decomposed into Fe-atoms. The temperature increases then monotonically and the main reaction zone of the flame is reached typically above 1000 K. The residence time between the decomposition of IPC and reaching the reaction zone in the low-pressure setup (30 mbar) was approximately 6–8 ms. Based on this set of process limits, the resulting parameters ranged from 25 to 200 ppm of IPC in argon at temperatures from 400 to 1200 K. The spacing in Fe-atom concentration was 25 ppm and 25 K in temperature, resulting in 264 support points. The total residence time was chosen to be 10 ms. Figure 11 depicts the key results of this parametric study in the temperature-time parameter space: panel (a) shows the waterfall plots of gas phase Fe-concentration for initial IPC loads of 50, 100, 150 and 200 ppm; panels (b) and (c) show the iso-line plots of Fe-atom concentration for initial IPC loads of 50 ppm and 200 ppm, used in this work.

Fig. 11
figure 11

Gas phase Fe-concentration calculated using nucleation theory approach [34] in the temperature-residence time parameter space: a waterfall plots considering four different initial loads of IPC: 50, 100, 150 and 200 ppm; b iso-line plot for initial IPC load of 50 ppm; c iso-line plot for initial IPC load of 200 ppm

Full size image

For a given value of temperature, the Fe-concentration rises during the first 1–3 ms manifesting the IPC decomposition; this rise is followed by a decay (except at the highest temperatures) once the supersaturated vapor of Fe-atoms starts to condense. For a given value of residence time the Fe-concentration at T < 450 K is negligible, since no precursor decomposition occurs. As the temperature rises towards 500 K, Fe-atoms emerge due to the IPC decomposition and then, the gas-phase Fe-concentration decays again, once the saturation vapor pressure is reached. With sufficient increase of the temperature (T > 1000 K), the saturation pressure rises, leading to the increase of gas-phase Fe, which is no longer consumed by condensation. This forms a “valley” of optimal Fe depletion in the temperature-time parameter space seen in Fig. 11.

Due to the small vapor pressure of bulk Fe, the Fe atoms are consumed from the gas phase quickly and the consumption increases with the growth of the initial IPC concentration. The initial nucleation is fast, followed by further coagulation and strong surface growth, which drives further decline of the gas-phase Fe concentration The effect becomes apparent already at the initial IPC concentrations around 50 ppm. The Fe-consumption process is temperature-dependent and reaches an optimum at \(\sim\) 650–700 K, matching well the early flame regime. At an initial IPC concentration of 200 ppm the IPC to Fe conversion efficiency drops to \(\sim\) 25% after \(\sim\) 1 ms residence time at 650 K. These findings indicate that realistic account for early iron nanoparticle formation, going beyond the incipient small clusters, can explain the fact that only a fraction of the initial IPC load is seen as gas-phase iron atoms. Note that the model based on the nucleation theory approach provides quite realistic estimation of the early iron particle size. The computed particle diameter reaches \(\sim\) 2 nm for completely fused particles, which is consistent with the observations reported by Sellmann et al. [30]. Deviations are attributed to the lack of an oxidation mechanism for particles in the model and the effects stemming from invasive probing in the experiment.

The existence of the optimal temperature window of Fe-atom depletion can provide a hint for the enhancement of Fe concentration at the annular region of the burner, observed in the flame experiments. Note, that at the low temperature boundary (see Fig. 11) the Fe-atoms depletion can increase by factor of about two when the temperature grows by several tens of degrees. Therefore, it is conceivable that in the pre-heat zone of the flame, where the temperatures are in the ballpark of the low-temperature boundary, enhanced depletion of Fe will be observed near the burner center, where the temperature is several tens of degrees higher than in the annular region.

5 Conclusions

Two-dimensional maps of gas-phase iron atom absolute concentrations were measured in downward-firing, premixed, low-pressure \(\hbox {H}_2\)/\(\hbox {O}_2\)/Ar flames doped with Fe(CO)\(_5\), using LIF. By utilization of the fluorescence emanating from excitation of the strong \(\hbox {a}^5\)D \(\leftarrow\) \(\hbox {y}^5\) \(\hbox {D}^0\) transition of Fe(I), we were able to observe attenuation of the fluorescence signal along the laser beam propagation direction due to substantial absorption of the excitation laser radiation. Due to the reflection symmetry of the flame, this fluorescence attenuation could be directly converted into local absorbance values and relative concentrations resolved along the line-of-sight. By taking into account the laser/absorber linewidth ratio, this relative concentration was straightforwardly converted to absolute values. This is a first-time elaborate demonstration of LIF utilization for absolute concentration imaging in a calibration-free fashion, similar to absorption techniques, while bypassing the use of dual counterpropagating beam arrangement or concurrent use of judiciously picked weak and strong transitions, utilized in previous studies. The proposed method is applicable to a wide category of burner configurations, possessing reflection symmetry, where strong absorber is monitored, e.g. metal atoms emerging during precursor decomposition in nanoparticle flame synthesis reactors, or OH radical in atmospheric pressure flames.

We find the measured Fe-atom concentration to be significantly lower than the injected loads of the Fe(CO)\(_5\) precursor, indicating conversion of the IPC to species other than atomic iron already in the close vicinity of the burner surface, such as iron clusters and particles. The radial distribution of the iron atoms exhibits significant enhancement in the annular region of the burner, similar to the past observations for other species, such as soot and \(\hbox {NH}_2\) radicals, despite the nominally “flat” burner configuration. Both the low-conversion efficiency of IPC to iron atoms and the toroidal shape of the iron atom distribution are not captured by two-dimensional CFD simulation incorporating recently proposed skeletal iron chemistry mechanism. These findings suggest that faithful description of atomic iron emerging from the IPC addition should employ mechanism including formation of realistic several nm size nanoparticles. These iron nanoparticles can contribute to Fe-atom consumption via surface condensation, while they hamper the release of Fe atom back to the gas phase via evaporation, decomposing instead by heterogeneous chemical transport oxidation routes. To circumvent the difficulties associated with incorporation of such detailed mechanism into CFD simulation and the lack of knowledge of the processes associated with heterogeneous oxidation of early formed iron nanoparticles, we have performed a feasibility parametric study based on nucleation theory approach, probing the relevant range of temperature-residence time space. The nucleation theory approach predicts formation of nanoparticles in several nm size range, forming via nucleation, coagulation and surface condensation. The nucleation theory-based parametric study qualitatively supports the experimental observations of the low IPC to Fe conversion efficiency and the enhancement of Fe-concentration in the annular region of the burner.