1 Introduction

Nonlinear Schrodinger equations NLSEs were the objective of numerous research works in the literature. It was inspected that these equations are integrable when the real and imaginary parts are taken linearly dependent [1,2,3]. A class of an infinite number of the stable bright and dark soliton, was obtained [3]. Non-local NLSE was introduced in [4]. In [5], the generalized Darboux transformation was performed to solve NLSE. The solutions of NLSE coupled with Maxwell equations were considered in [6]. It was shown that pulses propagation may lead to a varying refractive index Kerr medium [1], which in turn may produce a phase shift in the pulse [7]. Mathematically, when an extra nonlinear correction to the NLSE is considered, indeed, the equation, for nonlinear short-pulse propagation, has to include the pulse envelope derivative. In the study of a system of cold bosons in an optical lattice, the emergence of interesting quantum phenomena such as fragmentation and coherence are demonstrated [8].

There are several well-known methods for finding exact solutions of nonlinear Schrödinger equation, such as exponential rational function method [9, 10], the \(m+G^{\prime }/G\) [11], extended sinh-Gordon equation exponentiation method improved expansion method [12] and generalized logistic equation method [13].

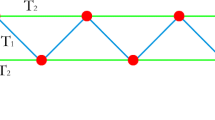
Optical lattices have are highly recognized tool to study many-body quantum physics for solid-state-type systems. A zig-zag optical lattice model of cold bosons was proposed in [14]. The continuum approximation based on a discrete equation governing a system of cold bosonic atoms in zig-zag optical lattices was derived. Exact solutions were found via the exp function method and the hyperbolic function methods [15]. In [16], a theoretical study on modulation instability and quantum discrete breather states in a system of cold bosonic atoms in zig-zag optical lattices was presented. A density-dependent gauge field may induce density-induced geometric frustration. That is the density-dependent hopping results in an effective repulsive or attractive interaction, and that for the latter case the vacuum may be destabilized leading to a strong compressible [17]. The ultracold bosons in zig-zag optical lattices present a rich physics due to the interplay between frustration induced by lattice geometry, two-body interactions. These features were demonstrated in [18]. The zig-zag form of displacements and transverse shear stresses need to be appropriately modeled by relaxation of the assumptions. The zig-zag structure model has many applications and simulations in classical theory was formulated in [19]. The effects of the speed of matter-wave propagation as a function of the lattice geometry was investigated in [20]. Indeed the zig-zag structure with the first- and second-neighbor interactions which may be referred to, as valence atoms lattice, sophisticate essentially the theory. A model of chain backbone of coupled particles, in the secondary structure, was suggested in [21], which was taken subjected to a 2D on site potential with a zig-zag relief. The structure of the crystal is completely determined by the zig-zag angle and stretching or compression of the zig-zag backbone by one lattice spacing [22]. The solitons correspond to local topological defects in crystalline polyethylene PE crystal tension, compression of a trans-zigzag chain on one lattice distance and tension were shown in [23].

In this work, a theoretical study on continuum analog to the discrete zig-zag optical lattice in a system of cold bosonic atoms is proposed. The model equation is dealt with by using the unified and generalized methods. The exact solutions reveal multi-geometric structures. The novelty of this work stems from the observation of zigzag-shaped pulses in zig-zag optical lattices. Furthermore, zig-zag self-phaser modulation with compression are found, obtained by using the unified method [24,25,26,27,28].

The comparison between the method used here and the known methods is done in the following:

  1. 1.

    In this paper, the unified method [24] presented by the author, was used. After this nomenclature , this method unifies all known methods such as, the tanh, modified, and extended versions, the F-expansion, the exponential, the \(G'/G\) expansion method.

  2. 2.

    On the other hand, the extended unified method [25] proposed, also by the author may be sufficient to replace the analysis of inspecting the symmetries of PDEs that arise by using Lie groups.

  3. 3.

    Using the generalized unified method [26], presented by the author, is more powerful tool than using the Hirota method.

2 Basic equations

2.1 The continuum model

Based on the discrete model equation [14], we propose the continuum version by

$$\begin{aligned}i\varphi _{t}(x,t)&=(\varepsilon _{0}-2(T_{1}-2T_{2}))\,\varphi (x,t)-2\delta ^{2}T_{2}\varphi _{x}(x,t)\nonumber \\&\quad -\delta ^{2}(T_{1}-2T_{2})\,\varphi (x,t)_{xx}\nonumber \\&\quad +U_{0}(N-1)\mid \varphi (x,t)\mid ^{2}\varphi (x,t)\,. \end{aligned}$$
(1)

Equation (1) is NLSE , where \(2\delta ^{2}T_{2}\)is the coefficient of the drift force, \(\delta ^{2}(T_{1}-2T_{2})\) is the dispersion coefficient and \(U_{0}(N-1)\) is the refractive index which is assigned to the polarization, if it self-focusing or self-defocusing according to when it positive or negative, respectively. In (1) \(T_{i},i=1,2\) are the two side lengths of the zig-zag optical lattice, \((\varepsilon _{0}-2(T_{1}-2T_{2}))/ 2\delta ^{2}T_{2}\) is the phase speed and \(\delta \ll 1\) is a small parameter. Here, it is assumed that \(T_{i}\ll 1,i=1,2.\)

2.2 Mathematical formulation

The zig-zag soliton in Eq. (1) has an impact on the propagation of pulses in optical fibers. That is, on the characteristic parameters, affecting its intensity, wave length, frequency, phase, polarization or spectral content. Thus, we are led to define the physical parameters that describe the propagation of optical pulses in such a complex medium [14]. To this issue, we write

$$\begin{aligned} \varphi (x,t)=\mid \varphi (x,t)\mid e^{i(\bar{k}x-\bar{\omega }t)}, \end{aligned}$$
(2)

where \(\mid \varphi (x,t)\mid\) stands for the intensity, \(\bar{k}\) and \(\bar{\omega }\) are the wave number and frequency which are defined in

$$\begin{aligned}\bar{k}&=\frac{\int \int _{\mathbb {R\times \mathbb {R^{+}}}}\mid \varphi (x,t)_{x}\mid dx\,dt}{\int \int _{\mathbb {R\times \mathbb {R^{+}}}}\mid \varphi (x,t)\mid dx\,dt},\nonumber \\ \bar{\omega }&=\frac{\int \int _{R\times \mathbb {R^{+}}}\mid \varphi (x,t)_{t}\mid dx\,dt}{\int \int _{\mathbb {R\times \mathbb {R^{+}}}}\mid \varphi (x,t)\mid dx\,dt}. \end{aligned}$$
(3)

The spectrum is defined by

$$\begin{aligned} \varPhi (k_{0},t)=\frac{1}{2\pi }\int _{R}\varphi (x,t)e^{-ik_{0}x}dx. \end{aligned}$$
(4)

Equations (3) and (4) will be detailed in Sect. 3.2.

Now, we find the analytic solutions of Eq. (1). To this end, we introduce a transformation that allow to inspect the waves produced by soliton–periodic wave collision, which is

$$\begin{aligned}\varphi (x,t) & =(\,u(x,t)+iv(x,t)\,)\,e^{i(kx-\omega t)}\nonumber \\ \mid \varphi (x,t)\mid &=\sqrt{u(x,t)^{2}+v(x,t)^{2}},\nonumber \\ Re\varphi (x,t)& =u(x,t)\,\cos (kx-\omega t)\nonumber \\&\quad -v(x,t)\,\sin (kx-\omega t)\,. \end{aligned}$$
(5)

We mention that the types of optical pulses that will be found when using Eq. (5) allow to distinguish whenever the collision is elastic or inelastic.

By substituting Eq. (5) into Eq. (1), we get the equations for the real and imaginary parts:

$$\begin{aligned}&(-1+N)Uu^{3}+u(-\omega +(-2+k^{2}\delta ^{2})T_{1}\nonumber \\&\quad -2(1+k^{2}\delta ^{2})T_{2}+\varepsilon _{0}\nonumber \\&\quad +(-1+N)U_{0}v^{2})+v_{t}+\delta ^{2}2T_{2}(kv-u_{x})\nonumber \\&\quad +2k(T_{1}-2T_{2})v_{x}\nonumber \\&\quad -(T_{1}-2T_{2})u_{xx})=0\,,\nonumber \\&\quad -(\omega +2T_{1})v+v(\varepsilon _{0}+(-1+N)U_{0}(u^{2}+v^{2}))\nonumber \\&\quad -u_{t}-2T_{2}\nonumber \\&\quad (v+\delta ^{2}k(u+kv-2u_{x})+v_{x}-v_{xx}))\nonumber \\&\quad +T_{1}\delta ^{2}k^{2}v-2ku_{x}-v_{xx})=0\,. \end{aligned}$$
(6)

We find the traveling waves solutions, and we introduce the transformations \(u(x,t)=U(z),\;v(x,t)=V(z),\;z=\mu x+\sigma t.\) When inserting these transformations into Eq. (6), we have

$$\begin{aligned}&(-1+N)U_{0}U^{3}+U(-\omega +(-2+k^{2}\delta ^{2})T_{1}\nonumber \\&\quad -2(1+k^{2}\delta ^{2})T_{2}+\varepsilon _{0}\nonumber \\&\quad +(-1+N)U_{0}V^{2})+\sigma V^{\prime }+\delta ^{2}(\mu (2kV^{\prime }\nonumber \\&\quad -\mu U^{\prime \prime })+2T_{2}(kV\nonumber \\&\quad +\mu (-U^{\prime }-2kV^{\prime }+\mu U^{\prime \prime })))=0,\nonumber \\&\quad +V(\varepsilon _{0}(-1+N)U_{0}(U^{2}+V^{2}))-\sigma U^{\prime }\nonumber \\&\quad +\delta ^{2}ST_{1}(k^{2}V-\mu 2kU^{\prime }+\mu V^{\prime \prime }))\nonumber \\&\quad -(\omega +2T_{2})V-2T_{2}(V+\delta ^{2}(kU+k^{2}V\nonumber \\&\quad +\mu (-2kU^{\prime }+V^{\prime }-\mu V^{\prime \prime })))=0. \end{aligned}$$
(7)

Here, the exact solutions of Eq. (7) (or(6)) are found by using the unified method [24,25,26,27,28]. This method asserts that solutions of a NLPDE are expressed in a polynomial or a rational functions in auxiliary functions that satisfy appropriate auxiliary equations.

3 Polynomial solutions of Eq. (7)

The solutions are represented in polynomial forms with an auxiliary function that satisfies an auxiliary equation, The solutions are represented in polynomial forms with an auxiliary function that satisfies an auxiliary equation:

$$\begin{aligned}U(z)& =\sum _{i=0}^{m_{1}}\,h_{i}\,g^{i}(z),\,\;V(z)=\sum _{i=0}^{m_{2}}\,p_{i}\,g^{i}(z)\,,\nonumber \\ g^{\prime }(z){}^{p} & =\sum _{i=0}^{pr}\,c_{i}\,g^{i}(z),\,p=1,2. \end{aligned}$$
(8)

We mention that, in Eq. (8), g(z) is the auxiliary function and the second equation is the auxiliary equation. The values of \(m_{1},m_{2}\) and r are determined from the balance and the consistency conditions, respectively. By balancing the highest order derivative with highest nonlinearity terms in Eq. (7), when \(p=1,\) the balance condition reads \(m_{i}=r-1,\) \(i=1,2\). The values of r are determined from the consistency condition. It is based on: (i) The number of equations that arise by substituting from (15) into (11)–(14), by setting the coefficients of \(g(z)^{i},\;i=0,1,...\) equal to zero, say \(r_{0}\). (ii) The numbers of the arbitrary parameters, \(\{,h_{i,},\,p_{i},\,c_{j}\}\) in Eq. (15), say d. This condition reads \(r_{0}-d\le m\), where m is highest order derivative in Eq. (11) (or (12) (here, \(m=2\)). We find that \(1\le r\le 3.\) The case when \(p=2\) can be analyzed by the same way, where \(\,m_{i}\) and r are found by using the balance and the consistency conditions.

It is worthy to mention that, when \(p=1\) the solutions in Eq. (8) are elementary (or implicit ) functions, while they are elliptic (periodic) functions when \(p=2.\)

3.1 The first case when \(p=2\) and \(r=2\)

In this case, Eq. (8) becomes

$$\begin{aligned}U(z) &=h_{1}g(z)+h_{0},\quad V(z)=p_{1}g(z)+p_{0},\nonumber \\ g^{\prime }(z)&=\sqrt{c_{4}g(z)^{4}+c_{2}g(z)^{2}+c_{0}}. \end{aligned}$$
(9)

By substituting Eq. (9) into Eq. (7), and for the real and imaginary parts to be linearly dependent, we take \(p_{0}=h_{0}p_{1}/h_{1}\). By setting the coefficients of \(g(z)^{j},j=0,1,...,\)equal to zero, we get

$$\begin{aligned}\sigma & =-\frac{1}{p_{1}}2\delta ^{2}\mu (kp_{1}T_{1}-(h_{1}+2kp_{1})T_{2}),\quad h_{0}=0,\nonumber \\ p_{1}&=\frac{\sqrt{-h_{1}^{2}(-1+N)U_{0}+2c_{4}\delta ^{2}\mu ^{2}T_{1}-4c_{4}\delta ^{2}\mu ^{2}T_{2}}}{\sqrt{(-1+N)U_{0}}},\nonumber \\ \omega & =\varepsilon _{0}+(-2+k^{2}\delta ^{2}-c_{2}\delta ^{2}\mu ^{2})T_{1}+\nonumber \\ \quad & 2T_{2}(-1-k^{2}\delta ^{2}+c_{2}\delta ^{2}\mu ^{2})\nonumber \\ &\quad +\frac{k\delta ^{2}\sqrt{-h_{1}^{2}(-1+N)U_{0}+2c_{4}\delta ^{2}\mu ^{2}T_{1}-4c_{4}\delta ^{2}\mu ^{2}T_{2}}}{h_{1}\sqrt{(-1+N)U_{0}}},\nonumber \\ \end{aligned}$$
(10)

where \(c_{i},\,i=0,2,4\) are arbitrary. Here we take

$$\begin{aligned} c_{4}=-m^{2},\;c_{2}=2m^{2}-1,\;c_{0}=-m^{2},\;g(z)=cn(z,m). \end{aligned}$$
(11)

The solutions are

$$\begin{aligned} u(x,t) &= {} h_{1}cn(z,m),\nonumber \\ v(x,t) & = {} \frac{\sqrt{-h_{1}^{2}(-1+N)U_{0}+2c_{4}\delta ^{2}\mu ^{2}T_{1}-4c_{4}\delta ^{2}\mu ^{2}T_{2}}}{h_{1}\sqrt{(-1+N)U_{0}}}cn(z,m)\,,\nonumber \\ z& = {} \mu x+\sigma t. \end{aligned}$$
(12)

The numerical results of the solutions in Eq. (12) are displayed in Fig. 1(i)–(iv) for \(Re\varphi (x,t)\) and \(\mid \varphi (x,t)\mid .\) (cf. Eq. (5)).

Fig. 1
figure 1

In i and iv the 3D plot to \(Re\varphi (x,t)\) and \(\mid \varphi (x,t)\mid\). In iii the contour plot of \(Re\varphi (x,t)\) is displayed, while in iii it is displayed against x for different values of t. When \(N=0.9,h_{1}=0.2,U_{0}=-0.1,T_{1}=0.08,T_{2}=0.1, m=0.999,k=5,\mu =0.9,\delta =0.1,\varepsilon _{0}=3\)

Full size image

Figure 1(i) and (iii) shows zig-zag pulses with self-phase modulation. Figure 1(ii) shows zig-zag optical lattice,in the dark regions.

We remark that in Fig. 1(iii) and (v) the optical pulses are sharp (shock-like) pulse, thus the collision is inelastic.

3.2 The second case when \(p=2\) and \(r=2\)

In this case, we use the solutions in Eq. (9), while the auxiliary equation

$$\begin{aligned} g^{\prime }(z)=g(z)\sqrt{a^{2}-b^{2}g(z)^{2}}. \end{aligned}$$
(13)

By substituting from Eq. (9) and Eq. (12) into Eq. (7), we have

$$\begin{aligned}\sigma &=-\frac{1}{p_{1}}(2\delta ^{2}\mu (kp_{1}T_{1}-(h_{1}+2kp_{1})T_{2})),\quad h_{0}=0,\nonumber \\ p_{1} & =\frac{\sqrt{-h_{1}^{2}(-1+N)U_{0}-2b^{2}\delta ^{2}\mu ^{2}T_{1}+4b^{2}\delta ^{2}\mu ^{2}T_{2}}}{\sqrt{(-1+N)U_{0}}},\nonumber \\ \omega & =\varepsilon _{0}+(-2+k^{2}\delta ^{2}-a^{2}\delta ^{2}\mu ^{2})T_{1}+\nonumber \\&\quad 2T_{2}(-1-k^{2}\delta ^{2}+c_{2}\delta ^{2}\mu ^{2}\nonumber \\&\quad +\frac{k\delta ^{2}\sqrt{-h_{1}^{2}(-1+N)U_{0}-2b^{2}\delta ^{2}\mu ^{2}T_{1}+4b^{2}\delta ^{2}\mu ^{2}T_{2}}}{h_{1}\sqrt{(-1+N)U_{0}}}. \end{aligned}$$
(14)

Finally, we get

$$\begin{aligned}g(z)&=\frac{a}{b}\,sech(a\,(z+B_{0}),\nonumber \\ u(x,t) & =\frac{a^{2}\,h_{1}}{b}\,sech(a\,(z+B_{0})\,,\nonumber \\ v(x,t) & =\frac{\sqrt{-h_{1}^{2}(-1+N)U_{0}-2b^{2}\delta ^{2}\mu ^{2}T_{1}+4b^{2}\delta ^{2}\mu ^{2}T_{2}}}{bh_{1}\sqrt{(-1+N)U_{0}}}\nonumber \\&\quad (a\,sech(a\,(z+B_{0})),\,N\ne 1. \end{aligned}$$
(15)

3.3 When \(p=1\) and \(r=2\)

In this case, we take the auxiliary equation

$$\begin{aligned} g^{\prime }(z)=c_{0}+c_{1}g(z)+c_{2}g(z)^{2}. \end{aligned}$$
(16)

By using Eqs. (9) and (16) into Eq. (7), we have

$$\begin{aligned}\sigma &=\frac{\mu \delta ^{2}}{p_{1}}((-2kp_{1}+3c_{1}h_{1}\mu -6c_{2}h_{0}\mu )T_{1}+2(h_{1}+2kp_{1}\nonumber \\&\quad -3c_{1}h_{1}\mu +6c_{2}h_{0}\mu )T_{2}),\quad c_{0}=\frac{h_{0}}{h_{1}^{2}}(c_{1}h_{1}-c_{2}h_{0}),\nonumber \\ \omega &=\varepsilon _{0}+(-2+k^{2}\delta ^{2}+2c_{1}^{2}\mu ^{2}\delta ^{2}-\frac{8c_{1}c_{2}h_{0}\mu ^{2}\delta ^{2}}{h_{1}}+\frac{8c_{2}^{2}h_{0}^{2}\mu ^{2}\delta ^{2}}{h_{1}^{2}T_{1}}\nonumber \\&\quad -\frac{1}{h_{1}^{2}}2(8c_{2}^{2}h_{0}^{2}\mu ^{2}\delta ^{2}-h_{1}\delta ^{2}(kp_{1}+8c1c2h_{0}\mu ^{2})\nonumber \\&\quad +h_{1}^{2}(1+k^{2}\delta ^{2}+2c_{1}^{2}\mu ^{2}\delta ^{2}))T_{2}. \end{aligned}$$
(17)

Finally, we have

$$\begin{aligned}g(z)&=\frac{c_{1}e^{c_{1}z}h_{1}-Aoe^{\frac{2c_{2}h_{0}z}{h_{1}}}h_{0}-c_{2}e^{c_{1}z}h_{0}}{(A_{0}e^{\frac{2c_{2}h_{0}z}{h_{1}}}-c_{2}e^{c_{1}z})h_{1}}\nonumber \\ u(x,t)&=\frac{e^{c_{1}z}(-c_{1}h_{1}+2c_{2}h_{0})}{-Aoe^{\frac{2c_{2}h_{0}z}{h_{1}}}+c_{2}e^{c_{1}z}},\quad v(x,t)=\frac{p_{1}}{h_{1}}u(x,t),\nonumber \\ z&=\mu (x+\frac{t\delta ^{2}}{p_{1}}((-2kp_{1}+3c_{1}h_{1}\mu -6c_{2}h_{0}\mu )T_{1}+2(h_{1}\nonumber \\&\quad +2kp_{1}-3c_{1}h_{1}\mu +6c_{2}h_{0}\mu )T_{2})),\nonumber \\ p_{1} & =\frac{\sqrt{-h_{1}^{2}(-1+N)U_{0}+2c_{2}^{2}\delta ^{2}\mu ^{2}T_{1}-4c_{2}^{2}\delta ^{2}\mu ^{2}T_{2}}}{\sqrt{(-1+N)U_{0}}}. \end{aligned}$$
(18)

The results in Eq. (18) are used to display the 3D plot and contour plots of \(Re\varphi (x,t)\) in Fig. 2(i) and (ii), respectively

Fig. 2
figure 2

i and ii When \(N=0.7,h_{1}=0.3,U_{0}=1.1,T_{1}=0.08,T_{2}=0.1,c2=0.07,k=5\), \(\mu =0.9,\delta =0.1,\varepsilon _{0}=3,c_{1}=0.3,A_{0}=0.5,p_{1}=2.5,h_{0}=1.3\)

Full size image

Figure 2i shows optical pulses with gaps and mixed smooth and sharp tops (bottoms), while Fig. 2(ii) shows local zigzag-shaped optical lattices.

3.4 Characteristics of the pulses propagation

Here, we investigate the content of the spectrum, the wave length, the frequency and intensity.

The spectrum content is shown in Fig. 3(i) and (ii), while the wave length, frequency, and the intensity of the pulses in optical lattices are shown in Fig. 3(iii)–(v).

Fig. 3
figure 3

i–iii In i and ii the 3D and contour plots are done, respectively, when \(N=1.7,h=0.03,T=0.3\) \(,T_{2}=0.1,c_{2}=-1.7,k=5,\mu =0.9,\delta =0.1,\varepsilon _{0}=3,c=0.03,A=0.5,p_{1}=2.5,h_{0}=1.3,U_{0}=1.5\)

Full size image

Figure 3(i) shows pulses with cusps, while ii shows random pulses in an optical lattice.

The optical lattice is self-focusing polarized.

4 Rational solutions of Eq. (7)

4.1 Coupled auxiliary equations

$$\begin{aligned} \begin{array}{c} U(z)=\frac{h_{0}+h_{1}g_{1}(z)+h_{2}g_{2}(z)}{s_{0}+s_{1}g_{1}(z)+s_{2}g_{2}(z)},\quad V(z)=\frac{p_{0}+p_{1}g_{1}(z)+p_{2}g_{2}(z)}{s_{0}+s_{1}g_{1}(z)+s_{2}g_{2}(z)},\\ \\ g_{1}^{\prime }(z)=c_{1}g(z)+c_{2}g_{2}(z),\quad g_{2}^{\prime }(z)=c_{1}g(z)+c_{2}g_{2}(z). \end{array} \end{aligned}$$
(19)

For linearly dependent solutions, we take \(p_{2}=h_{2}p_{1}/h_{1},\;p_{0}=h_{0}p_{1}/h_{1}\). When inserting Eq. (19) into Eq. (7), we get

$$\begin{aligned} \begin{array}{c} \sigma =-\frac{2\delta ^{2}}{p_{1}}\mu (kp_{1}T_{1}-(h_{1}+2kp_{1})T_{2}),\;d_{2}=\frac{-c_{2}s_{1}^{2}+c_{1}s_{1}s_{2}+d_{1}s_{2}^{2}}{s_{1}s_{2}},\\ \\ \omega =\left(k^{2}\delta ^{2}+\frac{1}{2}\left(-4+c_{1}^{2}\mu ^{2}\delta ^{2}+\frac{2c_{1}d_{1}s_{2}\mu ^{2}\delta ^{2}}{s_{1}}+\frac{d_{1}^{2}s_{2}^{2}\mu ^{2}\delta ^{2}}{s_{1}^{2}}\right)\right)T_{1}\\ \qquad+\left(-2-2k^{2}\delta ^{2}+\frac{2kp_{1}\delta ^{2}}{h_{1}}-c_{1}^{2}\mu ^{2}\delta ^{2}-\frac{2c_{1}d_{1}s_{2}\mu ^{2}\delta ^{2}}{s_{1}}-\frac{d_{1}^{2}s_{2}^{2}\mu ^{2}\delta ^{2}}{s_{1}^{2}}\right)T_{2}+\varepsilon _{0},\\ \\ p_{1}=\frac{\sqrt{(c_{1}s_{1}+d_{1}s_{2})^{2}\mu ^{2}\delta ^{2}T_{1}-2(h_{1}^{2}(-1+N)U_{0}+(c_{1}s_{1}+d_{1}s_{2})^{2}\mu ^{2}\delta ^{2}T_{2})}}{\sqrt{2}\sqrt{(-1+N)U_{0}}}.\\ \\ \end{array} \end{aligned}$$
(20)

Finally, we have

$$\begin{aligned} \begin{array}{c} g_{1}(z)=\frac{e^{(c_{1}-\frac{c_{2}s_{1}}{s_{2}})z}(d_{1}s_{2}^{2}A_{0}+c_{2}s_{1}(-s_{2}B_{0}+e^{\frac{c_{2}s_{1}z}{s_{2}}+\frac{d_{1}s_{2}z}{s_{1}}}+(s_{1}A_{0}+s_{2}B_{0})))}{c_{2}s_{1}^{2}+d_{1}s_{2}^{2}},\\ \\ g_{2}(z)=\frac{e^{(c_{1}-\frac{c_{2}s_{1}}{s_{2}})z}(c_{2}s_{1}^{2}B_{0}+d_{1}s_{2}((-1+e^{\frac{c_{2}s_{1}z}{s_{2}}+\frac{d_{1}s_{2}z}{s_{1}}}(s_{1}A_{0}+s_{2}B_{0})))}{c_{2}s_{1}^{2}+d_{1}s_{2}^{2}},\\ \\ u(x,t)=\frac{h_{1}(A_{0}e^{(c_{1}+\frac{c_{2}s_{1}}{s_{2}})z}s_{1}+Boe^{(c_{1}+\frac{c_{2}s_{1}}{s_{2}})z}s_{2}-s_{0})}{s_{1}(A_{0}e^{(c_{1}+\frac{c_{2}s_{1}}{s_{2}})z}s_{1}+Boe^{(c_{1}+\frac{c_{2}s_{1}}{s_{2}})z}s_{2}+s_{0})},\quad v(x,t)=\frac{p_{1}}{h_{1}}u(x,t),\\ \\ z=\mu (x-2kt\delta ^{2}T_{1}+\frac{2(h_{1}+2kp_{1})t\delta ^{2}T_{2}}{p_{1}}). \end{array} \end{aligned}$$
(21)

The results in Eq. (21) are used to display \(Re\varphi (x,t)\) in Fig. 4(i) and (ii) for the 3D and contour plots, respectively. In (iii) it is displayed against x for different values of t.

Fig. 4
figure 4

i–iii In i and ii the 3D and contour plots for Req(x, t) are done, respectively. In iii it is displayed against x for different values of t. When \(N=0.7,h_{1}=0.3,U_{0}=1.1\), \(T_{1}=0.2,T_{2}=0.08,s_{2}=0.7,s_{1}=1.5\), \(s_{0}=-2.3,d=0.5,s_{2}=-1.1,k=5,\varepsilon _{0}=7.5,\mu =0.9,\delta =0.1,c_{1}=0.3\), \(A_{0}=0.5,B_{0}=1.5,h_{0}=1.3\)

Full size image

Figure 4(i) and (iii) shows zig-zag optical lattice with self-phase modulations and compression, while (ii) shows local zig-zag optical lattice.

4.2 Case when \(r=2\) and \(p=1\)

We write

$$\begin{aligned}U(z) &=\frac{h_{0}+h_{1}g(z)}{s_{0}+s_{1}g(z)},\quad V(z)=\frac{p_{0}+p_{1}g(z}{s_{0}+s_{1}g(z}),\nonumber \\ g^{\prime }(z) & =c_{0}+c_{1}g(z)+c_{2}g(z){}^{2},\quad p_{0}=\frac{h_{0}p_{1}}{h}. \end{aligned}$$
(22)

Inserting Eq. (22) into Eq. (7) results in:

$$\begin{aligned}\sigma & =-\frac{2\delta ^{2}}{p_{1}}\mu (kp_{1}T_{1}-(h_{1}+2kp_{1})T_{2}),\nonumber \\ c_{0}& =\frac{c_{1}(h_{0}s_{1}+_{1}s_{0})-2c_{2}h_{0}s_{0}}{2h_{1}s_{1}},\nonumber \\ \omega & =\varepsilon _{0}+\frac{1}{2h_{1}s_{1}}(2h_{1}s_{1}(-2+k^{2}\delta ^{2})\nonumber \\&\quad +(c_{1}h_{1}-2c_{2}h_{0})(c_{1}s_{1}-2c_{2}s_{0})\mu ^{2}\delta ^{2})\,,\nonumber \\&\quad T_{1}-2T_{2})-2(2s_{1}(h_{1}+k(h_{1}k-p_{1})\delta ^{2})\,,\nonumber \\&\quad p_{1}=\frac{\sqrt{-2h_{1}^{2}(-1+N)U_{0}+(c_{1}s_{1}-2c_{2}s_{0})^{2}\mu ^{2}\delta ^{2}(T_{1}-2T_{2})}}{\sqrt{2(-1+N)U_{0}}}. \end{aligned}$$
(23)

The solutions of Eq. (7) are:

$$\begin{aligned} u(x,t) & =\frac{\psi _{1}}{\psi _{2}},\nonumber \\ \quad \psi _{1}& =\sqrt{h_{1}}(c_{1}h_{1}-2c_{2}h_{0})\sqrt{s_{1}}\nonumber \\&\quad +h_{1}\sqrt{c_{1}h_{1}-2c_{2}h_{0}})\sqrt{c_{1}s_{1}-2c_{2}s_{0}})\nonumber \\&\quad \tan h \, \left (\frac{\sqrt{c_{1}h_{1}-2c_{2}h_{0}}\sqrt{c_{1}s_{1}-2c_{2}s_{0}}(z+A_{0}))}{2\sqrt{h_{1}s_{1}}}\right),\nonumber \\ \quad \psi _{2} & =\sqrt{h_{1}s_{1}}(c_{1}s_{1}-2c_{2}s_{0})\nonumber \\&\quad +\sqrt{c_{1}h_{1}-2c_{2}h_{0}}s_{1}\sqrt{c_{1}s_{1}-2c_{2}s_{0}})\nonumber \\&\quad \tan h \left(\frac{\sqrt{c_{1}h_{1}-2c_{2}h_{0}}\sqrt{c_{1}s_{1}-2c_{2}s_{0}}(z+A_{0}))}{2\sqrt{h_{1}s_{1}}}\right),\nonumber \\ v(x,t) & =\frac{p_{1}}{h_{1}}v(x,t). \end{aligned}$$
(24)

The results in Eq. (24) are used to display \(Re\varphi (x,t)\) in Fig. 5(i) and (ii).

Fig. 5
figure 5

i and ii The 3D and contour plots of \(Re\varphi (x,t)\) are displayed against x and t in (i) and (ii), respectively. When \(N=3,h_{1}=0.3,U_{0}=1.1,T_{1}=0.2,T_{2}=0.08,c_{2}=0.7,s_{1}=1.5,s_{0}=-2.3\), \(k=5,\varepsilon _{0}=7.5,\mu =0.9,\delta =0.1,c_{1}=0.3,A_{0}=0.5,B_{0}=1.5,p_{1}=2.5,h_{0}=-1.3\)

Full size image

Figure 5i and ii shows the same geometric structures as in Fig. 2(i) and (ii).

5 Case when \(r=2\) and \(p=2\)

In this case we use Eq. (22), but the auxiliary equation is

$$\begin{aligned} g^{\prime }(z)=\sqrt{c_{0}+c_{1}g(z)+c_{2}g(z){}^{2}}. \end{aligned}$$
(25)

By the same way we have

$$\begin{aligned}&\sigma =-\frac{2\delta ^{2}}{p_{1}}\mu (kp_{1}T_{1}-(h_{1}+2kp_{1})T_{2}),\nonumber \\&\quad s_{0}=\frac{c_{1}s_{1}}{c_{2}}-\frac{h_{0}s_{1}}{h_{1}},\;c_{0}=\frac{c_{1}^{2}}{4c_{2}},\nonumber \\&\quad \omega =\varepsilon _{0}+\frac{1}{h_{1}}(-1+N)(h_{1}^{2}+p_{1}^{2})Uo)/s_{1}^{2}\nonumber \\&\quad +(-2+k^{2}\delta ^{2})T_{1}\nonumber \\&\quad -(2(h_{1}+h_{1}k^{2}\delta ^{2}-kp1\delta ^{2})T_{2},\nonumber \\&\quad p_{1}=\frac{\sqrt{2h_{1}^{2}(-1+N)U_{0}-c_{2}s_{1}^{2}\mu ^{2}\delta ^{2}T_{1}+2c_{2}s_{1}^{2}\mu ^{2}\delta ^{2}T_{2}}}{\sqrt{2U_{0}(-1+N)}}. \end{aligned}$$
(26)

The solutions are

$$\begin{aligned} u(x,t)= & {} -\frac{h_{1}(\,(c_{1}h_{1}-A_{0}e^{\sqrt{c_{2}}\,z})h_{1}-2c_{2}h_{0})}{(\,(c_{1}h_{1}+A_{0}e^{\sqrt{c_{2}}\,z})h_{1}-2c_{2}h_{0})s_{1}},\nonumber \\ v(x,t)= & {} \frac{p_{1}}{h_{1}}u(x,t). \end{aligned}$$
(27)

6 Conclusions

A continuum model analog to the zig-zag optical lattice is established. Exact solutions of the model equations are found by using the unified method. Graphical representations of the results obtained are carried. They exhibit local zig-zag optical lattice. Further pulses with different geometric structures are observed. Mixed sharp and smooth pulses with local gaps occur. Also, zig-zag optical lattice with self-phase modulations is observed. We think that these results consolidate the pretension of zigzag-shaped optical lattice. Further, the collision of pulses is shown to be inelastic, which may be argued for the formation of sharp optical lattice with self-phase modulation and compression. We think that the results found, here, for the propagation of zigzag-shaped pulses in optical lattice are completely novel. It is inspected that the collision is locally elastic (or inelastic), which may be due to the occurrence of mixed smooth and sharp optical pulses. Further, it is found that the zig-zag optical lattice is self-focusing.