1 Introduction

Wavefront shaping techniques opened a whole new example in optics and engineering by controlling optical waves propagating through scattering media [1,2,3,4,5]. These include focusing beyond the diffraction limit [6, 7], image through turbid media [8, 9], and enhanced transmission through coupling to the open eigenmodes [2]. In these studies, the transmission matrix (TM), which encodes completely multiple scattering in the scattering material, is a mighty tool. The TM is the input–output relation for a basis of orthometric modes, and in essence, enables the restoration or prediction [10, 11]. Once it is obtained, the scattering medium is no longer a stochastic object, and the output field can be determinately related with the input field. The TM can be directly obtained by monitoring the output field for each input field [10], or it can be indirectly achieved by means of feedback algorithms [12].

For many years, it has been known that elastic multiple scattering would cause Anderson localization of optical waves, and that, even in a diffusive system, it introduces crucial correlations in the TM of a complex medium [13]. Thus, the TM is typically ill-conditioned [14]. The input field can be attained by TM inversion, and the ill-condition of the TM seriously affects the accuracy of phase distributions. Numerically, due to the fact that the solution to the inverse matrix does not rely continuously on the matrix elements, a tiny error in calculating the inverse matrix of the TM produces an extremely large error to the phase distribution. To solve this problem, Mickael and coworkers have applied singular value decomposition (SVD) to the TM before inversion [14]. The purport of SVD is to delete some of the singular values of the TM which are close to zero. This is a valid way to decrease the extent of the ill-condition of the TM, attaining receivable focusing results.

In this work, we study the ill-condition of the TM in detail. A condition number analysis is utilized to evaluate the extent of the ill-condition of the TM quantitatively. Based on this analysis, we propose our opinion that tiny singular values of the TM would introduce a large error in TM inversion. An idea of optimizing the singular values of the transmission matrix is proposed, which improves the accuracy and stability of the phase distribution. Then, we perform experiment to verify this idea. The conclusion summarizes the whole paper.

The ill-condition of the TM.

Waves propagating through complex random media experience multiple scattering. Unless the intensity of the optical wave is intense enough to bring about nonlinear optical effects, wave propagation is a linear course, which is described by a TM. The TM connects the input and output channels, which can be expressed by [15]

$$ E_{m}^{{{\text{out}}}} = \sum\limits_{n = 1}^{N} {t_{mn} E_{n}^{{{\text{in}}}} } , $$
(1)

where \(E_{m}^{{{\text{out}}}}\)(m = 1, 2, 3, …, M) is the electric field at the mth output channel; \(E_{n}^{{{\text{in}}}}\)(n = 1, 2, 3, …, N) is the electric field at the nth input channel; and \(t_{mn}\) is the element of the TM in the mth row and nth column. Equation 1 can be written as matrix form:

$$ \left( {\begin{array}{*{20}c} {E_{1}^{{{\text{out}}}} } \\ {E_{2}^{{{\text{out}}}} } \\ {E_{3}^{{{\text{out}}}} } \\ \vdots \\ {E_{M}^{{{\text{out}}}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {t_{11} } & {t_{12} } & {t_{13} } & \cdots & {t_{1N} } \\ {t_{21} } & {t_{22} } & {t_{23} } & \cdots & {t_{2N} } \\ {t_{31} } & {t_{32} } & {t_{33} } & \cdots & {t_{3N} } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {t_{M1} } & {t_{M2} } & {t_{M3} } & \cdots & {t_{MN} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {E_{1}^{{{\text{in}}}} } \\ {E_{2}^{{{\text{in}}}} } \\ {E_{3}^{{{\text{in}}}} } \\ \vdots \\ {E_{N}^{{{\text{in}}}} } \\ \end{array} } \right). $$
(2)

Here, the first matrix on the right is the TM, which can be obtained utilizing the approach described in Ref. [10]. Since we aim at achieving a focal point through the medium, the output field \(E_{m}^{{{\text{out}}}}\) is set to the single-channel optimizing mode, where the output channel of the focal point is one and the others are zero:

$$ \left( {\begin{array}{*{20}c} {E_{1}^{{{\text{out}}}} } & {E_{2}^{{{\text{out}}}} } & {E_{3}^{{{\text{out}}}} } & \cdots & {E_{M}^{{{\text{out}}}} } \\ \end{array} } \right)^{T} = (\begin{array}{*{20}c} 0 & \cdots & 0 & 1 & 0 & \cdots & 0 \\ \end{array} )^{T} , $$
(3)

where the superscript T denotes the matrix transpose. According to the TM inversion mentioned in Ref. [16], \(E_{n}^{{{\text{in}}}}\)(n = 1, 2, 3, …, N) can be theoretically attained as long as \(M \ge N\). However, the TM is representatively ill-conditioned, which severely influences the accuracy of \(E_{n}^{{{\text{in}}}}\). Most references emphasize that elastic multiple scattering would cause Anderson localization of optical waves, which induces important correlations in the TM of a scattering medium. The ill-condition of the TM is due to the correlations of the row vectors, which causes several approximate solutions [17, 18]. The correlation of the row vectors indicates degeneracy of the transmission matrix. Since the degeneracy of the transmission matrix, multiple solutions would be obtained by transmission matrix inversion.

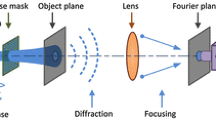
The basic structure of focusing coherent light through a scattering medium is shown in Fig. 1. A plane wave is incident on a spatial light modulator (SLM). The modulated light propagates through a disordered medium, and the scattered light is recorded by a detector. Using a correct phase distribution of the SLM, a focal point can be formed behind the medium. Suppose that

$$ {\varvec{E}}_{{{\mathbf{out}}}} = \left( {\begin{array}{*{20}c} {E_{1}^{{{\text{out}}}} } \\ {E_{2}^{{{\text{out}}}} } \\ {E_{3}^{{{\text{out}}}} } \\ \vdots \\ {E_{M}^{{{\text{out}}}} } \\ \end{array} } \right),\quad {\varvec{T}} = \left( {\begin{array}{*{20}c} {t_{11} } & {t_{12} } & {t_{13} } & \cdots & {t_{1N} } \\ {t_{21} } & {t_{22} } & {t_{23} } & \cdots & {t_{2N} } \\ {t_{31} } & {t_{32} } & {t_{33} } & \cdots & {t_{3N} } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {t_{M1} } & {t_{M2} } & {t_{M3} } & \cdots & {t_{MN} } \\ \end{array} } \right),\quad {\varvec{E}}_{{{\mathbf{in}}}} = \left( {\begin{array}{*{20}c} {E_{1}^{{{\text{in}}}} } \\ {E_{2}^{{{\text{in}}}} } \\ {E_{3}^{{{\text{in}}}} } \\ \vdots \\ {E_{N}^{{{\text{in}}}} } \\ \end{array} } \right). $$
Fig. 1
figure 1

Basic structure of focusing light through scattering media

Full size image

Then, Eq. (2) can be written as

$${\varvec{E}}_{{{\text{out}}}} = {\varvec{TE}}_{{{\text{in}}}} .$$
(4)

For simplicity, we assume that the number of output channels M equals the number of input channels N. Therefore, by solving the matrix equation, the solution of \({\mathbf{E}}_{{{\mathbf{in}}}}\) can be attained:

$$ {\varvec{E}}_{{{\text{in}}}} = {\varvec{T}}^{{ - 1}} {\varvec{E}}_{{{\text{out}}}} , $$
(5)

where T−1 is the inverse matrix of T. Assume a system with 256 input channels and 256 output channels (i.e. M = N = 256). The scattering medium is represented by a random matrix with uniform distribution. Thus, the matrix T can be measured using the approach described in Ref.[10]. If the output field is set to

$$ E_{m}^{{{\text{out}}}} = \left\{ {\begin{array}{*{20}c} {1,} & {m = 120} \\ {0,} & {{\text{others}}} \\ \end{array} } \right. $$
(6)

using Eq. (5), the input field Ein can be calculated. Using the full-field of Ein, we calculate the output field using the method of ray tracing. Here, ‘full-field’ means the amplitude and phase of the electric field. If we do not consider noise in this simulation (i.e. the TM is definitely precise), the intensity distribution of the output field is shown in Fig. 2a. In this case, the full-field inversion gives exactly the same solution. If we add 0–1.5% of random noise to T and Eout in Eq. (5) to simulate measurement errors, the intensity distribution of the output field is shown in Fig. 2b. In this case, we cannot see any focal point in the image plane, since this inversion is very unstable in the presence of noise. This phenomenon is called as the ill-condition of a matrix, which indicates that the solution of the linear system of equations is inaccurate. Figure 3 shows the amplitude and phase distribution of the incident field. Figure 3a and c are amplitude and phase distribution of no random noises (i.e. well-posed case), respectively, while Fig. 3b and d are amplitude and phase distribution with 0–1.5% of random noise (i.e. ill-posed case), respectively. The correlation coefficient between amplitude vector values in Fig. 3a and b is 0.043, while the correlation coefficient between phase vector values in Fig. 3c and d is 0.068. Therefore, there exist large differences between the profiles of well-posed and ill-posed inversion.

Fig. 2
figure 2

The intensity distribution of the output field. a Well-posed simulation; b ill-posed simulation

Full size image
Fig. 3
figure 3

Amplitude and phase distribution of Ein. a Amplitude distribution of well-posed condition; b amplitude distribution of ill-posed condition; c phase distribution of well-posed condition; d phase distribution of ill-posed condition

Full size image

Singular value decomposition and eigenchannel optimization

We further study the ill-condition of the TM by analyzing the singular values of the matrix. We perform singular value decomposition (SVD) of the TM

$$ T = \user2{UV,} $$
(7)

where \(\tau\) is a rectangular diagonal matrix with non-negative real numbers on the diagonal called singular values. V and U are unitary matrices mapping the input channels and eigenchannels to eigenchannels and output channels, respectively. The square of a singular value is called an eigenvalue. The physical meaning of the eigenvalue of the TM is the intensity transmittance coefficient of the corresponding eigenchannel. The eigenchannels with large eigenvalues are called open eigenchannels, while the eigenchannels with small eigenvalues are called closed eigenchannels. For the random scattering medium studied in Sect. 2, we plot eigenvalues after arranging them in descending order, which is shown in Fig. 4.

Fig. 4
figure 4

Eigenvalue distribution of the TM

Full size image

From Fig. 4, it can be seen that a large difference exists among the eigenvalues of the TM, and the smallest eigenvalue is close to zero. In fact, this is a general law for most disordered media. The largest eigenvalue is ~ 106 times larger than the smallest eigenvalue. Suppose that

$$ {{\varvec{\uptau}}} = \left( {\begin{array}{*{20}c} {\lambda_{1} } & 0 & \cdots & 0 \\ 0 & {\lambda_{2} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {\lambda_{N} } \\ \end{array} } \right), $$
(8)

where λi (i = 1,2,…,N) are the singular values of the TM. The diagonal elements of matrix τ are sorted in descending order, i.e. \(\lambda_{1} \ge \lambda_{2} \ge \cdots \ge \lambda_{N}\). The inverse matrix of T can be expressed as

$$ {\mathbf{T}}^{ - 1} = {\mathbf{V}}^{H} \left( {\begin{array}{*{20}c} {\frac{1}{{\lambda_{1} }}} & 0 & \cdots & 0 \\ 0 & {\frac{1}{{\lambda_{2} }}} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {\frac{1}{{\lambda_{N} }}} \\ \end{array} } \right){\mathbf{U}}^{H} , $$
(9)

where the superscript − 1 stands for the inverse matrix, and the superscript H denotes the conjugate transpose. As mentioned above, the smallest eigenvalue (or singular value λN) is close to zero, which means that \(\frac{1}{{\lambda_{N} }}\) becomes extremely large. In the process of calculating T−1 computationally, some system errors—such as discretization errors—would be magnified by \(\frac{1}{{\lambda_{N} }}\). Therefore, it is necessary to replace some of \(\frac{1}{{\lambda_{i} }}\;(i = 1,2,...,N)\) by \(\frac{1}{{\overline{\lambda }}}\) to reduce errors, where \(\overline{\lambda }\) is the average of λi and can be expressed as

$$ \overline{\lambda } = \frac{1}{N}\sum\limits_{i = 1}^{N} {\lambda_{i} } . $$
(10)

The condition number (CN) is an indispensable parameter that reflects the condition of a matrix. The CN of matrix T is defined as the ratio between the largest singular value and the smallest singular value:

$$ {\text{cond}}({\mathbf{T}}) = \left| {\frac{{\lambda_{1} }}{{\lambda_{N} }}} \right|, $$
(11)

where ‘| |’ stands for the absolute value. The larger the CN is, the more ill-conditioned the matrix will be. The CN of T−1 is equal to the CN of T. From Eq. 11, it can be seen that when we replace \(\lambda_{N}\) with \(\overline{\lambda }\;(\overline{\lambda } > \lambda_{N} )\), the value of cond (T) descends, which means the condition of the T−1 matrix becomes better than the original T matrix.

Table 1 shows the CNs of T−1 when the replaced singular values are in different ranges. The first and third columns are indices of replaced singular values, while the second and the fourth columns are the CNs of T−1. The indices of replaced singular values are in ranges 1–20 (step size: 1), 21–40 (step size: 1), …, 237–256 (step size: 1), 1–80 (step size: 4), 176–256 (step size: 4), in each of which 20 singular values are replaced by \(\overline{\lambda }\). In the following parts, when we mention the range of replaced singular values, it means the index range listed in Table 1. The results in Table 1 show that, if the number of replaced singular values is the same, the CNs of T−1 that correspond to the singular values replaced in the final range [e.g. 237–256 (step size: 1)] are smaller than those in other ranges. This result is mainly due to the fact that the singular values λi of T are sorted in descending order, which means that 1/λi are sorted in ascending order. If 1/λi in final ranges (i.e. large singular values of T−1) are replaced by \(1/\overline{\lambda }\), the maximum singular value of T−1 is decreased. Therefore, the CN of T−1 descends (see Eq. 11). The lowest CN in Table 1 corresponds to the indices in range 176–256 (step size: 4), indicating that some eigenchannels with medium eigenvalues should also be closed.

Table 1 Comparison of the CNs of the TM for different replaced singular values (N = 256)
Full size table

Table 1 indicates that the CN of T−1 when the singular values in range 176–256 (step size: 4) are replaced by \(1/\overline{\lambda }\) is smaller than the CN of T−1 when the singular values in range 1–80 (step size: 4) are replaced by \(1/\overline{\lambda }\). As mentioned above, a more accurate incident wavefront can be attained using a TM with a smaller CN. We verify this result through simulations. The enhancement factor of a focal point behind a disordered medium is defined as the ratio between the intensity of the focal point and the average intensity of the background. By comparing the enhancement factors of the focal points, we can judge that a range of replaced singular values is acceptable for TM inversion.

The comparison is between replacing the singular values in range 1–80 (step size: 4) and replacing those in range 176–256 (step size: 4) by \(1/\overline{\lambda }\). The incident wavefront is attained by

$$ {\hat{\mathbf{E}}}_{{{\text{in}}}} = {\hat{\mathbf{T}}}^{ - 1} {\mathbf{E}}_{{{\text{out}}}} , $$
(12)

where \({\hat{\mathbf{T}}}^{ - 1}\) is optimized T−1 with the replaced singular values mentioned above. The concrete simulation process is described as follows:

  • Generate a matrix with elements stochastically selected from a uniform distribution to substitute the disordered medium. Then, measure the TM of the disordered material according to the procedures described in Ref. [10].

  • Add 0–0.2% stochastic noises to the TM to simulate experimental errors. Calculate the incident wavefront \({\hat{\mathbf{E}}}_{{{\text{in}}}}\) using Eq. (12). The \({\hat{\mathbf{T}}}^{ - 1}\) in Eq. (12) is achieved by replacing the singular values in range 1–80 (step size: 4). Then the intensity of the focal point behind the medium is obtained using Eq. 1.

  • Calculate the incident wavefront again using Eq. 12. The \({\hat{\mathbf{T}}}^{ - 1}\) in Eq. 12 is achieved by replacing the singular values in range 176–256 (step size: 4). Then the enhancement of the focal point is achieved by Eq. 1.

The process is repeated 20 times. Thus, 40 enhancement factors can be attained, in which 20 for the replaced singular values in range 1–80 and 20 for the replaced singular values in range 176–256. The results are shown in Fig. 5. From Fig. 5, it is easy to see that the enhancement from the index range of 176–256 is higher than the enhancement from the index range of 1–80.

Fig. 5
figure 5

Simulated enhancement factors of the focal point behind the medium. The process is repeated 20 times and the results are sorted in ascending order. The blue triangles stand for the replaced singular values in range 1–80, while the red circles stand for the replaced singular values in range 176–256

Full size image

Methods of reducing errors of the inversion process

Popoff and coworkers proposed a pseudo-inversion method [19], in which the inverse operator is expressed as

$$ \hat{T}^{ - 1} = [T^{H} T + \sigma I]^{ - 1} T^{H} , $$
(13)

where the superscript H means conjugate transpose, s is the standard deviation of the environment noise, I is unit matrix.

As mentioned above, the condition of the TM is sensitive to the replaced singular values. Therefore, it is very important to select appropriate singular values of the TM for inversion. Here, we propose an idea to optimize the singular values using a simulated annealing algorithm. First, randomly generate 256 binary numbers (either 0 or 1) as the initial solution, in which each binary number corresponds to an index of a singular value. Here, 0 means the corresponding \(\lambda_{i}\) is replaced by \(\overline{\lambda }\), while 1 means that the corresponding \(\lambda_{i}\) keeps the same as its original value. Calculate the cost function of the initial solution. The cost function in this task is the intensity of the focal point behind the medium. Next, randomly perturb the initial solution to get a new solution. This perturbation means to randomly select half of the pixels and replace them by the other binary value. Then, calculate the cost function of the new solution. The new solution is accepted according to the Metropolis principle:

$$ P = \left\{ \begin{gathered} \exp \left( { - \frac{{E_{{{\text{new}}}} - E_{{{\text{old}}}} }}{{T_{k} }}} \right),\quad E_{{{\text{new}}}} - E_{{{\text{old}}}} < 0 \hfill \\ 1,\quad \quad \quad \quad \quad \quad \quad E_{{{\text{new}}}} - E_{{{\text{old}}}} \ge 0 \hfill \\ \end{gathered} \right. $$
(14)

where P is the acceptance probability, Enew is the value of the cost function of the new solution, and Eold is the value of the cost function of the old solution. Tk is the temperature of the k-th iteration, which can be expressed by

$$ T_{k} = \alpha^{k} T_{0} \quad (T_{0} > 0,\;k = 1,2,3,...) $$
(15)

where T0 is the initial temperature, and α is the decay factor. In this experiment, α = 0.99 and T0 = 90. This process is repeated indefinitely, until the intensity of the focal point is saturated. The output solution is shown in Fig. 6, which shows that the simulated annealing algorithm judges that all the singular values in the index range of 240–256 should be replaced by \(\overline{\lambda }\).

Fig. 6
figure 6

The output solution by simulated annealing algorithm. 0 means the corresponding \(\lambda_{i}\) is replaced by \(\overline{\lambda }\), while 1 means that the corresponding \(\lambda_{i}\) keeps the same as its original value

Full size image

The optimized singular values using the output solution in Fig. 6 are expected to attain a higher enhancement factor of the focal point. We verify the validity of the optimized singular values through experiment. We use the optical system shown in Fig. 1 to compare the enhancement factors from the optimized singular values in Fig. 6 with those from the replaced singular values in range 176–256 (step size: 4). We also compare this new algorithm with the method provided by Popoff [19]. The scattering medium in the experiment is a ground glass, and the wavelength of the incident light is 632.8 nm. The instrument model of the SLM is Holoeye Pluto 1080P, and the detector is a charge coupled device (CCD, Thorlabs). Due to the existence of random noise in the experiment, each experiment is performed 20 times, and the results are sorted in ascending order, which are shown in Fig. 7a. The comparison in Fig. 7a shows that the optimized singular values using a simulated annealing algorithm obtain the highest enhancement factor of the focal point among the three algorithms. The enhancement factor of pseudo-inversion method is higher than the enhancement factor of replaced singular values in range 241–256. Figure 7b–d shows intensity transmission through the scattering media. Figure 7b is the intensity transmission of replaced singular values in range 241–256, while Fig. 7c is the intensity transmission of pseudo-inversion method. Figure 7d is the intensity transmission of optimized singular values. The enhancement factors in Fig. 7b–d are 25.6, 43.2, and 48.7, respectively. The enhancement factor for an accurate solution is given as ~ pi/4*N, where N is the number of controlled optical modes. The enhancement factor of 200 is expected but the experimentally acquired factor was 50. The origin of the low enhancement factors is the noises in the experiment. Apparently, our proposed approach works very well in this noisy condition.

Fig. 7
figure 7

a Experimental enhancement factors of the focal point behind the medium (sorted in ascending order); b–d intensity transmission through the scattering media. b of replaced singular values in range 241–256; c of pseudo-inversion method; d of optimized singular values

Full size image

2 Conclusion

In this paper, we have studied the ill-condition of the TM in focusing light through disordered media. A method to optimize the singular values of the TM using a simulated annealing algorithm is proposed, which improves the enhancement factor of the focal point behind the medium. We have compared this method with previous algorithms by experiment, which shows that this new algorithm obtains the highest enhancement factor. Our study helps understanding a new aspect of wave propagation through scattering materials, and can be applied to biological imaging of highly disordered tissue.