Controlling the beam quality in DPALs by changing the resonator parameters

Abstract

The beam quality of diode-pumped alkali lasers (DPALs) is of major concern in the studies of these lasers. We report on experimental studies and modeling of the beam propagation factor M² in flowing-gas Cs DPALs with stable optical resonators and of its dependence on the resonator geometry. The measured values of M² are in agreement with those calculated using the optical model of multi-transverse mode operation (Auslender et al. in Opt Express 25:19767, 2017). Conditions for substantial improvement of the output laser beam quality, reducing M² to close to unity, are found. Changing the length of the resonator, and/or the radius of curvature of the high reflection mirror, leaving all other parameters of the laser unchanged, makes it possible to control the beam quality. Techniques for controlling M² in DPALs with wide-aperture beams have not been studied elsewhere and are very important for the applications of this laser. In addition to the optical model, a simple analytical method based on the model suggested by Siegman (IEEE J Quantum Electron 29:1212, 1993) is applied to the experimental results and predicts a simple scaling law for M² as a function of the size of the resonator fundamental mode.

1 Introduction

Extensive research on diode-pumped alkali lasers (DPALs) [1,2,3] has been conducted in the last 15 years, motivated by their potential for high wall-plug efficiency, good beam quality and scalability to high power. The main efforts have been aimed at increasing laser power and efficiency, while theoretical [4,5,6] and experimental [7, 8] studies of the output laser beam quality began only recently. The beam quality is characterized by the beam propagation factor, M², which represents the degree of variation of the beam from an ideal Gaussian beam. M² close to unity (< 1.2) was measured in a Cs DPAL with low, 12 W, pump power [7] and stable resonator. The focused pump beam diameter in that laser was comparable to the diameter of the fundamental Gaussian laser mode. Hence, only this mode oscillated, resulting in excellent beam quality. Higher order transverse modes could not oscillate because their diameters were larger than the diameter of the pump beam and the outer parts of the modes were absorbed by the unexcited Cs atoms.

In high-power DPALs, pumping is carried out by powerful diode lasers with wide-aperture beams. Their transverse sizes after focusing on the laser cell significantly exceed the size of the fundamental laser mode of a stable resonator, similar to that used in [7]. In this case, in addition to the fundamental resonator mode, high-order transverse modes located inside the pumped volume participate in lasing. Large divergence of these modes results in poor output beam quality. Comprehensive parametric study of the output beam quality of Cs DPALs pumped by wide-aperture beams with approximately 70 W power was reported in [8]. To change the pump beam diameter in the laser cell, this beam was focused by lenses with different focal lengths, whereas the geometry of the plano-concave optical resonator (similar to that used in Ref. [7]) and hence the size of the fundamental laser mode was not changed. However, even for rather tight focusing of the high-power pump beam applied in [8], the measured M² of the output laser beam was 15, i.e., very large, which means, as shown in [8], that several high-order transverse modes participate in the lasing. The simplest way to reduce the number of oscillating transverse modes leading to an improvement in the output laser beam quality is to increase the diameter of the fundamental laser mode of the stable resonator. This can be done by varying the resonator length and the curvature of the mirrors without changing the geometry of the pump beam.

It is noteworthy that changes in the geometry of a stable resonator can be used to improve the output laser beam quality of various large-bore lasers, e.g., CO₂ laser [9]. However, to the best of our knowledge, detailed studies of the influence of the stable resonator geometry on the beam quality have not been carried out for large-bore lasers and in particular for DPALs. Usually unstable resonators are used to reach small M² in large-bore lasers. However, according to recently published calculations [10], only unstable resonators with graded reflectivity mirrors (GRM) can provide for good beam quality in flowing-gas DPALs with M² < 2, whereas calculated M² for conventional unstable resonators with uniform reflectivity of the mirrors and optimal magnification corresponding to the maximum power is 10. The reason for such large M² is that in conventional unstable resonators the output beam is coupled out from the edge of the output coupling mirror, which results in large beam divergence in the far field due to the side lobes of the intensity profile in the near field. It is difficult to manufacture GRMs and they are very expensive; therefore, it is much easier to employ stable resonator with suitable geometry to reach high-beam quality. In addition, as shown in [10], M² in flowing-gas DPALs with stable resonators is less susceptible to flow velocity changes than in the same lasers with unstable resonators. Thus, the study of ways to improve the output beam quality in DPALs with stable resonators is very important.

2 Experiment and modeling

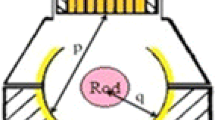
In the present paper, the dependence of M² on the resonator geometry and hence on the average diameter of the fundamental laser mode in the laser cell was studied experimentally in flowing-gas Cs DPAL with stable optical resonator. Schematics of the flowing-gas Cs DPAL with end-pumping geometry similar to that reported in Ref. [11] is depicted in Fig. 1. The gas mixture of 300 Torr of methane and 300 Torr of He at room temperature circulates in the closed loop flow system. The circulation is carried out by a gas blower. Liquid Cs, which serves as the alkali vapor source, is located upstream of the laser cell. The flowing system was heated by heating tapes to 130 °C, the temperature of the storage nipple containing the liquid Cs being 20 °C lower than that of the laser cell. Using a flowing-gas system allows to minimize the heating effects, which may cause a beam quality deterioration due to temperature gradients in the medium [4].

Fig. 1

Schematics of the flowing gas Cs DPAL with end-pump geometry. Pump beam of circular symmetry and a donut-shaped intensity profile was used

The diode laser in this setup produces 852-nm pump beam with optical power of up to 70 W with ultra-narrow band of 0.05 nm The pump beam of circular symmetry with a donut-shaped intensity profile was focused inside the alkali cell using 100-mm spherical lens. The pump beam waist diameter after focusing was 2.5 mm (measured as the second moment of the intensity profile) and the maximal diameter of the beam’s path inside the cell was 3.5 mm. The reason for such large diameter is the fact that the laser diode used in this setup produces a beam with poor quality (M² > 400). The system was operated at flow velocity of 3 m/s, using maximal pump power of 65 W.

The laser is equipped by a half-symmetric stable resonator [12], consisting of a plane output coupler (OC) and concave high reflector (HR) with a radius of curvature R, which are located at distance L (< R) apart. Such resonators are usually used in DPALs [7, 8]. The dependence of the diameter d (at 1/e² of the intensity) of the fundamental laser mode on the z-coordinate along the resonator optical axis is given by [12]

$$d(z) = 2w_{0} \sqrt {1 + \frac{{z^{2} }}{{z_{R}^{2} }}} ,$$

(1)

where

$$w_{0} = \left[ {\left( {\frac{{\lambda_{l} }}{\pi }} \right)^{2} L\left( {R - L} \right)} \right]^{1/4}$$

(2)

is the radius of the mode waist located at z = 0 at the OC, $\lambda_{l}$ is the laser wavelength and

$$z_{R} = \frac{{\pi w_{0}^{2} }}{{\lambda_{l} }} = \sqrt {L\left( {R - L} \right)} ,$$

(3)

is the Rayleigh length. The average fundamental mode diameter $\overline{d}$ in the short laser cell of length $l$(< < L, R) is equal with high accuracy (0.1%) for the geometry used in Refs. [7, 8]) to the beam diameter at the cell center: $\overline{d} = d(z = L - L_{{{\text{HR}}}} ) + O\left[ {\left( {l/L} \right)^{2} } \right],$ where $L_{{{\text{HR}}}}$ is the distance between the cell center and HR. Then using Eqs. (1) and (2) we get

$$\overline{d} = 2\sqrt {\frac{{\lambda_{l} }}{\pi }\sqrt {L\left( {R - L} \right)} \left[ {1 + \frac{{\left( {L - L_{{{\text{HR}}}} } \right)^{2} }}{{L\left( {R - L} \right)}}} \right]} .$$

(4)

Since R > L, it follows from Eq. (4) that for a given $L_{{{\text{HR}}}}$, $\overline{d}$ can be increased by increasing both R and L and reach values comparable with the diameter of the pump beam, resulting in single-mode oscillation and, hence, substantial improvement of the output beam quality.

The output laser power obtained for different resonator configurations was 16–21 W. In this setup we used HR mirrors with several radii of curvatures: 500, 1000, 2000 and 5000 mm. The distance L_HR between the cell center and HR was kept fixed at 65 mm and L was changed from 210 to 1000 mm. M² was measured by focusing the output beam by a spherical lens to capture variations of its radius along the optical axis by a beam profiling camera [8].

An optical model of multi-transverse mode operation reported in [5, 8] was applied for analyzing the experimental results and compared with a simple analytical model similar to that suggested in [9]. Conditions for substantial improvement of the output laser beam quality, reducing M² close to unity, are found. It is worth noting that the present method is much simpler than sophisticated methods for improving beam quality of solid-state lasers where intracavity optical elements were used for coherent combining of the beams emitted by different laser rods [13] or different parts of the intracavity multimode beam [14].

3 Results

Figure 2 shows the measured and calculated M² dependence on $\overline{d}$. The average diameter $\overline{d}$ is calculated by Eq. (4) using L, R and L_HR from the experiment. The dependence $M^{2} (\overline{d})$ is shown for two values of pump power: P_p = 65 W and P_p = 41 W. It is seen that for small $\overline{d} \sim 0.6{\text{ mm}}$, the values of M² are large (10–16) and increase with increasing P_p. As shown in [8], this increase is caused by the increase in the number of excited transverse modes participating in the lasing. As $\overline{d}$ is increased to 1.5–2 mm and approaches the pump beam diameter, M² drops to much smaller values, < 2, resulting in significant improvement of the laser beam quality. In this case, M² is almost independent of P_p and nearly single-mode operation of the laser takes place.

Fig. 2

Measured and calculated (by the optical model of multi-transverse mode operation [5, 8]) dependence of M² on $\overline{d}$ for P_p = 65 W and P_p = 41 W. As $\overline{d}$ approaches the size of the pump beam diameter, the laser operation approaches the single-mode regime. Analytical calculations of M² from Eq. (8) are performed for $d_{q\max } = 2$ mm

The dashed lines in Fig. 2 show the modeling results. The optical model of multi-transverse mode operation is based on calculations of the pump and laser beam intensities in the gain medium, where the laser beam intensity is a linear combination of the azimuthally-symmetric Laguerre–Gaussian modes [5]. In particular, for the donut-shaped pump beam, used in the present setup, the output laser beam is composed only from TEM_0q modes with zero radial indices [8]. The powers of the pump beam and of the transverse modes are found from the system of differential equations representing the Beer–Lambert law as explained in [5]. As seen in Fig. 2, good agreement is obtained between calculated and measured values of M².

Using the above-mentioned multi-mode model, we can evaluate the number of transverse modes participating in lasing for given P_p and $\overline{d}$. Figure 3 shows the calculated power distribution over the laser transverse-modes for P_p = 65 W and three different values of $\overline{d}$: 1.84 mm (M² = 1.63), 1.1 mm (M² = 4.16) and 0.6 mm (M² = 13.62). It is seen that in the case of the largest M², 10 transverse-modes oscillate, the highest order mode number being 30. At the same time in the smallest M² case, only two lowest order modes oscillate resulting in the aforementioned nearly single-mode laser operation. Note that the frequencies of the oscillating transverse modes are very close to each other [5] and that, due to the homogeneous broadening of the laser line, only one longitudinal mode oscillates with a frequency close to the center of the line [12]. As a result, the bandwidth of the laser spectrum is much narrower than the width of the pressure broadened gain profile (15 GHz). Figure 3 shows the calculated modal power distribution; measuring these distributions is beyond the scope of this article.

Fig. 3

Laser modal composition for 3 cases of $\overline{d}$, calculated by multi-transverse-mode model [5, 8]. For the values of $\overline{d}$ corresponding to large M² (gray bars), 10 transverse-modes lase, the highest order mode number being 30. For the smallest M² case (blue bars), only the two lowest order modes lase

4 Analytical approach

The dependence of M² on $\overline{d}$ shown in Fig. 2 can also be obtained using a simple approximate analytical approach to the description of the multi-transverse-mode lasing, similar to that suggested in [9]. Although this approach is inaccurate, it predicts the correct scaling law for the decrease of M² with increasing $\overline{d} .$ The normalized intensity distribution in the TEM_0q laser modes has the form [8]:

$$f_{q} \left( {r,z} \right) = \frac{8}{{\pi d^{2} (z)q!}}\left( {8\frac{{r^{2} }}{{d^{2} (z)}}} \right)^{q} \exp \left( { - 8\frac{{r^{2} }}{{d^{2} (z)}}} \right),$$

(5)

where r is the distance from the optical axis and $d(z)$ is given by Eq. (1). The radius $r_{q}$ of the transverse mode of the order q, defined as the largest r for which $f_{q} \left( {r,z} \right)$ equals to 1/e² of its maximum value over r (at given z) can be derived from Eq. (5):

$$r_{q} = \frac{d(z)}{{2\sqrt 2 }}\left( {\sqrt q + 1} \right).$$

(6)

Using the aforementioned assumption that in the short laser cell $d(z) \approx \overline{d}$ one gets from Eq. (6) the relation between q and the mode diameter $d_{q} \equiv 2r_{q}$:

$$q = \left( {\frac{{d_{q} \sqrt 2 }}{{\overline{d}}} - 1} \right)^{2} .$$

(7)

As suggested in Ref. [9] only the highest order transverse modes, for which the lasing is allowed, oscillate. The diameter of these modes $d_{q\max }$ is a little smaller than the pump beam waist diameter and the order of the highest mode $q_{\max }$ is given by Eq. (7) with $d_{q} = d_{q\max } .$ The diameter $d_{q}$ of the higher order modes (with $q > q_{\max }$) is larger than the pump beam diameter, hence, they will be absorbed and will not oscillate.

If a laser oscillates in an incoherent superposition of Laguerre–Gaussian TEM_0q modes with normalized power coefficients $|c_{q} |^{2}$ the factor M² for the resulting multimode beam will be given by a weighted sum over all the modes [8, 15]:

$$M^{2} = \sum\limits_{q = 0}^{{q_{\max } }} {|c_{q} |^{2} } (q + 1).$$

(8)

The coefficients $|c_{q} |^{2}$ are unknown and can be found only using the optical model [5, 8] described above (Sects. 2, 3). Assuming for simplicity that only the highest mode of the order $q_{\max }$ oscillates, we get $|c_{q} |^{2} = \delta_{{q_{\max } q}}$ and

$$M^{2} = q_{\max } + 1 = \left( {\frac{{d_{q\max } \sqrt 2 }}{{\overline{d}}} - 1} \right)^{2} + 1.$$

(9)

Note that for small $\overline{d}$ (corresponding to large M² >  > 1) Eq. (9) yields the following approximate expression for $M^{2}$:

$$M^{2} \approx 2\left( {\frac{{d_{q\max } }}{{\overline{d}}}} \right)^{2} .$$

(10)

The scaling law $M^{2} \sim \overline{d}^{ - 2}$ following from Eq. (10) is the same as that obtained in [9] for oscillating 1D Hermite–Gaussian modes that have the mathematical form $H_{n} (\sqrt 2 x/w)\exp ( - x^{2} /w^{2} ),$ where H_n is Hermitian polynomial of the order n and w is the radius of the fundamental mode with n = 0. For such modes, not only the scaling law but also the equation for M², which follows from the results of [9], has the same form as Eq. (10) under the assumption (for which Eq. (10) was derived) that only the highest order mode oscillates. Indeed, the order n of this oscillating mode with radius a is given by [9]:

$$n = \left( \frac{a}{w} \right)^{2} .$$

(11)

Then similarly to the derivation of Eq. (9), we obtain

$$M^{2} = 2n + 1 \approx 2\left( \frac{a}{w} \right)^{2} {\text{ (for }}n > > 1{),}$$

(12)

the last expression being identical to Eq. (10). If lower order modes participate in the lasing, M² is lower than that given by the last equation [9]. For example, in the case of hat-top intensity distribution in the laser beam, calculation performed in [9] yields $M^{2} = 1.3\left( {a/w} \right)^{2} ,$ whereas the experimental value of the quality factor in CO₂ laser is $M^{2} = \left( {a/w} \right)^{2}$ [9]. As noted in [9], the fact that the last experimental value is equal to the highest order n of the oscillating modes is just a coincidence.

Figure 2 shows the analytical dependence of M² on $\overline{d}$ calculated using Eq. (9) with $d_{q\max } = 2$ mm. The calculated results are in good agreement with the measured values. Note that in [9] the scaling law $M^{2} \sim \overline{d}^{ - 2}$ was not checked by comparison with experimental results since the experiments were performed for two resonators with very close values of $\overline{d} .$ The analytical method described above is, however, inaccurate because it is assumed that only the highest order transverse modes oscillate. This assumption was made for simplicity because the modal composition of the laser beam is unknown and can be found only using the accurate optical model of multi-transverse mode lasing described in Sects. 2 and 3. Nevertheless, the analytical method describes well the dependence of M² on $\overline{d}$ and can be used for rough estimates of the output beam quality in DPALs with stable resonators, although it is unable to predict the modal composition of the laser beam and the dependence of $M^{2}$ on the pump power. Note that $d_{q\max } = 2$ mm used as the fitting parameter of the analytical method is by 30% smaller than the average pump beam diameter in the laser cell. The reason for such a small value of $d_{q\max }$ is that it can be considered as the average radius of the transverse modes involved in the lasing, which is smaller than the radius of the pump beam.

Note that many transverse modes with close power values are involved in the oscillation in Cs DPAL with large M² (see gray bars in Fig. 3), and not only the highest order modes, as in a CO₂ laser [9]. The reason for it is the non-uniform distribution of the gain and pump intensity in DPAL, which differs significantly from the uniform distribution of gain in CO₂ laser [9].

5 Conclusions

The dependence of the beam propagation factor M² in flowing-gas Cs DPALs with stable optical resonators on the resonator geometry is studied experimentally and theoretically. Conditions for nearly single-mode laser operation resulting in substantial improvement of the output laser beam quality, reducing M² close to unity, are found. The beam quality of the output laser beam can be controlled by changing the length of the resonator, and/or the radius of curvature of the high-reflection mirror, leaving all other parameters of the laser unchanged. The presented technique for controlling M² in DPALs with wide-aperture beams has not been studied elsewhere and is very important for the applications of these lasers. The measured M² values are in agreement with those calculated using both the optical model of multi-transverse mode operation [5] and a simple analytical method similar to that suggested in [9]. Note that accurate values of M² were obtained using the multimode model while analytical formula provides for only a scaling law $M^{2} \sim \overline{d}^{ - 2}$ at large $M^{2}$ and can be used for rough estimates of the output beam quality in DPALs with stable resonators.