Bound states of chirped Airy–Gaussian beams in a medium with a parabolic potential

Abstract

Starting from the normalized dimensionless linear parabolic (Schrödinger-like) equation, by means of split-step Fourier numerical simulation, in this paper we investigate the interaction between two chirped Airy–Gaussian (CAiG) beams in a medium with a parabolic potential. We find that a parabolic potential provides interesting effects and supports the bound states of two CAiG beams. We also study the effect of chirps and found that large enough chirps will weaken the energy of bound states. Moreover, initial parameters of the beams, initial interval, amplitudes, and distribution factor, are taken into consideration as well.

1 Introduction

In 1979, Berry and Balazs first discovered that ideal Airy function was an exact solution of Schrödinger equation in the context of quantum mechanics [1]. However, true Airy wave packets, whose electric field profile is defined by an Airy function, are impractical as they contain an infinite amount of energy. Fortunately, Airy beams with finite energy were obtained experimentally by Siviloglou and Christodoulides in 2007 [2, 3]. This asymmetric beam has attracted wide attention on a world scale due to its unique properties. For example, it is diffraction free, and it exhibits self-acceleration and self-healing [3,4,5,6]. From the practical point of view, Airy beams have found useful applications, ranging from optical trapping [7] and optical switching [8] to plasma waveguide [9]. Recent analyses of temporal Airy pulses and spatial Airy beams suggest that different media have different effects on their propagation. When the pulses or beams propagate in nonlinear media, soliton is formed out of the main part of the energy about the Airy main lobe; Airy–soliton pairs are observed when Airy beams interact with each other [10,11,12]. In 2015, the propagation dynamic of chirped Airy pulse in an optical fiber was obtained analytically [13]. Strongly nonlocal and nonlinear media play crucial roles to make Airy pulse or beams propagate periodically [14, 15]. Such results have been discussed in numerous works. Furthermore, the dynamics of optical beams, such as Gaussian and Airy beams, in the context of the fractional Schrödinger equation (FSE) [16,17,18], have attracted great attention in recent years. Interestingly, in these studies the authors report that without potential and chirp, a one-dimensional (1D) Gaussian beam splits into two non-diffracting Gaussian beams, and a two-dimensional (2D) Gaussian beam undergoes conical diffraction during propagation. On the other hand, with linear chirp, both 1D and 2D Gaussian beams are diffraction free and their trajectories are deflected. Interestingly, the transmission, partial transmission/reflection, and total reflection of approximate diffraction-free beams are determined by the potential depth in the FSE with a double-barrier potential. When Airy beams are modeled by the potential barrier-induced fractional Schrödinger equation, the Lévy index plays an important role in diffraction, splitting, the number of reflected waves, and so on.

An Airy–Gaussian (AiG) beam can be seen as a more realistic Airy beam passing through Gaussian apertures. So AiG beams with finite energy retain some properties both of Airy and Gaussian beams. In consequence, AiG beam is becoming more and more popular today. Interestingly, the propagation properties of AiG beams indicate that self-bending is dependent on the distribution factor. Relevant numerical results are reported in Ref [19]. Thereafter, many investigations have been performed to understand the propagation of one AiG beam and interactions of two AiG beams [20, 21]. The results show that when the initial incident power of the AiG beam is within a certain range, a stable soliton arises; and single breather and breather pairs can be formed in the interaction of two AiG beams with enough intensity in saturable media and Kerr-like media. In addition, it is found that the interaction can be attractive or repulsive, depending on the relative phase, and as decreasing the interval between two AiG beams in the incidence, the intensity of the interaction increases. Moreover, chirp is found to support periodic and opposite intensity distribution of AiG beams [22].

In this paper, after introducing the normalized dimensionless linear parabolic (Schrödinger-like) equation under the paraxial approximation, we derive the interaction of two chirped Airy–Gaussian (CAiG) beams in a medium with a parabolic potential. We numerically find symmetric and/or asymmetric bound states generated by two separated CAiG beams. We find they are affected by the depth of the potential well, the distribution factor, the phase factor, amplitude and chirp.

2 Theoretical analysis

Under the paraxial approximation, the normalized dimensionless linear parabolic (Schrödinger-like [23, 24]) equation is described as:

$$ i\frac{\partial \varPhi }{\partial Z} + \frac{1}{2}\frac{{\partial^{2} \varPhi }}{{\partial X^{2} }} - V(X)\varPhi = 0, $$

(1)

where $\varPhi$ is the slowly varying envelope of the beam and V(x) represents the external potential of the medium. ${\text{X = }}{\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x {x_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${x_{0} }$}}$ and $Z = {\raise0.7ex\hbox{$z$} \!\mathord{\left/ {\vphantom {z {kx_{0}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${kx_{0}^{2} }$}}$ represent the dimensionless transverse coordinate and the propagation distance, respectively. $x_{0}$ is the transverse width and $kx_{0}^{2}$ is the Rayleigh range; $k = {\raise0.7ex\hbox{${2\pi n}$} \!\mathord{\left/ {\vphantom {{2\pi n} {\lambda_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\lambda_{0} }$}}$ is the wavenumber, $n$ is the refractive index of the medium with a parabolic potential, and $\lambda_{0}$ is the free-space wavelength. The parabolic potential is depicted as [14, 22, 25]

$$ V(X) = \frac{1}{2}\alpha^{2} X^{2} , $$

(2)

where $\alpha$ is the depth of the parabolic potential. In addition, the propagation of Airy and Airy–Gaussian beams in other media, such as ABCD optical system and graded index media, has been extensively studied [26,27,28,29].

Generally speaking, for a (1 + 1) dimensional CAiG beam, the initial field distribution can be written as [22]:

$$ \varPhi (X,Z = 0) = A_{0} Ai(X)\exp (aX)\exp ( - \chi_{0}^{2} X^{2} )\exp ( - i\beta^{\prime}X)\exp ( - i\beta X^{2} ), $$

(3)

where $A_{0}$ is the amplitude of the beam, $Ai\left( X \right)$ is the Airy function, and $a$ is the decay factor which is positive real to make the energy of the beam finite. $\chi_{0}$ is the distribution factor to amend field distribution of the beam, that is, when $\chi_{0}$ takes a small value, the beam tends to an Airy beam, and while it is large enough, the beam tends to a Gaussian beam. $\beta^{\prime}$ and $\beta$ represent the chirp factors of the beam. When $\beta^{\prime} = 0$ and $\beta = 0$, Eq. (3) shows the initial field distribution of the a AiG beam; when $\beta^{\prime} \ne 0$ and $\beta = 0$, Eq. (3) is the incident AiG beam with an initial velocity; when $\beta^{\prime} = 0$ and $\beta \ne 0$, Eq. (3) represents the incident CAiG beam with a quadratic chirp. In this paper, we only study the CAiG beam with a quadratic chirp, that is, $\beta^{\prime} = 0$, $\beta \ne 0$.

For the sake of further studying the interaction between two CAiG beams, we construct an initial incident beam consisting of two CAiG beams, whose field distribution can be expressed as:

$$ \begin{aligned} \varPhi (X,Z = 0) = A_{1} Ai(X - B)\exp [a(X - B)]\exp [ - \chi_{0}^{2} (X - B)^{2} ]\exp [ - i\beta_{1} (X - B)^{2} ] \hfill \\ + A_{2} \exp (iQ)Ai( - X - B)]\exp [a( - X - B)]\exp [ - \chi_{0}^{2} ( - X - B)^{2} ]\exp [ - i\beta_{2} ( - X - B)^{2} ], \hfill \\ \end{aligned} $$

(4)

where $A_{1}$ and $A_{2}$ are the amplitudes of the two CAiG beams, respectively. $B$ is the interval between the two CAiG beams. $\beta_{1}$ and $\beta_{2}$ represent the quadratic chirp factors of the two beams, respectively. $Q$ is the phase factor controlling the phase shift between the two CAiG beams, that is, when $Q = 0$, the two beams are in-phase, and for $Q = \pi$, they are out-phase. The interaction of two AiG beams is of great interest and has been studied in the context of the NLSE in some media [20, 21].

3 Simulation results

In this paper, numerical simulations are carried by using the split-step Fourier method [24, 30], which is a numerical method, dealing with the diffraction step and the nonlinear step separately, used to solve the nonlinear Schrödinger equation and to study the interaction between two chirped AiG beams in a medium with a parabolic potential based on Eq. (4). To better understand the interaction, we first study the propagation dynamics of a single chirped AiG beam based on Eq. (3). In the following numerical simulations, we take $a = 0.1$.

3.1 For a single CAiG beam

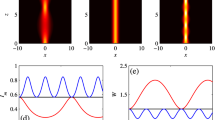
We first study the propagation of a single chirped AiG beam with varying $\alpha$ based on Eq. (3). In this case, we take $A_{0} = 2,\beta { = }0.03$.

Figure 1(a1, a2, a3) demonstrates that when $\alpha$ = 0, after a short distance, the energy of the beam will rapidly drop. This phenomenon is attributed to the diffraction effect. With the increase in $\chi_{0}$, the side lobes of the beam are weakened, and when $\chi_{0} { = }1$, the beam follows the Gaussian distribution. Moreover, the behavior of the energy diffraction changes drastically if $\alpha \ne 0$. When $\chi_{0}$ is small, Fig. 1(b1–b2) and (c1–c2) display interesting dynamics, that is, it exhibits a phenomenon similar to periodical oscillations, and the propagation curve exhibits an S shape. Also, we observe that with increasing $\alpha$, the oscillation period and the width of the beam decrease. When $\chi_{0} { = }1$, the propagation of the beam develops into the propagation of a Gaussian beam in a medium with a parabolic potential, as shown in Fig. 1(b3, c3).

Fig. 1

The propagation dynamics of a single CAiG beam in a medium with a parabolic potential for different $\alpha$ and $\chi_{0}$:(a1–c1)$\chi_{0}$ = 0.01, (a2–c2)$\chi_{0}$ = 0.1, (a3–c3)$\chi_{0}$ = 1 when $\beta { = }0.03$

3.2 For two CAiG beams

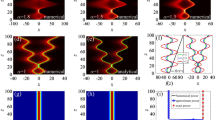
Figure 2 depicts the interaction of two CAiG beams with different values of $\chi_{0}$ at $Q = 0$ and $Q = \pi$, showing an interesting process. When $Q = 0$, the two beams are in-phase and the energy of the two beams converges to the center, and a periodic stable bound state is formed under the impact of both diffraction effect and parabolic potential. When $Q = \pi$, the two beams are out-phase and the energy of the two beams radiates symmetrically in opposite directions. As a result of the balance between diffraction effect and the influence of parabolic potential, a stable bound state is formed. No matter how large $Q$ is, when $\chi_{0}$ increases, the non-diffracting distance becomes short, the self-healing effect becomes weak, and their Airy patterns gradually break down. Conversely, with decreasing $\chi_{0}$, the non-diffracting distance increases and the self-healing effect becomes strong. When $\chi_{0}$ is large, the self-healing effect is very weak, as shown in Fig. 2(e1) and (e2). As a result, we can obtain the desired non-diffracting distance by changing $\chi_{0}$ in practical application.

Fig. 2

The interaction of two CAiG beams with varying $\chi_{0}$ when $A_{1} = A_{2} = 2,B = - 2$, $\alpha { = }0.2$, $\beta_{1} { = }\beta_{2} = 0.03$ for $Q = 0$(a1–e1) and $Q = \pi$(a2–e2)

As is shown in Fig. 3, we discuss the effect of parabolic potential on the interaction of two in-phase CAiG beams. When $\alpha { = }0$, we can view two beams interacting in free space. After a short interaction distance, the diffraction effect results in the rapid liberation of energy. When $\alpha \ne 0$, the two beams interact in a medium with a parabolic potential. From Fig. 3, we can see that bound breather forms in the interacting process. This is because the beams are rebounded back due to the potential well after outward diffraction. This will repeat periodically so that a periodic bound breathing phenomenon occurs. In this process, the energy of the beams is mainly concentrated on the breather. It is clear that, with increase in the potential strength $\alpha$, the period and the width of the breather decrease. The side lobes of the beams decrease as $\chi_{0}$ increases, resulting in less width as shown in Fig. 3(b3–d3). So, we can control the period and the width of the bound breather by changing $\alpha$ and $\chi_{0}$.

Fig. 3

The interaction of two in-phase CAiG beams with $\chi_{0} { = }0.01$ (the first line), $\chi_{0} { = }0.1$ (the second line) and $\chi_{0} { = }1$ (the third line), $\alpha$ = 0, 0.2, 0.4, 0.6 when $A_{1} = A_{2} = 2$, $\beta_{1} = \beta_{2} { = }0.03$ and $B = 1$

The results shown in Fig. 4 reveal indeed an effect which the interval between the two in-phase CAiG beams makes on their interaction. When the interval $B$ is negative, the main lobes of the two CAiG beams interact mainly, accompanied by the side lobes repulsing and then being bounced back by the attractive force from the potential well, propagating as periodic bound states. When the absolute value of the interval $B$ decreases, the attraction becomes stronger. When $B$ is positive and $B > 1$, the side lobes of the two CAiG beams interact mainly, the main lobes being on both sides, also forming periodic stable bound states. When $\chi_{0}$ is small, the strongest attraction is at $B{ = }0$, and when $\chi_{0}$ is large, it is at $B{ = }1$ as shown in Fig. 4(c1, c2) and (d3). Interestingly, we can clearly see that when $\chi_{0}$ is large enough, self-healing and side lobes of the beams are drastically weak, and the two beams interacting in a medium with parabolic potential behave as two Gaussian beams.

Fig. 4

The interaction of two in-phase CAiG beams with varying $B$ and different values of $\chi_{0}$: (a1–e1)$\chi_{0} { = }0.01$, (a2–e2)$\chi_{0} { = }0.1$, (a3–e3)$\chi_{0} { = }1$ when $A_{1} = A_{2} = 2$, $\alpha = 0.3$, $\beta_{1} = \beta_{2} { = }0.03$

Based on the results shown in Fig. 5, we have to realize that the amplitude has an important effect on the interaction between two CAiG beams. From the figure we can see that when the amplitudes of the two beams are not equal, interaction is more obvious on the larger amplitude side shown in Fig. 5(a1–a3) and (e1–e3). As the values of the amplitudes are closer to each other, the asymmetry is weaker, as shown in Fig. 5(b1–b3) and (d1–d3). But at the same amplitudes, energy evenly distributes on both sides [see Fig. 5(c1–c3)]. Furthermore, the influence of the distribution factor $\chi_{0}$ is similar to Figs. 2 and 4(a1, a2, a3). In fact, when $\chi_{0}$ increases from 0 to infinity, the field pattern of the beams will change from Airy distribution to Gaussian distribution.

Fig. 5

The interaction of two in-phase CAiG beams with varying amplitudes and different values of $\chi_{0}$:(a1–e1)$\chi_{0} { = }0.01$, (a2–e2)$\chi_{0} { = }0.1$, (a3–e3)$\chi_{0} { = }1$ when $B = - 3$, $\alpha = 0.3$, $\beta_{1} = \beta_{2} { = }0.03$

The influence of the phase factor $Q$ on the interaction of two CAiG beams is shown in Fig. 6, where we take the values $Q =$$- \pi$, $- \frac{2\pi }{3}$, $- \frac{\pi }{2}$, $- \frac{\pi }{3}$, 0, $\frac{\pi }{3}$,$\frac{\pi }{2}$, $\frac{2\pi }{3}$, $\pi$. $Q{ = }0$ means the two beams are in-phase. In this case, the two beams attract each other, and bound breather is built in the center. When $Q{ = } \pm \pi$, the two beams are out-phase and they repulse each other, but the repulsion is balanced by the attractive force from the potential well, obtaining bound breathing states. While $Q \ne 0$ and $Q \ne \pm \pi$, the beams transmit with center shift and energy deviation. In the case of $- \pi < Q < 0$, the center of the beams shifts to the right first and then propagates with periodic and opposite oscillation; in the situation of $0 < Q < \pi$, the center changes periodically and oppositely after turning to the left first. The smaller $\left| Q \right|$ is, the more the energy converges to the center. In addition, the value of $\chi_{0}$ only affects the whole energy of the beams, not the energy shift, so it will not be discussed in this part.

Fig. 6

The interaction of two CAiG beams in different initial phase factors with $Q$ = $- \pi$, $- \frac{2\pi }{3}$, $- \frac{\pi }{2}$, $- \frac{\pi }{3}$, 0, $\frac{\pi }{3}$, $\frac{\pi }{2}$, $\frac{2\pi }{3}$, $\pi$; $B = 1$, $\chi_{0} { = }0.1$, $A_{1} = A_{2} = 1$, $\alpha { = }0.3$, $\beta_{1} = \beta_{2} { = 0} . 0 3$

Figure 7 shows the influence of the positive and negative chirps for different distribution factors $\chi_{0}$. For small $\chi_{0}$, when the chirps are very small, they have almost no effects on the two beams [shown in Fig. 7(a1, a2)]; with large enough chirps, the total energy of the two beams are weakened extremely [shown in Fig. 7(c1, c2, d1, d2)]. When the chirps are larger, and they are positive [shown in Fig. 7(b1, b2)], the focusing effect exceeds the diffraction at the beginning; on the contrary, while the chirps are negative, diffraction will overtake the focusing effect at the beginning [shown in Fig. 7(e1, e2)]. When one chirp of the beams is positive and the other is negative, the positive chirped AiG beam has the same phenomena as in Fig. 7(b1) and (b2); the negative chirped AiG beam retains the phenomena in Fig. 7(e1) and (e2), then the beams will oppositely and periodically oscillate [shown in Fig. 7(f1) and (f2)]. Obviously, when the parameter $\chi_{0}$ is large enough, the beams will become chirped Gaussian beams, as shown in Fig. 7(a3–f3). These indicate that chirps have profound effect on the interaction between two CAiG beams.

Fig. 7

The interaction of two in-phase CAiG beams in different chirp parameters $\beta_{1} ,\beta_{2}$ and different values of $\chi_{0}$:(a1–f1)$\chi_{0} { = }0.01$, (a2–f2)$\chi_{0} { = }0.1$, (a3–f3)$\chi_{0} { = }1$ when $A_{1} = A_{2} = 1,B = - 2,\alpha = 0.3$

4 Conclusion

In summary, we mainly studied the interaction of two chirped AiG beams in a medium with a parabolic potential by way of numerical simulation. We found that bound states of the beams can be formed. The field patterns of these bound states depend strongly on the distribution factor χ₀: side lobes are gradually lost and the non-diffracting distance gets shorter and shorter with increase in χ₀. We also observed the effect of potential well, and found that potential well has a negative effect on the bound breathing period and width. In addition, the result showed that interval $B$ plays a decisive role on the main interaction between the main lobes or side lobes. Symmetric/asymmetric bound states can be obtained via choosing equal or unequal amplitudes of the two CAiG beams. We can also steer the center of the bound beams by tuning the initial phase factor $Q$. Finally, we found that small chirps have very little influence on the interaction and large enough chirps will reduce the energy of bound states.