1 Introduction

In the recent years, vortex beams carrying orbital angular momentum (OAM) have attracted much attention due to their fascinating properties and applications in a variety of fields such as optical microscopy [1], optical tweezers [2, 3], quantum state manipulation [4, 5], and quantum communications [6, 7]. Among these applications of the vortex beams, particular interest has been given to the optical communication due to their high channel capacity without increasing spectral bandwidth [7]. It has been well recognized that the vortex beams in turbulent atmosphere are affected by the turbulence [8, 9], and the OAM state will be confused with the neighbor one [10]. Furthermore, it was found that the transverse intensity profiles of vortex beams with non-diffracting characteristics are structurally preserved upon propagation in turbulence and have the self-healing property [11].

There are several types of the non-diffracting vortex beams, such as the Bessel beams [12], Airy beams [13, 14], and Hankel–Bessel beams [15]. Among them, the Bessel beam is a typical one, and is widely used in optical trapping and manipulation [16] and optical imaging [17]. Recently, a new non-diffracting vortex beam, the Lommel beam, was introduced [18], the beam of which can be described by a linear combination of Bessel modes with different axial projections of the wave vector and the transverse intensity profiles can be controlled by only one beam parameter. Furthermore, the significant advantage of the Lommel beams is due to its continuous change of OAM, while the Bessel beams contain only one discrete change. However, the Lommel beams require an infinite amount of energy and propagate indefinitely in the space without distortion. To confine their energy, mostly, a Gaussian windowing function is adopted, and then, the Lommel–Gaussian beam was introduced [19]. Ez-zariy al. studied the on-axis average intensity of a pertured Lommel–Gaussian beam in turbulent atmosphere [20]. Yu al. researched the OAM modal crosstalk of the Lommel–Gaussian beam through the turbulent ocean [21]. Subsequently, Yu al. analyzed the beam spreading and wander of a partially coherent Lommel–Gaussian beam in turbulent biological tissue [22]. Based on the beam superposition, Chen al. reported a group of sources to generate Lommel–Gaussian beams to analyze nonparaxial propagation [23]. However, to our knowledge, the propagation factor and angular width of laser beams, which are important parameters to value laser propagation feature in turbulent atmosphere, have not been reported. In this paper, we will discuss the effects of the atmospheric turbulence on the angular width and propagation factor of a Lommel–Gaussian beam. The appropriate parameters of the propagation for a Lommel–Gaussian beam in a turbulent atmosphere are obtained after analyzing the influences of beam and turbulent parameters on the propagation parameters using numerical simulations.

The rest of this paper is organized as follows: in Sect. 2, analytical expressions of the angular width and propagation factor of a Lommel–Gaussian beam propagating in atmospheric turbulence are obtained. Subsequently, the influences of different parameters of the structure constant, inner scale, outer scale, OAM quantum number, wavelength, asymmetry parameter, and and propagation distance on the propagation of a Lommel–Gaussian beam are analyzed and discussed in Sect. 3. Finally, conclusions are given in Sect. 4.

2 Theoretical formulation

The initial field distribution of a Lommel–Gaussian beam is expressed as [19]

$$E_{n} (\varvec{s},z = 0) = \sum\limits_{p = 0}^{\infty } {( - 1)^{p} (c)^{2p} } \exp [i(n + 2p) \varphi ]J_{n + 2p} (\beta \varvec{s})\exp \left[ { - \frac{{\varvec{s}^{2} }}{{w_{0}^{2} }}} \right],$$
(1)

where \(\varvec{s} = (s_{x} ,s_{y} )\) is a two-dimensional position vector, \(k = 2\pi /\lambda\) is the wave number with wavelength \(\lambda\), \(\beta\) is the beam’s scaling factor (\(\beta = k\sin \theta\), where \(\theta\) is the half cone angle of the incident beam), \(c\) is the asymmetry parameter, \(n\) is the OAM quantum number, and \(J_{n + 2p} ( \cdot )\) is the \(n + 2p\)th order of the first type of Bessel function, \(w_{0}\) is the beam waist width of the Gaussian envelope in initial field. When \(c = 0\), Eq. (1) reduces to the conventional expression of a Bessel–Gaussian beam.

The cross-spectral density (CSD) of a Lommel–Gaussian beam at \(z = 0\) is given as

$$\begin{aligned} W(\varvec{s}_{1} ,\varvec{s}_{2} ,0) = &\, E_{n} (\varvec{s}_{1} ,0)E_{n}^{ * } (\varvec{s}_{2} ,0) \\ = &\, \sum\limits_{p = 0}^{\infty } {\sum\limits_{{p^{'} = 0}}^{\infty } {} ( - 1)^{{p + p^{'} }} c^{2p} (c^{ * } )^{{2p^{'} }} } \exp [i(n + 2p) \varphi_{1} ]J_{n + 2p} (\beta \varvec{s}_{1} ) \\ & \times \exp [ - i(n + 2p^{'} ) \varphi_{2} ]J_{{n + 2p^{'} }} (\beta s_{2} )\exp \left[ { - \frac{{\varvec{s}_{1}^{2} + \varvec{s}_{2}^{2} }}{{w_{0}^{2} }}} \right], \\ \end{aligned}$$
(2)

where \(\varvec{s}_{1}\) and \(\varvec{s}_{2}\) specify two different points in the \(z = 0\) plane.

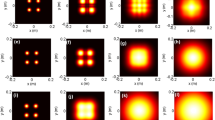
Figure 1 depicts the normalized transverse intensity distribution of a Lommel–Gaussian beam at the source plane. The calculation parameters are chosen as: \(w_{0} = 3\;{\text{cm}}\), \(\lambda = 632.8\;{\text{nm}}\), \(\beta = 80\;{\text{m}}^{ - 1}\), and \(n = 1\). It is clearly seen that the beam profile is determined by the value of the asymmetry parameter \(c\). When \(c\) is taken to a small value (\(c = 0\) corresponding to the case of a Bessel–Gaussian beam), the beam profile displays a circular symmetry. When \(c\) is adopted a big value, the beam profile displays axial symmetry and the direction of symmetry depends on \(c\).

Fig. 1
figure 1

Normalized transverse intensity of a Lommel–Gaussian beam at the source plane for different asymmetry parameters a \(c = 0\), b \(c = 0.1\), c \(c = 0.8\), and d \(c = 0.8i\)

Full size image

Based on the Bessel integral representation

$$\int_{0}^{2\pi } {\exp [i\rho \cos (\theta - \varphi )]\exp (im\theta )} {\text{d}}\theta = 2\pi i^{m} J_{m} (\rho )\exp (im \varphi ).$$
(3)

Then, Eq. (2) can expressed as

$$\begin{aligned} W(\varvec{s}_{1} ,\varvec{s}_{2} ,0) = & & \frac{1}{{(2\pi )^{2} }}\sum\limits_{p = 0}^{\infty } {} \sum\limits_{{p^{'} = 0}}^{\infty } {( - 1)^{{p + p^{'} }} c^{2p} (c^{ * } )^{{2p^{'} }} } \\ \, & \times \int_{0}^{2\pi } {} \int_{0}^{2\pi } {} W_{{\theta \theta^{'} }} (\varvec{s}_{1} ,\varvec{s}_{2} ,0)\exp [i(n + 2p)\theta - i(n + 2p^{'} )\theta^{'} ]{\text{d}}\theta {\text{d}}\theta^{'} , \\ \end{aligned}$$
(4)

where

$$W_{{\theta \theta^{'} }} (\varvec{s}_{1} ,\varvec{s}_{2} ,0) = \exp \left[ { - \frac{{\varvec{s}_{1}^{2} + \varvec{s}_{2}^{2} }}{{w_{0}^{2} }}} \right] \times \exp [i\beta (s_{{x\text{1}}} \cos \theta + s_{{y\text{1}}} \sin \theta - s_{{x\text{2}}} \cos \theta^{'} - s_{{y\text{2}}} \sin \theta^{'} )].$$
(5)

Using the summand difference vector notions

$$\varvec{s} = {{(\varvec{s}_{1} + \varvec{s}_{2} )} \mathord{\left/ {\vphantom {{(\varvec{s}_{1} + \varvec{s}_{2} )} 2}} \right. \kern-0pt} 2},\;\varvec{s}_{d} = \varvec{s}_{1} - \varvec{s}_{2} .$$
(6)

Equation (4) can expressed as

$$\begin{aligned} W(\varvec{s},\varvec{s}_{d} ,0) = & \frac{1}{{(2\pi )^{2} }}\sum\limits_{p = 0}^{\infty } {} \sum\limits_{{p^{'} = 0}}^{\infty } {( - 1)^{{p + p^{'} }} c^{2p} (c^{ * } )^{{2p^{'} }} } \\ & \times \int_{0}^{2\pi } {} \int_{0}^{2\pi } {} W_{{\theta \theta^{'} }} (\varvec{s},\varvec{s}_{d} ,0)\exp [i(n + 2p)\theta - i(n + 2p^{'} )\theta^{'} ]{\text{d}}\theta {\text{d}}\theta^{'} , \\ \end{aligned}$$
(7)

and

$$W_{{\theta \theta^{'} }} (\varvec{s},\varvec{s}_{d} ,0) = \exp \left[ { - \frac{{2\varvec{s}^{2} }}{{w_{0}^{2} }} - \frac{1}{{2w_{0}^{2} }}\varvec{s}_{d}^{2} } \right] + i\left( {{\mathbf{A}}_{ - } \varvec{s} + \frac{{{\mathbf{A}}_{ + } \varvec{s}_{d} }}{2}} \right),$$
(8)

where \({\mathbf{A}}_{ \pm } = \beta (\cos \theta \pm \cos \theta^{'} ,\sin \theta \pm \sin \theta^{'} ).\).

Using the extended Huygens–Fresnel principle, the received CSD of a Lommel–Gaussian beam in turbulence is written as [24,25,26]

$$\begin{aligned} W\left( {\varvec{\rho},\varvec{\rho}_{d} ,z} \right) = & \frac{1}{{(2\pi )^{2} }}\sum\limits_{p = 0}^{\infty } {} \sum\limits_{{p^{'} = 0}}^{\infty } {( - 1)^{{p + p^{'} }} c^{2p} (c^{ * } )^{{2p^{'} }} } \\ &\quad \times \int_{0}^{2\pi } {} \int_{0}^{2\pi } {} W_{{\theta \theta^{'} }} \left( {\varvec{\rho},\varvec{\rho}_{d} ,z} \right)\exp [i(n + 2p)\theta - i(n + 2p^{'} )\theta^{'} ]{\text{d}}\theta {\text{d}}\theta^{'} , \\ \end{aligned}$$
(9)

in which

$$\begin{aligned} W_{{\theta \theta^{'} }} \left( {\varvec{\rho},\varvec{\rho}_{d} ,z} \right) = & \left( {\frac{k}{2\pi z}} \right)^{2} \int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {W_{{\theta \theta^{'} }} (\varvec{s},\varvec{s}_{d} ,0)} } } } \\ & \times \exp \left[ {\frac{ik}{z}\left( {\varvec{\rho}- \varvec{s}} \right)\left( {\varvec{\rho}_{d} - \varvec{s}_{d} } \right) - H(\varvec{\rho}_{d} ,\varvec{s}_{d} ,z)} \right]{\text{d}}^{2} \varvec{s}{\text{d}}^{2} \varvec{s}_{d} , \\ \end{aligned}$$
(10)

where the following sum and difference vector notations are used

$$\varvec{\rho}= \text{(}\varvec{\rho}_{1} +\varvec{\rho}_{2} )/2,\varvec{\rho}_{d} =\varvec{\rho}_{1} -\varvec{\rho}_{2} .$$
(11)

The parameter \(H(\varvec{\rho}_{d} ,\varvec{s}_{d} ,z)\) in Eq. (10) denotes the intensity of the turbulence and is defined as [24, 26]

$$H(\varvec{\rho}_{d} ,\varvec{s}_{d} ,z) = 4\pi^{2} k^{2} z\int_{0}^{1} {{\text{d}}\xi \int_{0}^{\infty } {[1 - J_{0} (\kappa \left| {\varvec{s}_{d} \xi + (1 - \xi )\varvec{\rho}_{d} } \right|} } )]\varPhi_{n} (\kappa )\kappa {\text{d}}\kappa ,$$
(12)

where \(J_{0} ( \cdot )\) denotes the Bessel function of zero order, and \(\varPhi_{n} (\kappa )\) is the power spectrum of the refractive index fluctuations.

By use of the CSD \(W\left( {\rho ,\rho_{d} ,z} \right)\), the WDF is expressed as [24, 26]

$$h(\varvec{\rho}, \varphi ,z) = \left( {\frac{k}{2\pi }} \right)^{2} \int_{ - \infty }^{\infty } {\int_{{{ - }\infty }}^{\infty } {W(\varvec{\rho},\varvec{\rho}_{d} ,z)\exp ( - ik \varphi \cdot\varvec{\rho}{}_{d}){\text{d}}^{2} } }\varvec{\rho}_{d} .$$
(13)

Substituting Eq. (9) into Eq. (13), the WDF of a Lommel–Gaussian beam is given as

$$\begin{aligned} h(\varvec{\rho}, \varphi ,z) = & \frac{1}{{(2\pi )^{2} }}\sum\limits_{p = 0}^{\infty } {\sum\limits_{{p^{'} = 0}}^{\infty } {( - 1)^{{p + p^{'} }} c^{2p} (c^{ * } )^{{2p^{'} }} } } \\ & \times \int_{0}^{2\pi } {\int_{0}^{2\pi } {h_{{\theta \theta^{'} }} (\varvec{\rho}, \varphi ,z)\exp [i(n + 2p)\theta - i(n + 2p^{'} )\theta^{'} ]{\text{d}}\theta {\text{d}}\theta^{'} } } , \\ \end{aligned}$$
(14)

and

$$h_{{\theta \theta^{'} }} (\varvec{\rho}, \varphi ,z) = \frac{1}{{(2\pi )^{2} }}\left( {\frac{k}{2\pi }} \right)^{2} \int_{ - \infty }^{\infty } {\int_{{{ - }\infty }}^{\infty } {W_{{\theta \theta^{'} }} (\varvec{\rho},\varvec{\rho}_{d} ,z)\exp ( - ik \varphi \cdot\varvec{\rho}{}_{d}){\text{d}}^{2} } }\varvec{\rho}_{d} .$$
(15)

Substituting Eq. (10) into Eq. (15), after some operation as shown in Refs [26, 27], the formula of the WDF for the Lommel–Gaussian beam on turbulent propagation is given as

$$\begin{aligned} h_{{\theta \theta^{'} }} (\varvec{\rho}, \varphi ,z) = & \frac{1}{{(2\pi )^{2} }}\left( {\frac{k}{2\pi }} \right)^{2} \frac{{\pi w_{0}^{2} }}{2}\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {\exp } } } } \left[ { - \frac{{w_{0}^{2} {\mathbf{A}}_{{_{ - } }}^{\varvec{2}} }}{8} - \frac{{\varvec{\rho}_{\text{d}}^{\text{2}} }}{{\text{2}w_{0}^{2} }} + \frac{{i{\mathbf{A}}_{ + } }}{2}\varvec{\rho}_{d} } \right. \\ & - \left( {\frac{{w_{0}^{2} }}{8} + \frac{{z^{2} }}{{2w_{0}^{2} k^{2} }}} \right)\varvec{\kappa}_{d}^{\varvec{2}} + \left( {\frac{{i{\mathbf{A}}_{ + } z}}{2k} - \frac{{w_{0}^{2} {\mathbf{A}}_{ - } }}{4} - \frac{z}{{w_{0}^{2} k}}\varvec{\rho}{}_{d}} \right)\varvec{\kappa}_{d} - ik \varphi \cdot\varvec{\rho}{}_{d} - i\varvec{\rho \kappa }_{d} \\ & - \left. {H(\varvec{\rho}_{d} ,\varvec{\rho}_{d} + \frac{z}{k}\varvec{\kappa}_{d} ,z)} \right]{\text{d}}^{2}\varvec{\rho}_{d} d^{2}\varvec{\kappa}_{\varvec{d}}^{\varvec{2}} . \\ \end{aligned}$$
(16)

The moments of high-order moments of the WDF is expressed as [24,25,26]

$$< \rho_{x}^{{n_{1} }} \rho_{y}^{{n_{2} }} \theta_{x}^{{m_{1} }} \theta_{y}^{{m_{2} }} > = \frac{{\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {\rho_{x}^{{n_{1} }} \rho_{y}^{{n_{2} }} \theta_{x}^{{m_{1} }} \theta_{y}^{{m_{2} }} } } } } h(\varvec{\rho}, \varphi ,z){\text{d}}^{2}\varvec{\rho}{\text{d}}^{2} \varphi }}{{\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {h(\varvec{\rho}, \varphi ,z)} } } } {\text{d}}^{2}\varvec{\rho}{\text{d}}^{2} \varphi }}.$$
(17)

Substituting Eq. (14) into Eq. (17), the WDF of Lommel–Gaussian beam is given as follows:

$$< \rho_{x}^{{n_{1} }} \rho_{y}^{{n_{2} }} \theta_{x}^{{m_{1} }} \theta_{y}^{{m_{2} }} > \; = \frac{{\sum\limits_{p = 0}^{\infty } {\sum\limits_{{p^{'} = 0}}^{\infty } {\int_{0}^{2\pi } {\int_{0}^{2\pi } {\rho_{{x\theta \theta^{'} }}^{{n_{1} }} \rho_{{y\theta \theta^{'} }}^{{n_{2} }} \theta_{{x\theta \theta^{'} }}^{{m_{1} }} \theta_{{y\theta \theta^{'} }}^{{m_{2} }} } } } } \exp [i(n + 2p)\theta - i(n + 2p^{'} )\theta^{'} ]{\text{d}}\theta {\text{d}}\theta^{'} }}{{\sum\limits_{p = 0}^{\infty } {\sum\limits_{{p^{'} = 0}}^{\infty } {\int_{0}^{2\pi } {\int_{0}^{2\pi } {h_{{\theta \theta^{'} }} (\rho , \varphi ,z)} } } } \exp [i(n + 2p)\theta - i(n + 2p^{'} )\theta^{'} ]{\text{d}}\theta {\text{d}}\theta^{'} }},$$
(18)

where

$$< \rho_{x}^{{n_{1} }} \rho_{y}^{{n_{2} }} \theta_{x}^{{m_{1} }} \theta_{y}^{{m_{2} }} >_{{\theta \theta^{'} }} = \int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {\rho_{{x\theta \theta^{'} }}^{{n_{1} }} \rho_{{y\theta \theta^{'} }}^{{n_{2} }} \theta_{{x\theta \theta^{'} }}^{{m_{1} }} \theta_{{y\theta \theta^{'} }}^{{m_{2} }} } } } } h_{{_{{\theta \theta^{'} }} }} (\varvec{\rho}, \varphi ,z){\text{d}}^{2}\varvec{\rho}{\text{d}}^{2} \varphi .$$
(19)

Substituting Eq. (16) in Eq. (19), we obtain

$$<\varvec{\rho}^{2} >_{{\theta \theta^{'} }} = \left[ {\frac{{w_{0}^{2} }}{2} + \frac{{2z^{2} }}{{w_{0}^{2} k^{2} }} + \frac{{z^{2} }}{{4k^{2} }}({\mathbf{A}}_{x + }^{2} + {\mathbf{A}}_{y + }^{2} ) - \frac{{w_{0}^{4} }}{16}({\mathbf{A}}_{x - }^{2} + {\mathbf{A}}_{y - }^{2} ) + \frac{{4z^{2} }}{{k^{2} }}T} \right] \times \exp \left( { - \frac{{w_{0}^{2} {\mathbf{A}}_{ - }^{\varvec{2}} }}{8}} \right)\frac{{\pi w_{0}^{2} }}{2},$$
(20)
$$< \varphi^{2} >_{{\theta \theta^{'} }} = \left[ {\frac{2}{{w_{0}^{2} k^{2} }} + \frac{{z^{2} }}{{4k^{2} }}({\mathbf{A}}_{x + }^{2} + {\mathbf{A}}_{y + }^{2} ) + \frac{12}{{k^{2} }}T} \right]\exp \left( { - \frac{{w_{0}^{2} {\mathbf{A}}_{ - }^{\text{2}} }}{8}} \right)\frac{{\pi w_{0}^{2} }}{2},$$
(21)
$$<\varvec{\rho} \varphi >_{{\theta \theta^{'} }} = \left[ {\frac{2z}{{w_{0}^{2} k^{2} }} + \frac{{\beta^{2} z}}{{2k^{2} }}({\mathbf{A}}_{x + }^{2} + {\mathbf{A}}_{y + }^{2} ) + \frac{6z}{{k^{2} }}T} \right]\exp \left( { - \frac{{w_{0}^{2} {\mathbf{A}}_{ - }^{\varvec{2}} }}{8}} \right)\frac{{\pi w_{0}^{2} }}{2}.$$
(22)

Substituting Eqs. (20)–(22) in Eq. (18), we get

$$<\varvec{\rho}^{2} > = \frac{{w_{0}^{2} }}{2} + \frac{{2z^{2} }}{{w_{0}^{2} k^{2} }} + \frac{{\beta^{2} z^{2} }}{{2k^{2} }}\left( {\frac{{B_{n + 1} + B_{n - 1} }}{{2B_{n} }} + 1} \right) + \frac{{\beta^{2} w_{0}^{4} }}{8}\left( {\frac{{B_{n + 1} + B_{n - 1} }}{{2B_{n} }} - 1} \right) + \frac{{4z^{2} }}{{k^{2} }}T,$$
(23)
$$< \varphi^{2} > = \frac{2}{{w_{0}^{2} k^{2} }} + \frac{{\beta^{2} }}{{2k^{2} }}\left( {\frac{{B_{n + 1} + B_{n - 1} }}{{2B_{n} }} + 1} \right) + \frac{12}{{k^{2} }}T,$$
(24)
$$<\varvec{\rho} \varphi > = \frac{2z}{{w_{0}^{2} k^{2} }} + \frac{{\beta^{2} z}}{{2k^{2} }}\left( {\frac{{B_{n + 1} + B_{n - 1} }}{{2B_{n} }} + 1} \right) + \frac{6z}{{k^{2} }}T,$$
(25)

where \(B_{n} = \sum\nolimits_{p = 0}^{\infty } {\left| c \right|^{4p} I_{n + 2p} \left( {\frac{{\beta^{2} w_{0}^{2} }}{4}} \right),}\) and \(T = \frac{{\pi^{2} k^{2} z}}{3}\int_{0}^{\infty } {\kappa^{3} \varPhi_{n} (\kappa ){\text{d}}\kappa }\) represents the contribution of turbulent atmosphere.

Using the second moments of WDF, the propagation factor of laser beams is given as [24, 27]

$$M^{2} (z) = k( <\varvec{\rho}^{2} > < \varphi^{2} > - <\varvec{\rho} \varphi >^{2} )^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} .$$
(26)

Substituting Eqs. (23)–(25) into Eq. (26), the expression for a Lommel–Gaussian beam is expressed as

$$\begin{aligned} M^{2} (z) = & k\left\{ {\left[ {\frac{{w_{0}^{2} }}{2} + \frac{{2z^{2} }}{{w_{0}^{2} k^{2} }} + \frac{{\beta^{2} z^{2} }}{{2k^{2} }}\left( {\frac{{B_{n + 1} + B_{n - 1} }}{{2B_{n} }} + 1} \right) + \frac{{\beta^{2} w_{0}^{4} }}{8}\left( {\frac{{B_{n + 1} + B_{n - 1} }}{{2B_{n} }} - 1} \right) + \frac{{4z^{2} }}{{k^{2} }}T} \right]} \right. \\ & \times \left[ {\frac{2}{{w_{0}^{2} k^{2} }} + \frac{{\beta^{2} }}{{2k^{2} }}\left( {\frac{{B_{n + 1} + B_{n - 1} }}{{2B_{n} }} + 1} \right) + \frac{12}{{k^{2} }}T} \right] \\ \left. { - \left[ {\frac{2z}{{w_{0}^{2} k^{2} }} + \frac{{\beta^{2} z}}{{2k^{2} }}\left( {\frac{{B_{n + 1} + B_{n - 1} }}{{2B_{n} }} + 1} \right) + \frac{6z}{{k^{2} }}T} \right]^{2} } \right\}^{1/2} . \\ \end{aligned}$$
(27)

Equation (27) can be reduced to the case of a Lommel–Gaussian beam in free space when \(T = 0\).

If \(T = 0\) and \(c = 0\), Eq. (27) is easily reduced to the result of the Bessel–Gaussian beam in free space [28]:

$$M^{2} = \left\{ {\left[ {1 + n + \beta^{2} w_{0}^{2} I_{n + 1} \left( {\frac{{\beta^{2} w_{0}^{2} }}{4}} \right)/4I_{n} \left( {\frac{{\beta^{2} w_{0}^{2} }}{4}} \right)} \right] - \left( {\frac{{\beta^{2} w_{0}^{2} }}{4}} \right)^{2} } \right\}^{1/2} .$$
(28)

The angular width of a Lommel–Gaussian beam is written as [27, 29]

$$\begin{aligned} \varphi (z) = & ( < \left| { \varphi - < \varphi > } \right|^{2} > )^{1/2} = ( < \varphi^{2} > )^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \\ = & \sqrt {\frac{2}{{w_{0}^{2} k^{2} }} + \frac{{\beta^{2} }}{{2k^{2} }}\left( {\frac{{B_{n + 1} + B_{n - 1} }}{{2B_{n} }} + 1} \right) + \frac{12}{{k^{2} }}T} . \\ \end{aligned}$$
(29)

Equation (27) and (29) are the main result obtained in the present paper, which provides us with a convenient way to study the propagation properties of a Lommel–Gaussian beam in turbulent atmosphere.

3 Numerical calculations and analyses

For convenience of comparison, the normalized propagation factor \((M^{2} (z)/M^{2} (0))\) is adopted, and the Von Karman spectrum is chosen and expressed as follows [30]:

$$\varPhi_{n} (\kappa ) \approx 0.033C_{n}^{2} \frac{{\exp [ - ({{\kappa^{2} } \mathord{\left/ {\vphantom {{\kappa^{2} } {\kappa_{m}^{2} }}} \right. \kern-0pt} {\kappa_{m}^{2} }})]}}{{(\kappa^{2} + \kappa_{0}^{2} )^{{{\raise0.5ex\hbox{$\scriptstyle {\text{11}}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle \text{6}$}}}} }}(0 \le \kappa \langle \infty ),$$
(30)

where \(C_{n}^{2}\) is structure constant of turbulence, and \(\kappa_{0} = 1/L_{0}\), \(\kappa_{m} = 5.92/l_{0}\), \(L_{0}\), and \(l_{0}\) denote the outer and inner scales of turbulence. The parameters are set as follows: \(w_{0} = 3\;{\text{cm}}\), \(L_{0} = 10\;{\text{m}}\), \(l_{0} = 1\;{\text{cm}}\), \(\lambda = 632.8\;{\text{nm}}\), \(C_{n}^{2} = 10^{ - 15} \;{\text{m}}^{ - 2/3}\), \(\beta = 80\;{\text{m}}^{ - 1}\), and \(n = 1\). The other parameters are stated in the figure.

The normalized angular width of a Lommel–Gaussian beam on propagation through atmospheric turbulence with different OAM quantum numbers \(n\), wavelength \(\lambda\), and the absolute value of asymmetry parameter \(c\) are depicted in Fig. 2. The normalized angular width increases with the distance on propagation in turbulence. For a certain distance, the normalized angular width spreads slower with larger OAM quantum number or wavelength, i.e., the affect of turbulence on the normalized angular width is smaller. The normalized angular width is independent of \(\left| c \right|\) when the Lommel–Gaussian beams propagate in turbulence.

Fig. 2
figure 2

Normalized angular widths of a Lommel–Gaussian beam propagating in turbulent atmosphere with different a OAM quantum numbers \(n\), b wavelength \(\lambda\), and c modulus of asymmetry parameter \(c\), respectively

Full size image

Figure 3 presents the normalized angular width of a Lommel–Gaussian beam through atmospheric turbulence with different structure constant \(C_{n}^{2}\), inner scale \(l_{0}\), and outer scale \(L_{0}\), respectively. The normalized angular width for a Lommel–Gaussian beam becomes larger when the structure constant is larger or the inner scale is smaller, which indicates that under these conditions, the beam is more affected by the turbulence, and the beam quality is worse. The normalized angular width of a Lommel–Gaussian beam remains unaffected as distance increases in free space, i.e., it keeps invariant. It can also be seen that the outer scale has little effect on the normalized angular width.

Fig. 3
figure 3

Normalized angular width for a Lommel–Gaussian beam on propagation through atmospheric turbulence with different a structure constant \(C_{n}^{2}\), b inner scale \(l_{0}\), and c outer scale \(L_{0}\), respectively

Full size image

To analyze the relationship between propagation factor of a Lommel–Gaussian beam and its beam parameters, the normalized propagation factor for a Lommel–Gaussian beam propagating through turbulence with different OAM quantum numbers \(n\), wavelength \(\lambda\), and modulus of asymmetry parameter \(c\) are depicted in Fig. 4, respectively. The normalized propagation factor for a Lommel–Gaussian beam spreads faster in turbulence as the OAM quantum number and the wavelength is smaller. For a certain distance, the propagation factor of a Lommel–Gaussian beam with OAM quantum numbers (\(n \ne 0\)) increases more slowly than that of a Lommel–Gaussian beam without OAM quantum numbers (\(n = 0\)), which indicates that a Lommel–Gaussian beam with OAM quantum numbers has advantage over a Lommel–Gaussian beam without OAM quantum numbers for reducing the negative effect of turbulent atmosphere, and may be helpful in long-distance communications in atmospheric turbulence. This phenomenon can be physically interpreted by the fact that the Lommel–Gaussian beam with OAM quantum numbers contains screw wavefront dislocations, which have the stronger ability in reducing the effect of atmospheric turbulence than the beam without OAM quantum numbers. It is also found that the normalized propagation factor is independent of \(\left| c \right|\), which indicates that the beam’s transverse intensity profiles can be easily modified by changing the asymmetry parameter in various applications without affecting the propagation. As a comparison, the normalized propagation factor of the Bessel–Gaussian (BG, corresponding to the case of \(c = 0\)) beams under the same conditions is also depicted in Fig. 4a. The propagation properties of the BG beams are similar to that of the Lommel–Gaussian beams, whereas the continuous change of OAM makes the Lommel–Gaussian beams more desirable in practical applications and this is an important feature of the Lommel–Gaussian beams.

Fig. 4
figure 4

Normalized propagation factor for a Lommel–Gaussian beam propagating in turbulent atmosphere with different a OAM quantum numbers \(n\), b wavelength \(\lambda\), and c modulus of asymmetry factor \(c\), respectively

Full size image

Figure 5 presents the normalized propagation factor of a Lommel–Gaussian beam in atmospheric turbulence with different structure constant \(C_{n}^{2}\), inner scale \(l_{0}\), and outer scale \(L_{0}\), respectively. The normalized propagation factor for a Lommel–Gaussian beam spread more rapidly in turbulence when the structure constant is larger or inner scale is smaller, which indicates that under these conditions, the Lommel–Gaussian beam is more affected in turbulence, i.e., the beam quality is worse. It can be found that the normalized propagation factor is independent of distance when the propagating in free space. It can also be found that the outer scale has little effect on the beam quality.

Fig. 5
figure 5

Normalized propagation factor for a Lommel–Gaussian beam propagating through atmospheric turbulence with different a structure constant \(C_{n}^{2}\), b inner scale \(l_{0}\), and c outer scale \(L_{0}\), respectively

Full size image

4 Conclusion

In summary, analytical formulas of the propagation parameters of a Lommel–Gaussian beam propagating in turbulent atmosphere are derived. The influence of turbulent atmosphere and beam parameters on the propagation of the Lommel–Gaussian beam has been investigated. Within the range of parameters examined, it is shown that the as structure constant \(C_{n}^{2}\) is smaller, or OAM quantum number \(n\), inner scale \(l_{0}\) and the wave length \(\lambda\) is larger, the Lommel–Gaussian beam is preferable. The beam asymmetry can be easily changed by one beam parameter according to different practical applications without affecting the beam propagation. It is expected that this work will be useful for free space optical communications.