1 Introduction

Over the past decades, the propagation properties of laser beams passing through atmospheric turbulence have received more and more attention paralleling the evolution of laser beam applications. The spreading of a laser beam passing through the turbulent atmosphere possesses substantial applications such as free-space communications (Navidpour et al. 2007), active optical imaging (Hajjarian et al. 2010), remote sensing (Andrews and Phillips 1998) and so on. It is well known that during the propagation of light beam in atmospheric turbulence, the temperature and the pressure change thanks to the inhomogeneity of the atmosphere, as well as this variation leads to the change in the refractive index. This results in light intensity fluctuations that complicate beam propagation (Friehe et al. 1975) which limits its accuracy. So, understanding how optical beams react with the turbulent atmosphere is essential.

Up to now, the propagation properties of various types of laser beams in a turbulent atmosphere have been reported by a lot of researchers such as Cai and He (2006) studied the spreading of various dark hollow beams in a turbulent atmosphere. In the same year, Gbur (2014) investigated the properties of partially coherent beam in atmospheric turbulence. Recently, a detailed investigation of the propagation of multi-cosine-Laguerre-Gaussian correlated Schell-model beams in free space and atmospheric turbulence has been presented by Zhu et al. (2017). More recently, Teen et al. who established the Bessel-Gaussian beam propagation through the turbulence in free space optical communication (Arul Teen et al. 2018). Thereby, an analysis of flat-topped Gaussian vortex beam scintillation properties in atmospheric turbulence has been performed by Elmabruk and Eyyuboğlu (2019). Deng et al. (2020) have been derived the characteristics of high-power partially coherent laser beams propagating upwards in the turbulent atmosphere. The one after that year, Ma et al. (2021) developed the research on the propagation of partially coherent cosh-Gaussian beams through an ABCD optical system in non-Kolmogorov turbulence. Moreover, the influence of atmospheric turbulence on coherent beam combining for laser weapon systems has been established in the Jabczyński and Gontar (2021). After that, Xu et al. (2022) have examined the structurally stable beams in the turbulent atmosphere (Dark and antidark beams on incoherent background). In addition, Wang et al. (2023) have explored the second-order statistics of the Hermite-Gaussian correlated Schell-model beam carrying twisted phase propagation in a turbulent atmosphere. In the same context, our research group has also carried out a significant investigation in this area. Furthermore, these studies have involved several kinds of laser beams, including generalized Humbert–Gaussian beams (Nossir et al. 2021), Pulsed Hollow Higher-Order cosh-Gaussian beams (Benzehoua and Belafhal 2023), Schell-model beams (Chib et al. 2022), generalized Bessel-Laguerre beams (Boufalah et al. 2018), generalized spiraling Bessel beams (Saad et al. 2017), dark and antidark Gaussian beams (Yaalou et al. 2019), Hollow Gaussian beams (Khannous et al. 2016), Partially coherent laser beams (Nabil et al. 2022), a General Model vortex Higher-order cosh-Gaussian beam (Ebrahim et al. 2023) and truncated Bessel-modulated Gaussian beams (Belafhal et al. 2011).

In recent years, a new type of beam family called Whittaker–Gaussian (WG) beam was introduced by Lopezmago et al. (2009) as considered the universal solution of the paraxial wave equation in circular cylindrical coordinates. This beam is a particular case of the general circular beams (Bandres and Gutiérrez-Vega 2008) and can be expressed by either the Whittaker or the confluent Hypergeometric functions. The Whittaker–Gaussian beam is one of the most interesting research subjects in laser physics because of its large applications and its physical characteristics which have been thoroughly studied. So, to the best of our knowledge, this research hasn’t been examined elsewhere. Motivated by these features, this study looks at the evolution characteristics of the WG beam through a turbulent atmosphere. The rest of this paper is organized as follows: in the second Section, we investigate the source electric field of the WG beam and then we treat the received intensity expression of the beam spreading in atmospheric turbulence. The expression for the propagation of the WG beam in atmospheric turbulence by means of the extended Huygens–Fresnel integral and Rytov method is derived in the third Section. In the fourth Section, some numerical examples are presented and discussed versus the propagation distance under the change of the turbulence atmospheric and the incident beam parameters. Finally, we complete with a summary of our main results in the conclusion part.

2 Principle of the propagation of WG laser beam through a turbulent atmospheric

The electric field distribution of the WG beam at \(z = 0\) in the cylindrical coordinates system can be expressed as (Lopezmago et al. 2009; Nossir et al. 2023)

$$ E\left( {r_{0} ,z = 0,\theta_{0} } \right) = \left( {\frac{{ir_{0}^{2} }}{{2\omega_{0}^{2} }}} \right)^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0pt} 2}}} M_{{\frac{\mu }{2},\frac{m}{2}}} \left( {\frac{{ir_{0}^{2} }}{{2\omega_{0}^{2} }}} \right)\exp \left( { - \frac{{r_{0}^{2} }}{{\omega_{0}^{2} }}} \right)\exp \left( {im\theta_{0} } \right), $$
(1)

where \(r_{0}\) and \(\theta_{0}\) are the radial and azimuthal coordinates, respectively \(m\) is the Whittaker–Gaussian beams order, \(\omega_{0}\) is the beam waist width and the parameter \(\mu\) is a complex continuous radial order.

Using the explicit form of the special function \(M_{{\frac{\mu }{2},\frac{m}{2}}} \left( x \right)\) given by the Kummer function (Srivastava and Manocha 1984)

$$ M_{{\frac{\mu }{2},\frac{m}{2}}} \left( x \right) = x^{{\frac{m}{2} + \frac{1}{2}}} \exp \left( { - \frac{x}{2}} \right){}_{1}F_{1} \left( {\frac{m - \mu + 1}{2},m + 1;x} \right), $$
(2)

where \({}_{1}F_{1} \left( {a,b;x} \right)\) is the confluent hypergeometric function and by recalling the following series expansions of this last expression as (Srivastava and Manocha 1984)

$$ {}_{1}F_{1} \left( {a,b,z} \right) = \sum\limits_{t = 0}^{\infty } {\frac{{\left( a \right)_{t} }}{{\left( b \right)_{t} }}} \frac{{z^{t} }}{t!}. $$
(3)

Then, the expression of Eq. (1) may be rewritten in the following form

$$ E\left( {r_{0} ,z = 0,\theta_{0} } \right) = \left( {\frac{{ir_{0}^{2} }}{{2\omega_{0}^{2} }}} \right)^{\frac{m}{2}} \exp \left( {im\theta_{0} } \right)\exp \left( { - \frac{{r_{0}^{2} }}{{\omega_{0}^{2} }}} \right)\exp \left( { - \frac{{ir_{0}^{2} }}{{4\omega_{0}^{2} }}} \right)\sum\limits_{n = 0}^{\infty } {\frac{{\left( {\frac{m + 1 - \mu }{2}} \right)_{n} }}{{\left( {m + 1} \right)_{n} }}} \frac{{\left( {\frac{{ir_{0}^{2} }}{{2\omega_{0}^{2} }}} \right)^{n} }}{n!}. $$
(4)

This last equation represents the input field of the WG beam which is introduced as the product of the fundamental Gaussian beam and the infinite sum. Let us now consider the turbulent atmosphere illuminated by the Whittaker–Gaussian beam as seen in Fig. 1. According to Rytov's theory and the extended Collins formula, the electrical field distribution of a laser beam in a turbulent atmosphere along the z-axis is derived from the incident field at the source plane placed at \(z = 0\) as (Andrews and Phillips 1998; Born and Wolf 1999)

$$ E(\vec{\rho },z,t) = - \frac{ik}{{2\pi z}}\exp \left( {ikz} \right)\int\limits_{0}^{a} {\int\limits_{0}^{2\pi } {E(\vec{r}_{0} ,z = 0)\exp \,\left[ {\frac{ik}{{2z}}\left( {\vec{r}_{0} - \vec{\rho }} \right)^{2} + \psi \left( {\vec{r}_{0} - \vec{\rho }} \right) - 2i\pi ft} \right]} } d\vec{r}_{0} , $$
(5)

where the field at the point \(\vec{r}_{0} (r_{0} ,\theta_{0} )\) at the source plane is \(E(\vec{r}_{0} ,z = 0)\) and the field at the point \(\vec{\rho }(\rho ,\phi )\) in output plane is \(E(\vec{\rho },z,t)\), \(z\) is the propagation distance, \(k = 2\pi /\lambda\) is the wave number with \(\lambda\) is the wavelength of laser light in vacuum, \(a\) is the emitting aperture radius, \(\psi (\vec{r}_{1} ,\rho )\) is the solution to the Rytov method that characterizes the random part because of the turbulent atmosphere of the complex phase of a spherical wave, \(f\) and \(t\) represent the frequency and the time, respectively. Additionally, \(d\vec{r} = r_{0} dr_{0} d\theta_{0}\) is the elementary surface in the source plane.

Fig. 1
figure 1

Illustration of the geometry of the WG beam propagating through the turbulent atmosphere

Full size image

At the receiver plane, the average intensity is defined as

$$ \left\langle {I\left( {\vec{\rho },z} \right)} \right\rangle = \left\langle {E(\vec{\rho },z,t)E^{ * } (\vec{\rho },z,t)} \right\rangle , $$
(6)

where \(*\) signifies the complex conjugation and the angle brackets refer to the ensemble average over the medium statistics. From Eq. (5), the average intensity of the laser beam passing through the turbulent atmosphere is expressed as

$$ \begin{aligned} \left\langle {I\left( {\vec{\rho },z} \right)} \right\rangle &= \left( {\frac{k}{2z\pi }} \right)^{2} \int\limits_{0}^{a} {\int\limits_{0}^{a} {\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {\left\langle {E(\vec{r}_{1} ,0)E^{ * } (\vec{r}_{2} ,0)} \right\rangle } } } } \hfill \\ &\quad \times \exp \left[ {\frac{ik}{{2z}}\left( {\left( {\vec{r}_{1} - \vec{\rho }} \right)^{2} - \left( {\vec{r}_{2} - \vec{\rho }} \right)^{2} } \right)} \right]\left\langle {\exp \left[ {\psi \left( {r_{1} ,\rho } \right) + \psi^{ * } \left( {r_{2} ,\rho } \right)} \right]\,} \right\rangle d\vec{r}_{1} d\vec{r}_{2} . \hfill \\ \end{aligned} $$
(7)

Within the Rytov theory, the last term in angle brackets of Eq. (7) that defines the impact of turbulence on the propagation of a laser beam is given by (Andrews and Phillips 1998)

$$ \left\langle {\exp \left[ {\psi \left( {r_{1} ,\rho } \right) + \psi^{ * } \left( {r_{2} ,\rho } \right)} \right]\,} \right\rangle = \exp \left[ { - 0.5D_{\psi } \left( {r_{1} ,r_{2} ,\rho } \right)} \right] \cong \exp \left[ { - \frac{1}{{\rho_{0}^{2} }}\left( {\vec{r}_{1} - \vec{r}_{2} } \right)^{2} } \right]\,, $$
(8)

where \(D_{\psi } \left( {r_{1} ,r_{2} ,\rho } \right)\) is the phase structure function and \(\rho_{0} = \left( {0.545C_{n}^{2} k^{2} z} \right)^{{ - {3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0pt} 5}}}\) is the coherence length of a spherical wave propagating in the turbulent medium with \(C_{n}^{\,2}\) is the refractive index structure constant that determines the turbulent strength of the turbulent atmosphere. On substituting from Eqs. (4) and (8) into Eq. (7) and after some rearranging, we can express the average intensity of the WG beam after its propagation in atmospheric turbulent as

$$ \begin{aligned} < I\left( {\rho ,z} \right) > &= \left( {\frac{k}{2z\pi }} \right)^{2} \sum\limits_{{s_{1} = 0}}^{\infty } {\frac{{\left( {\frac{m + 1 - \mu }{2}} \right)_{{s_{1} }} }}{{\left( {m + 1} \right)_{{s_{1} }} }}} \frac{{\left( {\frac{i}{{2\omega_{0}^{2} }}} \right)^{{\frac{m}{2} + s_{1} }} }}{{s_{1} !}}\sum\limits_{{s_{2} = 0}}^{\infty } {\frac{{\left( {\frac{m + 1 - \mu }{2}} \right)_{{s_{2} }} }}{{\left( {m + 1} \right)_{{s_{2} }} }}} \frac{{\left( {\frac{ - i}{{2\omega_{0}^{2} }}} \right)^{{\frac{m}{2} + s_{2} }} }}{{s_{2} !}} \hfill \\ &\quad \times \int\limits_{0}^{a} {\int\limits_{0}^{a} {\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {e^{{i\left| m \right|\left( {\theta_{1} - \theta_{2} } \right)}} } } } } \exp \left[ { - \left( {\frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{ik}{{2z}} - i\frac{1}{{4\omega_{0}^{2} }}} \right)r_{1}^{2} } \right] \hfill \\ &\quad \times \exp \left[ { - \left( {\frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{ik}{{2z}} + i\frac{1}{{4\omega_{0}^{2} }}} \right)r_{2}^{2} } \right]\exp \left[ {\frac{ik}{z}\rho \left( {r_{1} \cos \left( {\theta_{1} - \psi } \right) - r_{2} \cos \left( {\theta_{2} - \psi } \right)} \right)} \right] \hfill \\ &\quad \times \exp \left[ {\frac{{2r_{1} r_{2} }}{{\rho_{0}^{2} }}\cos \left( {\theta_{1} - \theta_{2} } \right)} \right]r_{1}^{{m + 2s_{1} + 1}} dr_{1} d\theta_{1} r_{2}^{{m + 2s_{2} + 1}} dr_{2} d\theta_{2} . \hfill \\ \end{aligned} $$
(9)

In the next section, we will derive the axial intensity of the WG beam after passing through the atmospheric turbulent by the help of the last equation.

3 Axial intensity distribution of WG beam in turbulent atmosphere

For the calculation of the on-axis average intensity of the beam we focus on the expansion form of the hard aperture function \(H\left( r \right)\) into a finite sum of complex Gaussian functions written as (Wen and Breazeal 1988)

$$ H\left( r \right) = \sum\limits_{g = 1}^{N} {A_{g} \exp \left( {\frac{{ - B_{g} }}{{a^{2} }}r^{2} } \right)} , $$
(10)

where \(A_{g}\) and \(B_{g}\) mean the expansion and Gaussian coefficients, respectively and N signifies the number of the expansion terms that in the numerical simulation equal ten and \(a\) is the half-width of the rectangular function. We use the following integral formula (Gradshteyn and Ryzhik 1994)

$$ \int_{0}^{2\pi } {\exp \left[ { - im\theta_{1} + x\cos \left( {\theta_{1} - \theta_{2} } \right)} \right]} d\theta_{1} = 2\pi \exp \left( { - im\theta_{2} } \right)I_{m} \left( x \right), $$
(11)

where \(I_{m}\) is the modified Bessel function of order \(m\).

Making use of the integral formula (Gradshteyn and Ryzhik 1994)

$$ \int_{0}^{\infty } {x^{{\mu - \frac{1}{2}}} \exp \left( { - \alpha x} \right)} \,I_{2\nu } \left( {2\beta \sqrt x } \right)dx = \frac{{\Gamma \left( {\nu + \mu + \frac{1}{2}} \right)}}{{\Gamma \left( {2\nu + 1} \right)}}\beta^{2\nu } \left( {\frac{1}{\alpha }} \right)^{{\mu + \nu + \frac{1}{2}}} {}_{1}F_{1} \left( {\mu + \nu + \frac{1}{2};1 + 2\nu ;\frac{{\beta^{2} }}{\alpha }} \right), $$
(12)

where \(\Gamma \left( x \right)\) is gamma function.

By putting \(\rho = 0\) and inserting the aperture function of Eq. (10) and using of the integral formula of Eq. (11). Therefore, the Eq. (9) become

$$ \begin{aligned} < I\left( {0,z} \right) > &= \left( \frac{k}{z} \right)^{2} \frac{{\left( {\frac{1}{{\rho_{0}^{2} }}} \right)^{m} }}{{2\Gamma \left( {m + 1} \right)}}\sum\limits_{{s_{1} = 0}}^{\infty } {\frac{{\left( {\frac{m + 1 - \mu }{2}} \right)_{{s_{1} }} }}{{\left( {m + 1} \right)_{{s_{1} }} }}} \frac{{\left( {\frac{i}{{2\omega_{0}^{2} }}} \right)^{{\frac{m}{2} + s_{1} }} }}{{s_{1} !}}\sum\limits_{{s_{2} = 0}}^{\infty } {\frac{{\left( {\frac{m + 1 - \mu }{2}} \right)_{{s_{2} }} }}{{\left( {m + 1} \right)_{{s_{2} }} }}} \frac{{\left( {\frac{ - i}{{2\omega_{0}^{2} }}} \right)^{{\frac{m}{2} + s_{2} }} }}{{s_{2} !}} \hfill \\ &\quad \times \,\,\sum\limits_{{g_{1} = 1}}^{M} {A_{{g_{1} }} } \sum\limits_{{g_{2} = 1}}^{M} {A_{{g_{2} }} } \frac{{\Gamma \left( {m + s_{2} + 1} \right)}}{{\beta_{2}^{{m + s_{2} + 1}} }}\int\limits_{2}^{ + \infty } {r_{1}^{{2m + 2s_{1} + 1}} \exp \left( { - \beta_{1} r_{1}^{2} } \right){}_{1}F_{1} \left( {m + s_{2} + 1;m + 1;\frac{{r_{1}^{2} }}{{\rho_{0}^{4} \beta_{2} }}} \right)dr_{1} ,} \hfill \\ \end{aligned} $$
(13)

where

$$ \beta_{1} = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} - \frac{ik}{{2z}} - i\frac{1}{{4\omega_{0}^{2} }} + \frac{{B_{g} }}{{a^{2} }}, $$
(14a)

and

$$ \beta_{2} = \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }} + \frac{ik}{{2z}} + i\frac{1}{{4\omega_{0}^{2} }} + \frac{{B_{g} }}{{a^{2} }}. $$
(14b)

By employing the integral formula given by (Gradshteyn and Ryzhik 1994)

$$ \begin{aligned} &\int\limits_{0}^{\infty } {x^{\delta - 1} \exp \left( { - \mu{\prime} x} \right)} {}_{m}F_{n} \left( {\alpha_{1} ,\alpha_{2} ,...,\alpha_{m} ;\beta_{1} ,\beta_{2} ,...,\beta_{n} ;\lambda x} \right)dx \hfill \\ &\quad = \Gamma \left( \delta \right)\mu{\prime}^{ - \delta } {}_{m + 1}F_{n} \left( {\alpha_{1} ,\alpha_{2} ,...,\alpha_{m} ;\delta ;\beta_{1} ,\beta_{2} ,...,\beta_{n} ;\frac{\lambda }{{\mu{\prime} }}} \right), \hfill \\ \end{aligned} $$
(15)

with \(m \le n,{\text{Re}} \delta > 0;{\text{Re}} \mu{\prime} > 0,\) if \(m < n;{\text{Re}} \mu{\prime} > \lambda ,\)\(m = n\).

One obtains after tedious algebraic calculations, the expression for the on-axis average intensity distribution of the WG beam propagating through a turbulent atmosphere is reduced to

$$ \begin{aligned} < I\left( {0,z} \right) > &= \frac{{k^{2} }}{{z^{2} }}\frac{{\left( {\frac{1}{{\rho_{0}^{2} }}} \right)^{m} }}{{2^{2} \Gamma \left( {m + 1} \right)}}\sum\limits_{{s_{1} = 0}}^{\infty } {\frac{{\left( {\frac{m + 1 - \mu }{2}} \right)_{{s_{1} }} }}{{\left( {m + 1} \right)_{{s_{1} }} }}} \frac{{\left( {\frac{i}{{2\omega_{0}^{2} }}} \right)^{{\frac{m}{2} + s_{1} }} }}{{s_{1} !}}\sum\limits_{{s_{2} = 0}}^{\infty } {\frac{{\left( {\frac{m + 1 - \mu }{2}} \right)_{{s_{2} }} }}{{\left( {m + 1} \right)_{{s_{2} }} }}} \frac{{\left( {\frac{ - i}{{2\omega_{0}^{2} }}} \right)^{{\frac{m}{2} + s_{2} }} }}{{s_{2} !}} \hfill \\ &\quad \times \,\,\sum\limits_{{g_{1} = 1}}^{M} {A_{{g_{1} }} } \sum\limits_{{g_{2} = 1}}^{M} {A_{{g_{2} }} } \frac{{\Gamma \left( {m + s_{2} + 1} \right)}}{{\beta_{2}^{{m + s_{2} + 1}} }}\frac{{\Gamma \left( {m + s_{1} + 1} \right)}}{{\beta_{1}^{{m + s_{1} + 1}} }}{}_{2}F_{1} \left( {m + s_{2} + 1,m + s_{1} + 1;m + 1;\frac{1}{{\rho_{0}^{4} \beta_{1} \beta_{2} }}} \right), \hfill \\ \end{aligned} $$
(16)

where \({}_{2}F_{1} \left( . \right)\) represents the hypergeometric function. The closed form of the WG beam passing through the atmospheric turbulence given by Eq. (16) which is the main result finding of the current investigation. In the following, we discussed some numerical examples.

4 Results and discussions

In this part of the article, we will study the evolution properties of the axial intensity of the WG beam passing through atmosphere turbulent, based on the numerical calculation of the analytical expression established in Eq. (16) in terms of the characteristics of this medium and the parameters of the incident beam. The calculation parameters used in the present simulations are set as: \(\mu = 0.5,\)\(\omega_{0} = 0.02\;{\text{m}}\), \(\lambda = 632.8\;{\text{nm}},\) \(a = 0.15\;{\text{m}}\) and \(C_{n}^{2} = 1.10^{ - 14} \;{\text{m}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\).

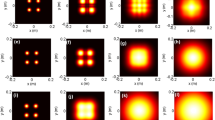
In order to investigate the influence of the strength of the atmospheric turbulence on the propagation behavior of a WG beam in the turbulent medium, we have illustrated in Fig. 2 the distribution of the intensity as a function of the propagation distance z for three values of the turbulent strengths \(C_{n}^{2}\). It can be clearly observed that the intensity distribution of the WG beam decreases much faster for high propagation distance when the turbulent strength \(C_{n}^{2}\) becomes large. Additionally, the axial intensity decreases with increasing of the beam order \(m\). We also notice from the same figure that beyond the first few hundred meters of the propagation distance \(z\) the average intensity increases by increasing this distance until it reaches a maximum then the axial intensity starts to change and decreases gradually for further propagation distance. However, the position of the maximum tends to small values of the propagation distance. Thus, we can deduce from this figure that in the near field, the axial intensity is equal to zero and remains unchanged. Moreover, the intensity profile takes on a wide shape with the decrease of \(C_{n}^{2}\) and becomes very focused with increasing the turbulent strength. Figure 3 illustrates the intensity evolution of the WG beam for weak turbulence and under the same conditions as in Fig. 2. In this figure, it is obvious that the intensity distribution decreases with the beam order but the size of the dark region of the beam enlarges. Conversely, we can observe from this figure that the position of the maximum is large with decreasing the turbulent strength. It’s also seen that the propagation of the beam becomes shorter when the turbulent strength is higher.

Fig. 2
figure 2

The intensity distribution of the WG beam versus the propagation distance \(z\) with different values of the turbulent strength (moderate turbulence regimes) and various values of the beam order: a \(m = 0,\) b \(m = 1\), c \(m = 3\) and d \(m = 4\)

Full size image
Fig. 3
figure 3

The intensity distribution of the WG beam as a function of the propagation distance \(z\) with different values of the turbulent strength (weak turbulence regimes) and various values of the beam order: a \(m = 0,\) b \(m = 1\), c \(m = 3\) and d \(m = 4\)

Full size image

It’s also observed from the plots that by increasing the turbulent strength the width of the lobe becomes smaller that is to say the propagation of the WG beam is very fast. We conclude that the propagation of the WG beam in the turbulent atmosphere is spreading more and more in the weak turbulent atmosphere. Figure 3 demonstrates that when the turbulent strength takes a larger value, the WG beam is more and more affected by the atmospheric turbulent. For convenience of comparison, we conclude that the beam is hardly influenced by the turbulent media in the far field. Additionally, the propagation of the WG beam is less resistant to the turbulence of the atmosphere when the turbulent strength is large. Finally, the WG beam is propagated at a longer propagation distance in the case of the weak turbulence regime reaching values greater than \(7.10^{4} \,{\text{m}}\) compared to the moderate turbulence regime which only reaches \(1.10^{4} \,{\text{m}}\), but it is preferable to study in the moderate turbulence range for application reasons.

To examine the impact of the beam waist \(\omega_{0}\) on the propagation of the WG beam, we have carried out in Fig. 4 the intensity distribution versus \(z\) for various values of the beam waist width. From these plots, it can be seen that the beam lobes become wider if the waist \(\omega_{0}\) is larger and the axial intensity is faster. However, the maximum propagation distance increases with an increase in the beam waist radius. Whereas the average axial intensity (initial hollow intensity distribution) keeps unchanged in the first few hundred meters of the field, afterwards the average intensity begins to rise as the propagation distance increases until a maximum of the intensity. After reaching this maximum value the intensity starts to decrease gradually.

Fig. 4
figure 4

The intensity distribution of the WG beam versus the propagation distance \(z\) with various values of the beam waist width \(\omega_{0}\) for fixed values of turbulent strength \(C_{n}^{2} = 1.10^{ - 14} \;{\text{m}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\) and different values the beam order: a \(m = 0,\) b \(m = 1\), c \(m = 3\) and d \(m = 4\)

Full size image

The effect of the wavelength on the intensity distribution of the WG beam is represented in Fig. 5, from which it is readily apparent that the axial intensity distribution is larger as the value of the wavelength decreases and the propagation is faster. Moreover, the average intensity profile takes on a wide shape with the increase of the wavelength \(\lambda .\) One might conclude that the speed of the decrease in the width of the dark spot in the center of the beam slows with decreasing of the beam order \(m\). Whereas, the axial average intensity is zero within the first tens of meters of the near field, further off in this distance, the intensity starts to change and is not equivalent to zero. Afterword, it is clearly indicating that the axial average intensity rises up to a maximum value of \(z\) after it decreases with the increase of the propagation distance.

Fig. 5
figure 5

The on-axis average intensity of the WG beams for various values of the wavelength \(\lambda\) \(\omega_{0}\) for fixed values of turbulent strength \(C_{n}^{2} = 1.10^{ - 14} \;{\text{m}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\) and four values of the beam order: a \(m = 0,\) b \(m = 1\), c \(m = 3\) and d \(m = 4\)

Full size image

It is obvious that atmospheric turbulence has a stronger effect on the shorter wavelength versus the axial intensity which means that the WG beam is more resistant to the atmospheric turbulence in the case of large values of the wavelength. Finally, we give in Fig. 6 the variation of the on-axis average intensity of the WG beam for several values of the parameter \(\mu\). From this figure, we can detect that the axial average intensity increases with \(\mu\). As in other figures, in the first propagation distance the axial intensity keeps unchanged and equals zero after that, it varies for higher values of the propagation distances. One can deduce that the influence of \(\mu\) is less visible for the large values of the beam order.

Fig. 6
figure 6

The axial intensity of the WG beam for different values of the parameter \(\mu\) \(\omega_{0}\) for fixed values of turbulent strength \(C_{n}^{2} = 1.10^{ - 14} \;{\text{m}}^{{{{ - 2} \mathord{\left/ {\vphantom {{ - 2} 3}} \right. \kern-0pt} 3}}}\) and various values of the beam order: a \(m = 0,\) b \(m = 1\), c \(m = 3\) and d \(m = 4\)

Full size image

5 Conclusion

In summary, based on the extended Huygens–Fresnel diffraction integral and the Rytov theory the propagation properties of a WG beam in atmospheric turbulence are treated theoretically. Graphical representations analyzing the impact of the turbulence strength and the source beam parameters on the studied beam are illustrated. Furthermore, results show that the profile of the WG beam remains unchanged and the intensity distribution increases quickly when the turbulent strength parameter increases for small values of the wavelength and for higher values of the beam waist width and the parameter \(\mu\). The results obtained in this work can be used to better understand the propagation properties of the WG beam in turbulent atmosphere, which are employed for optical communication, remote sensing domain, imaging and so on.