1 Introduction

The recent progress in nanofabrication techniques has enabled the development [1] of the artificially engineered materials with extraordinary electromagnetic properties that are not found in nature. One striking example of such materials is epsilon-near-zero (ENZ) metamaterials with dielectric permittivity |ε| ≪ 1 which have been shown to provide new approaches to the enhancement of light–matter interactions [2]. The remarkable property of ENZ material is that the phase velocity of light approaches an infinity. From the causality principle, it could be shown that ENZ material with very low intrinsic loss possesses a very low group velocity vg of electromagnetic wave propagation [3]. The effect of this low vg bears some analogy to the manipulating speed of light using ultracold sodium gas [4], heated Rubidium atoms [5], ruby crystal [6], photonic crystals [7], waveguides [8], and other systems [9, 10]. The advantages of the ENZ materials, such as availability of the high local fields and the fact that frequency mixing could be done without phase-matching, allow for the enhancement of the weak nonlinear-optical effects. As a result, ENZ material allows for control of self-focusing effects [11] and boosts the efficiency of second [12] and third harmonic generation [13]. The ENZ point also provides optimal conditions to observe self-trapping [14, 15].

Different physical realizations of ENZ structures are possible [2] including using multilayered structures [16] and transparent conducting oxides (TCO) [17]. The multi-layered Al:ZnO/ZnO metamaterial studied in this manuscript possesses the unique optical properties of optical transparency and high electrical conductivity. Atomic layer deposition for multi-layered Al:ZnO/ZnO samples offers an opportunity to tune dielectric constants to epsilon-near-zero spectral point in the near infrared (IR) for TM polarized wave by adjusting the doping concentration and/or thickness of the sample [18,19,20]. The presence of near-zero-dispersion significantly modifies familiar nonlinear optical parameters. Strong boundary effects and variation of the refractive index lead to the enhancement of the nonlinear effects in ENZ films. For example, recent experiments performed on Al-doped ZnO thin films show a sixfold increase of the Kerr nonlinear refractive index at the ENZ wavelength [21]. In addition, ENZ materials have a rapid change in permittivity for ENZ wavelength which could potentially lead to large second- and third-order dispersion parameters. The recent discoveries of novel nonlinear optical characteristics of TCO [21, 22], high potential for use of TCO for practical devices [23] and the recent development of compact IR sources of ultrashort pulses [24,25,26] motivated our numerical study of the ultrashort pulse propagation in the Al:ZnO/ZnO metamaterials at the epsilon-near-zero wavelength.

The ultra-short pulse shaping in the presence of nonlinearity and higher-order chromatic dispersion terms is not only a source of rich and fascinating physics [27, 28] but it can also provide novel techniques for practical laser devices [29, 30] which will be essential for modern optical communications and spectroscopy. Ultra-short pulse shaping could potentially provide a solution for metamaterial-based super-resolution imaging [31]. A generalized nonlinear Schrödinger equation describing the propagation of ultrashort pulses in the media exhibiting strong frequency dependent dielectric susceptibility was used to describe wave propagation in negative index material [32]. For the materials with strongly varying dispersive properties we need to take into consideration the limitation of the slow-varying envelope approximation [27] which was widely discussed in the literature [32, 33]. In this manuscript, we use an approach to ultrashort-pulse propagation which is based on the exact dispersion relation for the group velocity for the ENZ medium with negligible losses [3]. The results are also compared with the full wave analysis based on finite-difference time-domain (FDTD) numerical simulations.

Here in this paper, we present the results of a numerical investigation of ultrashort pulse propagation in the Al:ZnO/ZnO at the epsilon-near-zero wavelength. The influence of the various parameters of the Drude model for the Al:ZnO dielectric permittivity on the second-order dispersion of the ENZ metamaterial is investigated. The pulse propagation in the presence of enormous second-order dispersion and nonlinearity is studied. We show that when vg varies significantly across a spectral bandwidth of the initial pulse for the ENZ spectral point, the unique “soliton-like” propagation regime without nonlinearity is possible in multi-layered Al-doped ZnO metamaterial.

2 Ultra-short pulse propagation equation

Ultra-short pulse propagation can be described by the generalized Non-Linear Schrödinger (NLS) equation [27]:

$$\frac{{\partial A}}{{\partial z}}+{\beta _1}\frac{{\partial A}}{{\partial t}}+\frac{{i{\beta _2}}}{2}\frac{{{\partial ^2}A}}{{\partial {T^2}}}+\frac{\alpha }{2}A=i\gamma ({\omega _0})|A{|^2}A,$$
(1)

where A is the slowly varying pulse envelope, α is material loss, β1 is the first-order and β2 is second-order chromatic dispersion term, and γ is the non-linearity parameter. The nonlinearity parameter is defined as [27]:

$$\gamma ({\lambda _{\text{c}}})=\frac{{2\pi {n_2}({\lambda _{\text{c}}})}}{{{\lambda _{\text{c}}}{A_{{\text{eff}}}}}},$$
(2)

where λc is the crossing wavelength, n2(λc) (m2/W) is the nonlinear Kerr index, and Aeff (m2) is the effective mode area. It is important to note that in the regular materials, Eq. (1) is transformed in a frame of reference moving with a pulse at group velocity vg. However, for ENZ materials we need to include the term associated with β1 because vg is not constant across the input pulse spectrum.

The NLS equation is not easily solved analytically, aside for some specific situations, so the most common method of modeling pulse propagation is with the split-step Fourier (ssF) method. The ssF method is pseudo-spectral, in that it calculates the effects of dispersion and nonlinearity separately. This takes the form of two operators: \(\widehat {D}\) for dispersion and \(\widehat {N}\) for non-linearity:

$$\widehat {D}= - {\beta _1}\frac{\partial }{{\partial t}} - \frac{{i{\beta _2}}}{2}\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{\alpha }{2}.$$
(3)
$$\widehat {N}=i\gamma |A{|^2}.$$
(4)

The ssF method approximates the effects of each operator on the pulse propagation by applying dispersion in the Fourier domain and non-linearity in time. Typically, the accuracy of the ssF method is limited to the square of the step-size, h2 [27]. To minimize the error, the time grid was set to 100,000 units across 48,000 fs yielding accuracy on the order of 0.48 fs. The space grid spans 6000 units across 300 nm with a resolution of 0.05 nm.

For the numerical simulations, we choose an initial pulse with a Gaussian shape (TFWHM= 100 fs ≈ 1.665τ0). The thickness of the Al:ZnO/ZnO material was varied 100–700 nm which corresponds to the experimentally achieved thickness [34]. It is important to note that Al:ZnO/ZnO metamaterial typically possesses low intrinsic losses, e.g., the Im (ε⊥) = 0.0377 at λc = 1865 nm for Al:ZnO/ZnO metamaterial [18]. Therefore, the effect of a linear absorption α is negligible in our simulations.

First of all, we used ssF method to investigate the propagation of the initial pulse in the presence of nonlinearity only and neglected the effect of the operator \(\widehat {D}\). The nonlinearity parameter for bulk Al:ZnO was calculated γ = 9.84 × 10−3(1/kmW− 1), assuming the nonlinear refractive index n2 = 3.5 × 10−13 cm2/W [21] and a beam radius of 2 mm for free-space propagation. The estimated γ = 9.84 × 10−3 (W km)−1 is small compared to a typical single-mode fiber which has γ = 1 (W km)−1. The multilayered material would have a lower γ due to the additional presence of un-doped ZnO layers. Our numerical simulations show that effect of the nonlinearity is indeed negligible for propagation of a 100 fs pulse over the thickness of Al:ZnO/ZnO up to 1 µm. This is expected since LNL ~1 m (1 µJ pulse energy). It is important to note that nonlinearity will become important for ultrashort pulse propagation in photonic devices fabricated using ENZ materials which are able to confine light in the sub-wavelength volume [35]. Since nonlinearity varies significantly over the initial spectral bandwidth, this approach based on using the averaged nonlinearity parameter γ described above needs to be modified [14, 15, 36]. For the higher optical pulse intensities or/and confinement in the devices with sub-wavelength volume, the FDTD numerical method, described in Sect. 5, needs to be used.

Next, we used the numerical simulations to investigate the effect of the first-order and second-order chromatic dispersion terms. The propagation constant is defined by [27]:

$$\beta \approx \frac{{n(\omega )\omega }}{c},$$
(5)

where n(ω) is the refractive index as a function of frequency. The chromatic dispersion terms in Eq. (1) are defined as:

$${\beta _m}={\left( {\frac{{{d^m}\beta }}{{d{\omega ^m}}}} \right)_{\omega ={\omega _0}}},$$
(6)

where ω0 is the central frequency. Using these definitions, we can estimate β1 and β2 using predicted values for the refractive index of Al:ZnO/ZnO.

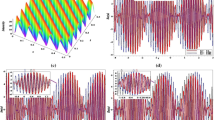
To illustrate the effect of each individual term for chromatic dispersion, β1 and β2, we choose to calculate the value of βm at the central frequency first (β1 = 1/vg = − 0.37 1/fs, β2 = 348.9 fs2/nm). The results of the numerical simulations for the propagation of the initial pulse in 300 nm of the Al:ZnO/ZnO metamaterial is shown in Fig. 1. As expected, the pulse is significantly broadened due to the enormous second-order dispersion β2 (Fig. 1a) (dispersion length LD = τ02/|β2| ~10.34 nm). If β1 is increased (the second order dispersion β2 is held constant), the overall broadening of the pulse remains unchanged but it offsets to the right from the initial position (top plot of the Fig. 1a). The spectral intensity remains unchanged (Fig. 1b) since the spectral phase has a quadratic dependence and the instantaneous frequency varies linearly.

Fig. 1
figure 1

Normalized intensity (a) and spectrum (b) for a 100 fs pulse propagated in 300 nm of the Al:ZnO/ZnO metamaterial. The corresponding phases in time (a) and spectral (b) domain are indicated by dashed line. The spectrum, intensity and phases for the initial pulse are presented at the bottom of a and b for comparison (dotted line)

Full size image

3 Drude model parameters and higher-order dispersion

From our results based on the averaged dispersion parameters (Fig. 1), we can expect that the multi-layered Al:ZnO/ZnO will be necessarily dispersive. Our goal is to investigate how various parameters for the Al:ZnO/ZnO permittivity affect chromatic dispersion. Our previous work [18] shows that first-order effective medium approximation [37, 38] provides a good model for the Al:ZnO/ZnO optical permittivity. Here, we assume 1:4 Al:ZnO/ZnO nano-layers ratio. To analyze the Al:ZnO/ZnO metamaterial, we used the Adachi model for ZnO [39] and the Drude model [40] for the Al:ZnO layer:

$${\varepsilon _{\text{D}}}={\varepsilon _\infty } - {f_{\text{D}}}\frac{{\omega _{{\text{p}}}^{2}}}{{{\omega ^2}+i\omega {\gamma _{\text{D}}}}},$$
(7)

where ω is the incoming light frequency, ωp is the plasma frequency, γD is the damping frequency, and ε∞ is the screening effect of the bound electrons in the material. To investigate the influence of each Drude parameter on the chromatic dispersion, we set to fD =0.4 and ε∞ =3, then allow ωp and γD to vary, as they are most representative of the material’s electronic behavior.

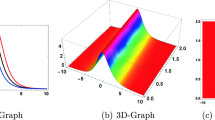
We found γD had the highest impact on the losses for ε⊥ (Fig. 2a) and the magnitude of β2 (Fig. 2c). This is consistent with our previous results of the ellipsometry analysis which also show [34] that ωp determines the spectral position of the crossing into hyperbolic dispersion, ωc. For this study, we choose to restrict ωp to 2.9 × 1015 Hz as this provides the shortest spectral crossing position within our fabrication capabilities [34]. The maxima of β1(ωc) and β2(ωc) for three values of γD, which are calculated by Eq. 6, are shown in Table 1.

Fig. 2
figure 2

a The calculated dielectric permittivity based on Drude model with varying γD values. b The chromatic dispersion term β1 which are calculated using Eq. (6) and Eq. (7) (Re (1/vg)). c The chromatic dispersion term β2 which are calculated using Eq. (6). The initial spectrum of a 100 fs pulse is indicated by dotted line. d Illustration of the ultrashort pulse transformation in ENZ Al:ZnO/ZnO metamaterial with 300 nm thickness

Full size image
Table 1 β1 and β2 values at crossing based on the Drude model with ωp = 2.9 × 1015 Hz
Full size table

One could expect that this method of calculating averaged β1 is not accurate in the case of ENZ material since phase velocity diverges at the ENZ point and vg will vary significantly along a spectral bandwidth of the initial pulse (Fig. 2b). For the low loss metamaterial at the ENZ observation frequency, the causality principle leads to the exact dispersion relation for vg =1/β1 [3]:

$${v_{\text{g}}}=c\sqrt {{\varepsilon ^\prime }(\omega )} {\left( {1+\frac{2}{\pi }\int\limits_{0}^{\infty } {\frac{{{\varepsilon ^{\prime \prime }}({\omega _1})}}{{{{(\omega _{1}^{2} - {\omega ^2})}^2}}}\omega _{1}^{3}\;{\text{d}}{\omega _1}} } \right)^{ - 1}},$$
(8)

where ε′ + iε″ are the material’s complex dielectric permittivity.

Using this definition for vg, (Eq. 8) we have calculated β1 over the bandwidth of the initial pulse using complex permittivity predicted by Drude model with ω p  = 2.9 × 1015 Hz and γD = 1011 Hz. The only limitation to our calculations comes from the known range of the Al:ZnO/ZnO permittivity. We limited the range of the integral from infinity to 25 1/fs to save computation time as higher ranges did not provide a significant difference. The imaginary part of permittivity ε″(ω1) was fixed to ε″(ωc). The largest difference between β1 calculated by Eq. (8) and Eq. (6) is the presence of imaginary terms (Fig. 2b).

4 Numerical simulations using the non-linear Schrödinger equation

Figure 3 shows the results of the numerical simulations for initial pulse propagation through different Al:ZnO/ZnO lengths (100–700 nm) when the chromatic dispersion values β1 are a function of frequency (a–e) or constant (f–j). The parameters for the real part of the chromatic dispersion β1 in Fig. 3a–e were calculated using Eq. (8) (Fig. 2b). The parameter for β2 was calculated using Eq. 6 (Fig. 2c). In addition, we choose to extend the derivative for β2 in Eq. 6 over the entire spectrum instead of just at the crossing frequency since β2 is changed significantly across the initial spectrum (Fig. 2c).

Fig. 3
figure 3

The normalized intensity and temporal phases for a 100 fs Gaussian pulse propagated through varying lengths. a–e The pulse propagated with β1 as calculated by Eq. 8 and β2 by Eq. 6. f–j The pulse propagated with β1 and β2 values set as the maximum values from Eq. 6

Full size image

The propagation of the initial pulse in the media with constant β1 and β2 (Figs. 3f–j, 4f–j) is characterized by a temporal pulse broadening up to ~ 7 ps as expected [27]. The temporal and spectral phases show quadratic dependence similar to presented in Fig. 2b, which is a signature of the temporal broadening due to second-order dispersion.

Fig. 4
figure 4

The normalized spectral intensity and spectral phases for a 100 fs Gaussian pulse propagated through various lengths. a–e The pulse propagated with β1 as calculated by Eq. 8 and β2 by Eq. 6. f–j The pulse propagated with β1 and β2 values set as the maximum values from Eq. 6. Temporal and spectral phases were calculated based on the method presented in [41]

Full size image

As the pulse propagates through the Al:ZnO/ZnO metamaterial (Fig. 2d), it become apparent that the vg plays a crucial role in pulse shaping (Fig. 3a–e). The pulse shape is almost preserved after propagating in 200 nm of the Al:ZnO/ZnO (Fig. 3b). The temporal phase (dashed line) is linear across the pulse width. Intuitively, it could be understood as if different frequencies would travel at different speeds within the pulse due to changing vg across the spectrum of the initial pulse. This variable change of vg is compensated by a temporal broadening due to β2. Therefore, the resulting pulse (Fig. 3b) has a constant instantaneous frequency. As the pulse propagate beyond 300 nm, this effect become weaker and the pulse experiences temporal broadening. The temporal phase becomes more quadratic after the sufficient distance (Fig. 3e). The spectrum of the propagating pulse remains almost unchanged even after propagation through the larger Al:ZnO/ZnO thicknesses (Fig. 4a–e) because the dispersion is the dominant effect. Additional numerical simulations for shorter pulses (up to 50 fs) show similar behavior. This type of ultrashort pulse propagation (Fig. 3a, b) resembles the fundamental soliton propagation in fibers [27] which results from mutual effects of the Kerr nonlinearity and second-order dispersion.

It is important to note that in spite of the fact that the pulse is in quasi-monochromatic regime, the slowly varying envelope approximation (SVEA) used for NLS equation (Eq. 1) might not be fully justified since longitudinal phase oscillations due to the diverging phase velocity could be comparable with the pulse envelope scale dynamics. While introducing group velocity vg using Eq. 8 takes into account the strong variation of vg along a spectral bandwidth of the initial pulse, the SVEA will break down for longer propagation distances and/or propagation in the presence of nonlinearity. Therefore, in the next section, we will provide a full wave analysis of the ultrashort pulse propagation in the presence of enormous dispersion.

5 Finite-difference time-domain method for ultrashort-pulse propagation

A full wave analysis study was performed using a finite-difference time-domain numerical algorithm which divides space and time into equal steps and simulates the time domain evolution of the Maxwell equations. Our FDTD numerical study for ultrashort pulse propagation in multilayered Al:ZnO/ZnO metamaterial was done using our home-build Python interface program and an open-source implementation of the FDTD method for electromagnetic applications, which was developed by MIT MEEP (MIT Electromagnetic Equation Propagation) [42]. MEEP FDTD implementation has been proven to be efficient for many applications [42] including the ultrashort pulse propagation in nonlinear graphene/silicon ridge waveguide [43] and the propagation of self-collimated ultrashort Gaussian pulses in a hybrid photonic crystal structure [44].

Propagation of the ultrashort pulse with the spectrum centered at the ENZ point is described by the Maxwell equations coupled to the permittivity model. The input pulse is assumed to have a Gaussian shape in time-domain with width of 100 fs. We assume that the light intensity distributes homogeneously at this area, and thus can simplify the simulation to one dimension. The real and imaginary part of the out of plane permittivity ε⊥ for the multilayered Al:ZnO/ZnO (Fig. 2a) are incorporated into MEEP code via the Lorentz permittivity model. We used a five pole Lorentz model [45, 46] to fit permittivity ε⊥ values for a spectral range between 1600 and 1900 nm using the Python’s nonlinear least square minimization and curve-fitting function [47] and the differential evolution method [48]. The fitting was optimized by finding a strong pole over a limited frequency range. If a strong pole was found, the range was kept for the next fitting. Otherwise, the range would be moved to an untested region. The mean-square-error (MSE) [18] for the fitting was MSE ~ 6.

The results of the one-dimensional FDTD simulations show that as the pulse propagates through the Al:ZnO/ZnO metamaterial (Fig. 5), the pulse gradually becomes asymmetric. In particular, the central peak of the real part of the electric field (Fig. 5h–j) remains relatively unchanged for propagating distances up to around 200 nm. For larger distances, the resulting pulse shows signs of deterioration which is indicated by a strong asymmetric sideband (Fig. 5k, l). The temporal intensity dependence has a characteristic asymmetric shift, similar to the one predicted using NLSE (Fig. 5a–c), which could intuitively be understood in terms of changing group velocity vg described in Sect. 4.

Fig. 5
figure 5

The normalized intensity (a–f) and the real part of the electric field (g–l) for a 100 fs Gaussian pulse propagated through varying lengths. Finite-difference time-domain method was used in numerical calculations

Full size image

It is important to note that the NLS equation (Eq. 1) based on SVEA and Eq. 8 allows for a qualitative prediction and an intuitive understanding of the physics of the ultrashort pulse shaping at the ENZ spectral point. Fast computational speed of the split-step Fourier method allows for the obtaining of an initial physical insight into ultrashort pulse propagation. However, for longer propagation distances, a full FDTD numerical study is necessary since errors in calculating group velocity vg via Eq. 8 due to limited spectral ranges and possible deviation from SVEA will strongly affect ultrashort pulse shaping for propagation distances beyond 300 nm. Our full FDTD study allows incorporation of ultrafast interband and intraband nonlinearities and variation of the dumping coefficient γD which will be a subject of our future studies.

6 Conclusions

In conclusion, we investigated the influence of the permittivity and material parameters predicted by the Drude model on chromatic dispersion and ultra-short pulse shaping in Al:ZnO/ZnO ENZ metamaterial. We found that the damping frequency, γD, had the highest impact on the material losses and the magnitude of second-order dispersion. The lower material losses and a high plasma frequency leads to a unique “soliton-like” propagation regime which allows for the chromatic terms, β2 and β1, to act together to prevent a temporal and spectral broadening for thicknesses up to 300 nm. It is important to note that this “soliton-like” propagation regime is characterized by the presence of only higher-order dispersion but not nonlinearity. Our numerical FDTD simulations show that as the pulse propagates through the Al:ZnO/ZnO metamaterial, the pulse gradually becomes asymmetric, resulting in the appearance of strong asymmetric sideband for propagation distances beyond 300 nm. Our approach to ultrashort-pulse propagation allows for an observation of the phase of the propagating ultrashort pulse which could be measured experimentally using well known techniques [41]. The resulting pulse has an almost linear temporal phase and the majority of the pulse energy is confined in the main peak for propagation distances up to 300 nm. This study will potentially be useful for applications in modern communications, spectroscopy and super-resolution imaging.