1 Introduction

Quantum entanglement versus separability of quantum systems, as a nonclassical exhibition of quantum states, is one of the most remarkable features of quantum theory which possesses numerous applications in recent decade [1,2,3]. Recently, study on this subject has become one of the main goals of quantum information science researches [4], since it is regarded as a resource for information processing in novel ways. For instance, entanglement is useful for quantum cryptography [5], quantum computation [6], quantum repeaters [7, 8], quantum teleportation [9, 10] and entanglement swapping [10, 11].

One of the most common approaches to realize the entanglement is making use of the projection measurement. Bell-state measurement as a projection measurement, entangles two particles without any direct interaction between them. When the particles A and C are entangled with particles B and D, respectively, a Bell-state measurement on the particles B and D will automatically collapse the state of the remaining two particles (A and C) into an entangled state. This striking application of the projection measurement is referred to as entanglement swapping [12,13,14,15]. It is noticeable that, this measurement entangles two particles B and D, too. Another method to create entanglement between particles B and D, if one of them is atom and the other is field, and occurring the entanglement swapping is interacting them in an optical cavity (cavity QED method). This method has been frequently reported in the literature [15, 16]. In particular, the entanglement swapping by cavity QED method has been used for the generation of tripartite entangled states [17, 18]. Entanglement swapping via the cavity QED method through the nonlinear atom–field interaction [19] and in the presence of dissipation [20, 21] have been recently done by us. In the framework of cavity QED, schemes already have been proposed which may open a route toward efficient quantum repeaters for long-distance quantum communication [22,23,24].

The two mentioned methods for entanglement swapping (cavity QED and Bell-state measurement), have also been employed similarly for quantum teleportation protocols. For example, Refs.  [25,26,27,28] have teleported the quantum states using Bell-state measurement and cavity QED methods, respectively. In quantum teleportation protocols, first suggested by Bennett et al. [9], an entangled state \(\,\left| \Psi \right\rangle _{AB}\) of systems A and B can be used as a quantum channel to teleport or send quantum information. In the other words, in such protocols, an unknown quantum state is transferred from one point to another, these points possibly being widely separated. We would like to emphasize that it is the unknown quantum state that is to be teleported, not the particle or particles in such states [29]. To realize the entanglement swapping in this paper, we utilize a system including two atom–field subsystems \((AF)_{1,2}\) and an ancillary mode a (a-mode) in the coherent state \(\,\left| {\alpha }\right\rangle _a=\text {exp}(-|\alpha |^2/2)\) \(\times \sum _{n=0}^{\infty }(\alpha ^n/\sqrt{n!})\,\left| {n}\right\rangle\), with the intensity \(|\alpha |^2=\bar{n}\). The states of the atom–field subsystems have been generated via the atom–field interaction in the standard Jaynes–Cummings model. Our goal is to generate the entanglement between two atoms \(A_{1}\), \(A_{2}\) and a-mode in the presence of two fields \({F}_{1}\), \(F_{2}\) and a-mode. When just two fields and a-mode exist and there is no atom to interact with these fields, the employment of the cavity QED method is not helpful. On the other hand, the Bell-state measurement method is not a usefully ideal method due to the difficulty of the realization of the Bell-state measurement in experiment [30] and the totally discrimination of the four known Bell-states is a hard task. Therefore, making use of the two customary methods which are mentioned above (cavity QED and Bell-state measurement), do not lead us to our purpose of entanglement swapping in the outlined model.

So, in this regard, a new method based on the Mach–Zehnder interferometer assisted with a nonlinear cross-Kerr medium [29, 31, 32] is presented. Utilizing the Kerr medium and cross-Kerr nonlinearities are particularly effective for purposes of the optical quantum information processing [33]. Our model is established on two single-mode quantized fields which are distinctly entangled with two 2-level atoms, and form the entangled states \((AF)_{1,2}\). These two-field states along with the a-mode (in the coherent state) are injected into the Mach–Zehnder interferometer and as a result, the even and odd coherent states (Schrödinger’s cat states) of the a-mode are generated. After detecting the fields, the subsystem including a-mode and both atoms becomes entangled together and a tripartite entangled state is prepared. In this step, we can calculate the success probability of the detecting process and the fidelity of the obtained entangled state relative to a maximally entangled state. Finally, with the help of the above-introduced Mach–Zehnder interferometer, we perform the teleportation of two-particle entangled state using a non-maximally entangled state (for quantum channel). It is worth noticing that the applied optical setups in both of the entanglement swapping and teleportation processes are assumed to be idealized. In other words, we ignore all dissipation sources like the cavity loss, qubit decay, high-efficiency detectors and so on, i.e., we suppose that the cavity is chosen so that it possesses high-quality factor, the qubits’ decay can be ignored and the detectors are of high efficiencies. This model may be prepared by utilizing high-quality factor cavities, appropriate Rydberg atoms and detectors with high efficiencies. The rest of this paper organizes as follows: in the next section, we briefly review the Mach–Zehnder interferometer where an external mode (which is initially in the coherent state) is coupled to an internal mode of interferometer through a cross-Kerr medium. In Sect. 3, we first pay attention to the generation of the atom–field entangled states \(((AF)_{1,2})\) via the standard Jaynes–Cummings model. These two entangled states along with an ancillary mode a as the external mode of Mach–Zehnder interferometer, form the total state of the system. In Sect. 4, we try to perform the entanglement swapping based on the Mach–Zehnder interferometer assisted with a nonlinear cross-Kerr medium as well as detecting method and show that how the a-mode is entangled with two atoms in a tripartite entangled state. Then, we investigate the corresponding quantities such as success probability of the detecting process, fidelity of the obtained entangled state relative to a suitable maximal entangled state and the degree of entanglement. In Sect. 5, we perform the entangled state teleportation with the help of the mentioned Mach–Zehnder interferometer. At last, we present a summary and concluding remarks in Sect. 6.

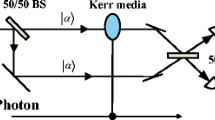
2 Mach–Zehnder interferometer: a brief review

In this section, we review the performance of a Mach–Zehnder interferometer, where its modes labeled as 1 and 2 are coupled to an external mode through a nonlinear cross-Kerr medium (Fig. 1). In this figure, \(\text {BS}_1\) and \(\text {BS}_2\) refer to the 50:50 beam splitters,Footnote 1 \(\text {D}_i\) and \(\text {M}_i\) (\(i=1,2\)) are detectors and mirrors, respectively, and the box labeled by \(\theta\) represents a phase shifter (PS) which is described by the operator [29, 31, 32, 34]

$$\begin{aligned} \hat{U}_{\text {PS}}=\text {e}^{i\theta \hat{c}^\dagger \hat{c}}. \end{aligned}$$
(1)

As is clear from Fig. 1, the phase shifter \(\theta\) leads to the phase change of the upper beam (i.e., mode 2 after passing the \(\text {BS}_1\)). Mode 1 after passing the \(\text {BS}_1\) together with the external mode a enter the cross-Kerr medium, so that the governing Hamiltonian is given by \(\hat{H}_{\text {CK}}=\hbar K\hat{a}^\dagger \hat{a}\hat{b}^\dagger \hat{b}\), where K is proportional to the third-order nonlinear susceptibility \(\chi ^{(3)}\). Accordingly, the unitary operator which determines the evolution of cross-Kerr medium is defined as

$$\begin{aligned} \hat{U}_{\text {CK}}=\text {e}^{-iK\hat{a}^\dagger \hat{a}\hat{b}^\dagger \hat{b}t}, \end{aligned}$$
(2)

where the operators \(\hat{a}^\dagger \hat{a}\) and \(\hat{b}^\dagger \hat{b}\) are, respectively, applied on the external mode a and mode 1 after passing the \(\mathrm {BS}_1\). Also, t is the interaction time and can be written in terms of the length of the Kerr medium (l) and the velocity of light in this medium (v), so that \(t={l}/{v}\).

Fig. 1
figure 1

Schematic representation of a Mach–Zehnder interferometer coupled to an external mode a through a nonlinear cross-Kerr medium

Full size image

The above-described apparatus which is usually employed to generate Schrödinger’s cat states [29, 31, 32], will be used here for our entanglement swapping and quantum teleportation purposes.

3 Model and basic equations

In the entanglement swapping process, some initially entangled systems are required, such that this entanglement is suitably switched to other new subsystems with the help of the entanglement swapping techniques. To achieve this purpose, we use two entangled states which have been previously prepared in an optical cavity via the atom–field interaction through the Jaynes–Cummings configuration. The Hamiltonian of this model (with \(\hbar =1\)) for each atom–field system is given by [35]:

$$\begin{aligned} \hat{H}_{(AF)_i}=\dfrac{1}{2}\omega _{A_i}\hat{\sigma }_{z_i}+\omega _{F_i}\big (\hat{a}_i^\dagger \hat{a}_i+\dfrac{1}{2}\big )+g_i(\hat{a}_i\hat{\sigma }_{+_i}+\hat{a}_i^\dagger \hat{\sigma }_{-_i}), \end{aligned}$$
(3)

where \(\hat{a}_i^\dagger\) and \(\hat{a}_i\) are the creation and annihilation operators of the ith field mode with frequency \(\omega _{F_i}\) which satisfies the relation \([\hat{a}_i,\hat{a}_i^\dagger ]=1\). The operators \(\hat{\sigma }_{z_i}\) and \(\hat{\sigma }_{\pm _i}\) are the Pauli spin operators of the ith atom, \(\omega _{A_i}\) are the atomic transition frequencies and \(g_i\) are the atom–field coupling constants (in the continuation, we assume \(g_1=g_2=g\)). The subscript \(i=1,2\) numbers each of the subsystems. Now, we suppose that the subsystem 1 contains atom \(A_1\) which initially is in the exited state \(\,\left| {e}_1\right\rangle\) and the field \(F_1\) in the vacuum state \(\,\left| {0}_1\right\rangle.\) After applying the Hamiltonian (3) for the interval of time \(t_1\), the atom–field entangled state results in

$$\begin{aligned} \left| {\psi (t_1)}\right\rangle _{{(AF)}_1}=\text {cos}(g t_1)\,\left| {e}\right\rangle _1\,\left| {0}\right\rangle _1-i\text {sin}(g t_1)\,\left| {g}\right\rangle _1\,\left| {1}\right\rangle _1. \end{aligned}$$
(4)

Choosing the interaction time as \(t_1={\pi }/{4g}\), we have

$$\begin{aligned} \,\left| {\psi ({\pi }/{4g})}\right\rangle _{{(AF)}_1}=\dfrac{1}{\sqrt{2}}\big (\,\left| {e}\right\rangle _1\,\left| {0}\right\rangle _1-i\,\left| {g}\right\rangle _1\,\left| {1}\right\rangle _1\big ). \end{aligned}$$
(5)

Similarly, we assume that the subsystem 2 consists of atom \(A_2\) and field \(F_2\) which are initially in the ground state \(\,\left| {g}\right\rangle _2\) and single-photon state \(\,\left| {1}\right\rangle _2\), respectively. After the interval time \(t_2\), the atom–field entangled state reads as

$$\begin{aligned} \,\left| {\psi (t_2)}\right\rangle _{{(AF)}_2}=\cos (g t_2)\,\left| {g}\right\rangle _2\,\left| {1}\right\rangle _2-i \sin (g t_2)\,\left| {e}\right\rangle _2\,\left| {0}\right\rangle _2. \end{aligned}$$
(6)

By tuning the interaction time as \(t_2={\pi }/{4g}\), we have

$$\begin{aligned} \,\left| {\psi ({\pi }/{4g})}\right\rangle _{{(AF)}_2}=\dfrac{1}{\sqrt{2}}\big (\,\left| {g}\right\rangle _2\,\left| {1}\right\rangle _2-i\,\left| {e}\right\rangle _2\,\left| {0}\right\rangle _2\big ). \end{aligned}$$
(7)

Considering the above two entangled states corresponding to subsystems 1, 2 in (5) and (7), it is readily found that the separable state vector of the whole system is of the form

$$\begin{aligned} \,\left| {\psi }\right\rangle _{(AF)_{1,2}}=\,\left| {\psi ({\pi }/{4g})}\right\rangle _{{(AF)}_1}\otimes \,\left| {\psi ({\pi }/{4g})}\right\rangle _{{(AF)}_2}. \end{aligned}$$
(8)

It is clearly known that by separable, we mean that the total subsystems are separable, however in each subsystem i (\(i=1, 2\)), the ith atom is entangled with the ith field. Then, making use of an ancillary mode a (which is in the coherent state \(\,\left| {\alpha }\right\rangle _a\)), the state of the total system, becomes the tensor product of the state in (8) and \(\,\left| {\alpha }\right\rangle _a\), i.e.,

$$\begin{aligned} \,\left| {\psi }\right\rangle _\text {total}&=\,\left| {\psi ({\pi }/{4g})}\right\rangle _{{(AF)}_1}\otimes \,\left| {\psi ({\pi }/{4g})}\right\rangle _{{(AF)}_2}\otimes \,\left| {\alpha }\right\rangle _a\nonumber \\&=\dfrac{1}{2}\big [\,\left| {e}\right\rangle _1\,\left| {g}\right\rangle _2\,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2\,\left| {\alpha }\right\rangle _a-i\,\left| {e}\right\rangle _1\,\left| {e}\right\rangle _2\,\left| {0}\right\rangle _1\,\left| {0}\right\rangle _2\,\left| {\alpha }\right\rangle _a\big ]\nonumber \\&\quad -\dfrac{1}{2}\big [i\,\left| {g}\right\rangle _1\,\left| {g}\right\rangle _2\,\left| {1}\right\rangle _1\,\left| {1}\right\rangle _2\,\left| {\alpha }\right\rangle _a+\,\left| {g}\right\rangle _1\,\left| {e}\right\rangle _2\,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2\,\left| {\alpha }\right\rangle _a\big ]. \end{aligned}$$
(9)

To perform the entanglement swapping process, this state is entered into the Mach–Zehnder interferometer which is indicated in Fig. 1. Two-field states \({F}_1\) and \({F}_2\) (which are indicated as \(\,\left| {m}\right\rangle _1\,\left| {n}\right\rangle _2\) with \(m,n=0,1\) in 9) are two entering modes 1,2 to the beam splitter 1 (\(\text {BS}_1\)) into the Mach–Zehnder interferometer. In addition, the coherent state \(\,\left| {\alpha }\right\rangle _a\) of the a-mode (in 9) enters into the cross-Kerr medium in this interferometer.

Fig. 2
figure 2

Sketch of the designed setup to perform the entanglement swapping process

Full size image

4 Entanglement swapping based on the Mach–Zehnder interferometer

To fulfill the entanglement swapping purpose, we must obtain the output state of the interferometer for each state entering it. As is seen in Fig. 2, the total state which is injected into the Mach–Zehnder interferometer, is a combination of the field states \({F}_1\), \({F}_2\) and \({F}_a\) indicated as \(\,\left| {m}\right\rangle _1\,\left| {n}\right\rangle _2\,\left| {\alpha }\right\rangle _a\) (\(m,n=0,1\)) in (9). For example, if the state \(\,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2\,\left| {\alpha }\right\rangle _a\) is injected in the interferometer, the output state of it is obtained as (see Appendix A)

$$\begin{aligned} \,\left| {\text {out}}\right\rangle _{\text {MZI}_1}=-\dfrac{1}{2}\big [i\,\left| {\widetilde{\psi _{o}}}\right\rangle _a\,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2+\,\left| {\widetilde{\psi _e}}\right\rangle _a\,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2\big ], \end{aligned}$$
(10)

where \(\,\left| {\widetilde{\psi _{o(e)}}}\right\rangle _a=[{N_{o(e)}}]^{-1}\,\left| {\psi _{o(e)}}\right\rangle _a\) with \(\,\left| {\psi _o}\right\rangle _a=N_o\big (\,\left| {\alpha }\right\rangle _a-\,\left| {-\alpha }\right\rangle _a\big )\) and \(\,\left| {\psi _e}\right\rangle _a=N_e\big (\,\left| {\alpha }\right\rangle _a+\,\left| {-\alpha }\right\rangle _a\big )\) are odd and even Schrödinger cat states, respectively, which have been introduced by Yurke and Stoler [36, 37]. Here, \(N_o=[2(1-\text {e}^{-2|\alpha |^2})]^{-1/2}\) and \(N_e=[2(1+\text {e}^{-2|\alpha |^2})]^{-1/2}\) are normalization factors. We should notice that the discrimination between even and odd coherent state superposition is an important issue in this content [38].Footnote 2 In a similar way (to “Appendix A”), considering the initial state \(\,\left| {0}\right\rangle _1\,\left| {0}\right\rangle _2\,\left| {\alpha }\right\rangle _a\) as the input state of the Mach–Zehnder interferometer, the output state is obtained as below

$$\begin{aligned} \,\left| {0}\right\rangle _1\,\left| {0}\right\rangle _2\,\left| {\alpha }\right\rangle _a\xrightarrow {\text {MZI}}\,\left| {\text {out}}\right\rangle _{\text {MZI}_2}=\,\left| {0}\right\rangle _1\,\left| {0}\right\rangle _2\,\left| {\alpha }\right\rangle _a, \end{aligned}$$
(11)

which may be expressed in terms of the even and odd Schrödinger’s cat states as below:

$$\begin{aligned} \,\left| {\text {out}}\right\rangle _{\text {MZI}_2}=\dfrac{1}{2}\,\left| {0}\right\rangle _1\,\left| {0}\right\rangle _2\big [\,\left| {\widetilde{\psi _o}}\right\rangle _a+\,\left| {\widetilde{\psi _e}}\right\rangle _a\big ]. \end{aligned}$$
(12)

Also, if the state \(\,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2\,\left| {\alpha }\right\rangle _a\) enters into the Mach–Zehnder interferometer, the output state reads as

$$\begin{aligned} \,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2\,\left| {\alpha }\right\rangle _a\xrightarrow {\text {MZI}}\,\left| {\text {out}}\right\rangle _{\text {MZI}_3}&=\dfrac{1}{2}\big [-i\,\left| {\widetilde{\psi _o}}\right\rangle _a\,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2\\ \nonumber&+\,\left| {\widetilde{\psi _e}}\right\rangle _a\,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2\big ], \end{aligned}$$
(13)

where we have supposed that \(Kt=\pi\) and \(\theta =\pi\). Finally, for the state \(\,\left| {1}\right\rangle _1\,\left| {1}\right\rangle _2\,\left| {\alpha }\right\rangle _a\), the resulted output state of Mach–Zehnder interferometer reads as

$$\begin{aligned} \,\left| {1}\right\rangle _1\,\left| {1}\right\rangle _2\,\left| {\alpha }\right\rangle _a\xrightarrow {\text {MZI}}&\,\left| {\text {out}}\right\rangle _{\text {MZI}_4}=\dfrac{1}{2\sqrt{2}}\,\left| {\widetilde{\psi _e}}\right\rangle _a\big [i\,\left| {2}\right\rangle _1\,\left| {0}\right\rangle _2\\ \nonumber&-i\,\left| {0}\right\rangle _1\,\left| {2}\right\rangle _2-\sqrt{2}\,\left| {1}\right\rangle _1\,\left| {1}\right\rangle _2\big ], \end{aligned}$$
(14)

where we have set \(2Kt=\pi\) and \(2\theta =\pi\). Summing up, replacing the relations (10) and (12)–(14) in (9), the whole state of the system after crossing the MZI becomes as

$$\begin{aligned} \,\left| {\Psi }\right\rangle _{\text {total}}&=-\dfrac{1}{4}\,\left| {e}\right\rangle _1\,\left| {g}\right\rangle _2\big [i\,\left| {\widetilde{\psi _o}}\right\rangle _a\,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2+\,\left| {\widetilde{\psi _e}}\right\rangle _a\,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2\big ]\nonumber \\&\quad -\dfrac{i}{4}\,\left| {e}\right\rangle _1\,\left| {e}\right\rangle _2\big [\,\left| {\widetilde{\psi _o}}\right\rangle _a+\,\left| {\widetilde{\psi _e}}\right\rangle _a\big ]\,\left| {0}\right\rangle _1\,\left| {0}\right\rangle _2\nonumber \\&\quad +\dfrac{1}{4\sqrt{2}}\,\left| {g}\right\rangle _1\,\left| {g}\right\rangle _2\,\left| {\widetilde{\psi _e}}\right\rangle _a\big [\,\left| {2}\right\rangle _1\,\left| {0}\right\rangle _2-\,\left| {0}\right\rangle _1\,\left| {2}\right\rangle _2+i\sqrt{2}\,\left| {1}\right\rangle _1\,\left| {1}\right\rangle _2\big ]\nonumber \\&\quad +\dfrac{1}{4}\,\left| {g}\right\rangle _1\,\left| {e}\right\rangle _2\big [i\,\left| {\widetilde{\psi _o}}\right\rangle _a\,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2-\,\left| {\widetilde{\psi _e}}\right\rangle _a\,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2\big ]. \end{aligned}$$
(15)

Now, detecting the state of field \(F_1\) in the single-photon state \(\,\left| {1}\right\rangle _1\), the total state of the system collapses to

$$\begin{aligned} \,\left| {\Psi }\right\rangle _{A_1A_2F_2a}&=-\dfrac{1}{4}\big (i\,\left| {e}\right\rangle _1\,\left| {g}\right\rangle _2\,\left| {\widetilde{\psi _o}}\right\rangle _a+\,\left| {g}\right\rangle _1\,\left| {e}\right\rangle _2\,\left| {\widetilde{\psi _e}}\right\rangle _a\big )\,\left| {0}\right\rangle _2\nonumber \\&\quad +\dfrac{i}{4}\,\left| {g}\right\rangle _1\,\left| {g}\right\rangle _2\,\left| {\widetilde{\psi _e}}\right\rangle _a\,\left| {1}\right\rangle _2. \end{aligned}$$
(16)

Henceforth, if we detect the state of field \(F_2\) in the vacuum state, the following state for the atom \(A_1\), atom \(A_2\) and a-mode is accessible

$$\begin{aligned} \,\left| {\Psi }\right\rangle _{A_1A_2a}=-\dfrac{N}{4}\big (i\,\left| {e}\right\rangle _1\,\left| {g}\right\rangle _2\,\left| {\widetilde{\psi _o}}\right\rangle _a+\,\left| {g}\right\rangle _1\,\left| {e}\right\rangle _2\,\left| {\widetilde{\psi _e}}\right\rangle _a\big ), \end{aligned}$$
(17)

where we have set N as a normalization factor. The generated entangled state in (17) is a tripartite entanglement of atom \(A_1\), atom \(A_2\) and a-mode. This state by assuming that the coherent amplitude \(\alpha\) is large enough, is transformed to a fully entangled state. Then, the entanglement is swapped from two subsystems \((AF)_1\) and \((AF)_2\) [expressed in (5) and (7), respectively], to a new system including \(A_1\), \(A_2\) and a-mode. In the following, to establish the reliability of the performed entanglement swapping process, we investigate the interesting criteria in the entanglement swapping process, including success probability as well as the fidelity.

4.1 Success probability

Success probabilities, respectively, for detecting the field \(F_1\) in the single-photon state \(\,\left| {1}\right\rangle _1\), and \(F_2\) in the vacuum state \(\,\left| {0}\right\rangle _2\) have been described by the following relations,

$$\begin{aligned}&\text {SP}_1=\dfrac{4N_e^2+1}{2(1+6N_e^2)},\end{aligned}$$
(18)
$$\begin{aligned}&\text {SP}_2=\dfrac{4N_e^2}{1+4N_e^2}. \end{aligned}$$
(19)

These quantities along with the total success probability (which is the product of \(\text {SP}_1\) and \(\text {SP}_2\)) are plotted in Fig. 3 versus the intensity of field (in the rest of this paper we refer to the intensity of the field briefly as the intensity of field).

Fig. 3
figure 3

Success probability of detecting the field \(F_1\) in the single-photon state \(\,\left| {1}\right\rangle _1\) (red dotted line), the field \(F_2\) in the vacuum state \(\,\left| {0}\right\rangle _2\) (blue dashed line) and the total success probability (black solid line) versus the intensity of field

Full size image

As is clear the success probability of detecting the state \(\,\left| {1}\right\rangle _1\) begins from its maximum value (i.e., 0.4) and by increasing the intensity of field, gently reaches the value 0.37 and remains constant for \(|\alpha |^2\gtrsim 2\). Also, the success probability of detecting the state \(\,\left| {0}\right\rangle _2\) begins from 0.5 and with increasing the intensity of field, ascends to its maximum value (i.e., 0.66) and remains constant for \(|\alpha |^2\gtrsim 2\). Finally, the total success probability begins from 0.2 and tends to 0.25 for \(|\alpha |^2\gtrsim 2\).

4.2 Fidelity

To demonstrate the similarity of the state (17) to the fully entangled state

$$\begin{aligned} \,\left| {\Phi }\right\rangle =\dfrac{1}{\sqrt{2}}\big (i\,\left| {e}\right\rangle _1\,\left| {g}\right\rangle _2\,\left| {\psi _o}\right\rangle _a+\,\left| {g}\right\rangle _1\,\left| {e}\right\rangle _2\,\left| {\psi _e}\right\rangle _a\big ), \end{aligned}$$
(20)

the fidelity may be used. The fidelity of two quantum states \(\,\left| {\Phi }\right\rangle\) and \(\,\left| {\Psi }\right\rangle _{A_1A_2a}\) which is defined as \(F=\big |\langle {\Phi |\Psi }\rangle _{A_1A_2a}\big |^2\) [4] is plotted in Fig. 4.

Fig. 4
figure 4

Fidelity of the state (17) relative to (20) versus the intensity of field

Full size image

As is clear, the fidelity is initiated from 0.5 for small values of the field intensity and slopes steeply up to 1 for \(|\alpha |^2\gtrsim 2\). The complete fidelity (i.e., 1) in the intensities \(|\alpha |^2\gtrsim 2\) means that the state \(\,\left| {\Psi }\right\rangle _{A_1A_2a}\) is entirely similar to the fully entangled state \(\,\left| {\Phi }\right\rangle\). This result is compatible with what is achieved from the state (17). This means that the state (17) for \(|\alpha |^2\gtrsim 2\) becomes a fully entangled state.

5 Quantum teleportation based on the Mach–Zehnder interferometer

As is stated, in teleportation protocol, Alice intends to transmit an unknown state to Bob using a quantum channel. In our proposal, teleportation of a two-particle entangled state is performed using a non-maximally entangled state (for quantum channel) with the help of the Mach–Zehnder interferometer.

Let us suppose the pair of entangled particles (particles 1 and 2) that Alice intends to transmit, is as follows:

$$\begin{aligned} \,\left| {\varphi }\right\rangle _{12}=\eta \,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2+\gamma \,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2, \end{aligned}$$
(21)

where \(\eta\) and \(\gamma\) are the unknown coefficients satisfactory \(|\eta |^2+|\gamma |^2=1\). Also, the quantum channel is a non-maximally entangled state as below:

$$\begin{aligned} \,\left| {\varphi }\right\rangle _{a34}=\eta '\,\left| {\alpha }\right\rangle _a\,\left| {0}\right\rangle _3\,\left| {1}\right\rangle _4+\gamma '\,\left| {-\alpha }\right\rangle _a\,\left| {1}\right\rangle _3\,\left| {0}\right\rangle _4, \end{aligned}$$
(22)

where the coherent state \(\,\left| {\pm \alpha }\right\rangle _a\) is related to the a-mode which was introduced in previous sections. In addition, the pairs of unknown coefficients \(\eta\), \(\gamma\) and \(\eta '\), \(\gamma '\) each of which satisfies the normalization condition. The initial state of total system including particles 1 and 2 together with the quantum channel reads as

$$\begin{aligned} \,\left| {\varphi }\right\rangle _{12a34}&=\,\left| {\varphi }\right\rangle _{12}\otimes \,\left| {\varphi }\right\rangle _{a34} \nonumber \\&=\eta \eta '\,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2\,\left| {\alpha }\right\rangle _a\,\left| {0}\right\rangle _3\,\left| {1}\right\rangle _4+\gamma \eta '\,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2\,\left| {\alpha }\right\rangle _a\,\left| {0}\right\rangle _3\,\left| {1}\right\rangle _4\nonumber \\&\quad +\eta \gamma '\,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2\,\left| {-\alpha }\right\rangle _a\,\left| {1}\right\rangle _3\,\left| {0}\right\rangle _4+\gamma \gamma '\,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2\,\left| {-\alpha }\right\rangle _a\,\left| {1}\right\rangle _3\,\left| {0}\right\rangle _4. \end{aligned}$$
(23)

Now, we enter the state \(\,\left| {m}\right\rangle _1\,\left| {n}\right\rangle _2\,\left| {\pm \alpha }\right\rangle _a\) with \(m,n=0,1\) in the interferometer which is shown in Fig. 1. By using the procedure outlined in the “Appendix A”, the following results are obtained:

$$\begin{aligned} \,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2\,\left| {\pm \alpha }\right\rangle _a\xrightarrow {\text {MZI}}\,\left| {\text {out}}\right\rangle _{\text {MZI}_5}&=\dfrac{1}{2}\big [\mp i\,\left| {\widetilde{\psi _o}}\right\rangle _a\,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2\\ \nonumber&\quad -\,\left| {\widetilde{\psi _e}}\right\rangle _a\,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2\big ], \end{aligned}$$
(24)
$$\begin{aligned} \,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2\,\left| {\pm \alpha }\right\rangle _a\xrightarrow {\text {MZI}}\,\left| {\text {out}}\right\rangle _{\text {MZI}_6}&=\dfrac{1}{2}\big [\mp i\,\left| {\widetilde{\psi _o}}\right\rangle _a\,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2\\ \nonumber&\quad +\,\left| {\widetilde{\psi _e}}\right\rangle _a\,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2\big ]. \end{aligned}$$
(25)

Then, the whole state of the system after crossing the Mach–Zehnder interferometer becomes as

$$\begin{aligned} \,\left| {\phi }\right\rangle _{12a34}&=\dfrac{1}{2}\,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2\big (-i\eta \eta '\,\left| {\widetilde{\psi _o}}\right\rangle _a+\gamma \eta '\,\left| {\widetilde{\psi _e}}\right\rangle _a\big )\,\left| {0}\right\rangle _3\,\left| {1}\right\rangle _4\nonumber \\&\quad -\dfrac{1}{2}\,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2\big (\eta \eta '\,\left| {\widetilde{\psi _e}}\right\rangle _a+i\gamma \eta '\,\left| {\widetilde{\psi _o}}\right\rangle _a\big )\,\left| {0}\right\rangle _3\,\left| {1}\right\rangle _4\nonumber \\&\quad +\dfrac{1}{2}\,\left| {1}\right\rangle _1\,\left| {0}\right\rangle _2\big (i\eta \gamma '\,\left| {\widetilde{\psi _o}}\right\rangle _a+\gamma \gamma '\,\left| {\widetilde{\psi _e}}\right\rangle _a\big )\,\left| {1}\right\rangle _3\,\left| {0}\right\rangle _4\nonumber \\&\quad +\dfrac{1}{2}\,\left| {0}\right\rangle _1\,\left| {1}\right\rangle _2\big (-\eta \gamma '\,\left| {\widetilde{\psi _e}}\right\rangle _a+i\gamma \gamma '\,\left| {\widetilde{\psi _o}}\right\rangle _a\big )\,\left| {1}\right\rangle _3\,\left| {0}\right\rangle _4, \end{aligned}$$
(26)

where \(\,\left| {\widetilde{\psi _{o(e)}}}\right\rangle _a\) have been defined after (10). Detecting the state of particle 1 in the state \(\,\left| {1}\right\rangle _1\) [with success probability \(\dfrac{1}{4}(\dfrac{\eta ^2}{N_o^2}+\dfrac{\gamma ^2}{N_e^2})\)] and particle 2 in the state \(\,\left| {0}\right\rangle _2\) (with success probability 1), the total state of system collapses to

$$\begin{aligned} \,\left| {\phi }\right\rangle _{a34}&=\dfrac{1}{2}\big (-i\eta \eta '\,\left| {\widetilde{\psi _o}}\right\rangle _a+\gamma \eta '\,\left| {\widetilde{\psi _e}}\right\rangle _a\big )\,\left| {0}\right\rangle _3\,\left| {1}\right\rangle _4\nonumber \\&\quad +\dfrac{1}{2}\big (i\eta \gamma '\,\left| {\widetilde{\psi _o}}\right\rangle _a+\gamma \gamma '\,\left| {\widetilde{\psi _e}}\right\rangle _a\big )\,\left| {1}\right\rangle _3\,\left| {0}\right\rangle _4. \end{aligned}$$
(27)

Now, we detect the state of the a-mode in two cases:

  • Detecting the state \(\,\left| {\widetilde{\psi _e}}\right\rangle _a\) for the a-mode: if the detection process results in the state \(\,\left| {\widetilde{\psi _e}}\right\rangle _a\), with the assumption \(\eta =\eta '\) and \(\gamma =\gamma '\), the (27) may be written as

    $$\begin{aligned} \,\left| {\phi }\right\rangle _{34}=\dfrac{\gamma }{2N_e^2}\big (\eta \,\left| {0}\right\rangle _3\,\left| {1}\right\rangle _4+\gamma \,\left| {1}\right\rangle _3\,\left| {0}\right\rangle _4\big ). \end{aligned}$$
    (28)

    So, the initial entangled state (21) of particles 1 and 2, is reconstructed for particles 3 and 4 and the quantum teleportation process is successfully carried out (a successful teleportation scheme results in the complete fidelity i. e., 1).

  • Detecting the state \(\,\left| {\widetilde{\psi _o}}\right\rangle _a\) for the a-mode: if the detection process results in the state \(\,\left| {\widetilde{\psi _o}}\right\rangle _a\), with setting \(\eta =\eta '\) and \(\gamma =\gamma '\), the relation (27) becomes as

    $$\begin{aligned} \,\left| {\phi '}\right\rangle _{34}=\dfrac{i\eta }{2N_o^2}\big (-\eta \,\left| {0}\right\rangle _3\,\left| {1}\right\rangle _4+\gamma \,\left| {1}\right\rangle _3\,\left| {0}\right\rangle _4\big ). \end{aligned}$$
    (29)

    Here, Bob only needs to make standard rotations on particles 3 and 4 (i.e., \(\hat{\sigma }_z\otimes \hat{I}\) on \(\,\left| {\phi '}\right\rangle _{34}\) ) to construct the initial entangled state (21). Then, again it is seen that the teleportation of the entangled state is fulfilled successfully.

We emphasize that the applied interferometer in the teleportation process has been considered clearly by ignoring of the loss, noise and other dissipative effects.

6 Summary and conclusion

In this paper, the entanglement swapping and quantum teleportation processes have been performed using the Mach–Zehnder interferometer assisted with a nonlinear cross-Kerr cell. As the first step in this study, we started with a brief review on the performance of the Mach–Zehnder interferometer in which mode 1 (after passing the \(\text {BS}_1\)) becomes coupled to an external mode through a cross-Kerr medium. Then, using this interferometer, we have paid attention to swap the entanglement and teleportation of an unknown quantum state. Since in the considered setup in this paper we have used two beam splitters, in a sense the content of this paper may be considered as an extension of our previous work in [39]. The total state in the entanglement swapping process is consisted of two entangled atom–field states \(((AF)_{1,2})\) (which have been generated using the interaction of atom and field via the Jaynes–Cummings model) and an ancillary mode a which is initially prepared in the coherent state. Injecting the state of two fields \(F_1\) and \(F_2\) and the a-mode (as the external mode of the interferometer) into the Mach–Zehnder interferometer and detecting the states of fields \(F_1\) and \(F_2\), has resulted in an entangled state between the atoms \(A_1\), \(A_2\) and the a-mode field. So, the entanglement swapping has been successfully performed from \((AF)_{1}\) and \((AF)_{2}\) to the \(A_1\)–\(A_2\)–a-mode. In the continuation, the quantum teleportation of an unknown entangled state has been performed using an unknown quantum channel using the Mach–Zehnder interferometer, too.

In this regard, we have evaluated a few interesting quantities in the entanglement swapping, including success probability of the detecting process, fidelity of the obtained entangled state relative to a suitable maximal entangled state and the degree of entanglement. In the evaluation of the total success probability of the detecting process, it has been demonstrated that this parameter after an initial increase, reaches its maximum value (i.e., 0.25) and remains constant for the intensity of the field \(|\alpha |^2\gtrsim 2\). Also, it has been observed that the value of fidelity for \(|\alpha |^2\gtrsim 2\) achieves its maximum possible value, i.e., 1. This fidelity means that the state (17) is completely similar to the maximally entangled state (20). As a comparison with the prior studies, in spite of Refs. [16, 40] and [13, 14] which, respectively, have utilized cavity QED and Bell-state measurement methods for the entanglement swapping, we have performed this process beyond the mentioned approaches with a new approach. In our proposal, the involving two fields \(F_{1}\), \(F_{2}\) and the a-mode (in the Mach–Zehnder interferometer) lead to the tripartite entangled state containing two atoms \(A_{1}\), \(A_{2}\) and a-mode. Summing up, in this paper we could generate the entangled state for three particles (atom \(A_1\), atom \(A_2\) and a-mode) via entanglement swapping process and applying a new implementation in comparison with Refs. [17, 18] through which tripartite entangled states have been produced. In addition, as a comparison with Refs. [25] and [26,27,28] which, respectively, have utilized Bell-state measurement and cavity QED methods for the quantum teleportation, we have teleported the two-particle entangled state using the Mach–Zehnder interferometer. We end this paper with mentioning that entanglement swapping in our previous works   [15, 19, 20, 39] has been performed using the well-known cavity QED method [16,17,18, 40] (the atom–field interaction in a cavity) or by tools such as a beam splitter by which a bipartite entangled state has been generated. However, our present work basically is based on neither of the latter mentioned methods nor the Bell-state measurement approach [13, 14]; instead, a Mach–Zehnder interferometer assisted with a nonlinear cross-Kerr cell is used (this is what has been newly done in this paper) by which a tripartite (instead of previously bipartite) entangled state has been generated in the introduced entanglement swapping process.