Interband and free charge carrier absorption in silicon at 800 nm: experiments and model calculations

Abstract

The average transmitted power of a Ti:sapphire femtosecond (fs) laser beam through thin, oxidized silicon (Si) membranes in the 10–30 $\, \upmu \text{m}$ thickness range at $45{^\circ }$ external angle of incidence at first increases with the incident average laser power and then decreases considerably. This stationary state behavior is quantitatively reproduced by a recently derived model using an effective absorption coefficient $\alpha _{\text {eff}} = \alpha _{1} + \alpha _{\text {FCA}}$, adding the coefficients of two independent linear absorption processes, $\alpha _{1}$ of the indirect interband transition and $\alpha _{\text {FCA}}$ of free charge carrier absorption (FCA). The relations between the empirical parameter $\alpha _{\text {FCA}}$ and the model parameters $n_{\text {eh}}$ (density of free charge carriers) and $\sigma _{\text {eh}}$ (absorption cross section of free charge carriers) are found to depend on the Si membrane thickness and are briefly discussed. Using different sample thicknesses, experimental evidence has been found for a nonlinear intensity dependence of $\alpha _{\text {FCA}}$∼$I_{0}^{n}$, where $1\le n \le 3$ shows systematic variation. The FCA model in combination with its empirical fit parameters allowed to fully calculate the transmission behavior of the Si membranes within the investigated sample thickness and laser power regimes.

1 Introduction

Silicon (Si) continues to be a prominent material in microelectronics, optoelectronics, micromechanics, solar cells, and increasingly in photonics (cf., e.g., [1]). Delicate Si devices can be shaped and/or modified by laser technology providing a manifold of remote, contactless, spatially confined and time controlled methods for, e.g., doping, annealing, crystallization, and ablation. Proper processing control requires, however, a detailed understanding of the linear and nonlinear optical phenomena in Si. Some of the nonlinear phenomena may occur simultaneously and be difficult to discriminate like, e.g., coherent two-photon absorption (TPA), free charge carrier absorption (FCA), and thermally induced absorption enhancement (TAE) [2].

FCA has a long history of more than half a century (cf., e.g., [3]), and was at first investigated by the standard spectroscopy and conventional free charge carrier generation. With the advent of lasers, the contactless and well-confined photo generation of free charge carriers has become amenable, convenient, and increasingly important. The bulk part of the FCA studies is, however, related to FCA in the wavelength range $\lambda > 0.9\, \upmu \text{m}$ with small (negligible) interference from the indirect interband transition of Si at $\lambda \le 1.13\, \upmu \text{m}$ ($1.1\, \text{ eV }$ optical band gap). Only a few papers address FCA in the spectral overlap region with the indirect and direct optical transitions (cf. [2, 4,5,6]). They differ fundamentally from the studies at long wavelengths: the generation of free charge carriers is dominated by 1-photon and 2-photon absorption at short and long wavelengths, respectively.

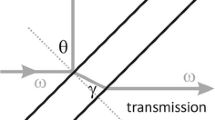
In this paper, a femtosecond (fs) Ti:sapphire laser tuned to $\lambda = 800\, \text{ nm }$ ($h\nu = 1.55\, \text{ eV }$) is applied to investigate the stationary state optical behavior of thin Si samples in the 10–$30\, \upmu \text{m}$ thickness range by measuring the average laser power of the fs pulse train transmitted through the membranes as a function of the incident laser power (Fig. 1). The main experimental findings provide an essential extension of our recent results [6] and address the membrane thickness d, the linear absorption coefficient $\alpha _{1}$, as well as the FCA coefficient $\alpha _{\text {FCA}}$ and its relations to the model parameters $n_{\text {eh}}$ (density of free charge carriers) and $\sigma _{\text {eh}}$ (absorption cross section of free charge carriers).

Fig. 1

Typical power dependences of the fs-laser beam reflection from and transmission through a thin silicon membrane with the contributions of linear absorption (broken line) and free charge carrier absorption (FCA, indicated by arrow) obtained for a pulse train at $800\, \text{ nm }$; inset: scheme of the experimental setup with external angle of incidence $\theta = 45^{\circ }$ and a propagation angle $\gamma = 11^{\circ }$ within silicon

2 Experimental

For the transmission measurements through the Si membranes, a Ti:sapphire laser beam tuned to $\lambda = 800\, \text{ nm }$ is applied to irradiate the Si samples at an external angle of incidence $\theta = 45^{\circ }$ (Fig. 1). The commercial fs oscillator (Spectra Physics, 3941-M3S, Tsunami) is pumped by a frequency doubled Nd:YVO$_4$ laser (Spectra Physics, Millenia V) with $5.5\, \text{ W }$ c.w. maximum output power and provides an average power up to $1\, \text{ W }$ at $80\, \text{ MHz }$ repetition rate. The pulse duration of $90\, \text{ fs }$ (fwhm) on the sample is determined by a custom built autocorrelator. The beam p-polarization is defined by a polarizing beam splitter (Thorlabs, Glan-laser polarizer, $10\, \text{ mm }$, CA, AR coating: 650–1050 nm) combined with two half-wave plates (Thorlabs, zero-order half-wave plate, $780\, \text{ nm }$) for power adjustment and polarization control. The beam is shaped by two lenses ($f = -50\, \text{ mm }$ and $f =35\, \text{ mm }$) and focused to a $1/e^{2}$ focal beam diameter of $(11.2\pm 2)\, \upmu \text{m}$ as determined by a z-scan measurement. The Rayleigh length amounts to $z_{\text {R}} = 0.12\, \text{ mm }$. The beam transmitted through the Si membrane is collected by a lens $f =125\, \text{ mm }$. A power meter (Thorlabs, PMD100D) is used to measure the reflected and transmitted powers.

The samples are prepared from commercial (100)-Si wafers ($370\, \upmu \text{m}$ thick) by chemical etching of one wafer side using tetramethylammonium hydroxide (TMAH) to produce thin membranes of $3\times 3\, \text{mm}^{2}$ area and a thickness d of $10 \le d \le 30\, \upmu \text{m}$ (details cf. Sect. 3.1). The wafers are slightly p-doped ($3\ldots 6\times 10^{14}\, \text{cm}^{-3}$). Prior to the investigations, the membranes are cleaned using acetone and $40\%$ hydrofluoric acid to remove dirt and old oxide layers, respectively. In contact with the air, the clean surfaces oxidize in the dark under ambient conditions reaching within 48 h an equilibrium thickness of $(2.5\pm 0.5)\, \text{ nm }$ (cf., e.g., [7]). In addition to the membrane thickness determination in Sect. 3.1, independent optical thickness measurements were performed using a Zeiss microscope Axio Imager.M2m in two ways. In case of intact membranes, the membrane thickness is derived from the difference between the wafer thickness ($370\, \upmu \text{m}$ specified and measured) and the measured depth of the etched square ($\approx$360 $\upmu \text{m}$) with an uncertainty of about ±5 $\upmu \text{m}$. The thickness homogeneity of the individual Si membranes is determined to ±1 $\upmu \text{m}$. In case of membrane fragments, the thickness measurement by direct inspection of the membrane cross section is relatively precise around ±0.2 $\upmu \text{m}$, but does not refer to the membranes used for the transmission measurements. It is assumed that preferably thin membranes are broken. Overall, the microscopic thickness measurements are in agreement with the results obtained in Sect. 3.1 (Fig. 3; Table 1).

Table 1 Parameters $(\alpha _{1}z_{\text {m}})$ and thickness $d_{i}$ of the Si membranes obtained from the linear absorption regime (Beer’s law, Fig. 3, index: lin) and the FCA model (Eqs. 5 and 7) used to fit the measurement points in Fig. 2b with exponent $n = 2$ (index: FCA, fix) and $n = \text {variable}$ (index: FCA, var); $d_{\text {mean}}$ is the average and $\Delta d_{\text {SD}}$ is the standard deviation of the three d values

3 Results and discussion

Laser beam reflection always displays a linear dependence on the incident laser power $P_{\text {in}}$ with $R = 0.15\,\pm \,0.01$ for the applied Si membranes without indicating a systematic thickness dependence (Fig. 2a). This finding is in agreement with previous reports (cf., e.g., [8, 9]) and confirms the validity of the Fresnel equations using the optical constants of the sample under ambient conditions, i.e., refractive indices $n_{\text {air}} = 1$, $n_{\mathrm{SiO}_{2}} = 1.45$ [10], and $n_{\text {Si}} = 3.69$ [11, 12] yielding $R = 0.155$.

Fig. 2

a Reflected laser power $P_{\text {ref}}$ with linear fit curves yielding reflectivity $R = 0.15\,\pm \,0.01$ and b average transmitted laser power $P_{\text {trans}}$ of a fs-laser pulse train ($\lambda = 800\, \text{ nm }$, $\tau _{\text {pulse}} = 90\, \text{ fs }$, repetition rate $80\, \text{ MHz }$, external angle of incidence $\theta = 45^{\circ }$) using thin Si membranes measured as a function of the incident average laser power $P_{\text {in}}$. The fit curves in part b originate from the FCA model described in Sect. 3.2 using a fixed exponent $n = 2$ (solid lines) and a variable exponent n (broken lines). Each Si membrane is labeled by a number and thickness ($d_{\text {mean}}$ from Table 1). The uncertainty of the measured power is $0.0005\, \text{ W }$, which yields error bars that are smaller than the symbols used. c Absorption coefficients $\alpha _{\text {FCA}}$ derived from Fig. 2b following the scheme of Fig. 1 by use of Eq. (3b), the value $\alpha _{1} = 785\, \text{cm}^{-1}$ and the d values from Table 1 (also cf. Sect. 3.2)

Figure 2b shows the measured laser beam transmission through the membranes as a function of the incident average laser power $P_{\text {in}}$ up to $0.8\, \text{ W }$. It is pointed out that the same transmission values are measured for rising or decreasing laser power $P_{\text {in}}$ (i.e., no hysteresis effects). The transmitted laser power $P_{\text {trans}}$ deviates considerably from linearity (Figs. 1, 2b): starting with an initial linear increase of $P_{\text {trans}}$ for low power $P_{\text {in}}$ ($< 0.2\, \text{ W }$ in Fig. 1), the transmitted power reaches an absolute maximum value at $P_{\text {in}} \approx 0.6\pm 0.1\, \text{ W }$ (Fig. 1). For higher laser power $P_{\text {in}}$, the transmitted power $P_{\text {trans}}$ decreases again (Fig. 2b). Contributions from internally reflected beams to the transmitted laser power $P_{\text {trans}}$ are neglected (<0.5%). Interference between the incoming and internally reflected beams is excluded, because the time for a pulse path forth and back through the membrane amounts to $\ge$250 fs being much longer than the $90\, \text{ fs }$ laser pulse duration.

Following the essence of our previous article [6], the discussion of the findings in Fig. 2b is focused on linear absorption (Beer’s law, indirect interband transition) in the low power region and FCA as the dominant effect controlling the experimental findings in the high power range (cf. Figs. 1, 2b; e.g., [2, 5, 6]).

The lifetime of thermalized electrons in the conduction band (CB) of Si, or equivalently, of thermalized electron–hole (eh) pairs ranges around $\tau _{\text {eh}}\approx 10^{-5}\, \text{s}$ for intrinsic and weakly doped Si samples [13,14,15]. This relatively long lifetime is much longer than the typical duration of ultrashort (ps to fs) or even short ($1\, \text{ ns }$ to $1\, \upmu \text{s}$) laser pulses. Therefore, eh pairs can accumulate during long laser pulses and/or during laser pulse trains used for the excitation of Si and thus generate additional absorption of the laser beam by free charge carriers. At our repetition rate of $80\, \text{ MHz }$ $\tau _{\text {rep}} = 1.25\times 10^{-8}\, \text{s}<< \tau _{\text {eh}}$. The accumulation of eh pairs during repetitively pulsed irradiation leads to a power dependent stationary density of eh pairs $n_{\text {eh}}$ which is determined by the ratio between the power dependent eh pair generation and its losses. Therefore, the laser beam transmission is approximated by Beer’s law (linear absorption) at low incident power $P_{\text {in}}$ and by additional linear absorption by free charge carriers (FCA) at high power, as shown in Fig. 1.

3.1 Linear laser beam absorption (Beer’s law)

In this section, the low $P_{\text {in}}$ power range of the linear absorption is considered and its validity region estimated. Beer’s law in its logarithmic form reads

$$\ln {(I(z_{\text {m}})/I_{0})} = -\alpha _{1}z_{\text {m}},$$

(1)

with $\alpha _{1}$ and $z_{\text {m}} = d/\cos {\gamma }$ being the linear absorption coefficient of Si at $\lambda _{\text {laser}}$ and the absorption pathlength within the Si membrane of thickness d under propagation angle $\gamma$ (Fig. 1), respectively. The intensities $I(z_{\text {m}})$ and $I_{0}$ in Eq. (1) refer to the laser beam intensities at the rear side in the Si membrane $I(z=z_{\text {m}})$ and the front side $I(z = 0)$ directly before the rear Si/SiO$_2$ interface and behind the front Si/SiO$_2$ interface, respectively. The relations between these intensities and the measured powers $P_{\text {trans}}$ and $P_{\text {in}}$ in Fig. 2 are established by assuming the proportionalities $I_{0} = \eta _{\text {in}}P_{\text {in}}T_{\text {air}/\text {Si}}$ and $I(z_{\text {m}}) = \eta _{\text {trans}}P_{\text {trans}}/T_{\text {Si}/\text {air}}$ with $T_{\text {air}/\text {Si}}$ and $T_{\text {Si}/\text {air}}$ being the intensity transmission factors ($T = 1 - R$, $R = \text {reflectivity}$). $\eta _{\text {in}}$ and $\eta _{\text {trans}}$ are the factors to convert the average laser power to the laser pulse intensity (averaged over the pulse duration and the beam cross section). With the assumption $\eta _{\text {in}} = \eta _{\text {trans}}$, i.e., assuming identical spatial and temporal beam profiles, both $\eta$ terms cancel. Using, furthermore, the relation $T_{\text {air}/\text {Si}}$ = $T_{\text {air}/\text {Si}} = T = 1 - R = 0.845$, the intensity terms $I_{0}$ and $I(z_{\text {m}})$ in Eq. (1) can be replaced by the measured values $P_{\text {in}}$ and $P_{\text {trans}}$ (Fig. 2), respectively, and yield:

$$\begin{aligned} \ln {(I(z_{\text {m}})/I_{0})} = \ln {(P_{\text {trans}}/P_{\text {in}})} - \ln {T^{2}} = -\alpha _{1}z_{\text {m}}. \end{aligned}$$

(2)

Equation (2) provides the basis of Fig. 3 and the option to empirically determine the product $\alpha _{1}z_{\text {m}}$ for each investigated Si membrane. As far as Beer’s law is applicable, the product $\alpha _{1}z_{\text {m}}$ should stay constant independent of $P_{\text {in}}$ and have a specific value for each membrane thickness $d = z_{\text {m}}\cos {\gamma }$. Consequently, the $P_{\text {in}}$ range of linear absorption (validity of Beer’s law) is characterized by the horizontal part of each trace in Fig. 3 as indicated by the broken lines. The abscissa scale is given in logarithmic units ($\ln {(P_{\text {in}}/\text {W})}$) for convenient presentation only.

The T value used in calculating the ordinate scale value in Fig. 3 is uncertain because the used refractive index of bulk amorphous SiO$_2$ need not necessarily apply to the thin layer of the natural oxide. $\Delta T = \pm 0.05$ corresponds to an uncertainty $\Delta n_{\mathrm{Si}O_2} = \pm 0.033$ in the refractive index of SiO$_2$. These uncertainties have been taken into account, together with the uncertainty in the measured $P_{\text {trans}}$ values of $\Delta P_{\text {trans}}$ $= \pm 0.0005\, \text{ W }$ to calculate the error bars in Fig. 3.

Fig. 3

Natural logarithm $\ln {(I(z_{\text {m}})/I_{0})} = \ln {(P_{\text {trans}}/P_{\text {in}})} - \ln {T^{2}} = -\alpha _{1}z_{\text {m}}$ (Eq. 2) with $I(z=z_{\text {m}})$ and $I_{0} = I_{z=0}$ being the laser beam intensities at the rear and at the front sides of the Si membrane as a function of the natural logarithm $\ln {P_{\text {in}}}$ of the average laser power $P_{\text {in}}$ incident onto the Si membranes. The boxes (broken lines) indicate the data points used to calculate $(\alpha _{1}z_{\text {m}})^{\text {lin}}$ and $d_{i}^{\text {lin}}$ for Table 1

For high power $P_{\text {in}}$, the traces $\ln {(P_{\text {trans}}/P_{\text {in}})} - \ln {T^{2}}$ turn strongly negative due to free charge carrier absorption (FCA, cf. Sect. 3.2). For thick membranes and small $P_{\text {in}}$ values, on the other hand, the turn of $\ln {(P_{\text {trans}}/P_{\text {in}})} - \ln {T^{2}}$ to negative values is attributed to measurement errors (baseline imperfections). The values of $(\alpha _{1}z_{\text {m}})^{\text {lin}}$ listed in Table 1 were obtained by averaging over the data points in the horizontal part of each curve, with the standard deviation taken as the error. The literature values for $\alpha _{1}$ cover a broad range from, e.g., $604\, \text{cm}^{-1}$ [16] to $1100\, \text{cm}^{-1}$ [17]. The value $\alpha _{1} = 604\, \text{cm}^{-1}$ was obtained by a z-scan measurement using a fs-laser pulse train at high repetition rate. Knowing now about considerable FCA under these conditions [6], this experimental result has to be reconsidered. From a recent paper $\alpha _{1} = 785\, \text{cm}^{-1}$ is obtained [18], which appears to be most reliable. The Si membrane thicknesses $d_{i}^{\text {lin}}$ listed in Table 1 were calculated with $\alpha _{1} = 785\pm 100\, \text{cm}^{-1}$, using the standard error propagation techniques.

In the paragraph above, the membrane thickness values $d_{i}$ were derived from the experimentally determined $(\alpha _{1}z_{\text {m}})_{i}$ product of Fig. 3 using the relation $d_{i} = (\alpha _{1}z_{\text {m}})_{i}(\cos {\gamma })/\alpha _{1}$. A second source of $(\alpha _{1}z_{\text {m}})_{i}$ values is, however, available from the $\exp {(-\alpha _{1}z_{\text {m}})}$ term in the FCA model (Eqs. 5, 7) in Sect. 3.2 and the related fit curve parameter F (Eq. 8). For clarity of the presentation, the above values $d_{i}$ and $(\alpha _{1}z_{\text {m}})_{i}$ derived from the linear absorption regime (Beer’s law) are in the following denominated $d_{i}^{\text {lin}}$ and $(\alpha _{1}z_{\text {m}})_{i}^{\text {lin}}$, while $d_{i}^{\text {FCA}}$ describe the thickness values extracted from the FCA model. The $d_{i}^{\text {lin}}$, $d_{\text {fix}}^{\text {FCA}}$, and $d_{\text {var}}^{\text {FCA}}$ values for a certain membrane in Table 1 agree with one another with a standard deviation $\pm \Delta d_{\text {SD}} < 1\, \upmu \text{m}$, meaning that the agreement of the d values is better than their individual errors. The averages of the three values are listed in the last column and used as labels in Figs. 2, 3, and 4.

Fig. 4

a Square root of the deviation $\Delta I_{\text {FCA}}/\eta$ [W] (cf. text) of the measured transmission values from the ideal behavior of Beer’s law (Eq. 9) plotted versus the average laser power $P_{\text {in}}$ [W] incident onto the Si membranes (thickness d given in figure). b Stationary density $n_{\text {eh}}$ of the free charge carriers obtained from the $\alpha _{\text {FCA}}$ values of Fig. 2c as a function of $P_{\text {in}}$ for the Si membranes of thickness d using Eq. (10) with fixed $n = 2$. c Stationary density $n_{\text {eh}}^{\text {var}}$ of free charge carriers obtained from the $\alpha _{\text {FCA}}$ values of Fig. 2c in the same way as before but using Eq. 10 with the variable values n given in Table 2

3.2 Free charge carrier absorption (FCA)

Recently, it was empirically found that the transmission of $590\, \text{ nm }$ dye laser and $800\, \text{ nm }$ fs-laser pulses through thin Si samples [6] can be modelled by use of the expressions:

$$\begin{aligned} I(z_{\text {m}}, I_{0})&=~I_{0}\exp {(-\alpha _{1}z_{\text {m}})} \quad \text{ for } \;I_{0} < I_{\text {c}} \end{aligned}$$

(3a)

$$\begin{aligned} I(z_{\text {m}}, I_{0})&=~(I_{0}-I_{\text {c}})\exp {(-\alpha _{1}z_{\text {m}})}\exp {(-\alpha _{\text {FCA}}z_{\text {m}})} \nonumber \\&\quad + I_{\text {c}}\exp {(-\alpha _{1}z_{\text {m}})} \quad \text{ for } \; I_{0} > I_{\text {c}} \end{aligned}$$

(3b)

with $\alpha _{\text {FCA}}$ representing the FCA contribution. In the low intensity regime $I_{0}\le I_{\text {c}}$, Beer’s law is applicable due to negligible FCA. Expression (3b) is valid for $I_{0} > I_{\text {c}}$ and allows to fit, e.g., a constant level of transmitted laser intensity $I(z_{\text {m}}, I_{0})$ for high $I_{0}$ values well above $I_{0}^{\text {max}}$ as observed at $590\, \text{ nm }$ with $I_{0}^{\text {max}}$ being the $I_{0}$ value for which $I(z_{\text {m}}, I_{0})$ reaches its maximum [6]. The physical meaning of $I_{\text {c}}$ can be interpreted as an $I_{0}$ threshold value below which electron/hole (eh) pairs are generated, but do not contribute to FCA, as shown, e.g., in Fig. 4, where $\Delta I_{\text {FCA}}\approx 0$ near the origin of the $P_{\text {in}}$ axis, with $\Delta I_{\text {FCA}}$ being the deviation of the experimental $I(z_{\text {m}})$ values from Beer’s law (also cf. Fig. 1). At least two reasons are conceivable for that: (1) part of the eh pairs are out of resonance with the incident laser beam photons or (2) the eh pairs built up in the first and final parts of (relatively short) laser pulses cannot fully contribute to FCA, i.e., part of the laser pulse will pass through the membrane without FCA. In the first case the $I_{\text {c}}$ value is expected to depend on the laser wavelength. In the second case-probably applicable to the dye laser pulse transmission at $590\, \text{ nm }$ and $250\, \text{ ns }$ duration [4]-$I_{\text {c}}$ will depend on the laser pulse duration relative to the (intensity dependent) eh pair build-up time.

The absorption coefficient $\alpha _{\text {FCA}}$ was previously shown [6] to follow the relation:

$$\begin{aligned} \alpha _{FCA}\approx n_{\text {eh}}\sigma _{\text {eh}}\left( n_{\text {eh}}\right) \approx \sigma _{0}n_{\text {eh}}^{2}\approx \sigma _{0}\left( \kappa \text {I}_{0}\right) ^{2} = \kappa _{2}I_{0}^{2} \end{aligned}$$

(4)

with $n_{\text {eh}}$ being the effective stationary density of eh pairs in the laser-irradiated volume. The absorption cross section $\sigma _{\text {eh}}(n_{\text {eh}})$ is proportional to the density $n_{\text {eh}}$ as could be derived from the findings in [19], i.e., $\sigma _{\text {eh}}\approx \sigma _{0}n_{\text {eh}}$ showing a nonlinear absorption response. Furthermore, it was assumed that $n_{\text {eh}}$ is homogeneous in the laser-irradiated volume and proportional to $I_{0}$ due to eh pair generation by 1-photon absorption. As a consequence, the FCA contribution in Eq. (3b) implies a quadratic dependence on $I_{0}$ in its exponent:

$$\begin{aligned} I(z_{\text {m}})&= ~(I_{0} - I_{\text {c}})\exp {(-\alpha _{1}z_{\text {m}})}\exp {(-\kappa _{2}I_{0}^{2}z_{\text {m}})} \nonumber \\&\quad + I_{\text {c}}\exp {(-\alpha _{1}z_{\text {m}})} \end{aligned}$$

(5)

or more generally

$$\begin{aligned} I(z_{\text {m}})&= ~(I_{0} - I_{\text {c}})\exp {(-\alpha _{1}z_{\text {m}})}\exp {(-\kappa _{n}I_{0}^{n}z_{\text {m}})} \nonumber \\&\quad + I_{\text {c}}\exp {(-\alpha _{1}z_{\text {m}})}, \end{aligned}$$

(6)

with $\kappa _{2,n}$ being the empirical constants and n the empirical variable parameter. Equation (6), i.e., $I(z_{\text {m}})$ = $f(I_{0},I_{\text {c}}, \alpha _{1}, \kappa _{n}, n, z_{\text {m}})$ together with the above relations (Sect. 3.1) between $I_{0}$ and $P_{\text {in}}$ as well as $I(z_{\text {m}})$ and $P_{\text {trans}}$ is transformed to the function of the measured values $P_{\text {trans}}$ = $f(P_{\text {in}}$, $P_{\text {c}}$, $\alpha _{1}$, $\alpha _{\text {FCA}}$, $z_{\text {m}}$) with $P_\text {c} = I_{\text {c}}/(\eta T)$:

$$\begin{aligned} P_{\text {trans}}(z_{\text {m}})&= ~T^{2}\exp {(-\alpha _{1}z_{\text {m}})}(P_{\text {in}}-{P_{\text {c}}}) \nonumber \\&\quad \times \exp {(-\alpha _{\text {FCA}}z_{\text {m}})} + T^{2}\exp {(-\alpha _{1}z_{\text {m}})P_{\text {c}}} \end{aligned}$$

(7)

or in an abbreviated form for convenient fitting

$$\begin{aligned} P_{\text {trans}}(z_{\text {m}}) = F_{n}\left[ \left( P_{\text {in}} - {P_{\text {c}}} \right) \exp {(-E_{n}P_{\text {in}}^{n})} + P_{\text {c}}\right] , \end{aligned}$$

(8)

with $F_{n} = T^{2}\exp {(-\alpha _{1}z_{\text {m}})}$ and $E_{n}$ = $\alpha _{\text {FCA}}z_{\text {m}}$ = $\kappa _{n}(\eta T)^{n}z_{\text {m}}$. Application of Eq. (8) is performed in two ways, i.e., with fixed $n = 2$ to test the above approximation for $\alpha _{\text {FCA}}$ and with variable n. Applying these two procedures to the $P_{\text {trans}}(P_{\text {in}})$ traces in Fig. 2b obtained for the Si membrane thickness series yields the parameters summarized in Table 2.

Table 2 Fit parameters for the $P_{\text {trans}}$($P_{\text {in}}$) traces in Fig. 2b obtained by the application of Eq. (8). The parameter values for variable n are graphed in Fig. 5

The fit curves obtained by Eq. (8) with fixed $n = 2$ or n as variable parameter are practically identical for thick membranes but differ in case of the two thinnest membranes (Fig. 2b). The fitting improvement by use of a variable exponent n is trivial from the mathematical point of view as there is one more free parameter available for optimization. On the other hand, the obtained $1.7 \le n \le 2.6$ values (Table 2) appear to be relevant for the physical meaning of the present findings (cf. Fig. 5b). The parameters $F_{n}$ and $F_{2}$ obtained with the variable exponent n and fixed $n = 2$, respectively (Table 2) are very similar (maximum deviation: $10\, \%$, membrane 1). The obtained parameters $E_{n}$ (or $E_{2}$) and $P_{\text {c,n}}$ (or $P_{\text {c},2}$) appear to depend on the membrane thickness (cf. discussion below).

Fig. 5

Fit parameters of the FCA model (Eq. 8) namely a $F_{n}$ (rhombes), n (triangles) from (Tab. 2) and the slopes of Fig. 4 (squares) and b relative density values $n_{\text {eh}}$ of free charge carriers as a function of the membrane thickness d; the values $n_{\text {eh}}$ were derived from the maximum $\alpha _{\text {FCA}}$ values in Fig. 2c recorded at $P_{\text {in}} = 0.8\, \text{ W }$ in three ways using in Eq. (10) the values $n = 1,2$ and $n = \text {variable}$ (Table 2). Proportionality factors are used for convenience of presentation ($F_{n}$: $\times 8$ and slope $\times 3$). The solid line in part a is an exponential fit curve (cf. text), whereas the dotted lines are guides for the eye only

The deviation of the laser intensity transmitted through the thin Si membrane from the small signal absorption behavior (Beer’s law) is essentially attributed to FCA (Fig. 1) and is mathematically described by

$$\begin{aligned} \Delta I_{\text {FCA}} =&~I^{0}(z_{\text {m}}, I_{0}) - I(z_{\text {m}}, I_{0})\nonumber \\ =&~\eta P_{\text {in}}T\exp {(-\alpha _{1}z_{\text {m}})} - \eta P_{\text {trans}}/T\nonumber \\ =&~\eta (P_{\text {in}}T\exp {(-\alpha _{1}z_{\text {m}})} - P_{\text {trans}}/T)\nonumber \\ =&~\eta (0.845P_{\text {in}}\exp {(-785\, \text{cm}^{-1}d_{i}/\cos {11^{\circ }})}\nonumber \\&- P_{\text {trans}}/0.845). \end{aligned}$$

(9)

In our previous paper [6], $(\Delta I_{\text {FCA}})^{0.5}$ was found to increase approximately linearly with the input power $P_{\text {in}}$ (or $I_{0}$), as shown in Fig. 4, of [6]. The calculated FCA contribution depends, however, on the assumed linear absorption behavior (Beer’s law) which has been revised in this paper with respect to the $\alpha _{1}$ and $z_{\text {m}}$ values (Sect. 3.1). Therefore, it appears interesting to check the FCA behavior of $\Delta I_{\text {FCA}}$ for the membrane thickness series of this paper under the revised conditions, i.e., with $\alpha _{1} = 785\pm 100\, \text{cm}^{-1}$ and the newly determined membrane thickness values from Table 1. For simplicity, Eq. (9) is divided by the constant scaling factor $\eta = 1.0\times 10^{11}\, \text{[pulse }\cdot {\mathrm{cm}}^{2}]^{-1}$ for the power law test of $\Delta I_{\text {FCA}}$ which is depicted in Fig. 4a.

At first sight, the square root of $\Delta I_{\text {FCA}}/\eta$ appears to increase (almost) linearly with the input power P $_{\text {in}}$ above a $P_{\text {in}}$ threshold $P_{\text {c}}$ which depends on the membrane thickness. This finding essentially confirms the previous results in [6]. The slope of the linear parts $d\sqrt{\Delta I_{\text {FCA}}/\eta }/d P_{\text {in}}$ = $(1/\sqrt{\eta })d\sqrt{\Delta I_{\text {FCA}}}/d(I_{0}/\eta T)$ = $(T\sqrt{\eta })d\sqrt{\Delta I_{\text {FCA}}}/d(I_{0})$ on the average decreases with increasing membrane thickness (Figs. 4a, 5a). The threshold $P_{\text {c}}$ on the $P_{\text {in}}$ axis for the linear behavior is difficult to determine and the values given in Fig. 4(a) are rough estimates only.

The physical meaning of parameter $F_{n} = T^{2}\exp {(-\alpha _{1}z_{\text {m}})}$ in Eq. (8) is straightforward and its values trivially show an exponential thickness dependence (fitted line in Fig. 5a) as expected, since the d values on the abscissa scale have been obtained from the $F_{n}$ parameter representing the linear interband absorption (Beer’s law).

The FCA effect, on the other hand, is represented by the absorption coefficient $\alpha _{\text {FCA}}$ (Fig. 2c) and the $\Delta I_{\text {FCA}}$ value (Fig. 4a). For its physical understanding the density $n_{\text {eh}}$ of free charge carriers, their absorption cross section $\sigma _{\text {eh}}$, and the relation $\sigma _{\text {eh}} = \sigma _{0}n_{\text {eh}}^{n-1}$ appear to be of utmost importance. Therefore, a selection of model values are displayed in Fig. 5 as a function of the membrane thickness d: value n from Table 2, the slope of Fig. 4a and the values $n_{\text {eh}}$ obtained from $\alpha _{FCA}$ in three ways using Eq. (10) with $n = 1,2$ and $n = \text {variable}$ (Table 2). In Fig. 5a the values n and the slope of Fig. 4a both decrease steadily with increasing membrane thickness.

The physical meaning of the parameter n is found in the relation

$$\begin{aligned} \alpha _{\text {FCA}}\approx n_{\text {eh}}\sigma _{\text {eh}}(n_{\text {eh}})\approx \sigma _{0}n_{\text {eh}}^{n}\approx \sigma _{0}(\kappa I_{0})^{n} = \kappa _{n}I_{0}^{n} \end{aligned}$$

(10)

that is the generalized form of Eq. (4), as was used in Eq. (6). Analysing the sequence of steps in Eq. (10), the value of n actually comes from the dependence of the absorption cross section $\sigma _{\text {eh}}$ on the density $n_{\text {eh}}$ of the eh pairs:

$$\begin{aligned} \sigma _{\text {eh}} = \sigma _{0}n_{\text {eh}}^{n-1}. \end{aligned}$$

(11)

Therefore, a change in the value of n corresponds to a change in the absorption cross section of the eh pairs as a function of the eh pair density. Evidently, the values $n_{\text {eh}}(d)$ obtained for $n = 1$ and 2 (Fig. 5b) show similar dependences from the membrane thickness, i.e., a steady decrease of $n_{\text {eh}}$ with thickness d. This attenuation results from a strongly decreasing rate of the average optical eh pair generation with increasing d values. The value $n = 1$ cannot a priori be excluded as it appears applicable for low $n_{\text {eh}}$ densities (Fig. 4 of Refs. [19, 20]). Assuming $3\times 10^{-18}\le \sigma _{\text {eh}}\le 2\times 10^{-17}\, \text{cm}^{2}$ (Fig. 3b of Ref. [5]) and applying it to the highest $\alpha _{\text {FCA}}$ values of this study yields, however, $n_{\text {eh}}$ values in the $1\times 10^{20}\, \text{cm}^{-3}$ to $5\times 10^{20}\, \text{cm}^{-3}$ range in which the $n_{\text {eh}}$ dependence of $\sigma _{\text {eh}}$ is no longer negligible (Fig. 4 of Ref. [19]). The values $n_{\text {eh}}(d)$ obtained for $n = \text {variable}$, on the other hand, display a maximum $n_{\text {eh}}$ value around d $\approx 20\, \upmu \text{m}$, indicating at least two counteracting effects. Taking into account that the $P_{\text {trans}}$ values in Fig. 2b are optimally fitted by $n = \text {variable}$, the related $n_{\text {eh}}$ values are assumed to be the most reliable ones. The preference of these $n_{\text {eh}}$ values is supported by additional findings:

In Table 2, the fit parameters $P_{\text {c},n}$ and $E_{n}$ as well as the threshold values from Fig. 4 appear to have a minimum around membrane thickness $d \approx 20\, \upmu \text{m}$ indicating a fundamental change in the FCA behavior. $P_{\text {c},n}$ and the threshold value of Fig. 4 both have the physical meaning of the constant part of the incident power ($P_{\text {c}} = I_{\text {c}}/\eta T$) that undergoes linear absorption, but no FCA.

Looking at Eqs. (10) and (11) the observed $n_{\text {eh}}(d)$ dependences may be traced back to the value $n_{\text {eh}}$ itself and/or to the $n_{\text {eh}}$ dependence of the absorption cross section $\sigma _{\text {eh}}$ via variations of the exponent n. The density $n_{\text {eh}}$ is controlled dynamically and represents a kinetic equilibrium between the laser induced generation of eh pairs and their losses. Their generation by the interband absorption in Si is determined by the $\alpha _{1}$ value and the incident laser power $P_{\text {in}}$. The losses of $n_{\text {eh}}$ pairs in the laser-irradiated Si volume, which is at the same time the probe volume for transmission, presumably occur mainly via (1) eh recombination at the front and rear Si/SiO$_2$ interfaces and (2) transverse diffusion of eh pairs out of the irradiated Si volume into the non-irradiated Si environment. Diffusion (2) should dominantly depend on the transverse $n_{\text {eh}}$ density gradient across the interface between the irradiated and non-irradiated parts of the Si membrane and show a weak membrane thickness dependence only. The eh pair losses (1) should, however, increase with the thickness dependent surface-to-volume ratio of the membranes and thus be highest for the thinnest membranes. As a preliminary result the $n_{\text {eh}}$ maximum at $d \approx 20\, \upmu \text{m}$ for $n = \text {variable}$ in Fig. 5b can qualitatively be rationalized by the balance between the counteracting effects of the laser beam attenuation (reduction of the eh pair generation rate) and the eh pair recombination at the front and rear Si/SiO$_2$ interfaces. These findings suggest to consider additionally physical effects next to the Si/SiO$_2$ interfaces which may be negligible in case of thick membranes, but are important for thin membranes.

At the rear Si/SiO$_2$ interface there is a region of spatial and temporal overlap of the incoming and the reflected laser beams. For $90\, \text{ fs }$ duration and refractive index $n_{\text {Si}} = 3.69$ [11, 12] the laser pulse in Si corresponds to a light disc of $d_{\text {las}}\approx 7.3\, \upmu \text{m}$ thickness. This results in a beam overlap sheet of $d_{\text {ov}}\approx d_{\text {las}}/2 \approx 3.6\, \upmu \text{m}$ thickness showing locally enhanced or reduced intensity for positive or negative interference between the incoming and the reflected beam parts, respectively. The sign of the interference depends on the phase change during laser beam reflection at the rear Si/SiO$_2$/air interfaces. The ratio $d_{\text {ov}}/d$ of the overlap sheet to the membrane thickness is inversely proportional to d and rises steeply for small d values.

Furthermore charge carrier injection from Si into SiO$_2$ is well known under the present laser irradiation conditions (cf., e.g., [21]). The pulse peak intensities incident on the sample amount up to $80\, \text{GW/cm}^{2}$ averaged over the beam cross section and the pulse duration. This leads to quasi-static electric fields $E_{\text {dc}}$ across both Si/SiO$_2$ interfaces. The field strengths and their penetration depth into the neighbouring Si membrane regions depend on the local laser intensities and the shielding of the electric charges intermediately fixed in the SiO$_2$ layers. The thickness of the depletion layers (depth of shielding) within the Si membrane next to the interfaces is estimated to lie in the 1–$1.5\, \upmu \text{m}$ region for the given p-dopant concentration (cf., e.g., [22]). This estimate assumes, however, an infinitely thick Si sample without laser excitation, i.e., free charge carriers originating from the dopant only. The eh pairs located in the electric field affected regions, that exist on both sides of the membrane [23, 24], are subject to different electric field strengths depending on their distance from the Si/SiO$_2$ interface. Therefore, it can be expected that features in the absorption spectrum of the affected eh pairs should be shifted due to the perturbation by the varying field, leading to a shifting and broadening of the FCA features of the eh pair population as a whole and, therefore, a change in the average $\sigma _{\text {eh}}$ value.

In our thickest sample ($\approx$30 $\upmu \text{m}$ thickness) the total depth of the $E_{\text {dc}}$ field and/or the laser beam overlap regions is small relative to the total thickness, and therefore, only a small fraction of the total number of eh pairs are perturbed. The remaining majority of the eh pairs are unperturbed and should show behavior characteristics similar to those found in thick (bulk) Si samples. In our thinnest sample of which the thickness ($\approx$10 $\upmu \text{m}$) is not much larger than that of the affected regions near the interfaces, a large fraction of the eh pairs are perturbed. Thus the FCA behavior becomes modified. The $n_{\text {eh}}$ dependence of the absorption cross section $\sigma _{\text {eh}}$ shows up, e.g., in the variable n values (Table 2) and the independently derived variable slopes in Fig. 4a.

A more detailed analysis of the above findings requires extended modelling of the discussed effects beyond the scope of the present study. In addition a more extensive experimental data basis will be helpful in order to disentangle the mutual interference between the model parameters $n_{\text {eh}}$, $\sigma _{\text {eh}}$, $\sigma _{0}$ and the exponent n, which all are enclosed in the single experimental value $\alpha _{\text {FCA}} = \alpha _{\text {FCA}}(n_{\text {eh}}, \sigma _{\text {eh}}, \sigma _{0}, n)$. One experimental approach to extend the data basis might use laser pulse trains at variable pulse repetition rates to change the relation between the eh pair generation rate (average input power $P_{\text {in}}$) and the average eh pair loss rate (available time for eh pair recombination between the laser pulses).

4 Summary and conclusion

The incidence of a Ti:sapphire fs-laser beam ($\lambda = 800\, \text{ nm }$, $\tau = 90\, \text{ fs }$, $80\, \text{ MHz }$) onto thin naturally oxidized, weakly B-doped Si membranes at $\theta = 45 ^{\circ }$ external angle of incidence and $\gamma = 11 ^{\circ }$ propagation angle in Si was investigated with respect to its reflection as well as its transmission. The reflectivity $R = 0.15\pm 0.01$ is found to be independent of the incident average laser power ($\le 0.8\, \text{ W }$) and pulse peak intensity ($\le$80 $\text{GW/cm}^{2}$).

The linear absorption (interband transition) is used to determine the membrane thickness d in the 10–$30\, \upmu \text{m}$ range by two ways, using either the linear absorption regime at low laser power (Beer’s law, sect. 3.1) or the related fit parameters of the applied FCA model (Sect. 3.2). Both routes lead to very similar results with a standard deviation $\Delta d_{\text {SD}} < 1\, \upmu \text{m}$ for a given value of the linear absorption coefficient $\alpha _{1}$, for which $\alpha _{1} = 785\, \text{cm}^{-1}$ [18] appears most reliable within the $600\, \text{cm}^{-1} \le \alpha _{1} \le 1200\, \text{cm}^{-1}$ literature value range.

The transmission behavior at high laser power is mainly attributed to free charge carrier absorption (FCA) and quantitatively reproduced by a recently derived FCA model [6] (Sect. 3.2). This model uses an effective absorption coefficient $\alpha _{\text {eff}} = \alpha _{1} + \alpha _{\text {FCA}}$ with $\alpha _{\text {FCA}}$ increasing with the average laser intensity (input power): $\alpha _{\text {FCA}} = \kappa _{n}I_{0}^{n}$ with $n \approx 2$. The FCA model with its empirical fit parameters allows to calculate quantitatively the transmission behavior of Si membranes within the investigated sample thickness, doping and laser power (intensity) regimes.

Some of the FCA fit parameters display extrema around the membrane thickness $d \approx 20\, \upmu \text{m}$ indicating a fundamental change in the FCA behavior. This finding is attributed to both thickness dependent counteracting effects and to physical effects next to the Si/SiO$_2$ interfaces which are negligible in case of thick Si membranes, but important for thin membranes.

Two counteracting effects are considered most important in controlling the dynamical equilibrium between the generation of free charge carriers and their losses by eh pair recombination: The laser beam power strongly attenuates (exponentially) along its path through the Si membrane by linear interband absorption and the power dependent FCA. Thus the average generation of eh pairs decreases drastically with increasing Si membrane thickness d. Increasing d values, on the other hand, reduce the relative loss rate of free charge carriers which is expected to be mainly controlled by eh pair recombination at the Si/SiO$_2$ interfaces.

Furthermore charge carrier injection from Si into SiO$_2$ builds up a quasi-static electric field $E_{\text {dc}}$ across the Si/SiO$_2$ interface which affects the neighboring Si region ($1\, \upmu \text{m}$ order of magnitude) according, e.g., to the dopant dependent shielding of $E_{\text {dc}}$. The depth dependent $E_{dc}$ affects the spectral properties of the electron/hole pairs in Si and thus the FCA. At the rear interface, on the other hand, interference between the incoming laser beam and its part reflected from the Si/SiO$_2$/air interfaces modifies the laser impact onto the Si membrane within a region of about $3.5\, \upmu \text{m}$ thickness.