1 Introduction

The volume fraction of soot particles in an aerosol is important for determining the impact of anthropogenic soot on ecosystems and human health. In situ measurements of this parameter can also elucidate the mechanisms that underlie soot formation, knowledge that is used to improve efficiency and reduce emissions of combustion processes. One diagnostic capable of quantifying these parameters is laser-induced incandescence (LII), in which aerosolized nanoparticles are heated to incandescent temperatures by a short laser pulse. The spectral incandescence from the nanoparticles is collected and imaged onto a detector, often photomultipliers (PMTs) equipped with band-pass filters [1]. The peak intensity of the soot incandescence depends on its temperature and is proportional to the soot volume fraction (SVF) present in the aerosol. The voltage measured by the PMTs can thus be expressed by the following [2]:

$${V_\lambda } = G{\eta _\lambda }{f_v}E({{\mathbf{m}}_\lambda })\frac{{6\pi }}{\lambda }{w_e}{I_{b,\lambda }}({T_{{\text{pe}}}}) + e,$$
(1)

where G is the PMT gain used during the measurements (treated as fixed and known), λ is the detection wavelength, η λ is the calibration coefficient that accounts for photoelectric conversion and optical collection efficiencies, f v is the soot volume fraction, E(m λ) is the absorption function of soot, w e is the equivalent laser sheet thickness, I b,λ is the blackbody spectral intensity at the detection wavelength, T pe is the equivalent peak temperature of the heated soot, and e is the measurement noise generated by the photon shot noise present in the PMTs and the Gaussian noise present in the electronics [2]. By relating peak LII measurements to this observation model, a practitioner can, therefore, infer the SVF, provided that the peak temperature is known, or if there is an established relationship between the LII signal and the SVF based on a known calibration source.

In auto-compensating laser-induced incandescence (AC-LII), the incandescence is simultaneously measured by two PMTs equipped with band-pass filters centered at different wavelengths. Two-color pyrometry is then used to estimate the effective peak temperature of the soot which, in turn, is used to infer a value for SVF from the voltage measurements [3]. In its classic form, AC-LII avoids the need for an absolute calibration, which greatly simplifies deployment of this diagnostic and makes the derived properties more robust to uncertainties in the calibration procedure.

While LII has widely been used to characterize soot-laden and synthetic nanoaerosols (e.g., refs. [1, 4–6]), there has been a little research which considers the uncertainty present in LII-derived quantities. Much of the work on uncertainty quantification has focused on time-resolved LII (TiRe-LII) measurements in which the objective is to infer particle size distribution parameters. Early attempts at uncertainty quantification have largely focused on sensitivity or perturbation analysis [7–11]. Daun et al. [12] examined the topology of the squared norm residuals and identified regions of high uncertainty. A more sophisticated analysis was developed by Crosland et al. [13], who investigated the propagation of uncertainty through the calibration of ICCDs and the AC-LII model through a large-scale Monte Carlo simulation.

The Bayesian framework for parameter inference has recently been adopted by the LII community to infer parameters such as volume fraction, temperature, and particle size distribution parameters. In this procedure, the measurements, v, and the quantities-of-interest (QoIs, such as soot volume fraction and peak temperature), x, are modeled as random variables with probability densities π(⋅) related by Bayes’ equation:

$$\pi ({\mathbf{x}}|{\mathbf{v}}) = \frac{{{\pi _{{\text{like}}}}({\mathbf{v}}|{\mathbf{x}}){\pi _{{\text{pri}}}}({\mathbf{x}})}}{{\pi ({\mathbf{v}})}}.$$
(2)

In the case of AC-LII, x = [f v , T pe]T and v=[V λ1, V λ2]T, where f v is the soot volume fraction, T pe is the peak particulate temperature, and v is a vector containing the measured voltages from the two photomultipliers. The likelihood, π like(v|x), quantifies the probability of an observed measurement, conditional on a particular parameter value in the context of measurement noise. The prior density, π pri(x), is a probabilistic representation of what is known or expected of the parameters based on knowledge available before the measurements are taken. The posterior, π(x|v), is a representation of the SVF and temperature accounting for the information in the measurements as well as the prior information. Finally, the evidence, π(v), is a normalization constant which ensures that the posterior satisfies the Law of Total Probability. The key benefits of the Bayesian framework over nonlinear least-squares regression are: (1) while nonlinear regression produces a single point estimate, the outcome of the Bayesian process is probability densities for the QoIs, the widths of which directly indicate the level of uncertainty present in these estimates [14, 15]; and (2) information contained in the measurement data can be combined with information known prior to the measurements in a statistically rigorous way, to reduce uncertainties in the QoIs.

Sipkens et al. [5] used the Bayesian framework to account for uncertainties due to measurement noise in their LII measurements on silicon nanoparticles. A Markov chain Monte Carlo (MCMC) technique was employed to approximate the posterior density of particle size distribution parameters. Sipkens et al. [16] subsequently used MCMC to estimate the posterior density of the mean primary particle size and thermal accommodation coefficient (TAC) from LII measurements on iron nanoparticles. More recently, Sipkens et al. [17] repeated a similar procedure in a comparative study of LII measurements on iron, silver, and molybdenum nanoparticles.

Hadwin et al. [15] presented the Bayesian technique of marginalization as a rigorous approach to uncertainty quantification. In this work, the uncertainty from the absorption function of soot, E(m λ), which is used in the AC-LII model, was discussed and the Principle of Maximum Entropy was employed to define prior distributions. The proposed prior distributions were then used to marginalize (integrate) the absorption function over the likelihood density, assuming that the absorption function is uniform with respect to wavelength. Further marginalization was carried out to obtain univariate probability densities and credibility intervals for SVF and peak temperature.

The present work extends and builds on our previous results by: (1) developing a framework through which the uncertainty present in multiple AC-LII parameters model and experimental parameters can be quantified; and (2) introducing a new technique which reduces the computational cost of quantifying the uncertainty in estimates computed with the AC-LII model. As a demonstration of this approach, experimental measurements collected from an ethylene-fueled laminar diffusion flame (described in Ref. [18]) are used to compute SVF and temperature and the associated uncertainties. These estimates are found using LII data corresponding to the peak signal intensity, to minimize uncertainty introduced by non-uniform primary particle temperatures caused by non-uniform cooling of different-sized particles. The uncertainty analysis presented in this work pertains to a specific apparatus, but can be generalized to other experimental arrangements.

Uncertainties in the nuisance parameters are modeled using maximum entropy priors. While Hadwin et al. [15] considered case of a single nuisance parameter, E(m λ), the present work considers the uncertainty introduced through calibration and a spatially non-uniform fluence profile [due, e.g., to coherent interference effects along with the uncertainty in E(m λ )], resulting in five nuisance parameters: E(m λ1), E(m λ2), η λ1, η λ2, and w e , where λ 1 and λ 2 are the two detection wavelengths. Increasing the number of nuisance parameters can dramatically increase the computational effort required for marginalization. To address this issue, we implement the Gaussian approximation technique, in which the posterior probability is modeled as a Gaussian distribution, Ν(μ, Γ), centered on the maximum a posterori estimate and Γ is the covariance matrix, derived from the Jacobian matrix (first-order sensitivities). Accordingly, the posterior probabilities are also approximated as Gaussian, and thus, marginalization can be done analytically.

The remainder of the paper is structured as follows: Sect. 2 and 3 discuss the experimental setup, the AC-LII model, and the tools required to compute estimates in the Bayesian framework. Section 4 explicates the uncertainty introduced into the LII inference procedure by the nuisance parameters, E(m λ ), η λ , and w e . Finally, the tools and prior densities that we have developed are applied to experimental AC-LII measurements in a laminar diffusion flame.

2 Laser-induced incandescence

2.1 Experimental setup

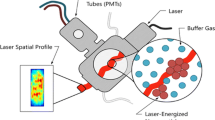
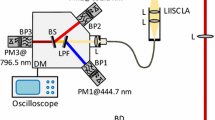
The measurements considered in this work were carried out on soot within an ethylene-fueled laminar diffusion flame operating under conditions described in Ref [18]. A schematic of the apparatus is shown in Fig. 1. Soot was energized using a Nd:YAG laser at an excitation wavelength of 1064 nm, and an average laser energy of 6.5 mJ/pulse at a height of 42 mm above the burner exit. A Silios diffractive optical element (DOE) and relay optics are used to shape the beam into a 2.5 mm × 2.5 mm square with a near top-hat profile, giving an average fluence of approximately 1 mJ/mm2. The solid acceptance angle of the detection optics transects the laser beam at an angle of 33.7°, which defines a roughly cylindrical probe volume having an average laser sheet thickness of 4.505 mm, i.e., the average detection pathlength subtended by the laser sheet [2]. (see Section 3 Figure 5 of Ref [2]. for more details.) The PMTs are Hamamatsu H5773 with built-in power supply and voltage divider circuits for dynode biasing. The PMTs are equipped with band-pass filters centered at λ 1 = 420 nm and λ 2 = 780 nm, respectively, and with a bandwidth less than 30 nm. More details regarding the apparatus and operating conditions of the flame are provided in Ref [18].

Fig. 1
figure 1

Schematic of LII experimental setup

Full size image

The peak voltages recorded from 1000 laser shots are plotted in Fig. 2, revealing a standard deviation of approximately 20% of the mean value. The main source of noise is shot noise, arising from the discrete nature of photon counting. Photon shot noise obeys a Poisson distribution, which can be modeled as a Gaussian distribution having a variance proportional to the observed voltage measurement. The PMT voltages are further corrupted by electronic noise, which is also Gaussian. Another source of noise comes from the shot-to-shot variations in the laser fluence profile, which induces a distribution of particle temperatures in the measurement volume. These effects combine to form an uncorrelated, unbiased Gaussian noise distribution, so the overall PMT voltage signals are themselves Gaussian [14, 19], as shown on the right of Fig. 2.

Fig. 2
figure 2

1000 peak PMT voltage measurements for the two measurement wavelengths and the associated normal distributions

Full size image

2.2 Auto-compensating laser-induced incandescence model

By applying Rayleigh–Debye–Gans fractal aggregate (RDG-FA) theory, which models the spectral incandescence from the laser-energized soot aggregates, which have a fractal structure comprised of nearly spherical primary particles (see Fig. 3 for example), as the sum of spectral incandescence from all primary particles within the probe volume [11, 12, 16], and neglecting signal trapping between the probe volume and the detector, the spectral intensity incident on each detector is given by the following:

$$I_{{\lambda ,d}} (t) = N_{p} w_{b} \int\limits_{0}^{\infty } {I_{{b,\lambda }} [T(d_{p} ,t){\text{]}}} C_{{abs}} (d_{p} )\pi (d_{p} )d(d_{p} ),$$
(3)

where N p is the number density of primary particles, I b,λ is the blackbody spectral intensity, T(d p , t) is the temperature of a primary particle with diameter d p , w b is the probe volume (beam) width, f v is the soot volume fraction, π(d p ) is the probability density of primary particle diameters, and C abs,λ (d p ) is their absorption cross section.

Fig. 3
figure 3

Example of a soot aggregate imaged using transmission electron microscopy (TEM)

Full size image
$${C_{{\text{abs}},\lambda }}\left( {{d_p}} \right) = \frac{{{\pi ^2}d_p^3}}{\lambda }E\left( {{{\mathbf{m}}_\lambda }} \right),$$
(4)

where E(m λ ) is the absorption function of soot. Note that N p π(d p )d(d p ) gives the number density of primary particles having a diameter between d p and d p + d(d p ). The number of primary particles per unit volume is related to the average primary particle diameter by the following:

$${N_p} = \frac{{6{f_v}}}{{\pi \overline {d_p^3} }}.$$
(5)

Equation (3) can be simplified greatly if the primary particles have a nearly uniform temperature, which is a reasonable approximation at the instant corresponding to the peak LII signal, assuming a spatially uniform fluence profile [20]. Under these circumstances, Eq. (3) can be simplified to:

$$I_{{\lambda ,d}} (t) = \frac{{6\pi }}{\lambda }f_{v} w_{b} I_{{b,\lambda }} \left[ {T\left( t \right)} \right]E\left( {{\mathbf{m}}_{\lambda } } \right).$$
(6)

Accounting for the finite spectral width of the band-pass filters, the peak PMT voltages can then be modeled as [2]:

$${V_\lambda } = G{\zeta _{{\text{opt}}}}{f_v}{w_b}\frac{{6\pi }}{\lambda }\int_\lambda E \left( {{{\mathbf{m}}_\lambda }} \right){I_{b,\lambda }}\left( {{T_p}} \right)\varvec{\uptheta}\left( \lambda \right)\tau \left( \lambda \right)\;d\lambda ,$$
(7)

where ζ opt is a constant that includes the efficiency of the relay optics and the solid angle subtended by the probe volume as viewed by the detector, T p is the peak temperature of the heated nanoparticles, Θ(λ) is the spectral response of the PMT, and τ(λ) is the filter transmission as a function of wavelength. The PMTs and filters are typically chosen, so that the spectral response is approximately flat over the wavelength of interest, so that an “equivalent filter” approximation, for the central wavelength λ c, can be made:

$${V_{{\lambda _c}}} = G{\zeta _{{\text{opt}}}}{f_v}{w_b}\frac{{6\pi }}{{{\lambda _c}}}E\left( {{{\mathbf{m}}_{{\lambda _c}}}} \right){I_{b,{\lambda _c}}}\left( {{T_p}} \right)\varvec{\uptheta}\left( {{\lambda _c}} \right)\tau \left( {{\lambda _c}} \right)\;{\Delta _{{\lambda _c}}},$$
(8)

where Δλc represents the PMT filter bandwidth. Finally, defining the calibration coefficient as η λc = ζ opt θ(λ c)τ(λ c)Δ λc results in Eq. (1).

This model is valid under the assumption that the peak temperature of the soot primary particles is nearly uniform within the probe volume, a condition which is not generally satisfied due to spatial inhomogeneity in the laser fluence. Even if optical techniques such as relay imaging [21] are introduced to produce a time-averaged “top-hat” profile, there is still considerable shot-to-shot variation in the fluence profile caused by the underlying stochastic nature of pulse generation in the laser medium and locally amplified by coherent interference. A more exact treatment considers the variation in blackbody spectral intensity across the laser sheet:

$$V_{{\lambda _{c} }} = G\zeta _{{{\text{opt}}}} f_{v} \frac{{6\pi }}{{\lambda _{c} }}E\left( {{\mathbf{m}}_{{\lambda _{c} }} } \right){\mathbf{\theta }}\left( {\lambda _{c} } \right)\tau \left( {\lambda _{c} } \right)\;\Delta _{{\lambda _{c} }} \int\limits_{x} {I_{{b,\lambda _{c} }} \left[ {T_{p} \left( x \right)} \right]} \;{\text{d}}x,$$
(9)

where x defines a location along the viewing axis of the detector across the laser sheet. Consequently, the temperature inferred from the ratio of PMT detector voltages:

$${T_{{\text{pe}}}} = \frac{{\frac{{hc}}{{{k_B}}}\left( {\frac{1}{{{\lambda _2}}} - \frac{1}{{{\lambda _1}}}} \right)}}{{\ln \left( {\frac{{{V_{{\lambda _1}}}{\lambda _1}^6{\eta _{{\lambda _2}}}E({{\mathbf{m}}_{{\lambda _2}}})}}{{{V_{{\lambda _2}}}{\lambda _2}^6{\eta _{{\lambda _1}}}E({{\mathbf{m}}_{{\lambda _1}}})}}} \right)}},$$
(10)

when h is Planck’s constant, c is the speed of light, and kB is the Boltzmann constant, is a biased average of the true temperature distribution T p (x) along the viewing axis of the detector across the laser sheet, and does not directly relate to the soot volume fraction as defined by Eq. (1).

To account for this effect, Snelling et al. [2] proposed an equivalent laser sheet thickness defined as follows:

$$w_{e} I_{{b,\lambda _{c} }} \left( {T_{{pe}} } \right) = \int\limits_{x} {I_{{b,\lambda _{c} }} \left[ {T_{p} \left( x \right)} \right]} \,{\text{d}}x.$$
(11)

which presumes T p (x) is known, e.g., from detailed knowledge of the fluence profile. Note that this equation implies that if T p (x) was uniform along the viewing axis, then w e corresponds to the geometric size of the laser sheet [2]. Using w e in Eq. (8) in place of w b ensures that the soot volume fraction is correctly related to the pyrometrically inferred peak temperature. Thus, provided the ratios E(m λ2)/E(m λ1) and η λ2/η λ1 are known, the peak soot temperature, in principle, is accurately modeled by the effective temperature even in the case of a non-uniform fluence profile, and the soot volume fraction can be estimated as:

$${f_v} = \frac{{{V_\lambda }}}{{E({{\mathbf{m}}_\lambda })\frac{{6\pi }}{\lambda }{\eta _\lambda }{w_e}{I_{b,\lambda }}({T_{pe}})}},$$
(12)

where λ is either λ 1 or λ 2. At longer cooling times, however, the polydisperse nature of the primary particle sizes will influence the effective temperature approximation, since larger particles are slower to cool, so the assumptions used to simplify Eq. (3) into Eq. (6) no longer hold. Instead, the effective temperature derived from Eq. (10) can be interpreted as an approximate temperature for the aerosol, skewed towards the temperature of larger and hotter nanoparticles [2].

3 Handling of nuisance parameters

The above measurement model, Eq. (1), contains several variables (E(m λ ), η λ , and w e ) that are not of immediate interest, but still must be accounted for in the analysis of the QoIs. Approaches for handling nuisance parameters conventionally center on algebraic elimination (i.e., minimizing the number of nuisance parameters by algebraic manipulation of the measurement equations); as a case in point, using ratio pyrometry to eliminate the detector solid angle from the temperature estimate, Eq. (10). When this fails, it is common practice to use a point estimate for the nuisance parameters, based on prior knowledge of their values. Unfortunately, this treatment severely underestimates the uncertainty in the QoIs, and also conceals biases that may arise from correlations between the parameters not captured by the governing equations.

In the previous work, Hadwin et al. [15] applied the robust Bayesian technique of marginalization to incorporate uncertainty in the value of E(m λ ) into the estimated posterior densities of SVF and peak temperature. Formally, the posterior uncertainty of the QoIs in x is obtained by marginalizing, or integrating out, the nuisance parameters γ, so that:

$$\pi ({\mathbf{x}}|{\mathbf{v}}) = \frac{{\int_{}^{} {{\pi _{{\text{like}}}}({\mathbf{v}}|{\mathbf{x}},{\mathbf{\gamma }}){\pi _{{\text{pri}}}}({\mathbf{x}},{\mathbf{\gamma }})d{\mathbf{\gamma }}} }}{{\pi ({\mathbf{v}})}},$$
(13)

which further simplifies to marginalization over the likelihood when the nuisance parameters are treated as statistically independent of the QoIs:

$$\pi ({\mathbf{x}}|{\mathbf{v}}) = \int_{}^{} {\pi ({\mathbf{x}},{\mathbf{\gamma }}|{\mathbf{v}})\;d{\mathbf{\gamma }}} = \frac{{{\pi _{{\text{pri}}}}({\mathbf{x}})}}{{\pi ({\mathbf{v}})}}\int_{}^{} {{\pi _{{\text{like}}}}({\mathbf{v}}|{\mathbf{x}},{\mathbf{\gamma }}){\pi _{{\text{pri}}}}({\mathbf{\gamma }})d{\mathbf{\gamma }}} .$$
(14)

Once the nuisance parameters are marginalized over the likelihood, the maximum a posteriori (MAP) estimate and credibility intervals can be computed [15]. The MAP estimate is the set of x values that maximize the posterior density, i.e., x MAP = argmax x [π(x|v)]. In the absence of prior information, the MAP corresponds to the maximum likelihood estimate (MLE), x MLE = argmaxx[π(v|x)], and, if the measurements are corrupted by identically distributed and independent measurement error, the MLE corresponds to the solution obtained by naïve least-squares minimization of the residual. Credibility intervals define a range within which the true value of the QoIs will fall with a specified probability (typically chosen to be 90% or 95%). The interval widths provide information about the levels of uncertainty in the estimate [14, 15].

Standard quadrature methods are highly efficient ways to evaluate the integral in Eq. (14) when its dimension is small, e.g., one or two nuisance parameters. The computational complexity quickly grows as the dimension increases, however, which often means that marginalization by direct integration is numerically intractable [19, 22–24]. Fortunately, there exist integration techniques which are less susceptible to the “curse of dimensionality”; the most widely used is Monte Carlo integration. If θ 1, θ 2 …, θ N is a sequence of independent identically distributed random variables with density π(θ), then:

$$\frac{1}{N}\sum\limits_{i = 1}^N f ({\theta _i}) \approx \int {f(\theta )\pi (\theta )d\theta .}$$
(15)

This means that nuisance parameters can be marginalized over the posterior by taking an average of the likelihood using values for γ sampled from the corresponding prior, π pri(γ). As the number of samples increases, the approximation converges to the true value of the integral at a rate proportional to \(1/\sqrt N\) [25]. This convergence rate can be improved through the use of various techniques, such as control variates, stratified sampling, and importance sampling, among others [26].

Even when Monte Carlo integration is used, marginalization can remain computationally intensive for problems involving a large number of nuisance parameters. For this reason, the most common approach for handling nuisance parameters is to use efficient optimization techniques and simultaneously estimate the nuisance parameters along with the QoIs. By including the nuisance parameters in the inference procedure, the uncertainty in these parameters is naturally incorporated into the estimate, since the variation of these parameters is considered while inferring the optimal values. In the Bayesian framework, this means that the posterior is updated to include the nuisance parameters:

$$\pi ({\mathbf{x}},{\mathbf{\gamma }}|{\mathbf{v}}) = \frac{{{\pi _{{\text{like}}}}({\mathbf{v}}|{\mathbf{x}},{\mathbf{\gamma }}){\pi _{{\text{pri}}}}({\mathbf{x}},{\mathbf{\gamma }})}}{{\pi ({\mathbf{v}})}} \propto {\pi _{{\text{like}}}}({\mathbf{v}}|{\mathbf{x}},{\mathbf{\gamma }}){\pi _{{\text{pri}}}}({\mathbf{x}}){\pi _{{\text{pri}}}}({\mathbf{\gamma }}).$$
(16)

Estimates, such as MAP or MLE, are subsequently computed using multivariate minimization algorithms (nonlinear programming or meta-heuristic) or with sample-based methods such as Markov chain Monte Carlo (MCMC) [14, 19]. However, incorporating the nuisance parameters into the estimate inevitably increases the dimensionality of the estimation problem, and thus, the stability of the inference problem decreases.

The inference problem is simplified when Gaussian densities are used for both the likelihood and prior models. In particular, the posterior, Eq. (16), becomes:

$$\pi ({\mathbf{x}},{\mathbf{\gamma }}|{\mathbf{v}}) \propto \exp \left( { - \frac{1}{2}\left\| {{\mathbf{L}}_{e} \left[ {{\mathbf{v}} - {\mathbf{v}}^{{{\text{mod}}}} ({\mathbf{x}},{\mathbf{\gamma }})} \right]} \right\|^{2} } \right)\exp \left( { - \frac{1}{2}\left\| {{\mathbf{L}}_{x} \left[ {{\mathbf{x}} - {\mathbf{x}}_{0} } \right]} \right\|^{2} } \right)\exp \left( { - \frac{1}{2}\left\| {{\mathbf{L}}_{\gamma } \left[ {{\mathbf{\gamma }} - {\mathbf{\gamma }}_{0} } \right]} \right\|^{2} } \right),$$
(17)

where v mod is the model connecting the QoIs and nuisance parameters to the measurements, cf. Equation (1), and L e , L x , and L γ are matrices, such that (L e T L e )−1 = Γ e , (L x T L x )−1 = Γ x, and (L γ T L γ )−1 = Γ γ, which are the covariance matrices for the noise, prior of x and γ, respectively. The variables x 0 and γ 0 are the expectations of the prior distribution of the QoIs and nuisance parameters. This form is useful, since the MAP estimate can now be written as a familiar least-squares minimization problem:

$$({\mathbf{x}},{\mathbf{\gamma }})_{{{\text{MAP}}}} = \arg \max \pi ({\mathbf{x}},{\mathbf{\gamma }}|{\mathbf{v}}) = \arg \min \left\{ {\left\| {{\mathbf{L}}_{e} \left[ {{\mathbf{v}} - {\mathbf{v}}^{{{\text{mod}}}} ({\mathbf{x}},{\mathbf{\gamma }})} \right]} \right\|^{2} + \left\| {{\mathbf{L}}_{x} \left[ {{\mathbf{x}} - {\mathbf{x}}_{0} } \right]} \right\|^{2} + \left\| {{\mathbf{L}}_{\gamma } \left[ {{\mathbf{\gamma }} - {\mathbf{\gamma }}_{0} } \right]} \right\|^{2} } \right\}\;,$$
(18)

which can be easily computed using the traditional least-squares techniques if v mod is linear, or using sequential quadratic programming if v mod is nonlinear [27].

The optimization problem in Eq. (18) presents a fast way to infer the MAP estimate, but does not aid in the definition of the posterior density. Equation (17) represents the posterior as a proportionality in terms of Gaussian distributions. Therefore, if v mod were linear, π(x,γ|v) would also be a normal distribution [14]. While the AC-LII measurement model, Eq. (1), is nonlinear with respect to temperature, but the posterior can still be approximated by a Gaussian distribution [14, 23, 28]:

$$\pi ({\mathbf{x}},{\mathbf{\gamma }}|{\mathbf{v}}) \approx \pi _{{{\text{apx}}}} ({\mathbf{x}},{\mathbf{\gamma }}) \propto \exp \left( { - \frac{1}{2}\left\| {{\mathbf{L}}_{{{\text{apx}}}} \left\{ {\left[ {\begin{array}{*{20}c} {\mathbf{x}} \\ {\mathbf{\gamma }} \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {{\mathbf{x}}_{{{\text{MAP}}}} } \\ {{\mathbf{\gamma }}_{{{\text{MAP}}}} } \\ \end{array} } \right]} \right\}} \right\|^{2} } \right)$$
(19)

where

$$\left( {{\mathbf{L}}_{{{\text{apx}}}}^{T} {\mathbf{L}}_{{{\text{apx}}}} } \right)^{{ - 1}} = {\mathbf{\Gamma }}_{{{\text{apx}}}} = \left( {{\mathbf{J}}_{{{\text{MAP}}}}^{T} {\mathbf{\Gamma }}_{e}^{{ - 1}} {\mathbf{J}}_{{{\text{MAP}}}} + \left[ {\begin{array}{*{20}c} {{\mathbf{\Gamma }}_{x}^{{ - 1}} } & 0 \\ 0 & {{\mathbf{\Gamma }}_{\gamma }^{{ - 1}} } \\ \end{array} } \right]} \right)^{{ - 1}} .$$
(20)

This approximation is made by considering the Jacobian of v mod evaluated at (x,γ)MAP, denoted by J MAP as a linear approximation of v mod.

The Gaussian approximation to the posterior simply requires the computation of the MAP estimate (the peak of the posterior) using Eq. (18), which is typically achieved through a least-squares minimization algorithm such as Gauss–Newton or Levenberg–Marquardt. Such algorithms are capable of returning the Jacobian upon convergence, which is then used to approximate the posterior uncertainty by computing Γ apx from Eq. (20).

4 Modeling the uncertainty in the AC-LII nuisance parameters

The uncertainty of the nuisance parameters is reflected by prior probability densities, which model what is known about the nuisance parameters. The prior distributions that one chooses for E(m λ ), η λ , and w e provide additional information to reduce the uncertainty in estimates of the QoI. In an ideal situation, the choice of included information should not unduly bias the posterior density towards a subjective prior belief or expectation, especially in the presence of a shallow likelihood density, since this would create a “self-fulfilling prophecy”. In other words, the posterior density would be dominated by a heuristically defined prior, and not the measurement data used to define the likelihood. To avoid this issue, we employ the Principle of Maximum Entropy [29–31], in which priors are defined, so that they are compatible with testable information (i.e., information that can be assessed for veracity through experimental means) and otherwise have minimal information content. The information content of a distribution has been shown to scale inversely with the information entropy:

$$h(\pi ) = - \int {\pi (x)\ln [\pi (x)]\;{\text{d}}x} .$$
(21)

Specific families of distributions will maximize h(π) subject to constraints derived from the available testable information. If all that is known about a parameter is that it must belong to an interval x ∈ [a, b], for example, then a uniform distribution between those values maximizes the information entropy. If a point estimate and some information of the spread of a parameter are available, a normal distribution will maximize h(π).

The following sections develop various simplified approaches that allow an estimate of the uncertainty present in the absorption function of soot, the calibration coefficients, and the equivalent laser sheet thickness.

4.1 Absorption function of soot

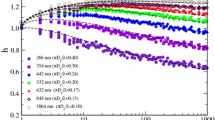
While the absorption function of soot has extensively been studied for decades, there remains little consensus about its value in the literature, or how it changes with wavelength in the visible spectrum. This is evidenced by the range of values plotted in Fig. 4. The difficulty in quantifying E(m λ ) originates from uncertain composition and structure of soot [32], which varies with both combustion chemistry, “maturity” [33, 34], and the measurement technique used to determine its value [35–37]. In the case of LII, it is likely further influenced by microstructure changes induced by laser heating [38]. Emission and absorption of ultraviolet and visible light by soot are also influenced by the presence of polycyclic aromatic hydrocarbons (PAHs) [39]. Even the accuracy of the RDG-FA models used to predict the absorption cross section of aggregates has been questioned [40, 41].

Fig. 4
figure 4

Values of E(mλ) for soot from the literature from Ref. [15], reproduced with permission

Full size image

In our previous work [15], we considered the range of values for E(m λ ) reported in the literature and invoked the Principle of Maximum Entropy to propose two priors. The first prior corresponded to a scenario in which there is little to no specific information on the origin of the soot, which would be the case for atmospheric measurements. In this case, the prior should reflect the increased level of uncertainty and incorporate more of the reported values. The second prior corresponded to soot generated from a well-characterized source operating under highly controlled laboratory conditions [42]. The width of the distribution for the second case was smaller than the first, due to the increase in certainty about the origins of the soot. In our previous work, both priors modeled E(m λ ) as uniform with respect to wavelength. Consequently, while the SVF was found to be highly sensitive to uncertainty in E(m λ ), the peak temperature defined through two-wavelength pyrometry obeyed a very narrow distribution having a width due entirely to shot noise. However, this treatment underestimates the uncertainty in the peak temperature (and consequently the SVF), since there is some theoretical basis to suspect that E(m λ ) may vary with wavelength, albeit in an uncertain way [32].

To incorporate this uncertainty into our analysis, in this work, both E(m λ1) and E(m λ2) are treated as jointly Gaussian random variables, again based on experiments carried out under controlled laboratory settings [42]. The mean of both E(m λ1) and E(m λ2) is set to 0.35, with a standard deviation of 0.03 based on the expected uncertainty in these variables. While a conservative uncertainty, estimate could be obtained by modeling these variables as independent, in reality, one would expect a high degree of correlation; loosely speaking, a portion of the E(m λ) uncertainty will affect all wavelengths in the same way (e.g., calibration uncertainty), while another portion will be wavelength-dependent due to the underlying (and uncertain) dispersive properties of soot. In particular, a correlation value of 0.75 for E(m λ) at 450 and 750 nm was calculated based on the statistical correlation present in the values reported by Coderre et al. [42]. Consequently, the prior for these variables is Ν(μ E(m),Γ E(m)), where

$${\mathbf{\mu }}_{{E({\mathbf{m}})}} = \left[ {\begin{array}{*{20}c} {0.35} \\ {0.35} \\ \end{array} } \right],\;\;{\text{and}}\;\;{\mathbf{\Gamma }}_{{E({\mathbf{m}})}} = 0.03^{2} \left[ {\begin{array}{*{20}c} 1 & {0.75} \\ {0.75} & 1 \\ \end{array} } \right].$$
(22)

4.2 Calibration coefficients

Calibration and analysis of the LII detection system are needed to relate the spectral incandescence of the heated soot within the probe volume to the voltages measured by the PMTs [2]. Snelling et al. [2] proposed a technique for calibrating a LII detection system in which the PMT voltage produced using a calibrated source, V CAL, is related to the collection optics and the spectral radiance of the calibration source, R S, through:

$${V_{{\text{CAL}}}} = {G_{{\text{CAL}}}}{\zeta _{{\text{opt}}}}\int_\lambda {{R_S}} (\lambda ,{T_{{\text{CAL}}}})\Theta (\lambda )\tau (\lambda )\;d\lambda ,$$
(23)

where G CAL is the gain used during the calibration, ζ opt represents the efficiency of the optics, T CAL is the temperature of the calibrated light source, Θ(λ) is the spectral response of the PMT, and τ(λ) is the filter transmission as a function of wavelength. In practice, the above integral is typically approximated by:

$$\int_\lambda {{R_S}} (\lambda ,{T_{{\text{CAL}}}})\Theta (\lambda )\tau (\lambda )\;d\lambda = {R_S}({\lambda _C},{T_{{\text{CAL}}}})\Theta ({\lambda _C})\tau ({\lambda _C}){\Delta _{{\lambda _C}}},$$
(24)

following Eq. (8). Substituting this approximation into Eq. (23) gives:

$${V_{{\text{CAL}}}} = {G_{{\text{CAL}}}}{\zeta _{{\text{opt}}}}{R_S}({\lambda _C},{T_{{\text{CAL}}}})\Theta ({\lambda _C})\tau ({\lambda _C}){\Delta _{{\lambda _C}}}.$$
(25)

which is rearranged to find:

$${\eta _{{\lambda _C}}} = {\zeta _{{\text{opt}}}}\Theta ({\lambda _C})\tau ({\lambda _C}){\Delta _{{\lambda _C}}} = \frac{{{V_{{\text{CAL}}}}}}{{{R_S}({\lambda _C},{T_{{\text{CAL}}}}){G_{{\text{CAL}}}}}}.$$
(26)

This definition incorporates all the optical parameters and is computed from measurements captured using the calibrated light source.

Equation (26) indicates that the uncertainty present in the calibration coefficient is induced by the uncertainties in the measured calibration voltage and spectral radiance of the calibration source. In particular, the voltage measurements are corrupted by Poisson-distributed photonic shot noise and Gaussian noise in the electronics [2], as described above. Beyond the measurement uncertainty, there can be systematic uncertainty in the spectral radiance. However, such uncertainties account for only ~1% for the PMT response [2], and can be neglected compared to the uncertainties due to measurement noise of the calibration voltage. Consequently, we neglect these uncertainties in this study.

The calibration for the measurements considered in this work was performed using a tungsten filament lamp within an integrating sphere (Sphere-Optics model SR-3A). If the measurement uncertainties of the calibration voltage were measured and spectral radiance of the integrating sphere was calculated, based on an independent external light source, during the LII calibration process, then Eq. (26) can be used to define a ratio distribution. In this case, however, only the values of η λ1 and η λ2 were computed. When the only information available is a point estimate of the parameter, an exponential distribution maximizes the information entropy of the prior density [29–31], assuming that the parameter is strictly positive. Thus, the exponential distributions, as shown in Fig. 5, are the maximum entropy prior densities for η λ1 and η λ2. To develop a more informative prior distribution for the calibration coefficients, the uncertainties involved with the external calibration of the integrating sphere and those associated with the calibration voltage need to be considered.

Fig. 5
figure 5

Maximum entropy prior distributions for the calibration coefficients. The red density is for λ = 780 nm, whereas the blue density is for λ = 420 nm

Full size image

4.3 Equivalent Laser Sheet Thickness

Non-uniform laser fluence can be accommodated via the equivalent beam thickness, Eq. (9), assuming that the spatial variation of the temperatures along the viewing axis of the detector and, therefore, the spatial variation of the fluence within the laser sheet are known. While the exact structure of these variations during an experiment is usually unknown, it is possible to generate a statistical model through a principal component analysis (PCA) of beam profile images captured for a set of independent shots.

The PCA technique relies on the Karhunen–Loève theorem, which represents a random field as a linear combination of orthogonal functions [43]. This is analogous to a Fourier series representation of a function on a compact set. When computing a Fourier series, the basis functions are fixed and consist of sinusoids of varying frequencies, whereas the basis functions in the Karhunen–Loève theorem are determined by the covariance function of the random field. This means, if F(x, y) represents the fluence at location (x, y) in the laser sheet, then:

$$F(x,y) = \bar F(x,y) + \sum\limits_{i = 1}^N {{\beta _i}} {f_i}(x,y),$$
(27)

where \(\bar F\) is the average spatial profile, f i (x, y) are the orthogonal basis functions, and β i are the random coefficients. The orthogonal basis functions can be computed from an eigenvalue decomposition of the sample covariance matrix constructed through an ensemble of laser sheet profiles. The resulting eigenvectors are then used as the orthogonal basis functions. The eigenvalues provide information about the β i coefficients, which are random variables that depend on the spatial variation of laser fluence. Synthetic fluence samples can then be generated by sampling the β i coefficients, which are modeled as normally distributed with a zero mean and variance equal to the ith eigenvalue.

To characterize the fluence variation within the laser sheet, a beam profile camera (Coherent Inc., LaserCam-HR) was used to capture images of the individual laser sheets. Images from 50 individual laser shots were used to build the PCA basis functions. Three of the images are shown in the top row of Fig. 6, in which the image counts were normalized, so that the peak count in each image is unity. Three simulated laser sheets generated using the sampling technique described above are shown in the bottom row of Fig. 6. The simulated laser sheets are nearly indistinguishable from the experimental measurements, demonstrating the effectiveness of the PCA analysis.

Fig. 6
figure 6

Top row experimentally observed laser sheets. Bottom row synthetic laser sheets generated using the PCA technique

Full size image

The simulated fluence profiles are then used to model the variation in primary particle temperature along the viewing axis of the detector, T(x). The variation in this temperature profile arises from the non-uniform laser fluence through Eq. (8). Strictly speaking, the spectral incandescence incident on the detector comes from the blackbody emission of primary particles located along the viewing axis over a ray emanating from the detector, integrated over the detector solid angle, which carves out the 3D probe volume in space. However, if we assume that the variations in fluence are isotropic, we can develop a simplified approximation to the uncertainty induced by a non-uniform laser sheet through a 1D integration over a single ray.

The local peak temperature at a location within the probe volume, in turn, can be connected to the local fluence by modeling the heat transfer during the laser pulse heating [4, 44]:

$$\frac{{dT}}{{dt}} = \frac{6}{{\pi {\rho _s}{c_s}d_p^3}}\left( {{q_{{\text{abs}}}} - {q_{{\text{cond}}}} - {q_{{\text{sub}}}} - {q_{{\text{rad}}}}} \right),$$
(28)

where T is the temperature of the soot, t is time, d p is the primary particle diameter, ρ s and c s are the density and specific heat capacity of the soot, q abs is the particle laser energy absorption rate, q cond is the particle energy loss rate through conduction, q sub is the particle energy loss rate through sublimation, and q rad is the particle energy loss rate through radiation, which is negligible and consequently excluded from the model [44]. The specific absorption, conduction, and sublimation models, detailed below, are taken from the Liu model in Refs [4, 44]. In particular, we model the laser energy absorption rate of soot nanoparticles occurs in the Rayleigh regime (following the RDG-FA model):

$${q_{{\text{abs}}}} = \frac{{{\pi ^2}d_p^3E({{\mathbf{m}}_\lambda })}}{\lambda }{F_0}q(t),$$
(29)

where F 0 is the fluence of the laser, q(t) is the normalized temporal profile of the laser pulse, so it integrates (with respect to time) to unity, and λ is the excitation wavelength of the laser. Note that in E(m λ ), Eq. (29) is evaluated at the excitation wavelength of the laser, 1064 nm, this means that the value of 0.4 is used in accordance with the Liu model from Refs [4, 44]. Conduction heat transfer is assumed to occur in the free molecular regime [18], so:

$${q_{{\text{cond}}}} = \frac{{\pi d_p^2{\alpha _T}{p_g}}}{{2{T_g}}}\sqrt {\frac{{R{T_g}}}{{2\pi {W_a}}}} \left( {\frac{{\gamma + 1}}{{\gamma - 1}}} \right)(T - {T_g}),$$
(30)

where α T is the thermal accommodation coefficient, p g is the pressure of the bath gas, T g is the bath gas temperature, R is the universal gas constant, W a is the effective molecular mass of air, and γ is the heat-capacity ratio. Finally, the rate of energy lost due to sublimation is given by:

$${q_{{\text{sub}}}} = - \frac{{\Delta {H_v}}}{{{W_v}}}\frac{{dM}}{{dt}},$$
(31)

where W v is the average molecular mass of the sublimed carbon clusters, and ΔH v is the enthalpy of formation of sublimed carbon clusters. The rate of particle mass lost through sublimation is:

$$\frac{{dM}}{{dt}} = - \frac{{\pi d_p^2{W_v}{\alpha _M}{p_v}}}{{RT}}{\left( {\frac{{RT}}{{2\pi {W_v}}}} \right)^{1/2}},$$
(32)

where α M is the mass accommodation coefficient, and p v is the partial pressure of sublimed carbon clusters. The temperature is then found simultaneously solving Eqs. (28) and (32) using a 4th order Runge–Kutta method, with model parameter values corresponding to the Liu model tabulated in Ref [44]. Our model implementation was verified by comparing the results to those from the Liu model reported in [44] when the same conditions are used. Further details concerning this model are available in Ref. [4], Ref. [44], and the references therein.

Equations (28) and (32) are solved for the peak temperature corresponding to each location in a randomly generated laser sheet profile. These results are then used to calculate w e via Eq. (11). Most of the model parameters are treated as fixed and known, even though they are often subject to considerable uncertainty, such as the thermal accommodation coefficient, α T , or the gas temperature, T g , which is justified since they do not strongly affect the peak primary particle temperature due to the dominance of the heating term in Eq. (28). The absorption model, on the other hand, has a strong influence on T p , and accordingly uncertainties in E(m λ ) and d p are included in the computation of peak temperatures. For given values of E(m λ ), d p , and the laser fluence distribution along the viewing axis, f(x), the temperature profile T(x) can be found, which is then used to compute a point estimate of w e from Eq. (11). The distribution for w e can be approximated by repeating this process using values sampled from distributions of E(m λ ), d p , and f(x). This sampling procedure is similar to the approach taken by Crosland et al. [13] and is equivalent to using Monte Carlo integration to compute:

$$\pi _{{{\text{pri}}}} (w_{e} ) = \iiint {\pi [w_{e} |E({\mathbf{m}}_{\lambda } ),d_{p} ,f(x)] \cdot \pi _{{{\text{pri}}}} [E({\mathbf{m}}_{\lambda } )] \cdot \pi _{{{\text{pri}}}} [d_{p} ]\; \cdot \pi _{{{\text{pri}}}} [f(x)] \cdot dd_{p} \cdot dE({\mathbf{m}}_{\lambda } )} \cdot df(x),$$
(33)

where π[w e | E(m λ ), d p , f(x)] is a Dirac delta density function centered at the value of w e generated using Eq. (11) with the equivalent peak temperature defined by Eq. (10) [14]. The prior for E(m λ ) is the one presented at the beginning of this section, i.e., π[E(m λ )] is a normal distribution with a mean 0.35 and a standard deviation of 0.03. The prior for the primary particle size was chosen to be a lognormal distribution with a geometric mean of 30 nm and a geometric standard deviation of 1.25, which is representative of typical values for the primary particles of in-flame soot for the measurement location used in the experiments [20]. The laser fluence is sampled using the PCA simulation technique described above.

The samples of w e were computed to have an average fluence of 1 mJ/mm2. The histograms of w e resulting from this procedure are shown in Fig. 7(a) for four combinations of E(m λ ) and d p . The distributions all have a long lower tail. The larger values of E(m λ ) shift the distribution to the right and decrease the spread. A larger E(m λ ) means that the particles absorb more energy (Eq. (29)) and thus reach higher temperatures, while the maximum temperature is limited due to the sublimation of carbon at high temperatures. Accordingly, a larger E(m λ ) results in a more uniform temperature distribution and hence a value of w e that is closer to the geometric size of the laser sheet. Variation in primary particle diameter has little effect on the position and shape of the distributions. The peak temperature, as we noted above, is minimally affected by the primary particle size because, at fluences corresponding to peak temperatures below the sublimation threshold (which is the case for F 0 = 1 mJ/mm2), both the sensible energy and primary particle absorption cross section are proportional to the d p 3, and thus, the peak primary particle temperature depends on fluence, but not on diameter. Moreover, when the fluence increases beyond the sublimation threshold (e.g., due to shot-to-shot variation in fluence, cf. Fig. 6), the peak temperature plateaus, since the additional absorbed energy mainly goes into sublimation, and thus, the peak temperature can be approximated as nearly uniform regardless of primary particle size. Figure 7b shows the prior probability density for w e which results from evaluating Eq. (33).

Fig. 7
figure 7

a Histograms of the simulated w e when E(m λ ) = 0.3, d p = 25 nm (Blue), E(m λ ) = 0.4, d p = 25 nm (Red), E(m λ ) = 0.3, d p = 45 nm (Black), and E(m λ ) = 0.4, d p = 45 nm (Green). b The estimated prior density for w e

Full size image

4.4 Prior for the gaussian approximation

Unfortunately, close examination of Eq. (1) reveals that an infinite set of candidate nuisance parameters exists that maximizes the prior and likelihood densities due to their multiplicative relationship. Moreover, since these variables are nuisance parameters, we have no interest in recovering their numerical values. To simplify the inference, we define two new composite parameters: c λ1 = E(m λ1) × η λ1 × w e and c λ2 = E(m λ2) × η λ2 ×w e . Thus, the nuisance parameter vector becomes γ c =[c λ1 c λ2]T, which now only involves two nuisance parameters, rather than five. This is an example of reducing the nuisance parameters through algebraic elimination.

The composite parameters c λ1 and c λ2 are composed of E(m λ ), η λ , and w e , so their corresponding probability densities are derived from those of the original parameters. Specifically, c λ will have a product distribution in the same way as that η λ can have a ratio distribution. Such densities typically do not have accessible closed forms, and consequently, sampling methods are used to approximate the distribution. The resulting samples closely follow normal distributions, as shown in Fig. 8, and accordingly, normal distributions are derived for π pri(c λ1) and π pri(c λ2).

Fig. 8
figure 8

Histogram and normal distribution fits for the variation within the composite nuisance parameters for λ = 780 nm (Red) and λ = 420 nm (Blue). The histograms are normalized to the total area sums to unity

Full size image

5 Quantifying uncertainty from experimental measurements

In this section, the posterior density of SVF and temperature are computed from experimental data. Two estimates of the posterior density, which include the uncertainty induced by the AC-LII parameters, are computed. The first approximation is computed using the technique of marginalization, in which nuisance parameters are integrated out of the likelihood density, so they are not included in the estimation process, but the uncertainty is still taken into account. The second technique computes the MAP estimate using Gauss–Newton (nonlinear least-squares) minimization and then makes the Gaussian approximation to the posterior. This approach combines the nuisance parameters into a single parameter, as they are all multiplied together, and estimates this composite parameter, γ c , along with SVF and temperature.

Figure 2 shows that the PMT voltages can be described by a normal distribution having a mean and width computed from the data shown in Fig. 2. Accordingly, the likelihood density is defined by

$$\pi _{{{\text{like}}}} ({\mathbf{v}}|{\mathbf{x}},{\mathbf{\gamma }}) = \pi _{e} ({\mathbf{v}} - {\mathbf{v}}^{{{\text{mod}}}} ) = \frac{1}{{2\pi \sigma _{{\lambda _{1} }} \sigma _{{\lambda _{2} }} }}\exp \left\{ { - \frac{{[V_{{\lambda _{1} }} - V_{{\lambda _{1} }}^{{\bmod }} ({\mathbf{x}},{\mathbf{\gamma }})]^{2} }}{{2\sigma _{{\lambda _{1} }}^{2} }} - \frac{{[V_{{\lambda _{2} }} - V_{{\lambda _{2} }}^{{\bmod }} ({\mathbf{x}},{\mathbf{\gamma }})]^{2} }}{{2\sigma _{{\lambda _{2} }}^{2} }}} \right\},$$
(34)

where v = [V λ1, V λ2]T are the measurements, x = [f v , T p ]T are the QoIs, γ = [E(m λ1), E(m λ2), η λ1, η λ2, w e ]T are the nuisance parameters, V λ1 and V λ2 are the sample mean of the measurements for the first and second channels with their respective standard deviations σ λ1 and σ λ2, π e is the probability density of the measurement errors, and V mod λ1, V mod λ2 are the voltages modeled by Eq. (1). The likelihood can be written more compactly as:

$$\pi _{{{\text{like}}}} ({\mathbf{v}}|{\mathbf{x}},{\mathbf{\gamma }}) = \pi _{e} ({\mathbf{v}} - {\mathbf{v}}^{{{\text{mod}}}} ) = \frac{1}{{2\pi |{\mathbf{\Gamma }}_{e} |^{{ - 1}} }}\exp \left\{ { - \frac{1}{2}\left\| {{\mathbf{L}}_{e} \left[ {{\mathbf{v}} - {\mathbf{v}}^{{{\text{mod}}}} ({\mathbf{x}},{\mathbf{\gamma }})} \right]} \right\|^{2} } \right\},$$
(35)

where

$$\left( {{\mathbf{L}}_{e}^{T} {\mathbf{L}}_{{\text{e}}} } \right)^{{ - 1}} = {\mathbf{\Gamma }}_{{\text{e}}} = \left[ {\begin{array}{*{20}c} {\sigma _{{\lambda _{1} }}^{2} } & 0 \\ 0 & {\sigma _{{\lambda _{2} }}^{2} } \\ \end{array} } \right].$$
(36)

Finally, prior densities need to be defined for the QoIs and the nuisance parameters to define the posterior density and perform marginalization. We consider three scenarios:

  1. a.

    The posterior with fixed nuisance parameters at γ = γ 0,

$$\pi ({\mathbf{x}}|{\mathbf{v}}) = \frac{{{\pi _{{\text{like}}}}({\mathbf{v}}|{\mathbf{x}},{\mathbf{\gamma }} = {{\mathbf{\gamma }}_0})}}{{\pi ({\mathbf{v}})}}.$$
(37)

These fixed values are chosen to be the mean value of the prior densities discussed in Sect. 4. In this scenario, the only uncertainty is due to measurement noise, while the other parameters are perfectly known. This procedure is most representative of the current practice followed by most LII practitioners.

  1. b.

    The marginalized posterior,

$$\pi ({\mathbf{x}}|{\mathbf{v}}) = \frac{1}{{\pi ({\mathbf{v}})}}\int {{\pi _{{\text{like}}}}({\mathbf{v}}|{\mathbf{x}},{\mathbf{\gamma }}){\pi _{{\text{pri}}}}({\mathbf{\gamma }})\;d{\mathbf{\gamma }}} .$$
(38)

This posterior is computed using the algorithm presented in the appendix of Ref [15]. In this work, however, the integral is multidimensional, so it is evaluated using Monte Carlo integration. In contrast to (a), this approach considers uncertainty in all the model parameters, as described in Sect. 3, and uses an accurate (albeit computationally expensive) technique to carry out the integrals needed to compute the posterior.

  1. c.

    The Gaussian approximation posterior,

$$\pi ({\mathbf{x}},{\mathbf{\gamma }}|{\mathbf{v}}) \approx \pi _{{{\text{apx}}}} ({\mathbf{x}},{\mathbf{\gamma }}) \propto \exp \left( { - \frac{1}{2}\left\| {{\mathbf{L}}_{{{\text{apx}}}} \left[ {\left[ {\begin{array}{*{20}c} {\mathbf{x}} \\ {\mathbf{\gamma }} \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {{\mathbf{x}}_{{{\text{MAP}}}} } \\ {{\mathbf{\gamma }}_{{{\text{MAP}}}} } \\ \end{array} } \right]} \right]} \right\|^{2} } \right)$$
(39)

where (x, γ)MAP and L apx are defined by Eqs. (18) and (20), respectively, with Γ x −1=0. Like (b), and this approach considers uncertainty introduced by measurement noise and imperfect knowledge of the nuisance parameters. In contrast to (b), however, the technique assumes a locally linear measurement model at x MAP, and, thus, requires no additional computational overhead beyond the Jacobian matrix.

A comparison of the posterior densities obtained through procedures (a) and (b) highlights the importance of considering the additional uncertainties due to imperfect knowledge of the nuisance parameters, while comparison of (b) and (c) will verify whether the Gaussian approximation is sufficiently accurate to estimate uncertainty without the excessive computational cost of marginalization.

The contour plots of the three estimated posterior densities are shown in Fig. 9. Figure 9 and Table 1 also show that the MAP estimates for the three cases are very similar. This result indicates that the MAP estimates for SVF and temperature are insensitive to uncertainty in the nuisance parameters, provided that the mean of the proposed prior distributions is used for each value of the nuisance parameters. Nevertheless, the most striking feature of these plots is that, when fixed values are used for the nuisance parameters without any consideration of the associated uncertainties, the posterior density is far narrower compared with the other two cases. In contrast, cases (b) and (c) show that marginalization or simultaneous estimation of the nuisance parameters effectively incorporates the uncertainty, modeled by the prior densities, present in the nuisance parameters.

Fig. 9
figure 9

Plot of the posterior densities for SVF and temperature when a fixed values are used for the nuisance parameters, b nuisance parameters are marginalized over the likelihood, and c when a Gaussian approximation is made to the posterior and the nuisance parameters are simultaneously estimated

Full size image
Table 1 MAP and 90% credibility interval estimates for soot volume fraction and temperature from the experimental data when the posterior is computed using fixed values for the nuisance parameters, the nuisance parameters are marginalized over the likelihood, and when the nuisance parameters are estimated using a Gaussian approximation
Full size table

Comparing the marginalized posterior in Fig. 9b with the Gaussian approximation in Fig. 9c shows that the Gaussian approximation misses the slight curvature and elongated tail present in the marginalized posterior. This can also be seen in the marginal distributions for SVF and peak temperature shown in Fig. 10. When the nuisance parameters are marginalized, the density has a long upper tail which is not captured by the Gaussian approximation. On the other hand, the area around the peak of the two posteriors is similar for both the marginalized posterior and Gaussian approximation, although the Gaussian approximation appears to slightly underestimate the uncertainty. This is confirmed with the estimated credibility intervals, shown in Table 1: the 90% credibility intervals for the marginalized distribution are approximately 35% wider than those found using the Gaussian approximation. However, given the approximately three order of magnitude reduction in computational effort, this estimate of uncertainty is considered to be quite satisfactory.

Fig. 10
figure 10

Plot of the marginalized posterior densities for a SVF and b temperature. In both plots, the blue curve is the distribution when fixed values are used for the nuisance parameters, the red curve is the distribution when the nuisance parameters are marginalized, and the purple curve corresponds to the Gaussian approximation to the posterior. The shaded area corresponds to the estimated 90% credibility interval for each marginal density

Full size image

6 Conclusions

Auto-compensating laser-induced incandescence is emerging as a reliable way to obtain spatially and temporally resolved estimates of particle volume fractions in soot-laden aerosols. It is essential, however, to interpret these estimates in the context of uncertainty. The present work uses Bayesian inference to account for the measurement noise in the spectral incandescence traces, arising mainly from photonic shot noise and electronic noise, the uncertainty in the radiative properties of soot (including spectral variation), as well as uncertainties introduced through the calibration procedure and a non-uniform, uncertain laser fluence profile. The Bayesian methodology provides a means to quantify uncertainty and explicates the role of prior knowledge in the inference procedure through the use of priors for both the nuisance variables and quantities-of-interest. If Gaussian priors are specified for the nuisance variables, which can be justified by the Principle of Maximum Entropy, calculating the maximum a posteriori estimate is reduced to solving a weighted least-squares minimization problem.

While it is essential to propose a comprehensive list of nuisance parameters to accurately estimate uncertainty in LII-derived estimates, marginalizing over these parameters requires a high-dimension integration that is time-consuming, and, in some cases, may be computationally-intractable. To overcome this drawback, we employed a Gaussian approximation of the posterior density. This approach only requires knowledge of the Jacobian matrix at the maximum a posteriori estimate, which is often a byproduct of least-squares minimization and thus requires little to no computational overhead. We found that this approach was able to reduce the computational effort by approximately three orders of magnitude.

It is important to emphasize that the objective of this paper is not to present a definitive uncertainty estimate that can be applied to all LII experiments, but to rather define a framework that can be adapted to arbitrary experimental configurations as new LII measurement techniques are developed, and extended to new sources of uncertainty as they become understood. For example, under some experimental conditions, the PMT response may become nonlinear. Similarly, we can improve our uncertainty estimate of the equivalent laser sheet thickness by considering the three-dimensional nature of the probe volume as well as uncertain TiRe-LII model parameters.

Finally, although this work focuses on estimating SVF and peak temperature, the Bayesian framework can also be used to interpret many aspects of time-resolved laser-induced incandescence. This framework has already been successfully applied to recover nanoparticle size distribution parameters and related uncertainties. More advanced techniques, like Bayesian model selection, or non-stationary estimation techniques to account for time varying or correlated uncertainties have great potential for guiding development of the models used to analyze TiRe-LII data.