1 Introduction

The unique electromagnetic properties of silicon nanoparticles have led to a multitude of existing and emerging roles in diverse areas of science and engineering. In medicine, for example, silicon nanoparticles may be used for biomedical diagnostics, targeted drug delivery, cancer therapy, cell tracking and labeling, and tissue engineering [1]. Photovoltaic device performance has undergone a paradigm shift with the introduction of nanoscale films containing silicon quantum dots, which can greatly increase photoelectric conversion efficiency [2]. Silicon nanoparticles also enhance the performance of other electronic equipment, including lithium-ion batteries [3], solid-state devices, LEDs, and printable electronics [4]. Gas-phase synthesis is the most economical route for mass production of silicon nanoparticles, but since the electromagnetic properties of silicon nanoparticles depend strongly on their size, these reactors must be designed and operated to produce nanoparticles having a highly controlled size distribution. Accordingly, there is a pressing need for an instrument that can make temporally and spatially resolved size measurements within the reactor to elucidate nanoparticle formation and growth mechanisms, pinpoint production problems, and eventually provide feedback for closed-loop control.

Time-resolved laser-induced incandescence (TiRe-LII), a combustion diagnostic normally used to measure the volume fraction and size of soot primary particles, is a promising candidate to fulfill this need. In this technique, a laser pulse heats the nanoparticles within a sample volume of aerosol to incandescent temperatures. Following the laser pulse, the spectral incandescence is measured as the nanoparticles equilibrate with their surroundings. Since larger nanoparticles cool more slowly than smaller nanoparticles, in principle the average size, and to some extent the size distribution, can be inferred from the observed spectral incandescence decay.

While TiRe-LII was initially conceived to measure the size and concentration of primary soot particles (e.g. [5–8]), several studies have investigated the feasibility of using this technique to size synthetic nanoparticles. Vander Wal et al. [9] first showed this approach could be viable for sizing metallic nanoparticles based on observed incandescence decay data, but they did not use the technique to recover particle sizes. Subsequent studies assessed the ability to extend TiRe-LII to size metal aerosols containing Ag [10], Fe [11–15], Mo [16, 17], and Ni [18] nanoparticles and oxide aerosols containing MgO [19], TiO2 [20, 21], Fe2O3 [22], and SiO2 [23] with varying success. The unique challenges associated with TiRe-LII measurements on synthetic nanoaerosols are due to the following: lower vaporization temperatures compared to carbonaceous nanoparticles, resulting in comparably weak signals [15]; high-temperature chemistry that may change the chemical composition of the nanoparticles [22]; and non-incandescent laser-induced emission from excited fragments and potential plasmas [9]. In this context, silicon is a promising material due to its high boiling point and because elemental silicon is chemically stable at high temperatures.

Despite the growing interest in gas-phase-synthesized silicon nanoparticles with well-defined properties, there have only been two prior attempts to size silicon nanoparticles using TiRe-LII [24, 25]. While strong TiRe-LII signals were obtained from the laser-heated Si nanoparticles in low-pressure plasmas, the subsequent analysis neglected the 1/λ dependence of emission and absorption efficiency in the Rayleigh regime [26], as well as the contribution of evaporation to nanoparticle cooling, which has been shown to be very important in low-pressure aerosols [27].

This paper presents pioneering experimental and theoretical work aimed at extending the capabilities of TiRe-LII to silicon nanoparticles. The paper describes the procedure and instrumentation used to collect the TiRe-LII data and briefly introduces the gas-phase synthesis process. The following section presents the heat transfer model required to analyze the TiRe-LII data, including the thermal accommodation coefficient, α, which is obtained by molecular dynamics for Si/Ar and Si/He, starting from first principles by using a combination of ab initio calculations and atomistic MD simulations to realistically model the gas/surface scattering that underlies α. Nanoparticle sizes inferred from the TiRe-LII data are found to be generally consistent with those found using Brunauer–Emmett–Teller (BET) analysis [28] and transmission electron microscopy (TEM) [29] on material from the same synthesis process.

2 Experimental procedure

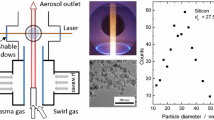
Gas-borne non-agglomerated silicon nanoparticles are produced from silane (SiH4) in a low-pressure microwave plasma flow reactor shown schematically in Fig. 1. The chamber is first evacuated and then purged with argon to remove potential contaminants (e.g., O2) that could react with the nanoparticles. Silane is premixed with dilution gases H2 and Ar at a pressure of 12 kPa so that the volume ratio of the constituents is approximately 1:12:60 for SiH4, H2, and Ar, respectively. The SiH4:H2:Ar core flow of 3.7 slm is surrounded by a Ar/H2 coflow that stabilizes the plasma. The microwave radiation of a 1,200-W magnetron is focused in the center of a 7.7-cm diameter quartz tube, producing a visible purple plasma in the lower region of the reactor shown in Fig. 2. Due to unipolar particle charging, plasma reactors form non-aggregated, electrostatically confined nanoparticles with a narrow nanoparticle size distribution; the microwave plasma reactor used here is known to produce single crystalline silicon nanoparticles with a geometric standard deviation of approximately σ g = 1.2 and nanoparticle sizes in the 5–50 nm range, depending on pressure and precursor concentration [30].

Fig. 1
figure 1

Schematic showing the experimental procedure: (1) mixing of inlet gases; (2) electrical discharge dissociation of silane; (3) nanoparticle formation; (4) in situ TiRe-LII nanoparticle sizing; and (5) ex situ BET nanoparticle sizing

Full size image
Fig. 2
figure 2

The stream of glowing silicon nanoparticles within the low-pressure plasma reactor (left), and the Artium 200M LII transmitter and receiver units arranged around the plasma reactor (right)

Full size image

Time-resolved laser-induced incandescence measurements are carried out 20 cm downstream from the plasma zone using the Artium 200M TiRe-LII system shown in Fig. 2. The instrument consists of a transmitter module containing a 1,064-nm Nd:YAG laser and optics, a receiver module containing collection optics and two photomultiplier tubes, and a computer for instrument control and data acquisition. Optical access to the aerosol is obtained through three quartz windows in the reactor walls. Inert gas flushing prevents particle deposition on the windows and allows continuous operation of the reactor for several hours. A laser pulse is shone across the reactor chamber through two opposite windows. The laser was operated with a repetition rate of 10 Hz. A nearly uniform “top-hat” beam profile with a square 2.8 mm × 2.8 mm cross section was generated by relay imaging an aperture into the measurement location where fluences were in the 0.12–0.16 J cm−2 range. The resulting incandescence signal of the laser-heated nanoparticles is detected through the third quartz window, perpendicular to the laser pulse; the probe volume is defined by intersection of the laser beam and the detector solid angle. The incandescence signal is split by a dichroic mirror, passed through two band-pass filters centered at 442 and 716 nm (full width at half maximum of 50 nm), and imaged onto the photomultiplier tubes. Further details of this procedure are provided in Ref. [6].

The spectral incandescence from the laser-heated nanoparticles can be modeled by integrating the incandescence emitted by all nanoparticle sizes

$$J_{\lambda } (t_{\text{i}} ) = C_{\lambda } \int\limits_{0}^{\infty } {\frac{{\pi d_{\text{p}}^{2} }}{4}Q_{{{\text{abs}},\lambda }} (d_{\text{p}} )P(d_{\text{p}} )I_{{{\text{b}},\lambda }} [T_{\text{p}} (t_{\text{i}} ,d_{\text{p}} )]{\text{d}}(d_{\text{p}} )}$$
(1)

where I b,λ is the blackbody spectral intensity, C λ is a constant that depends on the optical collection efficiency, laser fluence, and nanoparticle volume fraction, Q abs,λ is the absorption efficiency of the nanoparticles, and P(d p) is the probability density of nanoparticle diameters. The nanoparticle diameters are expected to be much smaller than the laser wavelength and the principal wavelengths of emitted radiation, and consequently, the nanoparticles emit and absorb in the Rayleigh limit:

$$Q_{{{\text{abs}},\lambda }} (d_{\text{p}} ) \equiv - 4xE({\mathbf{m}}_{\lambda } ) = 4\frac{{\pi d_{\text{p}} }}{\lambda }\text{Im} \left( {\frac{{{\mathbf{m}}_{\lambda }^{2} - 1}}{{{\mathbf{m}}_{\lambda }^{2} + 2}}} \right)$$
(2)

where x = πd p/λ is the nanoparticle size parameter and m λ  = n λ  + i·κ λ is the complex index of refraction for molten silicon [31]. The optical constants and E(m λ ) are plotted versus wavelength in Fig. 3.

Fig. 3
figure 3

Radiative properties of silicon [31] and calculated E(m λ ) as a function of wavelength

Full size image

The two color LII data are used to calculate a pyrometrically defined effective temperature

$$T_{\text{eff}} (t) = \frac{{hc_{\text{o}} }}{{k_{\text{B}} }}\left( {\frac{1}{{\lambda_{2} }} - \frac{1}{{\lambda_{1} }}} \right)\frac{1}{{\ln \left[ {K_{\text{opt}} \left( {\frac{{J_{{\lambda_{1} }} (t)}}{{J_{{\lambda_{2} }} (t)}}} \right)\left( {\frac{{E_{{{\mathbf{m}}_{{\lambda_{2} }} }} }}{{E_{{{\mathbf{m}}_{{\lambda_{1} }} }} }}} \right)\left( {\frac{{\lambda_{1} }}{{\lambda_{2} }}} \right)^{6} } \right]}}$$
(3)

where K opt accounts for the spectral variation of window transmissivity; this parameter was found to be K opt = 1.01 using a deuterium lamp over ultraviolet wavelengths and a xenon lamp over visible wavelengths. Sample incandescence data (averaged over 300 shots) and corresponding effective temperatures found using Eq. (3) is shown in Fig. 4.

Fig. 4
figure 4

TiRe-LII experimental data: scaled monochromatic incandescence and pyrometrically defined effective temperature

Full size image

The in situ size measurements of the silicon nanoparticles by TiRe-LII are complemented with the measurement of an average nanoparticle size calculated from their specific surface area as measured by BET analysis of silicon powder collected via a filter behind the reactor [28]. BET infers the specific surface area of nanoparticles from the physisorption of N2 by a sample of nanoparticle powder, which was kept at 150 °C and under vacuum overnight to remove residual water. Assuming that the nanoparticles are monodisperse spheres, the specific surface area can be converted to a representative nanoparticle diameter (corresponding to the Sauter mean diameter for a polydisperse powder) based on the knowledge of the sample mass and density. This technique is often used to determine the size of non-aggregated nanoparticles and has also been applied to size silicon nanoparticles produced from the reactor in previous studies [29]. Typical measurements carried out at CENIDE show a repeatability with <1 % variation in nanoparticle size, while a previous study that compared BET measurements of reference powders made independently by several laboratories showed a variation in the results below 5 % [32]. Although the BET analysis is done on the nanoparticles leaving the reactor, one would not expect the nanoparticle morphology to differ considerably between the TiRe-LII probe volume and the nanoparticle exit due to the strong Columbic repulsive forces between the Si nanospheres.

3 Heat transfer modeling

In TiRe-LII, the nanoparticle size distribution is inferred by regressing modeled spectral incandescence data, derived from a heat transfer model via Eq. (1), to experimental measurements. The laser-heated nanoparticles equilibrate with the surrounding bath gas according to

$$\rho c_{\text{p}} \frac{{\pi d_{\text{p}}^{3} }}{6}\frac{{{\text{d}}T_{\text{p}} }}{{{\text{d}}t}} = - q_{\text{cond}} (t,d_{\text{p}} ) - q_{\text{evap}} (t,d_{\text{p}} ) - q_{\text{rad}} (t,d_{\text{p}} )$$
(4)

where ρ, c p, T p, and d p are the nanoparticle density, specific heat, temperature, and diameter. The bulk density and specific heat of silicon are taken from Refs. [33, 34], respectively.

Since the silicon nanoparticles formed within the reactors are expected to be much smaller than the mean free molecular path in the bath gas, heat conduction takes place in the free molecular regime so that

$$q_{\text{cond}} (t,d_{\text{p}} ) = \pi d_{\text{p}}^{2} N_{\text{g}}^{{\prime \prime }} \left\langle {E_{\text{o}} - E_{\text{i}} } \right\rangle$$
(5)

where N g ″ = c g,t· n g/4 is the incident gas molecular number flux, n g = p g/(k B T g) is the number density, c g,t = [8k B T g/(πm g)]1/2 is the mean thermal speed of the gas molecules, and 〈E o − E i〉 is the average energy transferred to a gas molecule when a gas molecule scatters from the laser-heated nanoparticle. (As noted above, Columbic forces between the unipolar silicon nanoparticles result in aggregates having an open structure [29], so aggregate shielding is expected to be negligible). The energy transfer term is defined using the thermal accommodation coefficient

$$\alpha = \frac{{\left\langle {E_{\text{o}} - E_{\text{i}} } \right\rangle }}{{\left\langle {E_{\text{o}} - E_{\text{i}} } \right\rangle_{\hbox{max} } }}$$
(6)

where 〈E o − E i〉max = 2k B(T p − T g) for a monatomic gas. Equation (5) can be rewritten as [35]

$$q_{\text{cond}} (t,d_{\text{p}} ) = \pi d_{\text{p}}^{2} \frac{{p_{\text{g}} c_{{{\text{g}},{\text{t}}}} }}{{2T_{\text{g}} }}\alpha (T_{\text{p}} - T_{\text{g}} )$$
(7)

The thermal accommodation coefficient is found using molecular dynamics (MD) as described in the subsequent section of this paper. Free molecular heat conduction with argon and hydrogen molecules was considered simultaneously with two conduction terms identical to Eq. (7) except that p g is the gas partial pressure and c g,t, and α are specific to each gas species. Although the partial pressure of H2 is much lower than that of Ar, and α should also be much lower for H2 compared to Ar based on the relative molecular weights, free molecular heat conduction due to H2 molecules is still significant as its smaller mass translates into a higher c g,t and consequently a higher incident number flux of H2 molecules.

Evaporation in the free molecular regime is given by

$$q_{\text{evap}} (t,d_{\text{p}} ) = \varDelta H_{\text{v}} J_{\text{evap}} = \varDelta H_{\text{v}} \pi d_{\text{p}}^{2} \frac{{n_{\text{v}} c_{{{\text{v}},{\text{t}}}} }}{4}\zeta$$
(8)

where ΔH v is the enthalpy of vaporization per atom, J evap is the evaporating mass flux, n v = p v/(k B T p) is the vapor number density, c v,t = [8k B T p/(πm v)]1/2 is the mean thermal speed of the vapor, m v is the atomic mass of the vaporized species, and ζ is the sticking coefficient, 0 ≤ ζ ≤ 1, which accounts for the fraction of evaporated atoms that cannot escape the potential well and adsorb back onto the surface. In this work, we assume ζ = 1, since the high surface energy of the nanoparticle relative to the gas–surface potential well depth precludes reabsorption of evaporated Si atoms [15, 17]. The vaporized species is assumed to consist entirely of atomic silicon, which is supported by mass spectrometry measurements carried out by Tomooka et al. [36] over temperature ranges similar to those considered in this study. The enthalpy of vaporization, ΔH v, was found using Watson’s equation [37, 38]

$$\varDelta H_{\text{v}} = K(1 - T_{\text{r}} )^{0.38}$$
(9)

where K is a material constant, T r = T p/T cr is the reduced temperature, and T cr is the critical temperature of liquid silicon [39]. The constant can be solved using a known reference point on the vapor dome, most often the heat of vaporization at the boiling temperature and atmospheric pressure. Once ΔH v is known, the vapor pressure, p v, can be determined by the Clausius–Clapeyron relation [13]

$$\ln (p_{\text{v}} ) = - \frac{{\varDelta H_{\text{v}} }}{R}\frac{1}{{T_{\text{p}} }} + C$$
(10)

where R is the universal gas constant and C is a material constant. The vapor pressure is also corrected for the increased surface energy due to nanoparticle curvature using the Kelvin equation [40]

$$p_{\text{v}} = p_{{{\text{v}},{\text{o}}}} \exp \left[ {\frac{{4\gamma_{\text{s}} }}{{d_{\text{p}} \rho R_{\text{s}} T_{\text{p}} }}} \right]$$
(11)

where p v,o is the vapor pressure for a flat surface, γ s is the surface tension of the nanoparticle material, taken at the melting point [33], and R s is the specific gas constant. Recent studies (e.g. [41]) suggest that using the bulk value for γ s significantly underestimates the surface energy of nanoparticles. The influence of nanoparticle size on surface tension can be incorporated into the model using the Tolman equation [42]

$$\gamma_{\text{s}} = \frac{{\gamma_{{{\text{s}},{\text{o}}}} }}{{1 + {{4\delta } \mathord{\left/ {\vphantom {{4\delta } {d_{\text{p}} }}} \right. \kern-0pt} {d_{\text{p}} }}}}$$
(12)

where γ s,o is the bulk surface tension taken to be that of bulk silicon at 2,000 K [33] and δ is the Tolman length taken as the atomic diameter for δ/D ≥ 20. Figure 5 shows that this effect is negligible except for small particle sizes (<10 nm) and at lower nanoparticle temperatures. For moderately sized nanoparticles (~30 nm) and temperatures at which evaporation is important (>2,400 K), this model provides vapor pressures consistent with values measured above molten silicon as reported by Tomooka et al. [36] and Desai [34]. Figure 5 also shows that heat transfer due to evaporation corresponding to the vapor pressure from Ref. [34] is also consistent with values obtained through Eqs. (10–12).

Fig. 5
figure 5

Conduction, evaporation, and radiation as a function of surface temperature for silicon nanoparticles at 30 nm (left); and vapor pressure as a function of particle size using the bulk value and those corrected using Kelvin and Tolman equations (right)

Full size image

The nanoparticle mass lost due to evaporation is found by integrating J evap over the temperature decay. Since laser heating is excluded from the heat transfer model, mass loss was estimated by assuming the peak temperature for prevaled for 10 ns of laser heating as a worst-case scenario. This calculation showed that the nanoparticle mass would decrease less than 15 % (5 % reduction in d p) for all nanoparticles larger than 10 nm and only 4 % (2 % reduction in d p) for 30 nm nanoparticles. This is considered low enough that nanoparticle size was assumed to be static during the cooling process.

Finally, thermal radiation from the nanoparticles is given by [26]

$$q_{\text{rad}} (t,d_{\text{p}} ) = \int\limits_{0}^{\infty } {\pi d_{\text{p}}^{2} Q_{{{\text{abs}},\lambda }} (d_{\text{p}} )\pi I_{{{\text{b}},\lambda }} [T_{\text{p}} (t,d_{\text{p}} )]{\text{d}}\lambda }$$
(13)

Although thermal radiation from the laser-heated nanoparticles is the basis for TiRe-LII particle sizing, Fig. 5 shows that heat transfer due to thermal radiation is several orders of magnitude smaller than conduction and evaporation; consequently, radiation is neglected for the remainder of the analysis. Figure 5 also shows that the heat transfer due to evaporation decays very rapidly with decreasing temperature and becomes negligible below 2,250 K for most nanoparticle size classes.

4 Predicting the thermal accommodation coefficient using molecular dynamics

One of the main obstacles in extending TiRe-LII to new aerosols is that the thermal accommodation coefficient is unknown. Most published values for α (e.g. [43]) are found under conditions different from those encountered in TiRe-LII and thus cannot be applied directly to TiRe-LII analysis. Consequently, in most TiRe-LII experiments, α is inferred by comparing incandescence decay data to nanoparticle sizes found using ex situ analysis, such as TEM [11, 15, 44–46]. These accommodation coefficients are then used to infer nanoparticle sizes from other TiRe-LII data, a somewhat circular process.

It has been shown, however, that molecular dynamics (MD) can be used to predict this parameter for various gas–surface systems [47–49]. In the present work, this approach is used to predict α for the Si/Ar system over a range of surface and gas temperatures. We also carry out the same procedure for Si/He to investigate how the reduced gas molecular mass and potential well depth influences the accommodation coefficient.

The first step of this procedure is to define the interatomic potentials. The potential energy of silicon is defined using the Stillinger–Weber potential [50], consisting of two-body and three-body terms

$$U_{ij} (r_{ij} ) = \frac{1}{2}\sum\limits_{i} {\sum\limits_{j > i} {\phi_{2} (r_{ij} )} + \sum\limits_{i} {\sum\limits_{j \ne i} {\sum\limits_{k > j} {\phi_{3} (r_{ij} ,r_{ik} ,\theta_{ijk} )} } } }$$
(14)

The two-body term describes the Si–Si bonding within the crystal

$$\phi_{2} = \varepsilon A\left[ {B\left( {\frac{\sigma }{{r_{ij} }}} \right)^{p} - \left( {\frac{\sigma }{{r_{ij} }}} \right)^{q} } \right]\exp \left( {\frac{\sigma }{{r_{ij} - a\sigma }}} \right)$$
(15)

where r ij is the distance between the ith and jth atoms. The three-body term promotes the bond angle, θ ijk , between three silicon atoms

$$\phi_{3} = \lambda \varepsilon \left( {\cos \theta_{ijk} - \cos \theta_{0} } \right)^{2} \exp \left( {\frac{\gamma \sigma }{{r_{ij} - a\sigma }} + \frac{\gamma \sigma }{{r_{ik} - a\sigma }}} \right)$$
(16)

which keeps the silicon crystal in its diamond structure below its melting temperature. The parameterization for the Stillinger–Weber potential [50], summarized in Table 1, has been shown to replicate the empirically observed melting temperature and molten density of silicon [51]. To verify the physicality of the Stillinger–Weber potential for this application, the simulation density was compared to the experimental density used in the heat transfer model over a range of temperatures important to TiRe-LII analysis [33]. Figure 6 confirms that the density predicted by MD is within 10 % of the experimentally derived value.

Table 1 Parameterization for the Stillinger–Weber potential for silicon [50]
Full size table
Fig. 6
figure 6

MD-derived density of molten silicon averaged over the final 5,000 timesteps of the warming procedure, normalized by the published density over a range of surface temperatures [33]. Error bars denote two standard deviations of the mean

Full size image

The gas atoms interact with the surface atoms through a pairwise Morse potential

$$U_{ij} (r_{ij} ) = D\left[ {{\text{e}}^{{ - 2\lambda (r_{ij} - r_{\text{e}} )}} - 2{\text{e}}^{{ - \lambda (r_{ij} - r_{\text{e}} )}} } \right]$$
(17)

where D, λ, and r e are specific to the gas–surface molecular pair. These parameters are found by fitting superimposed pairwise potentials to the ground state energies derived from density functional theory (DFT) for gas atoms at various heights above a silicon surface. The silicon surface is represented by a 2 × 2 × 2 supercell of 64 atoms with a lattice parameter of 0.543 nm. The present work used the WIEN2k code [52] with the generalized gradient approximation (GGA) parameterization of the exchange and correlation functionals with RKM value of 5.0- and 12-k points in the irreducible Brillouin zone. RKM is the product of the largest plane-wave vector and the smallest muffin-tin radius in the system. Muffin-tin radii of 0.117 nm (for Si) and 0.106 nm (for Ar and He) were used. The DFT-derived parameterization of the Morse potential for the gas–surface interaction is given in Table 2 and plotted against the raw DFT data in Fig. 7. The binding energies shown in Fig. 7 are comparable to the 8 meV given by Bandler et al. [53] for helium in adsorption experiments and 20 meV given by Lau et al. [54] for argon in bombardment experiments.

Table 2 Pairwise Morse potential parameters between the gas and silicon atoms
Full size table
Fig. 7
figure 7

DFT-derived ground state energies for the Si/Ar and Si/He systems (symbols) and fitted Morse potentials (dashed lines)

Full size image

The above parameterization forms the basis of MD simulations of gas molecules scattering from the laser-heated silicon nanoparticle. Simulations were carried out using LAMMPS [55]. The silicon surface is modeled using 544 silicon atoms, initially arranged in a diamond crystal lattice. Periodic boundary conditions are applied on the lateral surfaces (perpendicular to the free surface) of the computational domain. The silicon is initially brought to the specified temperature by applying the Nosé–Hoover thermostat [56, 57] (NVT ensemble) with a damping constant of 0.1 ps for 30 ps. The simulation is continued for 5 ps under the NVE ensemble to ensure that the system has reached equilibrium conditions at the desired temperature, during which time the surface density is also tracked. At the conclusion of this simulation, the silicon atom positions and velocities are stored in a restart file.

The MD simulation forms the kernel of a Monte Carlo integration over 1,500 incident gas molecular trajectories. Incident gas velocities are sampled from a Maxwell–Boltzmann distribution at the prescribed gas temperature following [47], and the silicon atomic trajectories are initialized from the restart file. The atomic trajectories are then traced until the gas atom exceeds its initial height above the surface. The accommodation coefficient is then found by

$$\alpha = \frac{{{{m_{\text{g}} } \mathord{\left/ {\vphantom {{m_{\text{g}} } 2}} \right. \kern-0pt} 2}\left\langle {v_{2}^{2} - v_{1}^{2} } \right\rangle }}{{2k_{\text{B}} (T_{\text{p}} - T_{\text{g}} )}}$$
(18)

where m g is the gas molecular mass, and v 1 and v 2 are the incident and scattered gas molecular velocities, respectively. Figure 8a shows the progression of the initial warming process from a perfect silicon crystal lattice to an amorphous silicon molten surface at 2,500 K, while Fig. 8b shows an argon molecule directly scattering from the silicon surface.

Fig. 8
figure 8

Visualization of the molecular dynamics simulation: a a Nosé–Hoover thermostat is used to transform the silicon surface from its initial crystal configuration to amorphous molten silicon at 2,500 K, and b an argon molecule scatters directly from the silicon surface. Illustrated particles sizes are 70 % of the Van der Waals diameter

Full size image

For the MD study, a surface temperature of 2,500 K and gas temperature of 1,300 K were chosen since they are representative of TiRe-LII conditions, following previous MD studies [46–48]. Under these conditions, the accommodation coefficients for Si/He and Si/Ar were found to be 0.11 ± 0.01 and 0.36 ± 0.02, respectively, using 1,500 Monte Carlo trials. (Uncertainties correspond to two standard deviations of the mean.) These results follow the same general trend seen in the thermal accommodation coefficients versus potential well depth and reduced molecular mass calculated between monatomic gases and metals and graphite [49], as shown in Fig. 9.

Fig. 9
figure 9

MD-derived values of α versus potential well depth. Data for graphite are from Ref. [47], values for molybdenum, iron, and nickel are reported in Ref. [58], and values for silicon are the present study. Error bars denote two standard deviations of the mean

Full size image

The effect of gas temperature on the average energy transferred to the gas molecule, ΔE = 〈E o − E i〉, is plotted in Fig. 10 with T s held at 2,500 K. The change in translational normal and tangential energy components of the gas molecule is also plotted. While the increase in tangential translational energy is less than the normal component, it is larger than that observed by Daun et al. [47] between the graphite and both the monatomic gases and N2 [48]. This is almost certainly due to the greater surface roughness of liquid silicon compared to solid graphite; in the latter case, the thermal motion of carbon atoms is primarily normal to the exposed surface, so surface energy is transferred preferentially into the normal translational mode of the gas molecule. In contrast, the motion of atoms in molten Si is comparatively unconstrained, so energy is transferred into the normal and tangential modes. Similar trends were observed when comparing the MD-derived normal and tangential modes of the accommodation coefficients for molten Fe and Ni nanoparticles with those for Mo nanoparticles, which remain solid in TiRe-LII experiments [58].

Fig. 10
figure 10

Variation of ΔE = 〈E o − E i〉 of Si/Ar and Si/He with T g at T s = 2,500 K decomposed into: a the normal component; b the tangential component; and c the sum of both components. Error bars denote two standard deviations of the mean

Full size image

Figure 10 also shows that the average energy increase is zero when T s = T g, in accordance with the 2nd Law of Thermodynamics. The individual normal and tangential components of translational energy also appear to follow the same rule, suggesting that the normal and tangential modes of the gas molecule are uncoupled.

Figure 11 shows accommodation coefficients corresponding to change in gas molecular energies shown in Fig. 10. Because the denominator of Eq. (18) becomes very small when T s ≈ T g, a quadratic curve is fit to the points in Fig. 10 and is forced to cross zero when T s = T g in accordance with the 2nd Law. Substituting this expression into Eq. (18) gives a linear relationship between α and T g that is plotted in Fig. 11. The fitted curves generally lie within the error bounds (two standard deviations of the mean of the Monte Carlo trials) in the entire range of considered gas temperatures.

Fig. 11
figure 11

Variation of α for Si/Ar and Si/He with T g at T s = 2,500 K. Error bars denote two standard deviations of the mean

Full size image

Figure 12 shows the simulated change in energy transfer considering surface temperatures from 200 to 3,000 K for T g = 300 K. This plot reveals an inflection in the normal and tangential components of the gas molecular energies occurring when T s ≈ T melt, represented by the vertical dashed line in Fig. 12c. This is expected, particularly for the tangential component, due to increased mobility of the surface atoms in the liquid state as described above. Figure 12 shows that the thermal accommodation coefficients can be approximated by constant values above and below the melting temperature

$$\begin{gathered} \alpha_{{{{\text{Si}} \mathord{\left/ {\vphantom {{\text{Si}} {\text{Ar}}}} \right. \kern-0pt} {\text{Ar}}}}} = \left\{ {\begin{array}{*{20}c} {0.100,} \hfill & {T_{\text{s}} < T_{\text{m}} } \hfill \\ {0.347,} \hfill & {T_{\text{s}} > T_{\text{m}} } \hfill \\ \end{array} } \right. \hfill \\ \alpha_{{{{\text{Si}} \mathord{\left/ {\vphantom {{\text{Si}} {\text{He}}}} \right. \kern-0pt} {\text{He}}}}} = \left\{ {\begin{array}{*{20}c} {0.078,} \hfill & {T_{\text{s}} < T_{\text{m}} } \hfill \\ {0.107,} \hfill & {T_{\text{s}} > T_{\text{m}} } \hfill \\ \end{array} } \right. \hfill \\ \end{gathered}.$$
(19)
Fig. 12
figure 12

Variation of ΔE = 〈E o − E i〉 of Si/Ar and Si/He with surface temperature at T g = 300 K decomposed into: a the normal component; b the tangential component; and c the sum of both components. Error bars correspond to two standard deviations of the mean

Full size image

5 Analysis of TiRe-LII data

The MD-derived accommodation coefficients are then used to interpret the experimental TiRe-LII data. Silicon nanoparticle diameters are initially found by nonlinear regression of the experimental pyrometrically defined effective temperature, T eff, to the same effective temperature derived from a simulated incandescence signal found by solving Eq. (1). Since the procedure for inferring the nanoparticle size distribution from TiRe-LII data requires an initial condition of uniform nanoparticle temperatures (taken to be the peak temperature in the case of a “top-hat” beam profile), and because of a smoothing effect lasting several nanoseconds around the peak temperature, it is necessary to extrapolate a hypothetical peak nanoparticle temperature that would be compatible with the conduction and evaporation cooling models. Accordingly, instead of the experimentally observed peak temperature of 3,075 K, a somewhat higher initial temperature, T i = 3,100 K, was chosen as an initial condition to account for the smoothing effect at the peak.

A thermocouple was inserted in the central gas flow slightly above the TiRe-LII probe volume. After correcting for radiation losses from the probe, it indicated a gas temperature of 1,300 K, which is consistent with temperatures found through planar laser-induced florescence measurements carried out in a similar reactor [59].

Accounting for free molecular heat conduction by the H2 molecules requires knowledge of the \(\alpha_{{{\text{H}}_{2} }}\), which was not quantified using MD due to the complexity of deriving ab initio potentials for a polyatomic molecule. Since previous work has shown that the mass ratio and the thermal accommodation coefficient are closely related [47], H2 was modeled as monatomic and \(\alpha_{{{\text{H}}_{2} }}\) was assigned the value of α He = 0.11 due to similar mass of the two gases. Uncertainty introduced by this assumption is addressed later in the paper.

Based on detailed TEM studies of nanoparticles extracted from the same reactor (e.g., [32]), the nanoparticle sizes are known to follow a lognormal distribution

$$P(x) = \frac{1}{{x\sqrt {2\pi } \ln \sigma_{\text{g}} }}\exp \left[ {\frac{{ - (\ln x - \ln d_{{{\text{p}},{\text{g}}}} )^{2} }}{{2(\ln \sigma_{\text{g}} )^{2} }}} \right]$$
(20)

defined by the geometric standard deviation, σ g, and geometric mean particle diameter, d p,g, which is also the median diameter for a lognormal distribution. Figure 13 compares the modeled data corresponding to the maximum likelihood estimates (MLEs) of the lognormal distribution parameters, d p,g = 24.2 nm and σ g = 1.43, reported in Table 3. On the other hand, if the aerosols were monodisperse, the MLE nanoparticle diameter is 37.3 nm. Figure 13 also shows that the monodisperse model is unable to predict the incandescence decay at measurement times greater than 2 μs, which one would expect as the influence of polydisperse nanoparticle sizes on the incandescence decay becomes more pronounced at longer cooling times [46].

Fig. 13
figure 13

Experimentally observed pyrometric temperatures (solid line), and modeled temperature decays corresponding to the most probable monodisperse (long dash) and lognormal (short dash) nanoparticle size distributions. The monodisperse assumption is incapable of reproducing the observed pyrometric temperatures at longer cooling times due to the polydispersity of nanoparticle sizes

Full size image
Table 3 Most probable nanoparticle size distribution parameters and credible intervals
Full size table

Uncertainty in the distribution parameters caused by noise in the monochromatic incandescence measurements (due mainly to photomultiplier shot noise) was quantified using robust Bayesian analysis similar to the procedure described in Ref. [60]. In this approach, the posterior probability, P(x|b), of the hypothesized set of distribution parameters in x = [d p,g, σ g]T is defined by

$$P\left( {{\mathbf{x}}|{\mathbf{b}}} \right) = \frac{{P\left( {{\mathbf{b}}|{\mathbf{x}}} \right)P_{\text{pr}} ({\mathbf{x}})}}{{P\left( {\mathbf{b}} \right)}}$$
(21)

where P(b|x) is the likelihood of the observed data in b occurring for a hypothetical x, P pr(x) is the probability of x being correct based on prior knowledge of the distribution parameters, and P(b) scales the posterior probability so that the Law of Total Probability is satisfied. If the spectral incandescence data are contaminated with independent, normally distributed error, the likelihood is given by

$$P\left( {{\mathbf{b}}|{\mathbf{x}}} \right) = \prod\limits_{j} {\frac{1}{{\sqrt {2\pi \sigma_{j}^{2} } }}\exp \left\{ { - \frac{{\left( {T_{\exp ,j} - T_{\bmod ,j} } \right)^{2} }}{{2\sigma_{j}^{2} }}} \right\}}$$
(22)

where σ j is the expected standard deviation of the measured incandescence at the jth measurement time. The standard deviation increases at longer cooling times, as the signal-to-noise ratio in the incandescence traces drops with decreasing signal intensity [61]. In order to account for this fact, σ j is modeled by a quadratic function fitted to the standard deviations of the mean of 300 independent sets of incandescence data evaluated at every measurement time. The prior probability is defined as

$$P_{\text{pr}} ({\mathbf{x}}) = \left\{ {\begin{array}{*{20}c} {1,} \hfill & {{\text{if}}\;d_{{{\text{p}},{\text{g}}}} \ge 0\;{\text{and}}\;\sigma_{\text{g}} \ge 1} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(23)

since neither d p,g nor σ = ln(σ g) can hold non-positive values. While Eq. (19) defines a two-dimensional plot of the probability density of x, it is more convenient to quantify the uncertainty of a distribution parameter of interest with a credible interval over the marginalized probability densities of each variable. Since the marginalized posterior probabilities may be asymmetric, it is useful to define the credible interval using the highest density region (HDR) or highest density probability [62], which can be quantified using the density quantile approach [63]. In this case, a set of 10,000 samples, X = {x 1, x 2, …, x n }, is generated using a Markov Chain Monte Carlo (MCMC) algorithm [64]; these samples are then used to form marginalized posterior distributions for d p,g and σ g through kernel density estimation [65].

In Fig. 14, the MCMC samples are plotted over contours of the residual norm, showing the relationship between the samples and the region of minimal residual. The 95 % credible intervals and mean are given in Table 3. The maximum a posteriori (MAP) estimate of σ g = 1.43 obtained by minimizing the scaled residual is typical of a self-preserving distribution for an aerosol in which nanoparticle growth mechanisms have stabilized [66]. On the other hand, this value is larger than the σ g = 1.2 typically found from in situ particle mass spectrometry and ex situ TEM analysis [67]; the narrower distribution is also what one would expect based on the Coulomb repulsion of the charged nanoparticles [30].

Fig. 14
figure 14

MCMC samples laid over the L2 norm of the residual between experimental and modeled data. Histograms show the posterior distribution resulting from MCMC sampling, while the solid line corresponds to lognormal nanoparticle sizes that share a Sauter mean of d p,32 = 33.2 nm

Full size image

The large credible intervals associated with d p,g and σ g are typical of ill-posed inverse problems, since a wide range of nanoparticle size distributions exist that explain the experimental data within the standard deviation due to signal noise. Figure 14 shows that these solutions lie along a specified thin region of minimal residual. Daun et al. [68] demonstrated that this family of solutions approximately shares a narrow distribution of Sauter mean diameters, defined for a lognormal distribution as

$$d_{{{\text{p}},32}} = \frac{{\int\limits_{0}^{\infty } {d_{\text{p}}^{3} P(d_{\text{p}} ){\text{d}}d_{\text{p}} } }}{{\int\limits_{0}^{\infty } {d_{\text{p}}^{2} P(d_{\text{p}} )d{\text{d}}_{\text{p}} } }} = d_{{{\text{p}},{\text{g}}}} \exp \left[ {\frac{5}{2}\ln (\sigma_{\text{g}} )^{2} } \right]$$
(24)

Credible intervals for d p,32 are also reported in Table 3. As one would expect, the credible interval is considerably smaller than that found for d p,g since the ill-posedness of the problem is due to the narrow curvature of the residual function along the locus of distributions that share a common Sauter mean diameter.

We must also consider, separately, how model parameter uncertainty affects the recovered nanoparticle size distribution parameters. As noted above, the gas temperature within the probe volume is difficult to measure precisely due to the limited access afforded by the reactor geometry, but is approximately 1,300 K based on a thermocouple measurement in near the probe volume. An uncertainty of ±200 K is assigned as a conservative estimate of this uncertainty, primarily due to uncertainty in laser position with respect to the thermocouple location. The extrapolated initial nanoparticle temperature used in the sizing analysis is assigned an uncertainty of ±25 K, based on the difference between the experimentally observed peak temperature (3,075 K) and the assumed value (3,100 K). The thermal accommodation coefficient for H2 is assigned a conservative uncertainty of ±50 %. Uncertainties in ρ, c p, p g, γ s, T cr, and the MD-derived thermal accommodation coefficients are taken to be 10 % of their nominal values.

The impact of these uncertainties on the inferred size parameters is assessed through a perturbation analysis, in which the relative sensitivity coefficients, i.e., the product of the local sensitivity and the nominal model parameter value, are estimated through a central finite difference approximation. The error in an inferred parameter, y, due to uncertainty in a model parameter, x, can then be found using

$$\varepsilon \left( {y|x} \right) = {\text{PE(}}x )\times {\text{RSC(}}x,y )= {\text{PE(}}x )\times \left[ {x\frac{\partial y}{\partial x}} \right]_{{x_{0} }}$$
(25)

where ε is the error in the units of the inferred parameter, PE is the percentage error in a model parameter, and RSC is the relative sensitivity coefficient. Table 4 shows that these error bounds are comparable in magnitude to the credible intervals associated with signal noise.

Table 4 Relative sensitivity coefficients and estimated error for inferred nanoparticle size distribution parameters due to model parameter uncertainty
Full size table

Ex situ measurements made by BET analysis on a nanoparticle powder consisting of spherical, non-aggregated particles loosely connected by point contacts give an approximate diameter of 33.3 nm. This diameter can also be interpreted as the Sauter mean diameter since the nanoparticle size is derived from the ensemble volume of nanoparticles (found from the mass of the sample and bulk density of Si), divided by the specific surface area, which is inferred from N2 adsorption. This value is in excellent agreement with the TiRe-LII-derived Sauter mean of 33.2 nm and lies well within the error bars generated by measurement noise and model parameter uncertainty.

6 Conclusions

This paper describes the application of TiRe-LII to size silicon nanoparticles within a low-pressure microwave plasma reactor. Inferring nanoparticle sizes from TiRe-LII data requires a model of the free molecular heat conduction and evaporation through which the laser-heated nanoparticles equilibrate with the surrounding gas. Free molecular heat conduction depends on the thermal accommodation coefficient, which is calculated using molecular dynamics with DFT-derived gas/surface potentials. A parametric study elucidated how the thermal accommodation coefficient is expected to vary over a range of gas and particle temperatures.

The nanoparticle diameters were then inferred from the experimentally observed temperature decay, using a conduction model with separate terms for H2 and Ar and an evaporation model using Watson’s equation for the heat of vaporization. Maximum likelihood estimates of lognormal distribution parameters were found through Bayesian analysis; the geometric mean (and median) diameter of 24.2 nm is generally consistent with expected nanoparticle diameters, while the TiRe-LII-derived geometric standard deviation of 1.43 is larger than what is typically observed in TEM micrographs of silicon nanoparticle powders produced by the reactor. On the other hand, the Sauter mean diameter inferred from the TiRe-LII data matches the diameter found from BET analysis on a nanoparticle powder.

Ongoing work is focused on improving the evaporation model by including the influence of nanoparticle size on the surface energy used in the Kelvin equation. Uncertainty estimates will also be made more robust by combining the model parameter uncertainty and signal noise within an extended Bayesian framework. This lays the way for a more rigorous statistical treatment of TiRe-LII data and the possibility of obtaining more robust estimates of nanoparticle morphology by combining TiRe-LII data with other techniques that provide complementary information.