1 Introduction

In classical data transmission, repeaters are used to amplify data signals (bits) when they become weaker during their propagation through the transmission channel. In contrast to classical information, the above mechanism is impossible to realize when the transmitted data signals are the carriers of quantum information (qubits), which cannot be amplified or cloned without destroying the encoded information [1, 2]. Therefore, the carrier has to propagate along the entire length of the transmission channel which, due to various losses, leads to an exponentially decreasing probability to receive it intact at the end of the channel.

To circumvent this problem, the quantum repeater was proposed in the seminal Ref. [3] that encapsulates three building blocks such as (1) entanglement distribution, (2) entanglement purification, and (3) entanglement swapping, which have to be applied sequentially. Using the first building block, a large set of low-fidelity entangled qubit pairs is generated between all repeater nodes, which becomes distilled by the second block into a smaller set of high-fidelity entangled pairs. Entanglement swapping, finally, combines two purified entangled pairs distributed between the neighboring repeater nodes into one entangled pair leading to a gradually increasing distance of shared entanglement.

Obviously, quantum repeater schemes are not straightforward. The above-mentioned building blocks, for instance, require a feasible and reliable quantum logic, while low-fidelity entangled pairs have to be distributed over reasonably long distances. Up to now, only a few schemes, which distribute entanglement over the distance of 200 km using fiber-optic [4] and 100 km using free-space channel [5] between the nodes have been experimentally demonstrated. Nevertheless, motivated by a rapidly growing experimental and theoretical progress in the field of quantum communication, various quantum repeater schemes and single building blocks have been proposed [6–11].

In our previous paper [12], we already proposed a dynamical quantum repeater scheme in which the entanglement between the two neighboring repeater nodes was distributed using controlled displacements of input coherent light, while the generated low-fidelity entangled pairs were purified using ancillary (four-partite) entangled states. This scheme exploited solely the evolution of short chains of atoms coupled to optical cavities located in each repeater node, such that any explicit usage of quantum logical gates has been avoided. In the present paper, we propose an improved quantum repeater scheme that (as well) avoids two-qubit quantum logical gates and where the entanglement is distributed using a sequence of controlled phase shifts and displacements of input coherent light, while entanglement purification is free of ancillary entangled resources. This repeater scheme exhibits reasonable fidelities and repeater rates providing an attractive platform for long-distance quantum communication.

In particular, our entanglement distribution becomes very efficient, simple, and practical, as it only requires discriminating two optical coherent states with opposite signs, where each allows for conditionally preparing a certain two-qubit Bell state over the distance in two neighboring repeater nodes. This way, in the ideal loss-free case, maximum two-qubit entanglement can be deterministically generated with unit fidelity in the limit of large coherent state amplitudes. Note that in the present work, we focus on a standard (original) quantum repeater scheme as described above and based on the use of quantum memories and two-way classical communication. Other more recent approaches that make use of quantum error correction codes reduce or completely eliminate the need for storing quantum information and for employing two-way communication. As a result, extremely high rates are achievable in this new generation of repeaters (for a classification into three generations of quantum repeaters, see Ref. [13]).

The paper is organized as follows. In the next section, we describe in detail our practical quantum repeater scheme. We introduce and discuss the entanglement distribution, purification, and swapping protocols in Sects. 2.1, 2.2, and 2.3, respectively. In Sect. 2.4, we discuss a few relevant issues related to the implementation of our repeater scheme, while a brief analysis of final fidelities and repeater rates is given in Sect. 3 along with the summary and outlook.

2 Quantum repeater platform

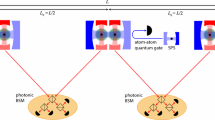
The main physical resources of our repeater scheme are (1) three-level atoms, (2) high-finesse optical cavities, (3) continuous and pulsed laser beams, (4) balanced beam splitters, and (5) photon detectors. In Fig. 1a, we display schematic view of our experimental setup that encapsulates two neighboring repeater nodes (B and C) and includes the entanglement distribution, purification, and swapping protocols in a single setup.

Fig. 1
figure 1

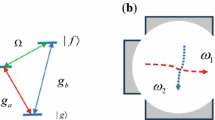
(Color online) a Sketch of experimental setup that realizes the two-node repeater scheme. In this setup, atoms in both repeater nodes are synchronously conveyed with the help of vertical optical lattices starting from the MOTs (oval regions) toward the resonators \(C_3\) (\(C_6\)). In the upper region (framed by a dashed rectangle), the atomic pairs become (one by one) entangled providing the entanglement resources for the next framed region, where the entanglement purification takes place. A successful purification round leads to an increase in fidelity associated with a stationary atomic pair, while the other pairs get projected once they leave the cavities \(C_2\) (\(C_5\)). In the final (lower) framed region, the atoms (associated with the purified atomic pair) enter the cavities \(C_3\) (\(C_6\)), where they get swapped with atoms (associated with other two purified atomic pairs) leading to a triple distance enlargement of shared entanglement. b The coherent state discrimination (CSD) setup. The coherent states \(| \pm \sqrt{\eta } \alpha \rangle\) encapsulated in Eq. (7) are guided into the upper input port of the beam splitter, while the ancilla coherent state \(| \dot{\iota }\,\sqrt{\eta } \rangle \alpha\) into the lower input port. c Structure of a three-level atom in the \(\varLambda\)-configuration subjected to the cavity and laser fields. See text for description

Full size image

In this setup, each repeater node encapsulates single-mode cavities \(C_1\), \(C_2\), and \(C_3\) (\(C_4\), \(C_5\), and \(C_6\)), single atoms conveyed along the setup with the help of two vertical optical lattices, two sources of weak coherent state pulses \(P_2\) and \(P_3\) (\(P_4\) and \(P_5\)), detectors \(D_3\) and \(D_4\) (\(D_5\) and \(D_6\)) connected to the neighboring node via a classical communication channel, and a magneto-optical trap (MOT) that provides atomic chains to be conveyed. The alignment of vertical lattices is such that the conveyed atoms cross cavities at their antinodes ensuring, therefore, a strong atom–cavity coupling regime. In addition, node B includes a source of weak coherent state pulses \(P_1\), while node C includes a coherent state discrimination (CSD) setup displayed in Fig. 1b. Finally, each repeater node encapsulates two optical lattices denoted as S and V (conveyors), where the atoms inserted into the V-conveyor are transported with a constant velocity through all three cavities, while the atoms in the S-conveyor can be slowed down or accelerated by demand.

For convenience, our setup is divided into three (framed by dashed rectangles) parts corresponding to three building blocks of a quantum repeater as mentioned in the introduction. Below, we clarify each part of our setup and explain all the manipulations and elements.

2.1 Entanglement distribution

In this part of setup, atoms 1 and 2 are extracted from the MOTs of each repeater node and inserted into the S-conveyors. Both atoms are initialized in the ground state \(| 0 \rangle\) and arrive simultaneously in the cavities \(C_1\) and \(C_4\). Each atom encodes a qubit by means of a three-level atom in the \(\varLambda\) configuration as displayed in Fig. 1c. In order to protect this qubit against the decoherence, the (qubit) states \(| 0 \rangle\) and \(| 1 \rangle\) are chosen as the stable ground and long-living metastable atomic states or as the two hyperfine levels of the ground state.

Once conveyed into the cavity \(C_1\) (\(C_4\)), atom 1 (2) couples simultaneously to the photon field of cavity and two continuous laser beams as displayed in Fig. 1c. The evolution of the coupled atom–cavity–laser system in the node B is governed by the Hamiltonian

$$\begin{aligned} H_\mathrm{R} = \frac{\hbar \, J_2}{2} \, \sigma ^X a^\dagger a, \end{aligned}$$
(1)

where \(\sigma ^X\) is the respective Pauli operator in the computational basis \(\{| 0 \rangle , | 1 \rangle \}\), while \(J_2\) is the effective coupling (see “Appendix,” where we show that the above Hamiltonian is produced deterministically in our setup). The evolution governed by \(H_\mathrm{R}\) reads

$$\begin{aligned} U_\mathrm{R}(\theta ) = \hbox {e}^{\dot{\iota }\,\theta \, \sigma ^X a^\dagger a}, \end{aligned}$$
(2)

where \(\theta = - J_2 \, t / 2\). This evolution implies a phase shift of the cavity field by the angle \(\theta\) or \((- \, \theta )\) conditioned upon the atomic state, where \(\theta\) is proportional to the atom–cavity–laser evolution time that, in turn, is inversely proportional to the velocity of conveyed atom.

In contrast to node B, the evolution of the coupled atom–cavity–laser system in the node C is governed by a sequence of two evolutions. While the second evolution is governed by the Hamiltonian (1), the first evolution is governed by the Hamiltonian

$$\begin{aligned} H_\mathrm{D} = \frac{\hbar \, J_1}{2} \left( a + a^\dagger \right) \sigma ^X , \end{aligned}$$
(3)

where \(J_1\) is the atom–field coupling (see “Appendix,” where we show that the above Hamiltonian is produced deterministically in our setup). The evolution governed by \(H_\mathrm{D}\) reads

$$\begin{aligned} U_\mathrm{D}(\beta ) = \hbox {e}^{\left( \beta \, a^\dag - \beta ^* a \right) \, \sigma ^X} = D \left( \beta \, \sigma ^X \right) , \end{aligned}$$
(4)

where \(\beta = - \dot{\iota }\,J_1 \, t / 2\). This evolution implies a displacement of the cavity field mode by the amount \(\beta\) conditioned upon the atomic state, where \(\beta\) is proportional to the atom–cavity–laser evolution time that, in turn, is inversely proportional to the velocity of conveyed atom. We remark that both Hamiltonians imply that the (fast-decaying) excited state \(| e \rangle\) remains almost unpopulated during the respective evolutions.

First, a pulse of a weak coherent light produced by the source \(P_1\) and characterized by a real amplitude \(\alpha\) interacts with the atom–cavity system in node B, where the cavity is prepared in the vacuum state. The evolution (2) leads to the atom–light entangled state

$$\begin{aligned} U_\mathrm{R} (\theta ) | \alpha \rangle | 0_1 \rangle = \frac{1}{\sqrt{2}} \left( | \hbox {e}^{\dot{\iota }\,\theta } \alpha \rangle | +_1 \rangle + | \hbox {e}^{-\dot{\iota }\,\theta } \alpha \rangle | -_1 \rangle \right) , \end{aligned}$$
(5)

where \(| + \rangle = \left( | 0 \rangle + | 1 \rangle \right) / \sqrt{2}\) and \(| - \rangle = \left( | 0 \rangle - | 1 \rangle \right) / \sqrt{2}\). The resulting coherent state from the cavity is outputted into the transmission channel between the nodes. Since we are dealing with a high-finesse cavity and since the fast-decaying atomic state \(| e \rangle\) remains almost unpopulated during the evolution, the dominant photon loss occurs in the optical fiber connecting the cavities \(C_1\) and \(C_2\) that plays the role of a transmission channel in our setup. Since photon loss increases with the length of the fiber, to a good approximation, we describe the loss using a beam splitter model that transmits only a part of the coherent light pulse through the channel,

$$\begin{aligned} | vac \rangle _E \, | \alpha \rangle \longrightarrow | \sqrt{1 - \eta } \, \alpha \rangle _E \, | \sqrt{\eta } \, \alpha \rangle , \end{aligned}$$
(6)

where the subscript E refers to an environmental light mode responsible for the fiber relaxation. In this expression, \(\eta = \hbox {e}^{-\ell / \ell _\circ }\) describes the attenuation of the transmitted light through the fiber, where \(\ell\) is the distance between the repeater nodes, while \(\ell _\circ\) is the attenuation length that can reach almost 25 km for fused-silica fibers at telecommunication wavelengths. Below, we set \(\ell _\circ = 25\) km.

Next, the attenuated light pulse interacts with the atom–cavity system in node C, where (as in node B) the cavity is prepared in the vacuum state. By tracing over the environmental degrees of freedom (mode with the subscript E), the evolution \(U_{R} (-\pi /2)\) in node B along with the sequence of evolutions \(U_{D} (- \dot{\iota }\,\sqrt{\eta } \, \alpha )\) and \(U_{R} (-\pi /2)\) in node C followed by an unconditional displacement \(D(\alpha \, \sqrt{\eta })\) leads to the entangled state between the atoms and optical modes (see Fig. 2)

$$\begin{aligned} \rho = \frac{1 + \hbox {e}^{- 2 \, \alpha ^2 (1 - \eta )}}{2} | p \rangle \langle p | + \frac{1 - \hbox {e}^{- 2 \, \alpha ^2 (1 - \eta )}}{2} | q \rangle \langle q |, \end{aligned}$$
(7)

where

$$\begin{aligned} | p \rangle= & {} \frac{1}{\sqrt{2}} \left( | \sqrt{\eta } \, \alpha \rangle | \phi _{1,2}^- \rangle + | - \sqrt{\eta } \, \alpha \rangle | \phi _{1,2}^+ \rangle \right) ; \end{aligned}$$
(8)
$$\begin{aligned} | q \rangle= & {} \frac{1}{\sqrt{2}} \left( | \sqrt{\eta } \, \alpha \rangle | \psi _{1,2}^- \rangle - | - \sqrt{\eta } \, \alpha \rangle | \psi _{1,2}^+ \rangle \right) , \end{aligned}$$
(9)

such that \(\langle p | p \rangle = \langle q | q \rangle = 1\), while \(\langle p | q \rangle = 0\).

Fig. 2
figure 2

(Color online) For each product state of two atoms (on the basis of \(\{ | + \rangle , | - \rangle \}\)), we display the evolution of the input coherent state \(| \alpha \rangle\) due to the sequence of three operations, namely (1) controlled phase shift \(U_R(-\pi /2)\) in node B, (2) controlled displacement \(U_D(-\dot{\iota }\,\alpha )\) in node C, and (3) controlled phase shift \(U_R(-\pi /2)\) in node C. In this figure, for simplicity, we set \(\eta = 1\) (lossless case)

Full size image

The (entangled with both atoms) light pulse is guided into the balanced beam splitter displayed in Fig. 1b and that is characterized by the transmissivity and reflectivity parameters \(T = 1 / \sqrt{2}\) and \(R = \dot{\iota }\,/ \sqrt{2}\), respectively. According to this coherent state discrimination (CSD) setup, the input pulse interferes with the (ancilla) coherent state \(| \dot{\iota }\,\sqrt{\eta } \, \alpha \rangle\) sent into another input port of the beam splitter. It can be readily checked that the coherent states \(| \pm \sqrt{\eta } \, \alpha \rangle\) encapsulated in Eq. (7) and supplemented by the ancilla state are transformed due to the beam splitter as follows:

$$\begin{aligned} | \dot{\iota }\,\sqrt{\eta } \, \alpha \rangle | \sqrt{\eta } \, \alpha \rangle \rightarrow | 0 \rangle | \dot{\iota }\,\sqrt{2 \, \eta } \, \alpha \rangle , \quad | \dot{\iota }\,\sqrt{\eta } \, \alpha \rangle | - \sqrt{\eta } \, \alpha \rangle \rightarrow | - \sqrt{2 \, \eta } \, \alpha \rangle | 0 \rangle . \end{aligned}$$
(10)

On the right-hand side of above equations, each ket vector in the expression corresponds to an output port of the beam splitter. Having two detectors resolving click or no-click detection events, there are three possible detection patterns, since the pattern \(\{\)click, click\(\}\) cannot happen. Among these patterns, the pattern \(\{\)no click, no click\(\}\) is inconclusive, while the remaining two patterns \(\{\)click, no click\(\}\) and \(\{\)no click, click\(\}\) lead to the desired state discrimination.

We compute first the respective probabilities of success

$$\begin{aligned} P^{\rm dist}= & {} \,{\text {Tr}} \left( \hat{\rho } | {\text {no click}}, {\text {click}} \rangle \langle {\text {no click}}, {\text {click}} | \right) \\= & {} \,{\text {Tr}} \left( \hat{\rho } | {\text {click}}, {\text {no click}} \rangle \langle {\text {click}}, {\text {no click}} | \right) = \,\frac{1}{2} \left( 1 - \hbox {e}^{-2 \, \eta \, \alpha ^2} \right) , \end{aligned}$$
(11)

where \(\hat{\rho }\) denotes the state \(\rho \, \otimes | \dot{\iota }\,\sqrt{\eta } \, \alpha \rangle \langle \dot{\iota }\,\sqrt{\eta } \, \alpha |\) being transformed in concordance with Eq. (10). Conditioned upon above detection patterns, the density function \(\hat{\rho }\) reduces to the one of two (atom–atom) entangled states

$$\begin{aligned} \tilde{\rho }_{-,f}^{1,2} = \frac{\langle {\text {no click, click}} | \, \hat{\rho } \, | {\text {no click, click}} \rangle }{P^{\rm dist}} = f \, | \phi ^-_{1,2} \rangle \langle \phi ^-_{1,2} | + (1-f) | \psi ^-_{1,2} \rangle \langle \psi ^-_{1,2} |; \end{aligned}$$
(12)

or

$$\begin{aligned} \tilde{\rho }_{+,f}^{1,2} = \frac{\langle {\text {click, no click}} | \, \hat{\rho } \, | {\text {click, no click}} \rangle }{P^{\rm dist}} = f \, | \phi ^+_{1,2} \rangle \langle \phi ^+_{1,2} | + (1-f) | \psi ^+_{1,2} \rangle \langle \psi ^+_{1,2} |, \end{aligned}$$
(13)

where the entanglement fidelity is given by the expression

$$\begin{aligned} f = \frac{1}{2} \left( 1 + \hbox {e}^{- 2 \, \alpha ^2 (1 - \eta )} \right) . \end{aligned}$$
(14)

If the output of photon detection yields the inconclusive pattern \(\{\)no click, no click\(\}\), then the atoms 1 and 2 should be discarded and the entanglement distribution protocol repeated using the next atomic pair conveyed by means of S-conveyors along the setup in both repeater nodes.

In this section, we developed a feasible scheme for distribution of atomic entanglement that is conditioned upon two detection patterns indicated above, where the total success probability associated with these patterns is \(2 \, P^\mathrm{dist}\), while the fidelity is given by the above expression. We exploit the controlled phase shift (2) in both repeater nodes supplemented by a controlled displacement in the second node. In contrast to Ref. [14] and our previous paper [12], this combined approach greatly simplifies the tripartite entangled state of light and two atoms [compare Eq. (7) in this paper to Eqs. (14) and (4) in the above-mentioned references]. More specifically, Eq. (7) encapsulates only two optical coherent states, which differ by a minus sign and are, therefore, much easier to discriminate. This simplification, in turn, implies a rather uncomplicated discrimination setup (CSD) displayed in Fig. 1b consisting of a single beam splitter and two photon detectors to resolve click and no-click events.

We emphasize that in the above-cited references, the entangled state of light and two atoms involve three different coherent states leading to a more demanding discrimination scheme. Specifically, the discrimination scheme in Ref. [14] requires two beam splitters and three unconditional displacements together with three photon detectors capable to resolve click and no-click events. Although the respective CSD scheme in our previous paper [12] requires a single beam splitter and one unconditional displacement, a notable difficulty poses the requirement to use photon number resolving detectors. As a consequence of simplified CSD in this paper, we obtain a much higher success probability (compare Eq. (11) in this paper to \({\mathcal {N}}_{-}/4\) in Ref. [12] and to \(P^{\rm total,USD}\) and \(P^{\rm total,ent}\) in Ref. [14]) leading, in turn, to much higher repeater rates. We remark that, in contrast to the controlled phase shift used in Ref. [14], in this paper, we exploit the evolution (2) based on \(\sigma ^X\) instead of \(\sigma ^Z\) and, moreover, we avoid manipulations of atomic states associated with the produced entangled state.

Finally, we note that Eq. (14) coincides with the respective fidelity obtained in our previous paper, in which we have mentioned that this fidelity is close to one when \(\alpha ^2 (1 - \eta ) \ll 1\). Since we considered one single purification round, this restriction led us to the regime \(\alpha ^2 \le 1\) that we considered through the paper. Due to four purification rounds considered in this paper, we succeed to relax this restriction and consider \(\alpha ^2 = 1,2,3\) (see below).

2.2 Entanglement purification

Assuming that the entanglement distribution was successful, atoms 1 and 2 are conveyed into the area, in which they are subjected to the (single-qubit) Hadamard transformation. Due to this unitary transformation, the states (12) and (13) take the form

$$\begin{aligned} \rho _{-,f}^{1,2}= &\, {} f \, | \psi ^+_{1,2} \rangle \langle \psi ^+_{1,2} | + (1-f) | \psi ^-_{1,2} \rangle \langle \psi ^-_{1,2} |, \end{aligned}$$
(15)
$$\begin{aligned} \rho _{+,f}^{1,2}= &\, {} f \, | \phi ^+_{1,2} \rangle \langle \phi ^+_{1,2} | + (1-f) | \phi ^-_{1,2} \rangle \langle \phi ^-_{1,2} |. \end{aligned}$$
(16)

Once atoms 1 and 2 enter the cavities \(C_2\) and \(C_5\), their (conveyed) velocities decrease gradually until zero, such that atoms remain trapped right inside the respective cavities.

At the same time, atoms 3 and 4 are inserted from MOTs into V-conveyors of both repeater nodes and transported with a constant velocity along the setup. Similar to atoms 1 and 2, this atomic pair is entangled and subjected then to the Hadamard gate. Assuming that the second entanglement distribution was successful, atoms 3 and 4 are now described by the state \(\rho _{-,f}^{3,4}\) or \(\rho _{+,f}^{3,4}\) having the structure of Eqs. (15) or (16), respectively. Atoms 3 and 4 are conveyed along the setup until they couple (simultaneously) to cavities \(C_2\) and \(C_5\) prepared both in the vacuum state. At this point, each of these cavities shares a pair of atoms 1, 3, and 2, 4, respectively.

Inside the cavities \(C_2\) and \(C_5\), these atomic pairs evolve due to the interaction governed by the Heisenberg XX Hamiltonians

$$\begin{aligned} H^{1,3}_{XX} = \frac{\hbar \, J_3}{2} \, \sigma _1^X \sigma _3^X, \quad {\text {and}} \quad H^{2,4}_{XX} = \frac{\hbar \, J_3}{2} \, \sigma _2^X \sigma _4^X, \end{aligned}$$
(17)

over the time period \(T = \pi / (2 \, J_3)\), where \(J_3\) is the effective coupling. The resulting density functions

$$\begin{aligned} \rho _{++,f}^{1-4}= &\, {} \hbox {e}^{- \dot{\iota }\,H^{1,3}_{XX} \, T / \hbar } \hbox {e}^{- \dot{\iota }\,H^{2,4}_{XX} \, T / \hbar } \left( \rho _{+,f}^{1,2} \otimes \rho _{+,f}^{3,4} \right) \hbox {e}^{\dot{\iota }\,H^{2,4}_{XX} \, T / \hbar } \hbox {e}^{\dot{\iota }\,H^{1,3}_{XX} \, T / \hbar }; \end{aligned}$$
(18)
$$\begin{aligned} \rho _{--,f}^{1-4}= &\, {} \hbox {e}^{- \dot{\iota }\,H^{1,3}_{XX} \, T / \hbar }\hbox {e}^{- \dot{\iota }\,H^{2,4}_{XX} \, T / \hbar } \left( \rho _{+,f}^{1,2} \otimes \rho _{-,f}^{3,4} \right) \hbox {e}^{\dot{\iota }\,H^{2,4}_{XX} \, T / \hbar } \hbox {e}^{\dot{\iota }\,H^{1,3}_{XX} \, T / \hbar }; \end{aligned}$$
(19)
$$\begin{aligned} \rho _{+-,f}^{1-4}= &\, {} \hbox {e}^{- \dot{\iota }\,H^{1,3}_{XX} \, T / \hbar } \hbox {e}^{- \dot{\iota }\,H^{2,4}_{XX} \, T / \hbar } \left( \rho _{+,f}^{1,2} \otimes \rho _{-,f}^{3,4} \right) \hbox{e}^{\dot{\iota }\,H^{2,4}_{XX} \, T / \hbar } \hbox {e}^{\dot{\iota }\,H^{1,3}_{XX} \, T / \hbar }; \end{aligned}$$
(20)
$$\begin{aligned} \rho _{-+,f}^{1-4}= &\, {} \hbox {e}^{- \dot{\iota }\,H^{1,3}_{XX} \, T / \hbar } \hbox {e}^{- \dot{\iota }\,H^{2,4}_{XX} \, T / \hbar } \left( \rho _{+,f}^{1,2} \otimes \rho _{+,f}^{3,4} \right) \hbox {e}^{\dot{\iota }\,H^{2,4}_{XX} \, T / \hbar } \hbox {e}^{\dot{\iota }\,H^{1,3}_{XX} \, T / \hbar }, \end{aligned}$$
(21)

describe four-partite entangled states. We remark that the above Heisenberg XX Hamiltonian is produced deterministically in our setup by coupling atoms (simultaneously) to the same cavity mode and two laser beams in the strong driving regime (see “Appendix” of Ref. [12]).

Being further conveyed along the setup, atoms 3 and 4 decouple from cavities \(C_2\) and \(C_5\), and get projected outside in the computational basis. Purification protocol is successful if the outcome of atomic projection reads

$$\begin{aligned}&\{ 0, 1 \} \quad {\text {or}} \quad \{ 1, 0 \} \quad {\text {for}} \quad \rho _{++,f}^{1-4} \quad {\text {and}} \quad \rho _{-+,f}^{1-4}, \end{aligned}$$
(22)
$$\begin{aligned}&\{ 0, 0 \} \quad {\text {or}} \quad \{ 1, 1 \} \quad {\text {for}} \quad \rho _{--,f}^{1-4} \quad {\text {and}} \quad \rho _{+-,f}^{1-4}. \end{aligned}$$
(23)

In this case, above detection patterns lead to the reduced density functions

$$\begin{aligned} \rho _{-,F_1}^{1,2}= & {} \frac{\langle 0_3, 1_4 | \rho _{++,f}^{1-4} | 0_3, 1_4 \rangle }{P^{\rm purif}_1} = \frac{\langle 1_3, 0_4 | \rho _{++,f}^{1-4} | 1_3, 0_4 \rangle }{P^{\rm purif}_1} = \frac{\langle 0_3, 0_4 | \rho _{+-,f}^{1-4} | 0_3, 0_4 \rangle }{P^{\rm purif}_1} \\= & {} \frac{\langle 1_3, 1_4 | \rho _{+-,f}^{1-4} | 1_3, 1_4 \rangle }{P^{\rm purif}_1} = F_1 | \psi ^+_{1,2} \rangle \langle \psi ^+_{1,2} | + (1 - F_1) | \psi ^-_{1,2} \rangle \langle \psi ^-_{1,2} |; \end{aligned}$$
(24)
$$\begin{aligned} \rho _{+,F_1}^{1,2}= & {} \frac{\langle 0_3, 1_4 | \rho _{-+,f}^{1-4} | 0_3, 1_4 \rangle }{P^{\rm purif}_1} = \frac{\langle 1_3, 0_4 | \rho _{-+,f}^{1-4} | 1_3, 0_4 \rangle }{P^{\rm purif}_1} = \frac{\langle 0_3, 0_4 | \rho _{--,f}^{1-4} | 0_3, 0_4 \rangle }{P^{\rm purif}_1} \\= & {} \frac{\langle 1_3, 1_4 | \rho _{--,f}^{1-4} | 1_3, 1_4 \rangle }{P^{\rm purif}_1} = F_1 | \phi ^+_{1,2} \rangle \langle \phi ^+_{1,2} | + (1 - F_1) | \phi ^-_{1,2} \rangle \langle \phi ^-_{1,2} |, \end{aligned}$$
(25)

where the purified fidelity and the success probability take the form

$$\begin{aligned} F_1 = \frac{f^2}{1 + 2 \left( f^2 - f \right) }, \quad P^{\rm purif}_1 = \frac{1}{2} - f + f^2. \end{aligned}$$
(26)

The above purified states preserve the rank 2 form and are characterized by the fidelity (26) displayed in Fig. 3a by a dotted curve. We remark that if the outcome of atomic projection disagrees with the patterns (22) and (23), the entanglement purification is considered unsuccessful. In this case, we discard all atoms and repeat both distribution and purification protocols using fresh atomic pairs conveyed from MOTs in each repeater node.

Fig. 3
figure 3

(Color online) a Purified fidelities \(F_1, F_2\), and \(F_4\) along with the swapped fidelity \(F_{\rm S}\) as functions of the initial fidelity (14). b Success probability \(P_\mathrm{pd}\) associated with the entanglement distribution and purification as a function of elementary repeater distance \(\ell\) displayed for \(\alpha ^2 = 1\) (solid curve), \(\alpha ^2 = 2\) (dotted curve), and \(\alpha ^2 = 3\) (dashed curve)

Full size image

Assuming that the entanglement purification is successful, atoms 5 and 6 are inserted from MOTs into V-conveyors and transported with a constant velocity along the setup. Similar to atoms 3 and 4, this atomic pair gets entangled, subjected to the Hadamard gate, and conveyed further into the cavities \(C_2\) and \(C_5\), such that each of these cavities shares a pair of atoms 1, 5, and 2, 6, respectively. In these cavities, atoms evolve due to the Heisenberg XX interaction over the time period T. Being further conveyed along the setup, atoms 5 and 6 are then projected in the computational basis. As before, the entanglement purification is successful if the outcome of atomic projection coincides with (22) and (23). In this case, we get the reduced density functions

$$\begin{aligned} \rho _{-,F_2}^{1,2}=\, & {} F_2 | \psi ^+_{1,2} \rangle \langle \psi ^+_{1,2} | + (1 - F_2) | \psi ^-_{1,2} \rangle \langle \psi ^-_{1,2} |, \end{aligned}$$
(27)
$$\begin{aligned} \rho _{+,F_2}^{1,2}=\, & {} F_2 | \phi ^+_{1,2} \rangle \langle \phi ^+_{1,2} | + (1 - F_2) | \phi ^-_{1,2} \rangle \langle \phi ^-_{1,2} |, \end{aligned}$$
(28)

where the purified fidelity \(F_2\) and the success probability \(P^{\rm purif}_2\) are computed using the iterative formulas

$$\begin{aligned} F_n= & {} \frac{f \, F_{n-1}}{1 - F_{n-1} + f \left( 2 \, F_{n-1} - 1 \right) }, \end{aligned}$$
(29)
$$\begin{aligned} P^{\rm purif}_n= & {} \frac{1}{2} \left( 1 - F_{n-1} + f \left( 2 \, F_{n-1} - 1 \right) \right) , \end{aligned}$$
(30)

where \(F_0 \equiv f\), while \(F_2\) is displayed in Fig. 3a by a dashed curve.

Assuming that the third purification (using atoms 7, 8) is successful, atoms 9 and 10 are conveyed along the setup and coupled then to the cavities \(C_2\), \(C_5\) in order to realize the last (fourth) purification round. In contrast to the sequence we described above, atoms 9 and 10 are not projected after they leave the respective cavities. Instead, atoms 1 and 2 are projected in the computational basis using the (nondestructive) projective measurements directly inside the cavities (see Sect. 2.4 below). In contrast to the patterns (22) and (23), the entanglement purification is successful if the outcome of atomic projection (atoms 1 and 2) reads

$$\begin{aligned}&\{ 0, 1 \} \quad {\text {or}} \quad \{ 1, 0 \} \quad {\text {for}} \quad \rho _{++,F_3}^{1,2,9,10} \quad {\text {and}} \quad \rho _{+-,F_3}^{1,2,9,10}, \end{aligned}$$
(31)
$$\begin{aligned}&\{ 0, 0 \} \quad {\text {or}} \quad \{ 1, 1 \} \quad {\text {for}} \quad \rho _{--,F_3}^{1,2,9,10} \quad {\text {and}} \quad \rho _{-+,F_3}^{1,2,9,10}. \end{aligned}$$
(32)

With the success probability \(P^\mathrm{purif}_4\), above patterns yield the reduced density functions

$$\begin{aligned} \rho _{-,F_4}^{9,10}= & \,{} F_4 | \psi ^+_{9,10} \rangle \langle \psi ^+_{9,10} | + (1 - F_4) | \psi ^-_{9,10} \rangle \langle \psi ^-_{9,10} |; \end{aligned}$$
(33)
$$\begin{aligned} \rho _{+,F_4}^{9,10}= &\, {} F_4 | \phi ^+_{9,10} \rangle \langle \phi ^+_{9,10} | + (1 - F_4) | \phi ^-_{9,10} \rangle \langle \phi ^-_{9,10} |, \end{aligned}$$
(34)

completely characterized by the fidelity \(F_4\) displayed in Fig. 3a by a dot-dashed curve. It is readily seen that we obtain an almost-unit-purified fidelity for \(f \ge 0.75\) using four (successful) purification iterations.

In this section, we developed a high-fidelity scheme for entanglement purification that leads (iteratively) to a gradual growth of the purified fidelity, and where the total probability of success

$$\begin{aligned} P_{{{\text{pd}}}} & = 2^{4} P_{1}^{{{\text{purif}}}} P_{2}^{{{\text{purif}}}} P_{3}^{{{\text{purif}}}} P_{4}^{{{\text{purif}}}} (2P^{{{\text{dist}}}} )^{5} \\ & = \left( {15f^{2} - 180f^{3} + 1130f^{4} - 4700{\mkern 1mu} f^{5} + 14,088f^{6} - 31,584f^{7} } \right. \\ & \quad + 53,776f^{8} - 69,600f^{9} + 67,648f^{{10}} - 48,000f^{{11}} + 23552f^{{12}} \\ & \quad - \left. {7168f^{{13}} + 1024f^{{14}} } \right)\left( {1 - {\text{e}}^{{ - 2\eta \alpha ^{2} }} } \right)^{5} , \\ \end{aligned}$$
(35)

is associated with four purification rounds which, in turn, encapsulates success probabilities of five entanglement distributions. By inserting Eq. (14) in the above expression, we display \(P_\mathrm{pd}\) in Fig. 3b as a function of \(\ell\) (encoded by \(\eta\)) for \(\alpha ^2 = 1\), 2, and 3. As expected, the total success probability decreases with the growth of the distance between the nodes. We emphasize that the sequence of steps utilized in this section can be related to the entanglement purification scheme C (so-called entanglement pumping) suggested in Ref. [15], in which the fidelity of a single low-fidelity entangled pair becomes gradually increased at the cost of all other low-fidelity entangled pairs available. Indeed, in our approach we also produced first the entangled pair (15) or (16) described by the fidelity \(F_0\) that became gradually increased up to \(F_4\) at the cost of entangled pairs associated with the atoms \(3, \ldots , 10\) and each described by the fidelity \(F_0\) as well.

In each node of proposed purification protocol, we exploit one evolution governed by the Heisenberg XX Hamiltonian (17) followed by a projection of a single atom in the computation basis. In contrast to our previous paper [12], in which we have utilized (1) a four-partite entangled state [see Eq. (8) in the above reference] generated in a probabilistic fashion through the cat state discrimination, (2) evolution governed by the Heisenberg XY Hamiltonian, and (3) projection of two atoms in each repeater node, the proposed approach greatly simplifies our protocol since we avoid any ancilla state and we postselect only the atomic state detection events associated with two atoms (and not four as in the previous paper). Due to these improvements, in this paper, we succeed to increase significantly the success probability \(P_\mathrm{pd}\) associated with the entire purification protocol [compare Eq. (35) with Eq. (26) in our previous paper].

We emphasize that a high purified fidelity obtained in this paper is the consequence of multiple purification rounds realized as an inherent part of our repeater scheme in this paper. Although we considered just four such rounds, our setup is capable of performing an arbitrary number of rounds at the cost of reduced success probability. The setup displayed in Fig. 1a of our previous paper, in contrast, is by design limited to a single purification round, such that an extension to four such rounds would require three additional cavities and six additional atoms in each repeater node along with three additional communication channels. Using this extended setup in the framework of approach proposed in our previous paper, we have checked that the purified fidelity obtained using four successive purification rounds is slightly smaller as the fidelity \(F_4\) obtained in this paper. However, since one successful purification round is conditioned upon the generation of the ancilla state (8) and atomic postselection (15), we obtained a much lower probability of success if compared with \(P_{{\rm pd}}\) derived above. This result leads, in turn, to a dramatically low success probability associated with the entire scheme and almost vanishing repeater rates.

2.3 Entanglement swapping

Assuming that the entanglement purification was successful, the (high-fidelity) entangled atoms 9 and 10 are conveyed along the setup to the swapping region displayed in the bottom rectangle of Fig. 1a. Here, atoms couple the cavities \(C_3\) and \(C_6\), both prepared in vacuum state. The conveyed atoms together with the trapped atoms form two atomic pairs 9, 12, and 10, 13. We recall that atoms 12 and 13 are entangled with atoms 11 and 14, respectively, where each pair is described by the mixed states \(\rho ^{11,12}_{\pm ,F_4}\) and \(\rho ^{13,14}_{\pm ,F_4}\) having the structure of Eqs. (33) and (34).

According to the entanglement swapping protocol we proposed in Ref. [12], each atomic pair evolves in cavities \(C_3\) and \(C_6\) due to the Heisenberg XX interaction utilized in the previous section. We remark that being applied on the separate states of an atomic pair (in the computational basis) over the time period \(T = \pi / (2 \, J_2)\), this evolution implies

$$\begin{aligned} | 1, 1 \rangle\longrightarrow & {} \frac{- \dot{\iota }\,}{\sqrt{2}} \left( | 0, 0 \rangle + \dot{\iota }\,| 1, 1 \rangle \right) ; \end{aligned}$$
(36)
$$\begin{aligned} | 0, 0 \rangle\longrightarrow & {} \frac{1}{\sqrt{2}} \left( | 0, 0 \rangle - \dot{\iota }\,| 1, 1 \rangle \right) ; \end{aligned}$$
(37)
$$\begin{aligned} | 1, 0 \rangle\longrightarrow & {} \frac{- \dot{\iota }\,}{\sqrt{2}} \left( | 0, 1 \rangle + \dot{\iota }\,| 1, 0 \rangle \right) ; \end{aligned}$$
(38)
$$\begin{aligned} | 0, 1 \rangle\longrightarrow & {} \frac{1}{\sqrt{2}} \left( | 0, 1 \rangle - \dot{\iota }\,| 1, 0 \rangle \right) , \quad \end{aligned}$$
(39)

such that the resulting states form the modified Bell basis

$$\begin{aligned} | {\mathbf {m}}_{a,b}^k \rangle = \hbox {e}^{- \frac{\dot{\iota }\,}{\hbar } H^{a,b}_{XX} \, T} \{ | 1_a, 1_b \rangle , | 0_a, 0_b \rangle , | 1_a, 0_b \rangle , | 0_a, 1_b \rangle \}, \end{aligned}$$
(40)

where \(k = 1,2,3,4\).

This observation suggests a deterministic realization of entanglement swapping using just two consecutive steps (1) atomic pairs 9, 12, and 10, 13 are subjected to the evolutions \(\hbox {e}^{- \frac{\dot{\iota }\,}{\hbar } H^{9,12}_{XX} \, T}\) and \(\hbox {e}^{- \frac{\dot{\iota }\,}{\hbar } H^{10,13}_{XX} \, T}\), respectively, that is followed by (2) projection of each atomic pair in the computational basis. Obviously, these two steps are equivalent with the atomic projection in the modified Bell basis (40), where the swapped state is given by the expression

$$\begin{aligned}&\frac{1}{{\mathcal {N}}} \left\langle {\mathbf {m}}_{9,12}^i, {\mathbf {m}}_{10,13}^j | \left( \rho ^{9,10}_{+,F_4} \otimes \rho ^{11,12}_{+,F_4} \otimes \rho ^{13,14}_{+,F_4} \right) | {\mathbf {m}}_{9,12}^i, {\mathbf {m}}_{10,13}^j \right\rangle \\&\quad = F_{\rm S} \, | \varphi ^{i,j}_{11,14} \rangle \langle \varphi ^{i,j}_{11,14} | + (1 - F_{\rm S}) | \chi ^{i,j}_{11,14} \rangle \langle \chi ^{i,j}_{11,14} |, \end{aligned}$$
(41)

taken here, for simplicity, for a particular case when all three entangled pairs have the structure of Eq. (34). In this expression, \({\mathcal {N}}\) is the normalization factor, the states \(\varphi ^{i,j}\) and \(\chi ^{i,j}\) are displayed in Table 1, while the swapped fidelity takes the form

$$\begin{aligned} F_\mathrm{S} = F_4 (3 - 6 \, F_4 + 4 \, F^2_4). \end{aligned}$$
(42)

As expected, the swapped density function (41) is diagonal in the standard Bell basis and is completely characterized by \(F_{\rm S}\) displayed in Fig. 3a by a solid curve.

In this section, we employed the swapping protocol introduced in our previous paper. This protocol is deterministic and exploits the same evolution as utilized in the previous section along with atomic projections. In contrast to the entanglement distribution and purification protocols, however, the swapping protocol is entirely characterized by the success probability \(P_\mathrm{sw}\) that is affected mainly by the efficiency of atomic projective measurements and can be close to one (see below). We conclude, therefore, that the total probability of success associated with the entanglement distribution, purification, and two swappings is given by the expression

$$\begin{aligned} P_\mathrm{total} = P^2_\mathrm{sw} \, P_\mathrm{pd} . \end{aligned}$$
(43)
Table 1 Pairs of Bell states identified with \(\varphi ^{i,j}\) and \(\chi ^{i,j}\) for given i (column) and j (row)
Full size table

2.4 Remarks on the implementation of our scheme

For simplicity, in the setup displayed in Fig. 1a, we considered just two repeater nodes (B and C), where the atomic pairs 11, 12 and 13, 14 were initially entangled and given both by Eq. (24). We are ready now to introduce the experimental setup that includes explicitly nodes A, B, C, and D. This setup is displayed in Fig. 4 and, in contrast to Fig. 1a, includes entanglement distribution and purification protocols associated with the (initially disentangled) atomic pairs 11, 12 and 13, 14. Simultaneously with the atomic pair 9, 10, these pairs are conveyed along the setup (but in the opposite direction) and follow the same sequence of interactions and projective measurements.

Fig. 4
figure 4

(Color online) Sketch of experimental setup that realizes the four-node repeater scheme

Full size image

We recall that all three building blocks of our repeater require projective measurements of atoms which are located inside and outside the cavity. The method of atomic nondestructive measurements demonstrated in Refs. [16, 17] enables projective measurements of atoms coupled (strongly) to a cavity field that fits perfectly in our experimental setup. The physical mechanism behind these measurements exploits the suppression of cavity transmission due to the strong atom–cavity coupling. Recall that each atom in our scheme is a three-level atom in the \(\varLambda\)-configuration (see Fig. 1c), where only the states \(| 0 \rangle\) and \(| e \rangle\) are coupled to the cavity field. If one such atom couples the cavity and is prepared in the \(| 0 \rangle\) state, such that the cavity resonance is sufficiently detuned from the atomic \(| 0 \rangle \leftrightarrow | e \rangle\) transition frequency, then the cavity transmission drops according to the atom–cavity detuning and atom–cavity coupling. On the other hand, the cavity transmission remains unaffected if the atom was prepared in the state \(| 1 \rangle\).

Once sufficiently many readouts of cavity transmission are recorded, this technique enables us to determine the state of a single atom with a high efficiency [16]. Since the atom–cavity coupling increases proportionally with the number of loaded (into cavity) atoms, the same technique enables us to distinguish the following three separate states of two atoms (1) \(| 0, 0 \rangle\), (2) \(| 0, 1 \rangle\) or \(| 1, 0 \rangle\), and (3) \(| 1, 1 \rangle\) (see [17]). We remark, however, that this approach cannot distinguish between the states \(| 0, 1 \rangle\) and \(| 1, 0 \rangle\) leading to an incompleteness of information about the swapped state (41) (see Table 1). In order to avoid this problem, one of the atoms in \(C_3\) (\(C_6\)) has to leave the cavity right after the inconclusive event occurs and be again projected outside the cavity.

The atomic projection outside the cavity is realized using a laser beam and a CCD camera located inside the oval regions displayed in Fig. 1a below the cavities \(C_2\) and \(C_5\). While the laser beam removes atoms in a given quantum state from the conveyor without affecting atoms in the other state (so-called push-out technique [18]), the CCD camera is used to detect the presence of remaining atoms via fluorescence imaging and determine, therefore, the state of each atom in question. In contrast to the previously discussed atomic projection, this technique is destructive, and thus, the projected atoms cannot be further utilized.

3 Summary and outlook

In the previous section, we have introduced our repeater scheme encapsulating three segments (four nodes) that corresponds to the overall distance of \(3 \, \ell\). The extension of the sketch shown in Fig. 4 to an arbitrary number N of segments is straightforward. With no loss of generality, we consider odd values of N corresponding to \(N+1\) repeater nodes or \(N-1\) swappings. Setting \(\alpha ^2 = 1, 2\), and 3, we display in Fig. 5a–c the overall distance as a function of N taken for the final fidelities \(F_\mathrm{final} = 0.8, 0.85, 0.9, 0.95\), which are identified with the fidelity obtained after \(N-1\) swapping operations. We infer from this figure that smaller values of \(\alpha ^2\) lead to larger overall distances, while the segment length \(\ell\) decreases with the increasing of N. We remark that this drawback is originated to the lack of repurification in our scheme that is supposed to act after each (or a few) swapping operation(s). We also emphasize that the obtained final fidelity is higher by about one order of magnitude as the respective fidelity obtained in our previous paper (compare, for instance, Fig. 5a to Fig. 5a in Ref. [12]).

Fig. 5
figure 5

(Color online) For the average photon numbers \(\alpha ^2 = 1\) (a), 2 (b), and 3 (c), we display the overall repeater distance \(L = N \, \ell\) as a function of N (number of segments) plotted for the final fidelities \(F_\mathrm{final} = 0.95\) (solid curve), 0.9 (dotted curve), 0.85 (dashed curve), and 0.8 (dot-dashed curve). For the average photon numbers \(\alpha ^2 = 1\) (d), 2 (e), and 3 (f), we display rescaled repeater rates (46) as functions of \(\ell\) (elementary length) plotted for the final fidelities \(F_\mathrm{final} = 0.95\) (solid curve), 0.9 (dotted curve), 0.85 (dashed curve), and 0.8 (dot-dashed curve). We remark using plots (d–f) along with plots (a–c), one can easily calculate rescaled repeater rates as functions of entire distance L

Full size image

Besides final fidelities, we calculate the repeater rates which, together with the success probabilities displayed in Fig. 3b, provide the main set of characteristics associated with a quantum repeater. Since the atomic (fast-decaying) excited states remain almost unpopulated and each atomic qubit is encoded by other two (long-living) states, we assume that the atomic coherence times exceed the overall time required to complete entanglement distribution, purification, and swapping in all repeater nodes. This assumption corresponds to a repeater with an ideal memory and implies that the only source of decoherence is the photon loss in the transmission channel.

We compute repeater rates (in units of pairs per second) using the following expression [19]

$$\begin{aligned} R = \frac{1}{T_{\circ} \, Z_N (P_\mathrm{total})}, \end{aligned}$$
(44)

where \(T_{\circ}\) is the total time required to distribute and purify an entangled pair over one repeater segment followed by two swappings, N is the number of segments, while

$$\begin{aligned} Z_N (P) = \sum _{j=1}^{N} \left( \begin{array}{c} N \\ j \end{array} \right) \frac{(-1)^{j+1}}{1 - (1 - P)^j}. \end{aligned}$$
(45)

According to the experimental setup displayed in Fig. 1a, the total time is composed of (1) interaction times required for entanglement distribution, purification, and swapping protocols, (2) time required for both destructive and nondestructive atomic projections, and (3) time required to communicate between the repeater nodes by means of coherent state light and classical communication. In contrast to the cases (1) and (2), the time (3) is readily computed using the relation \(14 \, \ell / \upsilon\), where \(\upsilon = 2 \times 10^8\) m/s is the velocity of light in the optical fiber. Without loss of generality, therefore, we express the total time as \(T_\circ = S \, 14 \, \ell / \upsilon\), where \(S > 1\) is a real number encoding the times (1) and (3) in terms of (3). By inserting this expression into Eq. (44), we consider the rescaled repeater rate

$$\begin{aligned} R \, S = \frac{\upsilon }{14 \, \ell \, Z_N (P_\mathrm{total})} \equiv \widetilde{R}. \end{aligned}$$
(46)

This rescaled repeater rate is determined by the triplet \(\{ \alpha , \ell , N \}\), which we extract from Fig. 5 for a given value of \(F_{\rm final}\). Setting \(\alpha ^2 = 1, 2\), and 3, we display in Fig. 5d–f the rescaled repeater rates as functions of \(\ell\) taken for the final fidelities \(F_\mathrm{final} = 0.8, 0.85, 0.9\), and 0.95. We infer from this figure that smaller values of \(\alpha ^2\) lead to smaller repeater rates \(\widetilde{R}\). We remark that this behavior was expected since small \(\alpha ^2\) imply a larger total distance L, which, in turn, leads to a reduction in the amount of produced entangled pairs (per second).

In this paper, a complete quantum repeater scheme that encapsulates entanglement distribution, purification, and swapping protocols was proposed. In contrast to conventional repeater schemes, we completely avoid two-qubit logical gates by exploiting cavity QED evolution along atomic projective measurements. Our repeater scheme has a conveyor-like structure, in which single atoms are inserted into one of two optical lattices and conveyed along the entire repeater node. At the same time, another chain of atoms is conveyed along the neighboring repeater node in a synchronous fashion. These two nodes form together a repeater segment, while the entire set of segments form the quantum repeater itself. In Figs. 1a and 4, the sketch of experimental setup was displayed and a detailed description of all necessary steps and manipulations was provided. A comprehensive analysis of success probabilities and final fidelities obtained after multiple purification and swapping operations was given. In addition, the comparison with regard to the results obtained in our previous paper has been provided.

In particular, our entanglement distribution here is based on a simpler coherent state discrimination measurement distinguishing only two coherent states with opposite signs, which can be easily and optimally done by linear optics and on–off detections. Following recent developments in cavity QED, finally, we briefly pointed to and discussed a few practical issues related to the implementation of our repeater scheme. We stress that although the physical resources utilized in our repeater are experimentally feasible, its explicit realization for a long-distance quantum communication still poses a serious challenge.