1 Introduction

The conventional correlation function of a partially coherent beam satisfies Gaussian distribution and usually is called Gaussian-correlated Schell-model function. Before 2007, only few papers were devoted to partially coherent beams with nonconventional correlations, such as J 0-correlated Schell-model source [1–3] and vortex-carrying partially coherent sources [4, 5]. Since Gori and collaborators first discussed the sufficient condition for devising the genuine correlation function of a partially coherent beam [6, 7], more and more attention is being paid to partially coherent beam with nonconventional correlation function [8–29]. Many extraordinary or unique properties of a partially coherent beam with nonconventional correlation function have been found, e.g., self-focusing and lateral shift of the intensity maximum on propagation [8–10], far-field flat-topped [11–13] or ring-shaped intensity profile formation [14–16], far-field radially polarization formation [17], self-splitting properties on propagation [18–20], and lattice-like intensity patterns formation on propagation [21, 22]. Different methods have been developed to generate a partially coherent beam with nonconventional correlation function [15, 25]. It was shown in [9, 10, 20, 26–28] that a partially coherent beam with nonconventional correlation function has an advantage over a partially coherent beam with conventional correlation function for reducing turbulence-induced degradation or scintillation and may be useful in free-space optical communication. A review on generation and propagation of partially coherent beams with nonconventional correlation functions is given in [29].

On the other hand, beam splitting is useful in many applications, such as optical imaging [30], particle trapping [31], atom guidance [32], and electron guidance [33]. In order to split one beam into two or more beams, one usually make use of anisotropic optical components or structures, such as beam splitter [34], phase gratings [35], photonic crystal [36], anisotropic metamaterial slab [37], and metallic nano-optic lens [38]. Recently, it was shown that some partially coherent beams with nonconventional correlation functions, such as rectangular cosine-Gaussian-correlated Schell-model (CGCSM) beam [18] and Hermite–Gaussian-correlated Schell-model (HGCSM) beam [19, 20], display self-splitting properties on propagation in free space, which may be useful in some applications, such as attacking multiple targets, trapping multiple particles, and guiding atoms, while the initial single beam spot of a HGCSM beam (or a rectangular CGCSM beam) only evolves into two or four beam spots on propagation in free space depending on its initial beam parameters [18–20].

As a typical kind of partially coherent beam with nonconventional correlation function, circular Laguerre–Gaussian-correlated Schell-model (LGCSM) beam displays circular ring-shaped (i.e., dark hollow) beam profile in the far-field although it has a Gaussian beam profile in the source plane [14]. Experimental generation of a circular LGCSM beam was first reported in [15]. It is was shown both theoretically and experimentally that one can generate a controllable optical cage by focusing a circular LGCSM beam near the focal plane, which may be useful for trapping particles or atoms [39]. Elliptical LGCSM beam was introduced and generated recently [16], and such beam displays elliptical dark hollow beam profile in the far-field. To our knowledge, no results have been reported up until now on a rectangular LGCSM beam (i.e., LGCSM beam whose degree of coherence is of rectangular symmetry). In this paper, our aim is to introduce the model for a rectangular LGCSM beam. The propagation properties of a rectangular LGCSM beam are totally different from that of a circular or elliptical LGCSM beam, e.g., it exhibits self-splitting properties on propagation in free space. The initial single beam spot of a rectangular LGCSM beam evolves into (m + 1) × (n + 1) beam spots on propagation with m and n being the beam orders; thus, the self-splitting properties of a rectangular LGCSM beam are more general than that of a HGCSM beam (or a rectangular CGCSM beam). Experimental generation of a rectangular LGCSM beam is also reported.

2 Rectangular Laguerre–Gaussian-correlated Schell-model beam: theoretical model

In the space–time domain, the statistical properties of a partially coherent beam are characterized by the mutual coherence function (MCF), which is defined as a two-point correlation function [6]

$$\Gamma \left( {{\mathbf{r}}_{1} ,{\mathbf{r}}_{2} } \right) = \left\langle {E^{ * } \left( {{\mathbf{r}}_{1} } \right)E\left( {{\mathbf{r}}_{2} } \right)} \right\rangle ,$$
(1)

where E denotes the field fluctuating in a direction perpendicular to the z-axis and the angular brackets denote an ensemble average.

The MCF of a partially coherent beam can be expressed in the following general form [40]

$$\varGamma \left( {{\mathbf{r}}_{1} ,{\mathbf{r}}_{2} } \right) = \sqrt {I\left( {{\mathbf{r}}_{1} } \right)I\left( {{\mathbf{r}}_{2} } \right)} \mu \left( {{\mathbf{r}}_{2} - {\mathbf{r}}_{1} } \right),$$
(2)

where \({\mathbf{r}}_{1} \equiv \left( {x_{1} ,y_{1} } \right)\) and \({\mathbf{r}}_{2} \equiv \left( {x_{2} ,y_{2} } \right)\) are two arbitrary position vectors transverse to the direction of propagation, I(r) is the intensity at point r, and \(\mu \left( {{\mathbf{r}}_{2} - {\mathbf{r}}_{1} } \right)\) is the degree of coherence (DOC). For a conventional Gaussian Schell-model beam (i.e., Gaussian-correlated Schell-model beam), both the intensity and the DOC satisfy Gaussian distribution [40]. For a circular or elliptical LGCSM beam, its intensity in the source plane satisfies Gaussian distribution, while its DOC satisfies circular or elliptical Laguerre–Gaussian distribution [14–16].

Now we introduce a new kind of partially coherent beam with nonconventional correlation function named rectangular LGCSM beam as a natural extension of a circular or elliptical LGCSM beam. The intensity and DOC of a rectangular LGCSM beam in the source plane are defined as

$$I\left( {\mathbf{r}} \right) = \exp \left( { - {\mathbf{r}}^{2} /2\sigma_{0}^{2} } \right),$$
(3)
$$\mu \left( {{\mathbf{r}}_{2} - {\mathbf{r}}_{1} } \right) = L_{m} \left[ {\frac{{\left( {x_{2} - x_{1} } \right)^{2} }}{{\delta_{0x}^{2} }}} \right]L_{n} \left[ {\frac{{\left( {y_{2} - y_{1} } \right)^{2} }}{{\delta_{0y}^{2} }}} \right]\exp \left[ { - \frac{{\left( {x_{2} - x_{1} } \right)^{2} }}{{2\delta_{0x}^{2} }} - \frac{{\left( {y_{2} - y_{1} } \right)^{2} }}{{2\delta_{0y}^{2} }}} \right],$$
(4)

where σ 0 denotes the transverse beam width, L i denotes the Laguerre polynomial of order i, and δ 0x and δ 0y denote the transverse coherence widths along the x and y directions, respectively.

To be a mathematically genuine or physically realizable correlation function, the MCF of a partially coherent beam should satisfy the condition of nonnegative definiteness and can be written in the following form [6]

$$\varGamma \left( {{\mathbf{r}}_{1} ,{\mathbf{r}}_{2} } \right) = \int {I\left( {\mathbf{v}} \right)} H^{ * } \left( {{\mathbf{r}}_{1} ,{\mathbf{v}}} \right)H\left( {{\mathbf{r}}_{2} ,{\mathbf{v}}} \right)d^{2} {\mathbf{v}},$$
(5)

where H is an arbitrary kernel and I is a nonnegative function.

Equation (5) can be expressed in the following alternative form [15]

$$\varGamma \left( {{\mathbf{r}}_{1} ,{\mathbf{r}}_{2} } \right) = \iint {\varGamma_{i} \left( {{\mathbf{v}}_{1} ,{\mathbf{v}}_{2} } \right)}H^{ * } \left( {{\mathbf{r}}_{1} ,{\mathbf{v}}_{1} } \right)H\left( {{\mathbf{r}}_{2} ,{\mathbf{v}}_{2} } \right)d^{2} {\mathbf{v}}_{1} d^{2} {\mathbf{v}}_{2} ,$$
(6)

where

$$\varGamma_{i} \left( {{\mathbf{v}}_{1} ,{\mathbf{v}}_{2} } \right) = \sqrt {I\left( {{\mathbf{v}}_{1} } \right)I\left( {{\mathbf{v}}_{2} } \right)} \delta \left( {{\mathbf{v}}_{1} - {\mathbf{v}}_{2} } \right).$$
(7)

Here, δ denotes the Dirac delta function. It is seen from Eqs. (6) and (7) that a partially coherent beam with required correlation function can be generated from an incoherent source with MCF \(\varGamma_{i} \left( {{\mathbf{v}}_{1} ,{\mathbf{v}}_{2} } \right)\) through propagation. Here, I and H denote the intensity of the incoherent source and the response function of the optical path, respectively.

Similar to Ref. [15], we set H in the following form

$$H\left( {{\mathbf{r}},{\mathbf{v}}} \right) = - \frac{i}{\lambda f}T\left( {\mathbf{r}} \right)\exp \left[ {\frac{i\pi }{\lambda f}\left( {{\mathbf{v}}^{2} - 2{\mathbf{r}} \cdot {\mathbf{v}}} \right)} \right],$$
(8)

with

$$T\left( {\mathbf{r}} \right) = \exp \left( { - {\mathbf{r}}^{2} /4\sigma_{0}^{2} } \right).$$
(9)

Here, H denotes the response function of the optical path which consists of free space of distance f, a thin lens with focal length f, and a Gaussian amplitude filter with transmission function given by Eq. (9).

Applying Eqs. (2)–(4) and (6)–(9), we find to generate a rectangular LGCSM beam from an incoherent source through propagation, and the intensity of the incoherent source should satisfy the following distribution

$$I\left( {\mathbf{v}} \right) = \left[ {H_{m} \left( {\frac{{\sqrt 2 v_{x} }}{{\omega_{0x} }}} \right)} \right]^{2} \left[ {H_{n} \left( {\frac{{\sqrt 2 v_{y} }}{{\omega_{0y} }}} \right)} \right]^{2} \exp \left[ { - \frac{{2v_{x}^{2} }}{{\omega_{0x}^{2} }} - \frac{{2v_{y}^{2} }}{{\omega_{0y}^{2} }}} \right],$$
(10)

where \(\omega_{0x} = \lambda f/\left( {\pi \delta_{0x} } \right)\) and \(\omega_{0y} = \lambda f/\left( {\pi \delta_{0y} } \right)\) are the beam widths along the x and y directions, respectively, and H i denotes Hermite polynomial of order i. Since I(v) is a nonnegative function, the correlation function for a rectangular LGCSM beam is indeed a mathematically genuine function and can be realized in experiment.

Under the condition of m = n = 0, the rectangular LGCSM beam reduces to the elliptical Gaussian-correlated Schell-model beam [15]. Under the condition of m = n = 0 and δ 0x  = δ 0y , the rectangular LGCSM beam reduces to the conventional Gaussian Schell-model beam [40–43].

Figure 1 shows the density plot of the square of the modulus of the DOC of the proposed rectangular LGCSM for different values of the beam orders m and n in the source plane. One finds from Fig. 1 that the density plot of the square of the modulus of the DOC of a rectangular LGCSM exhibits array distribution with rectangular symmetry and the numbers of the beamlets along x 1 − x 2 and y 1 − y 2 directions increase as the beam orders m and n increase, which are quite different from the density plot of the square of the modulus of the DOC of a circular or elliptical LGCSM beam [14–16]. Due to the array distribution of the DOC, the rectangular LGCSM beam exhibits self-splitting properties on propagation as shown later, which are also quite different from the propagation properties of a circular or elliptical LGCSM beam [14–16].

Fig. 1
figure 1

Density plot of the square of the modulus of the DOC of a rectangular LGCSM beam for different values of the beam orders m and n in the source plane

Full size image

3 Paraxial propagation of a rectangular Laguerre–Gaussian-correlated Schell-model beam through a stigmatic ABCD optical system

In this section, we derive the paraxial propagation formula for the MCF of a rectangular LGCSM beam passing through a stigmatic ABCD optical system and analyze its propagation properties.

Within the validity of the paraxial approximation, propagation of the MCF of a partially coherent beam through a stigmatic ABCD optical system can be studied with the help of the following generalized Collins formula [44, 45]

$$\begin{aligned} \varGamma \left( {{\varvec{\uprho}}_{1} ,{\varvec{\uprho}}_{2} } \right) = \frac{1}{{\left( {\lambda B} \right)^{2} }}\exp \left[ { - \frac{ikD}{2B}\left( {{\varvec{\uprho}}_{1}^{2} - {\varvec{\uprho}}_{2}^{2} } \right)} \right]\int {\int {\varGamma \left( {{\mathbf{r}}_{1} ,{\mathbf{r}}_{2} } \right)\exp \left[ { - \frac{ikA}{2B}\left( {{\mathbf{r}}_{1}^{2} - {\mathbf{r}}_{2}^{2} } \right)} \right]} } \hfill \\ \, \times \exp \left[ {\frac{ik}{B}\left( {{\mathbf{r}}_{1} \cdot {\varvec{\uprho}}_{1} - {\mathbf{r}}_{2} \cdot {\varvec{\uprho}}_{2} } \right)} \right]d^{2} {\mathbf{r}}_{1} d^{2} {\mathbf{r}}_{2} , \hfill \\ \end{aligned}$$
(11)

where \({\varvec{\uprho}}_{1} \equiv \left( {\rho_{1x} ,\rho_{1y} } \right)\) and \({\varvec{\uprho}}_{2} \equiv \left( {\rho_{2x} ,\rho_{2y} } \right)\) are two arbitrary transverse position vectors in the output plane, A, B, C, D are the elements of the transfer matrix for the stigmatic optical system, and \(k = 2\pi /\lambda\) is the wave number with λ being the wavelength.

Substituting Eqs. (2)–(4) into Eq. (11), after tedious integration, we obtain the following expression for the MCF of a rectangular LGCSM beam in the output plane

$$\begin{aligned} \varGamma \left( {{\varvec{\uprho}}_{1} ,{\varvec{\uprho}}_{2} } \right) & = \frac{{2\pi^{2} \sigma_{0}^{2} }}{{\left( {\lambda B} \right)^{2} }}\exp \left[ { - \frac{ikD}{2B}\left( {\rho_{xs} \rho_{xd} + \rho_{ys} \rho_{yd} } \right)} \right]\exp \left[ { - \frac{{\sigma_{0}^{2} }}{2}\left( {\frac{k}{B}} \right)^{2} \left( {\rho_{xd}^{2} + \rho_{yd}^{2} } \right)} \right] \\ \, & \quad \times \sum\limits_{{q_{x} = 0}}^{m} {\left( \begin{aligned} m \hfill \\ q_{x} \hfill \\ \end{aligned} \right)} \frac{{( - 1)^{{q_{x} }} }}{{q_{x} !}}\left( {\frac{1}{{\delta_{0x}^{2} }}} \right)^{{q_{x} }} \frac{{\left( {2i} \right)^{{ - 2q_{x} }} }}{{a_{x}^{{q_{x} + 1/2}} }}\exp \left( {\frac{{b_{x}^{2} }}{{4a_{x} }}} \right)H_{{2q_{x} }} \left( {i\frac{{b_{x} }}{{2\sqrt {a_{x} } }}} \right) \\ \, & \quad \times \sum\limits_{{q_{y} = 0}}^{n} {\left( \begin{aligned} n \hfill \\ q_{y} \hfill \\ \end{aligned} \right)} \frac{{( - 1)^{{q_{y} }} }}{{q_{y} !}}\left( {\frac{1}{{\delta_{0y}^{2} }}} \right)^{{q_{y} }} \frac{{\left( {2i} \right)^{{ - 2q_{y} }} }}{{a_{y}^{{q_{y} + 1/2}} }}\exp \left( {\frac{{b_{y}^{2} }}{{4a_{y} }}} \right)H_{{2q_{y} }} \left( {i\frac{{b_{y} }}{{2\sqrt {a_{y} } }}} \right), \\ \end{aligned}$$
(12)

with

$$\begin{aligned} a_{x} & = \frac{1}{{8\sigma_{0}^{2} }} + \frac{1}{{2\delta_{0x}^{2} }} + \frac{{\sigma_{0}^{2} }}{2}\left( {\frac{Ak}{B}} \right)^{2} ,\quad b_{x} = \frac{ik}{B}\rho_{xs} + \sigma_{0}^{2} \left( {\frac{k}{B}} \right)^{2} A\rho_{xd} , \\ a_{y} & = \frac{1}{{8\sigma_{0}^{2} }} + \frac{1}{{2\delta_{0y}^{2} }} + \frac{{\sigma_{0}^{2} }}{2}\left( {\frac{Ak}{B}} \right)^{2} ,\quad b_{y} = \frac{ik}{B}\rho_{ys} + \sigma_{0}^{2} \left( {\frac{k}{B}} \right)^{2} A\rho_{yd} . \\ \end{aligned}$$
(13)

In the above derivations, we have applied the following expansion and integral formulae

$$L_{n} (x) = \sum\limits_{q = 0}^{n} {\left( \begin{aligned} n \hfill \\ q \hfill \\ \end{aligned} \right)} \frac{{( - 1)^{q} }}{q!}x^{q} ,$$
(14)
$$\int_{ - \infty }^{\infty } {x^{n} } \exp \left[ { - \left( {x - \beta } \right)^{2} } \right]dx = \left( {2i} \right)^{ - n} \sqrt \pi H_{n} \left( {i\beta } \right).$$
(15)

The average intensity and the DOC of a rectangular LGCSM beam in the output plane are obtained as

$$I\left( {\varvec{\uprho}} \right) = \varGamma \left( {{\varvec{\uprho}},{\varvec{\uprho}}} \right),$$
(16)
$$\mu \left( {{\varvec{\uprho}}_{2} - {\varvec{\uprho}}_{1} } \right) = \frac{{\varGamma \left( {{\varvec{\uprho}}_{1} ,{\varvec{\uprho}}_{2} } \right)}}{{\sqrt {\varGamma \left( {{\varvec{\uprho}}_{1} ,{\varvec{\uprho}}_{1} } \right)\varGamma \left( {{\varvec{\uprho}}_{2} ,{\varvec{\uprho}}_{2} } \right)} }}.$$
(17)

Now we study the propagation properties of a rectangular LGCSM beam with the help of the above-derived formulae. First, we study the propagation properties of a rectangular LGCSM beam in free space. The transfer matrix for free space of distance z reads as

$$\left( {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 1 & z \\ 0 & 1 \\ \end{array} } \right).$$
(18)

Applying Eqs. (12) and (16)–(18), we calculate in Figs. 2 and 3 the normalized intensity distribution of a rectangular LGCSM beam on propagation in free space for different values of the beam orders m and n and in Fig. 4 the normalized intensity distribution of a rectangular LGCSM beam at z = 10 m in free space for different value of beam orders m and n with δ 0x  = δ 0y  = 0.2 mm, σ 0 = 1 mm, and λ = 632.8 nm. As shown in Figs. 2 and 3, the rectangular LGCSM beam exhibits self-splitting properties, i.e., the initial single beam spot evolves into multiple beam spots on propagation in free space, which are totally different from those of a circular or elliptical LGCSM beam [14–16]. Furthermore, the self-splitting properties of a rectangular LGCSM beam are also quite different from that of a HGCSM beam (or a rectangular CGCSM beam). As shown in [18–20], the initial single beam spot of a HGCSM beam (or a rectangular CGCSM beam) only evolves into two or four beam spots on propagation in free space, while the initial single beam spot of a rectangular LGCSM beam evolves into (m + 1) × (n + 1) beam spots on propagation with m and n being its beam orders (see Fig. 4).

Fig. 2
figure 2

Normalized intensity distribution of a rectangular LGCSM beam with m = n = 1 a in the ρ–z plane with ρ x  = ρ y on propagation, and b in the ρ x –ρ y plane at several propagation distances in free space

Full size image
Fig. 3
figure 3

Normalized intensity distribution of a rectangular LGCSM beam with m = n = 2 a in the ρ–z plane with ρ x  = ρ y on propagation, and b in the ρ x –ρ y plane at several propagation distances in free space

Full size image
Fig. 4
figure 4

Normalized intensity distribution of a rectangular LGCSM beam at z = 10 m in free space for different values of the beam orders m and n

Full size image

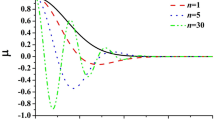
To show the influence of the initial coherence widths on the self-splitting properties, we calculate in Fig. 5 the normalized intensity distribution (cross-line ρ x  = ρ y ) of a rectangular LGCSM beam at z = 1.3 m in free space for different values of beam orders m, n and initial coherence widths with δ 0x  = δ 0y  = δ 0. One finds from Fig. 5 that the beam spot of a rectangular LGCSM beam evolves into multiple beam spots on propagation more rapidly with the increase in the beam orders m and n or with the decrease in the initial coherence widths. Thus, one can modulate the self-splitting properties by controlling the initial beam parameters. The extraordinary splitting properties of a rectangular LGCSM beam may be useful for attacking multiple targets simultaneously.

Fig. 5
figure 5

Normalized intensity distribution (cross-line ρ x  = ρ y ) of a rectangular LGCSM beam at z = 1.3 m in free space for different values of the beam orders m, n and initial coherence widths with δ 0x  = δ 0y  = δ 0

Full size image

To learn about the evolution properties of the DOC of the rectangular LGCSM beam on propagation, we calculate in Fig. 6 the density plot of the square of the modulus of the DOC of a rectangular LGCSM beam at several propagation distances in free space for different values of the beam orders m and n and in Fig. 7 the density plot of the square of the modulus of the DOC of a rectangular LGCSM beam at z = 50 m in free space for different values of the beam orders m and n with δ 0x  = δ 0y  = 0.2 mm, σ 0 = 1 mm, and λ = 632.8 nm. One finds from Fig. 6 that the square of the modulus of the DOC of the rectangular LGCSM beam exhibits array distribution in the source plane or at short propagation distance, while the array distribution gradually disappears on propagation in free space. With the increase in the beam orders m and n, the array distribution disappears more rapidly. Furthermore, it is interesting to find that the array distribution of the modulus of the DOC of a rectangular LGCSM beam evolves into diamond distribution on propagation when m and n are odd numbers, while the array distribution evolves into Gaussian distribution on propagation when m and n are even numbers. When m (or n) is an even number and n (or m) is an odd number, the distribution of the modulus of the DOC in the far-field looks like a Rugby. Thus, one can modulate the DOC of a rectangular LGCSM beam through varying its initial beam parameters.

Fig. 6
figure 6

Density plot of the square of the modulus of the DOC of a rectangular LGCSM beam at several propagation distances in free space for different values of the beam orders m and n

Full size image
Fig. 7
figure 7

Density plot of the square of the modulus of the DOC of a rectangular LGCSM beam at z = 50 m in free space for different values of the beam orders m and n

Full size image

Now we analyze the focusing properties of a rectangular LGCSM beam focused by a thin lens with focal length f. The distance between the source plane and the thin lens is f, and the distance between the thin lens and the output plane is z. The transfer matrix between the source plane and the output plane reads as

$$\left( {\begin{array}{*{20}c} A &\quad B \\ C &\quad D \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 1 &\quad z \\ 0 &\quad 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 1 &\quad 0 \\ { - 1/f} &\quad 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 1 &\quad f \\ 0 &\quad 1 \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {1 - z/f} &\quad f \\ { - 1/f} &\quad 0 \\ \end{array} } \right).$$
(19)

Applying Eqs. (12), (16), (17), and (19), we calculate in Fig. 8 the normalized intensity distribution of a focused rectangular LGCSM beam on propagation and in Fig. 9 the density plot of the square of the modulus of the DOC of a focused rectangular LGCSM beam on propagation with m = n = 3, δ 0x  = δ 0y  = 0.2 mm, σ 0 = 1 mm, λ = 632.8 nm, and f = 400 mm. From Fig. 8, one finds that a focused rectangular LGCSM beam exhibits splitting and combining properties on propagation, i.e., the initial single beam spot splits into (m + 1) × (n + 1) beam spots on propagation before the focal plane and these multiple spots combine to a single beam spot again on propagation after the focal plane. Although a focused HGCSM beam or a focused rectangular CGCSM beam also exhibits splitting and combining properties, its initial single beam spot only splits into two or four beam spots before the focal plane. The splitting and combining properties of a focused rectangular LGCSM beam may be useful for trapping multiple particle simultaneously in the focal plane and may be used to guide atoms along multiple channel near the focal plane. What is more, one finds from Fig. 9 that evolution properties of the square of the modulus of the DOC of a focused rectangular LGCSM beam on propagation are also interesting, i.e., the initial array distribution of the modulus of the DOC disappears gradually on propagation before the focal plane and the array distribution appears again on propagation after the focal plane. The distribution of the square of the modulus of the DOC of a focused rectangular LGCSM beam in the focal plane is similar to the corresponding results in the far-field.

Fig. 8
figure 8

Normalized intensity distribution of a focused rectangular LGCSM beam with m = n = 3 a in the ρ–z plane with ρ x  = ρ y on propagation, and b in the ρ x-ρ y plane at several propagation distances

Full size image
Fig. 9
figure 9

Density plot of the square of the modulus of the DOC of a focused rectangular LGCSM beam with m = n = 3 at several propagation distances

Full size image

4 Rectangular Laguerre–Gaussian-correlated Schell-model beam: experiment

In this section, we report experimental generation of a rectangular LGCSM beam and measure the propagation properties of a rectangular LGCSM beam focused by a thin lens.

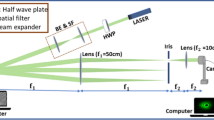
Figure 10 shows our experimental setup for generating a rectangular LGCSM beam and measuring its focusing properties. A He–Ne laser beam (λ = 632.8 nm) passes through a beam expander and goes toward a spatial light modulator (SLM, Holoeye LC2002), which acts as a phase grating designed by the method of computer-generated holograms. The phase grating for generating the beam whose intensity is given by Eq. (10) with different values of the beam orders m and n is shown in Fig. 11. The first-order diffraction pattern from the SLM is regarded as the beam whose intensity is given by Eq. (10) and selected out by a circular aperture (CA). The generated beam from the SLM illuminates a rotating ground-glass disk (RGGD) producing an incoherent beam whose intensity is given by Eq. (10). After passing through free space of distance f 1, a thin lens with focal length f 1, and a Gaussian amplitude filter (GAF), the generated beam becomes a rectangular LGCSM beam. The GAF is used to transform the beam profile of the beam from the RGGD into Gaussian beam profile; thus, the beam width σ 0 of the generated rectangular LGCSM beam is determined by the transmission function of the GAF and it is equal to 1 mm in our experiment. The square of the modulus of the DOC of the generated rectangular LGCSM beam and the corresponding results of the coherence widths (δ 0x and δ 0y ) are measured by the method described in [29], and Fig. 12 shows our experimental results of the square of the modulus of the DOC of the generated rectangular LGCSM beam for different values of the beam orders of m and n just behind the GAF. In our experiment, we have δ 0x  = δ 0y  = 0.1 mm.

Fig. 10
figure 10

Experimental setup for generating a rectangular LGCSM beam and measuring its focusing properties. BE beam expander, RM reflecting mirror, SLM spatial light modulator, CA circular aperture, RGGD rotating ground-glass disk, L 1, L 2 thin lenses, GAF Gaussian amplitude filter, CCD charge-coupled device, PC 1 and PC 2 personal computers

Full size image
Fig. 11
figure 11

Phase grating for generating the beam whose intensity is given by Eq. (10) with different values of the beam orders m and n

Full size image
Fig. 12
figure 12

Experimental results of the square of the modulus of the DOC of the generated RLGCSM beam for different values of the beam orders of m and n just behind the GAF with δ 0x  = δ 0y  = 0.1 mm

Full size image

The generated rectangular LGCSM beam first passes through a thin lens L 2 with focal length f 2 = 400 mm and then goes toward a charge-coupled device (CCD), which is used to measure the intensity distribution of the focused beam on propagation. The distance from the GAF to L 2 is equal to f 2, and the distance from L 2 to the CCD is equal to z; thus, the transfer matrix between the GAF and the CCD is given by Eq. (19) just by replacing f with f 2. The square of the modulus of the DOC of the focused rectangular LGCSM beam on propagation is also measured by the method described in [29]. Figures 13 and 14 show our experimental results of the intensity distribution of the generated rectangular LGCSM beam focused by a thin lens with focal length f 2 = 400 mm at several propagation distances for different values of the beam order m and n. Figure 15 shows our experimental results of the intensity distribution of the generated rectangular LGCSM beam focused by a thin lens with focal length f 2 = 400 mm in the focal plane for different values of beam orders m and n. One finds from Figs. 13, 14, and 15 that the generated rectangular LGCSM beam focused by a thin lens indeed exhibits splitting and combining properties on propagation. In the focal plane, the initial single beam spot splits into (m + 1) × (n + 1) beam spots as expected. Figure 16a, b shows our experimental results of the square of the modulus of the DOC of the generated rectangular LGCSM beam focused by a thin lens with focal length f 2 = 400 mm in the focal plane for different values of the beam orders m and n. For the convenience of comparison, the corresponding numerical results calculated by theoretical formulae are also shown (see Fig. 16c, d). From Fig. 16, we see that the square of the modulus of the DOC indeed exhibits diamond distribution for the case of m = n = 1 and Gaussian distribution for the case of m = n = 2 as expected. Our experimental results are consistent well with theoretical predictions, and only slight difference exists, which may be caused by the fluctuation of the source beam, the nonideal optical elements, and the resolution limits of the CCD.

Fig. 13
figure 13

Experimental results of the intensity distribution of the generated rectangular LGCSM beam with m = n = 1 focused by a thin lens with focal length f 2 = 400 mm at several propagation distances

Full size image
Fig. 14
figure 14

Experimental results of the intensity distribution of the generated rectangular LGCSM beam with m = n = 2 focused by a thin lens with focal length f 2 = 400 mm at several propagation distances

Full size image
Fig. 15
figure 15

Experimental results of the intensity distribution of the generated rectangular LGCSM beam focused by a thin lens with focal length f 2 = 400 mm in the focal plane for different values of beam orders m and n

Full size image
Fig. 16
figure 16

a, b Experimental results of the square of the modulus of the DOC of the generated rectangular LGCSM beam focused by a thin lens with focal length f 2 = 400 mm in the focal plane for different values of beam orders m and n, c, d the corresponding numerical results calculated by theoretical formulae

Full size image

5 Summary

We have introduced a new kind of partially coherent beam with nonconventional correlation function named rectangular LGCSM beam as a natural extension of recently introduced circular or elliptical LGCSM beam, and we have studied its propagation properties both theoretically and experimentally. We have found that a rectangular LGCSM beam exhibits self-splitting properties on propagation in free space and a focused rectangular LGCSM beam exhibits splitting and combining properties on propagation, which are totally different from that of a circular or elliptical LGCSM beam. Furthermore, we have found that the beam spot of a rectangular LGCSM beam splits into (m + 1) × (n + 1) beam spots on propagation with m and n being its beam orders, which are also quite different from other self-splitting beams, such as a HGCSM beam (or a rectangular CGCSM beam), whose beam spot only splits into two or four beam spots on propagation. Our experimental results verify our theoretical predictions. The extraordinary propagation properties of a rectangular LGCSM beam may be useful for manipulating multiple particles or attacking multiple targets simultaneously.