1 Introduction

Current flow through semiconductor devices is usually achieved by applying potential differences to contacts. Over the last 20 years, however, all-optical concepts to induce charge transport have sparked the interest of researchers. Such techniques are particularly appealing because currents can be located wherever one can focus an optical beam. In addition, the use of femtosecond pulses provides a THz bandwidth for current control—something contact-based methods cannot do. Depending on the symmetry of the material, different optical configurations can be utilized to induce electrical currents as well as pure spin currents. The most established example is current injection utilizing phase-stable superpositions of a fundamental beam \((\omega )\) and its second harmonic \((2\omega )\) [1, 2]. In a perturbative approach, it is related to a third-order optical nonlinearity \((\chi ^{(3)})\). It arises from a quantum interference of one- and two-photon absorption pathways across the direct gap \(E_G\) of a semiconductor which satisfies \(\hbar \omega < E_G < 2\hbar \omega\) and is allowed in any crystal structure. The process has been established in the prototypical material GaAs and subsequently applied to 2D systems, indirect semiconductors as well as nanostructures [3, 4]. It has also been observed at metal surfaces [5] and topological insulators [6].

The purpose of the present paper is to review our work on coherently controlled electrical currents in semiconductors. It comprises of three independent studies all of which are related to spectroscopy involving phase-related \(\omega /2\omega\) femtosecond pulse pairs interacting with GaAs microstructures.

In Sect. 2, we experimentally and theoretically investigate the power dependence of coherently controlled currents in bulk GaAs [7]. For moderate irradiances, it is well known that these currents are linked to the third-order optical nonlinearity \(\chi ^{(3)}(0;\omega ,\omega ,-2\omega )\). Here we focus on elevated irradiances where absorption saturation and ultimately the onset of Rabi oscillations contribute to the optical response. Current diagnostics is achieved electrically by recording the photoresponse of contacted specimens of low-temperature grown GaAs as a function of the relative phase of the \(\omega\) and \(2\omega\) pulses. Especially for stronger \(\omega\) irradiance, we find the magnitude of the coherently controlled current to be markedly reduced when compared to \(\chi ^{(3)}\)-expectation \({\mathrm {d}}J/{\mathrm {d}}t \propto E_\omega ^2 E_{2\omega }\). Theoretical simulations for the coherently controlled current based on the semiconductor Bloch equations and a 14 band \(\mathbf {k \cdot p}\) model agree well with the experimental trends.

In Sect. 3, we demonstrate a versatile scheme to analyze the phase structure of femtosecond pulses [8]. It relies on phase-sensitive \(\chi ^{(3)}\)-current injection driven by two time-delayed portions of an \(\omega\)/\(2\omega\) pulse pair. In particular, we are able to determine the group velocity dispersions of both the \(\omega\) and the \(2\omega\) part by a simple Fourier transform of the resulting current interferogram. We test the concept for 45-fs pulses at 1.45 \(\,\upmu\hbox {m}\) and directly compare it to second harmonic generation FROG.

In Sect. 4, we tackle a theoretical proposal by Liu et al. [9] for current detection utilizing coherently controlled currents. This proposal is based on the fact that both a current’s carrier distribution and the induced transition rates of the coherent control technique are asymmetric with respect to the crystal momentum. Depending on whether both exhibit the same or opposite asymmetry, the transmission of the input beams is expected to be either more or less increased due to state blocking. By controlling the asymmetry of the transition rates via the pulse pair’s relative phase, quantum interference control of electrical currents (QUIC) could be utilized to probe an anisotropic charge distribution via transmission measurements. In turn, this technique would allow to investigate ultrafast current dynamics by all-optical means. However, we find the currents’ signatures to be superimposed by nonlinear second harmonic generation in the sample which obstructs a verification of the theoretical ideas.

2 Signatures beyond the perturbative \(\chi ^{(3)}\)-Limit

The discussion in Sect. 2 follows the more detailed description in Ref. [7]. In particular, the present article is restricted to the main findings that reveal deviations from the established \(\chi (3)\)-picture of current injection while a number of additional experimental checks and verifications can be found in Ref. [7].

2.1 Theoretical model and simulation results

We follow the theoretical approach described in Ref. [11–13]. In short, we analyze the dynamical optoelectronic response using the multiband semiconductor Bloch equations (SBE) [11–13]

$$\begin{aligned} -i\hbar \left( \frac{\partial }{\partial t} {\mathrm {x}}^{\lambda \lambda '}_{{\mathbf {k}}} - \frac{\partial }{\partial t}\left. {\mathrm {x}}^{\lambda \lambda '}_{{\mathbf {k}}}\right| _{\mathrm {coll}}\right) &=(\epsilon ^{\lambda }_{{\mathbf {k}}} -\epsilon ^{\lambda '}_{{\mathbf {k}}}){\mathrm {x}}^{\lambda \lambda '}_{{\mathbf {k}}}\nonumber \\&\quad +\frac{e{\mathbf {A}}(t)}{m_0} \cdot \sum _{\upmu }\left[ {\varvec{\Pi }}^{\upmu \lambda }_{{\mathbf {k}}}{\mathrm {x}}^{\upmu \lambda '}_{{\mathbf {k}}}-{\varvec{\Pi }}^{\lambda '\upmu }_{{\mathbf {k}}}{\mathrm {x}}^{\lambda \upmu }_{{\mathbf {k}}}\right] , \end{aligned}$$
(1)

where \({\mathrm {x}}^{\lambda \lambda }_{{\mathbf {k}}}\equiv n^{\lambda }_{{\mathbf {k}}}\) is the population of electron with wave vector \({\mathbf {k}}\) in the band \(\lambda\) and \({\mathrm {x}}^{\lambda \lambda '}_{{\mathbf {k}}}\) with \(\lambda \ne \lambda '\) is the coherence between two bands \(\lambda\) and \(\lambda '\). The collision term \(\frac{\partial }{\partial t}\left. {\mathrm {x}}^{\lambda \lambda '}_{{\mathbf {k}}}\right| _{\mathrm {coll}}\) describes either the relaxation of population or the dephasing of coherence. Here, we treat this term in a phenomenological approach. We assume that the relaxation toward the quasi-equilibrium Fermi–Dirac distributions \(n^{\lambda }_{{\mathrm {FD}}}({{\mathbf {k}}},T)\) is given by \(\frac{\partial }{\partial t}\left. n^{\lambda }_{{\mathbf {k}}}\right| _{{\mathrm {coll}}}=-(n_{{\mathbf {k}}}^{\lambda }-n^{\lambda }_{{\mathrm {FD}}}({{\mathbf {k}}},T))/\tau _1\) and the dephasing is described by \(\frac{\partial }{\partial t}\left. {\mathrm {x}}^{\lambda \lambda '}_{{\mathbf {k}}}\right| _{{\mathrm {coll}}}=-{\mathrm {x}}^{\lambda \lambda '}_{{\mathbf {k}}}/\tau _2\). In the calculation, we use a typical value of 150 fs for both relaxation time \(\tau _1\) and dephasing time \(\tau _2\). In order to obtain the realistic band energy \(\epsilon _{{\mathbf {k}}}^\lambda\) and momentum matrix elements \({\varvec{\Pi }}^{\lambda \lambda '}_{{\mathbf {k}}}\) in Eq. (1), we employ a 14-band \({{\mathbf {k}}}\cdot {\mathbf {p}}\) theory with parameters for GaAs taken from Ref. [10]. The vector potential \({\mathbf {A}}\) in Eq. (1) is given by \({\mathbf {A}}(t)=-\int \nolimits _{-\infty }^t {\mathbf {E}}(t) dt\), where \({\mathbf {E}}(t)\) is the electric field of laser pulses. For the optical excitation of two colinearly polarized \(\omega\) and \(2\omega\) pulses, the field takes the form

$$\begin{aligned} E(t) & =\, E_\omega e^{-\frac{t^2}{2\tau _L^2}}\cos (\omega t+\phi _\omega )\nonumber \\&+E_{2\omega }e^{-\frac{t^2}{2\tau _L^2}}\cos (2\omega t+\phi _{2\omega }). \end{aligned}$$
(2)

Since we consider the optical excitation with energies far above the excitonic levels, the contribution of excitonic effects would be small and has been neglected in our calculations.

The population obtained from the SBE is used to evaluate the time-dependent current density

$$\begin{aligned} {\mathbf {J}}(t) =\frac{e}{m_0}\sum _{\lambda ,{\mathbf {k}}}{\varvec{\Pi }}_{{\mathbf {k}}}^{\lambda \lambda }n_{{\mathbf {k}}}^\lambda . \end{aligned}$$
(3)
Fig. 1
figure 1

Simulated dependence on the \(E_\omega\) amplitude for fixed \(E_{2\omega }\) amplitudes of current density at 100 fs after the pulse maximum. Here, incident pulses have a duration of \(\tau _L= 100\) fs, the \(2\omega\) pulse has photon energy of 1.6 eV, and the temperature is \(T=300\) K. The parabolic fits correspond to the perturbative \(\chi ^{(3)}\)-model

Full size image

We calculate the current density in GaAs bulk which is excited by Gaussian \(\omega /2\omega\) pulses with \(\tau _L= 100\) fs and \(2\hbar \omega =1.6\) eV. The phase relation \(\phi _{2\omega }-2\phi _\omega =\pi /2\) is chosen in order to maximize the current. The dependence of the calculated current density on the amplitude of the electric field \(E_{\omega }\) for fixed \(E_{2\omega }\) amplitudes is shown in Fig. 1. We note that our theoretical approach is also able to describe shift currents if off-resonantly excited bands, in particular, energetically higher conduction bands are included in the numerical evaluations [13].

2.2 Experimental setup and samples

The scheme of the experimental setup is shown in Fig. 2. The optical source for the current injection experiments is a commercial femtosecond Er:fiber laser (Toptica FFS). It delivers a 75-MHz pulse train of 250 mW average power and 90-fs pulse duration at a central wavelength of \(1.55\, \upmu{\mathrm{m}}\) such that \(2\hbar \omega = 1.6 \,{\mathrm{eV}} > E_G = 1.42\,{\mathrm{eV}}\) of GaAs at room temperature. The light is passed through a 2-mm BiBO nonlinear optical crystal to generate second harmonic radiation at 775 nm. A phase-stable superposition of co-polarized fundamental \((\omega )\) and second harmonic radiation \((2\omega )\) is synthesized in a two-color Michelson interferometer. A high-precision motorized stage and polarization optics ensure full control over the relative phase and the polarization state of the \(\omega /2\omega\) pulse pair. The light is focused onto the sample using an aspheric lens with a numerical aperture of NA = 0.26. Spot sizes are \(\approx (10 \, \upmu{\mathrm{m}})^{2}\) for \(\omega\) radiation and \(20\,\upmu{\mathrm{m}} \times 35\, \upmu{\mathrm{m}}\) for \(2\omega\) light. The photocurrent is extracted with a lock-in amplifier referenced to the exciting light that is mechanically chopped at 570 Hz. The sample is based on an annealed \(2\,\upmu{\mathrm{m}}\) thick low-temperature grown (LT-) GaAs epilayer on an intrinsic GaAs substrate. The most favorable aspect of this material is the possibility to characterize coherently controlled currents by metallic electrodes in the vicinity of the excitation. In essence, the short lifetime of unbound electrons in LT-GaAs inhibits dielectric charge relaxation and leads to a long-lived in-plane electrical dipole which manifests as a voltage drop between adjacent metal pads [2, 14]. We note that we have measured the lifetime of the unbound electron-hole pairs by time resolving the free-carrier absorption subsequent to photoexcitation. For the sample of this study, we find a reasonable lifetime of 1–2 ps.

Fig. 2
figure 2

Schematic of the experimental setup: An Er:fiber laser generates \(1.55 \, \upmu{\mathrm{m}}\) femtosecond pulses that are partially frequency doubled in a BiBO crystal. The individual intensity, the relative delay \(\tau\) and the polarization of the fundamental and the second harmonic can be controlled in a two-color interferometer. Both beams are focused on a contacted LT-GaAs sample; the photoinduced potential difference between the contacts is measured with a lock-in amplifier

Full size image

On the LT-GaAs specimen, gold electrodes with a gap of \(50\, \upmu{\mathrm{m}}\) are formed. Coherently controlled currents can be generated and electrically measured in the LT-GaAs substrate throughout the entire gap between the gold electrodes. Due to differing detection efficiencies, the magnitude of the phase-dependent signal in the external circuit varies with the distance between the excitation position and the electrodes as found before [14]. A phase-independent photocurrent offset reflects photoresponses from the illumination outside the center of the device. As expected from the response of Schottky contacts, it is most pronounced for excitations close to the electrodes. We therefore illuminate the center of the device to reduce potential influences of the metal contacts.

2.3 Irradiance dependence of the coherently controlled currents

Fig. 3
figure 3

Amplitude of the phase-dependent photoresponse for various combinations of illumination strengths \(I_{\omega }\) and \(I_{2 \omega }\). The dashed lines are quadratic dependences which correspond to the perturbative \(\chi ^{(3)}\)-model

Full size image

This section contains the central experimental results of the paper, i.e., the analysis of the magnitude of the coherently controlled current as a function of the \(\omega /2\omega\) irradiance. Since those data potentially not only reflect the photoinduced current strengths but are also influenced by the relaxation dynamics of the photoinduced electron-hole dipole, we have performed additional time-resolved experiments to produce a consistent overall picture of photocurrent generation, absorption saturation and carrier relaxation dynamics. For those additional measurements, we refer to the more detailed discussion in Ref. [7]. Figure 3 shows the magnitude of the injected current for numerous combinations of the field strengths \(E_\omega\) and \(E_{2\omega }\). The electric fields represent the peak field amplitudes of the pulses within the GaAs sample deduced from the incident optical intensity corrected for reflection losses. For comparison, the upper abscissa of Fig. 3 also contains information about the corresponding irradiance levels. The values for the current strengths are determined from the amplitude of the interferometric oscillations \(\propto \sin (2\phi _{\omega } - \phi _{2\omega })\) during optimum \(\omega\)/\(2\omega\) overlap. For all the \(E_{2\omega }\) irradiances used for Fig. 3, we observe a quadratic rise of the coherently controlled current as a function of a moderate field \(E_{\omega }\). This is consistent with the perturbative picture of coherent control whereby \({\mathrm {d}}J/{\mathrm {d}}t \propto E_\omega ^2 E_{2\omega }\) is expected. More interestingly, marked departures from this prediction are seen for field strength \(E_\omega \ge 0.5 {\mathrm{MV/cm}}\). Those saturation effects occur at very similar \(\omega /2\omega\) excitation strengths as predicted from the simulation results shown in Fig. 1. In particular, the \(E_\omega\) dependence seen in Fig. 3a matches the theoretical results for \(E_{2\omega } = 180\,{\mathrm{kV/cm}}\) in Fig. 1 very well. For moderate \(E_{2\omega }\) illumination (cf. Fig. 3c), the saturation effects in the experiment are more pronounced when compared to the theoretical expectation. Ultimately, even a pronounced decrease in the current as a function of the \(\omega\) field strength is visible in Fig. 3c. However, this current reduction is mainly governed by internal discharge effects due to the elevated carrier density generated by \(\omega\) irradiance [7].

We note that we have also analyzed current injection with perpendicularly polarized \(\omega\) and \(2\omega\) pulses. In such a configuration, current injection takes advantage of the element \(\eta _{xyyx}\) of the current injection tensor. \(\eta _{xyyx}\) is much smaller when compared to the element \(\eta _{xxxx}\) and gives rise to a current in the direction of the \(2\omega\) polarization [1]. In the experiment, the observed phase-dependent photoresponses are indeed markedly reduced to the values seen in Fig. 3. However, the current saturation looks very similar to the above results for parallel \(\omega\)/\(2\omega\) polarizations (data not shown). In addition, we observe increased current magnitudes but similar saturation effects in a sample with a gap of \(25 \upmu{\mathrm{m}}\) between the gold electrodes. Taken together, the saturation effects are therefore actually linked to the optical irradiance levels as opposed to potential saturation effects in the charge extraction.

We now want to comment about the direct comparability of the simulation results in Sect. 2.1 to the present experimental findings. First of all, a comparison of the absolute current magnitudes is beyond the scope of the study because the experimental values, e.g., depend on the location of the excitation spot on the metal-semiconductor-metal microstructure as well as the unknown efficiency of charge extraction into the contacts. The simulation takes into account a realistic description of the bandstructure of GaAs and an appropriate interaction of one- and two-photon absorption processes. However, the experiment is likely influenced by two additional factors: (i) We work with Gaussian pulse envelopes in time and space, whereas the simulation only considers plane waves with the temporal profile of the experiment. (ii) The experiments utilize LT-GaAs samples because its large defect density inhibits dielectric charge relaxation and leads to a long-lived in-plane electrical dipole which we in turn measure as a voltage drop between adjacent metal pads. The simulation, however, does only treat the current injection itself in pure GaAs and does not account for the charge accumulation and screening, i.e., a partial relaxation of the electrical dipole by the internal space charge field.

2.4 Conclusion

In conclusion, we have identified marked departures from the perturbative \(\chi ^{(3)}\)-expectation of \(\omega /2\omega\) current injection in bulk GaAs in both theory and experiment. They are directly linked to macroscopic state filling during the ultrafast light–matter interaction and lead to a significant current reduction at elevated irradiances. The results are of particular importance for a quantitative understanding of current injection in nanoscale devices where tightly focused femtosecond pulses easily reach the irradiances of the present study.

3 Phase retrieval of fs pulses utilizing \(\omega\)/\(2\omega\) quantum interference control

3.1 Motivation

Phase-resolved techniques have advanced the spectroscopic applications of laser light. Phase sensitivity can be achieved by frequency-resolved methods such as FROG (i.e., frequency-resolved optical gating) [15] or directly in the time domain. As an important example within the latter category, time-domain THz spectroscopy is now employed to analyze phenomena ranging from the dynamics of an electron-hole plasma in semiconductors [16] to THz control of magnetic excitations [17].

A few years ago, we have demonstrated a method for phase-sensitive spectroscopy which relies on the above field-sensitive third-order optical nonlinearity of current injection [18]. It is well known that phase-stable superpositions of transform-limited \(\omega\) and \(2\omega\) pulses incident on a semiconductor induce a coherently controlled electrical current according to [2]

$$\begin{aligned} \dot{J} \propto {E_{\omega }}^2E_{2\omega }\sin {\left( 2\phi _{\omega }-\phi _{2\omega } \right) } . \end{aligned}$$
(4)

Here, \(E_{\omega ,2\omega }\) denote the electric fields of the harmonically related and \(\phi _{\omega ,2\omega }\) their phases. In the experiment, we interferometrically scan the time delay \(\tau\) between the \(\omega\) and \(2\omega\) spectral components and detect the coherently controlled current induced in a semiconductor with a direct bandgap \(E_G\) satisfying \(\hbar \omega < E_G < 2\hbar \omega\). Current detection is performed in a time-integrating fashion, i.e., by analyzing charge accumulation at contacted ends of the semiconductor specimen. As a result, we measure the quantity \(I(\tau ) \propto \int {E_{\omega }}^2(t-\tau )E_{2\omega }(t)dt\). Taking advantage of the convolution theorem, its Fourier transform reads:

$$\begin{aligned} I(\nu ) = \int {I(\tau ) \exp {(-i2 \pi \nu \tau )}d\tau } \propto \left[ {E_{\omega }}(\nu )\right] ^2E_{2\omega }(\nu ) \end{aligned}$$
(5)

In particular, the spectral density \(I(\nu )\) contains the spectral density of the electric field of the \(2\omega\) pulse. We note that a modified experimental scheme discussed in 3.3 allows for a characterization of both the \(\omega\) and the \(2\omega\) field. In this subsection, our main aspect is the sensitivity of the scheme to amplitude and phase modifications of the \(2\omega\) spectral components upon transmission through a sample. To this end, we compare current interferograms detected with and without sample in the \(2\omega\) arm of the interferometer. In particular, transmission through the sample alters the electric field of the \(2\omega\) pulse to \(\tilde{E}_{2\omega }\). Consequently, we now detect a modified interferogram \(\tilde{I}(t)\propto \int {E_{\omega }}^2(t-\tau )\, \tilde{E}_{2\omega }(t)dt\) and compute the corresponding spectral density \(\tilde{I}(\nu )\). As evident from Eq. 5, the ratio of those two spectral densities reads: \(\tilde{I}(\nu )/I(\nu ) = \tilde{E}_{2\omega }(\nu )/E_{2\omega }(\nu )\). Most strikingly, this quantity is exactly the frequency dependent complex transmission coefficient \(\tilde{E}_{2\omega }(\nu )/E_{2\omega }(\nu ) = {\mathcal {T}}(\nu )e^{i\varPhi (\nu )}\) of the sample that induces the modification of the \(2\omega\) spectrum. This concept is similar to the use of an unbalanced Michelson interferometer [19]. However, the use of nonlinear current injection offers low background signals as well as the potential to characterize very weak \(2\omega\) fields.

Fig. 4
figure 4

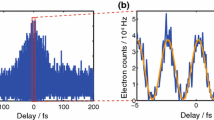
a Photocurrent as a function of delay between the \(\omega\) beam and the \(2\omega\) with an etalon in the \(2\omega\) arm [18]. b Amplitude (left axis) and phase (right axis) spectrum of the radiation transmitted through the etalon. The light solid line is a fit to the data. The inset shows a spectrum of the \(2\omega\) light transmitted through the etalon as measured with a spectrometer

Full size image

As an example, we analyze the spectral response of a Fabry–Pérot etalon with a low finesse of \({\sim }3\) [18]. It consists of a \(d= 152\, \upmu{\mathrm{m}}\) thick glass slide with \({\sim }30\,nm\) gold coverage on both surfaces. The optical setup is practically identical to the one shown in Fig. 2, and the etalon is inserted into the \(2\omega\) arm of the interferometer. As evident from the temporal scan in Fig. 4a, the insertion of the etalon leads to a substantially lower photocurrent signal and multiple backreflections. Amplitude and phase of the interferogram’s Fourier transform are shown in Fig. 4b. It shows pronounced equidistant peaks with a spacing of \(\Delta \nu = \frac{c}{2nd}\), where n is the refractive index of the glass. Their position agrees well with the intensity transmission of the etalon as detected with a fiber-coupled spectrometer of \(0.25\,{\mathrm{THz}}\) spectral resolution. The corresponding phase response of the etalon is shown as green curve in Fig. 4b. It consists of plateaus between adjacent Fabry–Pérot maxima and phase steps at those resonances. For a quantitative understanding, we compute the spectral phase for the etalon: The transmitted electric field of Gaussian pulses with temporal width \(\tau _p\) (full width half maximum) is given by (cf. Ref. [20])

$$\begin{aligned} E(\omega ) \propto \exp \left( -\frac{\tau _p^2 (\omega -\omega _0)^2}{16 \ln 2}\right) \frac{1}{1-r^2\exp {(i\omega \frac{2nd}{c})}} \end{aligned}$$
(6)

Here, \(\omega _0\) denotes the center frequency of the pulse, r the (real) field reflection coefficient, and c the speed of light. The spectral phase of the transmitted light can then be expressed as [21]

$$\begin{aligned} \varPhi _{\mathrm{Etalon}} = \arctan \left[ \frac{r^2\sin \left( \omega \frac{2{\mathrm{nd}}}{c}\right) }{1 - r^2\cos \left( \omega \frac{2{\mathrm{nd}}}{c}\right) }\right] - \varPhi _0(\omega ) \end{aligned}$$
(7)

where the phase term \(\varPhi _0(\omega ) = \frac{\omega x_0}{c}\) is related to the center position \(x_0\) of the pulse. The light solid line in Fig. 3b shows the theoretical expectation for the spectral phase with \(r = 0.93\) and \(n = 1.5\). It agrees very well with the experimental findings.

3.2 Experimental scheme

We now turn toward a modified scheme which allows for phase-sensitive characterization of both the \(\omega\) and the \(2\omega\) field. In essence, the emerging \(\omega /2\omega\) beam is split up and superimposed again to result in two time-delayed collinear beams. Governed by the scaling of the injection process, interferograms obtained by varying the relative temporal delay are modulated by both \(\omega\) and 2\(\omega\) carrier frequencies. A subsequent Fourier transform extracts important information about, e.g., the group velocity dispersion (GVD) of both \(\omega\) and 2\(\omega\) spectral components without a time-reversal ambiguity [8].

Fig. 5
figure 5

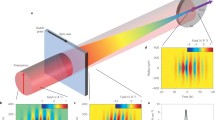
Experimental scheme [8]: A 0.5-mm-thick BBO generates the second harmonic (blue). An interferometer controls the delay \(\tau\) of the fundamental portion \(E^{(2)}_{\omega }\) (red) relative to a pulse pair composed of the remaining fundamental \((E^{(1)}_{\omega })\) and the second harmonic \(E_{2\omega }\). The emergent beam is focused onto a LT-GaAs sample with gold electrodes spaced 10 \(\upmu\hbox {m}\) apart. A lock-in amplifier measures the photoresponse. Inset geometry of the contacts and the optical polarizations

Full size image

The experimental setup is shown in Fig. 5. Pulse characterization is exemplarily realized for the output of a Coherent OPA 9850. It operates at \(1.45\, \upmu{\mathrm{m}}\) central wavelength and delivers 20 mW of \(t_{p,\omega }=\,\) 45-fs pulses (FWHM) at a repetition rate of 250 kHz. The pulses are frequency doubled in a 0.5-mm-thick BBO crystal. The \(\omega /2\omega\) pulse pair is passed through a Michelson interferometer. In one arm, a low-dispersive, 140 \(\upmu\hbox {m}\) thick Si-wafer blocks the second harmonic while a \(\lambda\)/2 plate tilts the remaining fundamental \(E^{(2)}_{\omega }\) to horizontal (x) polarization. The second arm contains an unaltered pulse pair consisting of the y-polarized fundamental \(E^{(1)}_{\omega }\) and the x-polarized second harmonic \(E_{2\omega }\). The pulse combination emerging from the interferometer is focused onto a contacted, low-temperature grown GaAs specimen at room temperature using a \(f=25\,mm\) parabolic mirror. On the chip, we use two gold contacts (spacing \({\sim }\)10 \(\upmu\hbox {m}\), tilted by \({\sim }\)45\(^{\circ }\) in the x–y-plane) for current extraction. If one records a current interferogram in this configuration (data not shown), it is strongly modulated with two carrier waves \(\omega _0\) and \(2\omega _0\), i.e., the pulses’ center frequencies. We will illustrate below that those two modulation frequencies arise from different beam combinations for current injection and their spectral phases ultimately reveal the phase structure of both \(\omega\) and \(2\omega\) pulses. Note that the Si-filter in the interferometer effectively suppresses any disturbing direct interference of two \(2\omega\) pulses.

3.3 Theoretical background of phase retrieval

A superposition of \(\omega\) and \(2\omega\) pulses induces a coherently controlled current with an injection rate of [1]:

$$\begin{aligned} \dot{\overrightarrow {\mathbf {J}}}= \mathop {\eta }\limits ^{\leftrightarrow } {\mathbf {E}}_\omega ^* {\mathbf {E}}_\omega ^* {\mathbf {E}}_{2\omega } \end{aligned}$$
(8)

\(\mathop {\eta }\limits ^{\leftrightarrow }\) is a fourth-rank tensor proportional to the imaginary part of \(\chi ^{(3)}(0;\omega ,\omega ,-2\omega )\). It shows negligible frequency dependence in the spectral region of interest [1, 3]. Note that we work with complex fields and denote the complex conjugate as, e.g., \({\mathbf {E}}_\omega ^*\). Physically relevant quantities are given by the real part. As a result of Eq. (8), current injection driven by two \(\omega\) and \(2\omega\) monochromatic waves with phases \(\varphi _{\omega ,2\omega }\) scales as \(\dot{J} \propto {E_{\omega }}^2E_{2\omega }\sin {\left( 2\varphi _{\omega }-\varphi _{2\omega } \right) }\). For the present pulsed configuration currents are induced with one y-polarized field \(E^{(1)}_\omega (t+\tau )\) and two x-polarized fields \(E^{(2)}_\omega (t)\) and \(E_{2\omega }(t+\tau )\) with relative timing \(\tau\). For a zincblende crystal such as GaAs, the largest elements of the current injection tensor are \(\eta _{xxxx} \approx 2 \eta _{yyxx}\) [1]. We implicitly assume a frequency independent \(\mathop {\eta }\limits ^{\leftrightarrow }\) and crystallographic axes aligned to the lab frame. We now restrict the consideration to the two current contributions which depend on the relative timing \(\tau\). They read:

$$\begin{aligned} \dot{J}_x= & {} \eta _{xxxx} \left[ E^{(2)}_\omega (t) E^{(2)}_\omega (t)\right] ^* E_{2\omega }(t+\tau ) \end{aligned}$$
(9)
$$\begin{aligned} \dot{J}_y= & {} \eta _{yyxx} \left[ E^{(1)}_\omega (t+\tau ) E^{(2)}_\omega (t)\right] ^* E_{2\omega }(t+\tau ) \end{aligned}$$
(10)

Intuitively, the term in Eq. (9) reflects a situation where the two \(\omega\) driving fields in Eq. (8) are derived from the same interferometer arm. In contrast, the two \(\omega\) fields originate from different interferometer arms to yield the current in Eq. (10). In the experiment, we interferometrically scan the delay \(\tau\) between the two interferometer arms and detect signatures \(I(\tau )\) of the coherently controlled current. Therefore, we expect signals \(I_x(\tau ) \propto \int \dot{J}_x {\mathrm {d}}t\) and \(I_y(\tau ) \propto \int \dot{J}_y {\mathrm {d}}t\). As the detector is tilted in the x–y-plane, we do not separately measure \(I_x(\tau )\) and \(I_y(\tau )\) but a superposition \(I(\tau )\). Due to the different \(\tau\)-dependence, the interferograms \(I_x(\tau )\) and \(I_y(\tau )\) feature carrier frequencies \(2\omega _0\) and \(\omega _0\), respectively [8].

We now analyze how phase distortions of the \(\omega\) and \(2\omega\) pulses manifest in the interference pattern \(I(\tau )\) and its FFT \(\hat{I}(\omega )\). The above expressions \(I_x(\tau )\) and \(I_y(\tau )\) represent different field convolutions of the driving \(\omega /2\omega\) pulse combinations. Utilizing the convolution theorem, their spectrum can be expressed by the Fourier transforms of the \(\omega /2\omega\) fields (\(\otimes\) denotes a convolution):

$$\begin{aligned} \hat{I_{x}}(\omega ) \propto \left[ \hat{E}_{\omega }^{(2)}(\omega ) \otimes \hat{E}_{\omega }^{(2)}(\omega )\right] ^* \cdot \hat{E}_{2\omega }(\omega ) \end{aligned}$$
(11)
$$\begin{aligned} \hat{I_{y}}(\omega ) \propto \left( \hat{E}_{\omega }^{(2)}(\omega )\right) ^* \cdot \left[ \left( \hat{E}_{\omega }^{(1)}(-\omega )\right) ^* \otimes \hat{E}_{2\omega }(\omega )\right] \end{aligned}$$
(12)

Such convolutions can be evaluated analytically for transform-limited and linearly chirped Gaussian pulses. Higher-order dispersions are incorporated numerically. The result of such a computation is a relation between the spectral phases of the incoming \(\omega /2\omega\) pulses and the phase properties of \(\hat{I}(\omega )\). Most importantly, we find GVDs \(\phi ''(\omega _0)\) and \(\phi ''(2\omega _0)\) to manifest as corresponding FFT phase curvatures \(D_{\omega _0}\) and \(D_{2\omega _0}\) at the respective center frequencies \(\omega _0\) and \(2\omega _0\). We restrict the consideration to the situation of moderate chirp \(|\phi ''(\omega _0)|\ll (t_{p,\omega })^2 = 2(t_{p,2\omega })^2\) where \(t_{p,\omega /2\omega }\) denotes the pulse durations (a more detailed discussion including stronger chirp can be found in Ref. [8]). In this limit, the phase curvatures \(D_{\omega _0}\) and \(D_{2\omega _0}\) are linked to the GVDs by

$$\begin{aligned} D_{\omega _0}= & {} \frac{10}{9}\phi ''(\omega _0) - \frac{4}{9} \phi ''(2\omega _0) \end{aligned}$$
(13)
$$\begin{aligned} D_{2\omega _0}= & {} \frac{1}{2}\phi ''(\omega _0) - \phi ''(2\omega _0) \end{aligned}$$
(14)

A further simplification is achieved by assuming \(\phi ''(2\omega _0)=\frac{1}{2} \phi ''(\omega _0)\) typical of second harmonic generation in a thin frequency doubler. In this situation, Eqs. (13) and (14) imply \(D_{\omega _0} = \frac{8}{9}\phi ''(\omega _0)\) and \(D_{2\omega _0}=0\).

3.4 Application of the phase retrieval technique

Fig. 6
figure 6

Spectral phases of the FFT of \(I(\tau )\)-traces for pulses of different chirp. Positive (negative) chirp is introduced by 5.3-mm SF11 (10-mm Infrasil). The lines are third-order polynomial fits

Full size image

We now use the above interferometric technique for the phase-sensitive characterization of chirped OPA pulses. To this end, we insert SF11 (Infrasil) glass slabs of different thickness and impose a positive (negative) GVD. Values of \(\phi ''(\omega _0)= +620\) fs2/cm (\(-\)160 fs2/cm) are expected from their Sellmeier equations. Fig. 6b shows the spectral phase of FFTs of exemplary current interferograms \(I(\tau )\) for unaltered, positively, and negatively chirped pulses. The linear contributions to the spectral phase have been subtracted as they only reflect temporal delays owing to the refractive indices. The phase within the fundamental peak around \(\omega _0\) depends pronouncedly on the material introduced into the beam path. In comparison to the reference measurement without additional material, the SF11 (Infrasil) adds a substantial positive (negative) phase curvature. In contrast, the spectral phase of the peak around \(2\omega _0\) depends little on the introduced material. This finding is in line with the picture put forward in Eq. (14) since frequency doubling of a chirped pulse implies \(\phi ''(2\omega _0)=\frac{1}{2} \phi ''(\omega _0)\). For a more quantitative analysis, we apply third-order polynomial fits to the spectral phases which are shown in Fig. 6. The extracted phase curvatures together with Eqs. (13) and (14) finally determine the GVDs \(\phi ''(\omega _0)\) and \(\phi ''(2\omega _0)\). We note that we do not further analyze the third-order terms here because they are small for the present configurations.

Fig. 7
figure 7

Results for the GVD \(\phi ''(\omega _0)\) measured by the coherent control technique (red symbols) and by FROG (blue symbols) for different chirp configurations [8]. The abscissa is calibrated by the Sellmeier equations for SF11 and Infrasil

Full size image

To provide a benchmark comparison to an established phase retrieval scheme, we also perform phase retrieval with second harmonic generation FROG [15]. The setup uses a 0.5-mm BBO and a fiber-coupled spectrometer. We use the freely available FROG code [22] to reconstruct the spectral phase of the pulse and to extract the GVD from its curvature.

Figure 7 depicts the final result for the measured GVD \(\phi ''(\omega _0)\) for various chirp configurations as imposed by SF11 and Infrasil glass slabs of different thickness. The error bars are related to the scatter of three independent sets of measurements. The abscissa is calibrated using the corresponding Sellmeier equations. The dashed line shows the theoretical expectation assuming that the unaltered OPA output has a residual GVD of \(\phi ''(\omega _0)= -50\) fs \(^2\). The FROG data nicely reveal the theoretically expected GVD even though our FROG setup is not particularly sensitive in unveiling very small GVDs. The GVDs extracted with the coherent control technique also agree very well with the theoretical expectation and show a similar small scatter around the dashed line. We note that the analysis of the spectral phase of the FFT of \(I(\tau )\) utilizes the Eqs. (13) and (14). For the most strongly chirped configurations shown in Fig. 7 the limit \(|\phi ''(\omega _0)|\ll (t_{p,\omega })^2\) starts to break down. Here the simplified analysis of the coherent control data suggests a somewhat smaller absolute value of the GVD compared to the theoretical expectation.

3.5 Conclusion

We have demonstrated a new phase retrieval scheme for ultrashort laser pulses. It relies on second harmonic generation in combination with phase-dependent current injection driven by two time-delayed portions of the emerging \(\omega /2\omega\) pulse pair. Most remarkably, the phase information can be extracted from a simple Fourier transform of a one-dimensional current interferogram. These ideas are tested for different chirp configurations of 45-fs pulses centered at \(1.45\,\upmu{\mathrm{m}}\) wavelength. A direct comparison to FROG indicates a similar sensitivity to the pulse’s GVD. Our scheme can be extended to much shorter pulses since current injection offers a broadband and spectrally flat nonlinear response [1, 3]. Since current injection occurs within the \({\sim }\)1 \(\upmu{\mathrm{m}}\) penetration depths of the \(2\omega\) light, phase mismatch in the detector is minimal. By choosing different detector materials, the scheme can be extended to various wavelength regimes.

4 All-optical current detection based on quantum interference control

4.1 Proposed detection scheme

Current measurements typically rely on the detection of a voltage drop across a resistor. In contrast, optical techniques for current detection have rarely been demonstrated so far. One approach relies on the analysis of the momentum of occupied electronic states by angle-resolved photoemission spectroscopy. Femtosecond time-resolved two-photon photoemission is a subtype of this approach and is based on an optical excitation of electrons via ultrafast laser pulses. As an example, such techniques have previously been utilized for time-resolved measurements of coherently controlled surface currents in copper [5]. The drawbacks of angle-resolved photoemission methods are their sophisticated detection schemes including electron optics and high vacuum conditions. An optical current measurement technique which is based on the analysis of transmitted or reflected laser beams would simplify the detection scheme. However, such a method may not rely on linear transmission or reflection alone. As an example for possible nonlinear interactions for current detection, current-induced second harmonic generation in GaAs has been demonstrated recently [23].

There exists a theoretical proposal by Liu et al. for current detection utilizing our above quantum interference control (QUIC) technique [9]. This proposal is based on the fact that both a current’s carrier distribution and the induced transition rates of QUIC are asymmetric with respect to the crystal momentum. Depending on whether both exhibit the same or opposite asymmetry, the transmission of the input beams is expected to be either more or less increased due to phase space filling. By controlling the asymmetry of the transition rates via the pulse pair’s relative phase, QUIC could be utilized to probe an anisotropic charge distribution via transmission measurements. In turn, this technique would allow to investigate ultrafast current dynamics by all-optical means. In the following, the proposal for charge current detection via QUIC is sketched, experimentally investigated, and discussed with respect to its practicability.

Fig. 8
figure 8

Illustration of optical current detection in a direct band gap semiconductor utilizing QUIC. The upper panels depict simplified band diagrams; differently shaded areas mark the electron and hole distribution. The lower panels represent side views of the sample. a The generation of a current via application of an external voltage corresponds to a \({\mathbf {k}}\)-shift of the electron and hole distribution. b The coherent superposition of a fundamental beam and its second harmonic induces transitions whose addressed crystal momentum \({\mathbf {k}}\) can be controlled by the beams’ relative phase. If the transitions at \({+}k\) are suppressed, the beams’ absorption is not influenced by the current’s carrier distribution. c If the transitions are excited at \(+k\), the beams’ absorption is reduced because of state blocking by the current’s carrier distribution

Full size image

The application of a static voltage to a semiconductor results in a current flow which is mediated by free carriers, i.e., electrons in the conduction band or holes in the valence bands. Without scattering, an external field would cause a monotonic increase in the crystal momentum. Carrier scattering limits the average \({\mathbf {k}}\)-shift to a field-dependent value determined by the mobility and momentum relaxation time of the charge carriers. The resulting asymmetry of the carrier distribution in \({\mathbf {k}}\)-space corresponds to a directed charge current. Fig. 8a shows the voltage-induced \({\mathbf {k}}\)-shift of an optically excited carrier distribution in the conduction and valence band. For simplicity, only two bands are shown. Both the electron and hole distribution are shifted in the same direction. The behavior of the hole distribution can also be interpreted as a positive k-shift of an electron distribution with respect to the energy minimum of the valence band. Owing to the opposite slope of both bands, electrons and holes move into opposite directions and their current contributions add up. We note that the displayed k-shift is exaggerated for clarity. Typically, the asymmetry of a voltage-induced current is relatively low, and only a small number of carriers which are not compensated by carriers with opposite velocities contribute to the current. Determined by the different mobility of electrons and holes, the average \({\mathbf {k}}\)-shift of the electron distribution typically exceeds the shift of the hole distribution.

In contrast to voltage-induced current generation, QUIC is an all-optical process. As detailed earlier, the coherent absorption of a fundamental beam and its second harmonic causes interfering one-photon and two-photon transitions at crystal momenta with opposite sign. The absolute value of the crystal momentum is determined by the photon energy. Controlled by the beams’ relative phase and their polarization, carriers are predominantly excited at \(+k\) or \(-k\). The resulting asymmetric electron and hole distributions correspond to directed electron and hole currents. In contrast to voltage-induced current generation, the asymmetry of the distributions is much more pronounced and a majority of the excited carriers may contribute to the current.

If both current generation processes are combined, the voltage-induced current may influence the optical transitions. Fig. 8b as well as c shows situations in which a fundamental beam and its second harmonic are incident onto a thin GaAs sample. Simultaneously, an external voltage induces a current in the sample. The external voltage causes a positive k-shift of the previously excited carrier distribution. The excitation could be either induced thermally or optically by an additional pump beam. Via appropriate polarization adjustment of the \(\omega /2\omega\) beams, the current is injected parallel to the voltage-induced current. Governed by the optical phase, the corresponding transitions are predominantly induced at \(-k\), as in Fig. 8b, or at \(+k\), as in c. Depending on whether the optical transitions at \(+k\) or \(-k\) dominate, the beams’ transmission is expected to be either more or less influenced by current-induced state blocking. In the latter case, as shown in Fig. 8b, optical transitions are induced between mostly unoccupied electronic states. The beams’ absorption is hardly influenced by the current’s carrier distributions which are centered at \(k>0\). However, if the optically addressed states are predominantly located at \(+k\), as shown in Fig. 8c, they are significantly influenced by the current. Owing to the occupation of electron and hole states at \(+k\) by the current, there are less states available for optical excitation. As a consequence, the beams’ absorption is reduced. In practice, this effect should be more pronounced for the second harmonic beam as one-photon transition rates are typically higher than two-photon transitions rates of the corresponding fundamental beam.

By analyzing the beams’ transmission as a function of their relative phase, QUIC in principle allows to probe the current direction all-optically. Since the in-plane angle of the coherently injected current can be controlled by the beams’ polarization, it should also be possible to derive an angle-resolved current map. In comparison, one- or two-photon absorption alone is only sensitive to the density of free carriers. As the induced transitions are symmetric with respect to the crystal momentum \({\mathbf {k}}\), only the average occupation in the bands is probed. The average occupation, however, does not change by application of an external voltage. QUIC only accounts for a small portion of the beams’ interaction with the semiconductor. In practice, the beams’ individual one- and two-photon absorption significantly exceeds the current-induced absorption saturation. However, the proposed current detection technique benefits from the explicit phase dependence of QUIC. By measuring the differential transmission with respect to the optical phase, the contribution of phase-independent one- and two-photon absorption cancels out and the current-induced transmission change remains. Therefore, Liu et al. [9] predict a high sensitivity of this technique.

4.2 Experimental implementation and sample

The optical current detection technique is exemplarily applied to a GaAs thin film in which a current is induced via application of an external voltage. Since the optical detection relies on QUIC, the experimental implementation partly resembles the QUIC setups for current injection layed out before.

Fig. 9
figure 9

Experimental scheme for current detection utilizing QUIC: One output beam of the fiber laser source is frequency doubled in a nonlinear crystal and steered into a two-color interferometer which allows to control the probe beams’ individual delay \(\tau\), their polarization and intensity (optics not shown). Both beams are collinearly focused on the 13 \(\upmu{\mathrm{m}}\) wide gap of two metal contacts on top of a thin GaAs sample. The second synchronized laser output is also frequency doubled to provide an additional second harmonic pump beam. It is focused on the same spot as the other beams to generate a spatial confined distribution of free carriers which is accelerated by an external voltage. The intensity of the transmitted probe beams is recorded with a photodiode. A filter in front of the photodiode allows to select a specific beam

Full size image

Figure 9 depicts the experimental implementation of the current detection technique. The FFS fiber laser is used as a light source. On the one side, it features a stable output with respect to the beams’ intensity as well as alignment. On the other side, it features a second synchronized beam output that is able to generate an additional second harmonic pump beam for current generation, as explained later. Both outputs emit 100-fs pulses with a central wavelength of 1550 nm. One output beam is frequency doubled in a nonlinear crystal to provide a train of two-color pulse pairs for QUIC. Via a subsequent interferometer, both components can be manipulated with respect to their individual intensity, polarization, and relative delay \(\tau\). In particular, a half-wave plate in one arm is used to achieve a parallel horizontal polarization of both harmonics. Furthermore, the interferometer allows to ensure a collinear propagation of both beams before these are focused onto the GaAs sample. To reduce back reflections that may distort the laser source, the sample is slightly tilted.

The sample consists of a thin layer of GaAs with gold contacts on top. First, a GaAs substrate was overgrown with a thin layer of AlAs and a GaAs layer of 1 \(\upmu{\mathrm{m}}\). Afterward, the substrate was locally removed from the back side via selective etching of predefined areas. The AlAs layer acted as etch stop and prevented the removal of the upper GaAs layer. Gold contacts on top of the windows were defined via optical lithography and metallic evaporation. To enhance mechanical stability, the sample was glued on a transparent glass substrate which in turn was glued into a sample holder with macroscopic electrical contacts. We use a pair of metallic contacts with a gap of 13 \(\upmu{\mathrm{m}}\). Measurements of the Franz–Keldysh spectrum evidence the existence of substantial in-plane electric fields when applying a voltage across the contact pair.

The pulse pairs are collinearly focused in the gap of two parallel metallic contacts. The focal spot diameters are approximately 20 \(\upmu\mathrm{m}\) for the fundamental beam and 25 \(\upmu\mathrm{m}\) for the second harmonic component. Simultaneously, an external voltage supply induces a horizontal current between the contacts. Owed to the horizontal polarization of the beams, both the pulse pairs and the voltage-induced current address the same crystal momenta. To measure the current’s influence on the beams’ transmission, the sample thickness has to be in the order of the absorption length or less. In the case of GaAs and a second harmonic wavelength of 775 nm, the absorption length amounts to 670 nm. As the photon energy is below the band gap, the absorption length of the fundamental beam is significantly higher than the absorption length of the second harmonic beam.

To enhance the amplitude of the voltage-induced current, the conductivity of the intrinsic GaAs layer is locally increased by optical excitation. For that purpose, the second synchronized laser output is also frequency doubled in a nonlinear crystal, resulting in a second harmonic beam of 20 mW power. A shortpass filter blocks the fundamental beam. The additional second harmonic pump beam allows to directly excite carriers in GaAs from a valence to the conduction band. It is focused on the same spot between the metal contacts as the pulse pairs. The minimum focal spot diameter of the pump beam is 20 \(\upmu\mathrm{m}\). A different angle of incidence minimizes disturbance of the pulse pairs’ transmission measurement. The delay \(\tau _\mathrm{pump}\) of the pump beam with respect to the pulse pairs is controlled with a motorized stage.

The transmitted pulse pairs are collected with a lens behind the sample and focused on a photodiode. An additional shortpass or longpass filter allows to select a specific beam. The induced photocurrent is proportional to the irradiance and recorded with a lock-in amplifier. The amplifier is either referenced to a chopper in a beam path or to a square-wave voltage which is applied to the sample to induce a modulated current. The latter is generated by a waveform generator which is connected to the contact pair. Alternatively, a constant-voltage source is used which is simultaneously able to precisely measure the induced current.

4.3 Application of the current detection technique

The optical current detection technique is now applied to a GaAs thin film. In essence, the pulse pairs’ transmission is measured as a function of their relative optical phase and the current amplitude which is induced in the window. The latter determines the asymmetry of the currents’ carrier distribution in \(\mathbf {k}\)-space. The relative phase of the pulse pair components determines the asymmetry of the optical transitions. If the transitions predominantly address electronic states which are already occupied by the current, the transmission is expected to be increased due to absorption saturation.

The absorption saturation and thus the sensitivity of the current detection technique depend on the mutual coherence of the pulse pairs. Therefore, special attention is paid to ensure collinear propagation and focusing of the pulse pair. To this end, the GaAs sample is exchanged with a beam profiler during adjustment. Furthermore, it is verified that the polarization of both pulse pair components coincides with the direction of the voltage-induced current. In this way, the pulse pairs and the current address the same electronic states.

In order to adjust the temporal overlap of the pulse pair components, the amplitude of the current injected by the \(\omega /2\omega\) pulse pair is measured. At peak intensities of about \(6\,\mathrm{GW/cm^2}\) for the fundamental beam and \(200\,\mathrm{MW/cm^2}\) for the second harmonic component, the maximum peak to peak current amplitudes in the external circuit are 200 nA. These relatively high current amplitudes are probably related to the small gap between the contacts.

The current to be probed is generated by an external voltage at the position where the additional pump beam is incident. The spatial overlap between the pump and the \(\omega /2\omega\) probe is adjusted by maximizing transient pump-probe signatures. The temporal separation \(\tau _\mathrm{pump}\) is set such that the pump precedes the \(\omega /2\omega\) probe by a few picoseconds. This delay ensures a quasi-thermalized carrier distribution with a well-defined asymmetry, determined by the external voltage.

After adjustment, the GaAs windows and the current within are probed by phase-dependent transmission measurements of one pulse pair component. For this purpose, the relative delay \(\tau\) of the pulse pair components is interferometrically varied around maximum temporal overlap while keeping the delay \(\tau _\mathrm{pump}\) of the pump beam constant. A photodiode behind the sample records the intensity of the transmitted beam. The pulse pair component to be monitored is selected by an additional longpass or shortpass filter in front of the photodiode.

Despite careful alignment, measurements of the fundamental beam component do not show a significant and reproducible phase-dependent transmission signal. However, this observation is not unexpected since the fundamental beam may only interact via two-photon transitions. Given the same illumination intensity, these are less likely than corresponding one-photon transitions. Therefore, the following measurements concentrate on the transmission of the second harmonic beam.

Fig. 10
figure 10

Differential transmission of the second harmonic pulse pair component as a function of the pulse pairs’ relative delay \(\tau\) and the voltage applied to the illuminated GaAs window. a Signal recorded with a constant voltage and the lock-in amplifier referenced to a chopper in the fundamental beam arm. b Signal recorded by referencing the lock-in amplifier to a square-wave voltage. Both signals are normalized to the total transmission of the second harmonic pulse pair component. A constant offset is subtracted from both graphs

Full size image

Figure 10a exemplarily depicts the transmission of the second harmonic pulse pair component. A lock-in amplifier records the response of the photodiode. It is referenced to a chopper in the arm of the fundamental pulse pair component. In this way, stray light by the second harmonic pump beam is suppressed. During the measurement, a fixed voltage of −10 V, 0 V, or +10 V is applied to the contacts. The approximate peak illumination intensities on the window are \(6\,\mathrm{GW/cm^2}\) (\(200\,\mathrm{MW/cm^2}\)) for the \(\omega\) (\(2\omega\)) pulse and \(700\,\mathrm{MW/cm^2}\) for the additional (second harmonic) pump beam. The delay \(\tau _\mathrm{pump}\) is set such that each pump pulse precedes a pulse pair by 2.5 ps.

The graph reveals distinct oscillations of the transmission with respect to the delay \(\tau\) with a period corresponding to the wavelength of the second harmonic pulse. The oscillation amplitudes are in the order of \(10^{-3}\) when normalizing the signal to the total intensity of the transmitted second harmonic probe pulse.

Apart from the oscillating signal, the recorded transmissions also contain phase-independent components in the order of \(10^{-2}\). These are probably caused by the optically induced increase in the total carrier density. Since the proposed optical current detection explicitly depends on the relative phase, the constant components are not analyzed in more detail and subtracted from the graph.

The voltage dependence of the oscillation amplitudes is less pronounced than expected. In particular, the oscillation is even present if no voltage is applied to the GaAs window. If oscillatory features are solely caused by the current-induced transmission increase detailed in Sect. 4.1, the oscillation would be expected to vanish if no current and thus no asymmetry of the carrier distribution is present. Therefore, these oscillations must have another origin that is discussed in more detail below.

Most strikingly, an increase in the applied voltage results in a significant shift of the oscillation with respect to the delay \(\tau\). In order to separate this effect from the voltage-independent oscillation, another measurement technique is used. Instead of the chopper in the fundamental beam arm, the lock-in amplifier is referenced to a square-wave voltage which alternates the voltage applied to the sample between 0  V and \(\pm 10\)  V. In this way, the measurement is only sensitive to voltage-induced transmission changes. Exemplary measurements of the voltage-induced transmission changes are shown in Fig. 10b obtained with the same irradiances as in panel a. Therefore, the differential transmission can be normalized in the same way. Furthermore, phase-independent offsets are subtracted. The two curves correspond to measurements employing square-wave voltages with the same amplitude of 10 V but different polarity. Both curves feature similar oscillation amplitudes and the same oscillation period as the curves in Fig. 10a. However, the phases of the two curves differ by \(\pi\) and therefore correlate with the orientation of the applied voltage. Such a behavior is in agreement with the voltage-dependent phase shift of the three curves in Fig. 10a. The observed oscillations can be thought of as a superposition of two slightly shifted oscillations, a voltage-independent component and a voltage-dependent component.

In order to investigate the underlying mechanism of the voltage-dependent component, the corresponding oscillation amplitudes are determined as a function of the illumination intensity. To this end, measurements as shown in Fig. 10b are repeated with different intensity combinations of both pulse pair components. If the intensity of the second harmonic component is kept constant, the extracted oscillation amplitudes scale linearly with the intensity of the fundamental beam. If the intensity of the fundamental component is kept constant, the oscillation amplitudes scale with the root of the second harmonic irradiance. Taken together, the phase-dependent transmission scales in the same way as the QUIC amplitude. However, the intensity dependence alone is not sufficient to identify QUIC as the origin of the transmission oscillation. At least, it can be concluded that the transmission signal originates from a nonlinear optical effect.

4.4 Influence of second harmonic generation

The fact that the transmission signal features a sinusoidal phase dependence even if no voltage is applied to the GaAs windows indicates the influence of another effect than current-induced absorption saturation. A likely candidate for such an effect is second harmonic generation (SHG) in the GaAs sample itself [24, 25]. If the fundamental pulse pair component is frequency doubled in the GaAs window, the emergent beam exhibits the same wavelength and propagation direction as the second harmonic pulse pair component. As a consequence, the illumination intensity on the photodiode would also be determined by the interference of the two second harmonic beams. In particular, the intensity would exhibit the same oscillation period as seen in Fig. 10a.

Fig. 11
figure 11

a Spectra of the second harmonic signal behind the GaAs sample at a fixed intensity of the fundamental input beam and different voltages applied to the contact pair. b Integrated intensity of the second harmonic peaks as a function of the fundamental beam intensity and the applied voltage. The curves correspond to parabolic fits

Full size image

SHG in the GaAs window can be identified by a spectral-resolved measurement. To this end, the photodiode behind the sample is exchanged with a spectrometer. During such a measurement, only the fundamental beam is focused on the GaAs window. The other two second harmonic beams are blocked as their high intensity would saturate the spectrometer. Indeed, if the fundamental beam is focused on the GaAs window, the spectrometer reveals a peak at the second harmonic wavelength. Such spectra are shown in Fig. 11a for an exemplary fundamental beam intensity of \(6\,\mathrm{GW/cm^2}\). By detecting the signal with a photodiode, the power of the emerging second harmonic component can be estimated to about \(0.3\,nW\).

The application of a voltage to the GaAs window significantly influences the amplitude of the SHG. As an example, a voltage of +20 V causes an increase of up to 50 %. In contrast, a negative voltage results in a slight decrease in the amplitude. It should be noted that the application of a voltage of \(\pm 10\)  V, as used in the previous measurements, has a qualitatively similar but less pronounced influence on the SHG amplitudes.

To confirm the signal as originating from SHG, its dependence on the input beam intensity is analyzed. Fig. 11b shows the integrated intensity of the second harmonic component as a function of the fundamental beam intensity and the applied voltage. As expected, the data agree well with quadratic dependences. If a positive or negative voltage is applied to the GaAs film, the respective scaling factor of the parabolic fits is higher or lower than without a voltage. The underlying mechanism of this voltage dependence is addressed later in the chapter. First, we discuss the influence of SHG on the previously presented transmission measurements.

During transmission measurements, the photodiode is simultaneously illuminated by the second harmonic beam which is generated in the sample \((E_{2 \omega , \mathrm{SHG}})\) as well as the transmitted second harmonic pulse pair component \((E_{2 \omega , \mathrm{probe}})\). As a consequence, both second harmonic beams interfere. The intensity on the detector can be described by a superposition of the corresponding electric field amplitudes E:

$$\begin{aligned}&| E_{2 \omega , \mathrm{probe}} + E_{2 \omega , \mathrm{SHG}}|^2 \propto I_{2 \omega , \mathrm{probe}} \nonumber \\& \quad + 2 \cos (\Delta \phi _{2 \omega }) \, \sqrt{I_{2 \omega , \mathrm{probe}} \cdot I_{2 \omega , \mathrm{SHG}}} + I_{2 \omega , \mathrm{SHG}} \end{aligned}$$
(15)

The first and third term on the right-hand side denote the individual transmitted intensities of the second harmonic pulse pair component and the beam generated in the sample, respectively. The additional term describes the interference of both beams. Its magnitude is determined by their relative optical phase. If the relative delay of the pulse pair components in the interferometer is continuously swept, the intensity oscillates with a period that corresponds to the second harmonic wavelength, as in Fig. 10. In order to quantify the influence of interference on the transmission measurements, the oscillation amplitude of the intensity is exemplarily calculated for the measurement shown in Fig. 10. The corresponding transmitted beam power \(I_{2 \omega ,\mathrm{probe}}\) is in the order of \(200\,\upmu\mathrm{W}\). As mentioned above, \(I_{2 \omega , \mathrm{SHG}}\approx 0.3 \, nW\). If normalized to the total transmission which is dominated by \(I_{2 \omega , \mathrm{probe}}\), the relative oscillation amplitude is given by \(2 \sqrt{I_{2 \omega ,\mathrm{SHG}}/I_{2 \omega ,\mathrm{probe}}}\). Inserting the above-mentioned intensities yields a relative interference amplitude of \(2 \cdot 10^{-3}\). This value exceeds the observed oscillation in Fig. 10a by a factor of 4. However, it must be taken into account that the calculation assumes optimum coherence of both beams which is not fulfilled in practice. As an example, the polarizations of both beams do not coincide but form an angle of about \(45^\circ\). As a consequence, the intensity interference is reduced compared to the calculation. Overall, it is therefore reasonable to attribute the voltage-independent oscillation in Fig. 10a to interference, caused by SHG in the sample. In the following, we further argue that it is also reasonable to attribute the voltage-dependent oscillation component in Fig. 10b to interference. In particular, the application of a voltage influences the second harmonic generation in the sample due to EFISH (electric-field-induced second harmonic generation).

EFISH refers to frequency doubling in a material by coupling of the incident beam’s electric field amplitude \(E_{\omega }\) with the amplitude of a static electric field \(E_\mathrm{DC}\) [26–28]. In terms of nonlinear optics, this effect is described by the fourth-rank tensor \(\chi ^{(3)}(-2 \omega ; \omega , \omega , 0)\). Omitting the optical polarizations for clarity, the material’s polarization P follows the relation

$$\begin{aligned} P_{\textit{EFISH}} \propto \chi ^{(3)}(-2 \omega ; \omega , \omega , 0) \, E^{2}_{\omega } \, E_\mathrm{DC}. \end{aligned}$$
(16)

Since the electric field amplitude of the emitted second harmonic beam scales linearly with the polarization P, the second harmonic intensity is proportional to the square of the fundamental beam intensity, as for regular SHG. Additionally, the second harmonic field amplitude is proportional to the static field amplitude \(E_\mathrm{DC}\). As a consequence, the phase is shifted by \(\pi\) upon a reversal of the constant field’s polarity [29].

Coming back to Fig. 11, the voltage-induced difference of the detected second harmonic intensity can be attributed to EFISH. Both conventional SHG and EFISH cause frequency doubling of the incident fundamental beam. As evident from the good agreement with the parabolic fits, the voltage-induced difference in amplitude follows the quadratic intensity dependence of EFISH. On the basis of reference transmission measurements with the second harmonic pulse pair component, it can be ruled out that the difference is simply caused by a voltage-dependent absorption in the sample. The fact that depending on the voltage polarity the intensity is either increased or decreased can be explained by interference. The spectrometer detects a superposition of two second harmonic components generated by conventional SHG as well as EFISH. Depending on their relative optical phase, these interfere constructively or destructively. While the optical phase of the conventional SHG component is fixed, the EFISH component depends on the orientation of the static field. As a result, the total intensity may be decreased upon application of a negative voltage. A simultaneous generation of an EFISH component as well as a field-independent SHG component in the sample is also consistent with the oscillations in Fig. 10a. As mentioned above, the voltage-induced phase shift can be interpreted as a superposition of two oscillations, a voltage-independent component as well as a voltage-induced component. The former can be explained by interference of the second harmonic pulse pair component with SHG in the sample. The voltage-induced oscillation can be attributed to interference with an EFISH component. Consistent with the field dependence of EFISH, the voltage-induced oscillation in Fig. 10b is shifted by \(\pi\) if the polarity is inverted.

We note that QUIC and the interference by second harmonic generation even exhibit the same intensity dependence such that a variation in the irradiances promises no further insight. As evident from Eq. (15), intensity interference is proportional to the square root of the intensity of both interfering second harmonic components. The intensity of second harmonic generation in the sample, in turn, is proportional to the squared intensity of the incident fundamental beam. Consequently, the oscillation amplitude scales with \(\sqrt{I_{2 \omega }} \, I_{\omega }\), similar to QUIC. As already mentioned, such a scaling is also observed for the amplitude of the voltage-induced oscillations of the transmission measurements.

In summary, it can be concluded that the presented transmission measurements are dominated, if not fully determined, by interference of second harmonic components generated by SHG and EFISH.

4.5 Conclusion

An experimental implementation of the optical current detection scheme proposed by Liu et al. [9] is presented as well as evaluated. The detection scheme is based on quantum interference control of electrical currents (QUIC) by a two-color pulse pair incident on the sample to be probed. Via the relative phase and polarization of the pulse pair components, the crystal momentum of the optically addressed electronic states can be controlled. If these electronic states are already occupied, the pulse pair’s transmission is expected to be increased due to absorption saturation. Such a selective absorption saturation would allow to sense an anisotropic carrier distribution which corresponds to the presence of a current. In particular, the current should manifest a dependence of the transmission on the pulse pair’s relative phase.

The presented implementation of the detection technique is designed for an exemplary analysis of a voltage-induced current in a thin GaAs sample. Via frequency doubling of ultrashort laser pulses in a nonlinear crystal and a subsequent interferometer, collinear coherent pulse pairs are provided; their components can be individually adjusted in intensity, relative delay, and polarization. In essence, the sample to be probed consists of a thin layer of GaAs with metallic contacts on top to apply a voltage. In order to increase the amplitude of the induced current, the sample is further excited by an additional laser beam. On the basis of independent control measurements, it can be demonstrated that the setup fulfills the fundamental requirements of the proposed detection technique. Measurements of QUIC in the sample confirm a precise and coherent superposition of the pulse pair components. Therefore, the pulse pairs allow for a selective optical excitation of electronic states. The calculated excitation density corresponds to a massive population of the electronic bands that should result in a significant influence on the pulse pairs’ transmission.

Despite careful design and optimization of the setup, the transmission measurements do not allow to deduce an influence by current-dependent saturation absorption. The central problem is that the measurements are affected by interference which can be attributed to second harmonic generation in the sample. The focused illumination of the GaAs sample by the fundamental beam results in frequency doubling which is verified by spectrally resolved measurements. An additional voltage application influences the frequency doubling in the sample by electric-field-induced second harmonic generation (EFISH). As a consequence, the transmitted second harmonic pulse pair component interferes with the additionally generated second harmonic beam. The resulting intensity interference on the detector features a similar phase- and voltage dependence as the predicted absorption saturation. Furthermore, QUIC as well as interference of the second harmonic beams follows the same intensity dependence. Therefore, a potential influence by current-dependent saturation absorption cannot simply be separated from the pronounced intensity interference.