1 Introduction

Soot volume fraction (SVF) is an important parameter in determining the impact of anthropogenic soot on ecosystems and human health. Within flames and engines the SVF also provides information about the chemical and transport processes that underlie combustion, which must be known to improve efficiency and reduce emissions. One diagnostic capable of quantifying this parameter is laser-induced incandescence (LII) [1], in which soot particles within a sample aerosol volume are heated to incandescent temperatures by a short laser pulse. The spectral incandescence from the soot particles is collected and imaged onto a spectrometer, an intensified charge-coupled device (ICCD), or photomultipliers equipped with bandpass filters. The soot volume fraction is proportional to the measured spectral incandescence [1] and can be quantified if the incandescence measurement has been calibrated. Alternatively, auto-correlated (AC), or two-color, LII estimates the soot temperature from the ratio of spectral incandescence measurements taken at two wavelengths [2, 3]; this parameter, combined with the spectral incandescence at a single wavelength, uniquely specifies the SVF.

While LII is widely used to measure various aerosol characteristics, the uncertainty associated with these measurements is infrequently discussed. Most uncertainty quantification in LII has focussed on time-resolved measurements, in which the incandescence following the laser pulse is used to infer parameters such as the median particle size and size distribution width. Lehre et al. [4, 5], for example, assessed the reliable range of nanoparticle sizes inferred from incandescence based on the sensitivity of the squared norm of the residuals (which they referred to as the Chi-squared parameter) to perturbations in the probability density of each size class. Daun et al. [6] also examined the topography of the squared norm of the residuals and made some suggestions of how to avoid uncertainties resulting from measurement noise. Kuhlmann et al. [7] extensively discussed the origins of various uncertainties in TiRe-LII experiments, but did not quantify how these uncertainties propagate through the model. Starke et al. [8] and Eremin et al. [9] attempted to quantify these analyses using a simple perturbation analysis under various TiRe-LII conditions. One of the few studies to directly address uncertainty in AC-LII-inferred SVF measurements is Crosland et al. [10], who considered how uncertainties in model parameters and noise in signals captured by intensified charge-coupled devices (ICCDs) propagate through the measurement model into SVF estimates. This was done through a Monte Carlo simulation in which repeated soot volume fraction calculations were made for an ensemble of laboratory measurements with model parameters sampled from prior distributions. Sipkens et al. [11] also directly quantified the uncertainty in particle size and distribution estimates inferred from TiRe-LII measurements made on metal nanoparticles. They used a perturbation analysis, following Starke et al. [8] and Eremin et al. [9], to estimate how model parameter uncertainty impacts the size distribution of molybdenum nanoparticles inferred from TiRe-LII, and a wild bootstrapping method [12] to compute the impact of measurement noise. The latter technique uses the empirical residuals calculated as the difference between experimental data and modeled data fit with a weighted least-squares analysis. These residuals are resampled and added to the least-squares solution to produce new empirical data sets. Repeating the inference gives a series of samples of the inferred parameters, which can be used to develop confidence intervals.

A more robust treatment employs the Bayesian methodology for inferring parameter values and the associated uncertainty. The Bayesian framework treats the parameters of interest, in this case the SVF and peak temperature, along with all other model parameters as random variables. As a result there is no single true value for these parameter values but a joint posterior probability distribution for all the values which the parameters can hold. Using the posterior distribution various types of estimates are possible, see Sect. 3, since Bayes’ theorem provides a mechanism to connect what is known or expected probabilistically about the parameters of interest with the information obtained through the measurement process [13]. Specifically, Bayes’ theorem states

$$\pi \left( {{\mathbf{x}}|{\mathbf{b}}} \right) = \frac{{\pi \left( {{\mathbf{b}}|{\mathbf{x}}} \right)\pi_{\text{pri}} \left( {\mathbf{x}} \right)}}{{\pi \left( {\mathbf{b}} \right)}} \propto \pi \left( {{\mathbf{b}}|{\mathbf{x}}} \right)\pi_{\text{pri}} \left( {\mathbf{x}} \right),$$
(1)

where b is a vector of observations, x is a vector of quantities of interest (QoI), and π(·) are probability densities. In the case of AC-LII, we typically have x = [f v, T p]T and b = v λ  = [V λ1, V λ2]T where f v is the soot volume fraction, T p is the peak particulate temperature, and v λ is a vector containing the measured voltages from the photomultipliers. The posterior, π(x|b), is a probabilistic representation of the SVF and temperature once we have observed the data and considered the uncertainties associated with the model, which connects SVF and temperature with the measurements. The likelihood, π(b|x), quantifies the probability of an observed measurement, conditional on a particular parameter value in the context of measurement noise. The prior density, π pri(x), is a probabilistic representation of what is known or expected of the parameters based on knowledge available before the measurements are taken. Finally, the evidence,

$$\pi ({\mathbf{b}}) = \int {\pi ({\mathbf{b}}|{\mathbf{x}})\pi_{\text{pri}} ({\mathbf{x}})} \;\text{d}{\mathbf{x}},$$
(2)

is a normalization constant which ensures that the posterior satisfies the Law of Total Probability. When x is of high dimension or there are ancillary model parameters, often called “nuisance parameters,” which must be inferred but are not of interest, the evidence can be hard to compute.

Quantities-of-interest (e.g., SVF) inferred from physical measurements are subject to a range of modeling errors and uncertainties. Some uncertainties can be easy to identify, such as photon shot noise, while others are more subtle, such as a non-uniform laser fluence profile [14] or signal trapping [3, 15]. The present work only considers the uncertainty associated with electron shot noise and the optical properties of soot, since they are expected to dominate the uncertainty in f v [10].

The absorption and emission properties of soot depend on the absorption function

$$E({\mathbf{m}}_{\lambda } ) = {\text{Im}}\left( {\frac{{{\mathbf{m}}_{\lambda }^{2} - 1}}{{{\mathbf{m}}_{\lambda }^{2} + 2}}} \right),$$
(3)

where m λ  = n λ  − ik λ is the complex index of refraction. Considerable variation exists in the reported radiative properties of soot, and moreover the reliability of some of these values is questionable [16]. This variation in the literature reflects the overall state of knowledge concerning E(m λ ), and consequently acts as a basis for a prior distribution.

Sipkens et al. [17] applied Bayesian techniques to estimate the uncertainty in mean particle size and distribution width for silicon nanoparticles. Uncertainties due to measurement noise were modeled using Markov chain Monte Carlo (MCMC) in a Bayesian framework, while uncertainties in the model parameters were estimated using a perturbation analysis. In a subsequent study, Sipkens et al. [18] attempted to simultaneously estimate the uncertainty resulting from the model parameters and measurement noise while inferring the mean particle size and thermal accommodation coefficient (TAC) for iron nanoparticles. Unfortunately, estimates were computed from a relatively small sample size as the MCMC procedure required substantial computational time to converge given the number of input parameters as well as their interrelation, which caused the posterior density to have a long, shallow topography that was difficult to integrate. A similar challenge arises when MCMC is used to compute estimates for the SVF using AC-LII data, but a novel solution that circumvents this issue is proposed.

In this work we consider estimating soot volume fraction and peak particulate temperature in the Bayesian framework. We propose a method which is able to quantify the uncertainty in such estimates resulting from uncertain or unreliable information about nuisance parameters such as absorption efficiency. Crosland et al. [10] addressed this issue by treating all the model parameters as stochastic variables which obey prescribed distributions based on SVF when the various model parameters were sampled from their respective distributions. Using this ensemble of soot volume fraction estimates they assessed the level of uncertainty of an estimate by examining the resultant histogram. This technique, while providing an estimate of the uncertainty, does not consider how appropriate the various combinations of the model parameters are in terms of the measurements and consequently will misrepresent the uncertainty associated with a measurement. The present technique is better able to account for odd or extreme combinations of these parameters through the inclusion of the density in the posterior and a formal treatment of the likelihood, thus improving uncertainty estimates.

Furthermore, there are philosophical and practical distinctions between Crosland et al.’s approach [10] and the methodology present here. The former work can be classified as a “frequentist” methodology, which, loosely stated, presumes that there exists one “true” SVF value, and the probability that the inferred value is “correct” is proportional to the frequency of this observation during replication. In contrast, the Bayesian approach conceives the QoI, nuisance parameters, and measurements as random variables described by probability densities, and the prior and measurement densities are propagated through Bayes’ equation to obtain the posterior densities. Moreover, the Bayesian method explicates the roles of prior and measurement information in the inference procedure, and we present a rigorous procedure for defining priors based on the Principal of Maximum Entropy [19].

The remainder of this paper is structured as follows: Sect. 2 presents the measurement model used to infer the soot volume fraction of an aerosol sample. Section 3 discusses how the model is incorporated into the Bayesian framework. Section 4 reviews the current state of knowledge of E(m λ ) and proposes a prior for this variable. Finally, in Sect. 5 we present numerical results when simulated and experimental data are used. The use of simulated data means the ground truth is known which allows us to demonstrate the ability of the Bayesian framework to quantify the uncertainty in soot volume fraction estimates, whereas, the use of the experimental data illustrates that these techniques are easily applied to practical LII applications.

2 Laser-induced incandescence

Figure 1 shows a schematic of a typical AC-LII experiment. A short laser pulse energizes nanoparticles contained in a sample volume of aerosol. The resulting spectral incandescence emitted by all nanoparticles of different sizes is given by

$$J_{\lambda } (t) = C_{\lambda } \int\limits_{0}^{\infty } {\frac{{\pi d_{\text{p}}^{2} }}{4}I_{{{\text{b}},\lambda }} \left[ {T\left( {d_{\text{p}} ,t} \right)} \right]Q_{{{\text{abs}},\lambda }} \left( {d_{\text{p}} } \right)\pi \left( {d_{\text{p}} } \right)\;{\text{d}}\left( {d_{\text{p}} } \right)},$$
(4)

where I b,λ is the blackbody spectral intensity, C λ is a constant that depends on the optical collection efficiency, laser fluence, and nanoparticle volume fraction, Q abs,λ is the absorption efficiency of the nanoparticles, and π(d p) is the probability density of nanoparticle diameters. The nanoparticle diameters are expected to be much smaller than the laser wavelength and the principal wavelengths of emitted radiation. Consequently, the nanoparticles are said to emit and absorb in the Rayleigh limit,

$$Q_{{{\text{abs}},\lambda }} \left( {d_{\text{p}} } \right) = 4\frac{{\pi d_{\text{p}} }}{\lambda }E\left( {{\mathbf{m}}_{\lambda } } \right).$$
(5)

The spectral incandescence is recorded with photomultipliers or a spectrometer and the detection voltage, V λ , can be modeled by [2]

$$V_{\lambda } = f_{\text{v}} E({\mathbf{m}}_{\lambda } )\frac{6\pi }{\lambda }\eta w_{\text{e}} E_{{{\text{b}},\lambda }} (T_{\text{p}} ) = f_{\text{v}} E({\mathbf{m}}_{\lambda } )\frac{{12\pi c^{2} h}}{{\lambda^{6} }}\eta w_{\text{e}} \left[ {\exp \left( {\frac{{C_{1} }}{{\lambda T_{\text{p}} }}} \right) - 1} \right]^{ - 1} ,$$
(6)

where C 1 = hc/k B, h is Planck’s constant, c is the speed of light, k B is the Boltzmann constant, λ is a measurement wavelength, f v is the soot volume fraction, E(m λ ) is the absorption efficiency at λ, η is the calibration coefficient that accounts for photoelectric conversion and optical collection efficiencies, w e is the equivalent laser sheet thickness, and E b,λ (T p) is the emissive power of a blackbody at the measurement wavelength and particulate temperature, T p.

Fig. 1
figure 1

Illustration of a typical setup for an LII experiment

Full size image

In AC-LII, it is common practice to approximate the temperature distribution of laser-energized nanoparticles by a single “effective” temperature inferred using the two measurement voltages recorded at the detection wavelengths,

$$\frac{{V_{{\lambda_{1} }} }}{{V_{{\lambda_{2} }} }} = \frac{{f_{\text{v}} E({\mathbf{m}}_{{\lambda_{1} }} )\frac{6\pi }{{\lambda_{1} }}\eta w_{\text{e}} E_{{{\text{b}},\lambda_{1} }} (T_{\text{e}} )}}{{f_{\text{v}} E({\mathbf{m}}_{{\lambda_{2} }} )\frac{6\pi }{{\lambda_{2} }}\eta w_{\text{e}} E_{{{\text{b}},\lambda_{2} }} (T_{\text{e}} )}} = \frac{{E({\mathbf{m}}_{{\lambda_{1} }} )\lambda_{2}^{6} \left[ {\exp \left( {\frac{{C_{1} }}{{\lambda_{2} T_{\text{p}} }}} \right) - 1} \right]}}{{E({\mathbf{m}}_{{\lambda_{2} }} )\lambda_{2}^{6} \left[ {\exp \left( {\frac{{C_{1} }}{{\lambda_{2} T_{\text{p}} }}} \right) - 1} \right]}}.$$
(7)

By invoking Wien’s approximation, exp[C 1/(λT p)] ≫ 1, Eq. (7) can be rearranged to obtain the effective temperature,

$$T_{\text{e}} = \frac{{C_{1} \left( {\frac{1}{{\lambda_{2} }} - \frac{1}{{\lambda_{1} }}} \right)}}{{\ln \left( {\frac{{V_{{\lambda_{1} }} \lambda_{1}^{6} E({\mathbf{m}}_{{\lambda_{2} }} )}}{{V_{{\lambda_{2} }} \lambda_{2}^{6} E({\mathbf{m}}_{{\lambda_{1} }} )}}} \right)}}.$$
(8)

Since the absorption cross section and sensible energy of soot primary particles are both proportional to the particle volume, the peak temperature of the soot primary particles should be nearly uniform provided that the laser fluence is spatially uniform. Consequently, in principle, the peak soot temperature is accurately modeled by T e, even in the case of a polydisperse particle size distribution, provided that the ratio E(m λ2)/E(m λ1) is known. At longer cooling times, the primary particle temperatures vary increasingly with variations in primary particle diameters, and consequently the effective temperature can be interpreted as a representative temperature of the ensemble, skewed toward the temperature of larger nanoparticles.

In general, however, the laser fluence profile is not uniform across the laser sheet, and consequently the peak temperature of soot particles obeys a distribution having a finite width. When a non-uniform laser sheet is considered the detection voltages are given by

$$V_{\lambda } = f_{\text{v}} E({\mathbf{m}}_{\lambda } )\frac{{12\pi c^{2} h}}{{\lambda^{6} }}\eta \int\limits_{x} {\left[ {\exp \left( {\frac{{C_{1} }}{\lambda T(x)}} \right) - 1} \right]^{ - 1} } {\text{d}}x,$$
(9)

where T(x) is the particulate temperature along the detector viewing axis across the laser sheet. The effective temperature coupled with the equivalent laser sheet thickness gives the approximation

$$w_{\text{e}} \left[ {\exp \left( {\frac{{C_{1} }}{{\lambda T_{\text{e}} }}} \right) - 1} \right]^{ - 1} = \int\limits_{x} {\left[ {\exp \left( {\frac{{C_{1} }}{\lambda T(x)}} \right) - 1} \right]^{ - 1} } {\text{d}}x.$$
(10)

By using the effective temperature estimate with the corresponding equivalent laser sheet thickness and rearranging Eq (6), the soot volume fraction can be estimated as

$$f_{\text{v}} = \frac{{V_{\lambda } }}{{E({\mathbf{m}}_{\lambda } )\frac{6\pi }{\lambda }\eta w_{\text{e}} E_{{{\text{b}},\lambda }} (T_{\text{e}} )}},$$
(11)

where λ is either λ 1 or λ 2 .

This estimate relies on knowledge of all parameters from the measurement model, which are imperfectly known at best. Through the use of Bayesian techniques we can incorporate this uncertainty into the estimation process, and consequently quantify the propagation of this uncertainty into the soot volume fraction estimate. In particular, we estimate the posterior density for both soot volume fraction and particulate temperature while marginalizing over the other parameters in the voltage model.

3 Bayesian estimation

There are two main differences between the approaches that dominate the LII literature and the Bayesian framework: (1) the Bayesian framework treats the QoI, in this case f v and T p, as well as ancillary model parameters and the measurement data, as random variables that obey a joint distribution, rather than having a single fixed value; and (2) the Bayesian framework integrates the information obtained from the measurement process, with all the knowledge available prior to the measurements (e.g., from other measurements and scientific theory) into a minimum covariance estimate.

Accordingly, the solution to an estimation problem within the Bayesian framework is the posterior density from Eq. (1), which can be rephrased with x = [f v, T p]T and b = v λ  = [V λ1, V λ2]T as

$$\pi \left( {f_{\text{v}} ,T_{\text{p}} |{\mathbf{v}}_{\lambda } } \right) = \frac{{\pi \left( {{\mathbf{v}}_{\lambda } |f_{\text{v}} ,T_{\text{p}} } \right)\pi_{\text{pri}} \left( {f_{\text{v}} ,T_{\text{p}} } \right)}}{{\pi \left( {{\mathbf{v}}_{\lambda } } \right)}} \propto \pi \left( {{\mathbf{v}}_{\lambda } |f_{\text{v}} ,T_{\text{p}} } \right)\pi_{\text{pri}} \left( {f_{\text{v}} ,T_{\text{p}} } \right).$$
(12)

In the present case, the observed voltages can be modeled as a function of the volume fraction and peak temperature, denoted hereafter as \(v_{\lambda }^{\bmod } \left( {f_{\text{v}} ,T_{\text{p}} ;E\left( {{\mathbf{m}}_{\lambda } } \right)} \right)\). In LII, the measurement noise is traditionally modeled as centered normally distributed [6], so the likelihood can be written as

$$\begin{aligned} \pi \left( {v_{\lambda } |f_{\text{v}} ,T_{\text{p}} } \right) = \pi_{e} \left[ {v_{\lambda } - v_{\lambda }^{\bmod } \left( {f_{\text{v}} ,T_{\text{p}} ;E(m_{\lambda } )} \right)} \right] \hfill \\ \propto \exp \left\{ { - \frac{1}{2}\left[ {v_{\lambda } - v_{\lambda }^{\bmod } \left( {f_{\text{v}} ,T_{\text{p}} ;E(m_{\lambda } )} \right)} \right]^{T} \varGamma_{e}^{ - 1} \left[ {v_{\lambda } - v_{\lambda }^{\bmod } \left( {f_{\text{v}} ,T_{\text{p}} ;E(m_{\lambda } )} \right)} \right]} \right\}, \hfill \\ \end{aligned}$$
(13)

where Γ e is the covariance matrix of the measurement noise cf [13, 20, 21].

Random variables in these problems are often summarized by point and spread estimates. Common point estimates are the maximum a posterior (MAP) or maximum likelihood (MLE) estimates, which correspond to the soot volume fraction and particulate temperature that maximize the posterior and likelihood densities, respectively. When a completely “uninformed” prior is used (i.e., π pri = 1) the MAP and MLE estimates coincide. Both the MAP and MLE estimates are computed using nonlinear optimization techniques; when the likelihood and posterior are Gaussian, the optimization problem involves quadratic programming techniques which are computationally efficient.

The Bayesian paradigm allows the estimation of the level of uncertainty through spread estimates. A typical spread estimate is defined by a credibility interval, or more generally, a credibility set. The α % posterior credibility set S α is chosen so

$$\mathop \smallint \nolimits_{{S_{\alpha } }}^{{}} \pi ({\mathbf{x}}|{\mathbf{b}})\;d{\mathbf{x}} = \frac{\alpha }{100}.$$
(14)

When dealing with multiple variables, it is typical to compute the credibility intervals for each variable using marginal distributions. Equation (14) must be augmented with an additional constraint to define a unique credibility set; the most intuitive choice is to define them so that the probabilities of an estimate falling above or below the estimate are equal; such credibility intervals are called equal tail credibility intervals. If the distribution is highly skewed, however, the resulting credibility intervals will be very wide. In this scenario, one can instead compute highest posterior density (HPD) credibility intervals, where the probability densities at the lower and higher interval limits are equal. Figure 2 schematically shows the difference in these two definitions. In this paper, we compute 90 % HPD credibility intervals.

Fig. 2
figure 2

Illustration of 95 % intervals computed using the equal tail (solid line) and highest posterior density (dashed line) methods

Full size image

As shown in Eqs. (1) and (12), the evidence, π(b), is needed to scale the posterior density so as to satisfy the Law of Total Probabilities; this step is essential for calculating uncertainty estimates through credibility intervals. As noted in the Introduction, carrying out the integral shown in Eq. (2) can be computationally difficult if x is high dimensional [21]. Instead, sampling methods, like Markov chain Monte Carlo (MCMC) simplify this integration. Markov chain Monte Carlo methods generate a sequence of random samples where each subsequent sample is accepted or rejected based on the relative value of the posterior at the current and sampled location. Although this means that there is a local correlation between the points, on a grander scale, it can be shown that the sequence of random samples generated through this technique is ergodic to the posterior distribution [22]. These samples can then be used to compute MAP or MLE estimates and credibility intervals.

The LII voltage model in Eq. (6) contains parameters, such as η, E(m λ ), and w e , other than the QoI, f v and T p. In the Bayesian lexicon these are “nuisance parameters.” In this work we treat the calibration coefficient, η, and the equivalent laser sheet thickness, w e , as deterministic and known, while E(m λ ) is treated as an unknown random variable that obeys a distribution. A typical approach to account for the uncertainty in E(m λ ) is to include it in x and simultaneously estimate it with f v and T p using Eq. (1). We attempted this, but found that the multiplicative relationship between f v and E(m λ ) gave the posterior density a long shallow ridge topography, which prevented the Markov chain from converging. Sipkens et al. [11] encountered a similar problem when trying to simultaneously estimate the particle size and thermal accommodation coefficient from TiRe-LII measurements on molybdenum nanoparticles. To circumvent this issue, we directly marginalize the absorption efficiency over the posterior, thereby eliminating the problems with this multiplicative relationship while simultaneously incorporating uncertainty in E(m λ ). Marginalizing over E(m λ) gives a likelihood function that applies for all possible values of E(m λ ), conditional on its probability density.

Since the only density in Eq. (12) which depends on E(m λ ) is the likelihood, we marginalize E(m λ ) over the likelihood

$$\pi \left( {{\mathbf{v}}_{\lambda } |f_{\text{v}} ,T_{p} } \right) = \int_{ - \infty }^{\infty } \pi \left[ {{\mathbf{v}}_{\lambda } |f_{\text{v}} ,T_{p} ,E\left( {{\mathbf{m}}_{\lambda } } \right)} \right]\pi_{\text{pri}} \left[ {E\left( {{\mathbf{m}}_{\lambda } } \right)} \right]\;{\text{d}}E\left( {{\mathbf{m}}_{\lambda } } \right),$$
(15)

and carry out the integral using Simpson’s rule for a range of values of f v, T p, and E(m λ ).

4 Defining a prior for the absorption function

The use of a fixed value or function for E(m λ ) when inferring QoI from LII data is an inappropriate choice, since this will understate the posterior density widths and cause the LII practitioner to misinterpret and place too much confidence in the results. On the other hand, it is also unreasonable to treat E(m λ ) as an “unknown” since some information is available about this parameter, and, from a practical standpoint, excluding prior information about E(m λ ) would result in an indefinite posterior density as described above. Accordingly, it is of paramount importance to define a reasonable prior distribution for E(m λ ).

There is considerable variation in the reported magnitude and wavelength dependence of the absorption function for soot, e.g., Ref. [16] and references therein. By considering these trends, and assessing the techniques used to derive such values, one can assess the general state of knowledge of E(m λ ). Coderre et al. [23] and Crosland et al. [10] attempt to reduce this variation by rationally filtering some of the reported optical properties on the basis of known deficiencies with the data collection or analysis. Unfortunately, even after filtering, there still exists a large variation of reported E(m λ ) in the literature that reflects the state of knowledge of the optical properties of soot; this variation should be reflected in the prior distribution.

Typical soot generated by combustion has a fractal aggregate structure composed of nearly spherical primary particles of approximately the same size as shown in Fig. 3. Absorption and scattering of light by soot aggregates is most often modeled by Rayleigh-Debye-Gans fractal aggregate (RDG-FA) theory [24]. While the scattering cross section of a soot aggregate increases nearly geometrically with the number of primary particles per aggregate, RDG-FA theory models the absorption cross section of the soot aggregate as the arithmetic superposition of the absorption by primary particles, which gives rise to Eqs. (4)–(6). Recent work casts some doubt on this simplification, however. Liu and Smallwood [25] and Yon et al. [26] used generalized multi-sphere Mie-solution (GMM) and the discrete dipole approximations (DDA) to calculate the scattering and absorption of soot aggregates in a sample volume and found that absorption by the aggregates in a sample volume is not exactly proportional to the superposition of the absorption by the primary particles. Although using RDG-FA theory to infer E(m λ ) from extinction measurements will introduce an error in the inferred E(m λ ) values, the error is somewhat mitigated if RDG-FA theory is also used to model absorption using biased E(m λ ) values (i.e., the inverse procedure), so in this work we neglect this source of uncertainty.

Fig. 3
figure 3

Soot aggregate imaged with a transmission electron microscope

Full size image

Other uncertainties in E(m λ ) arise from the uncertain origin of the soot particles. Some studies suggest that the absorption function changes with the H/C ratio [27, 28]. Other work found that changes in the H/C ratio may be informative, but other factors, such as height above burner, explain the variations in a more direct way [29, 30]. Cléon et al. [31] found that the absorption function varied with the age of the soot and Therssen et al. [32] demonstrated that the height above the burner has a similar effect, which was confirmed in Bladh et al. [33]. This behavior has been attributed to the existence of polycyclic aromatic hydrocarbons (PAHs), which absorb and emit light in the ultraviolet and visible wavelengths.

These manifold uncertainties are reflected in the range of reported E(m λ ) values for soot, which are plotted in Fig. 4. Values range (approximately) from 0.18 to 0.42. One common feature is that E(m λ ) is relatively flat across the visible spectrum, with the exception of Chang and Charalampopoulos [34] and Stagg and Charalampopoulos [35], who applied the dispersive (Drude) properties of graphite to soot to interpret their measurements, and found that E(m λ ) increases with wavelength below 500 nm. This feature is not observed by Coderre et al. [23], Krishnan et al. [36] and Kolyu and Faeth [37], however, which calls into question whether the dispersive properties of graphite can be applied to soot.

Fig. 4
figure 4

Values of E(m λ ) of soot from the literature

Full size image

Furthermore, the uncertainty in the value of E(m λ ) can change with the setting in which the estimation is being conducted. For example, one would expect a greater degree of uncertainty associated with the optical properties of atmospheric black carbon, given its ambiguous origin and age, compared to soot generated under specific laboratory conditions. This difference in information would subsequently be reflected in the prior through different variances placed on E(m λ ) for these two situations.

The choice of prior distribution can often compensate for the information deficit present in ill-posed problems, but it should not unduly bias the posterior density toward a subjective prior belief or expectation, i.e., a “self-fulfilling prophecy.” This strategy descends from the principle of indifference, which, loosely stated, argues that possible outcomes should be assigned equal probabilities in the absence of any additional information [38]. (A more detailed discussion is provided in [19].) Consequently, prior distributions that satisfy the idea of “fairness” exhibited by the principle of indifference can be generated by maximizing the information entropy subject to constraints derived from testable information. We do this using maximum entropy priors [38–40], which are compatible with testable information (i.e., information that can be assessed for veracity through experimental means) and otherwise have minimal information content, which scales inversely with the information entropy

$$h(x) = - \int {\pi (x)\ln [\pi (x)]\;{\text{d}}x} .$$
(16)

The foundation for this approach comes from Shannon’s [40] and Jaynes’ pioneering work [38, 39] on information theory, which argued that the information content of a probability density can be quantified as inversely proportional to its information entropy, which is analogous to entropy in thermodynamics. (In fact, Jaynes argues that thermodynamic entropy is a special case of information entropy [19].)

In the case of no testable information, no constraint is imposed and the information entropy is maximized by a uniform prior density. If the only information available is that the variable falls between two values, x∈[a, b], then the maximum entropy distribution will be a uniform distribution, or “plausible interval” π pr(x) = 1/(b − a), x∈[a, b], and π pr(x) = 0 otherwise [41]. If a point estimate and approximate distribution width of the random variables are known, the information entropy is maximized by a normal distribution with a mean equal to the point estimate and the standard deviation reflecting the known distribution width [19].

Being mindful of all these consideration, we propose two priors for E(m λ ): The first prior is for a case where there is little to no specific information on the origin of the soot, i.e., atmospheric measurements. In this scenario the prior should reflect the increased level of uncertainty and incorporate more of the reported values, the majority of which fall between 0.18 and 0.42 with the bulk of reported values around 0.3. (As shown in Fig. 4, the majority of studies report that E(m λ ) is constant with respect to wavelength, particularly in the case of “aged” soot [42].) Based on this observation, we propose a maximum entropy prior π W[E(m λ )] that models E(m λ ) as obeying a normal distribution with mean of 0.3 and standard deviation of 0.04, invariant of wavelength. A second prior is built to represent the uncertainty of E(m λ ) for soot generated based on the results of Coderre et al. [23] which is a well-characterized burner in terms of the uncertainty in E(m λ ). In this case we propose a prior distribution π T[E(m λ )] which is a Gaussian with a mean of 0.36 and standard deviation of 0.02. Figure 5 plots sample draws from these priors over experimental E(m λ ) data for both cases.

Fig. 5
figure 5

Plot of a the specific prior π W (purple diamonds) and b the general prior π T (green diamonds) with values found in literature

Full size image

5 Marginalization of the absorption parameter

In order to see how the uncertainty of the absorption parameter impacts the estimated posterior for SVF, we consider a series of estimates using simulated LII measurements. The simulated data, denoted by v λ , was generated by evaluating Eq. (6) when f v = 2 ppm, T p = 3950 K, η = 1, w e = 2.1 mm, λ 1 = 445 nm, λ 2 = 750 nm; these parameter values approximately correspond to measurements from a laminar diffusion flame [43]. The simulated data were corrupted by uncorrelated centered Gaussian noise with covariance Γ e corresponding to a standard deviation equivalent to 2 % of the simulated voltages, which is typical of electron shot noise present in measurements made using photomultiplier tubes [10]. The data were simulated assuming E(m λ1) = 0.356 and E(m λ2) = 0.376. In principle it would be possible to accommodate spectral variation of E(m λ ) through the prior, which would result in a greater level of uncertainty in the temperature estimates. In this work, however, we have chosen to derive the priors assuming that E(m λ ) is constant with respect to wavelength for three reasons: (1) This more accurately reflects the prior state of knowledge, which is imperfect as summarized in Fig. 4; (2) it simplifies the model so the focus will be on the Bayesian techniques introduced; and (3) it avoids “inverse crimes,” which arise when the data are perfectly compatible with the model and measurement noise is neglected [44].

Since there are only two QoI, f v and T p, we compute the posterior density through direct evaluation, instead of employing MCMC or similar techniques. This involves computation of the right hand side of the proportionality in Eq. (12) and scaling the resultant function, so it integrates to unity. The integral used to marginalize E(m λ ) over the likelihood was computed using Simpsons rule.

In order to see the effect of prior information and the marginalization of the absorption parameters, the posterior is computed for a range of situations. This computation is presented in two stages: In Sect. 5.1, the likelihood density is computed for various types of prior information regarding the absorption parameters; while in Sect. 5.2 the posterior density is computed with three different prior models for SVF and peak temperature.

5.1 Computation of the likelihood

In computing the posterior density for SVF and temperature, the first step is to calculate the likelihood density. Using the simulated data, we compute the likelihood density corresponding to two scenarios: assuming a fixed assumed value for absorption efficiency, which reflects the current standard of practice followed by most LII practitioners, and the marginalization of the absorption efficiency over the likelihood calculated using the priors models discussed at the end of Sect. 4. In Fig. 6 the two priors for the absorption efficiency are plotted alongside the true values of E(m λ1) and E(m λ2) used to generate the simulated measurements. These values agree well with the tight distribution π T, but lie on the edges of the wide distribution π W; this is done to highlight the effect of using badly chosen prior information. Specifically, we compute:

Fig. 6
figure 6

Plot of the prior densities used for the absorption efficiency and the values used to simulate the measurements. The dashed lines correspond to the E(m λ ) values used to generate the measurements

Full size image
  1. 1.

    The likelihood when E(m λ1) and E(m λ2) are assumed to equal 0.3, which is the mean of π W

    $$\pi_{{{\text{L}}_{1} }} (v_{\lambda } |f_{\text{v}} ,T_{\text{p}} ) = \pi_{e} [v_{\lambda } - v_{\lambda }^{\bmod } (f,T_{\text{p}} ;0.3)] = \frac{1}{{2\pi \sqrt {|\varGamma_{e} |} }}\exp \left( { - \frac{1}{2}\left\| {L_{e} \left[ {v_{\lambda } - v_{\lambda }^{\bmod } (f,T_{\text{p}} ;0.3)} \right]} \right\|^{2} } \right),$$
    (17)

    where L e denotes the Cholesky factor of Γ −1 e .

  2. 2.

    The likelihood when E(m λ1) and E(m λ2) are assumed to equal 0.36, which is the mean of π T

    $$\pi_{{{\text{L}}_{2} }} ({\mathbf{v}}_{\lambda } |f_{\text{v}} ,T_{\text{p}} ) = \pi_{e} [{\mathbf{v}}_{\lambda } - {\mathbf{v}}_{\lambda }^{\bmod } (f,T_{\text{p}} ;0.36)] = \frac{1}{{2\pi \sqrt {|\varGamma_{e} |} }}\exp \left( { - \frac{1}{2}\left\| {L_{e} \left[ {{\mathbf{v}}_{\lambda } - {\mathbf{v}}_{\lambda }^{\bmod } (f,T_{\text{p}} ;0.36)} \right]} \right\|^{2} } \right).$$
    (18)
  3. 3.

    The likelihood when E(m λ1) = E(m λ2) = E(m λ ) is marginalized and π W is used as the distribution of E(m λ )

    $$\pi_{{{\text{L}}_{3} }} ({\mathbf{v}}_{\lambda } |f_{\text{v}} ,T_{\text{p}} ) = \mathop \smallint \nolimits_{0}^{\infty } \pi_{e} \left[ {{\mathbf{v}}_{\lambda } - {\mathbf{v}}_{\lambda }^{\bmod } [f,T_{\text{p}} ;E({\mathbf{m}}_{\lambda } )]} \right]\pi_{W} \left[ {E({\mathbf{m}}_{\lambda } )} \right]\;\text{d}E({\mathbf{m}}_{\lambda } ).$$
    (19)
  4. 4.

    The likelihood when E(m λ1) = E(m λ2) = E(m λ ) is marginalized and π T is used as the distribution of E(m λ )

    $$\pi_{{{\text{L}}_{4} }} ({\mathbf{v}}_{\lambda } |f_{\text{v}} ,T_{\text{p}} ) = \mathop \smallint \nolimits_{0}^{\infty } \pi_{e} \left[ {{\mathbf{v}}_{\lambda } - {\mathbf{v}}_{\lambda }^{\bmod } [f,T_{\text{p}} ;E({\mathbf{m}}_{\lambda } )]} \right]\pi_{T} \left[ {E({\mathbf{m}}_{\lambda } )} \right]\;\text{d}E({\mathbf{m}}_{\lambda } ).$$
    (20)

It is worth noting that, in the context of information entropy, the information content of the absorption parameter prior varies inversely with width; π W is least informative, while the point estimates of E(m λ ) (0.3 and 0.36) have an information entropy of zero.

The contours of estimated likelihood densities of the soot volume fraction are depicted in Fig. 7. The marginal distributions for the temperature are approximately the same for all the likelihood densities. This indicates that the measurements contain a high level of information about the temperature of the soot in the aerosol when the absorption function is assumed to be constant. This stability would disappear if spectral variations of the absorption efficiency were considered. Also, we can see that in all cases the temperature corresponding to the peak of the densities (which is the maximum likelihood estimate) is smaller than the true value. This is also partly due to the fact that E(m λ ) has been incorrectly specified. As a result we expect soot volume fraction to be overestimated since temperature and soot volume fraction are negatively correlated [10].

Fig. 7
figure 7

The four different estimated likelihood densities π L1 (red), π L2 (yellow), π L3 (blue), π L4 (green). Ovals correspond to contours at 5 % of the peak value of the likelihood density. Histograms show the marginalized distributions for f v (above plot) and T p (right of plot). A single marginalized distribution is shown for T p as the distributions for all four likelihoods are nearly identical

Full size image

Table 1 summarizes the maximum likelihood estimates and the associated 90 % credibility intervals. The MLE estimates and credibility intervals for particulate temperature are all the same and are close to the true value, further indicating that the voltage measurements are informative about the particulate temperature. We can see that using a fixed value for the absorption efficiency (π L1 and π L2) results in credibility intervals which are narrow but do not contain the true value of soot volume fraction. When the absorption efficiency is marginalized (π L3 and π L4), on the other hand, the credibility intervals do contain the true value and are wider due to the additional uncertainty from the prior model of E(m λ ).

Table 1 MLE estimates and credibility intervals of soot volume fraction, in ppm, and peak temperature, in K, for the different likelihood models
Full size table

5.2 Computation of the posterior

The next steps are to select priors for the parameters to be estimated, f v and T p, and subsequently compute the posterior. We compute the posterior associated with the four likelihood densities from above (π L1, π L2, π L3, and π L4) found by marginalizing E(m λ ) with associated prior models. To illustrate the influence of the prior distribution the posterior is computed for three different types of prior information for f v and T p. In practice this prior information is informed by previous LII experiments, published data from similar experiments, numerical simulations, or general physical arguments. The first set of posteriors is computed when we expect soot volume fraction to fall between 1 ppm and 3 ppm and temperature to fall between 3500 K and 4000 K; in the maximum entropy formalism this prior knowledge results in a uniform distribution, denoted π pri1. The next set of posteriors is computed when a point estimate of f v and T p are known and expected; specifically, we expect f v = 2 ppm and T p = 3750 K. An exponential distribution maximizes information entropy when a point estimate of f v or T p is known. Hence, the prior corresponding to a point estimate treats f v and T p as independent exponential random variables with expectation set at 2 ppm and 3750 K, respectively. We shall denote the use of the exponential prior by π pri2. The final form of information is a combination of the first two, i.e., estimates of the distribution centers and widths. We expect that f v will be around 2 ppm and will rarely fall lower than 1 ppm and above 3 ppm; further, we expect the temperature to fall between 3500 and 4000 K and will have a value around 3750 K. In this case, information entropy is maximized by modeling f v and T p as independent normally distributed random variables with density denoted π pri3, with means of 2 ppm and 3750 K and standard deviations of 0.5 ppm and 125 K, respectively.

5.2.1 Uniform prior

An image of the uniform prior and the 5 % contours of the posterior for each of the likelihoods are shown in Fig. 8a, b, respectively. As we can see, there is no change in the distributions, except for π L3, when compared to Fig. 7. The uniform prior treats all points in the plausible set as being equally probable; consequently the only effect it has on the likelihood densities is to truncate values which are outside this plausible set. This effect is seen directly with π L3; here the long upper tail of the likelihood, due to the wide distribution used to marginalize E(m λ ), has been truncated as those values for soot volume fraction fall outside of the plausible set, whereas the other three densities (π L1, π L2 and π L4) are unaffected by the uniform prior, as over 99.99 % of the area under these densities fall completely within the plausible set. This behavior is further evident in Table 2, which summarizes the MAP estimates and the associated 90 % credibility intervals; the credibility interval estimates are unchanged when compared to Table 1, with the exception of the π L3. The uniform prior means the posterior corresponding to π L3 is truncated. This results in more weight on, and thus a higher probability density allocated to, the peak of the distribution. Hence, as there is now greater probability allocated to a smaller set, the HPD credibility intervals for this posterior are narrower than those computed for the π L3 likelihood density. Consequently, the credibility interval no longer contains the true value for the soot volume fraction.

Fig. 8
figure 8

Plot of a π pri1 which is the uniform prior for soot volume fraction and temperature, and b the four different estimated posterior densities corresponding to the following likelihoods: π L1 (red), π L2 (yellow|), π L3 (blue), π L4 (green). Ovals correspond to contours at 5 % of the peak value of the posterior density. Plots along the edges are the marginalized distributions for f v (above plot) and T p (right of plot). Note that the scales on the prior and posterior plots do not match

Full size image
Table 2 The MAP estimates and credibility intervals of soot volume fraction, in ppm, and peak temperature, in K, for the different likelihood densities when a uniform prior, πpri1 is used
Full size table

5.2.2 Exponential prior

An image of the exponential prior, π pri2, and the 5 % contours of the posteriors corresponding to each of the likelihood densities is shown in Fig. 9a, b, respectively. The exponential prior contains little information (i.e., it is wide) and prefers smaller values for f v and T p, so we can see the posterior distributions are slightly shifted. Table 3, which summarizes the MAP estimates and the associated 90 % credibility intervals, shows the same behavior with each of the MAP estimates being smaller than the MLE estimates and the 95 % percentile containing the greatest shift for each estimate. This shift in the posterior is small but improves over the uniform prior since the true value of soot volume fraction now falls inside the credibility interval for both cases where E(m λ ) has been marginalized. Also note that when the likelihood models π L1 and π L2 are used, the resulting posterior is barely affected by the exponential prior; this is because the prior contains very little information compared to the measurements. The results for the temperature behave in a similar way. The measurements contain a large amount of information about the temperature so the application of this prior leaves the marginal posterior density for temperature unmoved.

Fig. 9
figure 9

Plot of: a The exponential prior, π pri2, for soot volume fraction and temperature; b The four different estimated posterior densities corresponding to the following likelihoods: π L1 (red), π L2 (yellow), π L3 (blue), π L4 (green). Ovals correspond to contours at 5 % of the peak value of the posterior density. Plots along the edges are the marginalized distributions for f v (above plot) and T p (right of plot). Note that the scales on the prior and posterior plots do not match

Full size image
Table 3 The MAP estimates and credibility intervals of soot volume fraction, in ppm, and peak temperature, in K, for the different likelihood densities when πpri2, the exponential prior, is used
Full size table

5.2.3 Gaussian prior

An image of the Gaussian prior and the 5 % contours of the posterior for each of the likelihoods are shown in Fig. 10a, b, respectively. This prior contains the most information (a point and a spread estimate); consequently the resulting posterior densities are the most changed compared to the corresponding likelihood densities. The densities in which E(m λ ) is marginalized (π L3 and π L4) have been affected most; since these distributions are the widest, the information contained in the prior has a greater influence on the posterior densities. Consequently, the centers of the posteriors are shifted and the spread is reduced. In Table 4, which summarizes the MAP estimates and the associated 90 % credibility intervals, we can see that the information introduced by the prior has produced credibility intervals that contain the true value, except when the value of 0.3 was used for E(m λ ). Again, the posterior distribution of the temperature is virtually unchanged in comparison to the likelihood density.

Fig. 10
figure 10

Plot of a The Gaussian prior, π pri3, for soot volume fraction and temperature b The four different estimated posterior densities corresponding to the following likelihoods: π L1 (red), π L2 (yellow), π L3 (blue), π L4 (green). Ovals correspond to contours at 5 % of the peak value of the posterior density. Plots along the edges are the marginalized distributions for f v (above plot) and T p (right of plot). Note that the scales on the prior and posterior plots do not match

Full size image
Table 4 The MAP estimates and credibility intervals of soot volume fraction, in ppm, and peak temperature, in K, for the different likelihood densities when a Gaussian prior is used
Full size table

5.3 Application to laboratory measurements

As a final demonstration we apply the methodology described above to experimental AC-LII measurements carried out on a laminar diffusion flame generated with a coflow burner operating under conditions described in [45]. LII measurements were made at a height of 42 mm above the flame, using a 1064-nm Nd:YAG laser with a fluence of 6.5 mJ per pulse and firing with a rate of 10 Hz. A laser fluence which is approximately uniform was obtained through relay imaging. Incandescence from the laser-energized soot particles are imaged onto two photomultiplier tubes equipped with narrow bandpass filters centered at 420 and 780 nm. Voltages are measured at a sampling interval of approximately 1 ns, and the peak voltage from each channel is taken to correspond with the peak spectral incandescence at each detection wavelength. A more detailed description of the LII apparatus is provided in [45].

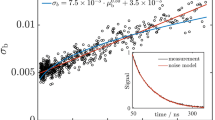
The measurement data, shown in Fig. 11, consist of peak PMT voltages from 100 sequential laser shots. The mean and variance of these shots were used as inputs in the Gaussian error model described in Eq. (13). While it is common practice among LII practitioners to simply use the average of the shot data, considering the variance of shot data allows an accurate characterization of the measurement error, which further improves the quality of the estimated uncertainty.

Fig. 11
figure 11

The 100 peak voltages from the two detection wavelengths, blue circles for 420 nm and red circles for 780 nm, with the mean values used as the measurements and associated two standard error bounds used for the variance are shown by the black solid and dashed lines respectively

Full size image

All nuisance parameters, apart from E(m λ ), are treated as deterministic and known. Calibration coefficients were computed using the approach of Snelling et al. [2] which gave values of η λ1 = 9.337 × 10−8 and η λ2 = 3.552 × 10−8 at 420 and 780 nm, respectively. Similarly, Snelling et al.’s approach was used to compute the equivalent laser sheet thickness when the detection angle was 33.7° giving a value of w e = 4.531 mm.

The likelihood densities are calculated using Eqs. (17)–(20), when the four different priors for E(m λ ) are used (note the same notation will be used as above). These likelihood densities, along with the three maximum entropy priors defined in the previous section, are used to compute the corresponding posterior densities. The densities computed from the laboratory measurements, shown in Fig. 12, and computed estimates, in Table 5, demonstrate much the same behavior as those found using simulated measurements. When a prior with a greater level of information is used the resultant distribution has a smaller spread; this is seen with both the priors on E(m λ ) and those placed on f v and T p. As was the case with simulated data, the probability density of T p inferred from experimental PMT voltages are largely unaffected by the choice of prior information. This is largely due to treating E(m λ ) as constant over wavelength is a simplification which loses much of the uncertainty present in T.

Fig. 12
figure 12

a Contours of the likelihood densities π L1 (red), π L2 (yellow), π L3 (blue), and π L4 (green) computed using the laboratory measurements. b Contours of the posterior densities computed from the likelihood densities when a Uniform prior is used. c Contours of the posterior densities computed from the likelihood densities when an Exponential prior is used. d Contours of the posterior densities computed from the likelihood densities when a Gaussian prior is used

Full size image
Table 5 The MAP estimates and posterior credibility intervals when the various likelihood densities and priors are used to infer soot volume fraction, in ppm, and peak temperature, in K, from experimental data
Full size table

6 Conclusions

In order to properly interpret soot volume fractions inferred from auto-correlated LII data, practitioners must qualify their measurements with estimates of the uncertainty that arise from both measurement noise and model parameter uncertainty. The present work presents a methodology that quantifies how these uncertainties impact the accuracy of soot volume fraction and peak temperature estimates by quantifying photomultiplier shot noise and model parameter uncertainty, and then uses Bayes’ equation to compute posterior densities of the quantities of interest. Point estimates can be obtained from the MAP estimate (or MLE estimate, if an uninformative prior is used), while credible intervals for each parameter of interest can be found from the corresponding marginalized posterior density. Bayes’ equation also facilitates incorporation of prior knowledge about the unknown parameters through Bayesian priors. This must be done with care to avoid introducing overly subjective interpretations of the prior information, which can unduly bias the posterior densities. We do this using maximum entropy priors, distributions which maximize information entropy subject to imposed constraints derived from testable information.

Inferred soot volume fraction and peak soot temperatures depend on the absorption function, E(m λ ). While there is little consensus in the literature on the value of E(m λ ), the majority of studies suggests that the absorption function is nearly constant over the wavelengths important to LII. Through the use of the maximum entropy principle, we proposed statistical priors for two different cases: a distribution which represents the overall state of knowledge of E(m λ ), appropriate for measurements on atmospheric soot of unknown origin, and a narrower distribution in which E(m λ ) is known with greater certainty, corresponding to a well-characterized soot source.

The uncertainty in the value of E(m λ ) was then considered when estimating the soot volume fraction from simulated and laboratory AC-LII data. While in some cases it is possible to treat nuisance parameters, like E(m λ ), as an additional quantity to be inferred, in this case the strong correlation between f v and E(m λ ) gave rise to a nearly indefinite posterior density topography. Consequently, we account for uncertainty from E(m λ ) by marginalizing the absorption parameters over the likelihood. Prescribing wide prior distributions (which are less informative) for E(m λ ) results in a wide likelihood density. This means the true values for soot volume fraction and temperature fell within the 90 % credibility intervals which were estimated.

We subsequently considered how different forms of prior information on f v and T p, coupled with the Principle of Maximum Entropy, influence the posterior density for these parameters. Three forms of prior information were considered: a plausible set (uniform distribution); a point estimate (exponential distribution); and a point estimate with spread information (normal distribution). In all cases the posteriors showed that the use of a prior with greater information content lead to improved estimates and smaller uncertainty.

When working with real AC-LII measurements a plethora of additional uncertainties are present such as: non-uniform laser fluence; absorption of the LII signal by other species; or errors in the timing of the signals due to minor variations in the photomultipliers and cable lengths. While these uncertainties are excluded from the present analysis, they will be accommodated in the Bayesian paradigm in future work. The Bayesian approach also facilitates design-of-experiment, since experimental parameters, such as the choice of measurement gating time or detection wavelengths, can be chosen to minimize the covariance of inferred QoI.

Furthermore, subsequent work will focus on extending the techniques developed in this paper to estimate the uncertainty associated with the size distribution of soot nanoparticles inferred from TiRe-LII data. Consideration of experimental TiRe-LII data will allow quantification of uncertainty in particle size estimates, and assessment of the computational TiRe-LII model through the use of Bayesian model plausibility techniques.