An effective method for calculating phase-matching conditions in biaxial crystals

Abstract

We present an effective method for calculating phase-matching conditions in biaxial crystals, especially for nonlinear orthorhombic crystals. Exploiting the angle definition introduced by Japanese mathematician Kodaira Kunihiko, we deduce the angular relations in geometry and obtain the expressions of refractive indices depending on angular orientation of wave vector k and optical axis angle. Then, we directly calculate the phase-matching conditions with BIBO crystal in spontaneous parametric down-conversion (SPDC) process and gain the optimum phase matching schemes for the type I and type II. On its basis, we discuss the angular gradients of the pump and emission wave refractive index near the exact phase matching direction and compare the SPDC with double-frequency process in geometrical relations of the refractive index ellipsoids. This method based on angle-dependent refractive index can be applied to three-wave interactions. It is convenient to calculate the phase matching parameters without solving the quadratic Fresnel equations.

1 Introduction

Nonlinear frequency conversion has attracted a great deal of attention because of its applications in laser technology and quantum optics. It is an interaction of light with matter, allowing for no conversion of energy, momentum and angular momentum. Since Franken et al. [1] first found the second-harmonic generation (SHG) in 1961, many others were studied following it, such as sum frequency (SF), difference frequency (DF), optical parametric amplifiers (OPA) and optical parametric oscillator (OPO). As crystal materials develop, nonlinear frequency conversion has made rapid progress in laser sources owing to its simplicity and wavelength flexibility [2–6]. From 1995, the first demonstration of high-efficiency polarization entanglement generation with BBO crystal [7], spontaneous parametric down-conversion (SPDC) in nonlinear crystals has been the mainstay for entanglement production in quantum optics [8, 9]. This entangled photon source based on SPDC has strong correlations beyond the classical physics limitation and has great potential applications in quantum information processing. Nevertheless, the phase mismatching and low nonlinear optical coefficient of uniaxial crystal confine its application in high-intensity source of multi-entangled photon pairs. Thus, there is a renewed interest in calculation of the phase matching parameters for biaxial crystals, especially the applications in non-classical optics.

Generally, nonlinear crystals are classified as uniaxial crystals and biaxial crystals by optical birefringence phenomenon. Comparing with uniaxial crystal, the biaxial crystals normally have two different refractive index ellipsoids, and the traditional ordinary and extraordinary waves are no longer valid. Both the intrinsic polarizations correspond to extraordinary waves, with the wave vector not coinciding with Poynting vector inside crystal. The work about phase-matching conditions must be done accurately, which is influenced by the pump radiation wavelength and crystal temperature. As biaxial crystal has two optical axes with complex optical structure, the calculation of phase matching parameters is so complicated that less work has been done. Yao et al. [10] first calculated phase-matching conditions in biaxial crystals. They make biaxial crystal equivalent to uniaxial crystal, with the two optical axes symmetrically distributed around the wave vector. In the following years, the improved methods for phase matching in biaxial crystals are worked out [11–16]. In these studies, they mainly focus on optical second-harmonic generation, and the refractive indices under phase-matching conditions are all obtained by solving quadratic Fresnel equations. Recently, new nonlinear orthorhombic biaxial crystals have become increasingly important for nonlinear frequency conversion for its highly effective nonlinear coefficient, especially in quantum entanglement generation [17, 18]. We used Yao’s method to calculate the parameters for SPDC process, such as temporal and spatial walk-off, the acceptance angles, spectral acceptance bandwidth and effective nonlinear coefficient. We still do not avoid solving quadratic Fresnel equations. These approaches are complicated and cannot gain the angular derivative of refractive index in phase matching direction, which influences the spatial distribution of entangled photons [19, 20]. In crystal optical, the two refractive indexes of biaxial crystal can be easily worked out by wave normal Fresnel equations with $\theta_{1}$, $\theta_{2}$, which are angles between wave vector and two optical axes. However, there is no knowledge about the angles $\theta_{1}$, $\theta_{2}$ applied in nonlinear frequency conversion. It is worth to explore the angular relation of refractive index in biaxial crystals. This work can introduce a convenient method to calculate the phase-matching conditions, and it is crucial for studying the unique characters of the angular derivative of refractive index in biaxial crystal.

Here, we focus on the angle calculation and angle-dependent refractive index in biaxial crystals and present a straightforward method for calculating the phase matching in SPDC process. Applying the angle definition introduced by Japanese mathematician Kodaira Kunihiko, we deduce the expressions of refractive indices dependent on the angular orientation of wave vector and optical axis angle in biaxial crystal. Then taking biaxial crystal BiB₃O₆ (BIBO) as an example, we calculate the phase-matching conditions and obtain the optimum phase matching directions for two types of collinear phase matching. Comparing the SPDC with double-frequency process in biaxial crystals, we know how to choose the refractive index ellipsoids of the pump and emission waves according to angular gradient of refractive index near the exact phase matching direction. It permits convenient calculation of phase matching parameters in biaxial crystals, and it offers a new way to determine which ellipsoids the pump and emission waves will take.

2 The angular calculation

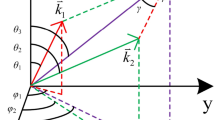
For biaxial crystals under principal coordinates system designated as (xyz), we can calculate refractive index at any directions by wave normal Fresnel equations. However, the crystal parameters, in fact, are measured in crystallographic coordinates system (abc), whose axes are not parallel to those in principal coordinates system. Therefore, in order to find the angle dependence of refractive index, we rotate the principal coordinates system (xyz) $\phi$ around z axis and acquire coordinates $x^{\prime}y^{\prime}z^{\prime}$, and then, we rotate the above coordinate ($x^{\prime}y^{\prime}z^{\prime}$) $\theta$ around $y^{\prime}$ axis and get coordinates $x^{\prime\prime}y^{\prime\prime}z^{\prime\prime}$, where $\theta$ represents the polar angle relative to the optical z axis in plane $x^{\prime}z^{\prime}$ and $\phi$ represents the azimuthal angle measured from x axis in the xy plane. The schematic in Fig. 1 shows the coordinate transformation of dielectric axis (xyz), crystal principal axis (abc) and laboratory frame ($x^{\prime\prime}y^{\prime\prime}z^{\prime\prime}$). The two optical axes designated as C₁ and C₂ distribute symmetrically about z axis, and the angles between z and C₁, C₂ are $\varOmega$, $- \varOmega$, respectively. Moreover, $\theta_{1}$, $\theta_{2}$ are angles between wave vector k and C ₁, C ₂, and $\theta^{\prime}$, $\theta^{\prime\prime}$ are angles between z axis and the projections of k in the yz and xz plane.

Fig. 1

Schematic showing the coordinate transformation of the dielectric axis ($xyz$), the crystal principal axis (abc) and the laboratory frame ($x^{{\prime \prime }} y^{{\prime \prime }} z^{{\prime \prime }}$)

Proved by wave normal Fresnel equations [21], the refractive indexes of two perpendicular linear polarized beams $n_{1,2}$ can be calculated by

$$ \frac{1}{{n_{1,2}^{2} }} = \frac{{\cos^{2} \left[ {\left( {\theta_{1} \pm \theta_{2} } \right)/2} \right]}}{{n_{x}^{2} }} + \frac{{\sin^{2} \left[ {\left( {\theta_{1} \pm \theta_{2} } \right)/2} \right]}}{{n_{z}^{2} }}, $$

(1)

where $n_{x}$ and $n_{z}$ are the indexes in x and z directions, respectively. When we take the upper (lower) sign “+” (“−”) in the two terms of right side, we get $n_{1}$ ($n_{2}$). Thus, the angles $\theta_{1}$ and $\theta_{2}$ are key parameters for calculating the refractive index. More importantly, the derivative of refractive index is crucial for phase-matching conditions in nonlinear frequency conversion and decides the birefringence anisotropy in space distribution which can be applied in the problem of quantum entangled wave packet distribution.

For nonlinear frequency conversion process, we generally express the signal and idler wave vectors in laboratory frame defined by the rotated axes ($x^{{\prime \prime }} y^{{\prime \prime }} z^{{\prime \prime }}$), which is convenient to calculate the output efficiency. In crystal’s dielectric axes (xyz), it is easier to solve the refractive index exerting an influence on phase-matching conditions and birefringence anisotropy. Therefore, in order to applied the crystal parameters at will, we can seek the angular conversion relations between the dielectric axis (xyz) and the laboratory frame ($x^{{\prime \prime }} y^{{\prime \prime }} z^{{\prime \prime }}$) systems. With the method of angle projecting and the angle definition introduced by Japanese mathematician Kodaira Kunihiko [22], we obtain the expressions of $\theta_{1}$, $\theta_{2}$ with usual angles $\varOmega$, $\theta$ and $\phi$ which are presented below.

In dielectric coordinate system, the optical axis angle $\varOmega$ in Fig. 1 can be expressed by [23]

$$ \varOmega = \arcsin \left( {\frac{{n_{z} }}{{n_{y} }}\sqrt {\frac{{n_{y}^{2} - n_{x}^{2} }}{{n_{z}^{2} - n_{x}^{2} }}} } \right) , $$

(2)

where $n_{x}$, $n_{y}$ and $n_{z}$ are the principal refractive indices in x, y and z directions, respectively. They are constants for a given crystal. According to geometrical description in Fig. 1, we project the wave vector k ($\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{OK}$) and line segment $\overline{zK}$ onto zy, xz plane and get the projections $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{OK_{1} }}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{OK_{2} }}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{zK_{1} }}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{zK_{2} }}$, respectively. Then, the value of $\theta$ can be calculated by

$$ \tan \theta = \frac{{\overline{zK} }}{{\overline{Oz} }}. $$

(3)

Since $\overline{{zK_{1} }}$ is the projection of $\overline{zK}$ in yz plane, the edges and angles in the right-angled triangle zK₁K meet the relation of

$$ \overline{{zK_{1} }} = \overline{zK} \cdot \cos (\pi /2 - \phi ). $$

(4)

In yz plane, $\theta^{{\prime }}$ is the included angle of Oz and OK ₁ . Applying the relation of Eq. (4), its tangent value is

$$ \tan \theta^{{\prime }} = \frac{{\overline{{zK_{1} }} }}{{\overline{Oz} }} = \frac{{\overline{zK} \cdot \cos (\pi /2 - \phi )}}{{\overline{Oz} }} = \tan \theta \cdot \cos (\pi /2 - \phi ). $$

(5)

According to cosine theorem in tetrahedron O-C ₂zK₁, it can be written as

$$ \cos (\angle C_{2} OK_{1} ) = \cos \theta^{{\prime }} \cdot \cos (\varOmega ), $$

(6)

where $\angle C_{2} OK_{1}$ represents the included angle of lines OC ₂ and OK ₁ .

For $\overline{{zK_{2} }}$ is the projection of $\overline{zK}$ in xz plane, the right-angled triangle zK₂K meets the relation below:

$$ \overline{{zK_{2} }} = \overline{zK} \cdot \sin (\pi /2 - \phi ). $$

(7)

In the xz plane, utilizing the result of Eq. (7), the tangent value of $\theta^{{\prime \prime }}$ can be expressed by

$$ \tan \theta^{{\prime \prime }} = \frac{{\overline{{zK_{2} }} }}{{\overline{Oz} }} = \frac{{\overline{zK} \cdot \sin (\pi /2 - \phi )}}{{\overline{Oz} }} = \tan \theta \cdot \sin (\pi /2 - \phi ). $$

(8)

According to cosine theorem in tetrahedron O-C ₁ zK ₂, it can be written as

$$ \cos (\angle C_{1} OK_{2} ) = \cos \theta^{{\prime \prime }} \cdot \cos ( - \varOmega ), $$

(9)

where $\angle C_{1} OK_{2}$ represents the included angle of lines OC ₁ and OK ₂ .

From the geometrical description in Fig. 1, we can get the below relationships

$$ \angle C_{1} OK_{2} = \varOmega - \theta^{{\prime \prime }} , $$

(10a)

$$ \angle C_{2} OK_{2} = \theta^{{\prime \prime }} - ( - \varOmega ). $$

(10b)

In the xy ($\theta = 90^\circ$) plane, we use the cosine theorem and get the relations below:

$$ \cos (\angle C_{1} OO^{{\prime }} ) = \cos (\pi /2 - \varOmega ) \cdot \cos \phi , $$

(11a)

$$ \cos (\angle C_{2} OO^{\prime } ) = \cos (\pi /2 - | - \varOmega |) \cdot \cos (\pi - \phi ). $$

(11b)

In the K ₂ OK plane, the line segment $\overline{{K_{2} K}}$ is perpendicular to $\overline{{K_{2} O}}$, and it is parallel to $\overline{{zK_{1} }}$. We can easily get the following equations:

$$ \overline{{K_{2} K}} = \overline{{zK_{1} }} = \overline{zK} \cdot \cos (\pi /2 - \phi ), $$

(12)

$$ \overline{{K_{2} O}} = \overline{Oz} /\cos \theta^{{\prime \prime }} . $$

(13)

The tangent value of $\angle K_{2} OK$ is gained by

$$ \tan \angle K_{2} OK = \frac{{\overline{{K_{2} K}} }}{{\overline{{K_{2} O}} }} = \frac{{\overline{zK} \cdot \cos (\pi /2 - \phi )}}{{\overline{Oz} /\cos \theta^{\prime\prime}}} = \tan \theta \cdot \cos (\pi /2 - \phi ) \cdot \cos \theta^{{\prime \prime }} . $$

(14)

Similar to above process, we use the cosine theorem in tetrahedron O-KK ₂ z and get

$$ \cos \theta = \cos \angle K_{2} OK \cdot \cos \theta^{{\prime \prime }} . $$

(15)

For common conditions of $0^\circ \le \theta < 90^\circ$ and $0^\circ \le \phi \le 90^\circ,$ in tetrahedrons O-KK ₂ C ₁ and O-KK ₂ C ₂, we can get the following relations according to cosine theorem:

$$ \begin{aligned} \cos \theta_{1} & = \cos \angle K_{2} OK \cdot \cos (\angle C_{1} OK_{2} ) \\ & = \cos \{ \arctan [\tan \theta \cdot \cos ({\pi \mathord{\left/ {\vphantom {\pi {2 - }}} \right. \kern-0pt} {2 - }}\phi ) \cdot \cos \theta^{{\prime \prime }} ]\} \cdot \cos (\varOmega - \theta^{\prime \prime } ) \\ & = (\cos \theta /\cos \theta^{\prime \prime } ) \cdot \cos (\varOmega - \theta^{\prime \prime } ) \\ \end{aligned} , $$

(16)

$$ \begin{aligned} \cos \theta_{2} & = \cos \angle K_{2} OK \cdot \cos (\angle C_{2} OK_{2} ) \\ & = \cos \{ \arctan [\tan \theta \cdot \cos ({\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2} - \phi ) \cdot \cos \theta^{{\prime \prime }} ]\} \cdot \cos [\theta^{{\prime \prime }} - ( - \varOmega )] \\ & = (\cos \theta /\cos \theta^{{\prime \prime }} ) \cdot \cos (\theta^{{\prime \prime }} + \varOmega ) \\ \end{aligned} , $$

(17)

where $\theta^{{\prime \prime }} = \arctan (\tan \theta \cdot \cos \phi )$. While in the range of $90^\circ < \theta \le 180^\circ$ and $0^\circ \le \phi \le 90^\circ$, we get the same relations with $\theta^{{\prime \prime }} = - \arctan (\tan \theta \cdot \cos \phi )$. When $\theta = 90^\circ ,\;0^\circ \le \phi \le 90^\circ$, we can get the expressions of $\theta_{1}$, $\theta_{2}$ from Eqs. (11a), (11b):

$$ \cos \theta_{1} = \cos (\angle C_{1} OO^{{\prime }} ) = \sin \varOmega \cdot \cos \phi , $$

(18)

$$ \cos \theta_{2} = \cos (\angle C_{2} OO^{{\prime }} ) = - \sin \varOmega \cdot \cos \phi . $$

(19)

Equations (16)–(19) are the angle transformations between the dielectric axis (xyz) and the laboratory frame ($x^{{\prime \prime }} y^{{\prime \prime }} z^{{\prime \prime }}$). Knowing the parameters of $\varOmega$, $\theta$ and $\phi$, we can obtain $\theta_{1}$, $\theta_{2}$ in dielectric axis, which can be used to calculate the refractive index easily in Eq. (1). The angular relations of the wave vector and the two optical axes can be used to calculate the phase matching parameters and to deduce the angular derivative of refractive index in spatial distribution in biaxial crystals.

In above demonstration, Eqs. (16) and (17) give the angular dependence in conditions of $0^\circ \le \phi \le 90^\circ$, $0^\circ \le \theta \le 180^\circ \;(\theta \ne 90^\circ )$. According to the angle definition introduced by Kodaira Kunihiko, $\theta^{{\prime }}$ and $\theta^{{\prime \prime }}$ in fact can be thought as the projections of $\theta$ in yz and xz plane. From Eqs. (5) and (8), we can get the expressions of $\theta^{{\prime }}$ and $\theta^{{\prime \prime }}$ as following:

$$ \theta^{{\prime }} = \arctan (\tan \theta \cdot \sin \phi ), $$

(20a)

$$ \theta^{{\prime \prime }} = \arctan (\tan \theta \cdot \cos \phi ). $$

(20b)

In Eq. (20a), $\theta^{{\prime }}$ is a monotone increasing function of $\phi$, with the smallest value of $0^\circ$ at $\phi = 0^\circ$ and the biggest value of $\theta$ at $\phi = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}$; on the contrary, $\theta^{{\prime \prime }}$ in Eq. (20b) decreases monotonously from $\theta$ to $0^\circ$. For $\theta = 90^\circ ,\;0^\circ \le \phi \le 90^\circ$ shown in Fig. 2, the wave vector k is on $x^{{\prime }}$ axis, and the angles $\theta_{1}$, $\theta_{2}$ become $\angle C_{1} OO^{{\prime }}$, $\angle C_{2} OO^{{\prime }}$, which can be calculated by Eqs. (18) and (19) according to the cosine theorem in tetrahedrons.

Fig. 2

Schematic diagram of the angle relations in biaxial crystal for $\theta = 90^\circ$

When $\phi = 0^\circ$, we can get $\theta^{{\prime }} = 0$, $\theta^{{\prime \prime }} = \theta$ according to Eqs. (5) and (8). Substituting $\theta^{{\prime \prime }}$ into Eqs. (16) and (17), the cosine of $\theta_{1}$, $\theta_{2}$ can be simplified as

$$ \cos \theta_{1} = \cos (\varOmega - \theta ), $$

(21a)

$$ \cos \theta_{2} = \cos (\varOmega + \theta ). $$

(21b)

Figure 3 gives the geometric sketch of angle relations for $\phi = 0^\circ$. We can see that the wave vector k is in xz plane, and the projections of $\theta$ in yz and xz plane are $\theta^{{\prime }} = 0$ and $\theta^{{\prime \prime }} = \theta$, respectively. It is clear that the angles between k and two optical axes (C ₁, C ₂) are $\theta_{1} = \left| {\theta - \varOmega } \right|$ and $\theta_{2} = \theta + \varOmega$. These results coincide with the discussion in Eq. (21).

Fig. 3

Schematic diagram of the angle relations in biaxial crystal for $\phi = 0^\circ$

Similar to above process, we get $\theta^{{\prime }} = 90^\circ$, $\theta^{{\prime \prime }} = 0^\circ$ for $\phi = 90^\circ$ from Eqs. (5) and (8). Equations (16) and (17) are simplified as

$$ \cos \theta_{1} = \cos \theta_{2} = \cos \theta \cdot \cos \varOmega . $$

(22)

Figure 4 is the geometric sketch of angle relations for $\phi = 90^\circ.$ In this case, the wave vector k is in yz plane, and the projections of $\theta$ in yz and xz plane are $\theta^{{\prime }} = 90^\circ$, $\theta^{{\prime \prime }} = 0^\circ$. We find the angles $\theta_{1}$, $\theta_{2}$ equal, because the plane formed by k and y axis is perpendicular to the xz plane, and C ₁, C ₂ distribute symmetrically about z axis. According to the cosine theorem in tetrahedrons O-KzC ₁ and O-KzC ₂, we get the relations of $\cos \theta_{1} = \cos \theta_{2} = \cos \theta \cdot \cos \varOmega$ which are coincided with the discussion in Eq. (22).

Fig. 4

Schematic diagram of the angle relations in biaxial crystal for $\phi = 90^\circ$

If the crystal axis angle $\varOmega = 0$, there is the relation of $\theta_{1} = \theta_{2} = \theta$. The biaxial crystal becomes uniaxial crystal, and Eq. (1) can be simplified as

$$ n_{o} = n_{x} \quad {\text{and}}\quad \frac{1}{{n_{e}^{2} }} = \frac{{\cos^{2} \theta }}{{n_{x}^{2} }} + \frac{{\sin^{2} \theta }}{{n_{z}^{2} }}, $$

(23)

where $\theta$ is the angle between the wave vector and optical axis, $n_{o}$, $n_{e}$ are the refractive indexes of ordinary and extraordinary beam in uniaxial crystal.

From the above analyzation, we conclude that Eqs. (16)–(19) give the expressions of angles $\theta_{1}$, $\theta_{2}$ with the parameters of $\varOmega$, $\theta$, $\phi$ under the conditions of $0^\circ \le \theta \le 180^\circ$ and $0^\circ \le \phi \le 90^\circ$. If we know the three angles, we can get the values of $\theta_{1}$ and $\theta_{2}$ that can be used to calculate the refractive indexes of two perpendicular linear polarized beams in monolithic crystal and orthorhombic crystal. The optical axis angle $\varOmega$ is defined by the principal refractive indices, which are influenced by wavelength, temperature and so on. The refractive indices here contain two space angles $(\theta_{1} ,\,\theta_{2} )$, so we can take advantage of it to study the characters of phase-matching conditions easily and refractive index angular distribution. Besides, the above demonstration is based on monolithic crystal, yet this method can be extended to triclinic crystal through a more angular projecting process.

3 A direct method for phase-matching conditions

The refractive index value of two perpendicular linear polarized beams at any direction can be calculated by Eq. (1). It can be written by

$$ n_{1} = \frac{{n_{x} n_{z} }}{{\sqrt {n_{z}^{2} \cos^{2} [(\theta_{1} + \theta_{2} )/2] + n_{x}^{2} \sin^{2} [(\theta_{1} + \theta_{2} )/2]} }}, $$

(24a)

$$ n_{2} = \frac{{n_{x} n_{z} }}{{\sqrt {n_{z}^{2} \cos^{2} [(\theta_{1} - \theta_{2} )/2] + n_{x}^{2} \sin^{2} [(\theta_{1} - \theta_{2} )/2]} }}. $$

(24b)

where $\theta_{1}$, $\theta_{2}$ are deduced in Eqs. (16)–(19), by exploiting the angle definition introduced by Japanese mathematician Kodaira Kunihiko [23].

In nonlinear optics, the output efficiency of nonlinear frequency conversion is a key parameter. We should firstly consider the phase-matching conditions, which is a complex problem in biaxial crystals. At present, all the work about it needs to solve quadratic Fresnel equations. Here, we introduce a direct method to calculate phase-matching conditions with the angular dependence of refractive index. Taking SPDC as an example, one incident photon is split into a pair of lower-energy correlated photons. It obeys the conservation laws of energy and momentum under phase-matching conditions, which can be written by

$$ \omega_{p} = \omega_{s} + \omega_{i} , $$

(25a)

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{k}_{p} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{k}_{s} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{k}_{i} , $$

(25b)

where $\omega_{p}$, $\omega_{s}$, $\omega_{i}$ are the frequency of incident photon, and two down-converted photons, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{k}_{p}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{k}_{s}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{k}_{i}$ are the corresponding wave vectors of pump, signal and idler beams. In the SPDC process, the two down-converted photons have equal frequency ($\omega_{s} = \omega_{i} = \omega$).

Generally, there are two transmitting lights in a biaxial crystal, which are called the ‘‘fast,’’ with a smaller refractive index, and the ‘‘slow,’’ with a bigger one. The momentum conservation has the following forms:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{k}_{p} ({\text{slow}}) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{k}_{s} ({\text{fast}}) + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{k}_{i} ({\text{fast}}), $$

(26a)

$$ \overrightarrow {k}_{p} ({\text{slow}}) = \overrightarrow {k}_{s} ({\text{fast}}) + \overrightarrow {k}_{i} ({\text{slow}}). $$

(26b)

Equation (26a) is the type I phase matching configuration, and Eq. (26b) is the type II.

The wave vectors are generally expressed as $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{k}_{l} = n_{l} (\theta_{l} ,\phi_{l} )\frac{{\omega_{l} }}{c}\hat{k}_{l}$ (l = p, s, i) for convenience, where $n_{l}$ is the refractive index for photons in direction of phase matching, $\hat{k}_{l}$ is the unit vector, and $\theta_{l}$, $\phi_{l}$ are the corresponding polar angle and azimuthal angle. For the collinear degenerate down-conversion considered, it satisfies the relation $\omega_{i} = \omega_{s} = {{\omega_{p} } \mathord{\left/ {\vphantom {{\omega_{p} } 2}} \right. \kern-0pt} 2}$. Equation (26) can be simplified in the form of refractive indices:

$$ 2n_{ps} (\theta ,\phi ) = n_{sf} (\theta ,\phi ) + n_{if} (\theta ,\phi ), $$

(27a)

$$ 2n_{ps} (\theta ,\phi ) = n_{sf} (\theta ,\phi ) + n_{is} (\theta ,\phi ), $$

(27b)

where $n_{l,m}$ (l = p, s, i; m = slow, fast) are the refractive indices of fundamental and SPDC waves, respectively. Combining Eqs. (24) and (27) together, we can get the relations of phase matching angles $(\theta ,\phi )$ for type I and type II. It is the key for calculating the phase matching characters.

In our numerical simulations, we choose BIBO as the monolithic biaxial crystal, with the parameters from Hellwig’s data at room temperature [24]. We first calculate optical axis angle $\varOmega$ in Eq. (4) based on Sellmeier coefficients of dispersion relation; then, we numerically calculate Eqs. (24) and (27) and obtain the relationships between phase matching angles $(\theta ,\phi )$. Figure 5a depicts the type I phase matching angles with a fundamental wavelength of 405 nm, while Fig. 5b is the type II phase matching at wavelength 810 nm. It is interesting to note that there are two possible phase matching solutions for a given azimuthal angle $\phi$ in SPDC, which is generally called double-phase-matching conditions. These relations are fundament for analyzing other parameters, such as the effective nonlinear coefficient $d_{\text{eff}}$.

Fig. 5

Relations of phase matching angles $(\theta ,\phi )$ in SPDC, a the type I at a fundamental wavelength of 405 nm, b the type II at a fundamental wavelength of 810 nm

In monolithic BIBO crystal, the effective nonlinearity coefficient can be expressed as [25]

$$ \begin{aligned} d_{\text{eff}}^{\text{sff}} & = - [d_{11} \cos^{2} \phi - d_{12} (3\cos^{2} \phi - 1)]\cos^{2} \theta \sin \phi \\ & \quad - d_{13} \sin^{2} \theta \sin \phi - d_{14} \sin 2\theta \cos 2\phi \\ \end{aligned} , $$

(28a)

$$ d_{\text{eff}}^{\text{sfs}} = [d_{11} \sin^{2} \phi + d_{12} (3\cos^{2} \phi - 2)]\cos \theta \cos \phi + d_{14} \sin \theta \sin 2\phi . $$

(28b)

Equations (28a) and (28b) are the type I and the type II phase matching configuration, respectively, and $d_{1j}$ (j = 1, 2, 3, 4) is the matrix tensor meeting the Kleinman symmetry condition [26].

Taking the normalized values of BIBO, $d_{11} = 2.53\;{\text{ pm/V}}$, $d_{12} = 3.2\;{\text{ pm/V}}$, $d_{13} = - 1.76\;{\text{ pm/V}}$ and $d_{14} = 1.66\;{\text{ pm/V}}$, we numerically simulate Eqs. (28) with the relationships of phase matching angle in Fig. 5 and acquire the effective nonlinearity coefficient varying with azimuthal angle. Figure 6a describes the relation of $d_{\text{eff}}$, $\theta$ and $\phi$ at a fundamental wavelength of 405 nm for the type I phase matching, while Fig. 6b presents the type II at a fundamental wavelength of 810 nm. The solid line and dash line are both corresponding to $0^\circ < \theta < 90^\circ,$ $90^\circ < \theta < 180^\circ,$ respectively. The $d_{\text{eff}}$ for the type I in Fig. 6a has the maximum value of 3.483 pm/V at $\phi = 90^\circ$, $\theta = 152^\circ$ in the case of $90^\circ < \theta < 180^\circ$. For the type II in Fig. 6b, the maximal value of $d_{\text{eff}}$ is about 2.539 pm/V at $\phi = 11.5^\circ$, $\theta = 42.8^\circ$. These results indicate that the optimum direction of type I phase matching is in principal plane, which coincides with our previous work [15], yet the best one for type II is in non-principal plane ($\phi = 11.5^\circ$).

Fig. 6

Variation relation of $d_{\text{eff}}$ along with azimuthal angle $\phi$, a the type I at a fundamental wavelength of 405 nm, b the type II at a fundamental wavelength of 810 nm

From the discussion above, we can obtain the specified phase-matching conditions by constructing the energy and momentum conserving algorithm for different nonlinear process. We apply the angle-dependent refractive indices of biaxial crystals in Eq. (24) to phase-matching conditions and get linear relations of refractive indices with angles $(\theta ,\phi )$, avoiding the complexity of solving quadratic Fresnel equations. It is a convenient method for calculating the phase matching parameters, especially for biaxial crystal.

4 The superiority of angular dependence of refractive index

To demonstrate the superiority of the method above, we introduce a degenerate type I collinear phase matching in biaxial crystals shown in Fig. 7, meeting the conditions of $k_{1} = k_{2} = k_{p} /2$ and $\vec{k}_{p} \parallel \vec{k}_{1} \parallel \vec{k}_{2} \parallel Oz^{{\prime \prime }}$. The point B, where the two different refractive index ellipsoids intersect, satisfies the phase-matching condition. The direction of laser beams is strictly along the line OB. Here, we consider the collinear degenerate type I SPDC in principal plane for simplification, just as in uniaxial crystals. So, the SPDC emission occurs in small vicinities of exact phase matching directions.

Fig. 7

Umbilicate point for maximal phase matching in biaxial crystal; pump and emission wave vector directions for collinear in the given detection

With the hypotheses of near axis and wide crystal, the function $n(\theta ,\phi )$ is approximated by its zero and first orders of Taylor expansion. The linear detuning is

$$ \delta \equiv \vec{k}_{p} (\theta ,\phi ) - \vec{k}_{1} (\theta ,\phi ) - \vec{k}_{2} (\theta ,\phi ) = \left( {\omega_{p} /c} \right)n_{p}^{{\prime }} (\theta_{0} ,\phi_{0} )/n_{p} (\theta_{0} ,\phi_{0} ), $$

(29)

where

$$ n_{p}^{{\prime }} (\theta_{0} ,\phi_{0} ) = \left. {\left\{ {[dn_{p} (\theta ,\phi )/d\theta + dn_{p} (\theta ,\phi )/d\phi ] - [dn_{1} (\theta ,\phi )/d\theta + dn_{1} (\theta ,\phi )/d\phi ]} \right\}} \right|_{\begin{subarray}{l} \theta = \theta_{0} \\ \phi = \phi_{0} \end{subarray} } . $$

(30)

In Eq. (29), $n_{p}^{{\prime }} (\theta_{0} ,\phi_{0} )$ is the gradient of refractive index at $(\theta_{0} ,\phi_{0} )$, and the linear detuning $\delta$ does not equal zero.

From Eqs. (29) and (30), the angular gradient of the pump wave refractive index $n_{p}^{{\prime }}$ is near the phase matching direction $oz^{{\prime \prime }}$, and its absolute value $\left| {n_{p}^{{\prime }} } \right|$ has a homologous relationship equivalent to the eccentricity of the ellipsoid. Known from afore-discussed results in part three, BIBO has a maximal value of $d_{\text{eff}}$ in $yz$ plane for the type I phase matching in SPDC process. In this case, the second part of $n_{p}^{{\prime }}$ in Eq. (30) turns into zero, and its absolute value reaches the maximum. The two different refractive index ellipsoids in a biaxial crystal evolve as one sphere and one circumrotating ellipsoid just as uniaxial crystals, corresponding to the case of $(e \to o + o)$. In double-frequency process, we should choose the case of $(e + e \to o)$ to make the absolute value of $n_{p}^{{\prime }}$ gain the maximum. In other words, if we want to obtain the optimum phase matching for type I in BIBO, the pump wave should take the circumrotating ellipsoid, and the SPDC or double-frequency wave take the sphere. Thus, utilizing the angular dependence of refractive index, it is easy to decide the phase matching angles, and it has superiority of ascertaining which ellipsoid the pump and emission waves will take.

5 Conclusions

In conclusion, we have presented a direct method for calculating the phase matching in a collinear three-wave mixing process based on angle-dependent refractive index in biaxial crystals. Applying the definition of angle introduced by Japanese mathematician Kodaira Kunihiko, we deduced the angular relations between the wave vector and the two optical axes in geometry and obtained the expressions of refractive indices depending on angular orientation $(\theta ,\phi )$ and optical axis angle $\varOmega$. Taking the parameters of BIBO crystal in SPDC process, we calculated effective nonlinear coefficients with angular dependence of refractive index and gained the optimum phase matching directions for the type I and type II. Furthermore, we discuss the angular gradient of the pump and emission wave refractive indexes near the phase matching direction, ascertaining which refractive index ellipsoids the pump and emission waves will take. This approach is convenient to calculate the phase-matching conditions and has superiority in assuring the space distribution of pump and emission waves in quantum optics.