1 Introduction

The reflection properties of cone mirrors were studied since the seventeenth century, when the catoptric anamorphoses were exploited [1]. Anamorphosis is a procedure for drawing an image that appears distorted and indecipherable when seen frontally, the image becoming intelligible from an eccentric viewpoint and/or when reflected by a suitably shaped mirror [2–6]. Anamorphic techniques have been used to hide confidential information, as well as for the pleasure of the perspective illusion [4]. Recently, cone mirrors were proposed and tested as panoramic imaging tools, e.g., in machine vision, surveillance, robot navigation [7–9], pipeline inspection [10], and endoscopy [11]. The optimum design of mirror-based optical systems requires to know exactly where the virtual image of the mirror is formed. Unfortunately, the only available calculations of the virtual image of reflecting cones are those for empty cone mirrors, used as alignment tools in the “axicon” configuration, that is, when the light source facing the bottom of the cone is reflected by the inner cone surface [12–14]. In this paper, we present the first analytical calculations and experimental results of the virtual image surface of solid cone mirrors (outer reflecting surface) having a vertex angle <90°, which are used, e.g., to decipher hidden patterns on the plane of the cone’s base, like in the case of anamorphoses. Our results show the cone’s virtual image surface has a not intuitive 3D shape.

2 Conical imaging, state of the art

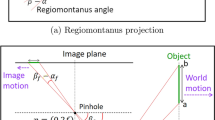
Let us draw the original picture inside a circle divided into a number of sectors [1]. These sectors are reported at the basis of a solid cone mirror, and a line is drawn to the observer from each point which delimits sectors. The intersection of each line with the cone gives the point of reflection of the corresponding point on the plane of the cone’s base. For example, in Fig. 1, the point K at the base of the cone corresponds to the point Q. In this way, each sector of the original circle is deformed in sectors of annuli having different radii. The original writing or image is restored when the observer looks at the deformed (anamorphic) picture on the table reflected by a suitable cone mirror, see Fig. 2.

Fig. 1
figure 1

Side view of a cone mirror in X, Z. The observer in E sees the point Q of the image on the plane reflected in the point (x r, 0, z r) of the cone’s surface, as if it were in K

Full size image
Fig. 2
figure 2

a Anamorphosis by conical deformation of a confidential message. The anamorphosis acts as a cryptography tool. b Software decipher of the message by inverting Eq. (1). c Experimental decipher by placing the conical mirror in the center of the anamorphosis in a. The observer above the apex of the mirror perceives the deciphered writing as if it were at the base of the cone. We used a cone mirror with h = 18 cm and ρ = 4.5 cm made by a film of PET (polyethylene terephthalate)

Full size image

Figure 2a shows how the central part of the original writing is spread along the whole peripheral circle. Both radial inversion and angular spread generate an anamorphic writing impossible to decipher without the cone mirror having the right height and diameter.

In mathematical terms, the conical anamorphosis is a mapping of concentric rings of radius r transformed to rings of radius r′ when reflected off the conical surface. In the geometrical approach, see Fig. 1, considering the center of the cone’s base as being the center of a coordinate system, geometrical calculations give the relationship between r′ and r as [2, 4, 5]:

$$r^{\prime } = r + 2 h\left( {\frac{\rho - r}{\rho - hA}} \right)\left( {\frac{{1 - AB - A^{2} }}{B + 2A}} \right)$$
(1)

where h is the height of the cone, ρ is the radius of the cone’s base, A = r/(d + h) where d is the distance between the observer and the cone apex, and B = (h 2 − ρ 2)/(ρh). Due to geometrical constraints, r′ > ρ > r.

In the common case, the observer in Fig. 1 is at a distance d ≫ h, Eq. (1) simplifies as:

$$r^{{\prime }} \approx r + 2 h^{2} \frac{\rho - r}{{h^{2} - \rho^{2} }} = r + \frac{2(\rho - r)}{{1 - \tan^{2} \varphi }}.$$
(2)

where ϕ is the half angle of the cone’s apex. This approximation requires h > ρ, that is, ϕ < 45°.

Equations (1) and (2) have been exploited to create conical anamorphoses [2–5], often using dedicated software [6], and the results are satisfactory, as shown in Fig. 2. However, we were not able to find in literature an exact analysis of the surface where the virtual image of solid conical mirrors lies. Indeed, there is a general agreement [2–6] to accept the geometric approach of Nicéron [1], see Fig. 1, which implicitly considers the virtual image surface of solid cone mirrors to lie in the plane of the cone’s base.

3 Conical imaging, the exact treatment

Where is the virtual image of an anamorphic drawing when observing its reflection by the cone mirror from the point E of Fig. 1? The cone mirror can be considered to be a combination of a plane mirror in XZ, YZ and a convex one in XY, see Fig. 3. The line z g on the cone’s side lies on the plane mirror. The plane normal to z g generates an ellipse running around the cone which represents the convex mirror. The optical axes of both components are inclined by half of the cone’s apex angle ϕ with respect to the base of the cone. The flat component of the cone mirror (meridional plane) generates a point-like virtual image, while the convex component (sagittal plane) generates a virtual image lying on a focal line. This discrepancy leads to astigmatic aberrations [9].

Fig. 3
figure 3

Geometry of the cone mirror relevant to the calculation of the virtual image surface. See text for symbols explanation

Full size image

To calculate the focal line of the convex component associated with a generic point on the anamorphic plane, let us determine the focal length of the mirror in the reflection point (x r, y r, z r), that is, its curvature radius. With reference to Figs. 1 and 3, the equation of the cone is

$$x^{2} + y^{2 } - \frac{{\rho^{2} }}{{h^{2} }}(z - h) ^2= 0,$$
(3)

while the equation of the line on the cone’s side for Y = 0 is

$$z_{\text{g}} (x) = - \frac{h}{\rho }x + h.$$
(4)

The plane perpendicular to (4), passing in the generic point (x r, 0, z r) in Fig. 3 is given by

$$z_{\text{n}} (x) = \frac{\rho }{h}x + z_{\text{r}} - \frac{\rho }{h}x_{\text{r}} .$$
(5)

The intersection of the cone (3) and the plane (5) gives the ellipse

$$x^{2} + y^{2} - \frac{{\rho^{2} }}{{h^{2} }}\left( {\frac{\rho }{h}x + z_{\text{r}} - \frac{\rho }{h}x_{\text{r}} - h} \right)^{2} = 0,$$

whose semi-axes are, in modulus,

$$S_{ \hbox{min} } = x_{r} \sqrt {\frac{{1 + t^{2} }}{{1 - t^{2} }}}$$

and

$$S_{\hbox{max} } = x_{r} \frac{{\sqrt {1 + t^{2} } }}{{1 - t^{2} }}$$

where t = ρ/h = tanϕ. We can deduce the curvature radius R of the convex axis of the conical mirror in the generic point (x r , 0, z r ) of its surface which reflects the point Q to the observer E (see Fig. 1) as

$$R(x_{\text{r}} ) = \frac{{S_{ \hbox{min} }^{2} }}{{S_{ \hbox{max} } }} = x_{\text{r}} \sqrt {1 + t^{2} } ,$$

that is,

$$R(z_{\text{r}} ) = \frac{{t(h - z_{\text{r}} )}}{{{ \cos }\,\phi }}.$$
(6)

The distance q(z r ) of the image of a generic point Q(r′) from the cone surface reflected in (x r , 0, z r ) toward E is given by the paraxial mirror equation as follows:

$$\frac{1}{{Q_{ \bot } }} + \frac{1}{{q(z_{\text{r}} )}} = - \frac{2}{{R(z_{\text{r}} )}}$$
(7)

where Q ⊥ is the minimum distance of Q(r′) from the line (4). The function q(z r) is the focal line we are looking for. Using Eqs. (6) and (7), simple but tedious passages give the effective distance of the image of a generic point Q(r′) from the cone surface as:

$$q(z_{r} ) = \frac{{t(h - z_{r} )(r^{{\prime }} - \rho )(1 + t^{2} )}}{{t(h - z_{r} )(1 + t^{2} ) + 2(r^{{\prime }} - \rho )}}\cos \phi$$
(8)

where we omitted the negative sign: this means the distance q(z r) in Eq. (8) is taken from the cone surface to the inside of the cone. The intersection of Eq. (8) with the line of sight gives the position of the image of the anamorphic point Q(r′) reflected in (x r, 0, z r). In fact, the line of sight is the segment from E to the virtual image point of the flat component of the cone mirror, which passes in (x r, 0, z r), see Fig. 1.

Finally, Eq. (1) gives the coordinate r corresponding to Q(r′), and repeating this procedure for each point Q(r′) of the anamorphic drawing, we obtain the wished surface Z ima(r) of the virtual image of the anamorphosis.

Figure 4 shows the plots of Z ima(r) as a function of r/ρ for some ϕ values. Note that the virtual image surface does not coincide at all with the plane of the cone’s base, as it was implicitly assumed in [1–6]. Rather, it is a 3D surface which starts from the circumference delimiting the base of the cone, becomes negative (i.e., it goes under the base) for some values of r and ϕ, then rises to the apex, looking like the hat of a witch, see Fig. 5.

Fig. 4
figure 4

Plot of the calculated virtual image surface Z ima(r) in the plane XZ versus r/ρ for different values of ϕ. The solid straight line shows the cone surface, as a reference

Full size image
Fig. 5
figure 5

The grid represents the calculated 3D surface of the virtual image of the cone mirror with ϕ = 38.7°, which is also shown as a reference

Full size image

4 Experimental

We made a number of different cone mirrors using a polished solid acrylic glass, films of PET and papers of shiny mirror-like materials. Putting a CMOS camera (640 × 480 pixels) perpendicular to the cone’s base and adjusting the manual focus, we found the best focal plane of the virtual image of a drawing on the table at a given radial position of the cone, see Fig. 6. Cone mirrors are astigmatic [9], that is, the reflected sagittal and meridional rays generate virtual images at different locations. As a consequence, the measured best focal plane was in the position of least confusion between the sagittal and tangential focus. In our experimental conditions, the depth of field (DOF) of the camera was 0.3 cm.

Fig. 6
figure 6

a Schematic of the setup to measure the virtual image of a drawing on the plane of the base of the cone mirror. In order to measure negative values of the height of the virtual image (that is, points of the virtual image below the cone’s base), we put the cone mirror on a shim on the table. b Example of the image of a drawing reflected near the base of the cone mirror. c Measurement of the focus height using a graduated scale on an inclined plane put on the table

Full size image

We repeated the measurement for different radial positions of each cone mirror and several times for each radial position. Typical results are shown in Fig. 7.

Fig. 7
figure 7

Dashed line plot of the calculated virtual image surface Z ima(r) in the plane XZ of the cone with Φ = 14.6°. Circles are the measured points of the virtual image. The solid line shows the cone surface, as a reference

Full size image

In addition, for each cone mirror having ϕ > 26°, we measured the minimum value of the negative height of the virtual image next to the base, which is foreseen in Figs. 4 and 5, and the results are summarized in Fig. 8.

Fig. 8
figure 8

Solid line calculated plot of the modulus of the largest negative height of the image plane normalized to the cone’s height versus the half angle ϕ of the cone’s apex. Circles experimental results

Full size image

5 Discussion

Both analytical calculations (Eq. 8) and experiments (Figs. 7, 8) demonstrate that the surface of the virtual image of cone mirrors has a complicated 3D shape, see Figs. 4 and 5. Then, the question is why we perceive a ‘well restored’ image of conical anamorphoses (see, e.g., Fig. 2) as if it were a 2D drawing at the base of the cone mirror, in apparent agreement with the geometric imaging construction in Fig. 1. The reason may be due to concomitant causes. Namely, conical anamorphoses are best reconstructed when looking at their reflection by the cone mirror with one eye only (to avoid the depth perception of binocular vision [2–4]) and when observed from a distance at least four times the cone’s height. For example, the experimental image in Fig. 2c was seen and framed at a distance of 110 cm from the base of the cone mirror, which is six times the cone’s height. In this case, the DOF of our eye can be roughly estimated by the formula used for cameras, namely

$${\text{DOF}} \approx \frac{{2s^{2} c}}{fD} \approx 1 1\;{\text{cm,}}$$
(9)

where s = 110 cm is the distance between object and eye’s lens, c ≈ 2.6 μm is the average size of a photoreceptor in the central part of the retina, f ≈ 1.7 cm is the focal length of the lens, and D = 0.35 cm is the diameter of the pupil in normal illumination conditions [15]. Equation (9) gives a DOF which is not large enough to prevent the perception of different locations of the virtual image surface across the 18 cm height of the cone mirror. Despite this, we see the whole image reflected by the cone at focus. The apparent contradiction is due to the different DOF definition for cameras (see Eq. 9) and for human eyes in ophthalmology [16], which involves, among other parameters, the neural contrast sensitivity function and the difference between vision and perception due to brain’s elaboration of the image [15, 16]. In addition, we have to take into account our innate tendency to accommodate the whole image at focus, reducing the size of the pupil to further increase the depth of field of the eye. Note that the change of pupil’s size is an automatically triggered, non-conscious mechanism, and therefore, it is independent of our will [16]. Finally, as we perceive the whole image as if it were at focus, the statistics of the previous experience [17] suggest us that we are observing a flat 2D image located at the base of the cone.

6 Concluding remarks

We have presented, to the best of our knowledge, the first analytical calculation and experimental results of the virtual image surface of solid cone mirrors having a vertex aperture 2ϕ < 90°, which are used to decipher hidden drawings and/or pictures on the plane of the cone’s base, as in the case of catoptric anamorphoses, see Fig. 2. Our results demonstrate that the virtual image of cone mirrors lies on a not intuitive 3D surface (see Figs. 4, 5, 7) thus showing how the commonly used geometric approach (see Fig. 1) is inadequate to find the correct virtual image position. We have also briefly discussed the visual perception processes leading to perceive the virtual image of conical anamorphosis on a flat 2D surface, much different from the one measured.

Our analytical method can be generalized to cone mirrors having 2ϕ > 90° as those used as panoramic imaging tools [7–11]. However, in this case, the intersection of the cone (Eq. 3) and the plane (Eq. 5) gives an hyperbola instead of an ellipse in Fig. 3. This extension may be the object of a next paper.