1 Introduction

The cubic complex Ginzburg–Landau equation describes a vast variety of phenomena from nonlinear waves to second-order phase transitions, from superconductivity, superfluidity, and Bose–Einstein condensation to liquid crystals and strings in field theory [1]. In optics, this equation describes a diversity of systems, namely laser systems, soliton transmission lines, nonlinear cavities with external pump, and parametric oscillators [2]. Some special solutions of this model, such as the pulsating, erupting, and creeping solitons, were found some years ago in numerical simulations [3, 4]. The erupting soliton was also found experimentally, in passively mode-locked solid state laser, where the higher-order effects might have some influence [5]. In particular, it has been observed that third-order dispersion can cause an asymmetry of the pulse explosions [5], in spite of the fact that such asymmetry can also occur in absence of higher-order effects [5, 6]. The interaction among the higher-order effects becomes particularly important for stable femtosecond pulse generation by passively mode-locked lasers [7]. Taking into account such higher-order effects is also useful for understanding several nonlinear phenomena affecting the transmission of femtosecond pulses in an optical transmission line [8].

The influence of higher-order effects on pulsating, erupting, and creeping solitons has been investigated recently [9–16]. Tian et al. [9] observed that the effect of the nonlinear gradient terms, i.e., the cumulated effect of the self-steepening (SST) and intrapulse Raman scattering (IRS), can dramatically change the periodic behavior of such pulses. The effect of the third-order dispersion (TOD) on the same pulses has also been analyzed in Ref. [10]. In particular, it was found that for some values of the TOD parameter, both the pulsating and creeping solitons can achieve a fixed-shape. On the other hand, in Ref. [11], it has been shown that under the influence of IRS and TOD, the plain-pulsating and creeping solitons can lose their pulsating behavior and be transformed in fixed-shape solitons. In order to achieve this objective, the negative TOD is more convenient for plain-pulsating solitons, whereas the positive TOD is more adequate for creeping solitons. Moreover, if the three higher-order effects act together, the explosions of an erupting soliton can be drastically reduced and even eliminated, also yielding a fixed-shape pulse [11–16]. In this paper, we have studied numerically some characteristics of the fixed-shape pulses that emerge from the pulsating, erupting, and creeping solutions of the quintic CGLE under the influence of intrapulse IRS, SST, and TOD.

In Sect. 2, we present the governing equation, corresponding to a generalized version of the cubic-quintic complex Ginzburg–Landau equation. The regions, in the parameter space, where the fixed-shape solutions emerge from the pulsating, erupting, and creeping are numerically obtained in Sects. 3, 4, and 5, respectively. There, we also characterize their velocities, shapes, and chirp. Finally, the main conclusions are summarized in Sect. 6.

2 The governing equation

In this work, we will consider a generalized form of the CGLE in order to include some higher-order effects, namely the intrapulse IRS, the SST, and the TOD:

$$ i\frac{\partial u}{\partial Z} + \frac{D}{2}\frac{{\partial^{2} u}}{{\partial T^{2} }} + \left| u \right|^{2} u = i\delta u + i\beta \frac{{\partial^{2} u}}{{\partial T^{2} }} + i\varepsilon \left| u \right|^{2} u + i\mu \left| u \right|^{4} u - \nu \left| u \right|^{4} u + {\text{H}} . {\text{O}} . {\text{E}} . $$
(1)
$$ {\text{H}} . {\text{O}} . {\text{E}} .= i\frac{{\beta_{3} }}{6}\frac{{\partial^{3} u}}{{\partial T^{3} }} - {\text{is}}\frac{{\partial (\left| u \right|^{2} u)}}{\partial T} + \tau_{R} u\frac{{\partial \left| u \right|^{2} }}{\partial T} $$
(2)

The optical envelope u in Eq. (1) is a complex function of two real variables, i.e., \( u = u(T,Z) \), where T is the retarded time in the frame moving with the pulse, and Z is the normalized propagation distance or the cavity round-trip number in passively mode-locked lasers. Concerning the other parameters in Eq. (1), D is the group velocity dispersion (GVD) coefficient, with D = ±1, depending on whether the GVD is anomalous or normal, respectively; β stands for spectral filtering (β > 0); δ is the linear gain or loss coefficient; ε accounts for nonlinear gain-absorption processes; μ if negative represents the saturation of the nonlinear gain; and ν if negative corresponds to the saturation of the nonlinear refractive index. The three terms in Eq. (2) describe the higher-order effects, where β 3 accounts for the TOD, s accounts for SST, and \( \tau_{R} \) is the coefficient related to intrapulse IRS.

In order to solve numerically the generalized CGLE given by Eqs. (1) and (2), a split-step Fourier method [17] has been used. The numerical simulations were carried out using a step size of 0.004 along the Z direction, and a step size of 0.01, with 8,192 points, along the T direction. Absorbing boundary conditions were used, as described in Ref. [18]. The criterion for the existence of fixed-shape pulses was constant energy along the propagation distance or damped energy oscillations whose amplitude was just 5 % of the average value.

3 Pulsating solitons

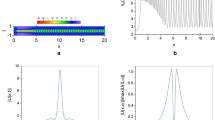
Figure 1a represents the amplitude evolution of a CGLE soliton, in the absence of higher-order effects (β 3 = τ R  = s = 0), for the following set of parameters values: δ = −0.1, β = 0.08, ε = 0.66, μ = −0.1, and ν = −0.1. The initial condition is an unitary amplitude sech(T) pulse. As the pulse propagates, its shape evolves periodically, with a period of Z ≈ 14, and with zero velocity. This periodic solution corresponds to the pulsating soliton found in [3].

Fig. 1
figure 1

Amplitude evolution for a pulsating soliton, a in the absence of higher-order effects, (β 3 = τ R  = s = 0), and b in the presence of higher-order effects, (β 3 = −0.05, τ R  = 0.01, s = 0.005), for the following set of parameters values: δ = −0.1, β = 0.08, ε = 0.66, μ = −0.1, and ν = −0.1

Full size image

Figure 1b illustrates the evolution of a fixed-shape (FS) pulse, emerging from the pulsating soliton in the presence of three higher-order effects, namely the TOD (β 3 = −0.05), the intrapulse IRS (τ R  = 0.01), and the SST (s = 0.005). This solution has nonzero velocity.

In our previous work [11], we studied the impact of TOD on pulsating solitons in the presence of the gradient effects, (IRS and SST). Hence, if positive TOD was added, the oscillations of amplitude are reduced. On the other hand, if negative TOD was considered, the oscillations of amplitude could be drastically reduced and the emerging pulse could achieve a fixed-shape.

Figure 2a shows the region in the (β 3, τ R ) plane in which FS pulses, emerging from pulsating solitons, were found numerically. In order to better complement our work, we assumed a constant value for the SST parameter, s = 0.005, as in our previous work [11]. For β 3 and τ R in the region below the curve, the numerical solutions do not converge to FS pulses. Our results show that FS solutions exist for both positive and negative TOD. However, the majority of the region area corresponds to negative TOD. For some parameters inside the FS region, we have also confirmed that the same fixed-shape solutions are obtained with different initial pulse shapes and energies; however, we noted that the convergence rate may depend on these initial conditions.

Fig. 2
figure 2

a Region in the parameter plane (τ R , β 3) in which fixed-shape pulses, emerging from the pulsating soliton (Fig. 1a), exist (dark region). The parameter value of the SST effect is constant (s = 0.005). The three circles show the locations of the solutions represented in Fig. 3. b Pulse velocities versus τ R , (upper graphic), and versus β 3, (lower graphic), for three different values of β 3 and τ R , respectively. (The other parameter values are as follows: δ = −0.1, β = 0.08, ε = 0.66, μ = −0.1, and ν = −0.1)

Full size image

The three circles show the locations of the three particular solutions represented in Fig. 3.

Fig. 3
figure 3

a Amplitude profile, and b frequency chirp, for s = 0.005, β 3 = −0.03 and τ R  = 0.01 (solid curves), β 3 = −0.08 and τ R  = 0.025 (dashed curves), and for β 3 = 0.03 and τ R  = 0.02 (dashed-dotted curves). (The other parameters values are as follows: δ = −0.1, β = 0.08, ε = 0.66, μ = −0.1, and ν = −0.1)

Full size image

Figure 2b shows the pulse velocities, \( v \approx \left( {\frac{\Updelta T}{\Updelta Z}} \right), \) versus τ R , (upper graph), and versus β 3, (lower graph), for three different values of β 3 and τ R , respectively, in the region of existence. The upper graph shows that the pulse velocities grow approximately linearly with τ R and that they are independent of the value of β 3, (β 3 = −0.1, −0.05, 0.01), since the curves are superposed, with the same slope. In this case, the velocity is positive, and all the pulses move rightward, similarly to what happen to the pulse represented in Fig. 1b. The lower graph also shows that the pulse velocities do not depend on the value of β 3, i.e., it is approximately constant for each τ R value. The velocities are higher for higher τ R , (τ R  = 0.01, v ≈ 0.2), (τ R  = 0.02, v ≈ 0.5), (τ R  = 0.03, v ≈ 0.8), as should be expected from the results shown in the upper graph.

Figure 3a shows the amplitude profiles, and Fig. 3b the frequency chirp (minus the time derivative of the phase, −∂φ/∂T), for three different pulses (circles in Fig. 2a). The three pulse amplitude profiles and their frequency chirp are quite similar, no matter the signal and magnitude of TOD, and of IRS. The pulse amplitude profiles resemble that of a slightly asymmetric flattop soliton. The frequency chirp is negative at the leading edge, attaining its minimum value before it starts to grow linearly over the pulse central region. After reaching its positive maximum, it decreases to zero, at the trailing edge.

4 Erupting solitons

Figure 4a shows the amplitude evolution of a CGLE soliton, in the absence of higher-order effects (β 3 = τ R  = s = 0), for the following set of parameter values: δ = −0.1, β = 0.125, ε = 1.0, μ = −0.1, and ν = −0.6, for an initial sech(T) pulse. This solution corresponds to the erupting soliton found in [3].

Fig. 4
figure 4

Amplitude evolution for an erupting soliton, a in the absence of higher-order effects, (β 3 = τ R  = s = 0), and b in the presence of higher-order effects, (β 3 = 0.1, τ R  = 0.275, s = 0.005), for the following set of parameter values: δ = −0.1, β = 0.125, ε = 1.0, μ = −0.1, and ν = −0.6

Full size image

As the pulse propagates, it becomes covered with small ripples which seem to move downward along the two slopes of the soliton, in such a way that after a short distance, the pulse is covered with this seemingly chaotic structure. When the ripples increase in size, the soliton cracks into pieces, after which the pulse evolves in order to restore its shape. This process repeats along the propagation distance, but never exactly in equal periods, and the explosions can even become slightly asymmetric, i.e., do not occur simultaneously on both slopes, as is illustrated in the figure.

A different scenario can occur if the pulse propagates under the simultaneous presence of, for example, the three higher-order effects [11], as illustrated in Fig. 4b. In this case, the propagation of the pulse (Fig. 4a) in the presence of IRS (τ R  = 0.275), positive TOD (β 3 = 0.1), and SST (s = 0.005) does not show any explosion. The emerging pulse is a FS solution that moves rightward with nonzero velocity. The pulse is asymmetric, with a short and slightly steeper leading edge, if compared with the long trailing edge.

Figure 5a shows the region, in the (β 3, τ R ) plane in which FS pulses, emerging from the erupting soliton, were found numerically. We kept the SST parameter value constant, s = 0.005, the same value assumed in [11]. The three circles show the locations of the three particular solutions represented in Fig. 6.

Fig. 5
figure 5

a Region in the parameter plane (τ R , β 3) in which fixed-shape pulses, emerging from the erupting soliton (Fig. 4a), exist (dark area). The parameter value of the SST effect is constant (s = 0.005). The three circles show the locations of the three particular solutions represented in Fig. 6. b Pulse velocities versus τ R , (upper graph), and versus β 3, (lower graph), for three different values of β 3 and τ R , respectively. (The other parameters values are as follows: δ = −0.1, β = 0.125, ε = 1.0, μ = −0.1, and ν = −0.6.)

Full size image
Fig. 6
figure 6

a Amplitude profile, and b frequency chirp, for s = 0.005, β 3 = 0.3 and τ R  = 0.8 (solid curves), β 3 = 0.15 and τ R  = 0.4 (dashed curves), and for β 3 = 0.05 and τ R  = 0.25 (dashed-dotted curves). (The other parameters values are as follows: δ = −0.1, β = 0.125, ε = 1.0, μ = −0.1, and ν = −0.6)

Full size image

For β 3 and τ R in the region below the curve, the numerical solutions do not converge to FS solutions. In this part of the work, only positive TOD was considered. However, FS pulses that emerge from erupting solitons can exist for both signs of TOD [11, 12]. Also, in the case of erupting solitons, other tests were done with different initial pulse profiles and energies and the same FS pulses were obtained.

Figure 5a also shows that for small values of TOD parameter (0 ≤ β 3 ≤ 0.05), the required value of τ R for FS pulses to exist tends to increase as β 3 decreases. In order to transform an erupting pulse into FS, the required values of τ R are at least one order of magnitude higher than for the case of the pulsating soliton.

Figure 5b shows the pulse velocities versus τ R , (upper graph), and versus β 3, (lower graph), for three different values of β 3 and τ R , respectively, all in the region of existence of FS.

In the upper graph, the pulse velocities decrease approximately linearly with τ R . This behavior should be expected, since in the presence of IRS, the erupting pulse tends to move leftward [11, 12]. The absolute value of the curve slope is smaller for the smaller value of β 3 (β 3 = 0.05) and is higher for the higher values of β 3 (β 3 = 0.15, 0.3), with the higher values of velocity occurring for β 3 = 0.3. These results for velocity versus τ R are in good agreement with the study made in Ref. [16].

The lower graph illustrates the velocity dependence on the β 3 parameter, for three different values of τ R . This dependency is not linear, but quite similar, in all the considered ranges of β 3. The higher values of velocity occur for the smaller value of τ R . For \( \beta_{3}\, \lesssim\, 0.12, \) the velocity grows slowly, as should be expected since in the presence of TOD, the pulse moves rightward. For \( 0.12\, \lesssim\, \beta_{3}\, \lesssim\, 0.18, \) an unexpected decrease occurs, since the values of SST and IRS are constant. This unexpected behavior could be, for instance, due to some pulse complexity. In fact, a previous work [14] has shown that on the stationary regime, the erupting soliton can exhibit a dual-pulse spectrum. For \( \beta_{3} \gtrsim 0.18, \) the pulse velocities grow approximately linearly with β 3, for the three different values of τ R , almost at the same rate, since the curves slopes are similar. However, the velocities are more negative for the higher values of τ R .

Figure 6 shows three examples of pulses amplitude profiles (a) and its frequency chirp (b) (circles in Fig. 5a). The peaks of each of the three pulses have been centered in T = 0, 10, 20, respectively, for convenience. As it may be observed, the pulses profiles are asymmetric, and the peak amplitudes have almost the same value (2.5 ≤ amplitude ≤ 2.6). The pulse shapes have some differences between them. In the left pulse (dashed-dotted curve, β 3 = 0.05, τ R  = 0.25), the leading edge is longer than the trailing edge and exhibits a small peak structure. These ripples grow and decay, without the occurrence of any explosion. Both central and right pulses have similar profiles (dashed and solid curves, respectively). The leading edges are steeper than the trailing edges, in both cases. However, the right pulse (solid curve) exhibits a steep leading edge and some small humps in the pulse top. In general, the small peaks appear in connection with high values of β 3. More details about these pulse top humps can be found in Ref. [16].

From Fig. 6b (upper graph), it can be seen that the frequency chirp is positive at the leading edge and negative at the trailing edge, whereas it has a negative slope over the pulse central region. The oscillations of the frequency chirp (T < −2) appear in combination with amplitude oscillations on the leading edge. On the other hand, the small oscillations of the frequency chirp (T > 5) are connected with very small-amplitude oscillations on the trailing edge. For central and right pulses (dashed and solid curves, respectively), the frequency chirp profiles are similar to the latter except for the absence of oscillations. It may also be observed that the pulse with a steeper leading edge (solid curve) has a more abrupt change of chirp across the pulse central region, almost vertical, possibly associated with the pulse top humps.

5 Creeping solitons

Graph in Fig. 7a represents the amplitude evolution of a CGLE soliton, in the absence of higher-order effects (β 3 = τ R  = s = 0), for the following set of parameters values: δ = −0.1, β = 0.101, ε = 1.3, μ = −0.3, and ν = −0.101, for an initial sech(T) pulse. This solution corresponds to the creeping soliton found in [3]. This pulse is a rectangular pulse with two fronts and a sink (due to energy loss) at the top. The two fronts pulsate back and forth relative to the sink asymmetrically at the two sides [3]. The shape of the creeping soliton resembles the shape of a composite pulse [19, 20].

Fig. 7
figure 7

Amplitude evolution for a creeping soliton, a in the absence of higher-order effects, (β 3 = τ R  = s = 0), and b in the presence of higher-order effects, (β 3 = 0.006, τ R  = 0.005, s = 0.002), for the following set of parameters values: δ = −0.1, β = 0.101, ε = 1.3, μ = −0.3, and ν = −0.101

Full size image

Figure 7b shows the amplitude evolution for the creeping soliton in the simultaneous presence of the three higher-order effects (β 3 = 0.006, τ R  = 0.005, s = 0.002). The emerging pulse is a FS pulse that moves rightward with constant velocity, and also, the FS pulse resembles an asymmetric composite pulse.

Figure 8a shows the region, in the (β 3, τ R ) plane where FS pulses, emerging from the creeping soliton, were found numerically. We kept the SST parameter value constant, s = 0.002, the same value assumed in [11]. The three circles show the parameter location of the three particular solutions represented in Fig. 9. This region (dark area) is a small and very irregular area, if compared with the region of existence of FS pulses emerging from pulsating and erupting solitons. The region and its border were estimated considering as initial condition, an unitary sech(T) pulse. The convergence to a FS pulse usually occurs at least in 350 normalized distances, but in some cases, they are observable only after 500 normalized distances. Moreover, in some limited cases, the FS was achieved outside the region of existence but at discrete sites, i.e., it was not possible to find them in the surrounding area of the (β 3, τ R ) plane. And finally, tests carried out with other initial conditions, particularly with different energies and peak powers, showed, in some cases, a convergence to a different FS, with the same peak power, maybe due to the pulse complexity. Eventually, the pulse itself could be faced as a bound state of a plain pulse and fronts, and a coexistence of different pulses may occur as in the CGLE [19]. More research is necessary.

Fig. 8
figure 8

a Region in the parameter plane (τ R , β 3) in which fixed-shape pulses, emerging from the creeping soliton (Fig. 7a), exist. The parameter value of the SST effect is constant (s = 0.002). The three circles show the location of the three particular solutions represented in Fig. 6. b Pulse velocities versus τ R , for β 3 = 0.01 and s = 0.002. The circles refer to particular simulations. (The other parameters values are: δ = −0.1, β = 0.101, ε = 1.3, μ = −0.3, and ν = −0.101)

Full size image
Fig. 9
figure 9

a Amplitude profile, and b frequency chirp, for s = 0.002, β 3 = 0.0075 and τ R  = 0.005 (solid curves), β 3 = 0.01 and τ R  = 0.01 (dashed curves), and for β 3 = 0.02 and τ R  = 0 (dashed-dotted curves). (The other parameters values are as follows: δ = −0.1, β = 0.101, ε = 1.3, μ = −0.3, and ν = −0.101)

Full size image

Figure 8b show the pulse velocities versus τ R , (upper graph), for β 3 = 0.01 and s = 0.002, in the region of existence of FS. The circles refer to particular simulations. The pulse velocities grow approximately linearly with τ R , up to τ R  ≈ 0.0035 (A). At that point, a velocity discontinuity occurs, and the pulses move leftward, until τ R reaches 0.006 (B). Between A and B, the velocity still grows approximately linearly with τ R , at the same rate as before. For τ R beyond point B, the pulse moves rightward and the velocity still grows approximately linearly with τ R , at the same rate. This unexpected behavior may again be attributed to pulse complexity.

Figure 9 shows three examples of pulse amplitude profiles (a) and their frequency chirp profiles (b) (circles in Fig. 8a). The pulse on the right (dashed curve) was centered in T = 10, for convenience. The two pulses on the left (solid and dashed-dotted curves) seem to be a mirror image of the pulse on the right. The amplitude profile of these two pulses resembles that of an asymmetric composite pulse. In the leading edge, the pulses are similar to a narrow composite pulse, whereas in the trailing edge, the pulses are similar to a wide composite pulse [19]. For the pulse represented in the right, the composition is reversed. The frequency chirp of the two pulses on the left is negative at the leading edge and attains its minimum value before it starts to grow linearly over the pulse central region. After reaching a positive maximum, it decreases to a local minimum, increases a little bit to a local maximum, and after that decreases, in a nonlinear way, to zero, at the trailing edge. Note that the irregular evolution of the chirp, at the leading and trailing edges, is associated with amplitude fluctuations in the same edges. The chirp profile represented by the dashed line is a point reflection image of the chirp profiles of the other pulses.

6 Conclusions

We have studied numerically some of the characteristics of the fixed-shape solutions that emerge from the pulsating, erupting, and creeping solitons whenever higher-order effects, namely the intrapulse IRS, SST, and TOD, are added to the quintic CGLE.

We have found regions of existence of FS solitons in the (τ R , β 3) parameter space. We also studied the dependence of velocities on the IRS parameter, for FS pulses in those regions. In general, the pulse velocity absolute values grow linearly with the Raman parameter. On the other hand, the dependence of the FS pulse velocities on TOD exhibits a different behavior for pulsating or erupting solitons. The pulse shapes and chirps were also presented. In general, in the region of their existence, the shapes of the emerging FS pulses do not change significantly when emerging from pulsating solitons, whereas they can exhibit different profiles if emerging from erupting or creeping solitons.