Fast wavefront sensing using a hardware parallel classifier chip

Abstract

In most applications of laser technology and optics the beam quality, the ability to focus a laser beam and the achievement of a good optical resolution play an important role. The compensation of distortions using adaptive optics requires fast wavefront measurement. Classical wavefront analysis schemes use matrix operations, which show a nonlinear computation time dependence with matrix size, making it difficult to achieve high-speed control loops at a high resolution. A novel wavefront sensor system is presented using a massively parallel k-nearest neighbor classifier chip in an embedded hardware setup. Our miniaturized sensor is able to detect one optical distortion within about 80 μs allowing its use for high-speed adaptive optics applications.

1 Introduction

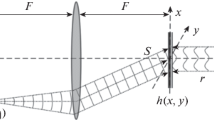
In most applications of laser technology and optics, the beam quality, the ability to focus a laser beam and the achievement of a good optical resolution play an important role. Unfortunately, these properties are often limited by distortions of the wavefront of the light beam. For the compensation of these distortions, adaptive optics may be used. It allows to compensate a phase distortion by use of a deformable mirror. Therefore, it is necessary to measure the phase front of the incoming or emitted radiation. This may be done by a Shack–Hartmann sensor (SHS) which uses a lens array creating a spot grid in the focal plane [2], as shown in Fig. 1.

Fig. 1

Setup of a SHS and the resulting spot distribution on the detector chip

The shift of the measured spots, compared to their reference position, is then a measured for the local phase front slope [2]. By integration, the real phase front may be determined except for an absolute offset.

Especially for applications such as atmospheric reconnaissance or laser beam correction, a very fast measurement method is required to allow a correction in close real time. For example, the correction of the aberrations induced by the atmosphere requires a measurement frequency of several kHz, to still allow compensation of fast fluctuations. Of course, the adaptive mirror needs to be driven as well with those frequencies. Currently, the image from the Shack–Hartmann lens array is captured by a camera and transferred to a computer, which treats this image sequentially, i.e., it determines the spot shifts, then the phase gradients, and finally by integrating the phase. This process is running quite slowly compared to the frame rates of the fast cameras available today. The reasons for this are as follows:

• The high amount of data which needs to be transferred from the camera to the computer that performs the processing. On common personal computers (PC), the image processing often takes more time than the acquisition interval between two consecutive images. This prevents the use of the highest measurement frequency of the camera; high-speed applications need to temporarily buffer the images and to process them after the measurement.

• Sequential data processing, i.e., centroid extraction, calculation of the spot shifts, phase front slopes integration.

Hence, a fast measurement method and its affiliated setup, which allow real-time wave front measurement at high frequencies, require large computational resources, and in consequence a high-performance computer.

Field programmable gate array (FPGA) or application-specific integrated circuit (ASIC) devices allow to remove the “von Neumann” bottleneck, the memory access, limiting the performance of classical computers. They feature massively parallel data processing at low system frequencies, resulting in an increase in performance while lowering the power consumption. Many existing hardware wavefront measurement solutions [3, 4, 5] concentrate on fast centroid extraction, i.e., transforming the Shack–Hartmann sensor spot pattern in a spot displacement matrix as fast as possible and with low latency. But for the centroid analysis, i.e., obtaining the optical distortions in form of Zernike polynomials or driving a deformable mirror in an adaptive optics setup, still a PC computer will be required.

To cope with this, at ISL, we developed a novel prototype of a completely PC-less wavefront sensing system for industrial applications as a mobile, autonomous wavefront sensor or for use in integrated adaptive optics systems. It analyses 11 × 11 lens array cells at a camera resolution of 640 × 480 pixels. The most important optical distortions (Zernike polynomials up to order 4) are determined in about 1.2 ms after termination of the centroid detection process. The resulting measurement frequency up to 830 Hz (limited by the chosen Shack–Hartmann sensor camera) makes our sensor suitable for high-speed adaptive optics applications. By associating a FPGA device to an ASIC hardware classifier chip [6], a significant gain in performance could be achieved compared to existing FPGA-only solutions [7].

An alternate approach for achieving maximum measurement speeds without the need of a computer is the use of electro-optic parallel processors as described in [8]. Nevertheless, the complex optical setup of the presented modal wavefront sensor makes it very expensive and less flexible, i.e., changing the type of distortions to be detected by the sensor requires building of custom optical masks. Furthermore, the optical design makes it difficult to distinguish between more than about 20 different types of optical distortions.

2 The used hardware classifier chip

Efficient data processing, for embedded wavefront analysis, requires recognition and sorting tasks which are highly nonlinear and time-consuming, even with a powerful computer. Almost all computers (PC, DSP, CISC, RISC) are using a central processing unit (CPU) and separate instruction and data memories. Current improvements in computer architecture rely on multi-core processors in order to execute several instructions in parallel. However, the data transfer between core and memory still remains the bottleneck. New performances are expected only through a new massively parallel structure, processing multiple instructions on multiple data simultaneously. In this way, we have investigated a new architecture of natively parallel processors. It implements 1,024 identical parallel processors on the same ASIC component (CogniMem [9]) addressed and working in parallel and having the capability to learn and to recognize patterns in real time (10 μs). CogniMem is a neural processor implementing two operating mode: radial basis function (RBF [10]) and k-nearest neighbors (kNN [11]). It performs parallel real-time pattern recognitions according to the L ₁ norm-distance d(x) evaluation between an incoming vector V of dimension 256 (256 words of 8 bits) and a set of reference vectors V _r of the same length (Eq. 1):

$$d_j(x) = \sum \limits^{256}_{i=1} \left| V_{j_i} - V_{{\hbox{r}}_i} \right|, \quad j = 1:1,024$$

(1)

Because of the native parallel processing, the response time remains constant. Therefore, the classification time does not depend on the number of committed processors. Each prototype vector V _n is locally stored by one of the 1,024 available cells. In the RBF mode, the key point of this technology is that the developer does not have to worry about the network topology nor about the connection weighting process. These time-consuming tasks are now automatically performed at the electronic level. The second mode of the ASIC CogniMem, used in our classification application, is the k-nearest neighbor (kNN). The kNN search still remains a problem in research, e.g., in industrial domains requiring content retrieval, classification, matching estimation. The exhaustive kNN search algorithm specificities are as follows:

• It computes the distances between the query point V (red cross Fig. 2) and each of the reference points V _n (blue points Fig. 2),

• The k-nearest neighbors are trivially determined using a sorting algorithm.

Fig. 2

kNN search in R ₂ with k = 3 (i.e., list limited to 3 over 1,024 for this example) using the Euclidean distance

The kNN algorithm issues an ordered list of distances with the corresponding class number. In spite of searching and sorting algorithm improvements and new PC powerful computational resources (GPU with CUDA [11]), the memory access and the computation time remain the main drawbacks of this classifier on a PC computer. Now, a breakthrough technology (CogniMem) brings an efficient solution to overcome this time-consuming approach. We will demonstrate that it is possible to use this very fast and PC-free classifier for the development of an embedded Shack–Hartmann wavefront analyzer.

3 Description of the algorithm

3.1 Feature extraction

In order to use the classifier chip for wavefront recognition tasks, the first step is to define a feature extraction method, which transforms the physically measured wavefront, the Shack–Hartmann sensor (SHS) image, to an input vector compatible with the used classifier chip.

A micro-lens array transforms the wavefront inclination to luminous spots displacements measured by a CMOS camera sensor. Knowing the optical characteristics of the CMOS sensor, the used lens array and the mounting properties, a specific square region of pixels in the SHS image corresponding to each lens array may be assigned. Figure 3 shows an example: 9 lens array analysis zones have been defined. The SHS is calibrated in the way that an incoming plane wavefront will generate a local light spot maximum in the center of the assigned pixel region of each lens array cell. If the wavefront is distorted, the light spot maxima will be displaced from the center. Provided that incoming distorted wavefronts are optically limited in their inclination angle, a way that a light spot generated by a specific lens array cell will never appear in the pixel area of an adjacent lens array cell. The spot displacements may be defined as relative displacements from the center position of each lens array cell. Figure 4 shows an example SHS spot displacement pattern discretized to a grid of relative spot displacements in the range of [−4 … 4] for each axis. For simplicity reasons, a very small lens array grid of 3 × 3 lenses has been chosen at a very large discretization to explain the concept. The classifier itself is able to process lens array grids of up to 11 × 11 lenses with a relative spot displacement resolution of 256.

Fig. 3

SHS image and selection of lens array cell analysis zones

Fig. 4

Representation of SHS spot displacements within each lens array cell by a 2D grid, serialization of the data to a vector

The spot position within each lens array cell C _x is described by its relative X and Y coordinates, e.g., X = 0, Y = −2 for lens array cell C ₁. As the classifier chip needs a vector as input pattern for the classification process, the relative pixel coordinates of each light spot in each cell will be serialized to a vector in the next step. Equation 2 shows the vector corresponding to the example in Fig. 4.

$$V= \{0, -2, 2, -2, 3, -2, 1, -1, 2, -1, 3, -1, 1, 0, 2, 0, 3, 0\}$$

(2)

3.2 Learning phase

For use of the classifier chip for recognition of optical distortions, it needs to be trained first in order to recognize basic patterns of optical distortions. Such basic patterns might be for example the optical distortions described by the Zernike polynomials (e.g., Tilt, Focus, Koma, etc.), see Fig. 5. Our smart wavefront sensor application uses one classifier chip. It has been taught to detect the optical distortions corresponding to the first 15 orders of Zernike polynomials at a resolution of 0.05 λ and sampling data from 11 × 11 micro-lenses (see Fig. 6). For easier description of the developed recognition algorithm, a simplified case will be used in the following sections. Only 4 patterns will be learned to the classifier, restricted to 3 × 3 micro-lenses. Figure 7 shows the learned patterns. Pattern P ₀ is the reference pattern, indicating that a plain wavefront has been detected (Zernike polynomial Z ⁰₀ ). Pattern P ₁ is a simplified focus distortion (Zernike polynomial Z ²₀ ), and patterns P ₂ and P ₃ are tilt distortions (Zernike polynomials Z ¹₁ and Z ¹₋₁ ).

Fig. 5

Wave front mode orders in Zernike polynomials

Fig. 6

Classifier database containing the first 15 orders of Zernike polynomials at a resolution of 0.05 λ

Fig. 7

SHS spot displacements patterns learned to the classifier, corresponding to basic optical distortions (e.g., Zernike polynomials)

3.3 Recognition phase

After successful training of the classifier, the chip is ready for wavefront recognition and decomposition of a wavefront to the previously learned basic patterns.

The patented [6], iterative decomposition algorithm works as follows:

• 1. Serialization of the initially measured spot displacements pattern to a vector V _x

• 2. Presentation of the vector V _x to the previously trained classifier

• 3. Get the recognition result P _y

• 4. Subtract the vector V _y  = V(P _y ) corresponding to the recognized pattern P _y from the vector that has been presented to the classifier in step 2. The resulting vector V _x  = V _x  − V _y will be the one presented to the classifier in the next iteration step.

• 5. Add the identifier of pattern P _y to the list of the result parts of the decomposition result.

• 6. Is P _y the pattern learned as zero wavefront distortion (pattern P ₀ in the example)?

  • (a) Yes: go to step 7.

  • (b) No: go back to step 2.

• 7. End of the decomposition process, and the remaining vector V _RX = V _x corresponds to the decomposition rest, which may not be decomposed furthermore (extend classifier database to have it recognized next time).

Figure 8 shows a typical decomposition process with an example pattern R ₀ that is compatible to the previously learned database (Fig. 7). To furthermore illustrate how the previously described iterative algorithm works, the whole algorithm with all iterations will be explained in detail by means of this example.

Fig. 8

Decomposition of a SHS measurement to a linear combination of known spot displacement patterns learned to the classifier

We start by serializing the measured spot displacement pattern to a vector (Step 1). Equation 3 shows this starting vector V(R ₀).

$$V(R_0) = \{0, -2, 2, -2, 3, -2, 1, -1, 2, -1, 3, -1, 1, 0, 2, 0, 3, 0\}$$

(3)

When presenting this vector to the classifier, the chip’s parallel architecture compares which of the previously learned patterns P ₀, P ₁, P ₂ or P ₃ matches best the presented vector V(R ₀). This is done by calculating the distance value between the presented vector V(R ₀) and the vector of each learned pattern V(P ₀) up to V(P ₃). Equation 4 shows how the distance value d(R _x P _y ) is calculated for a presented vector V(R _x ) and a pattern vector V(P _y ) with each vector consisting of n elements.

$$d(R_x P_y) = \sum\limits_{i=0}^n \left| V(R_x)[i] - V(P_y)[i] \right|$$

(4)

Equation 5 shows the distances to each reference pattern P _x determined by the classifier after presentation of the vector V(R ₀).

$$\begin{aligned} d(R_0 P_0) & = 26\\ d(R_0 P_1) & = 26\\ d(R_0 P_2) & = 23\\ d(R_0 P_3) & = 19 \end{aligned}$$

(5)

The vector V(P ₃) is the best matching pattern for the presented vector V(R ₀) as it produces the smallest distance in the comparison process. This means that the pattern P ₃ is one part of the presented pattern R ₀. In the next step (Equation 6), the recognized vector V(P ₃) is subtracted from the presented vector V(R ₀). The resulting vector V(R ₁) will be the one that will be presented to the classifier in the next iteration step.

$$\begin{aligned} V(R_1) & = V(R_0) - V(P_3)\\ & = \{-1, -2, 1, -2, 2, -2, 0, -1, 1, -1, 2, -1, 0, 0, 1, 0, 2, 0 \} \end{aligned}$$

(6)

Equation 7 shows the distances to each reference pattern P _x determined by the classifier after presentation of the vector V(R ₁).

$$d(R_1 [P_0, P_1, P_2, P_3]) = [19, 17, 16, 16]$$

(7)

This time the classifier is not able to decide whether the pattern P ₂ or the pattern P ₃ is best matching the presented pattern R ₁. In this case, one of both may be chosen, and it does not matter which. In this example, we will choose the pattern P ₂. Again the difference V(R ₂) between the recognized vector V(P ₂) and the presented vector V(R ₁) is calculated (Eq. 8).

$$\begin{aligned} V(R_2) & = V(R_0) - V(P_3) - V(P_2)\\ & = \{-1, -1, 1, -1, 2, -1, 0, 0, 1, 0, 2, 0, 0, 1, 1, 1, 2, 1\} \end{aligned}$$

(8)

The iterative process is repeated as shown in Fig. 8 until the pattern P ₀, which references zero wavefront distortion, is recognized. This is the case after presentation of the pattern R ₄ to the classifier. This concludes the iterative decomposition process. Equation 9 shows the resulting decomposition of the original pattern R ₀. The vector V(R _X ) is the decomposition rest (Eq. 10), i.e., a vector that may not be decomposed using the previously learned classifier.

$$V(R_0) = 2 \times V(P_3) + V(P_2) + V(P_1)$$

(9)

$$V(R_X) = \{-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 \}$$

(10)

The presented algorithm may be easily adapted to different kinds of sampling functions.

4 Hardware demonstrator

In order to demonstrate the feasibility of our approach, the described principle and algorithm have been applied to the development of an autonomous hardware wavefront sensor (Fig. 9).

Fig. 9

Autonomous wavefront sensor using a hardware kNN classifier chip

The selected hardware platform implements the following components:

• Actel IGLOO low-power FPGA containing the developed algorithm

• CogniMem neural network chip for kNN hardware classification

• Aptina gray-level CMOS image sensor with a resolution of 720 × 576 and a pixel size of 6 μm

• Thorlabs 150 μm micro-lens array mounted in front of the CMOS sensor

• USB interface for system configuration

• I2C interface for connecting a compatible TFT display module or custom electronics

The wavefront sensor may be configured by connecting to a standard PC, but once configured it may be used fully autonomously by connecting a compatible TFT display module (Fig. 10). The TFT display allows real-time visualization of the measurement results without a computer.

Fig. 10

TFT display module for the wavefront sensor

The classifier chip has been taught to recognize the best linear combination of the first 15 Zernike polynomials (order 4) describing the incoming wavefront. The discretion interval is 0.05 λ. It may be improved by increasing the number of neurons of the classifier database, i.e., by adding a multiple CogniMem chips. In its current development state, our miniaturized sensor is able to detect the most dominant optical distortion of the wavefront within only about 80 μs.

5 Testing and validation

In order to test the accuracy of the developed sensor, a first simplified test case has been defined: The measurement of the distance between a laser source reduced to a point source (spherical emitting source) and our SHS (Figs. 11 , 12), using the sensor as focal spot detector.

Fig. 11

Experimental setup

Fig. 12

Spherical wave front displacement calculation

For this experiment, the defocus Z ²₀ Zernike polynomial (Fig. 5) contains all the information needed to calculate the focal distance to the emitting source. The distance d = R needs to be estimated (see Fig. 12)

The geometrical phase $\varphi_g$will be estimated by means of the spatial phase delay h and the wavelength λ (Eq. 11) as follows:

$$\varphi_g = \frac{2\pi}{\lambda} h$$

(11)

Geometrically, this is given by:

$$h = R - R \cos \alpha = R( 1 - \cos \alpha )$$

(12)

and for α ≪ 1, we obtain:

$$h \approx R \left( 1 - \left(1 - \frac{1}{2} \alpha^2 \right) \right) \approx R \frac{\alpha^2}{2}$$

(13)

As

$$r = R \sin \alpha \rightarrow r \approx \alpha R$$

(14)

we finally get:

$$\varphi_g = \frac{2\pi}{\lambda} \cdot \frac{r^2}{2R}$$

(15)

The phase relation given by the Z ²₀ Zernike polynomial can be written as:

$$\varphi_Z = \frac{2\pi}{\lambda} a^2_0 \cdot Z^2_0$$

(16)

with

$$Z^2_0 = \sqrt{3} \cdot \left( 2 \rho^2 - 1 \right)$$

(17)

The distance ρ, in polar coordinates, may be expressed as:

$$\rho = \frac{2r}{D}.$$

(18)

This results in

$$\varphi_Z = \frac{2\pi}{\lambda} a^2_0 \cdot \sqrt{3} \cdot \left(8 \frac{r^2}{D^2} - 1 \right)$$

(19)

The phase gradients of $\varphi_g$ and $\varphi_Z$ should be equal:

$$\frac{\partial \varphi_g}{\partial r} = \frac{\partial \varphi_Z}{\partial r}$$

(20)

By solving the resulting equation

$$\frac{2\pi}{\lambda} a^2_0 \cdot \sqrt{3} \cdot 16 \frac{r}{D^2} = \frac{r}{R} \cdot \frac{2\pi}{\lambda}$$

(21)

we obtain

$$R = \frac{D^2}{16 \sqrt{3} a^2_0} \quad\quad a^2_0\quad \hbox{in (m)}$$

(22)

$$R = \frac{D^2}{16 \sqrt{3} \lambda a^{2\ast}_0}\quad a^{2\ast}_0\quad \hbox{in}\,\lambda$$

(23)

Figure 13 is a comparison between classical and neural network algorithms without sub-pixel optimization, i.e., only the brightest spot within each lenslet zone is taken as the displacement spot.

Fig. 13

Comparison of the algorithm accuracies

These curves demonstrate that both algorithms follow the same line for small distances. As the distance increases, the gap between the theoretical and actual positions increases less for the classical algorithm. This is mainly due to the method to determine the (x, y) position of the spot maximum values (centroids). Our work focuses on the wavefront recognition, so the centroid detection has been implemented using a very simple method, which looks only for the maximum value of the pixels in each cell (each corresponding to one lens). No sub-pixel interpolation is performed, restricting our system to the CMOS sensor’s native pixel resolution of 25 × 25 pixels per micro-lens array cell.

To cope with this, several well-performing high precision centroid extraction techniques [3, 4, 5] are available. Sub-pixel resolutions of down to 0.125 pixels are supported by the CogniMem classifier chip in the presented optical setup, enabling the use of our prototype in small aberration closed-loop adaptive optics setups with few modifications.

6 Conclusion and perspectives

Classical wavefront analysis methods based on matrix calculations need expensive and power-consuming computers. The presented wavefront sensing method is an innovative approach, particularly well suited for embedded applications, i.e., integration in lasers for beam correction or battery-driven hand-held devices for ophthalmology.

The performance of our demonstrator is currently limited by the frame rate of the used low-cost CMOS sensor (only 60 frames per second). To remove this bottle-neck, a commercial high-speed camera (e.g., CameraLink or FireWire) needs to be interfaced to our system. Nirmaier et al. [12] propose an interesting alternate solution to this problem by combining the CMOS sensor and centroid detection electronics in one custom ASIC component, achieving bandwidths up to 300 Hz. As the previously cited techniques [3, 4, 5], their approach currently relies on a PC computer for the Zernike polynomials decomposition. Applying our analysis electronics (FPGA, CogniMem) to their novel sensor could solve this problem and contribute toward future very compact, high-speed and low-latency solutions for wavefront analysis and adaptive optics.

Our next step will be the integration of a high-speed CMOS sensor to improve the bandwidth of our sensor prototype. In our laboratory, we are also investigating novel hardware classifier concepts contributing to further improvements in the domain of wavefront sensing and high-speed adaptive optics.