1 Introduction

Nonlinear Schrödinger equation (NLSE) is a widespread model describing propagation of optical radiation in nonlinear media. Although being relatively simple, it describes such diverse phenomena as optical soliton formation [1], multi-soliton oscillations [2], femtosecond filaments [3], supercontinuum generation [4–6], etc. Since the discovery of the crucial role of the higher order dispersion terms resulting in radiation emitted by NLSE solitons [7–9], many subsequent studies have been devoted to the formation and tailoring processes of the supercontinuum generation in photonic crystal fibers (see e.g. [10, 11]). The primary cause of the soliton radiation is due to the presence of the resonant, with respect to the soliton frequency, modes of the continua (Cherenkov radiation). Much less attention was paid to the radiation of solitons, which reside in photonic band gaps (BGs), i.e., in the frequency ranges where the propagation of linear dispersive waves is forbidden, due to the modification of the linear dispersion by the periodically modulated refractive index. Gap solitons (GSs) were predicted and experimentally demonstrated in Bragg gratings [12–15] as the localized bounded states of the forward and backward propagating waves mutually coupled via the longitudinally modulated refraction index on the half-wavelength scale. Similar kind of the spatial GS exists in media with refractive index modulation in the transverse, say x, direction, and the light (soliton) propagates along the longitudinal, say z, direction [16, 17]. In the latter case, the spatial counterpart of the fiber grating is realized by means of the von Laue diffraction-grating scheme [18]. It is notable that the field configuration constituting the temporal GS is analogous to that in the waveguide array geometry of discrete solitons, which can be understood by a formal mapping between the 1D+time system (e.g., fiber grating) and the 2D system of the waveguide arrays.

Contrary to the classical solitons generated in a semi-infinite half-plane, GS is bounded by the maximum and minimum frequency values due to the finite width of the gap. This specifics can affect the stability of GS: as recently demonstrated [19], radiation into continuum modes is a possible physical reason for the instability of the GS behavior close to the middle of the BG. Such an instability was mentioned in the number of the studies [12, 20–22]. Our proposal is that the instability of GS close to the middle of the BG originates by the radiation from GS due to the four-wave mixing (FWM) process. Indeed, as far as the soliton frequency approaches the middle of the BG, conservation laws for the FWM between solitonic field and Bloch modes are satisfied, and a certain amount of the GS energy is radiated simultaneously into continua of linear waves of the upper and lower Bloch bands. Note that the FWM mechanism discussed here could be perceived as similar (from the viewpoint of parametric wave generation) to that proposed for intrinsic modes in [23].

The quasi 1D photonic lattices can be fabricated in bulk samples of photorefractive lithium niobate (LiNbO3) crystal possessing a defocusing nonlinearity of the saturating type [24]. Transparent LiNbO3 crystals with imprinted refractive index lattices are a convenient media for the studies of nonlinear photonics of periodic systems. Hence, it makes sense to explore how the saturation of the nonlinearity will affect the stability of GS behavior.

As only numerical solitary wave solutions of the NLSE in periodic potentials are known, it is difficult to predict how the saturation affects the radiation from BG soliton mediated by FWM. Therefore, the primary objective of this paper is to perform numerical analysis of the generalized NLSE with the periodically modulated refractive index and the saturating nonlinearity. We start from the dispersion calculation for two cases of periodic potentials and introduce a convenient method of the numerical analysis of solitons in the generalized NLS equation in Sect. 2. Further, in Sect. 3, we present our main numerical results, providing comparison of BG soliton propagation in one-dimensional optical lattice of harmonic and rectangular forms of the refractive index modulation and saturated defocusing nonlinearity.

2 GS in 1D modulated media

We consider a (microscopic) model for the complex field A(x, z) propagating in a bulk transparent media with the periodically modulated transverse coordinate. Our modeling is based on the numerical solution of the generalized NLSE. It is instructive to start this study from the linear analysis, i.e., to consider propagation of linear waves in specific periodic potentials.

2.1 The band structure: linear case

The propagation of linear optical waves in media with the periodically modulated refractive index is most straightforwardly described calculating eigenstates and corresponding eigenenergies of the linear part of the NLSE operator. Here, we restrict our analysis to one-dimensional harmonic \(U(x)=\cos(x)\) and the periodic nearly rectangular shape potential, which was considered as follows:

$$ U(x)= \sum_{n=-N}^N \exp[-(x-2 \pi n)^{10}]. $$
(1)

Both potentials are shown in Fig. 1.

Fig. 1
figure 1

Harmonic a and nearly rectangular b periodic potentials used in modeling

Full size image

Further throughout the paper, non-dimensional variables are used; therefore, the period of modulation was set to 2π. Accordingly, the reciprocal-lattice vector (k B  = 2π/d, with d being the period of the lattice) becomes unity.

In order to calculate the band structure (eigenenergies and eigenvectors) of the operator:

$$ i \frac{\partial A}{\partial z}+\frac{\partial^2 A(x,z)}{\partial^2 x}-2mU(x)A(x,z), $$
(2)

 we apply the Bloch’s theorem and use the form  \(\exp(ikx)a(x)\) for the z independent part of the optical field. Here, a(x) = a(x + 2lπ) is the periodic function with integer  \(l=-N,-N+1,\ldots,N-1,N\), where 2N + 1 is the number of modulation periods considered.

Function U(x) in Eq. (2) stands for the transverse profile of the periodically modulated refractive index. Note that (2) has only one free parameter—the modulation depth m, as the both space coordinates x and z are normalized to make the diffraction coefficient and the modulation wave number unity.

By expanding functions a(x) and U(x) into Fourier series:

$$ a(x)=\sum_{n=-\infty}^{\infty} a_n \exp[i(k-n)x), U(x)=\sum_{n=-\infty}^{\infty}u_n \exp(inx), $$
(3)

the band structure of the linear waves, expressed as a function ω(k), can be calculated by numerically solving the eigenvalue problem of the operator (2):

$$ 2 m \sum_{j=-\infty}^{\infty} u_j a_{n+j}+(k-n)^2 a_n=\omega(k) a_n, $$
(4)

By truncating the series (3) to the finite number of harmonic components M = 10, we arrive to the determinant of the size 21 × 21, giving the dispersion curves ω(k) shown in Fig. 2.

Fig. 2
figure 2

Band structure (dispersion curves ω(k)) obtained by numerically solving the eigenvalue problem of the linear operator (2) for harmonic a and rectangular b potentials (m = 0.1). In both cases, the dispersion of uncoupled waves (m = 0) is represented by the dashed lines. The corresponding Bloch states (forming band continua) are depicted by solid lines. Shadings visualize a semi-infinite gap above the 1-st Bloch band and two finite gaps in the dispersion of the periodic structures

Full size image

The dashed lines in Fig. 2 indicate the dispersion of the uncoupled harmonic components of the propagating field in the case m = 0, whereas the solid lines indicate the dispersion of the (Bloch) modes, formed due to the refractive index modulation. Filled areas show the regions forbidden for the propagation of linear waves, where BG solitons reside. (Note, that both first and second gaps are deeper for the case of the rectangular potential, as compared to harmonic one with the same modulation amplitude m). Further, we restrict our analysis to the BG solitons in the first gap, fixing the reference frequency (ω = 0) into the middle of the gap and normalizing in such a way that gap edges appear at ω =  ±0.5.

2.2 Calculation procedure: radiation from the BG soliton

For modeling of the solitary waves propagating in the 1D modulated structure with saturation effects, we use the following form of the NLSE:

$$ i \frac{\partial A}{\partial z}=\frac{\partial^2 A}{\partial^2 x}+\frac{|A|^2 A}{1+ \gamma_{sat}|A|^2}-2mU(x) A +i \alpha A. $$
(5)

 The coefficient γ sat in Eq. (5) characterizes the saturation which limits the magnitude of the maximum amplitude of the soliton. This, in turn, leads to such well known effects as preventing collapse in self-focusing of optical beams (see e.g. [25]). Further (in Sect. 3), it is shown that saturation affects the FWM process, and eventually the radiation from BG soliton, which is the main result of the present paper.

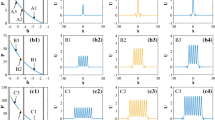
The role of the last term (amplification/attenuation characterized by the coefficient α) on the right hand side of Eq. 5 has to be discussed separately. Note that in order to inspect how the saturation affects the GS, it is convenient to tune the frequency ω of this solution throughout the gap. Unfortunately, such a solution is not available analytically for the NLSE with a periodic potential. Therefore, we have realized our idea numerically using the following method: firstly, a stable soliton wave has been found numerically in the area near the gap edge where its energy and frequency (ω) remain stable. After that, small amplification was turned on and the soliton field was amplified adiabatically. Proceeding with this amplification, we were able to tune the soliton frequency ω smoothly throughout the gap. The solitons amplified adiabatically using the above described procedure are shown in Fig. 3.

Fig. 3
figure 3

Modulus of the BG soliton amplitude near the middle of the gap, obtained by numerical analysis of Eq. (5) with the Kerr nonlinearity (γ sat = 0) for harmonic and nearly rectangular potentials. Non-vanishing radiation in the wings of the field profile, as compared to the initial BG soliton profile (shown in the insets) should be noted

Full size image

In our recent study using the same approach, we have found that the GS in defocusing Kerr nonlinear media (with the harmonic form of the potential) exists and is stable near the upper band edge (ω ≃ 0.5) only and becomes unstable for their eigenfrequencies around the middle (ω ≃ 0) of the band gap, due to radiation into the mode continua of the upper and lower bands. We demonstrate here such behavior of the BG solitons for the periodic harmonic and near-rectangular shape potentials in Fig. 4. Recall that the propagation (longitudinal) coordinate z in Eq. (5) is normalized to diffraction length, and the adiabatic amplification rate is α = 10−5. Such a weak amplification ensures adiabatic tuning of the numerical solution for the BG soliton through the gap. Nonzero radiation, generated by soliton and propagating toward the boundaries of integration region, depicted in Fig. 3a, b should be noted. As the dissipative boundaries are considered in numerical integration, they do not affect the soliton propagation (being sufficiently remote from it), but absorb the outgoing radiation. As a consequence of this radiation, BG soliton loses the energy, and its frequency increases from the middle of the gap if the amplification (coefficient α in Eq. 5) is turned off.

Fig. 4
figure 4

Evolution of the adiabatically amplified GS in the 1D modulated media with the pure Kerr nonlinearity with harmonic a and rectangular b potentials. Density plots show |A(x,z)|2 evolution during adiabatic amplification (with α × 10−5) until the middle of the BG is reached, where the radiation from BG soliton is generated. (ω = 0 corresponds to the soliton frequency in the center of the gap.)

Full size image

3 BG soliton in case of saturated nonlinearity

Here we explore the radiation (if any) from the GS for two different forms of the potential U(x), by numerical integration of the generalized NLSE (5). The strength of the saturation of nonlinearity is characterized here by the coefficient γ sat. The profiles of the BG solitons in the middle of the gap (for the cases of the Kerr nonlinearity) are shown above in Fig. 3. We supplement this case by additional plots (see Fig. 5) providing comparison for the evolution of frequency ω(z) of the amplified GS in the 1D photonic crystal with the pure Kerr nonlinearity for harmonic (a) and nearly rectangular (b) potentials. Frequency ω(z) was evaluated numerically as:

$$ \omega(z)=\left\langle \frac{\partial \arg[A(x,z)]}{\partial z}\right\rangle_x, $$

where \(\langle \ldots \rangle_x\) means averaging over the transverse coordinate x.

Fig. 5
figure 5

Evolution of the BG soliton frequency in the first BG of 1D modulated media with the pure Kerr nonlinearity with harmonic a and nearly rectangular b potentials. Lines (from right to left both panels) correspond to frequency evolution for different amplification coefficients α × 105 = 1, 2, 3, 4, 5, respectively. Zero frequency ω = 0 corresponds to the center of the gap)

Full size image

The only difference is a slightly prolonged distance of propagation for the case of the rectangular potential (shown in Fig. 5a, b, respectively) before the radiation from the BG soliton becomes observable. This feature is due to the fact that the rectangular potential possesses a broader BG as compared to the case of the harmonic potential (see Fig. 2).

Having examined the stability of the 1D BG soliton in the Kerr media with defocusing nonlinearity, we clarify next whether the recently discovered [19] feature (radiation from the GS) persists in situation with the saturating nonlinearity of the same (defocusing) sign. Following the above analysis of the evolution of the GS in the photonic band gap, we consider first the case of “moderate” saturation: γ sat = 1. In this case, as can be concluded from the Fig. 3, the saturation effects of the nonlinearity are negligible in the upper half of the BG. Probably, this is the reason why GS behavior pictured in Fig. 6a does not show significant changes, comparing to the case of Kerr nonlinearity. Evolution of the soliton frequency along the propagation distance ends at a frequency in the middle of the BG and is identical for both forms of the potential U(x), and therefore, only the case for the rectangular potential is shown here. Furthermore, it has been found that the BG soliton frequency increases from the middle of the gap, after the amplification was turned off, like in the case without the saturation. On the other hand, quite a different result was obtained in the case of strong saturation, i.e., for γ sat = 5. In this case, as shown in Fig. 6b for the nearly rectangular potential U(x), no signatures of the GS radiation have been seen for the frequencies around the middle of the BG. The soliton remains stable in the middle of the gap and, surprisingly, continues being stable even in the lower half of the BG. Solitons are destroyed (not shown here) only at the frequency below the lower edge of the BG, i.e., entering into the second continuum of the Bloch states.

Fig. 6
figure 6

Evolution of the BG soliton frequency in the first gap of the 1D modulated media with the saturating nonlinearity and rectangular periodic potential given by Eq. 1. Cases of the moderate (γ sat = 1) and strong (γ sat = 5) saturation of nonlinearity are shown in panels (a) and (b), respectively. Note that the GS is stable everywhere in the gap, in case of saturating nonlinearity (b)

Full size image

In Fig. 7, we show the calculated dependence of GS radiative loss rate (blue points) and minimum frequency ω min which can be reached by adiabatic amplification of the GS (red squares), as a function of saturation parameter. Quantitative changes (gradual disappearance of radiative instability of GS) occur at around 2 ≤ γ sat ≤ 3. It is instructive to relate the current results with the previous findings [26, 27], whereas GSs in the defocusing nonlinear media have been simulated numerically and observed experimentally. Considering the values for relevant parameters (radiation wavelength and the lattice period) close to those used in experiments [26, 27] (0.5 and 10 μm, respectively), we arrive at 100 μm for the diffraction length. Distances at which radiation destroys GS are of order of ten diffraction lengths, as follows from calculations. Therefore, 10 mm might be realistic distance at which stabilizing effects of the saturating nonlinearity can show itself in experimental situations similar to [26, 27].

Fig. 7
figure 7

Maximum GS relative loss rate (blue points) around the middle of the BG and minimum possible GS frequency (red squares) dependencies on the saturation parameter γ sat

Full size image

4 Conclusions

We have analyzed the stability of the spatial gap soliton behavior in a transparent media with the periodically modulated refractive index. In the framework of the generalized NLSE, with a periodic potential and saturating nonlinearity, we have confirmed some of our earlier predictions on the radiation from the spatial GS in the middle of the gap for the moderate saturation coefficient (when the nonlinearity is essentially of Kerr-type). Additionally, we have demonstrated that the radiation from BG soliton decreases for larger coefficient of the saturating nonlinearity and disappears completely for the sufficiently high saturation. The effect can be understood physically taking into account that the saturation of nonlinearity breaks the optimal phase relation for the energy transfer due to the FWM process, from solitonic field to continuum modes.