1 Introduction

In recent years, considerable attention has been paid to the propagation properties of stochastic electromagnetic beams in isotropic and anisotropic media. One significant aspect of this research is that much work has been done to investigate the propagation properties in free space [1–3] and turbulent atmosphere [4–11]. Also, some papers have appeared on polarization changes in beams propagating through optical fibers [12], human tissues [13, 14], compound photonic crystal [15] and chiral media [16], etc. Oceanic turbulence is another medium which may significantly affect polarization properties of a stochastic beam [17, 18]. Recently, the interest in optical underwater communications, imaging and sensing appeared [19, 20] and it has become important to investigate how oceanic turbulence affects spectra of stochastic electromagnetic beams. But compared with the turbulent atmosphere, light propagating through oceanic turbulence is a relatively unexplored topic.

On the other hand, it is more appropriate to introduce the aberration as a phase function that modifies the wave front for the propagation of a laser beam [21, 22]. As is well known, the aberration may emerge while the laser beam passes though an optical system. In this sense, it is worth studying the propagation characteristics of the beam with aberration. According to the investigation concerning the aberration, the size and the shape of the beam were strongly influenced by the aberration [23–26]. The characterization and propagation of Gaussian laser beams in the paraxial approach are well known and established [27, 28]. In this first-order linear regime, the optical system can be described in terms of its ABCD matrix. The width, divergence and radius of curvature of a generalized laser beam are defined in a search for Gaussian beam equivalent parameterization in the plane of interest [29–31], and the departure from this ideal situation is described by the quality factor M 2. When the paraxial regime is lost or cannot be applied, some extensions of the theory should be used [32]. A common situation occurs in which the paraxial approach fails when aberrations are present. Using the ray model, one can treat aberrations by tracing the trajectories of the light along the optical system and applying the basic rules of light ray propagation. For laser beam propagation, it is more appropriate to introduce the aberration as a phase function that modifies the wave front of the laser beam [21, 22, 33]. This phase function is usually located on the exit pupil of the system, it means the departure of the actual wave front with respect to a spherical wave front [34]. Some aberrations are well described within the ABCD formulation. These aberrations are defocus (in the paraxial approach, it corresponds to a spherical wave front) and astigmatism (which should be described by means of the tensor formulation of the ABCD matrix [28, 35]).

To the best of our knowledge, there are no papers dealing with the influence of the astigmatism on the propagation characteristics of laser beams in oceanic turbulence. In this paper, with the method of the cross-spectral density matrix [36], we derive a general analytic formula of a stochastic electromagnetic beam propagating in the oceanic turbulence. To illustrate the theory, we consider an example to illustrate the evolution of the spectral density distribution and the spectral degree of polarization of a typical electromagnetic GSM beam propagating in the oceanic turbulence. For simplicity, we ignore absorption and particle scattering and deal only with the effects of the fluctuating refractive index.

2 Theory

Let us consider a random, statistically stationary electromagnetic beam propagating close to the z-axis from the plane z = 0 to the half-space z > 0. The second-order coherence and polarization properties of the beam may be characterized by a 2 × 2 cross-spectral density matrix of the random electric field defined by the formula [36]

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {W} (\rho_{1} ,\rho_{2} ,z;\omega ) = [W_{ij} (\rho_{1} ,\rho_{2} ,z;\omega )] = [\langle E_{i}^{*} (\rho_{1} ,z;\omega )E_{j} (\rho_{2} ,z;\omega )\rangle ],\quad (i = x,y;j = x,y), $$
(1)

where \( E_{x} (\varvec{\rho},z,\omega ) \) and \( E_{y} (\varvec{\rho},z,\omega ) \) are the components of the random electric field in the x and y directions, respectively, at frequency ω, at a point\( r = (\varvec{\rho},z) \) in the half-space z > 0. Here, \( \varvec{\rho} \) denotes a two-dimensional position vector of a point in the xy plane. The x and y directions are perpendicular to the z-axis. The asterisk denotes the complex conjugate, and the angular brackets denote the ensemble average.

The elements of the cross-spectral density matrix at the source plane can be expressed by

$$ W_{ij}^{(0)} (\rho_{1}^{\prime } ,\rho_{2}^{\prime } ;\omega ) = \sqrt {S_{i}^{(0)} (\rho_{1}^{\prime } ;\omega )} \sqrt {S_{j}^{(0)} (\rho_{2}^{\prime } ;\omega )} \mu_{ij}^{(0)} (\rho_{1}^{\prime } ,\rho_{2}^{\prime } ;\omega ),\quad (i = x,y;j = x,y) , $$
(2)

where \( S_{i}^{(0)} \) represents the spectral density of the component E i of the electric field in the source plane, and \( \mu_{ij}^{(0)} \) denotes the spectral degree of correlation between the components E i and E j of the electric field in the source plane.

Using the paraxial form of the generalized Huygens–Fresnel principle, the elements of the cross-spectral density matrix at the two points \( (\varvec{\rho}_{{{\kern 1pt} 1}} ,z) \) and \( (\varvec{\rho}_{{{\kern 1pt} 2}} ,z) \) in the transverse plane z = const > 0 are given by [8]

$$ \begin{aligned} W_{ij} (\varvec{\rho}_{1}^{\prime } ,\varvec{\rho}_{2}^{\prime } ,z;\omega ) &= \left( {\frac{k}{2\pi z}} \right)^{2} \int {\int {d^{2} } }\varvec{\rho}_{1}^{\prime } \int {\int {d^{2}\varvec{\rho}_{2}^{\prime } } } W_{ij}^{(0)} (\varvec{\rho}_{1}^{\prime } ,\varvec{\rho}_{2}^{\prime } ;\omega ) \hfill \\&\quad \times \exp \left( {\frac{{ - ik\left( {\left( {\varvec{\rho}_{1} \varvec{ - \rho }_{1}^{\prime } } \right)^{2} - \left( {\varvec{\rho}_{2} \varvec{ - \rho }_{2}^{\prime } } \right)^{2} } \right)}}{2z}} \right) \hfill \\ &\quad\times \left\langle {\exp \left( {\psi^{ * } \left( {\varvec{\rho}_{1} ,\varvec{\rho}_{1}^{\prime } ,z;\omega } \right)} \right) + \left( {\psi \left( {\varvec{\rho}_{2} ,\varvec{\rho}_{2}^{\prime } ,z;\omega } \right)} \right)} \right\rangle_{m} K(\varvec{\rho}_{1}^{\prime } ,\varvec{\rho}_{2}^{\prime } ) \hfill \\ \end{aligned} , $$
(3)

where \( \left\langle \ldots \right\rangle_{m} \) denotes averaging over the ensemble of statistical realizations of the oceanic turbulence. \( \psi \) is the random part of the complex phase of a spherical wave propagating in the turbulent medium from the point \( (\varvec{\rho}^{\prime } ,0) \) to the point \( (\varvec{\rho},z) \). It is assumed here that the fluctuations of the light beam and of the oceanic turbulence are statistically independent, i.e. averaging over these parameters can be done separately. As the aberration is taken into consideration here, then the propagator K is given by the following formula [37]:

$$ K(\varvec{\rho}_{1}^{\prime } ,\varvec{\rho}_{2}^{\prime } ) = \exp \left( {ik[\Upphi (\varvec{\rho}_{1}^{\prime } ) - \Upphi (\varvec{\rho}_{2}^{\prime } )]} \right) , $$
(4)

where \( \Upphi \) is the wave aberration function. Here, we consider only the effect of astigmatism, and other aberrations are neglected. The wave aberration function for astigmatism is characterized by [37]

$$ \Upphi (x,y) = C_{6} (x^{2} - y^{2} ) , $$
(5)

where C 6 is the astigmatic coefficient.

In Eq. (3), the angular bracket that describes the turbulence effect can be approximated as below [9, 37]:

$$ \begin{gathered} \left\langle {\exp \left( {\psi^{ * } \left( {\rho_{1} ,\rho_{1}^{\prime } ,z;\omega } \right)} \right) + \left( {\psi \left( {\rho_{2} ,\rho_{2}^{\prime } ,z;\omega } \right)} \right)} \right\rangle_{m} \hfill \\ \cong \exp \left[ { - \frac{{\pi^{2} k^{2} z}}{3}\left[ {(\rho_{1} - \rho_{2} )^{2} + (\rho_{1} - \rho_{2} )(\rho_{1}^{\prime } - \rho_{2}^{\prime } ) + (\rho_{1}^{\prime } - \rho_{2}^{\prime } )^{2} } \right]\int {\kappa^{3} \Upphi_{n} (\kappa )d\kappa } } \right] \hfill \\ = \exp \left[ {\frac{{ - (\rho_{1} - \rho_{2} )^{2} - (\rho_{1} - \rho_{2} )(\rho_{1}^{\prime } - \rho_{2}^{\prime } ) - (\rho_{1}^{\prime } - \rho_{2}^{\prime } )^{2} }}{{\rho_{0}^{2} (z)}}} \right] \hfill \\ \end{gathered} , $$
(6)

then we obtain

$$ \rho_{0} = \left( {\frac{3}{{\pi^{2} k^{2} z\int\limits_{0}^{\infty } {\kappa^{3} } \Upphi_{n} (\kappa )d\kappa }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} , $$
(7)

where \( \rho_{0} \) is the coherence length of a spherical wave propagating in the turbulent medium.

The model for the spatial power spectrum of the refractive index fluctuations of the oceanic water was obtained from Ref. [38] as linearized polynomial of two variables: the temperature fluctuations and the salinity fluctuations. The model is valid under the assumption that the turbulence is isotropic and homogeneous and, hence, required only specification of the one-dimensional spectrum, which has the form

$$ \Upphi_{n} (\kappa ) = 0.388 \times 10^{ - 8} \varepsilon^{ - 1/3} \kappa^{ - 11/3} \left[ {1 + 2.35(\kappa \eta )^{2/3} } \right]f(\kappa ,w,\chi_{T} ), $$
(8)

where \( \varepsilon \) is the rate of dissipation of turbulent kinetic energy per unit mass of fluid which may vary in range from 10−4 to 10−10 m2/s3, \( \eta = 10^{ - 3} \) being the Kolmogorov micro-scale (inner scale), and

$$ f(\kappa ,w,\chi_{T} ) = \frac{{\chi_{T} }}{{w^{2} }}(w^{2} e^{{ - A_{T} \delta }} + e^{{ - A_{S} \delta }} - 2we^{{ - A_{TS} \delta }} ), $$
(9)

with \( \chi_{T} \) being the rate of dissipation of mean-square temperature, \( A_{T} = 1.863 \times 10^{ - 2} ,A_{S} = 1.9 \times 10^{ - 4} ,A_{TS} = 9.41 \times 10^{ - 3} , \) and \( \delta = 8.284(\kappa \eta )^{4/3} + 12.978(\kappa \eta )^{2} , \) w being the relative strength of temperature and salinity fluctuations, where in the ocean water can vary in the interval [− 5;0], attaining the upper bound for the maximum salinity-induced optical turbulence.

3 An example

To illustrate the propagation characterization of a stochastic electromagnetic beam with astigmatism in the oceanic turbulence, we consider a stochastic electromagnetic beam generated by an electromagnetic Gaussian Schell-model source. We assumed, for simplicity, that the off-diagonal elements of the cross-spectral density matrix of the beam in source plane have zero value (i.e. \( W_{xy}^{(0)} (\varvec{\rho}_{1}^{\prime } ,\varvec{\rho}_{2}^{\prime } ;\omega ) = W_{yx}^{(0)} (\varvec{\rho}_{1}^{\prime } ,\varvec{\rho}_{2}^{\prime } ;\omega ) = 0 \)). For such a source [39], the spectral densities of electric field components are given by expressions in the form

$$ S_{i}^{(0)} (\varvec{\rho}_{1}^{\prime } ,\omega ) = I_{i} \exp ( -\varvec{\rho}^{\prime 2} /2\sigma_{i}^{2} ),(i = x,y) $$
(10)

and the degree of correlation of the electric field has the form

$$ \mu_{ii}^{(0)} (\varvec{\rho}_{2}^{\prime } \varvec{ - \rho }_{1}^{\prime } ;\omega ) = \exp \left( { - \frac{{(\varvec{\rho}_{2}^{\prime } \varvec{ - \rho }^{\prime } )^{2} }}{{2\delta_{ii}^{2} }}} \right),(i = x,y), $$
(11)

where the parameters I i , \( \sigma_{i} \) and \( \delta_{ij} \) are independent of the position but may depend on the frequency.

To simplify the subsequent analysis, we will take

$$ \sigma_{x} = \sigma_{y} = \sigma_{0} . $$
(12)

Finally, Eq. (2) can be rewritten as

$$ \begin{gathered} W_{ii}^{(0)} (x_{1}^{\prime } ,x_{2}^{\prime } ,y_{1}^{\prime } ,y_{2}^{\prime } ;\omega ) = I_{i} \exp \left[ { - \left( {\frac{{x_{1}^{\prime 2} + x_{2}^{\prime 2} }}{{4\sigma_{0}^{2} }} + \frac{{y_{1}^{\prime 2} + y_{2}^{\prime 2} }}{{4\sigma_{0}^{2} }}} \right)} \right] \hfill \\ \times \exp \left[ { - \left( {\frac{{\left( {x_{1}^{\prime } - x_{2}^{\prime } } \right)^{2} }}{{2\delta_{ii}^{2} }} + \frac{{\left( {y_{1}^{\prime } - y_{2}^{\prime } } \right)^{2} }}{{2\delta_{ii}^{2} }}} \right)} \right],(i = x,y) \hfill \\ \end{gathered} $$
(13)

where \( (x^{\prime } ,y^{\prime } ) \) denote transverse coordinates of a point\( \varvec{\rho^{\prime}} \) in the source plane.

On substituting from Eqs. (4), (6) and (13) into Eq. (3), and after tedious integration, we obtain the expression for the elements of the cross-spectral density matrix of the beam in the plane z = const > 0:

$$ W_{ii} (x,y,z;\omega ) = \frac{{I_{i} }}{{\sqrt {\Updelta_{1i} \Updelta_{2i} } }}\exp \left[ { - \frac{1}{{2\sigma_{0}^{2} }}\left( {\frac{{x^{2} }}{{\Updelta_{1i} }} + \frac{{y^{2} }}{{\Updelta_{2i} }}} \right)} \right],(i = x,y) , $$
(14)

where

$$ \Updelta_{1i} = (1 - 2zC_{6} )^{2} { + }\left( {\frac{z}{{k\sigma_{0} }}} \right)^{2} \left( {\frac{1}{{4\sigma_{0}^{2} }} + \frac{1}{{\delta_{ii}^{2} }}} \right) + \frac{{2z^{2} }}{{\sigma_{0}^{2} k^{2} \rho_{0}^{2} }} , $$
(15)
$$ \Updelta_{2i} = (1 + 2zC_{6} )^{2} { + }\left( {\frac{z}{{k\sigma_{0} }}} \right)^{2} \left( {\frac{1}{{4\sigma_{0}^{2} }} + \frac{1}{{\delta_{ii}^{2} }}} \right) + \frac{{2z^{2} }}{{\sigma^{2} k^{2} \rho_{0}^{2} }}. $$
(16)

According to Eq. (3), the expressions for the intensity (spectral density) distribution and the spectral degree of polarization of the beam in the propagation field (z > 0) are, respectively, given by [8]

$$ I(\varvec{\rho},z;\omega ) = Tr\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {W} (\varvec{\rho},\varvec{\rho},z;\omega ) $$
(17)

and

$$ P(\varvec{\rho},z;\omega ) = \sqrt {1 - \frac{{4Det\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {W} (\varvec{\rho},\varvec{\rho},z;\omega )}}{{[Tr\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {W} (\varvec{\rho},\varvec{\rho},z;\omega )]^{2} }}} . $$
(18)

with Eqs. (17) and (18), and by using Eq. (14), the intensity distribution of an electromagnetic GSM beam with astigmatism propagating through oceanic turbulence can be expressed as

$$ I(x,y,z;\omega ) = \frac{{I_{x} }}{{\sqrt {\Updelta_{1x} \Updelta_{2x} } }}\exp \left[ { - \frac{1}{{2\sigma_{0}^{2} }}\left( {\frac{{x^{2} }}{{\Updelta_{1x} }} + \frac{{y^{2} }}{{\Updelta_{2x} }}} \right)} \right] + \frac{{I_{y} }}{{\sqrt {\Updelta_{1y} \Updelta_{2y} } }}\exp \left[ { - \frac{1}{{2\sigma_{0}^{2} }}\left( {\frac{{x^{2} }}{{\Updelta_{1y} }} + \frac{{y^{2} }}{{\Updelta_{2y} }}} \right)} \right] $$
(19)

and the spectral degree of polarization has the form

$$ \begin{aligned} P(x,y,z;\omega )& = \left\{ {\left| {\frac{{I_{x} }}{{\sqrt {\Updelta_{1x} \Updelta_{2x} } }}\exp \left[ { - \frac{1}{{2\sigma_{0}^{2} }}\left( {\frac{{x^{2} }}{{\Updelta_{1x} }} + \frac{{y^{2} }}{{\Updelta_{2x} }}} \right)} \right]} \right.} \right. \hfill \\&\quad \left. {\left. { - \frac{{I_{y} }}{{\sqrt {\Updelta_{1y} \Updelta_{2y} } }}\exp \left[ { - \frac{1}{{2\sigma_{0}^{2} }}\left( {\frac{{x^{2} }}{{\Updelta_{1y} }} + \frac{{y^{2} }}{{\Updelta_{2y} }}} \right)} \right]} \right|} \right\} \hfill \\ &\quad\times \left\{ {\frac{{I_{x} }}{{\sqrt {\Updelta_{1x} \Updelta_{2x} } }}\exp \left[ { - \frac{1}{{2\sigma_{0}^{2} }}\left( {\frac{{x^{2} }}{{\Updelta_{1x} }} + \frac{{y^{2} }}{{\Updelta_{2x} }}} \right)} \right],} \right. \hfill \\&\quad \left. { + \frac{{I_{y} }}{{\sqrt {\Updelta_{1y} \Updelta_{2y} } }}\exp \left[ { - \frac{1}{{2\sigma_{0}^{2} }}\left( {\frac{{x^{2} }}{{\Updelta_{1y} }} + \frac{{y^{2} }}{{\Updelta_{2y} }}} \right)} \right]} \right\}^{ - 1} \hfill \\ \end{aligned} $$
(20)

4 Numerical calculations and discussions

We will now investigate the properties of an astigmatic stochastic electromagnetic beam propagating in oceanic turbulence with the help of the numerical calculations. Unless it is specified, we will assume the following values of parameters of the source and of the turbulent ocean: \( \lambda = 632.8\;{\text{nm}},I_{x} = 1,I_{\text{y}} = 0.25,C_{6} { = }0.001,\sigma_{0} = 2\;{\text{cm}},\delta_{xx} = \delta_{yy} = 20\;{\text{mm}},\chi_{T} = 10^{ - 9} ,\varepsilon = 10^{ - 4} ,w = - 2.5. \)

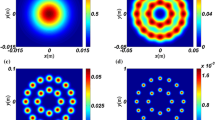
Figure 1 indicates the changes in the light intensity along the z-axis of astigmatic electromagnetic GSM beams passing through the oceanic turbulence with different parameters \( \chi_{T} ,\varepsilon ,w,\delta_{xx} \) and \( \delta_{yy} . \) It is evident from Fig. 1 that for larger values of \( \chi_{T} ,w \) and for smaller values of \( \varepsilon ,\delta_{xx} ,{\text{and}}\delta_{yy} \), the light intensity along the z-axis becomes smaller. It is known that \( \chi_{T} \) represents the strength of the oceanic turbulence. Therefore, as the strength of oceanic turbulence becomes larger, the light intensity becomes smaller. w being the relative strength of temperature and salinity fluctuations, where in the ocean water can vary in the interval [-5;0], attaining the upper bound for the maximum salinity-induced optical turbulence. It is, therefore, evident that the light intensity takes the maximum when temperature fluctuations in the ocean dominate salinity fluctuations. \( \delta_{xx} ,\delta_{yy} \) indicate the degree of coherence of the source, so when the degree of coherence of the source becomes larger, the light intensity becomes larger. At the same time, we can see that as the light intensity becomes smaller, the point taking the maximum of the light intensity will be closer to the origin.

Fig. 1
figure 1

Changes in the light intensity along the z-axis of astigmatic electromagnetic GSM beams propagating through the oceanic turbulence with different a \( \chi_{T} \), b \( \varepsilon \), c \( w \), d \( \delta_{xx} ,\delta_{yy} \)

Full size image

Figure 2a, b show the changes in the light intensity along the x-axis and y-axis of astigmatic electromagnetic GSM beams passing through the oceanic turbulence with different parameter \( \chi_{T} . \) Like the Fig. 1a, as the strength of the oceanic turbulence becomes larger, the light intensity along the x-axis and y-axis changes smaller. However, different from Fig. 1a, the point taking the maximum of the light intensity along the x-axis and y-axis is located at the origin. Although the changes in the light intensity along the x-axis and y-axis are similar, the propagation distance along the y-axis is farther than the x-axis. In addition, the strength of the oceanic turbulence has little effect on propagation distance along the y-axis, whereas for the x-axis case, as the strength of the oceanic turbulence becomes larger, despite the light intensity changes smaller, the propagation distance becomes farther. The similar phenomenon can also be found in Figs. 3 and 4.

Fig. 2
figure 2

Changes in the light intensity along the x-axis and y-axis of astigmatic electromagnetic GSM beams passing through the oceanic turbulence with different parameter \( \chi_{T} \)

Full size image
Fig. 3
figure 3

Changes in the light intensity along the x-axis and y-axis of astigmatic electromagnetic GSM beams passing through the oceanic turbulence with different parameter z

Full size image
Fig. 4
figure 4

Changes in the light intensity along the x-axis and y-axis of astigmatic electromagnetic GSM beams passing through the oceanic turbulence with different astigmatic coefficient C 6

Full size image

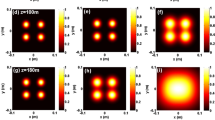
Figure 5a–d show the changes in the light intensity along the z-axis of astigmatic electromagnetic GSM beams passing through the oceanic turbulence with different value of C 6. When there is no astigmatism, the point taking the maximum of the light intensity is located at the origin. Under astigmatism case, the light intensity has a maximum value which the point taking the maximum value is not at the origin. In addition, the point becomes much closer to the origin as the astigmatic coefficient becomes larger. Furthermore, as the astigmatic coefficient becomes larger, the maximum value increases rapidly, and the width of the light intensity becomes shorter rapidly. This phenomenon is completely different from our expectation.

Fig. 5
figure 5

Changes in the light intensity along the z-axis of astigmatic electromagnetic GSM beams passing through the oceanic turbulence with different astigmatic coefficient C 6

Full size image

Figure 6a–d show the spectral degree of polarization along the z-axis with different values of astigmatic coefficient. From these figures, we observe that astigmatism can affect the polarization, and the degree of polarization in the far field is independent of the astigmatism of the source. We also observe that as the astigmatic coefficient increases to a certain order of magnitude, the degree of polarization is hardly affected by oceanic turbulence. Furthermore, it is shown that when the astigmatic coefficient is large enough, the degree of polarization is invariant all along the z-axis and it is hardly affected by free space diffraction or oceanic turbulence. This phenomenon is clearly seen in Fig. 6b–d.

Fig. 6
figure 6

Effect of different strengths of astigmatism on the spectral degree of polarization (on axis) in free space and oceanic turbulence

Full size image

Figure 7a–d shows the effect of astigmatism on the spectral degree of polarization in another point of view. From these figures, we can also conclude that as astigmatic coefficient becomes larger, the degree of polarization is less changed during propagation both in the free space and in the oceanic turbulence case.

Fig. 7
figure 7

Spectral degree of polarization (on axis) for different values of astigmatic coefficient C 6 in free space and oceanic turbulence

Full size image

5 Concluding remarks

In this paper, we investigate the effect of astigmatism on the spectral density distribution and the spectral degree of polarization both in oceanic turbulence and in free space. On the basis of the cross-spectral density matrix, the analytical formulae for the spectral density distribution and the spectral degree of polarization are derived. The Gaussian Schell-model source with astigmatism is chosen as the numerical example. The results have shown that for larger values of \( \chi_{T} ,w \) and for smaller value of \( \varepsilon ,\delta_{xx} \) and \( \delta_{yy} \), the light intensity along the z-axis becomes smaller. Furthermore, we found that although the change in the light intensity along the x-axis and y-axis is similar, the propagation distance along the y-axis is farther than the x-axis under the same conditions, and then we investigated the effect of astigmatic coefficient C 6 on the light intensity along the z-axis and found a phenomenon that completely different from our expectation. Finally, the results have shown that different strengths of astigmatism have different effects on the spectral degree of polarization. Our results might be crucial for operation of communication and sensing systems involving ocean turbulence channels.