Extension of the classical Fabry–Perot formula to 1D multilayered structures

Abstract

In any field theory the interaction of a wave packet with a multilayered potential is of high theoretical and practical relevance. In the present work we show an extension to any number of layers of the classical Fabry–Perot formula that works for any level of absorption, any thickness of the composing layers, any number of layers, any angle of incidence and for evanescent waves as well. More specifically, the ability of dealing with input evanescent waves and complex metal-based structures is of special interest for superlenses analysis and design. Some explicit examples in electromagnetism are also discussed.

1 Introduction

The study of the interaction between a wave packet and a multilayered structure plays a key role in many different contexts. For instance, one could be interested in computing the probability of tunnelling of a particle through a barrier or in studying the dynamics of charge carriers in a crystal. In electromagnetism, where the role of the potential is played by the index of refraction n, the propagation of a field through stratified media finds important applications in thin films technology (optical antireflection coating [1]), cloaking [2], spectroscopy (interferential mirrors or filters [3]), in superresolution imaging via metamaterials [4–9] and in non-linear optics [10, 11]. Except for very simple cases, where closed-form expressions for the transmission and reflection coefficients of a wave interacting with the multilayer are available, in most cases one has to resort to some numerical methods. Among these numerical approaches, the most popular one is probably the so-called transmission-matrix (or T-matrix) approach [12]. In this method, the electric and magnetic fields in any layer of the structure are expressed in terms of a forward and backward propagating plane wave with unknown complex amplitudes to be determined by imposing the proper boundary conditions at the interfaces between two adjacent layers. This numerical method is applicable not only to planar multilayers, but also to more complex inhomogeneous scatterers as, for instance, when diffraction gratings are present as well. Because of some numerical instabilities shown by the T-matrix approach to analyze the scattering from gratings (especially when evanescent waves are present), other numerical techniques have been developed during the years, to overcome these problems [13–15]. One of the most successful is surely represented by the S-matrix algorithm [16, 17], that has the advantage of being stable and, in some conditions, faster than the T-matrix approach. However, better performances are reached at the cost of a higher complexity of the algorithm [18, 19]. Although many different methods have been introduced in the past to calculate the complex amplitudes of the fields reflected and transmitted by multilayers, as far as we know an explicit extension of the fundamental Fabry–Perot formula to any number of layers is still missing. The solution we introduce, apart from being exact, can also be convenient from a computational point of view. The paper is organized as follows. In Sect. 2 we describe the foundations of the theory and we derive the closed-form expression for the reflected and transmitted field for a generic structure made of many layers of homogeneous media. In Sect. 3 we show the validity of our findings by discussing some specific example. Some useful formulas regarding energy conservation and the Poynting vector for oblique incidence are reported, for reader’s commodity, in the Appendix 1. Finally, the main results of our work are summarized in Sect. 4.

2 Extension of the Fabry–Perot formula to any number of layers

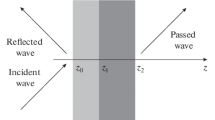
Although the results of our work are very general and hold for any wave field theory, from now on we will focus on electromagnetism only. Let us begin with the simplest layered structure one can analyze, which is made of only two media filling the whole space. In that case only one interface is present and the reflection and transmission coefficients (for s- and p-polarization) are analytically given by the Fresnel formulas [20]. Some complexity is added when another medium of thickness d is inserted. In Fig. 1 the three-medium structure is shown, with i meaning the input medium where the incident monochromatic wave is coming from and o denoting the output medium. The middle medium is labelled by 1. We will refer to a N-media structure when there are N − 2 media separating the input medium i from the output medium o. For a system made of three media (i, 1, o) one has, for the transmission and reflection coefficients, denoted by coefficients t and r, respectively

$$ t = \frac{t_{i,1} t_{1,o}\exp{(i k_{z1}d_1)}}{1-r_{1,o}r_{1,i}\exp{(i 2k_{z1} d_1)}} $$

(1)

$$ r = r_{i1}+\frac{t_{i,1} t_{1,o} r_{1,o} \exp{(i k_{z1}d_1)}}{1-r_{1,o}r_{1,i}\exp{(i 2k_{z1} d_1)}} $$

(2)

where $k_{z1}=\sqrt{k_0^2 n_1^2-k_{x1}^2}$ is the z component of the wavevector in the medium 1, d ₁ is its thickness, and Fresnel reflection and transmission coefficients at each interface (t _i,1, t _1,o , r _1,o , r _1,i ) are shown in the Fig. 1a. Also, we have denoted the index of refraction of the medium 1 by n ₁ and with k _x1 the x component of the wave vector in the medium. Equations 1 and 2 are known as Fabry–Perot (FP) formulas for a single-cavity [21]. These formulas are usually derived by literally listing all the multiple internal reflections that take place in the structure. In this way one discovers that the resulting transmitted (reflected) field has the form of a geometrical series and that Eq. 1 simply follows by summing up the series. The advantage of the FP formula resides in the fact that it is exact and it is valid for metals, strong absorbers, input evanescent waves and for any thickness d ₁. These are very appealing properties that would be highly desirable to keep also for more complex structures, that is, when N > 3. In order to do so, let us re-derive Eq. 1 by using another approach. The physical processes taking place in a single cavity are illustrated in Fig. 1a. One can describe these processes by considering the transmitted wave as the output in a block-diagram scheme as in Fig. 1b. In that block diagram, ξ represents the complex amplitude of incident wave, η the complex amplitude of the output wave, η ₁ is the amplitude in medium 1 right after being transmitted by the i/1 interface and η ₂ is the amplitude right before the 1/o interface. As it is clear from the diagram, a wave which passes through the first interface, propagates in layer 1 and then can either exit via the second interface or do another round trip into the medium 1. This second path is represented, in the block diagram, by the feedback loop linking η ₂ to η ₁. It is easy to write the node equation connecting η ₁ and η ₂, leading to

$$ t_{\hbox{FP1}}^{(1)} = \frac{\eta_2}{\eta_1} = \frac{\exp{(i k_{z1}d_1)}}{1-r_{1,o}r_{1,i}\exp{(i 2k_{z1} d_1)}} $$

(3)

By t ⁽¹⁾_FP1 we have denoted the Fabry–Perot transmission of order 1 for the layer 1, where the meaning of the term order will be clear in a moment. From the diagram it is also evident that η ₁ = t _i,1 ξ and η = η ₂ t _1,o , so that the relation between input and output reads

$$ \frac{\eta}{\xi} = t_{i,1} t_{\hbox{FP1}}^{(1)} t_{i,o} = \frac{t_{i,1} t_{1,o}\exp{(i k_{z1}d_1)}}{1-r_{1,o}r_{1,i}\exp{(i 2k_{z1} d_1)}} $$

(4)

Equation 4, which coincides with Eq. 1, provides also a clear physical picture of the transmission as a whole. In fact, once all the multiple reflections are taken into account by the transmission t ⁽¹⁾_FP1 , the total transmitted field is obtained simply by multiplying the input complex amplitude ξ by all the transmission coefficients of all the interfaces and all the Fabry–Perot-like transmissions. For reason of space we do not show the derivation of Eq. 2 concerning the reflection coefficient, but it is straightforward to realize that a similar reasoning applies. When the concept of FP transmission is introduced, the equivalent scheme for the whole structure can be further simplified as shown in c of Fig. 1.

Fig. 1

Incident, reflected and transmitted waves for a three-media layered structure (a). The presence of the two interfaces gives rise to a infinite set of internal reflections. The total reflected and transmitted field are built by summing the geometrical series that derives from the infinite set of internal reflections. We also show the block diagram equivalent to the three-media structure (b) and the equivalent scheme where all the multiple reflections are accounted for by means of the first-order FP transmission t ⁽¹⁾_FP1 (c)

The next step is to consider a structure made of four media (i,1,2,o). For this structure (N = 4, Fig. 2) one has to list all the countable paths that an incident wave can take to go from the input to the output medium. In order to derive the analytical expression for the transmitted and reflected wave, we need to draw the corresponding block diagram as we have done for the one-cavity structure. The corresponding plot, when looking at the transmitted wave, is shown in Fig. 2b. This time we have to write down two node equations. Additionally, one should note that from a physical point of view the two cavities are not identical. In fact, the second cavity, linking the amplitudes η ₃ and η ₄, is an ordinary Fabry–Perot cavity as in the previous example. We will call it a first-order FP cavity. For this cavity, the only feedback loop comes from the output interface of the cavity (interface 2/o in this case). On the other hand, the cavity that connects the amplitude η ₁ and η ₂ has a two-way feedback. One loop comes from the output interface of the cavity (interface 1/2 in the example) and the other from the last interface for the whole structure (interface 2/o). We will refer to this cavity as a second-order FP cavity. Generalizing, we will say that we deal with a mth-order FP cavity when there are m feedback loops reaching the input interface of the cavity. From the simplified diagram in Fig. 2b it is easy to obtain the total transmission t

$$ t=\frac{\eta}{\xi}=t_{i,1}t^{(1)}_{\rm {FP 2}}t_{1,2}t^{(2)}_{\rm {FP 1}}t_{2,o} $$

(5)

where

$$ t^{(2)}_{\hbox{FP 1}}= \frac{\exp{(ik_{z1}d_{1}})}{1-r_{1,2}r_{1,i}\exp{(2ik_{z1}d_{1})}- r_{2,o}r_{1,i}t_{1,2}t_{2,1}t^{(1)}_{\hbox{FP 2}}\exp{(2ik_{z1}d_{1})}\exp{(ik_{z2}d_{2}})} $$

(6)

and

$$ t^{(1)}_{\hbox{FP 2}}=\frac{\exp{(ik_{z2}d_{2}})}{1- r_{2,o}r_{2,1}\exp{(2ik_{z2}d_{2}})} $$

(7)

In Eqs. 6 and 7, t ^(q)_FPm denotes a FP transmission of order q linked to the mth layer. It follows that once the index of refraction and thickness of each layer are known, it is possible to write the analytical expression for the total transmission t (and reflection r). This approach can be extended to any number of layers since the corresponding block diagram can be always drawn and the relative nodes' equations easily derived. However, it would be not so handy to write down each time all the nodes' equations to solve the problem (although one could always let a computer program do it). Interestingly, the expression for t ^(q)_FPm can be derived by induction for any order q. This can be achieved by giving the physical interpretation of the terms appearing in the form of the FP transmissions, as written in Eqs. 6 and 7. If we have a closer look at Eq.6, we see that the numerator simply contains the one-way propagation factor $\exp{(i k_{z1} d_{1}})$ through the layer 1. The denominator is more complex but has an organized structure. In fact, in the expression

$$ 1-r_{1,2}r_{1,i}\exp{(2ik_{z1}d_{1})}-r_{2,o}r_{1,i}t_{1,2}t_{2,1}t^{(1)}_{\hbox{FP 2}}\exp{(2ik_{z1}d_{1})}\exp{(ik_{z2}d_{2}}) $$

(8)

different terms appear, each one associated to a particular sub-cavity of the whole structure. We can figure out which cavity we are dealing with by simply looking at the reflection coefficients present in each term. For instance, the term $r_{1,2}r_{1i}\exp{(2ik_{z1}d_{1})}$ refers to the cavity with interfaces 1/i and 1/2 (as suggested by the presence of the two reflection coefficients r _1,2 r _1,i ). The propagation factor $\exp{(2ik_{z1}d_{1})}$ accounts for a double propagation into the cavity in medium 1 (which is indeed the medium bounded by the two interfaces 1/i and 1/2). The second term refers to the cavity with boundaries 2/o and 1/i (which explains the presence of the two reflection coefficients r _2,o r _1,i ). For this second cavity the propagation must take into account for the propagation and transmission through the interfaces that the wave meets in its trip. This explains the presence of the terms $t_{1,2}t_{2,1}t^{(1)}_{\hbox{FP 2}}\exp{(2ik_{z1}d_{1})}\exp{(ik_{z2}d_{2}}).$

Fig. 2

Incident, reflected and transmitted waves for a four-media layered structure (a). We also show the block diagram equivalent to the four-media structure (b) and the equivalent scheme where all the multiple reflections are accounted for by means of the first and second FP transmissions, t ⁽¹⁾_FP1 and t ⁽¹⁾_FP2 , respectively (c)

To generalize, for a structure made of N media, $(i,1,2,3,\ldots,N-2,o),$ we will need to compute (N − 2) FP transmission coefficients. The FP transmission of order q = N − m − 1 is linked to the medium in the layer m, with $m=1,\ldots N-2,$ and takes the form

$$ \begin{aligned} t^{(N-m-1)}_{{\hbox{FP}}m} = \exp{(i k_{z_m}d_{m})}\{1-r_{m,m-1} r_{m,m+1}\exp{(2 i k_{z_m}d_{m})}\\ - r_{m,m-1}\exp{(2i k_{z_m}d_{m})}\sum_{l=m+1}^{N-2}[r_{l,l+1} (\prod_{p=m}^{l-1}t^{(N-p-2)}_{{\hbox{FP}}p+1} \exp{(i k_{z_p+1}d_{p+1})}t_{p,p+1}t_{p+1,p})]\}^{-1} \end{aligned} $$

(9)

where we have denoted the thickness of generic medium s by d _s and the z component of the wave vector as $k_{zs}. r_{s,s^{\prime}} (t_{s,s^{\prime}})$ is the reflection (transmission) coefficient between the media s and $s^{\prime}.$ Note that the notation r _1,0 refers to r _1,i .

The transmission of the whole structure then becomes (for a N-media structure there are N − 1 interfaces)

$$ t = \prod_{l=0}^{N-2} t_{l,l+1} \prod_{m=1}^{N-2} t^{(N-m-1)}_{{\hbox{FP}} m} $$

(10)

where t _0,1 = t _i,1 and t _N−2,N−1 = t _N−2,o are Fresnel’s transmission coefficients at the input and output interfaces, respectively. Equations 9 and 10 represent the main result of the present work. They allow us to compute the expression for the total transmission of a 1D multilayered structure with no limitation concerning level of absorption, thickness of layers, angle of incidence or presence of evanescent waves (either incident or generated inside the structure). Although Eq. 10 becomes more complex when N becomes large, it is important to notice that a computer program can be used to derive it, without any approximation. In this sense, all advantages of the proposed solution are preserved. Similarly, an expression for the total reflection can be computed, that reads

$$ r = r_{i,1}+ \sum_{m=1}^{N-2}\left\lbrace r_{m,m+1} \left[ \prod_{p=1}^{m}t^{(N-p-1)}_{{\hbox{FP}} p}t_{p-1,p}t_{p,p-1}\exp{(i k_{z_{p}}d_{p})}\right] \right\rbrace $$

(11)

where it is assumed, to simplify the notation, that t _0,1 = t _i,1, t _1,0 = t _1,i , r _1,0 = r _1,i , r _N-2,N−1 = r _N-2,o .

3 Examples

Let us now apply the results of the previous section to some specific example. Let us consider first an all-dielectric structure with N = 6 media (i, 1, 2, 3, 4, o) with indices of refraction [n _i  = 1, n ₁ = 1.5, n ₂ = 3, n ₃ = 2, n ₄ = 1.5, n _o  = 1] and thicknesses [d ₁ = 35 nm, d ₂ = 50 nm, d ₃ = 1,582 nm, d ₄ = 20 nm]. The wavelength λ is 632.8 nm. In Fig. 3 the reflection and transmission coefficients for both the s- and p-polarization are shown versus the normalized wavevector k _x /k ₀ of the incident plane wave. A calculation of the Poynting vector (Fig. 3c) shows that the energy is perfectly preserved for any incident k _x and any polarization, as it should be for a perfectly dielectric structure. It is important to recall that the simple condition $\vert r\vert^2 + \vert t\vert^2=1$ is valid only for normal incidence (i.e., when k _x  = 0), with no absorption present and when the input and output are the same medium. The most general expression for energy conservation can be obtained by passing through the definition of the Poynting vectors for the incident, reflected and transmitted wave. For reader’s commodity, we describe in the Appendix 1 such general expression, for s- and p-polarization.

Fig. 3

Reflection and transmission through a dielectric 1D all-dielectrics structure with media (i, 1, 2, 3, 4, o). The indices of refraction are (n _i  = 1, n ₁ = 1.5, n ₂ = 3, n ₃ = 2, n ₄ = 1.5, n _o  = 1) and thicknesses (d ₁ = 35 nm, d ₂ = 50 nm, d ₃ = 1,582 nm, d ₄ = 20 nm). a, b Show the absolute values for the reflection and transmission coefficients for s- and p-polarization cases, respectively. c The components of the time-averaged Poynting vector are plotted, for both states of polarization and for the reflected and transmitted field, respectively. The (blue) solid line is the z component of the Poynting vector for the reflected field for the s-polarization case while the (red) dotted line refers to the transmitted field for the same polarization. The (red) dashed line refers to the z component of the Poynting vector for the transmitted field for the p-polarization case while the (blue) dashed–dotted line refers to the reflected field for the p-polarization case. It is easy to check that energy conservation is obtained in closed-form

As second example, we would like to show how the proposed solution deals with lossy media. To do this, we consider two different structures. One structure (which we will call structure A) is made of two media, air and silver, for which the reflection and transmission are known in analytical form. The other (structure B) is a stack with six media (i, 1, 2, 3, 4, o), where the input and output media are air (n _i  = n _o  = 1), the medium 1 is silver with n ₁ = 0.13455 + i3.9865 and the medium 3 is gold with n ₃ = 0.19715 + i3.0899. The media 2 and 4 are glass with n ₂ = n ₄ = 1.5. The wavelength λ = 632.8 nm. The thickness of each layer for the structure B are the following: d ₁ = d _Ag (variable between 10 nm and 1 μm), d ₂ = 10 nm, d ₃ = 10 nm and d ₄ = 20 nm. In the example we compare the reflection from the structures A and B, for k _x /k ₀ = 0.5 and s-polarization, when the thickness of the silver layer in the structure B is changed from 10 nm to 1 μm. In this case, we expect that on increasing the thickness of the silver layer in the structure B its corresponding total reflection should tend to the reflection shown by the structure A, where silver fills the whole half-space. The reflection for the structure A, that can be computed analytically by means of Fresnel equations, is equal to r ^A _s  = 0.9864 in this specific case. From Fig. 4 we see that when the thickness of the silver layer, in the structure B, reaches about 120 nm then the reflection |r ^B _s | in that case tends to the asymptotic value of 0.9864, as expected. However, also under those conditions, we can still compute the small transmission through the whole stack B ; for instance, when d _Ag = 1 μm one finds $|t^{\hbox{B}}_s|=3.109\,\times\,10^{-18}.$

Fig. 4

Reflection and transmission through a dielectric 1D lossy stack made of six media (i, 1, 2, 3, 4, o) for k _x /k ₀ = 0.5 and s-polarization of light. The input and output media is vacuum (n _i  = n _o  = 1), the medium 1 is silver with n ₁ = 0.13455 + i3.9865 and the medium 3 is gold with n ₃ = 0.19715 + i3.0899. The media 2 and 4 are dielectric with n ₂ = n ₄ = 1.5. The wavelength is λ = 632.8 nm. The thicknesses of each layer for the structure B are the following: d ₁ = d _Ag (variable between 10 nm and 1 μm), d ₂ = 10 nm, d ₃ = 10 nm and d ₄ = 20 nm. In the plots the transmission |t _s | and reflection |r _s | are shown as function of the thickness of the layer of silver, indicated by d _Ag, which varies from 10 nm to 1 μm. The reflection tends to the ideal value (0.9864), typical of a silver half-space in air, for d _Ag > 120 nm

This specific example has also been simulated by means of an in-house version of the T-matrix approach. The results for the reflection and transmission coefficients obtained through the two different methods agreed up to the machine precision. A comparison on the computation time is more delicate. In case the closed-form solution we propose here is calculated by means of a computer program, then the time needed to compute it grows as N ². This computation time essentially accounts for time needed to derive the analytical expression for the transmission and reflection coefficients. However, the computational time for a T-matrix approach grows as N. We have found that for N < 20,25 layers the algorithm to compute the solution proposed in this work is always faster than the T-matrix method. Above that value, the T-matrix method becomes faster. However, it is important to stress that the calculation of the extended Fabry–Perot formula derived in this work, for a given N, is required only once. For any successive use there is no need to compute it again. In this case the extended Fabry–Perot formula is always notably faster than any numerical method.

We have also considered another application of the method, namely the case of a periodic structure of finite sizes consisting of 16-period of a n ₁ − n ₂ bilayer, with n ₁ = 1.5 (glass) and n ₂ = 5.47166 + i0.81627 (germanium), embedded in air. The relative thicknesses have been set to d _glass = 40 nm and d _Ge = 5 nm, respectively. In this case, we have considered the incident wave being either a homogeneous or an evanescent wave in air, of wavelength λ = 632 nm. Finally, the transmission and reflection coefficients of the same structure, with a perturbing air-layer of thickness 100 nm between the 16th and the 17th layer, have been computed. All results are shown in Fig.  5. Also in this case the extended Fabry–Perot formula gives the transmitted and reflected fields without problems and with an agreement with a T-matrix method up to machine precision.

Fig. 5

Reflection and transmission through a periodic structure without (a, b) and with perturbing layer (c, d). The main structure consists of 16 periods of glass-germanium (d _glass = 40 nm, d _Ge = 5 nm), embedded in air. The thickness of the perturbing layer (air) is d = 100 nm. The wavelength is λ = 632.8 nm

4 Conclusions

To summarize, in the present work we have shown how to extend the classical Fabry–Perot formula to a stratified 1D multilayer with any number of layers. Our findings are applicable to layers of any thickness, level of absorption and to any incident field (evanescent or not). We have provided a scheme to derive the closed-form expression for the fields once the structure of interest is known. The main difference with respect to iterative calculation methods that have been introduced in the past resides in the fact that the solution we proposed uses an iterative scheme only to compute the closed-form expression of the total transmission or reflection, with no numerical approximations. In this sense, the solution is exact. This is also confirmed by a check on energy conservation for dielectric structures, where energy is mathematically preserved, with no numerical approximation. The advantage is not only from a computational point of view (no numerical instability, potentially much faster computation time) but opens the way to a better understanding of the physics as well. We believe that our results can be useful in many different contexts as thin-films theory, photonic band-gap crystals, near-field superlens or evanescent wave enhanced spectroscopy.

Appendix 1: energy conservation

In this appendix we recall some expressions for the Poynting vectors of the incident, reflected and transmitted fields. They are used to check that the analytical expression for the transmitted and reflected fields, as derived in the paper, do not violate the energy conservation every time we are in the presence of a non-dissipative system.

When the incident wave has the x component of the wave vector different from zero (i.e., we are not at normal incidence) the expression of energy conservation can be obtained by deriving the expression of the z component of the Poynting vectors for the incident, reflected and transmitted wave, respectively. In addition, this has to be done separately for s- and p-polarization. Let us start with the s-polarization case.

1.1 S-polarization case

Let us assume that the incident wave has an electric field component of type

$$ E_y^{(1)}(x,z) = A_E^{(i)} \exp{(i {\bf k}^{(i)}\cdot{\bf r})} $$

(12)

with k ⁽ⁱ⁾ = (k ⁽ⁱ⁾ _x , 0, k ⁽ⁱ⁾ _z ) the wave vector of the incident field and r = (x, y, z). The energy flow along z for the incident field can be written, starting from the definition of the Poynting vector as

$$ \left\langle {\bf S}\right\rangle = \frac{1}{2} Re\{{{\bf E}\times{\bf H^{\star}}}\} $$

(13)

We need to look at the z component for the incident, reflected and transmitted field. After simple algebra we obtain,

$$ \left\langle {S_z^{(i)}}\right\rangle = \frac{1}{4} \frac{|A_{E}^{(i)}|^2}{\omega \mu_i} [k_{z}^{(i)}+(k_{z}^{(i)})^{\star}] $$

(14)

where ω is the angular frequency and μ _i is magnetic permeability of the input medium i. For the Poynting vectors of the reflected and transmitted field we get,

$$ \left\langle {S_z^{(rs)}}\right\rangle = \frac{1}{4} |r_s|^2 \frac{|A_{E}^{(i)}|^2}{\omega \mu_r} [k_{z}^{(r)}+(k_{z}^{(r)})^{\star}] $$

(15)

(k ^(r) _z  = k ⁽ⁱ⁾ _z and μ _i  = μ _r , since incident and reflected wave lie in the same medium),

$$ \left\langle {S_z^{(ts)}}\right\rangle = \frac{1}{4} |t_s|^2 \frac{|A_{E}^{(i)}|^2}{\omega \mu_t} [k_{z}^{(t)}+(k_{z}^{(t)})^{\star}] $$

(16)

with obvious meaning of the notation. To check energy conservation, we look at the following normalized quantity

$$ \frac{\left\langle {S_z^{(rs)}}\right\rangle +\left\langle {S_z^{(ts)}}\right\rangle }{\left\langle {S_z^{(i)}}\right\rangle } =|r_s|^2+ |t_s|^2 \frac{\mu_i}{\mu_t} \frac{[k_{z}^{(t)}+(k_{z}^{(t)})^{\star}]}{[k_{z}^{(r)}+(k_{z}^{(r)})^{\star}]} $$

(17)

that should always (i.e., for all k _x ) be equal to one for absorption-free systems. In case k ⁽ⁱ⁾ _x  = 0 (normal incidence), in absence of absorption and with same input and output medium, Eq. 17 reduces to the well-known form |r _s |² + |t _s |² = 1.

1.2 P-polarization case

In this case it is easier to consider the y component of the incident magnetic field

$$ H_y^{(1)}(x,z) = A_H^{(i)} \exp{(i {\bf k}^{(i)}\cdot{\bf r})} $$

(18)

For the z component of the Poynting vector of the incoming field we obtain

$$ \left\langle {S_z^{(i)}}\right\rangle = \frac{1}{4} \frac{|A_{H}^{(i)}|^2}{\omega \varepsilon_{i}} [k_{z}^{(i)}+(k_{z}^{(i)})^{\star}] $$

(19)

All formulas derived in the previous subsection can be extended to the current case by replacing r _s and t _s by r _p and t _p and μ by $\varepsilon$ in the medium. After doing that we get

$$ \frac{\left\langle {S_z^{(rp)}}\right\rangle +\left\langle {S_z^{(tp)}}\right\rangle }{\left\langle {S_z^{(i)}}\right\rangle } =|r_p|^2+ \frac{n_{\hbox{input}}^2}{n_{\hbox{output}}^2}|t_p|^2 \frac{[k_{z}^{(t)}+(k_{z}^{(t)})^{\star}]}{[k_{z}^{(r)}+(k_{z}^{(r)})^{\star}]} $$

(20)

which represents the energy conservation formula for the p-polarization case.