Transparent Multilayer Electromagnetic Structures Based on Metal Metamaterials

Abstract—Layered isotropic structures including layers of metamaterial are considered. Two-layer and multilayer symmetric structures, as well as a structure with a continuous change in material parameters, have been investigated. For the first time, the conditions of transparency of such structures and structures derived from them are presented. It is shown that the boundaries of the regions of no passage of the wave correspond to the conditions of transparency of such structures. It is shown that for transparency parity-time (PT) symmetric structures in electrodynamics and optics, additional conditions are required, in contrast to the structures presented.

INTRODUCTION

The study of inhomogeneous layered media in electrodynamics and optics has been carried out for more than a hundred years. The literature describes infinite and bounded structures [1–11], studies the behavior of various types of waves, considers guiding [11] and resonance [4, 5] structures, and isotropic [1‒5] and anisotropic media [6–8, 10].

A large number of microwave [4, 5] and optical devices [1, 7] have been developed on the basis of inhomogeneous media. Recently, various structures and devices using metamaterials have been of great interest to researchers [7, 12–14]. In particular, it was proposed to use metamaterials for the production of flat lenses, invisible coatings, elements of photonic switching systems and emitting devices.

Since 2007, studies have been presented describing the so-called parity-time (PT) symmetric structures [15–19]. In the simplest case, these are two-layer structures of the same thickness with complex conjugate dielectric and magnetic permeabilities. The authors proposed, in particular, to use them as transparent structures, as well as to compensate for losses in dielectric layers [18, 19]. To describe them, as a rule, operator methods were used, which were developed in detail in quantum physics [18, 19]. Papers [20–22] also describe a special case PT structure, a medium when the real parts of permittivity and permeability tend to zero. As shown by the author, such structures are indeed transparent, in contrast to general case PT symmetrical optical and electromagnetic structures.

However, it should be noted that as early as 2006, the so-called spatially symmetric structures without forbidden regions were described [23, 24]. These structures included layers of an ordinary dielectric and metamaterial of equal thickness with the same modulus and opposite in sign dielectric and magnetic permeability. Obviously, such media can be transparent.

The main goal of this study is to find conditions for the transparency of arbitrary layered media and media with continuously varying parameters in terms of the material parameters of the medium. For research, we used the transformation operator method [1, 3–8, 23, 24], which was widely used earlier to describe both isotropic and anisotropic structures and which is adequate for these cases in the framework of a linear problem.

1 TRANSPARENCY CONDITIONS OF A MULTILAYER STRUCTURE

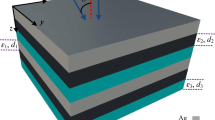
Let us consider the conditions for the transparency of an arbitrary layered, primarily two layer, structure. The dielectric and magnetic permeabilities of the layers in this case are complex. Let a plane electromagnetic wave with frequency $\omega ~$ falls on such a structure at an arbitrary angle (Fig. 1).

Fig. 1.

The geometry of the two-layer structure.

The behavior of a wave in such a structure can be described using a transformation operator that connects the tangential components of the field at its boundaries [1–8]:

$${\mathbf{\hat {U}}} = {\mathbf{\hat {L}}}{{{\mathbf{\hat {U}}}}_{0}}~,$$

(1)

where ${{{\mathbf{U}}}_{{0~}}}$ is the operator of the state of the tangential components of the field at boundary $z = {{z}_{0}}$ and ${\mathbf{U}}~$ is the operator of the state of the tangential components of the field at boundary $z = {{z}_{2}}.$ Then, for a TE-wave we have [1]

$${\mathbf{U}} = \left| {\begin{array}{*{20}{c}} {{{E}_{x}}} \\ {{{H}_{y}}} \end{array}} \right|,\,\,\,\,{{{\mathbf{U}}}_{0}} = \left| {\begin{array}{*{20}{c}} {{{E}_{{x0}}}} \\ {{{H}_{{y0}}}} \end{array}} \right|,$$

(2)

by analogy for TM-waves [1]:

$${\mathbf{U}} = \left| {\begin{array}{*{20}{c}} {{{E}_{y}}} \\ {{{H}_{x}}} \end{array}} \right|,\,\,\,\,{{{\mathbf{U}}}_{0}} = \left| {\begin{array}{*{20}{c}} {{{E}_{{y0}}}} \\ {{{H}_{{x0}}}} \end{array}} \right|.$$

(3)

The transformation operator of a two-layer structure, in accordance with the method [1–11], is found as the product of the layer transformation operators:

$${\mathbf{\hat {L}}} = {{{\mathbf{\hat {L}}}}_{1}}{{{\mathbf{\hat {L}}}}_{2}},$$

(4)

where the matrix of the operator of the first layer has form [1–5]

$${{{\mathbf{L}}}_{1}} = \left| {\begin{array}{*{20}{c}} {\cos {{\varphi }_{1}}}&{ - \frac{j}{{{{p}_{1}}}}\sin {{\varphi }_{1}}} \\ { - j{{p}_{1}}\sin {{\varphi }_{1}}}&{\cos {{\varphi }_{1}}} \end{array}} \right|.$$

(5)

Here, ${{\varphi }_{1}} = {{k}_{0}}{{n}_{1}}{{d}_{1}}\cos {{\theta }_{1}}$ is the optical thickness of the first layer, $~{{k}_{0}} = \omega \sqrt {{{\varepsilon }_{0}}{{\mu }_{0}}}$ is the wave number in free space, $~{{n}_{1}} = \sqrt {{{\varepsilon }_{1}}{{\mu }_{1}}~~} ~{{\;}}$ is the refractive index of the material of the first layer, ${{\theta }_{1}}$ is the angle of refraction in the first layer, $~{{p}_{1}} = \sqrt {{{{{\varepsilon }_{1}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{1}}} {{{\mu }_{1}}}}} \right. \kern-0em} {{{\mu }_{1}}}}}$ is the wave conductivity of the layer (for a wave of TE-type), ${{p}_{1}} = ~\sqrt {{{{{\mu }_{1}}} \mathord{\left/ {\vphantom {{{{\mu }_{1}}} {{{\varepsilon }_{1}}~}}} \right. \kern-0em} {{{\varepsilon }_{1}}~}}}$ is the wave impedance of the layer (for a wave of TM-type), ${{d}_{1}}$ is the layer thickness, and $j = \sqrt { - 1} .$ The second layer operator matrix is written as

$${{{\mathbf{L}}}_{2}} = \left| {\begin{array}{*{20}{c}} {\cos {{\varphi }_{2}}}&{ - \frac{j}{{{{p}_{2}}}}\sin {{\varphi }_{2}}} \\ { - j{{p}_{2}}\sin {{\varphi }_{2}}}&{\cos {{\varphi }_{2}}} \end{array}} \right|.$$

(6)

Here, similarly to the first layer, ${{\varphi }_{2}} = {{k}_{0}}{{n}_{2}}{{d}_{2}}\cos {{\theta }_{2}}$ is the optical thickness of the second layer, $~{{n}_{2}} = \sqrt {{{\varepsilon }_{2}}{{\mu }_{2}}}$ is the refractive index of the material of the second layer,$~{{\theta }_{2}}$ is the angle of refraction in the second layer, ${{p}_{2}} = \sqrt {{{{{\varepsilon }_{2}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{2}}} {{{\mu }_{2}}}}} \right. \kern-0em} {{{\mu }_{2}}}}}$ for the TE-type wave, ${{p}_{2}} = \sqrt {{{{{\mu }_{2}}} \mathord{\left/ {\vphantom {{{{\mu }_{2}}} {{{\varepsilon }_{2}}}}} \right. \kern-0em} {{{\varepsilon }_{2}}}}}$ for the TM-type wave, and ${{d}_{2}}$ is the layer thickness.

Obviously, the structure under consideration will be transparent if reflection coefficient R is zero, and transmission coefficient T is equal to 1. In accordance with [1], the reflection and transmission coefficients of the structure are in form

$$\begin{gathered} R = \frac{{\left( {{{L}_{{11}}} + {{L}_{{12}}}{{p}_{l}}} \right){{p}_{1}} - \left( {{{L}_{{21}}} + {{L}_{{22}}}{{p}_{l}}} \right)}}{{\left( {{{L}_{{11}}} + {{L}_{{12}}}{{p}_{l}}} \right){{p}_{1}} + \left( {{{L}_{{21}}} + {{L}_{{22}}}{{p}_{l}}} \right)}}~, \\ T = \frac{{2{{p}_{1}}}}{{\left( {{{L}_{{11}}} + {{L}_{{12}}}{{p}_{l}}} \right){{p}_{1}} + \left( {{{L}_{{21}}} + {{L}_{{22}}}{{p}_{l}}} \right)}}~, \\ \end{gathered} $$

(7)

where ${{L}_{{km}}}$ are the elements of transformation operator matrix (4). Thus, the transparency condition is defined by expression

$$\left( {{{L}_{{11}}} + {{L}_{{12}}}{{p}_{l}}} \right){{p}_{1}} - \left( {{{L}_{{21}}} + {{L}_{{22}}}{{p}_{l}}} \right) = 0.$$

(8)

This coefficient depends on both the parameters of the layered structure included in the elements of the transformation matrix ${{L}_{{km}}}$ and on environmental parameters ${{p}_{1}},$ ${{p}_{l}}.$

If the structure is required to be transparent regardless of the parameters of its environment, then from (8) it follows that condition

$${\text{tr}}{\mathbf{L}} = 2,$$

(9)

where ${\text{tr}}{\mathbf{L}}~$ is the matrix trace. Indeed, taking into account the continuity of the tangential components of the fields at the boundaries of the structure, the necessary condition for transparency is the equality of the components of these fields at the output of the structure to the corresponding components of the fields at its input:

$$\left| {\begin{array}{*{20}{c}} {{{E}_{{x0}}}} \\ {{{H}_{{y0}}}} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} {{{L}_{{11}}}}&{{{L}_{{12}}}} \\ {{{L}_{{21}}}}&{{{L}_{{22}}}} \end{array}} \right|\left| {\begin{array}{*{20}{c}} {{{E}_{{x0}}}} \\ {{{H}_{{y0}}}} \end{array}} \right|.$$

(10)

In this case, solution (10) gives (9) and, accordingly, condition (8) is satisfied (see the Appendix). In this case, it is known from the theory of periodic media that condition (9) determines the boundaries of the regions of no passage of a wave in an infinite periodic structure with the corresponding two-layer period [1‒4] described by operator (4).

Thus, a two-layer structure will be transparent if condition (9) is satisfied for the corresponding periodic structure the period of which is the considered bounded structure.

In a more general case, the operators for transforming a multilayer structure with an arbitrary number of layers are found:

$${\mathbf{\hat {L}}} = \prod\limits_{i = M}^1 {{{{{\mathbf{\hat {L}}}}}_{i}}} ~,$$

(11)

where ${{{\mathbf{\hat {L}}}}_{i}}$ is the operator’s ith layer and M is the number of layers. Then, to ensure transparency, equality (9) is satisfied.

Now consider a periodic structure with N periods including an arbitrary number of layers. Obviously, such a structure will be transparent if the amplitudes of the fields at its input and output are equal, and the resulting phase shift by N periods will be $2\pi m$ ($m = \pm 1, \pm 2, \ldots$). In this case, the phase shift in one period is equal to $\varphi = {{2\pi m} \mathord{\left/ {\vphantom {{2\pi m} N}} \right. \kern-0em} N}.$ Then, taking into account the transformation matrix for one period, we write

$$\left| {\begin{array}{*{20}{c}} {{{E}_{{x0}}}\exp \left( {j\varphi } \right)} \\ {{{H}_{{y0}}}\exp \left( {j\varphi } \right)} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} {{{L}_{{11}}}}&{{{L}_{{12}}}} \\ {{{L}_{{21}}}}&{{{L}_{{22}}}} \end{array}} \right|\left| {\begin{array}{*{20}{c}} {{{E}_{{x0}}}} \\ {{{H}_{{y0}}}} \end{array}} \right|,$$

(12)

where ${{L}_{{11}}},$ ${{L}_{{12}}},$ ${{L}_{{21}}},$ ${{L}_{{22}}}$ are elements of the transformation matrix for a multilayer period. Whence, taking into account (8), we obtain the condition for the transparency of a periodic multilayer structure with N periods and an arbitrary number of layers in a period in form

$${\text{tr}}{\mathbf{L}} = \left| {2\cos \varphi } \right|.$$

(13)

Thus, a multilayer structure with an arbitrary number of layers is transparent if its parameters correspond to the boundaries of the wave propagation regions of the corresponding periodic structure determined by condition (9). A multilayer periodic structure with N periods will be transparent if its parameters correspond to the wave propagation regions and condition (13) is satisfied.

Figure 2 shows an illustration of expression (13) using an example of a structure that includes four periods. In this case, the phase shift of the electric (magnetic) field vector in one period is $\pi {\text{/}}2,$ at the end of the fourth period, the phase shift of the electric field strength of vector $~{{E}_{9}}$ is $2\pi ,$ and the amplitude of vector $~{{E}_{9}}$ is equal to the amplitude of vector $~{{E}_{0}}$ at the beginning of the first period. Note that Fig. 2 shows a non-spatial rotation of vector E, and the dependence of the current phase of the wave on the spatial coordinate. For definiteness, the direction of the electric field vector is taken as zero phase ${{E}_{0}}$ along the positive direction of the Oy-axis.

Fig. 2.

Illustration of the transparency condition for a four-layer periodic structure.

2 TWO-LAYER SYMMETRIC DIELECTRIC-METAMATERIAL STRUCTURE

With the advent of metamaterials with simultaneously negative dielectric and magnetic permeabilities, the production of completely transparent layered structures has become much easier. Indeed, condition (9) can be satisfied when using a spatially symmetric isotropic dielectric–isotropic metamaterial structure. For this, it is necessary that for the layers of the two-layer structure, conditions ${{\varepsilon }_{{{\text{meta}}}}} = - {{\varepsilon }_{{\text{d}}}},$ ${{\mu }_{{{\text{meta}}}}} = - {{{{\mu }}}_{{\text{d}}}},$ ${{d}_{{{\text{meta}}}}} = {{d}_{{\text{d}}}}$ are satisfied (Fig. 3). In this case, the permittivity and permeability in the general case are complex quantities. Thus, in accordance with the methodology [1, 3], transformation operator matrix $~{{{\mathbf{\hat {L}}}}_{1}}$ of a single dielectric layer has form (5), and transformation operator matrix ${{{\mathbf{\hat {M}}}}_{1}}$ of a layer of an isotropic metamaterial is written in form

$${{{\mathbf{M}}}_{1}} = \left| {\begin{array}{*{20}{c}} {\cos {{\varphi }_{1}}}&{\frac{j}{{{{p}_{1}}}}\sin {{\varphi }_{1}}} \\ {j{{p}_{1}}\sin {{\varphi }_{1}}}&{\cos {{\varphi }_{1}}} \end{array}} \right|.$$

(14)

Indeed, the positive signs of the elements of the side diagonal are determined by the fact that the wavenumbers for the metamaterial have negative signs. Obviously, matrices (5) and (14) are mutually inverse (${{{\mathbf{M}}}_{1}} = {\mathbf{L}}_{1}^{{ - 1}}$). Then,

$${\mathbf{\hat {L}}} = {{{\mathbf{\hat {L}}}}_{1}}{{{\mathbf{\hat {M}}}}_{1}} = {\mathbf{\hat {I}}}~,$$

(15)

where ${\mathbf{\hat {I}}}$ is the single operator. It’s obvious that ${\text{tr}}{\mathbf{\hat {I}}} = 2.$ Therefore, taking into account (7), such a structure is transparent.

Fig. 3.

Dependence of the dielectric (a) and magnetic (b) permeability of the layers on the spatial coordinate: $\varepsilon _{{\text{1}}}^{'},$ $\varepsilon _{{\text{1}}}^{{"}}$ are the real and imaginary parts of the dielectric constant of an ordinary dielectric, $d$ is the thickness of dielectric and metamaterial layers.

Thus, a rule can be formulated: a two-layer spatially symmetric structure, which includes layers of an ordinary dielectric and an isotropic metamaterial of the same thickness, is transparent for any angles of incidence if the following conditions are met: ${{{{\varepsilon }}}_{{{\text{meta}}}}} = - {{{{\varepsilon }}}_{{\text{d}}}},$ ${{{{\mu }}}_{{{\text{meta}}}}} = - {{{{\mu }}}_{{\text{d}}}}.$

In a more general case, a two-layer spatially symmetric structure is transparent if it includes a dielectric layer and a metamaterial layer with arbitrary thicknesses and complex material parameters that satisfy the condition of equality of their electromagnetic thicknesses in modulus ${{{{\varphi }}}_{{\text{d}}}} = {{{{\psi }}}_{{{\text{meta}}}}}.$

As an example, Fig. 4a shows the distribution of the electric field of TE-waves from spatial coordinate z in the spatially symmetric structure of the thickness of the dielectric and metamaterial layers $~{{d}_{1}} = {{d}_{2}} = 0.01~$ m, dielectric and magnetic permeability of dielectric ${{\varepsilon }_{1}} = 15.3,$ ${{\mu }_{1}} = 1$, respectively, the dielectric and magnetic permeability of metamaterial ${{\varepsilon }_{1}} = - 15.3,$ ${{\mu }_{1}} = - 1$, and accordingly, frequency $f = {{10}^{9}}$ Hz. Figure 4b shows the distribution of the electric field of TE-waves from spatial coordinate z for the case of different layer thicknesses and equal electromagnetic thicknesses. The thicknesses of the dielectric and metamaterial layers are $~{{d}_{1}} = 0.01$ m and ${{d}_{2}} = 0.005$ m, respectively, the dielectric and magnetic permeability of the dielectric ${{\varepsilon }_{1}} = 15.3,$ ${{\mu }_{1}} = 1,$ dielectric and magnetic permeability of the metamaterial ${{\varepsilon }_{1}} = - 61.2,$ ${{\mu }_{1}} = - 1,$ and frequency $f = 2.4 \times {{10}^{9}}$ Hz.

Fig. 4.

The structure of the normalized electric field in a two-layer symmetric structure: (a) for the case of equal layer thicknesses and equal electromagnetic thicknesses (b) for the case of different layer thicknesses and equal electromagnetic thicknesses.

Thus, numerical calculations confirm the correctness of the theoretical results. The field values at both boundaries of the structures are equal for the selected layer parameters, and, therefore, the structure is transparent.

3 MULTILAYER SYMMETRIC DIELECTRIC-METAMATERIAL STRUCTURE

Consider multilayer transparent structures including an arbitrary number of dielectric and metamaterial layers. First of all, consider a four-layer structure that includes two layers of an ordinary dielectric of the same thickness with complex material parameters ${{\varepsilon }_{1}},$ ${{\mu }_{1}},$ ${{\varepsilon }_{2}},$ and ${{\mu }_{2}},$ described by operators ${{{\mathbf{\hat {L}}}}_{1}}$ and $~{{{\mathbf{\hat {L}}}}_{2}}$ respectively, and two layers of metamaterials of the same thickness with parameters ${{\varepsilon }_{3}} = - {{\varepsilon }_{1}},$ ${{\mu }_{3}} = - {{\mu }_{1}},$ ${{\varepsilon }_{4}} = - {{\varepsilon }_{2}},$ and ${{\mu }_{4}} = - {{\mu }_{2}},$ described by operators ${{{\mathbf{\hat {M}}}}_{1}}$ and ${{\widehat {~{\mathbf{M}}}}_{2}}$ respectively. Figure 5a shows an example of the dependence of the dielectric constant on the spatial coordinate for a four-layer optically transparent structure. A similar dependence exists for the magnetic permeability (Fig. 5b). Obviously, the resulting transformation operator of such a structure is found as

$${\mathbf{\hat {L}}} = {{{\mathbf{\hat {L}}}}_{2}}{{{\mathbf{\hat {L}}}}_{1}}{{{\mathbf{\hat {M}}}}_{1}}{{{\mathbf{\hat {M}}}}_{2}} = {\mathbf{\hat {I}}}~.~$$

(16)

Fig. 5.

Dependences of valid ${\text{Re}}\left( \varepsilon \right)$ and imaginary ${\text{Im}}\left( \varepsilon \right)$ parts of the dielectric (a) and magnetic (b) permeabilities from spatial coordinate z for a transparent structure.

Indeed, in accordance with the previous section, we define ${{{\mathbf{\hat {L}}}}_{1}}{{{\mathbf{\hat {M}}}}_{1}} = {\mathbf{\hat {I}}}$ and then $~{\mathbf{\hat {L}}} = {{{\mathbf{\hat {L}}}}_{2}}{\mathbf{\hat {I}}}{{{\mathbf{\hat {M}}}}_{2}} = {{{\mathbf{\hat {L}}}}_{2}}{{{\mathbf{\hat {M}}}}_{2}} = {\mathbf{\hat {I}}}.$ Thus, condition (8) is satisfied and the considered four-layer structure is transparent.

In a more general case, a symmetric multilayer structure is transparent if the number of dielectric layers is equal to the number of layers of a metamaterial of arbitrary thickness and, in pairs, for all layers, the condition ${{{{\varphi }}}_{i}} = - {{{{\psi }}}_{i}},$ where ${{{{\varphi }}}_{i}}$ is the optical thickness of the ith dielectric layer and $~{{{{\psi }}}_{i}}$ is the optical thickness of the ith layer of the metamaterial.

Moreover, in accordance with the theory of layer permutation stated in [3], a change in the order of alternation of layers in a given transparent structure does not affect the calculation result. Indeed, it can be shown that

$$\begin{gathered} {\mathbf{\hat {L}}} = {{{{\mathbf{\hat {M}}}}}_{2}}{{{{\mathbf{\hat {L}}}}}_{2}}{{{{\mathbf{\hat {L}}}}}_{1}}{{{{\mathbf{\hat {M}}}}}_{1}} \\ = {{{{\mathbf{\hat {L}}}}}_{2}}{{{{\mathbf{\hat {M}}}}}_{2}}{{{{\mathbf{\hat {L}}}}}_{1}}{{{{\mathbf{\hat {M}}}}}_{1}} = {{{{\mathbf{\hat {M}}}}}_{2}}{{{{\mathbf{\hat {L}}}}}_{1}}{{{{\mathbf{\hat {M}}}}}_{1}}{{{{\mathbf{\hat {L}}}}}_{2}} = \ldots = {\mathbf{\hat {I}}}~. \\ \end{gathered} $$

(17)

The validity of expression (18) can also be verified by simple multiplication of the matrices of operators. To do this, consider ${{{\mathbf{\hat {L}}}}_{2}}{{{\mathbf{\hat {M}}}}_{2}}{{{\mathbf{\hat {L}}}}_{1}}{{{\mathbf{\hat {M}}}}_{1}}.$ Because $~{{{\mathbf{\hat {L}}}}_{1}}{{{\mathbf{\hat {M}}}}_{1}} = {\mathbf{\hat {I}}}$ and ${{{\mathbf{\hat {L}}}}_{2}}{{{\mathbf{\hat {M}}}}_{2}} = {\mathbf{\hat {I}}},$ then ${{{\mathbf{\hat {L}}}}_{2}}{{{\mathbf{\hat {M}}}}_{2}}{{{\mathbf{\hat {L}}}}_{1}}{{{\mathbf{\hat {M}}}}_{1}} = {\mathbf{\hat {I}}}.$ Similarly, it can be shown that since ${{{\mathbf{\hat {L}}}}_{1}}{{{\mathbf{\hat {M}}}}_{1}} = {\mathbf{\hat {I}}},$ then ${{{\mathbf{\hat {M}}}}_{2}}{{{\mathbf{\hat {L}}}}_{1}}{{{\mathbf{\hat {M}}}}_{1}}{{{\mathbf{\hat {L}}}}_{2}} =$ ${{{\mathbf{\hat {M}}}}_{2}}{\mathbf{\hat {I}}}{{{\mathbf{\hat {L}}}}_{2}} = {{{\mathbf{\hat {M}}}}_{2}}{{{\mathbf{\hat {L}}}}_{2}} = {\mathbf{\hat {I}}},$ etc. Hence, the conclusion is obvious that this four-layer structure is also transparent in any order of layers.

In the general case, for an optically transparent structure, one can write

$$\sum\limits_{i = 1}^N {{{{{\mathbf{\hat {L}}}}}_{i}}{{{{\mathbf{\hat {M}}}}}_{i}}} = {\mathbf{\hat {I}}}~,$$

(18)

where ${{{\mathbf{\hat {L}}}}_{i}}$ are operators of dielectric layers with complex dielectric ${{\varepsilon }_{i}}$ and magnetic ${{\mu }_{i}}$ permeabilities, ${{{\mathbf{\hat {M}}}}_{i}}$ are operators of layers of a metamaterial with a complex dielectric $- {{\varepsilon }_{i}}$ and magnetic $- {{\mu }_{i}}$ permeabilities. Moreover, based on the theory [3], it can be argued that the order of alternation of layers does not affect the transparency conditions of the structure.

Figure 6a shows the distribution of the electric field of TE-waves in a structure including two dielectric layers with thicknesses ${{d}_{1}} = {{d}_{2}} = ~0.01$ m, dielectric constants ${{\varepsilon }_{1}} = 17.3,$ ${{\varepsilon }_{2}} = 4.3$ respectively, and magnetic permeabilities ${{\mu }_{1}} = 1.1,$ ${{\mu }_{2}} = 1.1$ respectively and two layers of metamaterial with thicknesses ${{d}_{3}} = {{d}_{4}} = 0.01~$ m, dielectric constants ${{\varepsilon }_{3}} = - 4.3,$ ${{\varepsilon }_{4}} = - 17.3$ respectively, and magnetic permeabilities ${{\mu }_{3}} = - 2.1,$ ${{\mu }_{4}} = - 1.1$ respectively. Figure 6b shows the calculation results for the case when the order of alternation of the second and third layers is changed. In both cases, the fields at the output of the structure are equal to the fields at its input, i.e., condition (9) is satisfied and the structures are transparent.

Fig. 6.

The structure of the normalized electric field in a four-layer electromagnetic structure for the cases: normal order of layers (1, 2, 3, 4) (a) and inverted order of layers (1, 3, 2, 4) (b).

4 MEDIA WITH CONTINUOUS PARAMETERS

Generalizing this result for a structure with continuously varying parameters (Fig. 7), we find that the structure is transparent if the real and imaginary parts of both the permittivity and permeability are centrally symmetric functions with respect to the origin (z = 0). In this case, obviously, it is necessary to fulfill conditions

$$\int\limits_{ - d}^d {\varepsilon \left( z \right)dz} = 0;\,\,\,\,\int\limits_{ - d}^d {\mu \left( z \right)dz} = 0.$$

(19)

Fig. 7.

Illustration of continuously changing parameters.

Note that for conditions (19) to be satisfied, the structure does not have to have spatial symmetry. First of all, above we are talking about symmetry for electromagnetic thicknesses. Moreover, based on the results of [3], in the case of continuously varying parameters under conditions (19), dependences $\varepsilon \left( z \right)$ and $\mu \left( z \right)$ can be anything.

5 PT-SYMMETRIC STRUCTURES

It was indicated in [15–19] that the condition of PT symmetry in electrodynamics and optics is the complex conjugation of the dielectric and magnetic permeabilities of the layers, i.e., in the case of a two-layer structure for one of the layers, the material parameters have form ${{\varepsilon }_{1}} = \varepsilon {\kern 1pt} ' + j\varepsilon {\kern 1pt} '',$ ${{\mu }_{1}} = \mu {\kern 1pt} ' + j\mu {\kern 1pt} '',$ for the second layer ${{\varepsilon }_{2}} = \varepsilon {\kern 1pt} ' - j\varepsilon {\kern 1pt} '',$ ${{\mu }_{2}} = \mu {\kern 1pt} ' - j\mu {\kern 1pt} ''.$ In this case, the Hamiltonians of the layers will be complex conjugate. However, this is not a sufficient condition for the transparency of the considered electromagnetic or optical structure. Indeed, the matrices of the operators of both layers have form (5), and their product is not the identity matrix. Let’s show it.

$$\begin{gathered} {\mathbf{L}} = {{{\mathbf{L}}}_{1}}{{{\mathbf{L}}}_{2}} = \left| {\begin{array}{*{20}{c}} {\cos \left( {\varphi _{{\text{1}}}^{'} + j\varphi _{{\text{1}}}^{{"}}} \right)}&{ - \frac{j}{{{{p}_{1}}}}\sin \left( {\varphi _{{\text{1}}}^{'} + j\varphi _{{\text{1}}}^{{"}}} \right)} \\ { - j{{p}_{1}}\sin \left( {\varphi _{{\text{1}}}^{'} + j\varphi _{{\text{1}}}^{{"}}} \right)}&{\cos \left( {\varphi _{{\text{1}}}^{'} + j\varphi _{{\text{1}}}^{{"}}} \right)} \end{array}} \right| \\ \times \,\,\left| {\begin{array}{*{20}{c}} {\cos \left( {\varphi _{{\text{1}}}^{'} - j\varphi _{{\text{1}}}^{{"}}} \right)}&{ - \frac{j}{{{{p}_{2}}}}\sin \left( {\varphi _{{\text{1}}}^{'} - j\varphi _{{\text{1}}}^{{"}}} \right)} \\ { - j{{p}_{2}}\sin \left( {\varphi _{{\text{1}}}^{'} - j\varphi _{{\text{1}}}^{{"}}} \right)}&{\cos \left( {\varphi _{{\text{1}}}^{'} - j\varphi _{{\text{1}}}^{{"}}} \right)} \end{array}} \right|, \\ \end{gathered} $$

(20)

where for the TE-type wave

$${{p}_{1}} = \sqrt {\frac{{{{\varepsilon }_{1}}}}{{{{\mu }_{1}}}}} = \sqrt {\frac{{\varepsilon _{{\text{1}}}^{'} + j\varepsilon _{{\text{1}}}^{{"}}}}{{\mu _{{\text{1}}}^{'} + j\mu _{{\text{1}}}^{{"}}}}} ~;\,\,\,\,{{p}_{2}} = \sqrt {\frac{{{{\varepsilon }_{2}}}}{{{{\mu }_{2}}}}} = \sqrt {\frac{{\varepsilon _{{\text{2}}}^{'} - j\varepsilon _{{\text{2}}}^{{"}}}}{{\mu _{{\text{2}}}^{'} - j\mu _{{\text{2}}}^{{"}}}}} ~,$$

(21)

$\varphi _{{\text{1}}}^{'}$ is the real part of the electromagnetic thickness and $\varphi _{{\text{1}}}^{{"}}$ is the imaginary part of the electromagnetic thickness. It follows from (20), (21) that ${{{\mathbf{\hat {L}}}}_{1}}{{{\mathbf{\hat {L}}}}_{2}} \ne {\mathbf{\hat {I}}}.$ Moreover, condition (9) is not automatically satisfied for (21). Indeed, the trace of matrix (20) is equal to

$$\begin{gathered} {\text{tr}}{\mathbf{L}} = {\text{tr}}\left( {{{{\mathbf{L}}}_{1}}{{{\mathbf{L}}}_{2}}} \right) = \frac{1}{2}\left( {2 + \frac{{{{p}_{1}}}}{{{{p}_{2}}}} + \frac{{{{p}_{2}}}}{{{{p}_{1}}}}} \right)\cos \left( {2\varphi _{{\text{1}}}^{'}} \right) \\ + \,\,\frac{1}{2}\left( {2 - \frac{{{{p}_{1}}}}{{{{p}_{2}}}} - \frac{{{{p}_{2}}}}{{{{p}_{1}}}}} \right){\text{cosh}}\left( {2\varphi _{{\text{1}}}^{{"}}} \right). \\ \end{gathered} $$

(22)

Obviously, in (22), ${\text{tr}}\left( {{{{\mathbf{L}}}_{1}}{{{\mathbf{L}}}_{2}}} \right) \ne 2$ with arbitrary parameters of the structure.

To satisfy the transparency conditions for such systems, it is necessary to satisfy identities (9) or (13). So, the two-layer PT symmetric structure, described by complex-conjugate permittivity and permeability, can be transparent only if additional conditions are met. This means that its use for these tasks is impractical. Exceptions are media with zero real parts of the permittivity and permeability described in [20–22]. However, such media are a special case of media presented in [23, 24] and this study.

CONCLUSIONS

Thus, layered isotropic media are considered, including layers of dielectric and metamaterial. First of all, the conditions for the transparency of an inhomogeneous, in particular, a layered structure, both from a conventional dielectric and with layers of an isotropic metamaterial, were obtained. It is shown that the condition for the transparency of a multilayer structure is that the parameters of the corresponding periodic structure belong to the boundary of the forbidden region. In other words, the trace of the transformation operator matrix must be equal to two in absolute value. The case of permutation of layers is considered and it is shown that the order of alternation of layers does not affect the conditions for the transparency of the structure when these conditions are met. It is also shown that for the transparency of so-called PT symmetric structures require the fulfillment of additional conditions obtained in this study.

It should be noted that the currently known metamaterials are resonant structures; therefore, in practice, spatially symmetric structures can be completely transparent only in a narrow frequency range.

APPENDIX

The condition for the transparency of an isotropic structure is the equality of the field components at its output to the field components at its input:

$$\left| {\begin{array}{*{20}{c}} {{{E}_{x}}} \\ {{{H}_{y}}} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} {{{E}_{{x0}}}} \\ {{{H}_{{y0}}}} \end{array}} \right|.$$

(A.1)

Further, given that the components of the fields at the output of the structure can be obtained using the transformation operator matrix as

$$\left| {\begin{array}{*{20}{c}} {{{E}_{x}}} \\ {{{H}_{y}}} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} {{{L}_{{11}}}}&{{{L}_{{12}}}} \\ {{{L}_{{21}}}}&{{{L}_{{22}}}} \end{array}} \right|\left| {\begin{array}{*{20}{c}} {{{E}_{{x0}}}} \\ {{{H}_{{y0}}}} \end{array}} \right|,$$

(A.2)

we obtain equation

$$\left| {\begin{array}{*{20}{c}} {{{E}_{{x0}}}} \\ {{{H}_{{y0}}}} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} {{{L}_{{11}}}}&{{{L}_{{12}}}} \\ {{{L}_{{21}}}}&{{{L}_{{22}}}} \end{array}} \right|\left| {\begin{array}{*{20}{c}} {{{E}_{{x0}}}} \\ {{{H}_{{y0}}}} \end{array}} \right|.$$

(A.3)

Let us write (A.3) in scalar form

$$\left\{ {\begin{array}{*{20}{c}} {{{E}_{{x0}}} = {{L}_{{11}}}{{E}_{{x0}}} + {{L}_{{12}}}{{H}_{{y0}}}} \\ {{{H}_{{y0}}} = {{L}_{{21}}}{{E}_{{x0}}} + {{L}_{{22}}}{{H}_{{y0}}}} \end{array}} \right..$$

(A.4)

Expressing from second equation (A.4)${{H}_{{y0}}},$ substituting it into the first equation in (A.4) and performing simple algebraic transformations, we obtain

$${{L}_{{11}}} + {{L}_{{22}}} = 1 + {{L}_{{11}}}{{L}_{{22}}} - {{L}_{{12}}}{{L}_{{21}}}.$$

(A.5)

Taking into account that the transformation matrix of an isotropic structure is always unimodular [1, 3], that is, ${{L}_{{11}}}{{L}_{{22}}} - {{L}_{{12}}}{{L}_{{21}}} = 1,$ we obtain the final expression that determines the transparency condition for the layered isotropic structure:

$${\text{tr}}{\mathbf{L}} = {{L}_{{11}}} + {{L}_{{22}}} = 2.$$

(A.6)

In this case, any phase shift, even with equal field amplitudes at the input and output, indicates the opacity of the structure, since the phase shift will lead to a rotation of the polarization plane.