Fractional Fourier transform of Airy beams

Abstract

An analytical expression of an Airy beam passing through a fractional Fourier transform (FRFT) system is presented. The effective beam size of the Airy beam in the FRFT plane is also derived. The influences of the order of FRFT, the modulation parameter, and the transverse scale on the normalized intensity distribution and the effective beam size of an Airy beam in the FRFT plane are examined. The order of FRFT controls the effective beam size and the orientation of the beam spot. The modulation parameter affects the effective beam size and the number of lateral side lobes. The normalized intensity distribution and the effective beam size are both proportional to the transverse scale.

1 Introduction

An Airy beam is the solution of the force-free Schrödinger equation. An Airy beam does not spread out in vacuum [1] and has the characteristic of freely accelerating [2, 3]. The self-healing properties, the evolution of the Poynting vector and angular momentum, and the phase behavior of the Airy beam have been investigated [4–6]. Different methods such as the method of geometrical optics and the method of the Wigner distribution function (WDF) have been proposed to explain the intriguing features of an Airy beam [7, 8]. The propagation of Airy beams has been examined in free space [9], in water [10], in a nonlinear medium [11, 12], and in turbulence [13, 14], respectively. Airy beams can be used in optical micromanipulation and all-optical switching [15–18].

The ordinary Fourier transform is vital to physical optics and optical information processing. Suppose that a piece of graded-index fiber with the proper length L is required for performing a Fourier transform of an input image. If the graded-index fiber is cut into pieces, a piece of length pL (p < 1) just performs the fractional Fourier transform (FRFT) of the input image. As an image can be described indirectly and uniquely by a WDF, the FRFT also indicates that the WDF is rotated by an angle of $\varphi = {{p\pi } \mathord{\left/ {\vphantom {{p\pi } 2}} \right. \kern-\nulldelimiterspace} 2}$ where p is the order of FRFT [19]. The FRFT has been widely used in the beam analysis, the beam shape and the signal process [20, 21]. The FRFTs of many kinds of laser beams have been widely investigated [22–26]. To the best of our knowledge, however, the research in the FRFT of Airy beams has not been reported elsewhere. In the remainder of this paper, therefore, the FRFT is applied to treat the propagation of Airy beams. An analytical expression for the FRFT of an Airy beam is derived, and the properties of an Airy beam in the FRFT plane are graphically illustrated.

2 Fractional Fourier transform of Airy beams

In the Cartesian coordinate system, the z-axis is taken to be the propagation axis. The initial distribution of an Airy beam in the source plane z = 0 is described by [2, 3]

$$ E(x_{0} ,y_{0} ,0) = Ai\left( {\frac{{x_{0} }}{{w_{0} }}} \right)Ai\left( {\frac{{y_{0} }}{{w_{0} }}} \right)\exp \left( {\frac{{ax_{0} }}{{w_{0} }} + \frac{{ay_{0} }}{{w_{0} }}} \right), $$

(1)

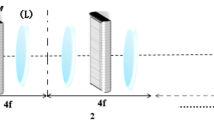
where w ₀ is the transverse scale, Ai(·) is the Airy function, and a is the modulation parameter. Optical system for performing the fractional Fourier transform is shown in Fig. 1. Figure 1(a) denotes the Lohmann I system, and Fig. 1(b) the Lohmann II system. P₁ and P₂ are the input and the output planes, respectively. The Airy beam incidents in the input plane, and we observe the intensity distribution of the Airy beam in the output plane. f is the standard focal length. In Fig. 1(a), the focus of the spherical lens is ${f \mathord{\left/ {\vphantom {f {\sin \varphi }}} \right. \kern-\nulldelimiterspace} {\sin \varphi }}$. In Fig. 1(b), the focus of the lens is ${f \mathord{\left/ {\vphantom {f {\tan \left( {{\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}}} \right. \kern-\nulldelimiterspace} {\tan \left( {{\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}}$; $\varphi = {{p\pi } \mathord{\left/ {\vphantom {{p\pi } 2}} \right. \kern-\nulldelimiterspace} 2}$, and p is the order of FRFT. In Fig. 1(a), the distance between the input and output planes is $2d = 2f\tan \left( {{\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-\nulldelimiterspace} 2}} \right)$. In Fig. 1(b), the distance between the input and output planes is $d^{\prime} = f\sin \varphi$.

Fig. 1

Optical system for performing the fractional Fourier transform. a Lohmann I system, b Lohmann II system

The Lohmann I optical system is described by the following transfer matrix

$$ R_{1} = \left( {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 1 & d \\ 0 & 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 1 & 0 \\ {{{ - \sin \varphi } \mathord{\left/ {\vphantom {{ - \sin \varphi } f}} \right. \kern-\nulldelimiterspace} f}} & 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 1 & d \\ 0 & 1 \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \varphi } & {f\sin \varphi } \\ {{{ - \sin \varphi } \mathord{\left/ {\vphantom {{ - \sin \varphi } f}} \right. \kern-\nulldelimiterspace} f}} & {\cos \varphi } \\ \end{array} } \right). $$

(2)

And the Lohmann II optical system is described by the transfer matrix

$$ R_{2} = \left( {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 1 & 0 \\ {{{ - \tan \left( {{\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} \mathord{\left/ {\vphantom {{ - \tan \left( {{\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} f}} \right. \kern-\nulldelimiterspace} f}} & 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 1 & {d^{\prime}} \\ 0 & 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 1 & 0 \\ {{{ - \tan \left( {{\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} \mathord{\left/ {\vphantom {{ - \tan \left( {{\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} f}} \right. \kern-\nulldelimiterspace} f}} & 1 \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \varphi } & {f\sin \varphi } \\ {{{ - \sin \varphi } \mathord{\left/ {\vphantom {{ - \sin \varphi } f}} \right. \kern-\nulldelimiterspace} f}} & {\cos \varphi } \\ \end{array} } \right) . $$

(3)

Therefore, the Lohmann I optical system and the Lohmann II optical system are equivalent. The Airy beam passing through a Lohmann optical system obeys the well-known Collins integral formula:

$$ E(x,y) = \frac{\exp (ikz)}{i\lambda B}\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {E(x_{0} ,y_{0} ,0)} } \exp \left\{ {\frac{ik}{2B}[A(x_{0}^{2} + y_{0}^{2} ) - 2(x_{0} x + yy_{0} ) + D(x^{2} + y^{2} )]} \right\}dx_{0} dy_{0} . $$

(4)

Substituting Eq. (1) into Eq. (4), the transformation formula of an Airy beam through an ABCD paraxial optical system reads as

$$ E(x,y) = \frac{\exp (ikz)}{i\lambda B}\exp \left[ {\frac{{ikD(x^{2} + y^{2} )}}{2B}} \right]E(x)E(y), $$

(5)

with E(x) and E(y) given by

$$ E(x) = \int_{ - \infty }^{\infty } {Ai\left( {\frac{{x_{0} }}{{w_{0} }}} \right)\exp \left( {\frac{{ax_{0} }}{{w_{0} }}} \right)} \exp \left[ {\frac{ik}{2B}(Ax_{0}^{2} - 2x_{0} x)} \right]dx_{0} , $$

(6)

$$ E(y) = \int_{ - \infty }^{\infty } {Ai\left( {\frac{{y_{0} }}{{w_{0} }}} \right)\exp \left( {\frac{{ay_{0} }}{{w_{0} }}} \right)} \exp \left[ {\frac{ik}{2B}(Ay_{0}^{2} - 2yy_{0} )} \right]dy_{0} . $$

(7)

Eq. (6) can be rewritten as

$$ E(x) = \exp \left( {\frac{ax}{{Aw_{0} }} - \frac{{ikx^{2}}}{2BA} + \frac{{ia^{2} B}}{{2Az_{r} }}} \right)\int_{ - \infty}^{\infty } {Ai\left( {\frac{{x_{0} }}{{w_{0} }}} \right)} \times\exp \left\{ {\frac{ikA}{2B}\left[ {\left( {\frac{x}{A} -\frac{{aw_{0} B}}{{iAz_{r} }}} \right) - x_{0} } \right]^{2} }\right\}, $$

(8)

where $z_{r} = kw_{0}^{2}$ represents the Rayleigh length. We note that the convolution of two functions, $f_{1} (\tau )$ and $f_{2} (\tau )$, is defined by [27]

$$ f_{1} (\tau ) \otimes f_{2} (\tau ) = \int_{ - \infty }^{\infty } {f_{1} (x_{0} )f_{2} (\tau - x_{0} )} dx_{0} , $$

(9)

where ⊗ denotes the convolution. Therefore, Eq. (6) can be rewritten in the form of the convolution:

$$ E(x) = \exp \left( {\frac{ax}{{Aw_{0} }} - \frac{{ikx^{2} }}{2BA} + \frac{{ia^{2} B}}{{2Az_{r} }}} \right)\left[ {f_{1} \left( {\frac{x}{A} - \frac{{aw_{0} B}}{{iAz_{r} }}} \right) \otimes f_{2} \left( {\frac{x}{A} - \frac{{aw_{0} B}}{{iAz_{r} }}} \right)} \right], $$

(10)

where the auxiliary functions $f_{1} (\tau )$ and $f_{2} (\tau )$are given by

$$ f_{1} (\tau ) = Ai\left( {\frac{\tau }{{w_{0} }}} \right), $$

(11)

$$ f_{2} (\tau ) = \exp \left( {\frac{ikA}{2B}\tau^{2} } \right). $$

(12)

The convolution theorem of the Fourier transform has the following property [27]

$$ f_{1} (\tau ) \otimes f_{2} (\tau ) = \int_{ - \infty }^{\infty } {f_{1} (\xi )f_{2} (\xi )\exp ( - i\xi \tau )} d\xi , $$

(13)

where the auxiliary functions $f_{1} (\xi )$ and $f_{2} (\xi )$ are the Fourier transform of $f_{1} (\tau )$ and $f_{2} (\tau )$, respectively. $f_{1} (\xi )$ and $f_{2} (\xi )$ are given by [27]

$$ f_{1} (\xi ) = \frac{1}{{\sqrt {2\pi } }}\int_{ - \infty }^{\infty } {Ai\left( {\frac{\tau }{{w_{0} }}} \right)\exp (i\xi \tau )} d\tau = \frac{{w_{0} }}{{\sqrt {2\pi } }}\exp \left( { - \frac{{iw_{0}^{3} }}{3}\xi^{3} } \right), $$

(14)

$$ f_{2} (\xi ) = \frac{1}{{\sqrt {2\pi } }}\int_{ - \infty }^{\infty } {\exp \left( {\frac{ikA}{2B}\tau^{2} } \right)\exp (i\xi \tau )} d\tau = \sqrt \frac{iB}{kA} \exp \left( { - \frac{iB}{2kA}\xi^{2} } \right). $$

(15)

Therefore, Eq. (10) is found to be

$$ \begin{aligned} E(x) &= w_{0} \sqrt {\frac{iB}{2\pi kA}} \exp \left( {\frac{ax}{{Aw_{0} }} - \frac{{ikx^{2} }}{2BA} + \frac{{iBa^{2} }}{{2Az_{r} }}} \right)\int_{ - \infty }^{\infty } {\exp \left[ { - \frac{{iw_{0}^{3} }}{3}\xi^{3} - \frac{iB}{2kA}\xi^{2} + \left( {\frac{{aw_{0} B}}{{Az_{r} }} - i\frac{x}{A}} \right)\xi } \right]} d\xi \\ &= w_{0} \sqrt {\frac{iB}{2\pi kA}} \exp \left[ {\frac{ax}{{Aw_{0} }} - \frac{a}{2}\left( {\frac{B}{{Az_{r} }}} \right)^{2} - \frac{i}{12}\left( {\frac{B}{{Az_{r} }}} \right)^{3} + \frac{{ia^{2} B}}{{2Az_{r} }} + \frac{iBx}{{2A^{2} z_{r} w_{0} }} - \frac{{ikx^{2} }}{2BA}} \right] \\ &\quad\times \int_{ - \infty }^{\infty } {\exp \left[ { - \frac{i}{3}\left( {w_{0} \xi + \frac{B}{{2Az_{r} }}} \right)^{3} } \right]} \exp \left\{ { - i\left[ {\frac{x}{{Aw_{0} }} - \left( {\frac{B}{{2Az_{r} }}} \right)^{2} + \frac{iaB}{{Az_{r} }}} \right]\left( {w_{0} \xi + \frac{B}{{2Az_{r} }}} \right)} \right\}d\xi .\end{aligned} $$

(16)

The Airy function can be written in terms of the integral representation:

$$ Ai(u) = \frac{1}{2\pi }\int_{ - \infty }^{\infty } {\exp \left( { - \frac{i}{3}x^{3} } \right)\exp ( - iux)} dx. $$

(17)

Accordingly, Eq. (16) can be analytically expressed as

$$ E(x) = \sqrt {\frac{i\lambda B}{A}} Ai\left[ {\frac{x}{{Aw_{0} }} - \left( {\frac{B}{{2Az_{r} }}} \right)^{2} + \frac{iaB}{{Az_{r} }}} \right]\exp \left[ {\frac{ax}{{Aw_{0} }} - \frac{a}{2}\left( {\frac{B}{{Az_{r} }}} \right)^{2} - \frac{i}{12}\left( {\frac{B}{{Az_{r} }}} \right)^{3} + \frac{{ia^{2} B}}{{2Az_{r} }} + \frac{iBx}{{2A^{2} z_{r} w_{0} }} - \frac{{ikx^{2} }}{2BA}} \right]. $$

(18)

Similarly, Eq. (7) turns out to be

$$ E(y) = \sqrt {\frac{i\lambda B}{A}} Ai\left[ {\frac{y}{{Aw_{0} }} - \left( {\frac{B}{{2Az_{r} }}} \right)^{2} + \frac{iaB}{{Az_{r} }}} \right]\exp \left[ {\frac{ay}{{Aw_{0} }} - \frac{a}{2}\left( {\frac{B}{{Az_{r} }}} \right)^{2} - \frac{i}{12}\left( {\frac{B}{{Az_{r} }}} \right)^{3} + \frac{{ia^{2} B}}{{2Az_{r} }} + \frac{iBy}{{2A^{2} z_{r} w_{0} }} - \frac{{iky^{2} }}{2BA}} \right]. $$

(19)

Therefore, the analytical transformation formula of an Airy beam through an ABCD paraxial optical system yields:

$$ \begin{aligned} E(x,y) &= \frac{1}{A} \exp\left( {ikz + \frac{ikC\rho^{2}}{2A}} \right)Ai\left[ {\frac{x}{Aw_{0} } - \left( {\frac{B}{2Az_{r}}} \right)^{2} + \frac{iaB}{Az_{r}}} \right]\exp \left[ {\frac{ax}{Aw_{0}} - \frac{a}{2}\left({\frac{B}{Az_{r} }} \right)^{2} - \frac{i}{12}\left({\frac{B}{Az_{r} }} \right)^{3} + \frac{ia^{2} B}{2Az_{r} } + \frac{iBx}{2A^{2} z_{r} w_{0} }} \right] \\ &\quad\times Ai\left[ {\frac{y}{Aw_{0}} - \left( {\frac{B}{2Az_{r}}} \right)^{2} + \frac{iaB}{Az_{r}}} \right]\exp \left[{\frac{ay}{Aw_{0}} - \frac{a}{2}\left( {\frac{B}{Az_{r}}}\right)^{2} - \frac{i}{12}\left( {\frac{B}{Az_{r}}} \right)^{3} + \frac{ia^{2} B}{2Az_{r}} + \frac{iBy}{2A^{2} z_{r} w_{0} }}\right], \end{aligned}$$

(20)

where $\rho = (x^{2} + y^{2} )^{1/2}$. Substituting Eq. (3) into Eq. (20), we can obtain the output field distribution for the Airy beam in the FRFT plane. The Airy beam through a Lohmann optical system follows a ballistic trajectory in the x–z and y–z planes that are described by the following parabolas.

$$ x = y = \frac{{w_{0} f^{2} \sin \varphi \tan \varphi }}{{4z_{r}^{2} }} . $$

(21)

If $\sin \varphi = 0$, it means $p = 2q(q = 0,\,1,\,2,\, \cdots )$. In this case, the output field distribution of the Airy beam in the FRFT plane reduces to

$$ E(x,y) = Ai\left( {\frac{x}{{w_{0} }}} \right)Ai\left( {\frac{y}{{w_{0} }}} \right)\exp \left( {\frac{ax}{{w_{0} }} + \frac{ay}{{w_{0} }}} \right)\exp (ikz). $$

(22)

The case of p = 1 corresponds to the ordinary Fourier transform case. In this case, the Airy beam through a Lohmann optical system is simplified to be

$$ E(x,y) = \frac{{w_{0}^{2} }}{4\pi }\exp \left[ {\frac{1}{3}\left( {a - \frac{{ikw_{0} x}}{f\sin \varphi }} \right)^{3} + \frac{1}{3}\left( {a - \frac{{ikw_{0} y}}{f\sin \varphi }} \right)^{3} } \right]. $$

(23)

The intensity of the output field for the Airy beam in the FRFT plane is given by

$$ I = \left| {E(x,y)} \right|_{{}}^{2} . $$

(24)

The effective beam size of the Airy beam in the x- and y-directions of the FRFT plane is defined as [28]:

$$ W_{j} = \sqrt {2\frac{{\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {(j - j_{C} )^{2} \left| {E(x,y)} \right|^{2} dxdy} } }}{{\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {\left| {E(x,y)} \right|^{2} dxdy} } }}} , $$

(25)

where j = x or y, j _C is the first moment radius and is given by

$$ j_{C} = \frac{{\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {j\left| {E(x,y)} \right|^{2} dxdy} } }}{{\int_{ - \infty }^{\infty } {\int_{ - \infty }^{\infty } {\left| {E(x,y)} \right|^{2} dxdy} } }}. $$

(26)

The effective beam sizes of the Airy beam in the x- and y-directions of the FRFT plane yields [14]

$$ W_{x} = W_{y} = \frac{1}{2a}\left[ {8a^{3} + 2a\left( {\frac{f\tan \varphi }{{z_{r} }}} \right)^{2} + 1} \right]^{1/2} w_{0} \left| {\cos \varphi } \right|. $$

(27)

3 Numerical calculations and analyses

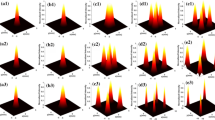
According to the obtained analytical expression, the properties of an Airy beam in the FRFT plane are numerically investigated. The x- and y-directions are separable in the formulae derived above. Moreover, they have the same form. Therefore, we first only consider the x-direction. As the Airy beam depends on the parameters p, a, and w ₀, the influences of these three parameters on the intensity distribution in the FRFT plane are investigated. In the following calculations, λ = 0.53μm and f = 1,000 mm. Figure 2 represents the normalized intensity distribution in the x-direction of an Airy beam with different fractional order p in the FRFT plane. a = 0.1 and w ₀ = 1 mm in Fig. 2. The variation of normalized intensity distribution with the fractional order p is periodic, and the period is 2. When p < 1, the lateral side lobes are located at the left side. In this case, moreover, the beam spot of the Airy beam decreases with increasing the value of p. When 2 ≥ p > 1, the lateral side lobes are located at the right side. In this case, however, the beam spot of the Airy beam increases with increasing the value of p. This dramatic phenomenon can be interpreted as follows. When 2 ≥ p > 1, A = cos(pπ/2) is a negative number, and B = fsin(pπ/2) is still positive. Therefore, the light distribution in the x-direction I _x is given by

Fig. 2

Normalized intensity in the x-direction of an Airy beam with different fractional order p in the FRFT plane

$$ I_{x} = \frac{1}{{\sqrt {\left| A \right|} }}\left\{ {Ai\left[ {\frac{ - x}{{\left| A \right|w_{0} }} - \left( {\frac{B}{{2Az_{r} }}} \right)^{2} - \frac{iaB}{{\left| A \right|z_{r} }}} \right]} \right\}^{2} \exp \left[ {\frac{ - 2ax}{{\left| A \right|w_{0} }} - a\left( {\frac{B}{{Az_{r} }}} \right)^{2} } \right]. $$

(28)

The minus sign before x results in that the lateral side lobes are located at the right side.

Figure 3 shows the normalized intensity in the x-direction of an Airy beam with different a in the FRFT plane; p = 1.75 and w ₀ = 1 mm. With increasing the value of a, the number of lateral side lobes decreases and the main peak expands. When a is relatively large, all the lateral side lobes disappears. Now, we investigate the influences of the parameter w ₀ on the normalized intensity distribution in the x-direction of an Airy beam in the FRFT plane. When varying the parameter w ₀ and the rest of parameters being kept invariant, the normalized intensity in the x-direction also changes. If the transversal coordinate is scaled by x/w ₀, the normalized intensity in the x-direction keeps invariant with varying the parameter w ₀. The corresponding figures are omitted to save space.

Fig. 3

Normalized intensity in the x-direction of an Airy beam with different parameter a in the FRFT plane

Figure 4 represents the contour graph of the normalized intensity distribution of an Airy beam with different parameter a and p in the FRFT plane. Other parameters are same as those in Fig. 2. Apparently, the modulation parameter a determines the number of the lateral side lobes. The smaller the modulation parameter a is, the larger the number of the lateral side lobes is. The value of the fractional order p affects the spot size of the Airy beam. Contour graph of the normalized intensity distribution of an Airy beam in free and the FRFT spaces is shown in Fig. 5. a = 0.05 and the unmarked parameters are same as those in Fig. 2. When p < 1, the beam spot of the Airy beam in the FRFT plane is similar to that of the Airy beam propagating in free space. The only difference is the size of the beam spot. When 2 ≥ p > 1, the beam spot of the Airy beam in the FRFT plane rotates π compared to that of the Airy beam propagating in free space. The aforementioned phenomenon can be understood as follows. The process of p from 0 to 1 is just that of the propagation of the Airy beam from the source plane to the far-field plane. The process of p from 1 to 2 is just that of the reflex of the Airy beam from the far-field plane to the input plane. There is only a dominant lobe in the beam spot of the Airy beam in the Fourier transform plane, and all the lateral side lobes disappear. As p = 1, it corresponds to the Fraunhofer diffraction, which describes the far-field beam pattern.

Fig. 4

Contour graph of the normalized intensity distribution of an Airy beam with different parameter a and p in the FRFT plane. a a = 0.05 and p = 0.5; b a = 0.1 and p = 0.5; c a = 0.05 and p = 1.75; d a = 0.1 and p = 1.75

Fig. 5

Contour graph of the normalized intensity distribution of an Airy beam in free and the FRFT spaces, a = 0.05. a Free space, z = f; b FRFT space, p = 0; c FRFT space, p = 1; d FRFT space, p = 1.75

Figure 6 represents the effective beam size in the x-direction of the FRFT plane as function of p, a, and w ₀; a = 0.1 and w ₀ = 1 mm in Fig. 6(a). p = 0.5 and w ₀ = 1 mm in Fig. 6(b). a = 0.1 and p = 0.5 in Fig. 6(c). When p ≤ 1, the effective beam size in the x-direction decreases with increasing the value of p. When 2 ≥ p > 1, the effective beam size in the x-direction increases with increasing the value of p. With increasing the value of a, the effective beam size in the x-direction first decreases and then slowly increases. With increasing the value of a, the number of lateral side lobes quickly decreases and the main peak slowly expands, which results in the decreasing of effective beam size. When further increasing a, all the lateral side lobes disappears and only the main peak expands, which results in the increasing of effective beam size slowly. With increasing the value of w ₀, the effective beam size in the x-direction scaled by W _x /w ₀ is nearly invariant, which means that the effective beam size in the x-direction, W _x , is proportional to w ₀.

Fig. 6

a The effective size in the x-direction of an Airy beam in the FRFT plane as a function of p; a = 0.1. b The effective size in the x-direction of an Airy beam in the FRFT plane as a function of a; p = 0.5. c The effective size in the x-direction of an Airy beam in the FRFT plane as a function of w ₀; a = 0.1 and p = 0.5

4 Conclusions

An analytical expression of an Airy beam passing through a FRFT system is derived. The normalized intensity distribution of an Airy beam in the FRFT plane is graphically illustrated, and the influences of the different parameters on the normalized intensity distribution and the effective beam size are discussed. The order of FRFT p not only affects the beam spot size of an Airy beam, but also controls the orientation of the beam spot. When p ≤ 1, the effective beam size decreases with increasing the value of p, and the beam spot of the Airy beam in the FRFT plane is similar to that of the Airy beam propagating in free space. When 2 ≥ p>1, the effective beam size increases with increasing the value of p, and the beam spot of the Airy beam in the FRFT plane rotates π compared to that of the Airy beam propagating in free space. The modulation parameter a influences on the number of lateral side lobes of an Airy beam in the FRFT plane. With increasing the value of a, the effective beam size first decreases and then slowly increases. The normalized intensity distribution and the effective beam size are proportional to the transverse scale w ₀.