Airy-related beams generated from a higher-order cosine-hyperbolic-Gaussian beam passing through a multiple Airy transforms optical system

Abstract

The present paper investigates the propagation properties of a higher-order cosine-hyperbolic Gaussian beam passing through n-times Airy transforms optical system. The intensity distribution, centroid, beam width, and propagation factor (M²-factor) of the output beam are obtained analytically, and their features are analyzed with numerical examples. It is demonstrated that the resulting beam can be expressed as a finite superposition of Airy modes, and its spot profile is Airy–like. The numerical results show that the main m peak intensity is wider and the number of secondary lobes of the light spot decrease as the number of the Airy transforms is increased. The beam’s shift is larger when the decentered parameter b or the number of the Airy transforms increases. The beam width and M²-factor are smaller when the Airy control parameters are decreased. Furthermore, under certain parameter conditions the transverse intensity may exhibit intensity modulation bands; the structure of these bands depends strongly on the number of Airy transforms. It is also found that the non-diffracting propagation distance of the transformed beam in free space decreases as the number of Airy transforms or the Airy control parameter $\alpha$ increases. The results of this study may be beneficial for beam shaping of Airy beams.

1 Introduction

During the last few decades, numerous works have been devoted to the mathematical transformations that are commonly used in physics, such as the Fourier transform, Hankel transform, Hilbert transform, Fourier–Bessel transform, Airy transform, etc. Many optical systems dealing with these transformations have been designed for optical applications, e.g., beam shaping, beam analysis, image processing, signal processing, beam conversion (Davis et al. 1998, 2000; Ozaktas et al. 2001; Goodman 2005; Widder 1979; Jiang et al. 2012a, b), and so on. In addition, the so-called Airy beams (Berry et al. 1979; Siviloglou et al. 2007a) have received great interest from physics researchers due to their unique features such as non-diffraction, ballistic trajectory, and self-healing (Siviloglou et al. 2007a, b; Broky et al. 2008). These beams have a large potential for many fields such as particle clearing (Baumgartl et al. 2008), optical micromanipulation (Ellenbogen et al. 2009), plasma physics (Polynkin et al. 2009; Ouahid et al 2018a, b), optical switching (Chremmos et al. 2012), optical trapping (Jia et al. 2012a, b), optical routing (Rose et al. 2013), and so on. And extensive research has been devoted to different ways of generating Airy and Airy-related beams (Dai et al. 2009; Cottrell et al. 2009; Dolev et al. 2009; Jiang et al. 2012a, b; Ez-zariy et al. 2016; Yaalou et al. 2019a, b, 2020a, b; Zhou et al. 2020, 2021; Huang et al. 2022).

On the other hand, the higher-order cosine-hyperbolic Gaussian beam (HOChGB) is known as a mathematical model, which was introduced in 2009 by Zhou et al. (2009) to describe a type of flattened light beam. The beam possesses two key parameters, namely the decentered parameter and the beam order, and can describe a broad range of well-known light beams, such the Gaussian beam, cosh (or cosine)-Gaussian beam, cosh (or cosine)-squared-Gaussian beam and higher-order cosine-Gaussian beam (Casperson et al. 1997; Lu et al. 1999) among others. The beam parameters permit a high control of the beam intensity pattern, which may be useful for practical applications in free space optics (FSO), higher power efficiency techniques, micro-optics, beam shaping, beam splitting techniques, plasma physics, etc. During the last few years, the propagation properties of a HOChGB in various optical systems have been investigated. Different characteristics of a HOChGB in free space, in a fractional Fourier transform system, in uniaxial crystals, through a focusing lens system, in the turbulent atmosphere, the vectorial beam properties, the beam propagation factor, and kurtosis parameter have been studied (Zhou 2009, 2011; Li et al 2010a, b; Luo et al. 2015; Hricha et al. 2020, 2021a, b; El Halba et al. 2021). Very recently, we have shown theoretically that a new Airy-related beam can be obtained from a HOChGB passing through an Airy transform optical system (ATOS) (Yaalou et al. 2020b). In the cited work, it was demonstrated that the profile of the generated Airy-related beam can be controlled by adjusting the parameters of the incident HOChGB or the ones associated with the Airy transforms system. The present work is aimed at extending the previously cited study to generate other structured light beams from a HOChGB. We, therefore, propose to examine the transformation of a HOChGB by a series of successive Airy transform optical systems (Zhou et al. 2022). The remainder of the paper is organized as follows: In the forthcoming Section, the theoretical model of HOChGB propagating through n-times Airy transforms optical system is presented, and the analytical expressions of the output field and its main propagation characteristics such as the centroid, the beam width, and the beam propagation factor (M²-factor) are derived theoretically. In addition, the propagation dynamic formula of the transformed HOChGB in free space is derived based on Huygens-Fresnel diffractive integral. In the third Section, numerical results are given to discuss the characteristics of the output beam as a function of the input beam parameters and the control parameter of the optical system. And the free space propagation after the beam passes the Airy transform system is analyzed with illustrative examples. Finally, the main results of this work are outlined in the conclusion part.

2 Theoretical model for a HOChGB propagating through n-times Airy transforms optical system

The multiple Airy transforms of an arbitrary light beam can be realized by passing the beam through a series of identical Airy transform optical systems (ATOS). Each ATOS consists of a 4f optical setup including a spatial light modulator (SLM). The phase modulation $\varphi {\kern 1pt} {\kern 1pt} \left( {x,y} \right)$ imposed by SLM has the form (Jiang et al. 2012b)

$$\varphi {\kern 1pt} {\kern 1pt} \left( {x,y} \right) = \frac{{\left( {\alpha {\kern 1pt} {\kern 1pt} k} \right)^{3} x^{3} + \left( {\beta {\kern 1pt} {\kern 1pt} k} \right)^{3} y^{3} }}{{3f^{3} }} - \left( {4k{\kern 1pt} f + \pi } \right),$$

(1)

where the real-valued α and β are the Airy control parameters in the x and y directions, respectively. $\left( {x,y} \right)$ are the Cartesian coordinates in the SLM plane, $k = \frac{2\pi }{\lambda }$ the wave number and f is the focal length of the thin lens.

A schematic diagram of the n-times Airy transforms optical system is shown in Fig. 1, which illustrates the input and the output planes, and the sequence of n successive individual ATOS. The first two lenses and the first SLM constitute the ATOS element.

Fig. 1

Diagram of n-times Airy Transform optical system

Under the paraxial approximation, the multiple (n-times) Airy transformations of an electric field ${\rm E}_{0} \left( {x_{0} } \right)$ can be expressed in one-dimensional space (1D) by the following iterative formula (Jiang et al. 2012b; Zhou et al. 2022)

$${\rm E}_{n} \left( x \right) = \frac{1}{\left| \alpha \right|}\,\int\limits_{ - \infty }^{ + \infty } {} E_{n - 1} \left( {x_{0} } \right)\,Ai\left( {\frac{{x - x_{0} }}{\alpha }} \right)dx_{0} ,$$

(2)

where n (= 1, 2, …) denotes the n^th Airy transform element, $x_{0}$ and $x$ are the 1D transversal coordinates at the input and output planes, respectively, α the Airy control parameter in a 1D transverse direction, and Ai(.) denotes the Airy function.

Now, let us assume an incident HOChGB at the input plane z = 0 with the electric field of the form (Zhou et al. 2009; Yaalou et al. 2020b)

$$E_{0} \left( {x_{0} ,y_{0} ,z = 0} \right) = \cosh^{p} \left( {\frac{{b_{x} x_{0} }}{{\omega_{0} }}} \right)\,\cosh^{q} \left( {\frac{{b_{y} y_{0} }}{{\omega_{0} }}} \right)\,\exp \left( { - \frac{{x_{0}^{2} + y_{0}^{2} }}{{\omega_{0}^{2} }}} \right),$$

(3)

where $\left( {x_{0} ,y_{0} } \right)$ are the transverse coordinate at the initial plane, cosh(.) is the hyperbolic cosine function, $\omega_{0}$ is the waist size of the Gaussian part, b_x and b_y are the decentered parameters associated with cosh(.), p and q are the beam orders along the x-and y-directions, respectively.

Equation (3) describes a general HOChGB with an asymmetrical profile in the x and y-directions, and the factors b_x, b_y, p and q are the key parameters of the beam. In the special case b_x = b_y and p = q, one obtains the symmetrical HOChGB (Zhou et al. 2009). Besides, as the beam is separable in the x-and y-directions, the 1D space representation is then convenient to study the paraxial propagation of the beam. Thus, in the following, we assume the following one-dimensional form for the incident HOChGB

$$E_{0} \left( {x_{0} ,z = 0} \right) = \cosh^{p} \left( {b_{x} \frac{{x_{0} }}{{\omega_{0} }}} \right)\exp \left[ { - \left( {\frac{{x_{0} }}{{\omega_{0} }}} \right)^{2} } \right],$$

(4)

where b_x is the decentered parameter and p is the beam order.

Using the explicit form of cosh (.) and recalling the binomial formula

$$\left( {{\text{X}}{\kern 1pt} {\kern 1pt} + {\kern 1pt} {\text{Y}}{\kern 1pt} } \right)^{{\text{p}}} {\kern 1pt} = {\kern 1pt} \sum\limits_{{{\text{s}} = {0}}}^{{\text{p}}} {{\text{C}}_{{\text{s}}}^{{\text{p}}} } \,{\text{X}}^{{\text{s}}} \left( {\text{Y}} \right)^{{^{{_{{{\text{p}} - {\text{s}}}} }} }} \;,{\text{ with}}\;{\text{C}}_{{\text{s}}}^{{\text{p}}} = {\kern 1pt} \frac{{\text{p!}}}{{{\text{s!}}\left( {{\text{p}} - {\text{s}}} \right)\,{!}}}$$

(5)

Equation (4) can then be rewritten as

$$E_{0} \left( {x_{0} ,z = 0} \right) = \frac{1}{{2^{p} }}\sum\limits_{s = 0}^{p} {A_{s} } \,\exp \left[ { - \frac{1}{{\omega_{0}^{2} }}\left( {x_{0} - b_{x}^{s} } \right)^{2} } \right],$$

(6a)

with

$$A_{s} = {\text{C}}_{{\text{s}}}^{{\text{p}}} \exp \left( {\frac{{b_{x}^{s} }}{{\omega_{0} }}} \right)^{2} \;,{\text{ and}}\;b_{x}^{s} = b_{x} \omega_{0} \left( {s - \frac{p}{2}} \right)$$

(6b)

This means that a HOChGB can be regarded as a finite superposition of decentered Gaussian beams with the same waist. Substituting from Eq. (6a) into Eq. (2), and performing the n times successive iterations by using the following integral formula (Zhou et al. 2022; Vallée et al. 2004)

$$\frac{1}{2\pi }\int\limits_{ - \infty }^{ + \infty } {\exp \left( {\frac{{iu^{3} }}{3} + iAu^{2} + iBu} \right)\,} dt\, = \exp \left( {\frac{{2iA^{3} }}{3} - iAB} \right)\,Ai\left( {B - A^{2} } \right),$$

(7)

after performing lengthy integral calculations (see the detailed calculation in the appendix part) one can obtain the output field as

$${\rm E}_{n} \left( x \right) = \frac{1}{{2^{p} }}\left( {\frac{\left| \alpha \right|}{\alpha }} \right)^{n - 1} \frac{{2\sqrt {\pi \tau_{\alpha } } }}{{n^{1/3} }}\sum\limits_{s = 0}^{p} {A_{s}^{{}} } \exp \left( {\frac{{2\,\tau_{\alpha }^{3} }}{{3\,n^{2} }} + \frac{{\tau_{\alpha } \,\left( {x - b_{x}^{s} } \right)\,}}{n\,\alpha }} \right)Ai\left( {\frac{{x - b_{x}^{s} }}{{n^{1/3} \,\alpha }} + \frac{{\tau_{\alpha }^{2} }}{{n^{4/3} }}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,$$

(8)

with $\tau_{\alpha } = \frac{{\omega_{0}^{2} }}{{4\,\alpha^{2} }}$. Hence, the 2D field expression ${\rm E}_{n} \left( {x,y} \right)$ of the generated beam reads

$${\rm E}_{n} \left( {x,y} \right) = \,{\rm E}_{n} \left( x \right)\,{\rm E}_{n} \left( y \right).$$

(9)

Equation (9) is a main analytical solution that indicates that n-times Airy transform of a HOChGB can be deemed as a superposition of decentered finite Airy beams with appropriate weights and decay coefficients. This means that the suggested optical system can be used as a tool to convert a HOChGB into an Airy–like beam with controllable parameters.

From Eq. (9) one can distinguish the following special cases:

• When p = q = b_x = b_y = 0, one obtains the output electric field corresponding to a Gaussian beam after n times Airy transforms (Zhou et al. 2022)

  $$\begin{gathered} E^{G}_{n} \left( {x,y} \right) = 4\pi \left( {\frac{{\left| {\alpha \beta } \right|}}{\alpha \beta }} \right)^{n - 1} \frac{{\sqrt {\tau_{\alpha } \tau_{\beta } } }}{{n^{2/3} }}\,\exp \left( {\frac{{2\,\tau_{\alpha }^{3} }}{{3\,n^{2} }} + \frac{{\tau_{\alpha } \,x\,}}{n\,\alpha }} \right)Ai\left( {\frac{x\,}{{n^{1/3} \,\alpha }} + \frac{{\tau_{\alpha }^{2} }}{{n^{4/3} }}} \right){\kern 1pt} {\kern 1pt} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left( {\frac{{2\,\tau_{\beta }^{3} }}{{3\,n^{2} }} + \frac{{\tau_{\beta } \,y\,}}{n\,\beta }} \right)Ai\left( {\frac{y}{{n^{1/3} \,\beta }} + \frac{{\tau_{\beta }^{2} }}{{n^{4/3} }}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} . \hfill \\ \end{gathered}$$

  (10)

• For p = q = 1, i.e., with an incident Cosh-Gaussian beam, one may obtain

  $$E^{ChG}_{n} \left( {x,y} \right) = \pi \left( {\frac{{\left| {\alpha \beta } \right|}}{\alpha \beta }} \right)^{h - 1} \frac{{\sqrt {\tau_{\alpha } \tau_{\beta } } }}{{n^{2/3} }}\exp \left( {\frac{{b^{2} }}{2}} \right)\,g_{n} \left( x \right)\,\,g_{n} \left( y \right),$$

  (11a)

where

$$\begin{gathered} g_{n} \left( u \right) = \exp \left( {\frac{{2\,\tau_{\alpha }^{3} }}{{3\,n^{2} }} + \frac{{\tau_{\alpha } \,\left( {u + b\omega_{0} /2} \right)\,}}{n\,\alpha }} \right)\,Ai\left( {\frac{{u + b\omega_{0} /2\,}}{{n^{1/3} \,\alpha }} + \frac{{\tau_{\alpha }^{2} }}{{n^{4/3} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, + \exp \left( {\frac{{2\,\tau_{\alpha }^{3} }}{{3\,n^{2} }} + \frac{{\tau_{\alpha } \,\left( {u - b\omega_{0} /2} \right)\,}}{n\,\alpha }} \right)\,Ai\left( {\frac{{u - b\omega_{0} /2\,}}{{n^{1/3} \,\alpha }} + \frac{{\tau_{\alpha }^{2} }}{{n^{4/3} }}} \right), \hfill \\ \end{gathered}$$

(11b)

with u = x or y.

• For n = 1, i.e., when the system is a single ATOS, one will obtain the field expression of an Airy-transformed HOChGB, which is consistent with the result of Ref. (Yaalou et al. 2020b).

Following the standard definition, the centroid of the output beam is defined from the first-order moment intensity as (Martinez-Herrero et al. 1993; Zhou et al. 2019)

$$X_{n} = \frac{{\int\limits_{ - \infty }^{ + \infty } {x\,\left| {E_{n} \left( x \right)} \right|^{2} dx} }}{{\int\limits_{ - \infty }^{ + \infty } {\,\left| {E_{n} \left( x \right)} \right|^{2} dx} }}.$$

(12)

By substituting Eq. (8) into Eq. (12), and after performing the integral expressions above, one can find that

$$X_{n} = \,\alpha \,\left( {\frac{ - n}{{4\tau_{\alpha } }} + \frac{{\tau_{\alpha }^{2} }}{n}} \right) + \frac{{\sum\limits_{s = 0}^{p} {A_{s}^{2} } \left( {b_{s} - \frac{{\alpha \tau_{\alpha }^{2} }}{n}} \right)}}{{\sum\limits_{s = 0}^{p} {A_{s}^{2} } }}.$$

(13)

The beam spot width $W_{n}$ and the divergence angle $\theta_{n}$ are defined based on the second-order intensity moments. Along the x-direction, one can write (Zhou et al. 2019)

$$W_{n} = \sqrt {\frac{{\int\limits_{ - \infty }^{ + \infty } {x^{2} \,\left| {E_{n} \left( x \right)} \right|^{2} dx} }}{{\int\limits_{ - \infty }^{ + \infty } {\,\left| {E_{n} \left( x \right)} \right|^{2} dx} }} - X_{n}^{2} } ,$$

(14)

and

$$\theta_{n} = \frac{1}{k}\sqrt {\frac{{\int\limits_{ - \infty }^{ + \infty } {\,\left| {\frac{{\partial \,E_{n} \left( x \right)}}{\partial \,x}} \right|^{2} dx} }}{{\int\limits_{ - \infty }^{ + \infty } {\,\left| {E_{n} \,\left( x \right)} \right|^{2} dx} }}} .$$

(15)

Inserting from Eq. (8) into Eqs. (14)-(15), one can obtain the following analytical results

$$W_{n} \, = \left| {\frac{\alpha }{{\sum\limits_{s = 0}^{p} {A_{s}^{{}} } }}} \right|\,\,\left| {\frac{{n^{2} }}{{8\tau_{\alpha }^{2} }} + \tau_{\alpha } } \right|^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} \,,$$

(16)

and

$$\theta_{n} = \frac{1}{{k\omega_{0} }}.$$

(17)

Equation (17) indicates that the divergence of the beam is independent of the number of the Airy transforms; the quantity depends only on the waist size of the incident beam and the wave number k. The cross-second-order moment $\left\langle {X_{n} \theta_{n} } \right\rangle$ is defined by

$$\left\langle {X_{n} \theta_{n} } \right\rangle = \frac{\pi }{ik}\frac{{\int\limits_{ - \infty }^{ + \infty } {\,\left[ {\frac{{\partial E_{n}^{*} \left( x \right)}}{\partial x}E_{n} \left( x \right) - \frac{{\partial E_{n} \left( x \right)}}{\partial x}E_{n}^{*} \left( x \right)} \right]dx} }}{{\int\limits_{ - \infty }^{ + \infty } {\,\left| {E_{n} \left( x \right)} \right|^{2} dx} }},$$

(18)

where the asterisk denotes the complex conjugation. Since the amplitude of the output field is purely real, one gets $\left\langle {X_{n} \theta_{n} } \right\rangle = 0$. The beam propagation factor (or M²-factor) is defined as

$$M_{n}^{2} = 2k\left( {W_{n}^{2} \theta_{n}^{2} - \left\langle {X_{n} \theta_{n} } \right\rangle^{2} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} .$$

(19)

The substitution of Eqs. (16) and (17) into Eq. (19) yields

$$M_{n}^{2} = \frac{2}{{\omega_{0} }}\left| {\frac{\alpha }{{\sum\limits_{s = 0}^{p} {A_{s}^{{}} } }}} \right|\,\,\left| {\frac{{\,n^{2} }}{{8\tau_{\alpha }^{2} }} + \tau_{\alpha } } \right|^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} \,.$$

(20)

To investigate the propagation of the light spots, after the HOChGB passes through the multiple Airy transforms system in free space, we use the Huygens–Fresnel formula (Collins 1970). In the x-direction, the propagated beam can be expressed as

$$E\left( {x,z} \right) = \sqrt {\frac{ik}{{2\pi z}}} \int\limits_{ - \infty }^{ + \infty } {E_{0} \left( {x_{0} ,z = {\kern 1pt} 0} \right)\exp \left\{ { - \frac{ik}{{2z}}\left[ {\left( {x - x_{0} } \right)^{2} } \right]} \right\}dx_{0} } {\kern 1pt} {\kern 1pt} ,$$

(21)

where $E_{0} \left( {x_{0} ,{\kern 1pt} z = {\kern 1pt} {\kern 1pt} 0} \right)$ and $E\left( {x,z} \right)$ are the fields at the source plane z = 0 and receiver plane z, respectively. z is the distance from the initial plane. $k = \frac{2\pi }{\lambda }$ is the wave number and λ is the wavelength of the light beam. By inserting Eq. (8) into Eq. (21), and using the convolution theorem of the Fourier transform (Vallée 2004; Gradshteyn 1994), and after long integral calculations (see the detailed calculation in the appendix part) the propagating beam reads as

$$\begin{gathered} E\left( {x,z} \right) = \frac{\alpha }{{2^{p} }}\left( {\frac{\left| \alpha \right|}{\alpha }} \right)^{n - 1} \sqrt {\frac{{4\pi \,\alpha \,\tau_{\alpha } \,n^{1/3} }}{\,z\,}} \exp \left( {\frac{{2\,\tau_{\alpha }^{3} }}{{3\,n^{2} }}} \right)\exp \left( { - \frac{{ikx^{2} }}{2z}} \right)\sum\limits_{s = 0}^{p} {A_{s}^{{}} } \exp \left( {\frac{{ - b\tau_{\alpha } \,\,}}{n\,\alpha }} \right)\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left\{ {\frac{{z^{2} \tau_{\alpha } }}{{2k^{2} \,n\,\alpha }} - \frac{{\,z^{3} \,\alpha^{3} \,n}}{{12k^{3} \,}} + \frac{ik}{{2z}}\,\left( {\frac{{iz\tau_{\alpha } }}{kn\,\alpha } - x} \right)^{2} + \frac{i\,z\,x}{{2k}} + \frac{{i\,z\,\alpha \tau_{\alpha }^{2} }}{\,2k\,n} + - \frac{i\,z\,b}{{2k}}} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times Ai\left( {\frac{x}{{n^{1/3} \,\alpha }} + \frac{{\,\tau_{\alpha }^{2} }}{{\,n^{4/3} }} - \frac{b}{{\alpha \,n^{1/3} }} - \,\frac{{\,z^{2} \,\alpha^{2} \,n^{2/3} }}{{4k^{2} \,}} - \frac{{iz\tau_{\alpha } }}{{k\,n^{4/3} \,\alpha^{2} }}} \right). \hfill \\ \end{gathered}$$

(22)

3 Numerical results and discussion

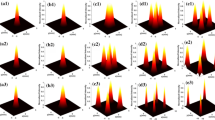
To discuss the properties of the generated beam we present in this Section some typical numerical examples based on the formulas derived above with different parameter conditions. Figure 2 illustrates the 1D normalized intensity distribution of a second order HOChGB (p = 2) after n-times Airy transforms for a small and a large value of b (in the simulation we take typically b as 0.1 and 4 respectively). The other calculation parameters are set as $\omega_{{0}} = 0.1\,{\text{mm}}$ and $\alpha = 2\,\,{\text{mm}}$. It can be seen from the plots that the output beam has an Airy-like pattern. The peak intensities are larger and side peaks decrease as the number of the Airy transforms n increases. In addition, one can note that when the decentered parameter b increases, the side peaks become weaker. Yet, the central peak intensity remains almost unchanged.

Fig. 2

The (1D) normalized intensity distribution of a HOChGB after n times Airy transforms, with p = 2 and $\omega_{0} = 0.1\,mm$. The top, middle, and bottom rows are respectively b = 0.1, b = 4, and b = 8. (a.1–3) n = 2, (b.1–3) n = 3, (c.1–3) n = 6 and (d.1–3) n = 12

One can see from Fig. 3 the drastic change in the light spot when the number of the Airy transforms is increased.

Fig. 3

Normalized intensity distribution of the output electrical field with b = 4, $\omega_{0} = 0.2\,{\text{mm}}$ and $\alpha = 2\,{\text{mm}}$ after n-times Airy transforms with p = 6: a n = 2; b n = 4, c n = 6 and d n = 8

The structure of the generated beam pattern is due to the interference of the individual Airy components (see Eq. (8)). The Airy modes evolve differently, and their interference becomes stronger when n is increased. This will give more characteristics richness to the output beam when the beam order p or the parameter b is larger.

Figure 4 displays the profile of the output beam for different values of p (p = 2, 4, and 6). It can be observed from this figure that a larger value of p leads to peak oscillation bands. The number and structure of these peak bands depend crucially on both parameters b and p.

Fig. 4

1D normalized intensity distribution and the contour graph (top and bottom row respectively) of the output beam, for different parameter values of b after 2-times Airy transforms. With $\omega_{0} = 0.2\,mm$$\alpha = \beta = 2\,mm$, and for p = q = 2, p = q = 4 and p = q = 6. (a.1–3) b = 0.1, (b.1–3) b = 1.5, (c.1–3) b = 2 and (d.1–3) b = 4

The evolution of the output beam centroid versus the Airy control parameters, for different values of n (n = 1, 2, 4, and 8), is depicted in Fig. 5. The plots show that the beam centroid shifts in the negative (or positive) direction when α is positive (or negative), and the shift becomes larger as n is increased. One can note also that the beam spot shift decreases strongly as the beam order p is increased.

Fig. 5

The evolution of the center of gravity of the output electrical field after n-times Airy transforms for b = 2 and $\omega_{0} = 0.5\,mm$ versus the control parameter $\alpha$. a p = 2 and b p = 6

The influence of the b-parameter on the output beam is given in Fig. 6, the plots show the evolution of the beam’s centroid versus b for different n, with p = 2 and 6. As can be observed from Fig. 6 the centroid of the beam shifts toward the optical axis as b increases, and for a certain value of b, the centroid keeps its position unchanged at the center.

Fig. 6

The evolution of the centroid of a HOChGB after n-times Airy transforms versus the beam parameter b, with $\alpha = 2\,\,mm$. a p = 2 and b p = 6

Figure 7 illustrates the effect of changing the sign of the Airy control parameters α and β on the beam after 2-times Airy transforms. It can be seen that the position and orientation of the output light spot are directly determined by the signs of α and β. The light spot appears in the first quadrant when α and β are negative and in the third quadrant when these parameters are both positive.

Fig. 7

The evolution of the center of gravity of the output electrical field after 2-times Airy transform for b = 0.1 (Top row) and b = 4 (Bottom row) with $\omega_{0} = 0.2\,mm$ and p = q = 2 versus the sign of the control parameters α and β. (a.1–2) $\alpha = \beta = 2\,mm$, (b.1–2) $- \,\alpha = \beta = 2\,mm$, (c.1–2) $\alpha = \, - \beta = 2\,mm$ and (d.1–2) $\alpha = \,\beta = \, - 2\,mm$

Figure 8 demonstrates the effect of the control parameters α and β on the beam after 2-times Airy transforms. It can be seen that as α and β increase, the central peak and side lobes intensities increase, too.

Fig. 8

The evolution of the output electrical field for b = 0.1 and n = 2 with $\omega_{0} = 0.2\,mm$ and p = q = 2 versus different values of the control parameters α and β. a $\alpha = \beta = 2\,mm$, b $\alpha = \beta = 4\,mm$ and c $\alpha = \beta = 6\,mm$

The above results show that by choosing properly the initial beam parameter b and the optical system's conditions, one can adjust broadly the intensity pattern and localization of the generated Airy-related beam.

The beam width and M² factor behaviors are depicted in Fig. 9. Their evolutions exhibit bowl-shaped curves. One can note that as the parameter n is increased, the evolution curve bends more, i.e., the evolution rate of beam width and M²-factor become larger. One can note also that the beam width remains almost constant when the value of α is smaller.

Fig. 9

The evolution of the spot size (Top row) and the beam propagation factor (bottom row) of the output electrical field after n-times Airy transforms for b = 2 and $\omega_{0} = 0.5\,mm$ versus the control parameter α. (a.1–2) p = 2 and (b.1–2) p = 6

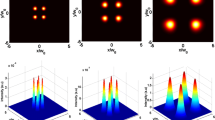
Figure 10 shows the asymmetry of the beam intensity when the parameters b along the x and y-direction (b_x and b_y) are different. This means that one can control the distribution of the beam's side lobes in the x- or y-directions by properly choosing the value of b_x and b_y.

Fig. 10

Normalized intensity distribution of the HOChGB after 3-times Airy transforms, with $\omega_{0} = 0.2\,mm$, p = q = 4, $\alpha = \beta = 2\,mm$, and $b_{x} = 1$. The Upper and lower rows for the three-dimensional and contour intensity patterns, respectively. a $b_{y} = 2$, b $b_{y} = 2.5$, c $b_{y} = 3$ and d $b_{y} = 4$

Figures 11 and 12 illustrate the propagation dynamics of the field after n-Airy transforms with n = 1, 2, 4 and 6.

Fig. 11

Normalized intensity distribution of the output electrical field in the x–z plane for $\lambda = 0.5\,\,\mu m$ with b = 0.1, $\omega_{0} = 0.1\,mm$ and $\alpha = 3\,mm$ after n-times Airy transforms with p = 2. n = 1, b n = 2, c n = 4 and d n = 6

Fig. 12

a: Normalized intensity distribution of the output electrical field in the x–z plane 6-times Airy transforms for $\lambda = 0.5\,\,\mu m$, b = 0.1, $\omega_{0} = 0.1\,mm$ and p = 2. a $\alpha = 1.5\,mm$, b $\alpha = 3\,mm$, c $\alpha = 4\,mm$ and d $\alpha = 6\,mm$. b: Normalized intensity distribution of the output electrical field in the x–z plane 6-times Airy transforms for $\lambda = 0.5\,\,{\mu m}$, b = 0.1, $\omega_{0} = 0.1\,{\text{mm}}$ and p = 2. a $\alpha = 1.5\,{\text{mm}}$ and b $\alpha = 3\,{\text{mm}}$

One can see that the non-diffracting propagation distance of the transformed beam decreases as the number of Airy transform or the control parameter $\alpha$ increases. In other words, the propagation distance of the Airy transformed beam can be controlled by adjusting these parameters.

4 Conclusion

The paraxial propagation of a HOChGB through n-times Airy transforms optical system is studied theoretically. The spatial characteristics of the generated beam, such as the field amplitude, the centroid, beam width, and propagation factor (M²-factor), are derived in closed form. And their evolutions are analyzed numerically versus the system parameters. From analytical and numerical results, it is demonstrated that the transformed beam is Airy-like. And its spatial characteristics depend closely on the beam order, the decentered beam, and the number of Airy transforms. It is shown that the profile of the generated beam can be controlled broadly by adjusting the optical system parameters and the initial beam parameters. Furthermore, the non-diffracting propagation distance of the transformed beam decreases as the number of Airy transforms or the control parameter $\alpha$ increases. This study may be beneficial for beam shaping and micromanipulations using Airy beams.

Appendix

The first Airy transform of a Gaussian can be performed by using the Plancherel-Parceval rule of the Fourier transform (Gradshteyn et al. 1994)

$$\int\limits_{ - \infty }^{ + \infty } {\,f_{1}^{*} \left( x \right)\,\,f_{2} \left( x \right)\,dx} \, = \int\limits_{ - \infty }^{ + \infty } {\,F_{1}^{*} \left( t \right)\,\,F_{2} \left( t \right)\,dt} \,\,,$$

(25)

where $F_{1} \left( t \right)\,$ $F_{2} \left( t \right)$ and are the Fourier transform of $f_{1} \left( x \right)\,$ $f_{2} \left( x \right)$ and respectively. The asterisk * represents the complex conjugate. So we have,

$$E_{1} \left( x \right) = \frac{1}{\left| \alpha \right|}\int\limits_{ - \infty }^{ + \infty } {\,\exp \left( {\frac{{ - x_{0}^{2} }}{{\omega_{0}^{2} }}} \right)\,\,Ai\,\left( {\frac{{x - x_{0} }}{\alpha }} \right)\,dx_{0} } \, = \,\int\limits_{ - \infty }^{ + \infty } {\,f_{1}^{*} \left( {x_{0} } \right)\,\,f_{2} \left( {x_{0} } \right)\,dx_{0} } \,$$

(26)

The Fourier transforms $f_{1} \left( x \right)\,$ and $f_{2} \left( x \right)$ takes the following forms

$$F_{1} \left( t \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {\exp \left( {\frac{{ - x_{0}^{2} }}{{\omega_{0}^{2} }}} \right)} \exp \left( {itx_{0} } \right)\,dx_{0} \, = \frac{{\omega_{0} }}{\sqrt 2 }\exp \left( {\frac{{ - \omega_{0}^{2} \,t^{2} }}{4}} \right),$$

(27)

and

$$F_{2} \left( t \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {Ai\,\left( {\frac{{x - x_{0} }}{\alpha }} \right)\,} \exp \left( {itx_{0} } \right)\,dx_{0} \, = \frac{\alpha }{{\sqrt {2\pi } }}\exp \left( {\frac{{i\alpha^{3} \,t^{3} }}{3} + itx} \right)$$

(28)

Now, by recalling the following integral formula (Vallée et al.2004)

$$\frac{1}{2\pi }\int\limits_{ - \infty }^{ + \infty } {\exp \left( {\frac{{iu^{3} }}{3} + iAu^{2} + iBu} \right)\,} dt\, = \exp \left( {\frac{{2iA^{3} }}{3} - iAB} \right)\,Ai\left( {B - A^{2} } \right).$$

(29)

The first Airy transform of any incident Gaussian beam in the x-direction is found to be

$$E_{1} \left( x \right) = 2\sqrt {\pi \,\tau_{\alpha } } \exp \left( {\frac{{2\tau_{\alpha }^{3} }}{3} + \frac{{\tau_{\alpha } \,x}}{\alpha }} \right)\,Ai\left( {\frac{x}{\alpha } + \tau_{\alpha }^{2} } \right),$$

(30)

with $\tau_{\alpha } = \frac{{\omega_{0}^{2} }}{{4\,\alpha^{2} }}$.

Following the same derivation process, the second, third, fourth and the fifth Airy transform of a Gaussian beam take the form

$$E_{2} \left( x \right) = \frac{{\left| \alpha \right|2\sqrt {\pi \,\tau_{\alpha } } }}{{2^{2/3} \,\alpha }}\exp \left( {\frac{{\tau_{\alpha }^{3} }}{6} + \frac{{\tau_{\alpha } \,x}}{2\alpha }} \right)\,Ai\left( {\frac{x}{{2^{1/3} \alpha }} + \frac{{\tau_{\alpha }^{2} }}{{2^{4/3} }}} \right),$$

(31)

$$E_{3} \left( x \right) = \frac{{\left| \alpha \right|2\sqrt {\pi \,\tau_{\alpha } } }}{{3^{2/3} \,\alpha }}\exp \left( {\frac{{2\tau_{\alpha }^{3} }}{27} + \frac{{\tau_{\alpha } \,x}}{3\alpha }} \right)\,Ai\left( {\frac{x}{{3^{1/3} \alpha }} + \frac{{\tau_{\alpha }^{2} }}{{3^{4/3} }}} \right),$$

(32)

$$E_{4} \left( x \right) = \frac{{\left| \alpha \right|2\sqrt {\pi \,\tau_{\alpha } } }}{{4^{2/3} \,\alpha }}\exp \left( {\frac{{\tau_{\alpha }^{3} }}{24} + \frac{{\tau_{\alpha } \,x}}{4\alpha }} \right)\,Ai\left( {\frac{x}{{4^{1/3} \alpha }} + \frac{{\tau_{\alpha }^{2} }}{{4^{4/3} }}} \right),$$

(33)

and

$$E_{4} \left( x \right) = \frac{{\left| \alpha \right|2\sqrt {\pi \,\tau_{\alpha } } }}{{5^{2/3} \,\alpha }}\exp \left( {\frac{{2\tau_{\alpha }^{3} }}{75} + \frac{{\tau_{\alpha } \,x}}{4\alpha }} \right)\,Ai\left( {\frac{x}{{5^{1/3} \alpha }} + \frac{{\tau_{\alpha }^{2} }}{{5^{4/3} }}} \right).$$

(34)

Consequently, the n-times ATOS of any Gaussian field has the following expression (Zhou et al. 2022)

$$E_{n} \left( x \right) = \left( {\frac{\left| \alpha \right|}{\alpha }} \right)^{n - 1} \frac{{2\sqrt {\pi \tau_{\alpha } } }}{{n^{1/3} }}\exp \left[ {\frac{2}{3}\frac{{\tau_{\alpha }^{3} }}{{n^{2} }} + \frac{{\tau_{\alpha } }}{n}\left( {\frac{x}{\alpha }} \right)} \right]Ai\left( {\frac{x}{{n^{1/3} \alpha }} + \frac{{\tau_{\alpha }^{2} }}{{n^{4/3} }}} \right),$$

(35)

therefore, the n-times ATOS for a decentered Gaussian field gives

$$E_{n} \left( {x - a} \right) = \left( {\frac{\left| \alpha \right|}{\alpha }} \right)^{n - 1} \frac{{2\sqrt {\pi \tau_{\alpha } } }}{{n^{1/3} }}\exp \left[ {\frac{2}{3}\frac{{\tau_{\alpha }^{3} }}{{n^{2} }} + \frac{{\tau_{\alpha } }}{n}\left( {\frac{x - a}{\alpha }} \right)} \right]Ai\left( {\frac{x - a}{{n^{1/3} \alpha }} + \frac{{\tau_{\alpha }^{2} }}{{n^{4/3} }}} \right).$$

(36)

This last expression is the Eq. (8) of the manuscript.

The free space propagation is directly obtained by substituting Eq. (8) into Eq. (21), so this yields

$$\begin{gathered} E\left( {x,z} \right) = \sqrt {\frac{ik}{{2\pi B}}} \frac{1}{{2^{p} }}\left( {\frac{\left| \alpha \right|}{\alpha }} \right)^{n - 1} \frac{{2\sqrt {\pi \tau_{\alpha } } }}{{n^{1/3} }}\sum\limits_{s = 0}^{p} {A_{s}^{{}} } \exp \left( {\frac{{2\,\tau_{\alpha }^{3} }}{{3\,n^{2} }}} \right)\exp \left( {\frac{{ - b\tau_{\alpha } \,\,}}{n\,\alpha }} \right)\,\exp \left( { - \frac{{ikDx^{2} }}{2B}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \int\limits_{ - \infty }^{ + \infty } {Ai\left( {\frac{{x_{0} - b}}{{n^{1/3} \,\alpha }} + \frac{{\tau_{\alpha }^{2} }}{{n^{4/3} }}} \right)\exp \left[ { - \frac{ik}{{2B}}\left( {Ax_{0}^{2} - 2xx_{0} } \right) + \frac{{\tau_{\alpha } x_{0} \,\,}}{n\,\alpha }} \right]dx_{0} } {\kern 1pt} {\kern 1pt} , \hfill \\ \end{gathered}$$

(37)

or

$$\begin{gathered} E\left( {x,z} \right) = \frac{1}{{2^{p} }}\left( {\frac{\left| \alpha \right|}{\alpha }} \right)^{n - 1} \frac{{\sqrt {2ik\tau_{\alpha } } }}{{n^{1/3} \,z}}\sum\limits_{s = 0}^{p} {A_{s}^{{}} } \exp \left( {\frac{{2\,\tau_{\alpha }^{3} }}{{3\,n^{2} }}} \right)\exp \left( {\frac{{ - b\tau_{\alpha } \,\,}}{n\,\alpha }} \right)\,\exp \left( { - \frac{{ikx^{2} }}{2z}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \int\limits_{ - \infty }^{ + \infty } {Ai\left( {\frac{{x_{0} - b}}{{n^{1/3} \,\alpha }} + \frac{{\tau_{\alpha }^{2} }}{{n^{4/3} }}} \right)\exp \left[ { - \frac{ik}{{2z}}x_{0}^{2} + \left( {\frac{ikx}{z} + \frac{{\tau_{\alpha } }}{n\,\alpha }} \right)x_{0} } \right]dx_{0} } . \hfill \\ \end{gathered}$$

(38)

Let us assume that

$$\begin{gathered} E_{a} \left( {x,z} \right) = \int\limits_{ - \infty }^{ + \infty } {Ai\left( {\frac{{x_{0} - b}}{{n^{1/3} \,\alpha }} + \frac{{\tau_{\alpha }^{2} }}{{n^{4/3} }}} \right)\exp \left[ { - \frac{ik}{{2z}}x_{0}^{2} + \left( {\frac{ikx}{z} + \frac{{\tau_{\alpha } }}{n\,\alpha }} \right)x_{0} } \right]dx_{0} } \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \int\limits_{ - \infty }^{ + \infty } {Ai\left( {\frac{{x_{0} - b}}{{n^{1/3} \,\alpha }} + \frac{{\tau_{\alpha }^{2} }}{{n^{4/3} }}} \right)\exp \left\{ {\left( {\frac{ - ik}{{2z}}} \right)\,\left[ {x_{0}^{2} - 2\,\left( {x - \frac{{iz\tau_{\alpha } }}{kn\,\alpha }} \right)x_{0} } \right]} \right\}dx_{0} } , \hfill \\ \end{gathered}$$

(39)

so

$$E_{a} \left( {x,z} \right) = \exp \left\{ {\left( {\frac{ik}{{2z}}} \right)\left( {x - \frac{{iz\tau_{\alpha } }}{kn\,\alpha }} \right)^{2} } \right\}\int\limits_{ - \infty }^{ + \infty } {Ai\left( {\frac{{x_{0} - b}}{{n^{1/3} \,\alpha }} + \frac{{\tau_{\alpha }^{2} }}{{n^{4/3} }}} \right)\exp \left\{ {\left( {\frac{ - ik}{{2z}}} \right)\,\left[ {x_{0}^{{}} - \left( {x - \frac{{iz\tau_{\alpha } }}{kn\,\alpha }} \right)} \right]^{2} } \right\}dx_{0} } .$$

(40)

Let us consider that $X_{0} = \frac{{x_{0} - b}}{{n^{1/3} \,\alpha }} + \frac{{\tau_{\alpha }^{2} }}{{n^{4/3} }}$, so $x_{0} = n^{1/3} \,\alpha \,\left( {X_{0} - \frac{{\tau_{\alpha }^{2} }}{{n^{4/3} }}} \right) + b$, one finds

$$\begin{gathered} E_{a} \left( {x,z} \right) = \left( {n^{1/3} \,\alpha } \right)\exp \left\{ {\left( {\frac{ik}{{2z}}} \right)\left( {\frac{{iz\tau_{\alpha } }}{kn\,\alpha } - x} \right)^{2} } \right\}. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \int\limits_{ - \infty }^{ + \infty } {Ai\left( {X_{0} } \right)\exp \left\{ {\left( {\frac{ - ik}{{2z}}} \right)\,\left[ {\left( {n^{1/3} \,\alpha } \right)\,X_{0} - x - \frac{{\alpha \,\tau_{\alpha }^{2} }}{n} + \frac{{iz\tau_{\alpha } }}{kn\,\alpha } + b} \right]^{2} } \right\}dX_{0} } \hfill \\ \end{gathered}$$

(41)

Then,

$$\begin{gathered} E_{a} \left( {x,z} \right) = \left( {n^{1/3} \,\alpha } \right)\exp \left\{ {\left( {\frac{ik}{{2z}}} \right)\left( {\frac{{iz\tau_{\alpha } }}{kn\,\alpha } - x} \right)^{2} } \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \int\limits_{ - \infty }^{ + \infty } {Ai\left( {X_{0} } \right)\exp \left\{ {\left( {\frac{ - ik}{{2z\,\alpha \,n^{1/3} \,}}} \right)\,\left[ {X_{0} - \left( {\frac{x}{{n^{1/3} \,\alpha }} + \frac{{\,\tau_{\alpha }^{2} }}{{\,n^{4/3} }} - \frac{{iz\tau_{\alpha } }}{{k\,n^{4/3} \,\alpha^{2} }} - \frac{b}{{\alpha \,n^{1/3} }}} \right)} \right]^{2} } \right\}dX_{0} } , \hfill \\ \end{gathered}$$

(42)

or

$$\begin{gathered} E_{a} \left( {x,z} \right) = \left( {n^{1/3} \,\alpha } \right)\exp \left\{ {\left( {\frac{ik}{{2z}}} \right)\left( {\frac{{iz\tau_{\alpha } }}{kn\,\alpha } - x} \right)^{2} } \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \int\limits_{ - \infty }^{ + \infty } {Ai\left( {X_{0} } \right)\,\exp \left\{ {\left( {\frac{ - ik}{{2z\,\alpha \,n^{1/3} \,}}} \right)\,\left[ {\left( {\frac{x}{{n^{1/3} \,\alpha }} + \frac{{\,\tau_{\alpha }^{2} }}{{\,n^{4/3} }} - \frac{{iz\tau_{\alpha } }}{{k\,n^{4/3} \,\alpha^{2} }} - \frac{b}{{\alpha \,n^{1/3} }}} \right) - X_{0} } \right]^{2} } \right\}dX_{0} } . \hfill \\ \end{gathered}$$

(43)

We note that the convolution of two functions, $f_{1} \left( X \right)$ and $f_{2} \left( X \right)$ are defined as (Gradshteyn et al. 1994)

$$f_{1} \left( t \right) \otimes f_{2} \left( t \right) = \int\limits_{ - \infty }^{ + \infty } {f_{1} \left( {t_{0} } \right)f_{2} \left( {t - t_{0} } \right)dt_{0} } ,$$

(44)

where $\otimes$ is the convolution product. Therefore, Eq. (43) turns out to be

$$\begin{gathered} E_{a} \left( {x,z} \right) = \left( {n^{1/3} \,\alpha } \right)\exp \left\{ {\left( {\frac{ik}{{2z}}} \right)\left( {\frac{{iz\tau_{\alpha } }}{kn\,\alpha } - x} \right)^{2} } \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\left[ {f_{1} \left( {\frac{x}{{n^{1/3} \,\alpha }} + \frac{{\,\tau_{\alpha }^{2} }}{{\,n^{4/3} }} - \frac{{iz\tau_{\alpha } }}{{k\,n^{4/3} \,\alpha^{2} }} - \frac{b}{{\alpha \,n^{1/3} }}} \right) \otimes f_{2} \left( {\frac{x}{{n^{1/3} \,\alpha }} + \frac{{\,\tau_{\alpha }^{2} }}{{\,n^{4/3} }} - \frac{{iz\tau_{\alpha } }}{{k\,n^{4/3} \,\alpha^{2} }} - \frac{b}{{\alpha \,n^{1/3} }}} \right)} \right]\,\,, \hfill \\ \end{gathered}$$

(45)

where the auxiliary functions are

$$f_{1} \left( t \right) = Ai\left( t \right)\,\,and\,f_{2} \left( t \right) = \exp \left( {\frac{ - ik}{{2\,z\,n^{1/3} \,\alpha }}t^{2} } \right).$$

(46)

The convolution theorem of the Fourier transform has the following property (Vallée et al. 2004; Gradshteyn et al. 1994)

$$f_{1} \left( t \right) \otimes f_{2} \left( t \right) = \int\limits_{ - \infty }^{ + \infty } {f_{1} \left( m \right)f_{2} \left( m \right)\,\exp \left( { - imt} \right)dm} ,$$

(47)

where

$$f_{1} \left( m \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {Ai\,\left( t \right)} \exp \left( {i\,m\,t} \right)\,dt\, = \frac{1}{{\sqrt {2\pi } }}\exp \left( {\frac{{ - im^{3} }}{3}} \right),$$

(48)

and

$$f_{2} \left( m \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {\,\exp \left( {\frac{ - ik}{{2\,z\,n^{1/3} \,\alpha }}t^{2} } \right)} \exp \left( {i\,m\,t} \right)\,dt\, = \sqrt {\frac{{z\,\alpha \,n^{1/3} }}{ik\,}} \exp \left( {\frac{{ - z\,\alpha \,n^{1/3} }}{ik\,}m^{2} } \right),$$

(49)

Then, by using the following results (Vallée et al. 2004),

$$\int\limits_{ - \infty }^{ + \infty } {\exp \left( {\frac{{iu^{3} }}{3} + iAu^{2} + iBu} \right)\,} dt\, = 2\pi \exp \left( {\frac{{2iA^{3} }}{3} - iAB} \right)\,Ai\left( {B - A^{2} } \right),$$

(50)

then.

$\int\limits_{ - \infty }^{ + \infty } {\,\exp \left[ { - i\,\left( {\frac{{m^{3} }}{3} - \frac{{\,z\,\alpha \,n^{1/3} }}{2k\,}m^{2} + t\,m} \right)} \right]dm} = 2\pi \exp \left[ { - \frac{2}{3}\left( {\frac{{\,z\,\alpha \,n^{1/3} }}{2k\,}} \right)^{3} + \frac{{\,i\,z\,\alpha \,n^{1/3} \,t}}{2k\,}} \right]\,Ai\left( {t - \,\left( {\frac{{\,z\,\alpha \,n^{1/3} }}{2k\,}} \right)^{2} } \right)$. Therefore, (43) turns out to be

$$\begin{gathered} E_{a} \left( {x,z} \right) = \left( {n^{1/3} \,\alpha } \right)\sqrt {\frac{{2\pi \,z\,\alpha \,n^{1/3} }}{\,ik\,}} \exp \left\{ {\left( {\frac{ik}{{2z}}} \right)\left( {\frac{{iz\tau_{\alpha } }}{kn\,\alpha } - x} \right)^{2} } \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\,\exp \left[ { - \frac{2}{3}\left( {\frac{{\,z\,\alpha \,n^{1/3} }}{2k\,}} \right)^{3} + \frac{{\,i\,z\,\alpha \,n^{1/3} \,t_{x} }}{2k\,}} \right]\,Ai\left( {t_{x} - \,\left( {\frac{{\,z\,\alpha \,n^{1/3} }}{2k\,}} \right)^{2} } \right), \hfill \\ \end{gathered}$$

(51)

with $t_{x} = \left( {\frac{x}{{n^{1/3} \,\alpha }} + \frac{{\,\tau_{\alpha }^{2} }}{{\,n^{4/3} }} - \frac{{iz\tau_{\alpha } }}{{k\,n^{4/3} \,\alpha^{2} }} - \frac{b}{{\alpha \,n^{1/3} }}} \right)$.

So, Eq. (22) in the paper is obtained as.

$\begin{gathered} E\left( {x,z} \right) = \frac{\alpha }{{2^{p} }}\left( {\frac{\left| \alpha \right|}{\alpha }} \right)^{n - 1} \sqrt {\frac{{4\pi \,\alpha \,\tau_{\alpha } \,n^{1/3} }}{\,z\,}} \exp \left( {\frac{{2\,\tau_{\alpha }^{3} }}{{3\,n^{2} }}} \right)\exp \left( { - \frac{{ikx^{2} }}{2z}} \right)\sum\limits_{s = 0}^{p} {A_{s}^{{}} } \exp \left( {\frac{{ - b\tau_{\alpha } \,\,}}{n\,\alpha }} \right)\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left\{ { - \frac{2}{3}\left( {\frac{{\,z\,\alpha \,n^{1/3} }}{2k\,}} \right)^{3} + \frac{ik}{{2z}}\,\left( {\frac{{iz\tau_{\alpha } }}{kn\,\alpha } - x} \right)^{2} + \frac{{\,i\,z\,\alpha \,n^{1/3} \,t_{x} }}{2k\,}} \right\}\,\,Ai\left( {t_{x} - \,\left( {\frac{{\,z\,\alpha \,n^{1/3} }}{2k\,}} \right)^{2} } \right) \hfill \\ \end{gathered}$.

After some arrangements, one obtains.

$\begin{gathered} E\left( {x,z} \right) = \frac{\alpha }{{2^{p} }}\left( {\frac{\left| \alpha \right|}{\alpha }} \right)^{n - 1} \sqrt {\frac{{4\pi \,\alpha \,\tau_{\alpha } \,n^{1/3} }}{\,z\,}} \exp \left( {\frac{{2\,\tau_{\alpha }^{3} }}{{3\,n^{2} }}} \right)\exp \left( { - \frac{{ikx^{2} }}{2z}} \right)\sum\limits_{s = 0}^{p} {A_{s}^{{}} } \exp \left( {\frac{{ - b\tau_{\alpha } \,\,}}{n\,\alpha }} \right)\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left\{ {\frac{{z^{2} \tau_{\alpha } }}{{2k^{2} \,n\,\alpha }} - \frac{{\,z^{3} \,\alpha^{3} \,n}}{{12k^{3} \,}} + \frac{ik}{{2z}}\,\left( {\frac{{iz\tau_{\alpha } }}{kn\,\alpha } - x} \right)^{2} + \frac{i\,z\,x}{{2k}} + \frac{{i\,z\,\alpha \tau_{\alpha }^{2} }}{\,2k\,n} + - \frac{i\,z\,b}{{2k}}} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times Ai\left( {\frac{x}{{n^{1/3} \,\alpha }} + \frac{{\,\tau_{\alpha }^{2} }}{{\,n^{4/3} }} - \frac{b}{{\alpha \,n^{1/3} }} - \,\frac{{\,z^{2} \,\alpha^{2} \,n^{2/3} }}{{4k^{2} \,}} - \frac{{iz\tau_{\alpha } }}{{k\,n^{4/3} \,\alpha^{2} }}} \right) \hfill \\ \end{gathered}$.