Near-field and far-field spreading of partially coherent annular beams propagating through atmospheric turbulence

Abstract

Based on the extended Huygens–Fresnel principle, closed-form expressions for the Rayleigh range and the far-field divergence angle of partially coherent annular beams propagating through atmospheric turbulence are derived by using the Wigner distribution function (WDF). Taking the Rayleigh range and the far-field divergence angle as the characteristic parameters of near-field and far-field spreading, respectively, the spreading of partially coherent annular beams both in free space and in turbulence is studied in detail. It is found that the effect of the strength of turbulence and beam parameters (e.g., the spatial correlation length, the waist width, and the wave length) on the beam spreading in the near field is in agreement with that in the far field. However, in turbulence, the effect of the obscure ratio of annular beams on the spreading is different between in the near field and in the far field. Namely, in turbulence the beam spreading in the near field becomes smaller and the beam spreading in the far field becomes larger as the obscure ratio increases. In particular, the effect of turbulence on the Rayleigh range and the far-field divergence angle is nearly unchanged versus the obscure ratio when the spatial correlation length is small. The main results obtained in this paper are explained physically.

1 Introduction

Propagation of laser beams through atmospheric turbulence is a topic that has been of considerable theoretical and practical interest (e.g., remote sensing, tracking and long-distance optical communications) for a long time [1–4]. Laser beams are of special interest because of their high directionality. It would be useful in applications to utilize beams that are distorted as little as possible by the presence of turbulence. Much work has been carried out concerning the spreading of laser beams propagating through atmospheric turbulence, and it has been demonstrated that partially coherent beams are less sensitive to turbulence than fully coherent ones [5, 6], and higher-order mode laser beams are less sensitive to turbulence than Gaussian ones [7, 8].

It is very important to study the propagation of annular beams. High power laser usually uses unstable optical resonators as resonant cavities which produce an annular beam [9]. In many telescopes, there exist the annular apertures which create an annular beam [10]. The telescope is used in both the transmitter and the receiver in laser satcoms and Free Space Optics (FSO) systems [11]. The average intensity, coherence, and scintillation of an annular beam propagating through atmospheric turbulence were discussed in [3]. The average intensity and scintillation index of dark hollow beams (DHBs) in atmospheric turbulence was studied in [12, 13]. It is shown that DHBs have advantage over a Gaussian beam and flat-topped beam for overcoming the destructive effect of atmospheric turbulence from the aspect of scintillation [12, 13]. In 2008, we studied the directionality of partially coherent annular flat-topped beams, and found that there exist equivalent partially coherent annular beams which may generate the same directionality as the corresponding fully coherent Gaussian beam both in free space and in turbulence [14]. Recently, the M ²-factor of DHBs propagating through atmospheric turbulence was investigated in [15]. It is shown that the relative M ²-factor of a DHB with lower coherence, longer wavelength, and larger dark size is less affected by the atmospheric turbulence [15].

The Rayleigh range is used in the theory of lasers to characterize the distance over which a beam may be considered effectively non-spreading [9, 16]. On the other hand, the far-field divergence angle is used to denote the beam spreading in the far field. The aim of this paper is to study near-field and far-field spreading of partially coherent annular beams both in free space and in atmospheric turbulence, where the Rayleigh range and the far-field divergence angle are taken as characteristic parameters of near-field and far-field spreading, respectively. It is found that for partially coherent annular beams, in turbulence the effect of the beam obscure ratio on the spreading is different between in the near field and in the far field, which is quite different from the behavior of other laser beams. The main results obtained in this paper are explained in physical.

2 Theoretical formulae

The amplitude of the field of a fully coherent flat-topped beam in the plane z=0 is expressed as [17]

(1)

where ρ′≡(x′,y′) is the transverse vector in the plane z=0, w ₀ is the waist width of the Gaussian mode in the plane z=0, M and N are beam orders of flat-topped beams, and [17]

$$ \alpha_{m} = ( - 1 )^{m + 1}\frac{M!}{m!( M - m )!},\qquad p_{m} = \sum_{m = 1}^{M} \frac{\alpha_{m}}{m}, $$

(2)

α _n and p _n can be given if m and M in (2) are replaced by n and N, respectively.

The fully coherent annular beam can be modeled as the difference between two fully coherent flat-topped beams with different values of the waist width w ₀ and $w'_{0}$. And then the amplitude of the field of the fully coherent annular beam in the plane z=0 can be given by

(3)

where $w'_{0} = \varepsilon w_{0}$ and 0<ε<1,ε is called the obscure ratio of the annular beam.

The fully coherent beam can be extended to the partially coherent one by introducing a Gaussian term of the spectral degree of coherence $\mu^{(0)}(\boldsymbol{\rho}'_{1},\boldsymbol{\rho}'_{2},0)$. The cross spectral density function of the partially coherent annular beam in the source plane z=0 is expressed as [17, 18]

(4)

where

(5)

(6)

σ ₀ is the spatial correlation length of the source. $W_{022}( \boldsymbol{\rho}'_{1},\boldsymbol{\rho}'_{2},0 )$ can be obtained if w ₀ in (5) are replaced by $w'_{0}$. $W_{021}( \boldsymbol{\rho}'_{1},\boldsymbol{\rho}'_{2},0 )$ can be obtained if $w'_{0}$ and w ₀ in (6) are changed places with each other.

Based on the extended Huygens–Fresnel principle, the cross spectral density function of the partially coherent annular beams propagating through atmospheric turbulence in the plane z is expressed as [3]

(7)

where $\boldsymbol{\rho}' = ( \boldsymbol{\rho}'_{1} + \boldsymbol{\rho}'_{2} ) / 2, \boldsymbol{\rho}'_{d} = \boldsymbol{\rho}'_{1} - \boldsymbol{\rho}'_{2}, \boldsymbol{\rho} = ( \boldsymbol{\rho}_{1} + \boldsymbol{\rho}_{2} ) / 2$ and ρ _d =ρ ₁−ρ ₂ are new variables introduced. ρ ₁≡(x ₁,y ₁) and ρ ₂≡(x ₂,y ₂) are the transverse vectors in the plane z>0. k is the wavenumber related to the wave length λ by k=2π/λ. The term $\exp[ - H( \boldsymbol{\rho}_{d},\boldsymbol{\rho}'_{d},z ) ]$ represents the effect of the turbulence, and $H( \boldsymbol{\rho}_{d},\boldsymbol{\rho}'_{d},z )$ can be written as [3]

(8)

where J ₀(•) is the zero-order Bessel function of the first kind, Φ _n (κ) being the spatial power spectrum of the refractive index fluctuations of the turbulent atmosphere.

Recalling the formula

$$ \delta\bigl( \boldsymbol{\rho}'' - \boldsymbol{ \rho}' \bigr) = \frac{1}{( 2\pi )^{2}}\int\exp\bigl[ \pm\mathrm{i} \boldsymbol{\kappa}_{d} \cdot\bigl( \boldsymbol{\rho}'' - \boldsymbol{\rho}' \bigr) \bigr]\,\mathrm{d}^{2} \boldsymbol{\kappa}_{d}, $$

(9)

the cross-spectral density of the partially coherent annular beams in the source plane z=0 can be rewritten as

(10)

On substituting from (10) into (7), recalling the integral formula (9) again, and performing the integration with respect to ρ′ and $\boldsymbol{\rho}_{d}^{\prime}$ in (7) in turn, we obtain

(11)

Considering (4) and (11), W(ρ,ρ _d ,z) can be rewritten as

(12)

where

(13)

and W ₂₂(ρ,ρ _d ,z),W ₁₂(ρ,ρ _d ,z) and W ₂₁(ρ,ρ _d ,z) can be expressed in the similar way.

The WDF of field is very useful for handling partially coherent beams, which can be defined in terms of the cross-spectral density as [19]

$$ h( \boldsymbol{\rho} ,\boldsymbol{\theta} ,z ) = \biggl( \frac{k}{2\pi} \biggr)^{2}\int W( \boldsymbol{\rho} ,\boldsymbol{\rho}_{d},z )\exp( - \mathrm{i}k\boldsymbol{\theta} \cdot\boldsymbol{\rho}_{d} )\, \mathrm{d}^{2}\boldsymbol{\rho}_{d}, $$

(14)

where θ≡(θ _x ,θ _y ),kθ _x and kθ _y are the wave vector components along the x-axis and y-axis, respectively. Integration of function h over the angular variables θ _x and θ _y gives the beam intensity, and its integral over the spatial variables x and y is proportional to the radiant intensity of the field.

On substituting from (12) into (14), yields

(15)

where

(16)

h ₂₂(ρ,θ,z), h ₁₂(ρ,θ,z) and h ₂₁(ρ,θ,z) can be expressed if W ₁₁(ρ,ρ _d ,z) in (16) is replaced by W ₂₂(ρ,ρ _d ,z), W ₁₂(ρ,ρ _d ,z) and W ₂₁(ρ,ρ _d ,z), respectively.

On substituting from (13) into (16), and performing the integration with respect to ρ″ in (16), we obtain

(17)

where

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

and h ₂₂(ρ,θ,z),h ₁₂(ρ,θ,z) and h ₂₁(ρ,θ,z) can be obtained in the similar way.

The moments of the order n ₁+n ₂+m ₁+m ₂ of WDF are given by the expression [19]

$$ \bigl\langle x^{n_{1}}y^{n_{2}}\theta_{x}^{m_{1}} \theta_{y}^{m_{2}} \bigr\rangle = \frac{\iint x^{n_{1}}y^{n_{2}}\theta_{x}^{m_{1}}\theta_{y}^{m_{2}}h(\boldsymbol{\rho} ,\boldsymbol{\theta} ,z)\,\mathrm{d}^{2}\boldsymbol{\rho} \,\mathrm{d}^{2}\boldsymbol{\theta}}{\iint h(\boldsymbol{\rho} ,\boldsymbol{\theta} ,z)\,\mathrm{d}^{2}\boldsymbol{\rho} \,\mathrm{d}^{2}\boldsymbol{\theta}} . $$

(26)

On substituting (15) into (26), making use of the integral transform technique, after very tedious integral calculations (see Appendixes A and B), we obtain the second moments 〈ρ ²〉 and $\langle\theta_{x}^{2} \rangle$ of partially coherent annular beams propagating through atmospheric turbulence, i.e.,

(27)

(28)

where only $\langle\theta_{x}^{2} \rangle$ is given, $\langle\theta_{y}^{2} \rangle$ can be derived in the similar way, and $\langle\theta^{2} \rangle = \langle\theta_{x}^{2} \rangle + \langle\theta_{y}^{2} \rangle$. $\langle\rho_{0}^{2} \rangle$, $\langle\theta_{0}^{2} \rangle$ and $\langle\theta_{x0}^{2} \rangle$ represent the second moments in the plane z=0, which are given by

(29)

(30)

(31)

(32)

(33)

(34)

The meaning of second moments in physics is clear [20, 21], e.g., 〈ρ ²〉 is relative to the mean-squared width, and $\langle\theta_{x}^{2} \rangle$ is relative to the far-field divergence angle along the x-axis. From (27) and (28), the Rayleigh range and the far-field divergence angle along the x-axis can be derived, which are given as follows:

2.1 Rayleigh range

It is known that the Rayleigh range is defined as the propagation distance at which the cross-sectional area of a beam doubles [9, 20], i.e., $\langle\rho_{z_{R}}^{2} \rangle / \langle\rho_{0}^{2} \rangle = 2$, where $\langle\rho_{z_{R}}^{2} \rangle$ is the second moment in the z=z _R plane. From (27), we can conclude that the Rayleigh range z _R of partially coherent annular beams in turbulence is determined by the cubic equation, i.e.,

$$ ( 4 / 3 )Tz_{R}^{3} + \bigl\langle\theta_{0}^{2} \bigr\rangle z_{R}^{2} - \bigl\langle\rho_{0}^{2} \bigr\rangle = 0, $$

(35)

Among the three solutions of this cubic equation, there is only one real solution, which represents the Rayleigh range z _R , i.e.,

$$ z_{R} = \bigl[ - \bigl\langle\theta_{0}^{2} \bigr\rangle / 2 + \bigl\langle\theta_{0}^{2} \bigr \rangle^{2} / ( 4A ) + A \bigr] / 2T, $$

(36)

where

(37)

It is noted that (36) is valid whether the strength of turbulence is strong or weak, but (36) is invalid when T=0 (i.e., free space). For free space case, (27) reduces to $\langle\rho^{2} \rangle|_{\mathrm{free}} = \langle\rho_{0}^{2} \rangle + \langle\theta_{0}^{2} \rangle z^{2}$. Based on the definition of Rayleigh range, we have $z_{R} |_{\mathrm{free}} = \sqrt{\langle \rho_{0}^{2} \rangle / \langle \theta_{0}^{2} \rangle}$.

2.2 Far-field divergence angle

For convenience, the analysis is restricted to the two-dimensional case (i.e., only the far-field divergence angle along the x-axis is considered), but the extension to the three-dimensional case is straightforward. According to [20], and recalling (28), the far-field divergence angle along the x-axis is expressed as

$$ \theta_{\mathrm{sp}}^{(x)} = 2\sqrt{\bigl\langle \theta_{x}^{2} \bigr\rangle} = 2\sqrt{\bigl\langle \theta_{x0}^{2} \bigr\rangle + 2Tz}. $$

(38)

It is clear that (38) is also valid in free space, i.e., $\theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}} = 2\sqrt{\langle \theta_{x0}^{2} \rangle}$.

Equations (36) and (38) are the main analytical results obtained in this paper, which indicate that the Rayleigh range and the far-field divergence angle of partially coherent annular beams in turbulence depends on the strength of turbulence and the beam parameters (i.e., ε, σ ₀, w ₀, and λ).

3 Numerical calculation results and analysis

In this section, some numerical calculations are performed to illustrate the near-field and far-field spreading (i.e., the Rayleigh range z _R and the far-field divergence angle $\theta_{\mathrm{sp}}^{(x)}$) of partially coherent annular beams both in free space and in turbulence.

The modified Von Karman spectrum is adopted as a model of the atmospheric turbulence, i.e., [3]

$$ \varPhi_{n}(\kappa) = 0.033C_{n}^{2}\bigl( \kappa^{2} + 1/L_{0}^{2} \bigr)^{ - 11/6}\exp \bigl( - \kappa^{2}/\kappa_{m}^{2} \bigr), $$

(39)

where κ _m =5.92/l ₀, l ₀ and L ₀ are the turbulence inner scale and outer scale, respectively. $C_{n}^{2}$ is the refraction index structure constant, which describes how strong the turbulence is. Letting l ₀=0.01 m and L ₀=10 m, (33) reduces to $T = 0.716\pi^{2}C_{n}^{2}$.

It is noted that the larger z _R is, the smaller the near-field spreading is. Whereas, the larger $\theta_{\mathrm{sp}}^{(x)}$ is, the larger the far-field spreading is. Figures 1(a) and (b) give the Rayleigh range z _R and the far-field divergence angle $\theta_{\mathrm{sp}}^{(x)}$ versus the refraction index structure constant $C_{n}^{2}$ for different values of the obscure ratio ε. From Fig. 1, it can be seen that z _R decreases and $\theta_{\mathrm{sp}}^{(x)}$ increases as $C_{n}^{2}$ increases, namely, turbulence results in a beam spreading both in the near field and in the far field. However, in turbulence, z _R and $\theta_{\mathrm{sp}}^{(x)}$ increase when ε increases. Namely, in turbulence, the near-field beam spreading becomes smaller as the obscure ratio increases, but this situation reverses for the far-field beam spreading. It implies that in turbulence the effect of the obscure ratio on the beam spreading is different between in the near field and in the far field, which also can be seen in Figs. 2–5, and is explained physically in Sect. 4.

Fig. 1

Rayleigh range z _R (a) and far-field divergence angle $\theta_{\mathrm{sp}}^{( x )}$ (b) versus the refraction index structure constant $C_{n}^{2}$. M=N=10, σ ₀=3 cm, w ₀=2 cm, λ=632.8 nm

Fig. 2

Rayleigh range z _R |_free (a), z _R  (b), relative Rayleigh range z _R /z _R |_free (c), far-field divergence angle $\theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}}$ (d), $\theta_{\mathrm{sp}}^{( x )}$ (e), and relative far-field divergence angle $\theta_{\mathrm{sp}}^{(x)}/ \theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}}$ (f) versus the obscure ratio ε. M=N=10, w ₀=4 cm, λ=632.8 nm

The relative Rayleigh range (i.e., z _R /z _R |_free) and the relative far-field divergence angle (i.e., $\theta_{\mathrm{sp}}^{(x)}/ \theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}}$) are adopted to characterize the effect of turbulence on the Rayleigh range and the far-field divergence angle, where z _R |_free and $\theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}}$ are those in free space. It is clear that z _R /z _R |_free≤1 and $\theta_{\mathrm{sp}}^{(x)}/\theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}} \ge 1$, and the smaller z _R /z _R |_free and larger $\theta_{\mathrm{sp}}^{(x)}/ \theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}}$ mean the more the beam spreading is affected by turbulence. For different values of the spatial correlation length σ ₀, the z _R and z _R /z _R |_free versus the obscure ratio ε are given in Figs. 2(a), (b), and (c), respectively; the $\theta_{\mathrm{sp}}^{(x)}$ and $\theta_{\mathrm{sp}}^{(x)}/ \theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}}$ versus ε are shown in Figs. 2(d), (e), and (f), respectively. In free space, for large σ ₀ (e.g., σ ₀=9 cm) z _R is not monotonic versus ε, but has a tendency to increasing; for small σ ₀ (e.g., σ ₀=1 cm, 1.5 cm, and 3 cm) z _R increases as ε increases (see Fig. 2(a)). However, in turbulence, z _R increases as ε increases for different values of σ ₀ (see Fig. 2(b), which is explained physically in Sect. 4. From Fig. 2(c), it can be seen that z _R /z _R |_free is not monotonic versus ε for large σ ₀ (e.g., σ ₀=9 cm). For small σ ₀ (e.g., σ ₀=1 cm and 1.5 cm), z _R /z _R |_free is nearly unchanged versus ε because the small σ ₀ dominates beam spreading. On the other hand, $\theta_{\mathrm{sp}}^{(x)}$ increases and $\theta_{\mathrm{sp}}^{(x)}/ \theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}}$ decreases as ε increases for different values of σ ₀ (see Fig. 2(d)–(f)). Therefore, the far-field beam spreading is less affected by turbulence with increasing ε though the far-field beam spreading becomes larger with increasing ε.

The z _R , z _R /z _R |_free, $\theta_{\mathrm{sp}}^{(x)}$ and $\theta_{\mathrm{sp}}^{(x)}/ \theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}}$ versus the spatial correlation length σ ₀, the waist width w ₀, and the wave length λ are given in Figs. 3–5, respectively. From Figs. 3–5, it can be seen that both in free space and in turbulence, z _R increases and $\theta_{\mathrm{sp}}^{(x)}$ decreases as σ ₀ and w ₀ increase (see Figs. 3(a), (c), and 4(a), (c)), and λ decreases (see Figs. 5(a) and (c)). Namely, both near-field spreading and far-field spreading of partially coherent annular beams become smaller when σ ₀ and w ₀ increase, and λ decreases. Thus, the effect of σ ₀, w ₀, and λ on the beam spreading in the near field is in agreement with that in the far field. On the other hand, z _R /z _R |_free decreases and $\theta_{\mathrm{sp}}^{(x)}/ \theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}}$ increases as σ ₀ and w ₀ increase (see Figs. 3(b), (d), and 4(b), (d)), and λ decreases (see Figs. 5(b) and (d)). It implies that partially coherent annular beams with smaller σ ₀ and w ₀, and larger λ are less affected by turbulence than those with larger σ ₀ and w ₀, and smaller λ.

Fig. 3

Rayleigh range z _R  (a), relative Rayleigh range z _R /z _R |_free (b), far-field divergence angle $\theta_{\mathrm{sp}}^{( x )}$ (c), and relative far-field divergence angle $\theta_{\mathrm{sp}}^{(x)}/ \theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}}$ (d) versus the spatial correlation length σ ₀. M=N=10, w ₀=2 cm, λ=632.8 nm

Fig. 4

Rayleigh range z _R  (a), relative Rayleigh range z _R /z _R |_free (b), far-field divergence angle $\theta_{\mathrm{sp}}^{( x )}$ (c), and relative far-field divergence angle $\theta_{\mathrm{sp}}^{(x)}/ \theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}}$ (d) versus the waist width w ₀. M=N=10, σ ₀=3 cm, λ=632.8 nm

Fig. 5

Rayleigh range z _R  (a), relative Rayleigh range z _R /z _R |_free (b), far-field divergence angle $\theta_{\mathrm{sp}}^{( x )}$ (c), and relative far-field divergence angle $\theta_{\mathrm{sp}}^{(x)}/ \theta_{\mathrm{sp}}^{(x)} |_{\mathrm{free}}$ (d) versus the wave length λ. M=N=10, σ ₀=3 cm, w ₀=4 cm

4 Physical explanations

In this section, the physical explanations for the two results obtained above are given, i.e., (i) In free space z _R is not monotonic versus ε for large σ ₀, but in turbulence z _R increases as ε increases. (ii) Both in free space and in turbulence $\theta_{\mathrm{sp}}^{(x)}$ increases as ε increases. Namely, in turbulence the beam spreading in the near field becomes smaller and the beam spreading in the far field becomes larger as the obscure ratio increases.

To simplify the mathematical formulation of average intensity, our analysis is restricted to the two-dimensional case. Letting $\boldsymbol{\rho}'_{1} = \boldsymbol{\rho}'_{2}$ in (4), the intensity of partially coherent annular beams along the x-axis in the source plane z=0 is written as

(40)

Letting ρ _d =0 in (12), and using the quadratic approximation in Rytov’s phase structure function [22], after straightforward integral calculations we obtain the average intensity I(x,0,z) of partially coherent annular beams propagating through atmospheric turbulence in the plane z>0, i.e.,

(41)

where

$$ I_{11}( x,0,z ) = \frac{k}{2z}\sum_{m = 1}^{M} \sum_{m' = 1}^{M} \alpha_{m} \alpha_{m'}\frac{w_{0}}{\sqrt{Q_{1}S_{11}}} \exp\biggl( - \frac{k^{2}x^{2}}{4z^{2}S_{11}} \biggr), $$

(42)

with

(43)

(44)

and $\eta_{0} = ( 0.545C_{n}^{2}k^{2}z )^{ - 3/5}$ being the spatial coherence radius of a spherical wave propagating in turbulence. I ₂₂(x,0,z), I ₁₂(x,0,z), and I ₂₁(x,0,z) can be obtained in the similar way.

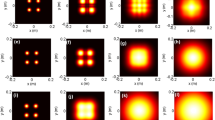
The normalized intensity distributions I(x,0,0)/I _max in the z=0 plane for different values of ε are shown in Fig. 6, where I _max is the maximum of intensity. The mean-squared width $\langle\rho_{0}^{2} \rangle$ in the z=0 plane versus ε is given in Fig. 7. It can be readily seen from Figs. 6 and 7 that $\langle\rho_{0}^{2} \rangle$ increases with increasing ε because the hole of annular beams becomes larger with increasing ε.

Fig. 6

Normalized intensity distribution I(x,0,0)/I _max. M=10, w ₀=4 cm

Fig. 7

Mean-squared width $\langle\rho_{0}^{2} \rangle$ versus the obscure ratio ε. M=N=10

It is known that the Rayleigh range is determined by the relative beam spreading comparing with the beam spreading in the waist plane z=0. The relative mean-squared width $\langle\rho^{2} \rangle / \langle\rho_{0}^{2} \rangle$ versus propagation distance z for different values of ε is plotted in Fig. 8. From Fig. 8(a), it can be seen that in free space $\langle\rho^{2} \rangle / \langle\rho_{0}^{2} \rangle$ is not monotonic versus ε. For example, for ε=0.2, 0.6 and 0.9 we have z _R =4421 m, 4172 m, and 4730 m, respectively, where relative mean-squared width $\langle\rho^{2} \rangle / \langle\rho_{0}^{2} \rangle$ reaches 2. Thus, z _R is not monotonic versus ε in free space. Figure 8(b) indicates that in turbulence ($C_{n}^{2} = 10^{ - 14}~\mathrm{m}^{ - 2/3}$) for ε=0.2, 0.6, and 0.9, we have z _R =1987 m, 2188 m, and 2458 m, respectively, where $\langle\rho^{2} \rangle / \langle\rho_{0}^{2} \rangle$ reaches 2. Therefore, in turbulence the beam spreading in the near field becomes smaller as the obscure ratio ε increases.

Fig. 8

Relative mean-squared width $\langle\rho^{2} \rangle / \langle\rho_{0}^{2} \rangle$ versus propagation distance z. M=10, σ ₀=9 cm, w ₀=4 cm, λ=632.8 nm

Figure 9 gives the normalized intensity distributions I(x,0,z)/I _max in the far field. It can be readily seen that in the far field the hollow profile of intensity distributions disappears and becomes bell-like profile for both free space and turbulence cases. It shows that both in free space (see Fig. 9(a)) and in turbulence (see Fig. 9(b)) the far-field spreading becomes larger as the obscure ratio ε increases.

Fig. 9

Normalized intensity distribution I(x,0,z)/I _max. M=10, σ ₀=2 cm, w ₀=4 cm, λ=632.8 nm, (a) z=10 km, (b) z=5 km

5 Conclusions

Based on the extended Huygens–Fresnel principle, the closed-form expressions for the Rayleigh range z _R and the far-field divergence angle $\theta_{\mathrm{sp}}^{(x)}$ of partially coherent annular beams in turbulence have been derived by using the WDF. Taking z _R and $\theta_{\mathrm{sp}}^{(x)}$ as the characteristic parameters of near-field and far-field spreading, respectively, the spreading of partially coherent annular beams propagating through atmospheric turbulence has been studied in detail. It has been found that turbulence results in beam spreading both in the near field and in the far field. The z _R decreases and $\theta_{\mathrm{sp}}^{(x)}$ increases as $C_{n}^{2}$ and λ increase, and σ ₀ and w ₀ decrease. It is known that, the larger z _R means the smaller near-field spreading, and the larger $\theta_{\mathrm{sp}}^{(x)}$ means the larger far-field spreading. Therefore, the effect of $C_{n}^{2}, \lambda, \sigma_{0}$, and w ₀ on the beam spreading in the near field is in agreement with that in the far field, which is quite different from that for the obscure ratio ε. In free space z _R is not monotonic versus ε for large σ ₀, but has a tendency to increasing. In turbulence z _R increases as ε increases. On the other hand, $\theta_{\mathrm{sp}}^{(x)}$ increases as ε increases both in free space and in turbulence. Therefore, the effect of the obscure ratio ε on the beam spreading is different between in the near field and in the far field. Namely, in turbulence the beam spreading in the near field becomes smaller and the beam spreading in the far field becomes larger as ε increases, which has been explained physically in this paper. In addition, for large σ ₀, the effect of turbulence on z _R versus ε is not monotonic; whereas the effect of turbulence on $\theta_{\mathrm{sp}}^{(x)}$ decreases monotonically as ε increases. For small σ ₀, the effect of turbulence on z _R and $\theta_{\mathrm{sp}}^{(x)}$ is nearly unchanged versus ε because the small σ ₀ dominates beam spreading. The results obtained in this paper will be useful in some applications, such as long-distance free-space optical communications and high-energy weapons, etc.

Appendices

Appendix A: Derivation of (27)

From (26) the second moment 〈x ²〉 can be rewritten as

$$ \bigl\langle x^{2} \bigr\rangle = ( E_{1} + E_{2} - E_{3} - E_{4} ) / E, $$

(45)

where

(46)

(47)

(48)

(49)

(50)

On substituting from (17) into (46), and performing the integration with respect to θ _x and θ _y in (46) in turn, we obtain

(51)

where δ denotes the Dirac delta function. To derive (51), we use the integral formula

$$ \int\exp( - \mathrm{i}sx) \,\mathrm{d}x = 2\pi\delta(s). $$

(52)

Recalling the integral formula

$$ \int f(x)\delta(x)\,\mathrm{d}x = f(0), $$

(53)

where f is an arbitrary function, and performing the integration with respect to ρ _dx and ρ _dy in (51) in turn, yields

(54)

And then, performing the integration with respect to x and y in (54) in turn, we obtain

(55)

To derive (55), we use (52) and the integral formula

$$ \int x^{2} \exp( - \mathrm{i}sx )\,\mathrm{d}x = - 2\pi \delta''( s ), $$

(56)

where δ″ is the second derivative of Dirac delta function δ.

Recalling the integral formulae (53) and

$$ \int f( x )\delta''( x )\,\mathrm{d}x = f''( 0 ), $$

(57)

where f′′ is the second derivative of an arbitrary function f, and performing the integration with respect to κ _dy and κ _dx in (55) in turn, we obtain

(58)

To obtain (58), (18) is used.

Similarly, E ₂ given by (47) can be expressed as

(59)

The E ₃ can be obtained if Q ₁, Q ₂ and R ₁ in (59) are replaced by Q ₃, Q ₄, and ε ² R ₁, and E ₄ can be obtained if Q ₁, Q ₂ and R ₁ in (59) are replaced by Q ₅, Q ₆, and ε ² R ₁.

The right-hand side of (50) is the total power of the beam at distance z, because of energy conservation; it is equal to the total power of the source, i.e.,

(60)

In view of (45), the expression for 〈x ²〉 has been derived. In a similar way, we can obtain the expression for 〈y ²〉. Consequently, the second moment 〈ρ ²〉 of partially coherent annular beams propagating through atmospheric turbulence has been derived, i.e.,

$$ \bigl\langle\rho^{2} \bigr\rangle = \bigl\langle x^{2} \bigr \rangle + \bigl\langle y^{2} \bigr\rangle = \bigl\langle \rho_{0}^{2} \bigr\rangle + \bigl\langle\theta_{0}^{2} \bigr\rangle z^{2} + ( 4 / 3 )Tz^{3}. $$

(61)

Equation (61) is just the same as (27) in the text, and $\langle\rho_{0}^{2} \rangle$ and $\langle\theta_{0}^{2} \rangle$ are defined as (29) and (30), respectively.

Appendix B: Derivation of (28)

From (26), the second moment $\langle\theta_{x}^{2} \rangle$ can be rewritten as

$$ \bigl\langle\theta_{x}^{2} \bigr\rangle = (F_{1} + F_{2} - F_{3} - F_{4})/E, $$

(62)

where

(63)

(64)

(65)

(66)

On substituting from (17) into (63), recalling the integral formulae (52) and (53), and performing the integration with respect to x,y,κ _dx , and κ _dy in (63) in turn, we obtain

(67)

Recalling the integral formulae (56) and (52), and performing the integration with respect to θ _x and θ _y in (67) in turn, yields

(68)

Recalling the integral formulae (53) and (57), and performing the integration with respect to ρ _dy and ρ _dx in (68) in turn, we obtain

(69)

To obtain (69), (18) is used.

Similarly, F ₂ given by (64) can be written as

(70)

The F ₃ can be obtained if Q ₁, Q ₂, and R ₁ in (70) are replaced by Q ₃, Q ₄, and ε ² R ₁, F ₄ can be obtained if Q ₁, Q ₂, and R ₁ in (70) are replaced by Q ₅, Q ₆, and ε ² R ₁.

Consequently, in view of (62),

$$ \bigl\langle\theta_{x}^{2} \bigr\rangle = \bigl\langle \theta_{x0}^{2} \bigr\rangle + 2Tz, $$

(71)

Equation (71) is just the same as (28) in the text, and $\langle\theta_{x0}^{2} \rangle$ is defined as (31).