1 Introduction

Firstly z-scan method was presented by M. Sheik Bahae et al. in 1989 using Gaussian decomposition method [1] and developed in 1990 [2]. After that, it has been widely used due to its appropriate properties regarding the measurement of the nonlinear optical refraction and absorption of many materials [3]. In 1994, Fresnel–Kirchhoff integral method (Fk method) was applied because of its ability to evaluate the electric field far from the exit plane of the sample [4] and later it was used in some similar studies [5, 6]. In 2010, FK method was used to calculate close-aperture z-scan [7]. One of the virtues of this method is the ability of measuring high nonlinear refractive index. This method is useful to evaluate the electric field in any point of the far field.

In this study, the real electrical field of Gaussian beam passing through a thin cubical nonlinear optical sample having both nonlinear absorption and refraction indices has been investigated. Also, Fresnel–Kirchhoff integral method has been applied as a useful tool to obtain the electric field in the far field. This expression merely could infer both the open- and close-aperture z-scan curves. After that, this method was used for TiO2 colloidal nanoparticles with the particle size ranging from 70 to 90 nm. Finally, the calculated results have been compared with the previous formulations and also a suitable curve-fitting method has been recommended to fit the experimental data to the appropriate theoretical ones.

2 Theory

Assuming a TEM 00 Gaussian beam of beam waist radius w 0 traveling in the +z direction, we could write the electric field as [8]

(1)

where E 0, \(w(z)=w_{0}\sqrt{1+\frac{z^{2}}{z_{0}^{2}}}\), \(z_{0}=\frac{kw_{0}^{2}}{2}\) and \(R(z)=z(1+\frac{z_{0}^{2}}{z^{2}})\) are the electric field at beam waist of the Gaussian beam, the beam radius at z, the diffraction length of the beam and the radius of curvature of the wavefront at z, respectively. The beam waist (focal point) is located at z=0. The parameters w and R of a Gaussian beam change during the propagation of the beam along the z-axis.

The equations describing the propagation of the optical field inside the nonlinear material take the form:

$$ \frac{d\Delta\varphi}{dz'}=-\Delta n(I)k$$
(2)

and

$$ \frac{dI}{dz'}=-\alpha(I)I.$$
(3)

It can be considered that a Gaussian beam passes through a thin third-order nonlinear optical sample with nonlinear refraction γ (MKS) located at z [1, 2]. In the case of a cubic nonlinearity and negligible nonlinear absorption, (2) and (3) can be solved to give the phase shift Δφ at the exit surface of the sample which simply follows the radial variation of the incident irradiance at a given position of the sample z. Thus,

$$ \Delta\varphi(z,r)=\frac{\Delta\varphi_0}{1+(\frac{z}{z_0})^2}\exp\bigl(-2r^2/w^2(z)\bigr)$$
(4)

where Δφ 0 is defined as the on-axis nonlinear phase shift at the beam focus, given by

$$ \Delta\varphi_0=k\gamma I_0L_{\mathrm{eff}}=k\Delta n L_{\mathrm{eff}}.$$
(5)

Here z, \(L_{\mathrm{eff}}=\frac{(1-e^{-\alpha L})}{\alpha}\), α, L and Δn=γI 0 are the distance between the sample and the beam waist, the effective length of the sample, the linear absorption coefficient, the sample thickness and the refraction change, respectively. The sample can be assumed as a thin sample by the thickness (L) significantly less than z 0.

Using the Fresnel–Kirchhoff diffraction theory, electric field at the exit plane of the sample is obtained as [6, 7]

(6)

The electric field in far field is obtained by means of free-space Fresnel–Kirchhoff diffraction integral at the Fraunhofer approximation. For a radial symmetric field, it equals a Hankell of Fourier–Bessel transform of the field, namely:

$$ E(\rho,z)=\frac{1}{i\lambda D}\int_0^{\infty}J_0(k\theta r)E_e(r,z)2\pi r\,dr$$
(7)

where J 0(x), θ and ρ are the zero-order Bessel function of the first kind, the far-field diffraction angle and the radial coordinate in the far-field observation plane, respectively. In the paraxial approximation, distance from the exit plane of the medium to the far-field observation plane (D) is related to the radial coordinate and the diffraction angle by ρ=Dθ. Therefore, we can write:

(8)

Using (8), we can write distribution pattern of irradiance as

(9)

where

$$ I'=\frac{cn_0\varepsilon_0}{2}\times\biggl(\frac{1}{\lambda D}\biggr)^2\times(2\pi E_0)^2\biggl(\frac{w_0}{w(z)}\biggr)^2e^{-\alpha L}$$
(10)

The magnitude of E 0 can be calculated simply through \(\frac{2}{w_{0}}\sqrt{\frac{P_{0}}{c\varepsilon_{0}n_{0}\pi}}\), where P 0 is the laser output power.

This formulation is useful when the absorption effect is reflected from close-aperture curve or at least the nonlinear absorption is considered neglected and there is almost a pure close-aperture curve. But when the nonlinear absorption is considered, the close-aperture curve includes both the nonlinear absorption and refraction effects. Thus, for a more real case, (2) and (3) will be reexamined after the following substitution [2]:

$$ \alpha(I)=\alpha+\beta I$$
(11)

This yields the irradiance distribution and phase shift of the beam at the exit surface of the sample as:

$$ I_e(z,r)=\frac{I(z,r)e^{-\alpha L}}{1+q(z,r)}$$
(12)

and

$$ \Delta\varphi(z,r)=\frac{k\gamma}{\beta}\ln\bigl(1+q(z,r)\bigr)$$
(13)

where q(z,r)=βI(z,r)L eff. Combining (12) and (13), the complex field at the exit surface of the sample can be obtained as

$$ E_e=E(z,r)e^{\frac{-\alpha L}{2}}(1+q)^{(-\frac{ik\gamma}{\beta}-\frac{1}{2})}$$
(14)

By using (7):

(15)

and

(16)

where I′ had been defined in (10). It is the most perfect relation for electric field of a Gaussian beam passing through a cubic nonlinear sample with some virtues. This technique is based on the FK method and could evaluate the passing electric far field. Furthermore, it is suitable for high optical nonlinearity cases which may include diffraction ring patterns [7]. The main virtue that distinguishes this method from other formulations is that the effect of all linear and nonlinear optical coefficients of the sample is presented in one formulation simultaneously.

Equation (16) could be utilized for simulation of both the open- and close-aperture z-scan curves, perfectly.

3 Experimental results and discussion

In the close-aperture z-scan study, a finite aperture of linear transmittance \(S=1-\exp(-\frac{2r_{a}^{2}}{w_{a}^{2}})\) (r a and w a being the aperture radius and the beam radius at the aperture plane, respectively) has been assumed which is placed at the far field so that the center of the aperture is located at the beam center. The transmitted power through the aperture can be simply calculated by

$$ P(z)=\int_0^{r_a}I(\rho,z)2\pi\rho \,dp$$
(17)

In open-aperture setup it is sufficient when r a →∞. The normalized transmittance could be calculated as well:

$$ T_{\mathrm{norm}}(z)=\frac{P(z,\Delta\varphi_0)}{P(z,\Delta\varphi_0=0)}$$
(18)

Equations 17 and 18 could be used for I(ρ,z) obtained from either (9) or (16) and could yield theoretical curves of open- (with r a →∞) and close-aperture (with a finite r a ) z-scan curves.

Now a suitable curve-fitting method to fit normalized experimental transmittance curves (\(T_{\mathrm{norm}}^{\exp}(z)\)) and theoretical ones (\(T_{\mathrm{norm}}^{\mathrm{the}}(z)\)) could be presented. For example, to find the best value of γ (β is considered known), the following procedures should be considered. First, \(T_{\mathrm{norm}}^{\exp}(z)\) is represented to the system as a one-dimensional array. Then, γ can be estimated in the range of γ min to γ max. After that, γ min is put in (16). Next, by using (17), (18), \(T_{\mathrm{norm}}^{\mathrm{the}}(z)\) can be obtained. After that, the residual sum of squares (SSE) is used) [9]:

$$ \mathit{SSE}=\sum_z\bigl[T_{\mathrm{norm}}^{\exp}(z)-T_{\mathrm{norm}}^{\mathrm{the}}(z)\bigr]^2$$
(19)

This process is repeated for the next values of γ. Finally, the minimum value of SSE gives the best value of γ. Replacing this value in (16)–(18) gives the best fitted curve. This process could be performed in other similar fitting processes.

In this study, a simple chemical procedure is used for the synthesis of TiO2 nanoparticles. At first, titanium isopropoxide Ti{OCH(CH3)2}4 solution (Merck, Purity 99 %) is dissolved in a mixture of methanol and ethanol (absolute grade) with molar ratio (1:1:10). Then, the solvent is stirred at 70 °C for 6 hours. Double-distilled water is drop-wise added into the solution at this temperature. The formation of TiO2 nanoparticles can be indicated by the color change of the solvent. After that, the obtained precipitate powder is filtered and washed several times with double-distilled water and ethanol to remove by-products. Finally, the sample is dried at 200 °C for 4 hours.

The origins of optical nonlinearities in materials and nanoparticles are different [10, 11]. The optical nonlinearity of aqua samples applied with continued wave laser beam with low intensity irradiation is usually contributed from two mechanisms: thermo-optical (thermal) effect and re-orientation of Kerr effect in liquids [11]. In thermo-optical effect, as the energy of a collection of particles or molecules increases, their macroscopic optical properties will be altered. For example, the refractive index reduces because of the thermal expansion and density decrease. When there is a linear relationship between laser irradiance and the refractive index, effective third-order nonlinearity will result. There is a relaxation time for this mechanism such that after it the system reaches the steady state and becomes time-independent [12]. In these conditions, all the time-independent relations that have been offered here are valid. The re-orientation of Kerr effect involves transitions between rotational energy level of a particle or molecule. It is non-resonant and therefore associated with the real part of susceptibility. This mechanism occurs in molecules or particles with different polarizabilities along their principle axes. Colloidal solution of nanoparticles in liquid solutions could exhibit either each of these behaviors or both of them. But for spherical nanoparticles such as TiO2 nanoparticles with considerable absorption coefficient, thermal effect is considerable.

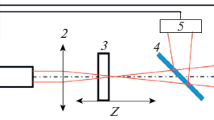
In this experiment, a colloidal solution containing 2.36 g/l of TiO2 nanoparticles in Ethanol (Merck, purity 99.6 %) was used. The average diameter of nanoparticles was 70–90 nm (Fig. 1). The solution was poured in a 1-mm quartz cell and radiated with a 48-mW He–Ne laser beam passing through the lens with wavelength of 633 nm, at room temperature. The waist of the beam at focus (z=0) became 30 μm (z 0=0.446 cm), while the light intensity was about 3397 W/cm2. In the close-aperture setup, an aperture with S=0.087 linear transition was used. The linear absorption of the sample was about α=1 cm−1.

Fig. 1
figure 1figure 1

(a) SEM image of TiO2 nanoparticles; (b) EDX analysis of TiO2 nanoparticles (98 % purity)

Full size image

At first, the normalized experimental open-aperture curve was fitted with the theoretical curve and the nonlinear absorption coefficient was evaluated. The transmitted power P e (z) was obtained by integrating (12) at z over r as follows:

$$ P_e(z)=P_ie^{-\alpha L}\frac{\ln[1+q(z,r=0)]}{q(z,r=0)}$$
(20)

where P i and P e (z) are the initial power to and the exit power from the sample, respectively.

Using the represented curve-fitting method with (20), β was calculated as 1.5×10−4 cm/W (Fig. 2). Substituting the β value in (20), the theoretical curve was obtained (Fig. 3b).

Fig. 2
figure 2

Calculated SSE curve (using (20)) versus β

Full size image
Fig. 3
figure 3

(a) Experimental data of open aperture z-scan; (b) theoretical fitted curve using (20); (c) theoretical fitted curve using (16)

Full size image

To evaluate the nonlinear refraction coefficient (γ), the β value was put in (16) and fitted by experimental results. Consequently, γ=−1.44×10−8 W/cm2 was obtained (Δφ 0=−0.464) (Fig. 4). Experimental and theoretical close-aperture curves are presented in Fig. 5.

Fig. 4
figure 4

Calculated SSE curve (using (16)) versus γ

Full size image
Fig. 5
figure 5

(a) Experimental close-aperture z-scan data of TiO2 nanoparticles; (b) fitted theoretical curve using (16)

Full size image

In the next step, these calculated results from (16) were compared with results obtained from (9). Dividing the normalized close-aperture curve having nonlinear absorption by the normalized open-aperture curve reflects the effect of nonlinear absorption and gives pure close-aperture curve (Fig. 6c). A close-aperture curve was obtained by putting γ=−1.44×10−8 W/cm2 in (9). Results are shown in Fig. 6(d). As can be observed, both obtained results are similar. This indicates that both of the methods (dividing the experimental normalized close-aperture curve by the open-aperture curve using (9), and application of (16) for experimental close-aperture curve) give the same result.

Fig. 6
figure 6

(a) Theoretical real close-aperture curve using (16); (b) theoretical open-aperture curve using (20); (c) pure close-aperture curve obtained by dividing curve (a) by (b); (d) pure close-aperture curve using (9)

Full size image

Not only is (16) useful to evaluate nonlinear refraction index but also it could be utilized to interpret the open-aperture curves. The open curve can be obtained by using this equation and substituting the above nonlinear absorption and refraction indices for an open aperture (S=0.99) replaced at z=55 cm (Fig. 3c). This curve is similar to the case when the power is instantly detected at the exit surface of the sample (Fig. 3b).

In the case of open-aperture z-scan, some researchers prefer to detect the transmitted power in far field due to avoid beam reflectance in the sample from the surface of the detector. If the feedback of the passing beam retransmits through the sample, lateral phenomena such as resonant effect and optical bistability effect would be inevitable [11]. This is why the surface of the detector is placed perpendicularly to the beam axis in the far field with a little invert angle in such a way that the reflected beam does not return through the sample.

It is of note that all the measurements have been performed in the steady-state conditions after passing the relaxation time.

4 Conclusions

Here, a diffraction model of nonlinear optical media interacting with a Gaussian beam by both the nonlinear refraction and absorption has been suggested based on Fresnel–Kirchhoff diffraction theory. This theory could explain the z-scan phenomenon in a new way. Numerical computations indicate that the shapes of the experimental z-scan curves could greatly be explained by this method. Because the exact nonlinear optical indices could be obtained, a proper curve-fitting method has been offered. By using this new method the calculated curves obtained from z-scan experiment of TiO2 nanoparticles colloidal solution in ethanol host with the particle size ranging from 70 to 90 nm have been analyzed. Also, the accuracy of this new method has been investigated by comparing the calculated results with the previous methods.