1 Introduction

During the past few years, the precision position measurement of an atom has been the subject of many recent studies because of its potential wide applications in trapping of neutral atoms, laser cooling [1], atom nano-lithography [2, 3], Bose–Einstein condensation [4, 5], and measurement of the center-of-mass wave function of moving atoms [6, 7]. Earlier studies for localization include the measurement of the phase shift of either the standing wave [8, 9] or the atomic dipole [10] due to the interaction of the atom with the standing-wave field, the entanglement between the atom’s position and its internal states [11], resonance imaging methods [12], etc.

Recently, it has been shown that quantum coherence and interference can give rise to some interesting phenomena, such as electromagnetically induced transparency [13, 14], spontaneously generated coherence [15, 16], multi-wave mixing [17, 18], enhancing Kerr non-linearity [19, 20], optical soliton [21, 22], and so on. Based on atomic coherence and quantum interference, many schemes have been proposed for one-dimensional (1D) atom localization. For example, Herkommer, Schleich, and Zubairy proposed a scheme in which the Autler–Townes spontaneous spectrum is used [23]. Qamar et al. suggested atom localization based on resonance fluorescence in a two-level system driven by a strong standing-wave field [24], and later Paspalakis and Knight proposed a quantum-interference-induced sub-wavelength atomic localization in a three-level Λ-type atom interacting with a classical standing-wave field and a weak probe laser field, and they found that the atomic position with high precision can be achieved via the measurement of the upper-state population of the Λ-type atom as the atom moves in the standing-wave field [25]. More recently, in a four-level atomic system with a closed-loop configuration, Zubairy and coworkers again showed that in two 1D atom localization schemes [26, 27] the phase of the standing-wave driving field played an important role in reducing the number of localization peaks from the usual four to two, leading to sub-half-wavelength localization. At the same time, Gong et al. presented two schemes [28, 29] based on double-dark resonance effects and demonstrated that the atom can be localized at the nodes of the standing-wave field, and the detecting probability can be increased to 1/2. Interestingly, instead of the measurement of the population in the excited state, the detection of the population in the ground state coupled to the standing-wave field leads to only two localization peaks in a unit wavelength region. This was shown by Agarwal and Kapale [30], who put emphasis on the momentum distribution and the role of the ratio of the intensities of the coupling and probe fields. Of course, some relative schemes for realizing 1D atom localization are also studied [31–35]. On the other hand, two-dimensional (2D) atom localization has also been extensively studied in the multilevel atomic system. The studies show that one can control 2D atom localization via the measurement of the upper-state or any ground-state population [36], via interacting double-dark resonances [37], via controlled spontaneous emission [38–41], or via the probe absorption spectrum [42–44].

In this work, we investigate the 2D atom localization behaviors in a four-level atomic system via controlled spontaneous emission in a single decay channel. It is found that the precision and resolution of the 2D atom localization can be significantly improved due to the quantum interference effects. Our work is mainly based on the [36–44], however, which is drastically different from those works. The major differences are obtained as follows. (i) The 2D atom localization patterns reveal that the maximal probability of finding an atom within the sub-half-wavelength domain of the standing waves can reach unity, which is increased by a factor of 2 or 4 compared with the previous proposed schemes for realizing 2D atom localization via controlled spontaneous emission in a single decay channel [38, 39] or from two coherent decay channels [40]. (ii) A few works have discussed efficient 2D atom localization behaviors via phase-dependent probe absorption spectrum [42, 43] or via phase-dependent spontaneous emission spectrum from two coherent decay channels [41], however, four or five fields are used to controlling the 2D atom localization behaviors. It is well known that the external fields are less convenient for experimental realization, which may be the serious reason to sophisticate the experimental setup. Unlike those works, only three fields are applied in present scheme, which make our scheme much more convenient in experimental realization. (iii) Because of the spatial-position-dependent atom-field interaction, the spontaneously emitted photon carries information about the position probability distribution. As a result, the atom can be localized when the spontaneously emitted photon is detected. The schemes [40, 41] for 2D atom localization via two spontaneous emission channels may bring some difficulties to photo-detection, while our work is also different from those investigations as we investigate the 2D atom localization behaviors via spontaneous emission in a single decay channel. This advantage also makes the present scheme much easier to carry out in experimental arrangements. Our paper is organized as follows: In Sect. 2, we present the theoretical model and establish the corresponding equations. The numerical results are shown in Sect. 3. In Sect. 4, some simple conclusions are given.

2 Model and dynamic equations

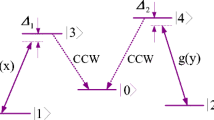
We consider the four-level atomic system as shown in Fig. 1. This system has one ground level |1〉 and three excited levels |2〉, |3〉, and |4〉. A probe field with Rabi frequency 2Ω p (frequency ω p ) is applied to the transition |2〉↔|1〉, while the transition |3〉↔|2〉 is driven by a composition of two orthogonal standing-wave fields S xy with position-dependent Rabi frequency 2Ω(x,y)=2Ω xy [sin(kx)+sin(ky)] (frequency ω xy ). The transition from the level |3〉 to the level |4〉 is assumed to be coupled by the vacuum modes in the free space.

Fig. 1
figure 1

Schematic diagram of a four-level atomic system

Full size image

Under the Hamiltonian in the Raman–Nath, the electric-dipole and rotating-wave approximations, the interaction Hamiltonian for the system is (ħ=1)

(1)

where Δ p =ω 2−ω p , Δ xy =ω 32−ω xy , and δ k =ω 34−ω k are the detunings of the probe field, the standing-wave fields S xy , and the vacuum modes, respectively. 2Ω xy =E xy μ 32/ħ and 2Ω p =E p μ 21/ħ are the Rabi frequencies for the relevant laser transitions. μ mn (m,n=1,2,3) are the dipole matrix elements and E j (j=p,xy) are the slowly varying amplitudes of the optical fields. b k is the annihilation operator for the kth vacuum mode with frequency ω k . g k stands for the coupling constant between the kth vacuum mode and the atomic transition |3〉↔|4〉.

The dynamics of this system can be described by using the probability amplitude equations. Then the wave function of the system at time t can be expressed in terms of the state vectors as

(2)

where the probability amplitude \(A_{i,0_{k}}(x,y;t)\) (i=1–3) represents the state of atom at time t when there is no spontaneously emitted photon in the kth vacuum mode, \(A_{4,1_{k}}(x,y;t)\) is the probability amplitude that the atom is in level |4〉 with one photon emitted spontaneously in the kth vacuum mode, and f(x,y) is the center-of-mass wave function of the atom.

The atom localization in our scheme is based on the fact that the spontaneously emitted photon carries information about the position of atom in the x–y plane as a result of the spatial position-dependent atom-field interaction. When we have detected at time t a spontaneously emitted photon in the vacuum mode of wave vector k, the atom is in its internal state |4〉 and the state vector of the system, after making appropriate projection over |Ψ(t)〉, is reduced to

(3)

where ℕ is a normalization factor. Thus, the conditional position probability distribution, i.e. the probability of finding the atom in the (x,y) position at time t is

(4)

which follows from the probability amplitude \(A_{4,1_{k}}(x,y;t)\).

Making use of the Schrödinger equation in the interaction picture, the dynamical equations for the atomic probability amplitudes are given by

(5a)
(5b)
(5c)
(5d)

where Γ=2π|g k |2 D(ω k ) is the spontaneous decay rate from level |3〉 to level |4〉 and D(ω k ) is the density of mode at frequency ω k in the vacuum.

Carrying out the Laplace transformations \(\tilde{A}(x,y;s)=\int_{0}^{\infty }e^{-st}A(x,y;t)\,dt\) (s is the time Laplace transform variable) for (5a)–(5d), we have the results

(6a)
(6b)
(6c)
(6d)

where \(f_{3}=\Delta_{p}+\Delta_{xy}-i\frac{\varGamma }{2}\) and f 4=Δ p +Δ xy −δ k . A i (0) (i=1–3) represents the probability amplitude at the initial time t=0. Finally, the conditional probability of finding the atom in level |4〉 with a spontaneously emitted photon of frequency ω k in the vacuum mode k is then given by

(7)

As the center-of-mass wave function of the atom f(x,y) is assumed to be nearly constant over many wavelengths of the standing-wave fields, the conditional position probability distribution W(x,y,;t→∞|4,1 k ) is determined by the filter function defined as

$$ F(x,y)_{2D}=\biggl \vert \frac{\varOmega _{p}\varOmega (x,y)A_{1}(0)+f_{4}\varOmega (x,y)A_{2}(0)+[f_{4}(f_{4}-\Delta_{p})-\vert \varOmega _{p}\vert ^{2}]A_{3}(0)}{f_{4}(f_{4}-\Delta_{p})(f_{4}-f_{3})-\vert \varOmega _{p}\vert ^{2}(f_{4}-f_{3})-\vert \varOmega _{c}\vert ^{2}f_{4}}\biggr \vert ^{2}.$$
(8)

3 Results and discussion

In this section, we analyze the conditional position probability distribution of the atom via a few numerical calculations based on the filter function F(x,y)2D in (8), and then address how the system parameters can be used to achieve 2D atom localization by controlled spontaneous emission. In the following numerical calculations we chose are set in units of constant γ, which should be in the order of MHz for rubidium or sodium atoms.

Filter function F(x,y)2D versus the positions (kx,ky)=(−π≤kx≤π, −π≤ky≤π) for different values of the detuning of spontaneously emitted photon is plotted in Fig. 2. As can be seen, the conditional position probability distribution depends strongly on the detuning of spontaneously emitted photon. For the case δ k =5γ, the peak maxima, which represent the most probable positions of the atom, are distributed in all four different quadrants of the x–y plane [see Fig. 2(a)]. When the detuning is tuned to δ k =10γ, the atom is mainly localized in quadrants I and III, and the peaks of the F(x,y)2D show crater-like patterns [see Fig. 2(b)]. On the condition of δ k =15γ, the localization peaks display a small-caliber crater-like pattern and a large-caliber crater-like pattern with different localization precision in quadrants I and III, and the atom localized at these circles [see Fig. 2(c)]. With the increase of the detuning to further higher values [i.e. δ k =20γ in Fig. 2(d)], the spatial distribution of the atom localization exhibits a spike-like pattern. From the above discussions, it is obvious that there is a strong correlation between the frequency detuning of the spontaneously emitted photon and the position of the atom. The measurement of a particular frequency corresponds to the localization of the atom within a sub-half-wavelength region of the standing-wave field.

Fig. 2
figure 2

Filter function F(x,y)2D versus positions (kx,ky)=(−π≤kx≤π, −π≤ky≤π) for different values of δ k . (a) δ k =5γ; (b) δ k =10γ; (c) δ k =15γ; and (d) δ k =20γ. The other parameters are Δ p =Δ xy =0, \(A_{1}(0)=A_{3}(0)=1/\sqrt{2}\), A 2(0)=0, Ω xy =10γ, Ω p =γ, and Γ=3γ

Full size image

In Fig. 3, we study the effect of the intensity of the probe field on the spatial distributions of the 2D atom localization. For a small intensity of the probe field, i.e. Ω p =2γ, the filter function shows two spike-like patterns in quadrants I and III [see Fig. 3(a)]. When the probe field is adjusted to Ω p =4γ, the two spike-like patterns become two crater-like patterns, as shown in Fig. 3(b). With a further increase of Ω p (Ω p =6γ), the spatial distributions of the filter function do not change, but the caliber of every crater-like pattern becomes wider. Simultaneously, the height of the small crater-like pattern in quadrant III becomes lower [see Fig. 3(c)]. However, when the intensity of the probe field reaches at an appropriate value [i.e. Ω p =10γ, in Fig. 3(d)], the localization peak in quadrant III has completely disappeared. In such a case, we can obtain a high-precision and high-resolution 2D atom localization, which can be attributed to the quantum interference effect induced by the probe field.

Fig. 3
figure 3

Filter function F(x,y)2D versus positions (kx,ky)=(−π≤kx≤π, −π≤ky≤π) for different intensity of the probe field. (a) Ω p =2γ; (b) Ω p =4γ; (c) Ω p =6γ; and (d) Ω p =10γ. The other parameters are Δ p =Δ xy =0, \(A_{1}(0)=A_{3}(0)=1/\sqrt{2}\), A 2(0)=0, Ω xy =10γ, δ k =20γ, and Γ=3γ

Full size image

Finally, two interesting ways for realizing 100 % probability of finding an atom within the sub-wavelength domain of the standing waves are exhibited in Figs. 4 and 5, respectively. From Figs. 4(a)–4(c), one can find that via adjusting the detunings of the probe and standing-wave fields, the filter function F(x,y)2D displays a crater-like pattern and the position of the localization peak changes obviously. Interestingly, when Δ p =15γ and Δ xy =−2γ, spatial distribution of the filter function shows a spike-like pattern in quadrant I. In such a condition, the probability of finding the atom in one period of the standing-wave fields is increased to 1, that is to say, the atom can be localized at a particular position and the 2D atom localization is indeed achieved efficiently. Therefore, the probability of finding the atom at a particular position is increased by a factor of 2 or 4 compared with the previous proposed schemes [36–40, 44]. The influences of the initial probability amplitudes on the spatial distributions of the 2D atom localization are depicted in Fig. 5. Clearly, the spatial distributions of the filter function F(x,y)2D are very sensitive to the initial probability amplitudes. The 100 % probability of finding an atom within the sub-half-wavelength domain of the standing waves can also be achieved for the case \(A_{2}(0)=A_{3}(0)=1/\sqrt{2}\) and A 1(0)=0 [see Fig. 5(d)]. According to the above discussions, one can realize that the detunings of the probe and standing-wave fields and initial probability amplitudes play important roles in the precision and spatial distribution of 2D atom localization.

Fig. 4
figure 4

Filter function F(x,y)2D versus positions (kx,ky)=(−π≤kx≤π, −π≤ky≤π) for different values of Δ p and Δ xy . (a) Δ p =15γ, Δ xy =0; (b) Δ p =0, Δ xy =10γ; (c) Δ p =15γ, Δ xy =10γ; and (d) Δ p =15γ, Δ xy =−2γ. The other parameters are Ω p =4γ, \(A_{1}(0)=A_{3}(0)=1/\sqrt{2}\), A 2(0)=0, Ω xy =10γ, δ k =20γ, and Γ=3γ

Full size image
Fig. 5
figure 5

Filter function F(x,y)2D versus positions (kx,ky)=(−π≤kx≤π, −π≤ky≤π) for different values of initial probability amplitudes. (a) A 1(0)=1, A 2(0)=A 3(0)=0; (b) \(A_{1}(0)=A_{3}(0)=1/\sqrt{2}\), A 2(0)=0; (c) \(A_{1}(0)=A_{2}(0)=1/\sqrt{2}\), A 3(0)=0; and (d) \(A_{2}(0)=A_{3}(0)=1/\sqrt{2}\), A 1(0)=0. The other parameters are Δ p =Δ xy =0, δ k =20γ, Ω xy =10γ, Ω p =2γ, and Γ=3γ

Full size image

Before concluding, let us briefly discuss the possible experimental realization of our proposed scheme for the present study. We consider, for instance, the cold atoms 87Rb (nuclear spin I=3/2) on the 5S-5P-5D transitions as a possible candidate [45]. The experimental system for this atomic scheme can be realized by the 87Rb atom with |5S 1/2,F=2〉, |5S 1/2,F=2〉, |5P 3/2,F=3〉, |5D 5/2,F=4〉, and |6P 3/2,F=3〉 behaving the |1〉, |2〉, |3〉, and |4〉 state labels, respectively. In this scheme, the atom, also moving in the z-direction, passes through the intersectant region of two orthogonal standing-wave laser fields, which are respectively aligned along the x and the y axes. The weak probe field propagates along the positive z direction. The composition of two orthogonal standing waves can be obtained by combining four identical beams, where a pair of identical beams propagate along the positive and negative x directions in the x–y plane while another pair of identical beams propagate along the positive and negative y directions in the x–y plane. The probe and control beams can be obtained from external cavity diode lasers. According to the above conditions, our scheme may be realized via the experiment proposed in [35].

4 Conclusions

To sum up, we have investigated the two-dimensional atom localization behaviors in a four-level atomic system via controlled spontaneous emission in a single decay channel. It is found that the precision and resolution of the 2D atom localization can be significantly improved due to the quantum interference effects. More importantly, the 2D atom localization patterns reveal that the maximal probability of finding an atom within the sub-half-wavelength domain of the standing waves can reach unity, which is increased by a factor of 2 or 4 compared with the previous proposed schemes [36–40, 44]. As a result, our scheme may be helpful in laser cooling or the atom nano-lithography via atom localization [46].