1 Introduction

The accelerating Airy beams are drawing much interest because they represent a novel class of nondiffracting field [1, 2] and because of their tremendous application potential in fields such as optical manipulation, filamentation, and nonlinear optics [3–8]. However, the Airy function is an oscillatory function and the Airy beams consist of decaying side lobes, and these side lobes may create deleterious effects for some applications [9, 10].

On the other hand, the fractional Fourier transform (FrFT) has been introduced into optics by Mendlovic and Ozaktas [11, 12] and Lohmann [13] in 1993. Since then, the FrFT has been found important applications in signal processing, optical image encryption, beam shaping and beam analysis [14–18]. Recently, the FrFT of various beams has been widely investigated, such as the flattened Gaussian beams [19], elliptical Gaussian beams [20], partially coherent Gaussian Schell beams [21, 22], a hollow Gaussian beam [23, 24], Lorentz–Gauss beams [25], and Ince–Gauss beams [26, 27]. However, to the best of our knowledge, the propagation characteristics of the Airy beams have not been studied through an ABCD system [28] with a hard-edge rectangular aperture.

In this paper, by expanding a hard-edged aperture function into a finite sum of complex Gaussian functions, we obtain the analytical formula for the propagation of the Airy beams in free space and through the FrFT system. According to the derived formulas, the propagation properties of the Airy beams in free space and through the FrFT plane with a hard-edged aperture are illustrated numerically. The influences of the different parameters on the normalized intensity distribution are also discussed.

2 Propagation of Airy beams through a hard-edge rectangular aperture

The electric field distribution of the Airy beams at the z=0 plane reads as

(1)

where E 0 is a constant, w 1 and w 2 are arbitrary transverse scales, Ai(⋅) is the Airy function, 0≤a<1 and 0≤b<1 are decay parameters.

Assuming a hard-edge rectangular aperture is located at the z=0 plane, the corresponding window function

$$ H(x,y) =\begin{cases}1&|x| \leq a_{1},\ |y| \leq b_{1}\\0&\mbox{else}\end{cases}$$
(2)

is expanded into a finite sum of complex Gaussian functions [29–31],

$$ H(x,y) =\sum_{j=1}^{N} \sum _{l=1}^{N}B_{l}B_{j}\exp\biggl(-\frac{C_{l} x^{2}}{a_{1}^{2}} \biggr)\exp\biggl(-\frac {C_{j} y^{2}}{b_{1}^{2}} \biggr),$$
(3)

where a 1 and b 1 are respectively the width and the height of the rectangular aperture, B l , B j , C l , C j are the coefficients, and N is the number of complex Gaussian terms and they can be found in Table 1 of [29].

The propagation of the Airy beams through a paraxial ABCD system with a hard-edge aperture satisfies the Collins integral [28]

(4)

where an unimportant phase factor has been negligible in (4).

Substituting (1) and (3) into (4), one can obtain

(5)

where \(c_{j}=C_{j}/b_{1}^{2}+i k A/(2B), c_{l}=C_{l}/a_{1}^{2}+i k A/(2B)\).

For unapertured case, i.e., a 1→∞ and b 1→∞, (5) can be changed into

(6)

In free space, A=1, B=z, C=0, D=1, (5) and (6) are the expressions for the propagation of the Airy beams with and without a hard-edge aperture in free space, respectively, and (6) is consistent with (3) of [32].

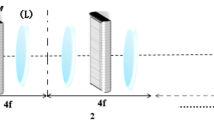
The Lohmann I optical system and the Lohmann II optical system are equivalent to perform the FrFT, as is shown in Fig. 1. f is the standard focal length. The focus of the lens is f/sinϕ, ϕ=pπ/2 and p is the order of FrFT. The distance between the input and output planes is 2d=2ftan(ϕ/2) in Fig. 1a, d′=fsinϕ in Fig. 1b. In the Lohmann I optical system and the Lohmann II optical system, A=cosϕ, B=fsinϕ, C=−sinϕ/f, D=cosϕ, (5) and (6) are analytical expressions for the output Airy beam distribution with and without a hard-edge aperture in the FrFT plane, respectively. It is not difficult to see from (5) and (6) that the variation of the normalized intensity distribution with the fractional order p is periodic, and the period is p=4. When p=1, the FrFT plane becomes the ordinary Fourier transform plane.

Fig. 1
figure 1

(Color online) Two kinds of optical transforming systems for performing FrFT: (a) one lens system; (b) two lenses system

Full size image

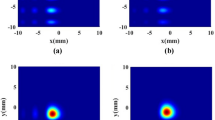
Figure 2 shows the normalized intensity distribution of the Airy beams through a hard-edge rectangular aperture in free space for Figs. 2(a)–2(c) the aperture sizes a 1=b 1=2 mm, and Figs. 2(d)–2(f) the aperture sizes a 1=b 1=10 mm, and Figs. 2(g)–2(i) the aperture sizes a 1=b 1=100 mm. The different columns represent the different propagation distances given in the top of the figure. The parameters are chosen λ=500 nm, w 1=w 2=1 mm, a=b=0.01. It is not difficult to find in Figs. 2(a)–2(c) that the side lobes of the Airy beams are truncated by the aperture and only the central lobe exists when the aperture sizes a 1=b 1=2 mm, and the central lobe still exhibits its most exotic features, i.e., its trend to freely accelerate, self bend, and diffract very slowly. Figures 2(d)–2(f) presents that the second side lobes and the central lobe of the Airy beams exist when the aperture sizes a 1=b 1=10 mm, and the Airy beams still exhibit their most exotic features, i.e., theirs trend to freely accelerate, self-bend, and almost diffract-free. When the aperture sizes approach to infinity, the whole Airy beams keep well; their features are the same as those in [1, 2]. Therefore, by choice the proper aperture size, the side lobes of the Airy beams can be controlled.

Fig. 2
figure 2

(Color online) Normalized intensity distribution of the airy beams through a hard-edge rectangular aperture in free space for (a–c) the aperture sizes a 1=b 1=2 mm, and (d–f) the aperture sizes a 1=b 1=10 mm, and (g–i) the aperture sizes a 1=b 1=100 mm. The different columns represent the different propagation distances given in the top of the figure. The parameters are chosen λ=500 nm, w 1=w 2=1 mm, a=b=0.01

Full size image

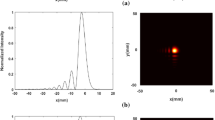
Figures 3, 4, 5, 6 present the normalized intensity distribution of the Airy beams through a hard-edge rectangular aperture in the FrFT plane, where the different fractional orders are given in the top of the figure. According to Figs. 3–6, it is easy to see that the beam shape in the FrFT plane remains invariant as 4q+1≤p≤4q+3 (q=0,1,2,…), 4q≤p≤4q+1 and 4q+3≤p≤4q+4, while the beam rotates 180∘ as p changes from 2q≤p≤2q+1 to 2q+1<p≤2q+2. When p=2q+1, the beam spot reaches minimum size, while for p=2q, the beam spot reaches maximum size. Therefore, the size of the beam spot in the FrFT plane can be controlled by choice of the fractional order p.

Fig. 3
figure 3

(Color online) Normalized intensity distribution of the airy beams through a hard-edge rectangular aperture in the FrFT plane, where the different fractional orders are given in the top of the figure. The parameters are the same as those in Fig. 2 except the fractional orders

Full size image
Fig. 4
figure 4

(Color online) All are the same as those in Fig. 3 except the fractional orders

Full size image
Fig. 5
figure 5

(Color online) All are the same as those in Fig. 3 except the fractional orders

Full size image
Fig. 6
figure 6

(Color online) All are the same as those in Fig. 3 except the fractional orders

Full size image

3 Conclusions

In conclusion, the propagation of the Airy beams through a hard-edge rectangular aperture has been investigated, and the analytical expressions for the Airy beams passing through free space and a FrFT system are derived. According to the derived formula, the normalized intensity distribution of the Airy beams in free space and in the FrFT plane with a hard-edge rectangular aperture is graphically illustrated with numerical examples, and the influences of the different parameters on the normalized intensity distribution are also discussed. The side lobes of the Airy beams can be controlled by choosing the proper aperture size. The beam spot size of the Airy beams in the FrFT plane can be controlled by the fractional order p and the aperture size.