1 Introduction

The Wigner distribution function (WDF) was first proposed to account for quantum corrections to classical statistical mechanics [1]. Now, the WDF provides a powerful tool in the description of coherent and partially coherent beams and their propagation in linear and nonlinear media [2]. The properties of the WDF of an optical beam through first-order optical systems have been investigated [3–5]. The WDF and its applications to optical problems especially in the field of partial coherence have been elaborated [6]. It is shown in [7] that for a Gaussian–Schell beam passing through a complex optical system and its WDF distribution, ABCD transform law holds. Based on the Wigner formalism for analyzing the propagation of partially coherent beams, an exact solution describing the self-similar dynamics of partially coherent beams in nonlinear and noninstantaneous Kerr media has been presented and analyzed [8]. The WDF has also been applied to the partially coherent nonparaxial beams [9, 10]. The WDF of a circular or rectangular aperture has been presented [11]. WDFs of Hermite–Gaussian and Laguerre–Gaussian modes have been derived and expressed in terms of Laguerre polynomials, respectively [12–14]. The WDF of an Airy beam has been used to explain the intriguing features of an Airy beam [15]. The WDF of Hermite–cosine-Gaussian beams through an apertured optical system has been examined [16]. Based on a linear systems approach, the WDF of volume holograms with arbitrary index modulation has been obtained [17]. An iterative method for simulating beam propagation in nonlinear media has been proposed by using the Hamiltonian ray tracing and the WDF [18].

Lorentz–Gauss beams are introduced to describe the radiation emitted by a single-mode diode laser [19, 20]. The Lorentz beam is a special case of Lorentz–Gauss beams. The properties of Lorentz and Lorentz–Gauss beams have been extensively examined [21–30]. To further analyze the properties of Lorentz and Lorentz–Gauss beams, in this paper we investigate the WDF of Lorentz and Lorentz–Gauss beams through a paraxial ABCD optical system. As the complementary error function emerges in the optical field of Lorentz and Lorentz–Gauss beams through a paraxial ABCD optical system, it is difficult to further obtain the analytical expression of the WDF. Therefore, the Hermite–Gaussian expansion of a Lorentz function is used in the source plane, which results in the outcome of an analytical expression of the WDF.

2 WDF of Lorentz and Lorentz–Gauss beams through a paraxial optical system

In the Cartesian coordinate system, the z-axis is taken to be the propagation axis. The Lorentz–Gauss beam in the source plane z=0 takes the form

$$ E(x,y,0) = E(x,0)E(y,0),$$
(1)

with E(j,0) given by

$$ E(j,0) = \frac{w_{0j}}{j^{2} + w_{0j}^{2}}\exp\biggl( -\frac{j^{2}}{w_{0}^{2}} \biggr),$$
(2)

where j=x or y (hereafter), w 0x and w 0y are the parameters related to the beam widths of the Lorentz part in the x- and y-directions, respectively, and w 0 is the waist of the Gaussian part. The Lorentz distribution can be expanded into the linear superposition of finite terms of Hermite–Gaussian functions [31]:

(3)

where N is the number of terms in the expansion. The weight coefficient σ 2m is given by [31]

(4)

where \(\operatorname{erfc}(\cdot)\) is the complementary error function. H 2m (⋅) is the 2mth-order Hermite polynomial. Therefore, (2) can be rewritten as follows:

$$ E(j,0) = \sqrt{\frac{\pi}{2}} \frac{1}{w_{0j}}\sum_{m = 0}^{N}\sigma_{2m} H_{2m}\biggl(\frac{j}{w_{0j}} \biggr)\exp\biggl( -\frac{j^{2}}{u_{j}^{2}} \biggr),$$
(5)

where

$$ \frac{1}{u_{j}^{2}} = \frac{1}{w_{0}^{2}} + \frac{1}{2w_{0j}^{2}}.$$
(6)

Since the two-dimensional Lorentz–Gauss beam is the product of two one-dimensional Lorentz–Gauss beams, we consider the WDF of a one-dimensional Lorentz–Gauss beam hereafter. The WDF that corresponds to a one-dimensional optical field in an observation plane is defined by [1]

(7)

where v x denotes the spatial-frequency variable in the phase space, and the asterisk means the complex conjugation. Substituting (5) into (7) and using the integral formulas [32]:

(8)
(9)
(10)

one can obtain the WDF of a Lorentz–Gauss beam in the j-direction of the source plane:

(11)

where [(s 1+s 2)/2] gives the greatest integer less than or equal to (s 1+s 2)/2. If w 0 tends to infinity, the Lorentz–Gauss beam reduces to be a Lorentz beam. In this case, we insert (3) into (7) and use the following integral formula [32]:

(12)

The WDF of a Lorentz beam in the j-direction of the source plane yields

(13)

where \(L_{2m_{1}}^{2m_{2} - 2m_{1}}( \cdot)\) is the associated Laguerre polynomial.

The propagation of a Lorentz–Gauss beam through a paraxial ABCD optical system is described by the Collins integral formula

(14)

where A,B,C, and D are the transfer matrix elements of the paraxial optical system. By using the integral formula [32]

(15)

the propagation of a Lorentz–Gauss beam through a paraxial ABCD optical system turns out to be

(16)

where α j is defined by

$$ \alpha_{j} = \frac{w_{0j}^{2}}{w_{0}^{2}} + \frac{1}{2} -\frac{ikAw_{0j}^{2}}{2B}.$$
(17)

Substituting (17) into (7), we can obtain the WDF of a Lorentz–Gauss beam through a paraxial ABCD optical system,

(18)

where the auxiliary parameters are defined as follows:

(19)
(20)
(21)

B=0 corresponds to an image-forming system. In this case, the output field of a Lorentz–Gauss beam yields

(22)

The corresponding WDF of a Lorentz–Gauss beam through an image-forming system is found to be

(23)

where the auxiliary parameters are defined by

(24)
(25)

We note that the value of σ 2m dramatically decreases with increasing the even number 2m: σ 0=0.7399,σ 2=0.9298×10−2, and σ 10=0.3008×10−6. Therefore, (11), (13), (18), and (23) converge quickly. The WDF of two-dimensional Lorentz and Lorentz–Gauss beams through a paraxial ABCD optical system can be readily obtained by virtue of the above results:

$$ W(x,y,v_{x},v_{y}) = W(x,v_{x})W(y,v_{y}).$$
(26)

3 Numerical calculations and analysis

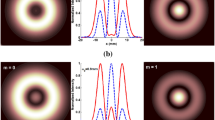
Now, the WDFs of Lorentz and Lorentz–Gauss beams propagating in free space are calculated by using the formulae derived above. As the WDFs in the x- and y-directions have the same variational law, we first only consider the WDF in the x-direction. Figures 1, 2, 3, and 4 represent the normalized WDFs of Lorentz and Lorentz–Gauss beams at several different observation planes in free space. The normalized WDF is given by W(x,v x )/W max(x,v x ), where the subscript denotes taking the maximum value. To conveniently describe the Lorentz–Gauss beam, a new parameter e j =w 0j /w 0 is introduced. If w 0 tends to infinity, e j trends to zero. In this case, the Lorentz–Gauss beam reduces to be a Lorentz beam. e x =0,0.5,1, and 3 in Figs. 1, 2, 3, and 4, respectively. In Figs. 1, 2, 3, and 4, the transversal spatial coordinate, the spatial frequency variable, and the axial propagation distance are scaled in proportion to 1/w 0x ,w 0x , and \(w_{0x}^{2}/\lambda\). The Lorentz–Gauss beam is predominated by the smaller one of the Lorentz and Gaussian parts. In the source plane, therefore, the pattern of WDF of a Lorentz–Gauss beam with small e x is similar to a Lorentz profile. The pattern of WDF of a Lorentz–Gauss beam with large e x in the source plane is similar to a Gaussian profile. When w 0x is equal to w 0, the pattern of WDF of a Lorentz–Gauss beam in the source plane is the modulation of the Gaussian profile by a Lorentz distribution. Upon propagation in free space, the pattern of WDF of a Lorentz–Gauss beam twists clockwise. Moreover, the pattern of WDF shrinks in the direction of the spatial frequency variable and elongates in the direction of the transversal spatial coordinate. With the increase of the parameter e x , the angle that the pattern of WDF rotates upon propagation also increases. For comparison, the normalized WDF of a Gaussian beam at several different observation planes in free space is also shown in Fig. 5. Comparing Fig. 3 with Fig. 5, we can find that the spatial extension of the Lorentz–Gauss beam is higher than that of the Gaussian beam. Normalized WDF in the x-direction of a Lorentz beam in the point x=0 of different observation planes of free space is shown in Fig. 6. Upon propagation in free space, the normalized WDF in the x-direction of a Lorentz beam in the point x=0 steepens. WDF offers the properties of optical beams both in the spatial domain and the frequency domain. Upon propagation, a Lorentz beam expands in the spatial domain. As a result, the normalized WDF in the x-direction becomes narrower as z is increased. Figure 7 represents normalized WDF in the x-direction of a Lorentz–Gauss beam at the point x=0 of different observation planes of free space; e x =1 in Fig. 7. Also, the normalized WDF of a Lorentz–Gauss beam in the point x=0 steepens upon propagation.

Fig. 1
figure 1

Contour graph of normalized WDF in the x-direction of a Lorentz beam at different observation planes in free space. e x =0. (a) z=0. (b) \(z = w_{0x}^{2}/\lambda\). (c) \(z = 5w_{0x}^{2}/\lambda\). (d) \(z = 10w_{0x}^{2}/\lambda\)

Full size image
Fig. 2
figure 2

Contour graph of normalized WDF in the x-direction of a Lorentz–Gauss beam at different observation planes in free space. e x =0.5. (a) z=0. (b) \(z = w_{0x}^{2}/\lambda\). (c) \(z =5w_{0x}^{2}/\lambda\). (d) \(z = 10w_{0x}^{2}/\lambda\)

Full size image
Fig. 3
figure 3

Contour graph of normalized WDF in the x-direction of a Lorentz–Gauss beam at different observation planes in free space. e x =1. (a) z=0. (b) \(z = w_{0x}^{2}/\lambda\). (c) \(z =5w_{0x}^{2}/\lambda\). (d) \(z = 10w_{0x}^{2}/\lambda\)

Full size image
Fig. 4
figure 4

Contour graph of normalized WDF in the x-direction of a Lorentz–Gauss beam at different observation planes in free space. e x =3. (a) z=0. (b) \(z = 0.4w_{0x}^{2}/\lambda\). (c) \(z =w_{0x}^{2}/\lambda\). (d) \(z = 2w_{0x}^{2}/\lambda\)

Full size image
Fig. 5
figure 5

Contour graph of normalized WDF in the x-direction of a Gaussian beam at different observation planes in free space. (a) z=0. (b) \(z = w_{0}^{2}/\lambda\). (c) \(z = 5w_{0}^{2}/\lambda\). (d) \(z =10w_{0}^{2}/\lambda\)

Full size image
Fig. 6
figure 6

Normalized WDF in the x-direction of a Lorentz beam at the point x=0 of different observation planes in free space

Full size image
Fig. 7
figure 7

Normalized WDF in the x-direction of a Lorentz–Gauss beam at the point x=0 of different observation planes in free space. e x =1

Full size image

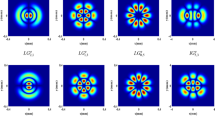
As the WDF represents the energy of a ray at a given space position (x,y) with an angle (v x ,v y ) [3, 33], we now analyze the novel properties of Lorentz and Lorentz–Gauss beams by their WDFs at different space positions at different propagation distances. The normalized WDFs of the Lorentz beam as functions of v x and v y at several different positions (x,y) are depicted in Figs. 8 and 9 for the source plane z=0 and the observation plane \(z =5w_{0x}^{2}/\lambda\), respectively. The WDF of the Lorentz beam at the origin (0,0) of the source plane is just a Lorentz-type profile. The WDF of the Lorentz beam at other points of the source plane is composed of a central dominant lobe and some side lobes. With the increase of the departure distance from the origin, the number of the side lobes also augments, and the pattern size of the central dominant lobe decreases. The WDF of the Lorentz beam at the origin of the observation plane \(z =5w_{0x}^{2}/\lambda\) is a rotated Lorentz distribution. With varying the point (x,y), the shape of the central dominant lobe of the WDF in the observation plane \(z = 5w_{0x}^{2}/\lambda\) also changes. Compared Fig. 9 with Fig. 8, the angular extension of the Lorentz beam in the observation plane \(z = 5w_{0x}^{2}/\lambda\) is smaller than that in the source plane. Secondly, the number of the side lobes of the WDF in the observation plane \(z = 5w_{0x}^{2}/\lambda\) is also smaller than that in the source plane.

Fig. 8
figure 8

Contour graph of normalized WDF of a Lorentz beam at several different points in the source plane. (a) x=y=0. (b) x=0 and y=w 0y . (c) x=−w 0x and y=−3w 0y . (d) x=3w 0x and y=3w 0y

Full size image
Fig. 9
figure 9

Contour graph of normalized WDF of a Lorentz beam at several points in the observation plane of \(z = 5w_{0x}^{2}/\lambda\). (a) x=y=0. (b) x=0 and y=w 0y . (c) x=−w 0x and y=−3w 0y . (d) x=3w 0x and y=3w 0y

Full size image

Figures 10 and 11 show the normalized WDFs of a Lorentz–Gauss beam with e x =e y =1 at different points in the source plane z=0 and in the observation plane \(z = 5w_{0x}^{2}/\lambda\), respectively. e x and e y of the Lorentz beam are equal to zero. With increasing the parameters e x and e y , the number of side lobes at the point other than the origin decreases. In the case of e x =e y =1, the side lobes in the WDF of the Lorentz–Gauss beam completely disappear. Moreover, the central lobe in the WDF of the Lorentz–Gauss beam tends to a Gaussian-type profile. The distinction of the Lorentz beam from the Gaussian beam is its high angular spreading. The above research denotes that the high angular spreading of Lorentz beam maybe caused by the side lobes in the WDFs. Also, the side lobe existing in the WDF of Lorentz beams results in the diffraction-free ranges of this kind of beams in the x- and y-directions \(2\pi w_{0x}^{2}/\lambda\) and \(2\pi w_{0y}^{2}/\lambda\), which are longer than that of the Gaussian beam.

Fig. 10
figure 10

Contour graph of normalized WDF of a Lorentz–Gauss beam at several different points in the source plane. e x =e y =1. (a) x=y=0. (b) x=0 and y=0.5w 0y . (c) x=−0.5w 0x and y=−0.75w 0y . (d) x=0.75w 0x and y=0.75w 0y

Full size image
Fig. 11
figure 11

Contour graph of normalized WDF of a Lorentz–Gauss beam at several different points in the observation plane of \(z =5w_{0x}^{2}/\lambda\). e x =e y =1. (a) x=y=0. (b) x=0 and y=0.5w 0y . (c) x=−0.5w 0x and y=−0.75w 0y . (d) x=0.75w 0x and y=0.75w 0y

Full size image

4 Conclusions

Based on the Collins integral formula and the expansion of Lorentz distribution, an analytical expression for the WDF of Lorentz and Lorentz–Gauss beams through a paraxial ABCD optical system is derived. The properties of the WDF of Lorentz and Lorentz–Gauss beams propagating in free space are demonstrated. The normalized WDFs of one-dimensional Lorentz and Lorentz–Gauss beams are plotted at several different observation planes. The normalized WDFs of two-dimensional Lorentz and Lorentz–Gauss beams at different spatial points are also depicted in several observation planes. The influences of the beam parameters on the WDF of Lorentz and Lorentz–Gauss beams in free space are also analyzed at different propagation distances. When e x and e y of the Lorentz–Gauss beam are far small, the side lobes exist in the WDF of the Lorentz–Gauss beam at the point other than the origin. With increasing the parameters e x and e y , the side lobes in the WDF of the Lorentz–Gauss beam at the point other than the origin gradually decrease and eventually disappear. The side lobes in the WDF of Lorentz beam result in its different properties from the Gaussian beam. This research is beneficial to the practical applications involving in the single-mode diode laser. Though here we only consider the coherent Lorentz and Lorentz–Gauss beams, the approach used here can also be extended to the partially coherent Lorentz and Lorentz–Gauss beams.