Average spreading of rectangular elliptical Gaussian beam array propagating in non-Kolmogorov turbulence

Abstract

The spreading properties of the rectangular elliptical Gaussian beam (EGB) array propagating in non-Kolmogorov turbulence are investigated by using the derived analytical expression for the root-mean-square (rms) beam width. The results indicate that the rms beam width of the EGB array is smaller than that of the circular Gaussian beam array for long-distance propagation. The optimum separation distances are proved to exist and have a strong dependence on the ratio of the waist width along the long axis to that along the short axis of the EGB. Further, the rms beam width in non-Kolmogorov turbulence is different from that in Kolmogorov turbulence.

1 Introduction

Optical propagation through a turbulent atmosphere is a very important subject in the case of remote sensing, imaging, and communication systems, and has attracted considerable interest in the past decades. Since the Kolmogorov model was introduced, it has been widely accepted and used to describe the atmospheric turbulence. However, recent experimental results have indicated great deviations from the Kolmogorov model in some portions of the atmosphere [1]. When the atmosphere is extremely stable, the turbulence is no longer homogeneous in three dimensions since the vertical component is suppressed [2]. The anisotropic turbulence in the stratosphere has been experimentally investigated [3]. The experimental results also have indicated that the Kolmogorov model cannot completely describe the turbulence near the tropopause [4]. For the propagation along the slant path, the turbulence shows non-Kolmogorov characters, and its spectral exponent depends strongly on the altitude [5]. It can be understood by the mechanisms of turbulent generation and dissipation being different at high and low altitudes, which results in the difference in turbulent spectra [6]. Further, the Kolmogorov model is only valid in the inertial subrange.

Therefore, a non-Kolmogorov model is presented in [7], which reduces to the Kolmogorov model only for the generalized exponent α=3.67. The average spreading of a Gaussian-Schell model beam propagating in non-Kolmogorov turbulence is investigated [8]. In the past decade, a variety of laser beam arrays have been widely studied because of their wide applications in the inertial confinement fusion and high-energy weapons. The propagation properties of beam arrays in turbulent atmosphere are investigated [9–12], respectively.

Elliptical Gaussian beams (EGBs) are often encountered in laser optics, material processing and nonlinear optics. EGBs possess high orbital angular momentum, which can be used for rotating micrometer-sized particles and cold atoms [13]. In addition, EGBs can be used to increase the conversion efficiency in second-harmonic generation instead of Gaussian beams [14]. The average intensity and scintillation index of EGB propagating in Kolmogorov turbulence are studied in [15, 16], respectively. However, to our knowledge, the propagation properties of EGB array in non-Kolmogorov turbulence have not been studied. In this letter, the average spreading of rectangular EGB array propagating along horizontal direction in non-Kolmogorov turbulence is investigated in detail by using the rms beam width. The results indicate that the rms beam width of the EGB array is larger than that of the circular Gaussian beam array for a short propagation distance. However, for a long propagation distance, the rms beam width of the EGB array is smaller than that of the circular Gaussian beam array. Therefore, it is more suitable to use the EGB array in long-distance propagation, which can improve the performance of the communication system.

2 Analytical formulas

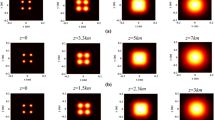
Assume that a rectangular beam array consisting of N×M equal beamlets with elliptical Gaussian profile is located on the source plane z=0 with the separation distances x ₀ and y ₀, as shown in Fig. 1. For simplicity, the formulas obtained below are for odd M and N. For even M and N, the formulas are valid by changing the range of m, p into 1−M/2 to M/2 and n, q into 1−N/2 to N/2. For the coherent combination, the cross-spectral density function of the rectangular EGB array is expressed as [17]

(1)

where w _0x and w _0y are the waist widths along the long axis and short axis of the beamlet.

Fig. 1

Schematic diagram of the rectangular beam array with the number of rows N=3 and that of columns M=5

Based on the extended Huygens–Fresnel principle, the average intensity of the rectangular EGB array propagating in a non-Kolmogorov turbulence is defined as [12]

(2)

where k=2π/λ is the wave number with the wavelength λ. The ensemble average term in (2) can be expressed as [12]

where κ is the magnitude of the two-dimensional spatial frequency and J ₀ is the Bessel function of the first kind and zero order.

The rms beam width of the rectangular EGB array in non-Kolmogorov turbulence is defined as [11]

$$ w_\mathrm{turb}=\biggl[\frac{2\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}(x^2+y^2)\langle I(x,y,z)\rangle \,\mathrm{d}x\,\mathrm{d}y}{\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\langle I(x,y,z)\rangle \,\mathrm{d}x\,\mathrm{d}y}\biggr]^{1/2}.$$

(3)

On substituting (2) into (3) and using the integral transform technique, after tedious integral calculations, we obtain

$$ w_\mathrm{turb}=\left(A+\frac{B}{k^2}z^2+\frac{8}{3}Tz^3\right)^{1/2},$$

(4)

where

and

$$T=\pi^2\int_0^{\infty}\kappa^3\varPhi _n(\kappa,\alpha)\,\mathrm{d}\kappa.$$

Considering the inner-scale and outer-scale effects, the non-Kolmogorov spectrum is defined as [7]

(5)

where A(α)=Γ(α−1)cos(απ/2)/(4π ²), κ ₀=2π/L ₀ and κ _m =c(α)/l ₀, in which c(α)={Γ[(5−α)/2]⋅A(α)⋅2π/3}^1/(α−5), L ₀ is the outer scale and l ₀ is the inner scale. Using the non-Kolmogorov spectrum, after some tedious mathematical manipulation, the term T is expressed as [10]

(6)

where $\beta=2\kappa_{0}^{2}-2\kappa_{m}^{2}+\alpha \kappa_{m}^{2}$ and Γ denotes the gamma function.

3 Theoretical results and analysis

In numerical simulations, for simplicity, the parameters λ=1550 nm, $\tilde{C}_{n}^{2}=1\times10^{-15}\ \mathrm{m}^{3-\alpha}$, M=5, N=3, L ₀=1 m and l ₀=0.01 m are kept fixed. Figure 2 plots the rms beam width w _turb of the rectangular EGB array as a function of the propagation distance z for several different w _0y /w _0x with the parameters x ₀=0.01 m, y ₀=0.01 m and α=3.8. The result indicates that w _turb of the EGB array is larger than that of the circular Gaussian beam (w _0x =w _0y ) array for a short propagation distance. However, for a long propagation distance, w _turb of the EGB array is smaller than that of the circular Gaussian beam array and w _turb of the EGB array is smaller for larger w _0y /w _0x .

Fig. 2

The rms beam width w _turb as a function of the propagation distance z for different w _0y /w _0x with x ₀=0.01 m, y ₀=0.01 m and α=3.8

The influences of the separation distances x ₀ and y ₀ on the rms beam width w _turb are studied in Fig. 3, where the parameters are z=10 km, α=3.8, (a) y ₀=0.01 m and (b) x ₀=0.01 m. The results indicate that for given y ₀, there is an optimum separation distance x _0m , which leads to a minimum rms beam width w _min, and x _0m decreases with the increase of w _0y /w _0x , as shown in Fig. 3(a). Moreover, the optimizing effect of x ₀ on w _turb is better for larger w _0y /w _0x , where the optimizing effect can be measured by (w _turb−w _min)/w _min. For given x ₀, there is an optimum separation distance y _0m which leads to a minimum rms beam width w _min, and y _0m increases with the increase of w _0y /w _0x , as shown in Fig. 3(b). Besides, the optimizing effect of y ₀ on w _turb is better for smaller w _0y /w _0x .

Fig. 3

w _turb as a function of (a) x ₀ and (b) y ₀ for different w _0y /w _0x with z=10 km, α=3.8, (a) y ₀=0.01 m and (b) x ₀=0.01 m

The results above are based on the case of α=3.8. However, the generalized exponent α is variable as the rectangular EGB array propagates in non-Kolmogorov turbulence. Next, the influence of α on w _turb is investigated. As shown in Fig. 4, when α is smaller than 3.67 and not close to 3, there is a larger w _turb compared with α=3.67 and when α is close to 3, w _turb decreases rapidly since in this case A(α) begins to decrease to zero. Besides, when α is larger than 3.67, there is a smaller w _turb. Further, for z=10 km, the rms beam width w _turb is smaller for larger w _0y /w _0x , which is consistent with the result indicated in Fig. 2.

Fig. 4

w _turb as a function of α for different w _0y /w _0x with z=10 km, x ₀=0.01 m and y ₀=0.01 m

4 Conclusions

In conclusion, the analytical expression for the rms beam width w _turb of the rectangular EGB array propagating in non-Kolmogorov turbulence is derived. The average spreading of the EGB array has been investigated numerically. The results indicate that w _turb of the EGB array is larger than that of the circular Gaussian beam array for a short propagation distance. However, for a long propagation distance, w _turb of the EGB array is smaller than that of the circular Gaussian beam array, which has great significance to a long-distance free space optical communication. Moreover, there are optimum separation distances x _0m and y _0m which lead to a minimum rms beam width w _min. The optimum separation distances have great dependence on the ratio w _0y /w _0x . Further, w _turb depends greatly on α, which manifests that the spreading and focusing ability of the EGB array propagating in non-Kolmogorov turbulence is so different from that in Kolmogorov turbulence that a specific treatment is required when non-Kolmogorov turbulence exists. Therefore, the non-Kolmogorov spectrum should be considered in the real system design.