1 Introduction

Cavity ringdown (CRDS) and cavity enhanced absorption spectroscopy (CEAS) are sensitive techniques, which have found widespread application in the measurement of trace amounts of gaseous absorbers [1–6]. The high sensitivity of these techniques is a result of the elongated light paths the photons travel inside an optical cavity, which consists of two or more highly reflective mirrors. The high reflectivity of the cavity’s mirrors does not only result in a long effective path of light (enhancement of a factor (1−R)−1), but also implies a very low transmission of the incident intensity into the cavity (T=1−R) [7]. This well-known trade-off between a long effective light path and high cavity transmission can be overcome by utilising narrow-band coherent light sources and exploiting the modal structure of the cavity [8]. For the most recent variant of CEAS, diode lasers (DL) are used as light sources and light leaking out of the cavity is reinjected into its source (optical-feedback—CEAS, OF-CEAS) [4, 5, 9–14]. An optical feedback with frequency filtered light is achieved by applying this method, with the result that the emission of the DL is locked to one of the resonance frequencies of the optical cavity. The portion of the reinjected light (feedback-rate) determines the frequency range of the DL, over which the locking takes place [4, 15].

All kinds of diode lasers are in principle sensitive to optical feedback. In the context of OF-CEAS, the suitability of distributed feedback diode lasers (DFB) [4, 5, 9–11] has been proven for the near and mid-infrared region. External cavity diode lasers have proven suitable for the visible range (ECDL)[12–14]. More recently, even quantum cascade lasers have been utilised [16, 17].

The most important consideration for any OF-CEAS setup is to avoid the reinjection of light, which has not been frequency-filter ed by the cavity, into the DL. This is commonly achieved by utilising a V-shaped cavity design [4] (refer to Fig. 2). Other suitable schemes include a linear cavity with injection via a glass plate in Brewster’s angle [13] and a three mirror ring cavity with an additional retro-reflector [18]. Lately, the OF-CRDS technique [13] has also been adopted to measure the extinction by aerosol particles [19].

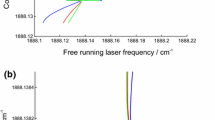
The common characteristic of all these optical feedback schemes is that the reinjection of the light into the laser diode has to take place with a well-defined constant phase. This is commonly achieved by matching the cavity length to the laser-cavity distance and additionally by active control of the position of a piezo-mounted mirror. The position of this mirror is usually found by minimising an error signal that is created from the signal of the transmitted light by some suitable algorithm. Figure 1 depicts an example of how the measured cavity transmission will typically look like, if the feedback-phase is well adjusted.

Fig. 1
figure 1

Cavity transmission with active feedback-phase regulation and weak water vapour absorption. The continuous sweep of the injection current results in an almost discrete tuning of the laser frequency. The laser remains locked to one longitudinal cavity mode over a wide range. Frequency jumps occur at the beginning and end of every mode. The symmetry around each transmission maximum indicates the correct adjustment of the feedback-phase

Full size image

We present, in the following pages, different approaches for the creation of an error signal from cavity transmission data, which can be exploited for the automatic online adjustment of the feedback-phase. For this purpose, it is first explained in Sect. 3, how the cavity transmission can be modelled. Subsequent, in Sect. 4, the modelled cavity transmission is used to analyse the suitability of different approaches with respect to features typically varying in an experiment. Finally, in Sect. 5, we present the performance of the regulator described Sect. 2.

2 Experimental

The OF-CEAS setup is depicted in Fig. 2. Light from a DFB diode laser (NLK1E5C1TA, λ=1.37 μm, NTT Electronics), placed on a linear translation stage (LTS), is focused by an aspheric lense and attenuated by two polarisation filters. It is coupled to the cavity via two mirrors, one of which (M Phase) is mounted on a piezo electric actuator (PZT) and used to adjust the feedback-phase. The PZT (PI, S-303) is driven by a piezo controller (Thorlabs MDT694A) not depicted in Fig. 2. The V-shaped cavity consists of the three mirrors M 1, M 2, and M 3 (Laytertec, low loss, R=1 m). Its branches L 1 and L 2 have a length of 0.5 m and the opening angle is α=2.9°. L 0, the distance between laser diode and cavity, is 1 m. This assures that only even or only odd modes are present in one scan [4].

Fig. 2
figure 2

Schematic of the optical and electrical setup: V-shaped cavity built of mirrors M1, M2, and M3, a DFB-laser mounted on a linear translation stage (LTS), attenuation optics, a piezo mounted mirror M Phase for feedback-phase regulation, and the photodiode (PD). The PD signal is evaluated by a DSP, generating the error-signal applied to the PZT. Optionally, a sine can be added

Full size image

The transmitted light (Cavity Output) is collected by a photo receiver (FEMTO HCA-S, 20 MHz, 105 V/A) and its signal is evaluated by the digital signal processor (DSP) based electronics, which calculates the error signal applied to the PZT. Optionally, an artificial disturbance (sine or step function) can be added to the DSP’s output, which is used to determine the achievable regulatory bandwidth for the feedback-phase and the step response in the setup. The experimental basis of the regulator in use is a microcontroller (Microchip Inc., dsPIC33F series) including a DSP unit, and the specific algorithms (refer to Sect. 4) are implemented in C code and assembly language. The microcontroller is placed on a printed circuit board (PCB), which also holds two 16-bit digital-analog-converters (DAC). One of the DACs is used for the output of the error-signal. The input-signal, i.e. the intensity behind the cavity, is sampled at 100 kHz with 12 bit resolution by the dsPIC33F’s internal analog-digital-converter (ADC).

Additional logic, which allows running an OF-CEAS experiment independently of other computers, was also implemented. For this purpose, the second DAC is available for the tuning of the laser frequency. It is used to generate a voltage ramp or any other arbitrary waveform, which can be fed into most diode laser drivers for analog modulation of the current. At the end of each frequency-scan, a TTL pulse can be produced in order to trigger the switch-off of the laser diode, which generates a ringdown event. The ringdown time is needed for the conversion of the cavity transmission signal to absorption coefficients [5].

3 Modelling of the cavity output signal

In the case of optical feedback, the diode laser and the optical cavity have to be regarded as a combined or coupled system. Based on results of Laurent et al. [20], Morville et al. [4] derived the dependency of the coupled laser frequency ω and the diode cavity mode frequency ω N :

(1)

In this equation, \(\mathcal{F}_{\mathrm{CAV}} = \frac{\pi R}{1-R^{2}}\) and \(\mathcal{F}_{\mathrm{DL}} = \frac{\pi\sqrt{R_{\mathrm{DL}}}}{1-R_{\mathrm{DL}}}\) are the finesse of the V-shaped and the diode laser’s cavity, respectively, with R→1 being the average mirror reflectivity and R DL the laser diode’s cavity reflectivity. κ is the feedback-rate, which is the ratio of the laser’s intensity and the intensity of the reinjected light. α is the Henry–Factor [21], ϑ=arctan(α), n 0 l LD the diode laser optical length, c the speed of light, L 1 and L 2 the length of the cavity arms and L 0 the distance between the laser diode and the cavity’s folding mirror. The frequency ω of the coupled system is implicitly given by the diode cavity mode frequency ω N , which can be controlled externally either by temperature or the laser diode injection current. Equation (1) describes the effect of locking the laser frequency to the resonance frequencies of the optical cavity. Note that the nomenclature used throughout the literature is not consistent. Morville et al. [4] use ω free instead of ω N and name it the free running laser frequency, which is the steady state solution of the rate equation without feedback (Eq. (1) in Laurent et al. [20]).

All sorts of environmental factors, like thermal drift, wind, or vibration introduce changes in the length L 0 and thereby change the feedback-phase. It is necessary to actively account for this phase and make corrections accordingly.

In order to account for a variable feedback-phase, the arguments of the both sine functions in the numerator of (1) have to be extended by an additional summand Φ, the feedback-phase, which yields:

(2)
(3)

Equation (1) cannot be solved analytically for the coupled frequency ω, but under the condition of a non-negative slope, numerical approaches for a solution exist. For this work, the straight-forward approach of analytically calculating the derivative of (1) and then numerically finding all its zero crossings (\(\omega^{\prime}_{n}=0\)) in a small region around (ω−ω RES)/FSR, where FSR is the external cavity’s mode spacing was used. This way the regions of non-negative slope are easily found and an invertible data set can be created. As the inverted data set is equally spaced in ω and not in ω N , it is interpolated to yield the frequency of the laser locked to a cavity mode.

In order to calculate a transmission signal that can be compared to the experiment, the cavity transmission H(ω), given in (4), has to be evaluated at that frequency.

$$H_{V}(\omega)=\frac{T^2}{(1-R^2)^2+4R^2 \sin^2(\frac{1}{2}\omega\tau +\frac{3\vartheta}{2})}. $$
(4)

In this equation τ is the light’s roundtrip time within the cavity, ϑ the argument of the mirror’s complex field-re flectivity, R the mirrors intensity reflectivity, and T its intensity transmission. A derivation of this equation is sketched in Appendix.

Computed transmission signals have been plotted in Fig. 3 for different values of the feedback-phase. The solid black curve represents an optimal adjustment, whereas the dashed red, and dashed bold blue curves are the result of small misalignment in different directions. The dotted pink, and dotted bold green curves correspond to larger misalignment. It has to be mentioned that slightly asymmetrical signals like the dashed red, and the dashed bold blue curve can still be used for the measurement of absorption coefficients, as usually only the peak-transmission of a mode is evaluated. As that is still at 25%, which is the theoretical maximum for a V-shaped cavity, it does correspond to the transmission at a cavity’s eigenfrequency. More information on the evaluation of raw data has been published by Kerstel et al. [5].

Fig. 3
figure 3

Calculated cavity transmission in the case of weak optical-feedback (κ=2×10−7) and various phasings

Full size image

4 Creation of an error-signal

In order to adjust for the feedback-phase, an error-signal has to be created. In 1991, Ohshima and Schnatz [22] published a scheme for locking to a single cavity mode, which directly employs the symmetry of the cavity transmission signal.

Further schemes—suitable for OF-CEAS, where tuning over many modes takes place—have been presented by Motto-Ros [23] and Baran et al. [11]. Both approaches have in common, that the feedback-phase correction is performed continuously, i.e. irrespective of the beginning and end of each mode.

Here, we present an approach to analyse for the symmetry of each individual mode, in order to achieve the highest possible regulatory bandwidth. This approach has two major functioning units: The finding of the modes and the application of the error-signal algorithms.

The most fundamental task in both parts is the calculation of the first derivative. Savitzky–Golay filters have been used for this work, as they allow for noise filtering and signal differentiation at the same time [24, 25]. Filter lengths between five and fifteen points turned out to be appropriate, and by using cyclic permutations of the filter, its application—a discreet convolution—comes down to a scalar product of two vectors. Although noise filtering and calculation speed are of minor interest for the simulations, both become important in a real experiment.

In a first step, the finding of the beginning and end of every mode is addressed. For this purpose, a zero crossing trigger on the raising slope of the first derivative of the cavity transmission signal is used as indicator. Between two trigger events the algorithms are applied to the cavity transmission. At the occurrence of the trigger, the final error signal is calculated and given as result. Especially for the finding of the modes, the noise reduction from Savitzky–Golay filters is beneficial, as it protects effectively from false trigger events. Additional protection is achieved by defining a minimum and maximum mode width, as well as a signal threshold.

In the following sections, different approaches for the error-signal generation are presented and discussed with respect to the criteria below for an ideal result. These are in essence four points:

  1. 1.

    Linearity (at least monotonicity) with respect to the phase over a wide range.

  2. 2.

    Independence of the signals intensity.

  3. 3.

    Independence of the mode width.

  4. 4.

    Analog or digital implementability.

A linear correlation is needed for PID regulators to perform well and a monotonic signal can be converted to a linear signal via a regulatory curve. The frequency scan of a diode laser is usually performed by scanning its injection current. This leads in principle to a variation of the laser’s intensity. Also, the presence of absorbers changes the amount of the cavity transmission, and by this reduces the amount of light fed back into the diode laser (feedback-rate), which comes to a smaller mode width. Finally, the algorithms should be simple enough, to be applied by analog electronics, or mode by mode on a conventional microcontroller. The methods presented in the following sections employ different features of the cavity transmission (compare to Fig. 3) to check its symmetry, though they all have the common characteristic that the first derivative is the basis for their mode of operation. In order to obtain the characteristics of a specific Error-method, it was applied to the phase dependent transmission (refer to 3) for different values of the feedback-phase. This procedure was repeated for different intensities (10%, 20%, …, 80%, 90%) at a fixed feedback-rate and then for different feedback-rates (10−6, 5×10−7, 10−7, 5×10−8) at a fixed intensity. The selected feedback-rates correspond in our case to locking ranges of about (2, 1.4, 0.7, and 0.5) FSR and an intensity decrease of 95%. By proceeding as outlined above, most practical conditions in an experiment are covered. The slight noise, which is visible in most characteristic curves, is a fragment of the interpolation process.

4.1 Edge steepness approach

In order to check the symmetry of the cavity transmission, its edge steepness, which is available from the derivative of the signal, can be used as an indicator. A very straightforward approach is to use the sum of maximum and minimum of the derivative as an error signal (ES-method). This scheme works because the increase (derivative maximum) and decrease (derivative minimum) in the intensity transmission are equally strong in the symmetric case, whereas in every other case one of those is stronger than the other. The difference in the steepness (difference of derivative minimum and maximum absolute values) gives the amplitude of the error signal, whereas the relative strength determines the direction.

Figure 4 depicts the characteristics of the ES-method for different intensities. It is obvious that this scheme depends on the intensity of the input signal, because the edge steepness, i.e. the change of intensity, is a function of the intensity itself. This behaviour can be compensated by normalising to the mode’s peak transmission. On the other hand, this method is almost independent of the locking range, i.e. the width of a single mode, which can be seen in Fig. 5. The reason for this can be understood as follows: In every case, the cavity transmission is negligible outside the locked area. During a mode-lock, the transmission traverses a unique, phase dependent shape. The shape is unique to the feedback-phase and either compressed or stretched with the feedback-rate. Hence, the intensity jumps are not a function of the mode-width, and thus the edge steepness is a stable indicator.

Fig. 4
figure 4

Error signal characteristics of the ES-method for different signal intensities with κ=10−6 and ϑ=1.4

Full size image
Fig. 5
figure 5

Error signal of the ES-method at fixed intensity of 70% and variable feedback-rate ϑ=1.4

Full size image

This scheme can easily be evaluated by a microcontroller based solution, as it is used here. The procedure requires only two comparisons and up to one write operation per data point involved. It is therefore extremely fast.

4.2 Weighted slope approach

Instead of evaluating the edge steepness directly, an alternative approach is to evaluate the overall slope, i.e. to integrate the derived signal. A direct integral would always have a zero result, but if the derivative is weighted, e.g. by some sort of nonlinear function, which is monotonic, the integral produces a usable error signal. The advantage of such an approach is that it can also be implemented in analog circuitry with reasonable effort. Some candidates for such functions are f(x)=x 3 (WS.1-method) or f(x)=sign (x)⋅(exp (|x|)−1). The exponential function is specifically interesting, as it describes the characteristics of bipolar transistors. A simple combination of a npn and a pnp transistor would do the job in this case. When using a microcontroller, the x 3 function is more suitable, because it can be calculated faster.

The weighted slope approach—implemented in the form of the WS.1-method—has the same compensable intensity dependency as the ES-method in Sect. 4.1. The WS.1-method is also almost independent of the locking-range, as the weighting favours strong slopes (frequency jumps), whereas small slope values, which are present in the locked area, become insignificant. Figure 6 shows a direct comparison of both methods with normalisation applied.

Fig. 6
figure 6

Comparison of the ES- and WS.1-method characteristics with normalization applied. κ=10−6 and ϑ=1.4

Full size image

A variant of the weighted slope approach was recently proposed by Baran et al. [11]. Instead of applying a non-linear weighting function to the derived signal, it is integrated with a different time constant (WS.2-method). For this work, a moving average filter is used to simulate the slow integration. The method’s characteristic for different intensities is plotted in Fig. 7 and is comparable to the one of the ES- and WS.1-method. The feedback-rate dependant characteristic is comparable to the one of SM-method in Sect. 4.3, which is shown in Fig. 9.

Fig. 7
figure 7

The WS.2-method characteristics for different signal intensities with κ=10−6 and ϑ=1.4

Full size image

4.3 Shifted maximum approach

A further method, presented by Motto-Ros [23], uses the position of the maximum within one mode as an indicator for the symmetry of the signal (SM-method). The feedback-phase is at its optimum value if the transmission maximum is located at the centre of the mode. The translation of the peak position to the error-signal is done by a threshold trigger applied to the derived signal. If the derived signal is higher than the upper threshold a constant positive signal is output, if it is lower than the lower threshold a negative value is output. Otherwise it is zero. Integrating over the output gives the error signal, which has been plotted in Fig. 8.

Fig. 8
figure 8

Error signal characteristics of the SM-method for different signal intensities. κ=10−6 and ϑ=1.4

Full size image

In contrast to the other methods presented, the SM-method is much less sensitive to the intensity of the input signal and, therefore, it is the best suited method for a simple analog implementation, as no normalisation of the signal is required. With respect to the influence of the feedback-rate, however, this method is less advantageous as can be seen from Fig. 9.

Fig. 9
figure 9

Error signal characteristics of the SM-method at fixed intensity of 70% and variable feedback-rate . ϑ=1.1

Full size image

4.4 Overview of the presented methods

Finally, the results from this chapter are summed up. Table 1 gives an overview of the presented methods with respect to the monotonic region of each, as well as to the mode width dependency. The intensity dependency is also given, but it has to be kept in mind that it is generally possible to compensate it by a normalisation procedure as outlined above.

Table 1 Overview of algorithms presented throughout Sect. 4
Full size table

5 Experimental results

In this section, the performance of the ES-method, implemented on a DSP, is evaluated in a real experimental setup. The results are generally the same, when the WS.1-method is used instead. The performance of the SM-method and the WS.2-method, employing analog implementations, was already presented elsewhere [11, 23].

5.1 Regulatory bandwidth under experimental conditions

In a first step, we determine the performance of the ES-method in terms of the regulatory bandwidth in a full experimental setup.

For this purpose, the regulator is connected to a piezo controller driving a piezo on which a mirror is mounted (see Fig. 2). An artificial disturbance of the phase was introduced via a sine of variable frequency, which was added to the correction signal and this way applied to the PZT. The idea behind this experiment is that the artificial disturbance results in a cyclic change of the feedback-phase. For slow disturbances, i.e. at low frequencies, the regulator electronics can follow the perturbation and eliminate it, whereas at higher frequencies the perturbation becomes too quick and can no longer be compensated. This behaviour is essentially the same as for a high pass filter, hence the phase regulator can be considered as such a filter and be characterised by the damping of the input. Accordingly the regulatory bandwidth is hereby defined as the frequency, at which the input disturbance experiences a damping of 3 dB. For this experiment, the amplitude of the sine was selected to approximately match a phase shift of 0.6 rad. The laser current is scanned by ramps of 5 Hz, which is the maximum scan rate achievable with our setup. Every ramp consists of 95 modes, hence the mode rate is 475 modes/s. Using the ES-method, the achieved regulatory bandwidth was 37 Hz (see Fig. 10).

Fig. 10
figure 10

Damping of the artificial phase disturbance by the regulator using the ES-method. The red lines mark the regulatory bandwidth of 37 Hz, which is the frequency that results in a 3 dB damping

Full size image

The PID parameters used are: P=0.17, I=0.5, and D=0.1. These values are the dimensionless parameters, as they are used by the PID routine included in the dsPIC DSC DSP Algorithm Library (Microchip Inc., Part Number: SW300022). They represent the best parameter set in terms of speed and stability that could be found. Although a correct choice for the PID parameters is crucial for a good performance, a relatively big variation of 10% for each one individually did change the bandwidth only by a few percent. It is also possible to find sets, which result in a higher bandwidth, though the increase in speed is generally accompanied by a less stable regulation.

5.2 Step response of the regulator

Finally, the regulator’s step response is given, which nicely demonstrates its function. Instead of the sine function used beforehand, a step function is added to the regulators output. The PID parameters used are the same as in Sect. 5.1. From this experiment, several insights can be gained. On the one hand, the response of the piezo system (PZT and driver) can be monitored, and on the other hand the number of modes needed to correct for the step-like perturbation can be measured. Figures 11 and 13 depict the step perturbation and response for a negative and a positive change, respectively.

Fig. 11
figure 11

Response of the regulator to a negative step like phase shift using the ES-method

Full size image

The figures yield immediately that the piezo system is a performance limiting factor in our setup, as the response to the step perturbation is not abrupt but has a significant settling time of about two modes. A stronger driver and a reduced mirror mass will certainly improve this. A full compensation of the step perturbation (excluding the settling delay) takes about 5 modes for a negative, and 3 for a positive step.

Whenever the regulator finds a new mode, a 5 V pulse is raised on one of its digital outputs. These pulses are depicted in both figures as red dots. Especially from Fig. 11, it can be seen that the regulator reliably detects the beginning and the end of each mode, even for strong perturbations and in the presence of parasitic modes. This reliable mode detection is a key feature, which has to be implemented with care. Figure 12 gives an additional example for the finding of the modes at the transition from one scan to the next. From this figure, two important features of the regulator can be deduced. The first point is again the reliable finding of the modes; this time in the case of a varying mode width due to the non-linear frequency to injection current relation of the diode laser. The second point is the rejection of the complicated tuning region just after the ringdown event at the end of the scan. If the transmission data between 50 ms and 60 ms was also used for the feedback-phase correction, it would introduce a significant disturbance.

Fig. 12
figure 12

Cavity transmission and mode finding in between two current ramps

Full size image
Fig. 13
figure 13

Response of the regulator to a positive step-like phase shift using the ES-method

Full size image

6 Conclusion and perspectives

In this work, different approaches for the generation of an error-signal for phase-locking in OF-CEAS were presented and analysed. Besides the previously published methods of Motto-Ros [23] (SM) and Baran [11] (WS.2), two further methods (ES and WS.1) were proposed. Detailed simulations of the error-signal to be expected from those methods gave the result that the ES- and the WS.1-method are equally well suited as direct error-signals, as they are almost independent of the mode width and can be normalised to the transmission intensity. The SM-method, on the other hand, is almost intensity independent, but has a stronger dependency on the mode width. The WS.2-method is dependent on both, intensity and mode width, of which at least the intensity dependency could be compensated in the same way it has been done for the other methods.

The feasibility of a reliable, dsp based, mode by mode feedback-phase correction—implementing the ES-method—was demonstrated, and its performance under experimental conditions evaluated. From the experiments, it is found that a bandwidth of 37 Hz could be achieved in our setup. The step response shows that this performance is currently limited by the piezo system.