1 Introduction:

Phase field (PF) or Ginzburg–Landau (G–L) theory is commonly used to capture various first-order solid–solid phase transitions (PTs) [1, 2] such as surface-induced martensitic PT [3,4,5], premelting at the external surfaces [6,7,8], solid-solid PT via intermediate melt [9,10,11,12], dislocation evolution [13,14,15], nanoscale interaction of PTs and dislocations [16,17,18,19,20], martensitic PT in diffrent length scale [21,22,23,24,25,26,27,28,29], crack propagation [30,31,32,33], nanovoids evolution [34, 35] etc. In this paper, PTs between austenite to martensitic variants and twinning between martensitic variants are considered. Martensitic PT can be defined as a first-order, diffusionless, and displacive transformation which plays a crucial role in the evolution of unique microstructures. It also shows interesting mechanical properties and nontrivial microstructure for different materials such as shape memory alloys [36,37,38,39,40,41,42,43,44,45]. During such transformation, the crystal lattice of austenite (A), the high-temperature cubic phase, transforms to martensite (T). T is a lower-symmetry lattice of the low-temperature phase. Such PTs happen mainly due to either mechanical stress or reducing temperature. This deformation can be characterized by the transformation strain tensor, \({\pmb {\varepsilon }}_{t}\), or Bain strain tensor. The existence of a finite number n of crystallographically equivalent variants of T can be implied from the relative symmetries of the A and T crystal lattices. All martensitic variants T\(_i\), \(i=1,2,\ldots ,n\) have the same components of \({\pmb {\varepsilon }}_{t}\) strain tensor in their respective crystallographic bases [46, 47]. In this PF theory, each of the T\(_i\) variants is described by an order parameter \(\eta _i\), \(i=1,2,\ldots ,n\). The evolution of each variant is described by the G–L equations. The G–L equations represent linear relationships between the rate of change of the order parameters, \(\dot{\eta }\), and generalized thermodynamic forces, X. The main computational advantage of the PF approach is that there is no need to explicitly track the interfaces. The interfaces evolve and form automatically from the solution of G–L equations. The solutions describe finite-width diffuse interfaces. Within such interfaces, the order parameters continuously change between their values in different phases. The main requirement of the thermodynamic potential is to possess the minima in order parameter space corresponding to A and each T\(_i\) variant and separated by an energy barrier[43, 48,49,50] for some temperature and stress ranges. In some theories, martensitic PT is described by the order parameters related to transformation strains [37, 40,41,42,43, 45, 51], while the order parameters in other models are the components of the strain tensor responsible for lattice instability [38, 39]. Here, the order parameters are related to the transformation deformation gradient tensor \({{\pmb {U}}}_{ti}\) for each martensitic variant. This is similar to PF theories described in [37, 40,41,42,43, 52,53,54]. The theory described in[40,41,42,43] have been generalized for large strain and lattice rotations [52, 55,56,57].

It is well known that material surface or interface is exposed to a biaxial tension [58]. The magnitude of the biaxial tension equals the surface energy \(\Gamma\). Due to this surface tension, there is a jump in normal stresses across an interface equal to \(2\Gamma /\xi\). Here \(\xi\) is the mean interface radius. This is also applicable to the case where interfaces do not support elastic stresses. However, most of the cases the material parameters for interfaces are unknown. Hence it is challenging to formalize simple constitutive equations that capture the complex, strongly heterogeneous properties, strains, and stresses fields across an interface. This problem has been overcome in [59, 60]. The interface stresses which is consistent with a sharp interface approach have been introduced for T–T interfaces [57, 59,60,61]. Moreover, the solid–solid and solid–liquid interfaces generate additional surface stress due to elastic deformations [59, 60]. More recently, multiphase PF theory for temperature- and stress-induced PTs are developed for n phases [62,63,64,65,66] and applied to martensitic PTs [62]. The PF theory in [54] only requires one-order parameter to describe variant–variant transformation and twinning. This formulation allows one to prescribe the twin interface energy and width and to introduce interface stresses consistent with the sharp interface limit. The thickness of the martensitic variant is of the order of 1 nm and they possess sharp tips. Hence, the interface stress plays a significant role in coherent elastic interfaces to reproduce non-trivial experimentally observed twinning microstructures [54, 62, 64].

In this paper, a PF model for PT between two martensitic variants and twinning between martensitic variants is presented from our previous theory [54] for a strict thermodynamic derivation of the PF equations that includes interface tension in the interfaces for both A–T and T–T PTs. This surface tension term is thermodynamically consistent with the sharp-interface limit for an arbitrary temperature and non-equilibrium interface. This PF theory is much more detailed and advanced than existing sharp-interface models for a coherent interface [67, 68]. Here, each martensitic variant is characterized by the rotation-free deformation of the crystal lattice. The key point is that martensite–martensite PT and all twinning within them are described with a single-order parameter. This significantly simplifies the description of martensite–martensite PT and multiple twinnings. In this theory, the total stress at the diffuse interface consists of elastic and dissipative parts. These stress components are evaluated from the solution of the coupled system of PF equations and viscoelasticity equations. From the solution of the stress components, interface stresses are obtained in the diffuse interface. The finite element method is implemented to solve the coupled PF and elasticity equations for cubic-to-tetragonal PT in NiAl alloy. The distribution and the effect of the interface tension are studied for both A–T and T–T interfaces. Additionally, problems on twinning in martensite and combined austenite-martensite and martensite-martensite PT and nanostructure evolution in a nanosize sample are solved. Some of the nontrivial experimentally observed microstructures of NiAl alloys which were reproduced in the simulations involving finite rotations [54], are analyzed in detail and corresponding stress distributions are shown during the morphological evolution. This includes bending, tip splitting, and twins crossing. Good quantitative agreement between simulation result and experimental micrograph for the bending angle is obtained. It is shown that the surface tension is an important factor influencing the stress and the PF solution significantly. This formulation can also be applied for liquid–liquid, solid–liquid, and liquid–gas diffuse interfaces and advances those theories consistent with the sharp interface approach for non-equilibrium conditions.

2 System of equations

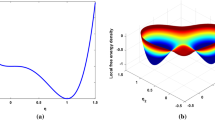
In this paper, two martensitic variants are considered which are denoted as T\(_1\) and T\(_2\). For generalization of n variants, PT is described by order parameter space of n-dimensional hypersphere [54]. Here, the austenite A is positioned at the origin (\(\Upsilon =0\), \(\vartheta =0\)) and the martensitic variants (T\(_1\) and T\(_2\)) are positioned at (\(\Upsilon =1\), \(\vartheta =0\)) and (\(\Upsilon =1\), \(\vartheta =1\)), respectively, as shown in Fig. 1a. The radial order parameter \(\Upsilon\), describes A\(\leftrightarrow\)T\(_1\) and A \(\leftrightarrow\)T\(_2\) PT. On the other hand, the angular order parameter \(\vartheta\), bounded by \(0 \le \vartheta \le 1\) describes twinning T\(_1\)\(\leftrightarrow\)T\(_2\) (variant–variant) transformations. Here, the angle between the radius vector \(\, { \Upsilon }\,\) and the positive axis of order parameter space is \(\,\pi \,\vartheta /2\,\). For generalized n variants, this description of order parameter space leads to the constraint \(\sum ^{n}_{i=1} \cos ^2 \left( \frac{\pi }{2} \vartheta _i \right) = 1\). This non-linear constraint significantly complicates the development of the thermodynamic potential which cannot satisfy all thermodynamic equilibrium and stability conditions for more than two martensitic variants. However, for single variant–variant or twinning transformation T\(_1\)\(\leftrightarrow\)T\(_2\), this constraint reduces to the linear constraint \(\vartheta _1+\vartheta _2=1\). For T\(_1\) and T\(_2\) variants, order parameter space and stress free Landau potential, \(\psi ^{l}\) are shown in Fig. 1 at thermodynamic equilibrium temperature between A and T.

Fig. 1
figure 1

a Schematic of the order parameter space with \(\Upsilon\) and \(\vartheta\); b contour plot of the stress-free Landau potential \(\psi ^{l} = \breve{\psi }^{\theta } +\psi ^\theta\), and c corresponding 3D plot of the potential surface at thermodynamic equilibrium temperature between \(\mathsf{A} - \mathsf{T}\) for NiAl. All the energies are in J/m\(^3\)

Full size image

The morphological evolution of martensitic microstructure and evolution of order parameters can be described by Ginzburg–Landau (G–L) equations. Thermodynamics and Landau–Ginzburg kinetics (see, e.g. [54]) lead to

$$\begin{aligned} \frac{1}{M_\Upsilon }\frac{\partial \Upsilon }{\partial t}= & {} -\frac{\rho }{\rho _0} \frac{\partial \psi ^h}{\partial \Upsilon }|_{\small {{\pmb {B}}}} +{{\pmb {\nabla }}} \cdot \left( \frac{\rho }{\rho _0} \frac{\partial \psi ^h}{\partial {{\pmb {\nabla }}} \Upsilon } \right) ; \nonumber \\ \frac{1}{M_\vartheta }\frac{\partial \vartheta }{\partial t}= & {} -\frac{\rho }{\rho _0} \frac{\partial \psi ^h}{\partial \vartheta }|_{\small {{\pmb {B}}}} +{{\pmb {\nabla }}} \cdot \left( \frac{\rho }{\rho _0} \frac{\partial \psi ^h}{\partial {{\pmb {\nabla }}} \vartheta } \right) . \end{aligned}$$
(1)

Here \({M_\Upsilon }\) and \({M_\vartheta }\) are the kinetic coefficients. These two set of equations describe A \(\leftrightarrow\)T\(_{1,2}\) and T\(_1 \leftrightarrow\)T\(_2\) PTs, respectively. The terms \({\partial \psi^h }/{\partial \Upsilon }\) and \({\partial \psi^h }/{\partial \vartheta }\) are calculated at constant finite strain \({{\pmb {B}}}\). The Helmholtz free energy is given by the following expression:

$$\begin{aligned} \psi ^h = \psi ^e( \Upsilon ,{{\pmb {B}}}, \vartheta , \theta ) + \frac{\rho _0}{\rho } \breve{\psi }^{\theta } +\psi ^\theta + \frac{\rho _0}{\rho }\psi ^\nabla , \end{aligned}$$
(2)

where \(\psi ^e({{\pmb {B}}}, \Upsilon , \vartheta , \theta )\) is the elastic part, \(\frac{\rho _0}{\rho } \breve{\psi }^{\theta }\) is the energy barrier between phases, \(\psi ^\theta\) is the phase transformation thermal driving force, and \(\frac{\rho _0}{\rho }\psi ^\nabla\) is the interfacial gradient energy.

Thermal part of the free energy \(\psi ^\theta\) is expressed as

$$\begin{aligned} \psi ^\theta = -\Delta s (\theta -\theta _\mathrm{e})q (\Upsilon ); \quad q (\Upsilon ) = 3\Upsilon ^2-2 \Upsilon ^3, \end{aligned}$$
(3)

where \(\theta _\mathrm{e}\) is the stress free A and T thermodynamic equilibrium temperature, and \(\theta _\mathrm{c}\) is the critical temperature for stress-free A. \(\breve{\psi }^{\theta }\) is the energy barrier term which is defined as

$$\begin{aligned} \breve{\psi }^\theta&= (3 \Delta s(\theta -\theta _\mathrm{e})+ A_0 \left( \theta - \theta _\mathrm{c} \right) ) \Upsilon ^2 (1-\Upsilon )^2\nonumber \\&\quad + \bar{A} \sum \, (1-\vartheta _1)^2 (1-\vartheta _2)^2 (3\Upsilon ^2-2 \Upsilon ^3), \end{aligned}$$
(4)

where \(A_0\) and \(\bar{A}\) characterize the barriers for A–T\(_{1, 2}\) and T\(_1\)–T\(_2\) transformations, respectively. The gradient energy is defined as

$$\begin{aligned} \psi ^\nabla = \frac{\beta _\Upsilon }{2} |{{\pmb {\nabla }}} \Upsilon |^2 + q (\Upsilon ) \frac{\beta _\vartheta }{4} \sum _{i=1}^{n}|{{\pmb {\nabla }}} \vartheta _i|^2 , \end{aligned}$$
(5)

where \(\beta _\Upsilon\) and \(\beta _\vartheta\) are gradient energy coefficients. The Cauchy stress tensor can be expressed as [54],

$$\begin{aligned} {\pmb {\sigma }}= & {} \frac{\rho }{\rho _0} {{\pmb {V}}} \cdot \frac{\partial \psi ^h}{\partial {{\pmb {B}}}} \cdot {{\pmb {V}}} - \frac{\rho }{\rho _0} \left( {{\pmb {\nabla }}} \Upsilon \otimes \frac{\partial \psi ^h}{\partial {{\pmb {\nabla }}} \Upsilon }\right) _s \nonumber \\&- \sum _{i=1}^{n-1} \frac{\rho }{\rho _0} \left( {{\pmb {\nabla }}} \vartheta _i \otimes \frac{\partial \psi ^h}{\partial {{\pmb {\nabla }}} \vartheta _i}\right) _s. \end{aligned}$$
(6)

Here, \({{\pmb {V}}}\) is the left stretch tensor, \({{\pmb {B}}}\) is the finite strain measure, \(\rho\) and \(\rho _0\) are the mass densities in the deformed and undeformed states. The Cauchy stress tensor can be represented as following:

$$\begin{aligned} {\pmb {\sigma }} = {\pmb {\sigma _\mathrm{e}}}+{\pmb {\sigma _{\mathrm{st}}}}. \end{aligned}$$
(7)

where \({\pmb {\sigma _\mathrm{e}}}\) is the elastic stress tensor which can be expressed as follows:

$$\begin{aligned} {\pmb {\sigma _\mathrm{e}}} =K\varepsilon _{\mathrm{0e}} {\pmb {I}}+ 2\mu {\pmb {e}}_\mathrm{e}, \end{aligned}$$
(8)

where \({\pmb {I}}\) is unit tensor. K and \(\mu\) are bulk and shear elastic moduli of phases, respectively. Additionally, \(\varepsilon _{\mathrm{0e}}\) and \({\pmb {e}}_\mathrm{e}\) are the elastic volumetric strain and the elastic deviatoric strain tensor, respectively. The term \({\pmb {\sigma _{\mathrm{st}}}}\) is defined as a non-mechanical type of stress called “surface tension” [54].

$$\begin{aligned} {\pmb {\sigma }}_{st}= & {} (\psi ^{\nabla }+\breve{\psi _{\theta }}){\pmb {I}}-\beta _{\Upsilon }{\pmb {\nabla }}\Upsilon \,\otimes \, {\pmb {\nabla }}\Upsilon \nonumber \\&-q(\Upsilon )\,\beta _{\vartheta }{\pmb {\nabla }}\vartheta \,\otimes \, {\pmb {\nabla }}\vartheta . \end{aligned}$$
(9)

Finally, for two martensitic variants, the G–L equations are simplified to

$$\begin{aligned} \frac{1}{M_{\Upsilon }}\, \frac{\partial \Upsilon }{\partial t}= & {} {\pmb {\sigma }}_\mathrm{e}{{\pmb {:}}}\left( {{\pmb {R}}}_\mathrm{e} \cdot \frac{\partial {{\pmb {U}}}_\mathrm{t}}{\partial \Upsilon } \cdot {{\pmb {U}}}_t^{-1}\cdot {{\pmb {R}}}_\mathrm{e}^t\right) _s \nonumber \\&- \frac{\rho }{\rho _o}\,\frac{\partial \psi ^\theta }{\partial \Upsilon }- \frac{\partial \breve{\psi ^\theta }}{\partial \Upsilon }-\frac{\partial {\psi ^\nabla }}{\partial \Upsilon }+ {\pmb {\nabla }}\cdot \left( \frac{\partial \psi ^\nabla }{\partial {\pmb {\nabla }}\Upsilon }\right) \nonumber \\= & {} {\pmb {\sigma }}_\mathrm{e}{{\pmb {:}}}\left( {{\pmb {R}}}_\mathrm{e} \cdot \frac{\partial {{\pmb {U}}}_\mathrm{t}}{\partial \Upsilon } \cdot {{\pmb {U}}}_t^{-1}\cdot {{\pmb {R}}}_\mathrm{e}^t\right) _s +\frac{6\Delta s (\theta -\theta _\mathrm{e})}{1+\varepsilon _\mathrm{o}}(1-\Upsilon )\Upsilon \nonumber \\&-6\bar{A}\Upsilon \vartheta ^2(1-\vartheta )^2(1-\Upsilon )\vartheta ^2 \nonumber \\&- 2A_0 \left( \theta _\mathrm{e} - \theta _\mathrm{c} \right) \Upsilon (1-3\Upsilon +2\Upsilon ^2) \nonumber \\&-3 \beta _{\vartheta }\Upsilon (1-\Upsilon )|{\pmb {\nabla }}\vartheta |^2+\beta _{\Upsilon } {\pmb {\nabla }}^2 \Upsilon ; \end{aligned}$$
(10)
$$\begin{aligned} \frac{1}{M_{\vartheta }}\, \frac{\partial \vartheta }{\partial t}= & {} {\pmb {\sigma }}_\mathrm{e}{{\pmb {:}}}\left( {{\pmb {R}}}_e \cdot \frac{\partial {{\pmb {U}}}_\mathrm{t}}{\partial \vartheta } \cdot {{\pmb {U}}}_t^{-1}\cdot {{\pmb {R}}}_e^t\right) _s \nonumber \\&- \frac{\partial \breve{\psi ^\theta }}{\partial \vartheta }+ {\pmb {\nabla }}\cdot \left( \frac{\partial \psi ^\nabla }{\partial {\pmb {\nabla }}\vartheta }\right) \nonumber \\= & {} {\pmb {\sigma }}_\mathrm{e}{{\pmb {:}}}\left( {{\pmb {R}}}_\mathrm{e} \cdot \frac{\partial {{\pmb {U}}}_\mathrm{t}}{\partial \vartheta } \cdot {{\pmb {U}}}_t^{-1}\cdot {{\pmb {R}}}_\mathrm{e}^t\right) _s -2\bar{A}\vartheta q(\Upsilon )(1-3\vartheta +2\vartheta ^2) \nonumber \\&+ \beta _{\vartheta } q(\Upsilon ) {\pmb {\nabla }}^2 \vartheta . \end{aligned}$$
(11)

3 Numerical results

3.1 Material parameters

In this paper, cubic to tetragonal PTs is considered for NiAl alloy. The corresponding material parameters are taken from [40, 41, 54]. The PF parameters used in the simulation are: \(a=3\), \(\theta _\mathrm{c}= -183\) K, \(\theta _\mathrm{e}= 215\) K, \(A_0=-3 \Delta s=4.42\) MPa K\(^{-1}\), \(\bar{A}=5320\) MPa, \({M_\Upsilon } = {M_\vartheta } = 2596.53\) m\(^2\)/Ns, \(\beta _\Upsilon = \beta _\vartheta = 5.18\times 10^{-10}\) N; \(\theta = 100\,\)K, unless otherwise stated. In the plane stress 2D FEM simulation, two martensitic variants: T\(_1\) and T\(_2\), are considered. The transformation strains in the cubic axes of T\(_1\) is \({\pmb {\varepsilon }}_{t1}=(0.2153,-0.0783,-0.0783)\) and T\(_2\) is \({\pmb {\varepsilon }}_{t2}=(-0.0783,0.2153,-0.0783)\). Twin interface energy is calculated as \(E_{\scriptscriptstyle TT}= 0.9583\) J/m\(^2\) and width \(\Delta _{\scriptscriptstyle TT}= 0.8323\) nm. For simplicity, isotropic linear elasticity is used. The values of bulk modulus \(K=112.85\,\) GPa and shear modulus \(\mu =65.14\,\) GPa are used. All external stresses are considered normal to the deformed surface.

3.2 Numerical implementation

The system of equations is implemented and solved with the finite element code COMSOL [69], using the arbitrary Lagrangian– Eulerian approach. The numerical procedure is well matched with the analytical solution [62, 63] for each interface (A–T\(_1\), A–T\(_2\) and T\(_1\)–T\(_2\)) for validation of the model. The order parameters are similar to concentrations of different species, while \({\pmb {\varepsilon }}_{\mathrm{t}}\) can be treated as concentration strain, which has a sophisticated dependence on concentration. Ginzburg–Landau equation has a similar structure with a diffusion equation with complex stress–concentration interaction and cross effect between the diffusion of different species though Fick’s law. Thus, Ginzburg–Landau equations are solved using transient diffusion equations in the deformed configuration [69]. Additionally, a structural application module is used to solve elasticity equations. Lagrange quadratic triangular elements have been used with five to six elements per interface width. This is implemented to achieve a mesh-independent solution [54]. Furthermore, the mesh independent solution is confirmed by varying size of the mesh from 0.05 to 0.1 nm. In order to minimize numerical error, the adaptive mesh generation is implemented which identifies the regions that require a high resolution and produce an appropriate mesh. Finally, G–L equations are solved by implementing the backward Euler integration technique and segregated time-dependent solver [69]. During simulations, the automatic time-stepping method with relative tolerance of \(10^{-5}\) is used. This application mode provides a more accurate solution for our problem.

3.3 Austenite–Martensite (A–T) interface

In this section, an equilibrium \(\mathsf{A}\)–\(\mathsf{T}_1\) interface is considered. The profile of order parameter; \(\Upsilon\) and the parts of energies which are localized in the interface; \(\breve{\psi }^\theta\) and \(\psi ^\nabla\) are presented in Fig. 2. More importantly, principal stress component; \(\sigma ^{yy}\) for the case considering surface tension \(\sigma ^{yy}_{\mathrm{st}}\) and without \(\sigma ^{yy}_{\mathrm{st}}\) for equilibrium \(\mathsf{A}\)–\(\mathsf{T}_1\) interface are shown in Fig. 3. Here first martensitic variant \(\mathsf{T}_1\) is considered. \(\mathsf{T}_1\) and \(\mathsf{T}_2\) are the equivalent energy phases. They are differed only by the transformation strain. The square sample of size 50  nm \(\times\) 50  nm is considered as an initial sample of austenitic state. The crystal lattice of \(\mathsf{T}_1\) is then rotated by \(\alpha =36.5^\circ\) in one part of the sample to get \({\pmb {\varepsilon }}_{t1}^y=0\) at the interface (Fig. 2a). This is resulted in the reduction of the internal stress at the vertical \(\mathsf{A}\)–\(\mathsf{T}_1\) interface and corresponding transformation strain component \({\pmb {\varepsilon }}_{t1}=(0.113,\, 0,\, 0.1305)\). Here, homogeneous stationary temperature \(\theta = \theta _\mathrm{e}= 215\) K is considered. In the left half of the sample, initial condition of order parameters are \(\Upsilon =0.001\) and \(\vartheta =0\) corresponding to \(\mathsf{A}\) and right part of the sample \(\Upsilon =0.999\) and \(\vartheta =0\) corresponding to \(\mathsf{T}_1\) are prescribed (see Fig. 1). The external stress is neglected in the deformed configuration. Initial condition for stress is \({\pmb {\sigma }}={\pmb {\sigma }}_{\mathrm{st}}\). When right part of the sample is transformed to \(\mathsf{T}_1\) for \(\Upsilon =0.999\), the deformed sample state is shown in Fig. 2a and corresponding stationary distribution of \(\Upsilon\) is shown in Fig. 2b near to the \(\mathsf{A}\)–\(\mathsf{T}_1\) interface, along the line passing through the middle of the square sample. Additionally, the local thermal energy that contributes to the interface stresses, \(\breve{\psi }^\theta\) is presented in Fig. 2c and gradient energy, \(\psi ^\nabla\) in Fig. 2d. For stress-free case, the distribution of \(\Upsilon\) matches exactly with analytical solution in [62, 63]. The distribution of the gradient energy, \(\psi ^\nabla\) coincides with the distribution of the local energy, \(\breve{\psi }^\theta\) for both \(\mathsf{A}\)–\(\mathsf{T}_1\) and \(\mathsf{A}\)–\(\mathsf{T}_2\) interfaces.

Fig. 2
figure 2

a Distribution of order parameter \(\Upsilon\) for \(\mathsf{A}\)–\(\mathsf{T}_1\) interface of initially squared austenitic sample of size \(50 nm \times 50 nm\). Martensitic variant \(\mathsf{T}_1\) is rotated by \(\alpha =36.5^{\circ }\) to get \({\pmb {\varepsilon }}_{t1}^y=0\) at \(\mathsf{A}\)–\(\mathsf{T}_1\) interface. b Stationary solution of \(\Upsilon\), c local energy \(\breve{\psi }^\theta\) and d gradient energy \(\psi ^\nabla\) near to \(\mathsf{A}\)–\(\mathsf{T}_1\) interface along the line passing through the middle of the square sample. All the energies are in J/m\(^3\)

Full size image

The distribution of \(\sigma ^{yy}\) considering \(\sigma ^{yy}_{\mathrm{st}}\) (see Fig. 3a, b) and neglecting \(\sigma ^{yy}_{\mathrm{st}}\) (see Fig. 3c, d) are shown. For \(\sigma ^{yy}_{\mathrm{st}}=0\), there is a significant stress \(\sigma ^{yy}\) distribution, concentrated at \(\mathsf{A}\)–\(\mathsf{T}_1\) interface. In this case, left most austenitic part is subjected to under compression while right most part of the \(\mathsf{T}_1\) is under tension. It is noteworthy to mention that the state of stress changed rapidly near to the interface as shown in Fig. 3d. The maximum value of \(\sigma ^{yy}_{\mathrm{st}}\) is almost equal to \(\sigma ^{yy}\) at the interface, as shown in Fig. 3b. Due to the asymmetry of the deformed geometry, there exist an asymmetry in \(\sigma ^{yy}_{\mathrm{st}}\) distribution. On the other hand, for the case where \(\sigma ^{yy}_{\mathrm{st}}\ne 0\), the magnitude of \(\sigma ^{yy}\) is much higher. It is noteworthy to mention that the distribution of \(\sigma ^{yy}_{\mathrm{st}}\) changes the overall distribution of \(\sigma ^{yy}\), increasing tensile stress and moving the maximum value to the center of the sample (see Fig. 3b).

Fig. 3
figure 3

Distribution of y-component of principal stress \(\sigma ^{yy}\) for \(\mathsf{A}\)–\(\mathsf{T}_1\) interface of initially austenitic squared sample of size 50 nm \(\times\) 50 nm for the cases (a) with surface tension \(\sigma ^{yy}_{\mathrm{st}}\) and c without \(\sigma ^{yy}_{\mathrm{st}}\). b Plot of \(\sigma ^{yy}\) considering \(\sigma ^{yy}_{\mathrm{st}}\) and d neglecting \(\sigma ^{yy}_{\mathrm{st}}\), along the line passing through the middle of the square sample. Variant \(\mathsf{T}_1\) is rotated by \(\alpha =36.5^\circ\) to get \({\pmb {\varepsilon }}_{t1}^y=0\) at \(\mathsf{A}\)–\(\mathsf{T}_1\) interface. All the stresses are in GPa

Full size image

3.4 Martensite–Martensite (T–T) interface

Here, pure \(\mathsf{T}_1\)–\(\mathsf{T}_2\) interface is considered in an initial austenitic square sample of size 50 nm \(\times\) 50 nm. Temperature is kept as 100 K, below equilibrium temperature \(\theta _e\). This condition ensures the formation of martensitic variants only. On the left part of the sample, the crystal lattice of \(\mathsf{T}_1\) is rotated by \(\alpha =36.5^\circ\) and on the right part \(\mathsf{T}_2\) is rotated by \(\alpha =-36.5^\circ\) to get \({\pmb {\varepsilon }}_{t1}^y={\pmb {\varepsilon }}_{t2}^y=0\). This choice of transformation strain relaxes internal stress at \(\mathsf{T}_1\)–\(\mathsf{T}_2\) interface. The corresponding transformation strains in the cubic axes are \({\pmb {\varepsilon }}_{t1}=(0.113,\,0,\,0.1305)\) and \({\pmb {\varepsilon }}_{t2}=(0.113,\,0,\,-0.1305)\) for \(\mathsf{T}_1\) and \(\mathsf{T}_2\) variants, respectively. On the left half of the sample, initial condition of order parameters are \(\Upsilon =1\) and \(\vartheta =0.001\) corresponding to \(\mathsf{T}_1\) and right part of the sample \(\Upsilon =1\) and \(\vartheta =0.999\) corresponding to \(\mathsf{T}_2\). One point of the external surface is completely fixed in x and y-directions and the other one is fixed in x-direction to avoid rigid body motion. There is no external stress considered in this case. The initial condition for stress is \({\pmb {\sigma }}={\pmb {\sigma }}_{\mathrm{st}}\). The stationary solution of deformed state of the sample is shown in Fig. 4a with finite interface. The profile of order parameter \(\vartheta\) is plotted close to \(\mathsf{T}_1\)–\(\mathsf{T}_2\) interface as shown in Fig. 4b. The profile of \(\vartheta\) is exactly matches with analytical solution in [62, 63] for the stress-free condition. Again, the distribution of gradient energy \(\psi ^\nabla\) coincides with the distribution of the local energy \(\breve{\psi }^\theta\), presented in Fig. 4c, d.

Fig. 4
figure 4

a Distribution of order parameter \(\vartheta\) for \(\mathsf{T}_1\)–\(\mathsf{T}_2\) interface of initially squared austenitic sample of size 50 nm \(\times\) 50 nm. Variant \(\mathsf{T}_1\) is rotated by \(\alpha =36.5^\circ\) and \(\mathsf{T}_2\) is rotated by \(\alpha =-36.5^\circ\) to get \({\pmb {\varepsilon }}_{t1}^y={\pmb {\varepsilon }}_{t2}^y=0\) at \(\mathsf{T}_1\)–\(\mathsf{T}_2\) interface. b Stationary distribution of \(\vartheta\), c local energy \(\breve{\psi }^\theta\) and d gradient energy \(\psi ^\nabla\) near to \(\mathsf{T}_1\)–\(\mathsf{T}_2\) interface along the line passing through the middle of the square sample. All the energies are in J/m\(^3\)

Full size image

For \(\sigma ^{yy}_{\mathrm{st}}=0\), the magnitude of \(\sigma ^{yy}\) is significantly high throughout the sample with stress reversibility in the interface as shown in Fig. 5c, d. At the midsection of the sample near to the interface, the zone of stress concentration is comparatively larger. Away from the interface, \(\mathsf{T}_1\) is under compression while \(\mathsf{T}_2\) is under tension. On the other hand, when \(\sigma ^{yy}_{\mathrm{st}} \ne 0\), the magnitude of \(\sigma ^{yy}\) is much higher in the interface (see Fig. 5a, b). In this case, the distribution of \(\sigma ^{yy}\) is symmetric with maximum value at interface due to contribution of \(\sigma ^{yy}_{\mathrm{st}}\). The maximum value of \(\sigma ^{yy}\) and \(\sigma ^{yy}_{\mathrm{st}}\) coincide at the interface as in Fig. 5b. Due to stress free boundary condition, \(\sigma ^{yy}\) is close to zero at the intersection of the interface and the free surface.

Fig. 5
figure 5

Distribution of y-component of principal stress \(\sigma ^{yy}\) for \(\mathsf{T}_1\)–\(\mathsf{T}_2\) interface of initially austenitic squared sample of size 50 nm \(\times\) 50 nm for the cases a with surface tension \(\sigma ^{yy}_{st}\) and c without \(\sigma ^{yy}_{st}\). b Plot of \(\sigma ^{yy}\) considering \(\sigma ^{yy}_{st}\) and d neglecting \(\sigma ^{yy}_{\mathrm{st}}\), along the line passing through the middle of the square sample. Variant \(\mathsf{T}_1\) is rotated by \(\alpha =36.5^\circ\) and \(\mathsf{T}_2\) is rotated by \(\alpha =-36.5^\circ\) to get \({\pmb {\varepsilon }}_{t1}^y={\pmb {\varepsilon }}_{t2}^y=0\) at \(\mathsf{T}_1\)–\(\mathsf{T}_2\) interface. All the stresses are in GPa. Distribution of y-component of principal stress \(\sigma ^{yy}\) for \(\mathsf{T}_1\)–\(\mathsf{T}_2\) interface of initially austenitic squared sample of size 50 nm \(\times\) 50 nm for the cases a with surface tension \(\sigma ^{yy}_{\mathrm{st}}\) and c without \(\sigma ^{yy}_{\mathrm{st}}\). b Plot of \(\sigma ^{yy}\) considering \(\sigma ^{yy}_{\mathrm{st}}\) and d neglecting \(\sigma ^{yy}_{\mathrm{st}}\), along the line passing through the middle of the square sample. Variant \(\mathsf{T}_1\) is rotated by \(\alpha =36.5^\circ\) and \(\mathsf{T}_2\) is rotated by \(\alpha =-36.5^\circ\) to get \({\pmb {\varepsilon }}_{t1}^y={\pmb {\varepsilon }}_{t2}^y=0\) at \(\mathsf{T}_1\)-\(\mathsf{T}_2\) interface. All the stresses are in GPa

Full size image

3.5 Bending and spliting of martentisitic tips in NiAl alloys

To validate the correctness of our theory and show the importance of interfacial stress to predict the experimental microstructure, some of the interesting and nontrivial experimentally observed microstructures for NiAl alloys [70,71,72] are reproduced. Since numerous alternative solutions may exist, initial conditions are chosen carefully. It is done with several steps as follows. First, an initial random distribution of order parameter \(\Upsilon\) is prescribed. The value of \(\Upsilon\) in the range [0; 0.45] is considered in a square sample of 50  nm \(\times\) 50  nm with the austenite lattice rotated by \(\alpha =45^\circ\) (see Fig. 6a). The initial value of \(\vartheta = 0.5\) was used throughout the sample. Normal displacement and shear stress are considered as zero in one horizontal surface and one vertical surface. In two other surfaces, constant biaxial normal strain of magnitude 0.01 is used. Shear stresses are prescribed zero at external surfaces. Plane stress condition is assumed. The temperature of \(\theta =50\) K is studied. Finally, the evolution of \(\Upsilon (2\vartheta -1)\) is presented in Fig. 6. It shows the transformation of the austenite into martensite and corresponding morphological evolution.

Fig. 6
figure 6

Left column: evolution of \(\Upsilon (2\vartheta -1)\) in a square sample of size 50 nm \(\times\) 50 nm. Partial A sample transformed into martensitic variants and twinning morphology observed as a stationary microstructure. Second and third columns: normal stress, \(\sigma _y\) and difference of two normal stress components, \(\sigma _x-\sigma _y\); right column: shear stress component, \(\sigma _{xy}\). Blue and red are for martensitic variants \(\mathsf{T}_1\) and \(\mathsf{T}_2\), respectively. All the values of stress are in GPa

Full size image

Martensitic varients try to form horizontal and vertical interfaces between twins and interfaces between martensite and austenite under angles \(\pm 45^\circ\), all corresponding to the invariant plane interfaces. Asymmetry in the initial condition provides the driving force for the formation of a horizontal twin structure. In between two martensitic twin austenite is observed near vertical sides to satisfy the symmetric boundary condition.

Fig. 7
figure 7

Left column: evolution of \(\Upsilon (2\vartheta -1)\) in a square sample of size 50 nm \(\times\) 50 nm with an initial condition shown in Fig. 6c. Second and third columns: normal stress, \(\sigma _y\) and difference of two normal stress components, \(\sigma _x-\sigma _y\); right column: shear stress component, \(\sigma _{xy}\). Blue and red are for martensitic variants \(\mathsf{T}_1\) and \(\mathsf{T}_2\), respectively. All the values of stress are in GPa

Full size image

Final solution from Fig. 6c is considered as initial solution for the next problem. Temperature is reduced to \(\theta = 0 K\). \(\beta _\vartheta\) is considered as \(\beta _\vartheta = 5.187\times 10^{-11}\) N which led to twin interface energy \(E_{\scriptscriptstyle MM}= 0.304\) J/m\(^2\) and width \(\Delta _{\scriptscriptstyle MM}= 0.262\) nm. The components of transformation strains have been changed to the values \({\pmb {U}}_{t1}=(k_1, k_2,k_2)\) and \({\pmb {U}}_{t2}=(k_2,k_1,k_2)\) with \(k_1=1.15\) and \(k_2=0.93\) corresponding to NiAl alloy in [70,71,72]. The value of \(\Upsilon\) is considered equal to 1 in the sample. During the evolution of microstructure, splitting of the initial twins is observed (Fig. 7). This the due to reduction in the interface energy.

Fig. 8
figure 8

a Comparison of simulation result with TEM image of NiAl alloy [70]. b zoomed part of simulation results from Fig. 7c; c TEM microscopy image of NiAl alloy [70]. Simulations reproduce tip splitting and bending angle of martensite twins. d Difference of two normal stress components, \(\sigma _x-\sigma _y\); f shear stress component, \(\sigma _{xy}\). Blue and red are for martensitic variants \(\mathsf{T}_1\) and \(\mathsf{T}_2\), respectively. All the values of stress are in GPa

Full size image

During the evolution, rigid vertical boundaries help the formation of high elastic energy in the absence of austenite. In order to reduce the high elastic stress, vertical twin formation has occurred. This twin microstructure formation is proportional in each of the vertical sides due to prescribed horizontal strain (Fig. 7a, b). In the final microstructure after twins are fully developed, bending and splitting of martensitic tips is observed (Figs. 7c, 8) similar to experiments [70, 71]. Since between T\(_1\) and T\(_2\) there is invariant plane interface, it requires mutual rotation of these variants by the angle \(\beta =12.1^\circ\) (\(\cos \beta = 2 k_1 k_2/(k_1^2+k_2^2)= 0.9778\)) [70]. Here the angle between horizontal and vertical variants T\(_2\) is \(1.5 \beta =18.15^\circ\), which is in good agreement with our simulations. Here interface between horizontal and vertical variants T\(_2\) is not invariant plane type interface due to large lattice rotations. It is worth mentioning that the narrowing and bending of the tips of one T\(_2\) horizontal plates due to the reduction of the boundary area. It is caused by a reduction in the internal stresses at this boundary. Measured angles between the tangent to the bent tip and horizontal line in the experiment [70] and in calculations (Fig. 8) are in good quantitative agreement.

Fig. 9
figure 9

Comparison of simulation result with TEM image of NiAl alloy [70]. a Final solution for \(\Upsilon (2\vartheta -1)\) in a sample and b its zoomed part near left side of a sample; c TEM microscopy image of NiAl alloy [70]. For both experiment and simulation, crossed twins are observed. d Difference of two normal stress components, \(\sigma _x-\sigma _y\); f shear stress component, \(\sigma _{xy}\). Austenite is represented as green. Blue and red are for martensitic variants \(\mathsf{T}_1\) and \(\mathsf{T}_2\). All the values of stress are in GPa

Full size image

In Fig. 7, the intermediate values of \(\vartheta\) in some regions during microstructure evolution in some regions (see \(t=125\) and 210)are noticeable. One twin penetrates in to region of another twin, results in crossed twins type microstructure. They were also observed in experiments [72]. In our simulations in Fig. 7, they represent intermediate stage of twin evolution. In some experiments they have been arrested and produced stable microstructure (Fig. 9). In our case, if \(\bar{A}\) is reduced to 0.532 GPa, such crossed twins became stable (Fig. 9). Moreover in Fig. 9, twins T\(_2\) are surrounded by twins T\(_1\), which is also observed in experiments [70]. In [72], twin boundaries consist of two different deformation variants that correspond to a case where the angle \(\alpha\) between the two types of twin planes is close to \(\alpha =85^\circ\) (Fig. 9c), which is in good agreement with our simulations (Fig. 9b). When observing the macrotwin boundaries as in Fig. 9c, it is seen that the large volume fraction of twin variant is close to parallel with the macrotwin interface and the tips of the smallest volume fraction of the twin variants are observed to curve towards the macrotwin boundaries, which is reproduced in our simulation in Fig. 9a. Moreover, most of the cases the twin planes are visibly bending or reorienting in areas close to the interface and the small microtwin variants penetrating into the other varients (see Figs. 8a, 9a). In these zones, the formation of a needle-like microtwin occurs which usually tapered to the microtwin boundary, and the penetrating microtwin variant tends to disappear. It is observed that these zones are subject to an extra bending deformation and some tip splitting which is also found in our simulation in Fig. 8a. However, the microtwin planes tend to bend gradually when approaching the macrotwin interface. Components of the stress fields, including interface stresses, are also shown. In most of the cases, they are excluded from the literature because of large artificial oscillations. Here there are no oscillations. Moreover, stress concentration has a regular character. This underlines the advantages of the current simulations. Since twin boundaries represent invariant plane, it is generally seen that in a sharp interface approach those invariant planes are stress-free and do not generate elastic energy. But in this model, large shear stress \(\sigma _{xy}\) is observed. \(\sigma _{xy}\) changes the sign across the twin interface. To accommodate the large alternating shears across a finite-width interface, large shear stress appears in the constraint sample. Thus, starting with a microstructure in Fig. 6, which is quite far from the final one, this model is able to reproduce three types of experimentally observed nontrivial microstructures of NiAl alloy involving finite rotations. This includes bending, tip splitting, and twins crossing. Good quantitative agreement between simulation result and experimental micrograph for the bending angle is obtained.

4 Conclusion

Summarizing, a PF approach of PTs between austenite to martensitic variants and twinning between martensitic variants is presented with the main focus on the effect of interfacial stress on phase transformations. This theory allows to introduce interface stress tensor which essentially transforms to biaxial tension. This model requires only one order parameter to describe variant–variant transformation and twinnings. The interface stresses do not contribute directly to the G–L equations but it can change the elastic stress. The finite element method is implemented to solve the coupled PF and elasticity equations for cubic-to-tetragonal PTs in NiAl alloy. The effects of interfacial stress are studied for both austenite–martensite and martensite–martensite interfaces. Additionally, problems on twinning in martensite and combined austenite–martensite and martensite–martensite transformations are shown. Different types of nontrivial experimentally observed microstructures which were reproduced in the simulations [54] are discussed in detail. It includes tip splitting, bending, and twins crossing. It is found that the interfacial stress is an important factor, influencing the stress distribution at interfaces and the PF solution significantly. This developed theory and expression for the interface stresses can be directly applied to other temperature- and stress-induced transformations such as liquid–liquid transformation, reconstructive phase transformations, amorphization/crystallization, evaporation, sublimation, melting, etc.