1 Introduction

Perovskite manganese oxides with the general formula Re1−xAxMnO3 (Re = rare-earth and A = divalent alkaline earth ions) have been revitalized in the last few years, this interest is due to their attractive electrical and magnetic properties [1,2,3,4,5] and their importance for several applications, such as in spintronics, information storage, magnetic recording media, gas sensors and magnetic refrigeration applications [6,7,8]. In addition, these materials have many advantages, such as their low production cost, convenient preparation, high refrigeration efficiency, small volume requirement and chemical stability. Besides, these materials are environment-friendly, non toxic and do not cause for noise pollution. This makes them attractive to further research in relation to the widely used refrigeration technology based on gas compression. To understand the different physical properties of these materials, many theories such as double-exchange (DE) interaction and Griffiths singularity have been proposed [9]. Basically, these physical phenomena are directly related to ferromagnetic (FM) or antiferromagnetic (AFM) interactions. According to DE phenomenon, the charge carrier of the system, for example, transfers from Mn3+ to Mn4+ via oxygen. Furthermore, the strong Hund’s coupling between the Mn site and for example, causes an FM interaction, while Mn3+–O2−–Mn3+ and Mn4+–O2−–Mn4+ super exchange (SE) interaction makes an AFM ordering. Consequently, according to the ratio of Mn3+/Mn4+ ions, these two orders can coexist in a single sample. However, DE phenomenon is insufficient to explain the importance of physical properties in manganites. In addition, Griffiths phase can explain these complex phenomena. Recently, Griffiths phase has been used to survey the magnetic properties of diverse compounds, such as: rare-earth inter-metallic compounds Tb5Si2Ge2 [10] and hole perovskite-doped manganites [11,12,13,14,15]. The existence of Griffiths phase is due to the presence of FM clusters in paramagnetic (PM) parts. Besides, the physical properties of perovskite managnites are highly influenced by other factors, such as the method of preparation and the doping level in the Re (La) or Mn site. For instance, doping LaMnO3 sample in the La site by Sr2+ involves the presence of the mixed valence Mn3+ and Mn4+ at the Mn site, and this compound (LaSrMnO3) becomes FM and conducting. These manganites are acquiring a growing interest in magnetic refrigeration technology for their large magnetocaloric effect (MCE) [16]. In addition, La0.67Ca0.33MnO3 presents a second-order transition at 272 K and a large MCE (− ∆SM = 3.6 J/kg K) under an applied magnetic field of 1 T [17]. Betancourt et al. have been reported that La0.67Ba0.33MnO3 sample shows a − ∆SM of 1.06 J/kg K under an applied magnetic field of 2.5 T at 340 K, which makes this sample a potential candidate for magnetic refrigeration [18]. The sample La0.67Ba0.22Sr0.11MnO3 presents large − ∆SM of about 2.26 J/kg K at µ0H = 5T and a Curie temperature (TC) at 450 K [19], while the value of − ∆SM = 4.91 J/kg K at TC = 350 K and µ0H = 5T for La0.67Ba0.23Ca0.1MnO3 composition [20]. However, its TC is remote from room temperature, restricting its applicability in traditional cooling devices.

To adjust these physical properties, Mn-site itself is doped with other transition elements such as In, Cr, Co, Fe, Ti, Al [19, 21,22,23,24]. Recently, it has been shown that with increasing the doping rate of Fe at B-site, TC and − ∆SM decrease [25]. Reshmi et al. state that the Ni substitution in La0.67Sr0.33MnO3 reduced TC to about room temperature but the maximum of − ∆SM decreased.

This paper aims at studying the effect of titanium on the structural, magnetic and MCE properties in La0.67Ba0.25Ca0.08MnO3 compound.

2 Experimental details

The flux method is a simple and low-cost strategy to prepare materials. It cannot affect the microstructure [26, 27]. In this process, for La0.67Ba0.25Ca0.08MnO3 sample, stoichiometric amounts of La2O3, BaCO3, CaCO3 and MnO2 precursors were taken in the appropriate molar ratio. For La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 sample, La2O3, BaCO3, CaCO3, MnO2 and TiO2 precursors were used. The mixture was ground in an agate mortar for 2 h with an appropriate quantity of KCl. The adding of KCl is to expedite thermal ionic diffusion in the solid state, thereby weakening the activation barriers to ceramic synthesis and sintering. In addition, it avoids the evaporation of precursors. The obtained powder was heated in an alumina crucible at 800 °C for 24 h. Then, it was washed with hot distilled water to remove KCl salts. The residue was dried at 100 °C in air. After being ground well, the powders were pressed at 105 Pa into circular pellets (e = 1 mm and d = 10 mm), then sintered in the air at 1000 °C for 24 h. The structure and phase purity of the prepared samples were verified by X-ray diffraction (XRD), using the “PANalytical X’Pert Pro” diffractometer with a Cukα radiation (λ = 1.5406 Å) at room temperature. Data refinement was obtained with 2θ from 10° to 70°, with a scanning step of 0.02° and a counting time of 18 s per step. The structural analysis was carried out by the standard Rietveld Method [28], using the program FULLPROF [29]. The microstructure was studied by scanning electron microscopy (SEM) on the as-obtained pellets using a ‘Phillips XL 30 microscope’. A semi-quantitative analysis was done at 20 kV accelerating voltage using energy dispersive X-ray analyses (EDX). The dc magnetic properties were carried out over a temperature range of 0–400 K in an applied magnetic field of 0.05 T in both zero-field cooled (ZFC) and field-cooled (FC) modes. These experiments were carried out using a BS2 and BS1 magnetometer developed in Louis Neel Laboratory of Grenoble.

3 Results and discussion

3.1 Structural analysis

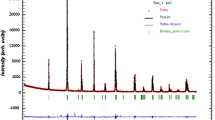
To study the structural properties of our samples, we carried out XRD analysis with CuKα radiation at room temperature. XRD diagrams of our samples are presented in Fig. 1. We can remark that our samples have a single phase without any detectable secondary phase, within the sensitivity limits of the experimental. Zooming the most intense peak, we can also remark a shift of peak to lower 2θ values (inset of Fig. 1).This explains the increase of the unit cell volume with increasing Ti content [30]. This confirms the incorporation of Ti (equal to 0.605 Å) at the Mn site and the ratio c/a exhibits the anisotropic contractions [31, 32]. The structural refinement indicates the rhombohedral structure with the space group \(R\overline{3} c\) (no. 167), in which La/Ba/Ca atoms at 6a (0, 0, 1/4) position, Mn/Ti at 6b (0, 0, 0) and O at 18e (x, 0, 1/4) position. The Rietveld analysis, is depicted in Fig. 2a, a* for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively. The quality of XRD data refinement is estimated by the adjustment indicator such as the weighted pattern Rwp, pattern Rp, and the goodness of fit χ2. A good agreement between the experimental and calculated XRD pattern is shown. The obtained results are summarized in Table 1. The increase of unit cell volume with increasing Ti is accompanied by an increase of dMn–O length and a decrease of θMn–O–Mn bond angle of MnO6 (Table 1). The crystal structure and the distances Mn–O for La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 sample were determined using “Diamond” program, based on the evaluated atomic positions. As shown in the inset (b*) of Fig. 2a*.

Fig. 1
figure 1

XRD patterns for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples. The inset shows the most intense peak of our samples (Bragg reflexions 104)

Full size image
Fig. 2
figure 2

(a) and (a*) show Rietveld plots of XRD data for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively. The inset (b*) shows the crystal structure, for La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 as an example. The inset (c) and (c*) show Williamson–Hall graph of our samples

Full size image
Table 1 Structural parameters of La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples deduced from Rietveld refinement of XRD data at room temperature
Full size table

To predict the stability of perovskite structure, Goldschmidt proposed a tolerance factor (t), defined as [33]:

$$t = \frac{{ < r_{A} > + < r_{O} > }}{{\sqrt 2 ( < r_{B} > + < r{}_{O} > )}},$$
(1)

where 〈rA〉, 〈rB〉 and 〈rO〉 are the average ionic radii of A, B and O perovskite sites, respectively. Generally, we can say that any sample has a perovskite structure if its t lies in the limits of 0.89 < t < 1.02 [34]. In our work, the values of t were found to be 0.942 and 0.941 for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively. Hence, our samples are in the stable range of perovskite structure.

From the reflection of 2θ values of XRD profile, the average crystallite size (Dsc) was calculated using Scherer’s equation. It is defined as [35]:

$$D_{\text{sc}} = \frac{K\lambda }{\beta \cos \theta },$$
(2)

where λ is the wavelength of the CuK⍺ radiation (λ = 1.5406 Å), K is a form factor of value 0.9, θ is the position of the peak in degrees and β is the width at mid-height of the most intense peak.

The obtained values of Dsc decrease from 34 to 30 nm, respectively, for La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 and La0.67Ba0.25Ca0.08MnO3. This proves the nano-metric size of our samples [36].

Another method can be used to calculate the average crystallite size, based on the analysis of all diffraction peaks. It is Williamson–Hall’s approach (WH), defined as [37]:

$$\beta \cos \theta = \frac{K\lambda }{{D_{\text{WH}} }} + 4\varepsilon \sin \theta .$$
(3)

The plot of βcosθ versus 4 sinθ is presented in inset (c) and (c*) of Fig. 2, La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively. The micro strain (ε) is extracted from the inverse of the slope of the linearly fitted data, and DWH is calculated from the root of the y intercept.

The values of DWH were equal to 137 and 99 nm, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively. We can see that these values are larger than Dsc. This difference is caused by the existence of strain, which contributes to the broadening of peaks [38]. The surface morphology of our samples was interpreted with SEM image as shown in the insets (b) and (b*) of Fig. 3a, a*, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3. The average particle sizes of the compounds were estimated using Image J software. After measuring the diameters of all the particles in SEM image, the obtained data were fitted with the log–normal function [39]:

$$f(D) = \left( {\frac{1}{{\sqrt {2\pi } \sigma D}}} \right)\exp \left[ { - \frac{{\ln^{2} \left( {\frac{D}{{D_{0} }}} \right)}}{{2\sigma^{2} }}} \right],$$
(4)

where D0 and σ are the median diameter obtained from the SEM and data dispersions, respectively. The insets (c) and (c*) of Fig. 3a, a*, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively, show the dispersion histogram. The mean diameter \(\left\langle {\left. D \right\rangle } \right.\, = \,D_{0} \,\exp ({{\sigma^{2} } \mathord{\left/ {\vphantom {{\sigma^{2} } {2)}}} \right. \kern-0pt} {2)}}\) and standard deviation \(\sigma_{D} \, = \,\left\langle {\left. D \right\rangle } \right.\,\,[\exp (\sigma^{2} ) - 1]^{1/2}\) were determined using fit results. The grain sizes observed by SEM were equal to 1.89 and 1.29 µm, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively. These are larger than those calculated by Scherer and Williams–Hall methods. This is because each particle observed by SEM consists of several crystallized grains [40, 41].

Fig. 3
figure 3

(a) and (a*) show EDX analysis for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively. Insets: (b) and (b*) show the typical SEM. The insets: (c) and (c*) show the histogram of the distribution of particle size

Full size image

To verify the existence of all elements in our studied sample, energy-dispersive X-ray analysis (EDX) was carried out at room temperature. EDX spectrum depicted in Fig. 3a, a*, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively, shows the presence of all elements. This confirms that there is no loss of any integrated elements during the sintering with in experimental errors. The typical cationic composition for our samples is listed in Table 2. This confirms the absence of secondary phases in the X-rays and the cationic composition of our samples.

Table 2 Results of EDX analysis
Full size table

3.2 Magnetic properties

After careful study of the structural and morphological properties, we studied the magnetic properties of La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3beginning with the zero-field-cooled (ZFC) and field-cooled (FC) magnetizations under an applied field of 0.05 T in the temperature range 0–400 K (Fig. 4). We can remark a net PM–FM transition, at their TC. TC, defined as the temperature corresponding to the peak of dM/dT in the M versus T curve, shown in inset of Fig. 4, are 300 and 287 K for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively. Additionally, a small divergence between ZFC and FC curves was noticed at the irreversibility temperature T = 264 and 258 K, respectively La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3. This phenomenon can be attributed to the appearance of an isotropic field generated from FM clusters [42].

Fig. 4
figure 4

Temperature dependence of the magnetization measured at magnetic field of 0.05 T for our samples. The plot of dM/dT versus T is depicted in the inset

Full size image

According to DE model, a lower TC is associated to a poor overlap between Mn3d and O2p orbitals. This caused a reduction in the charge carrier bandwidth (W), which led to the decrease of the exchange coupling of Mn3+–Mn4+ as well as TC [43].

W can be expressed empirically by [44]:

$$W = \frac{\cos \omega }{{d^{3.5} ({\text{Mn}} - {\text{O}})}},$$
(5)

where ω is the plane “inclination” angle of the bond given by \(\omega = {{(\pi - < {\text{Mn}} - {\text{O}} - {\text{Mn}} > )} \mathord{\left/ {\vphantom {{(\pi - < {\text{Mn}} - {\text{O}} - {\text{Mn}} > )} 2}} \right. \kern-0pt} 2}\) and dMn–O is the bond length [43]. The calculated values of W are listed in Table 1. With substitution Mn4+ by Ti4+, we can see that grain size decreases. This leads a decrease of θMn–O–Mn angles. This caused a reduction in the charge carrier W, which led to the decrease of the exchange coupling of Mn3+–Mn4+ as well as TC.

To get insight into the magnetic behavior in FM phase, we determined M(T) curves on FC modes by the conventional spin wave theory. Generally, in correlated electron systems such as: manganite; spin waves, their fluctuations and domain boundaries are quite common in influencing the ferromagnetism [45]. According to Lonzarich and Taillefer, [46] the magnetization in any manganite sample is governed by the spin wave theory. Regarding this theory, magnetization varies as T3/2 (Bloch’s law), at low temperatures. Another term was added over a wide range of temperatures; it is T2. While, close to TC, it varies as \(({{1 - T^{4/3} } \mathord{\left/ {\vphantom {{1 - T^{4/3} } {T_{\text{C}}^{4/3} )^{1/2} }}} \right. \kern-0pt} {T_{\text{C}}^{4/3} )^{1/2} }}\). Taking account of different parameters, in FM region, the magnetization data can be expressed by [46]:

$$M(T) = M_{0} + M_{3/2} T^{3/2} + M_{2} T^{2} ,$$
(6)

where M0 is the temperature independent spontaneous magnetization. From the best fit curves in Fig. 4, we can conclude that FM behavior La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples may be due to spin waves.

To understand the dynamics of spin, we determined the susceptibility (χ−1) as a function of temperature, as shown in Fig. 5. In PM region, all curves deviated from the linear behavior and showed a downturn in the curves, which is a characteristic of Griffiths phase [47, 48]. Griffith’s law suggested that the deviation from the Curie–Weiss’s law can be associated to the existence of FM clusters in PM region, signifying the presence of FM interaction.

Fig. 5
figure 5

Variation of the inverse susceptibility as a function of temperature for our samples. The inset shows the fit of the curve, at PM region, using Eq. 10 for La0.67Ba0.25Ca0.08MnO3 sample, as an example

Full size image

The Griffiths temperature (TG) is the maximum of the (d(χ−1)/dT) (T) curves [Inset (b) and (b*) of Fig. 6a, a*, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively]. It is grouped in Table 3.

Fig. 6
figure 6

(a) and (a*) show FC magnetization curves for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively. The insets (b) and (b*) show (d(1/χ)/dT) as a function of temperature for our samples

Full size image
Table 3 Magnetic data for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples
Full size table

From Figs. 5 and 6, the χ−1(T) curves present a nonlinear behavior, which indicates that the χ−1 (T) does not obey the Curie–Weiss’s law. However, it must follow Curie–Weiss’s law, in the region of T > TG. This indicates a typical PM behavior, defined as [49]:

$$\chi = \frac{C}{{T - \theta_{\text{cw}} }},$$
(7)

where θcw is Curie–Weiss temperature. C is the Curie constant, which present the inverse of the slope of the straight line. It is expressed by:

$$C = \frac{{N_{A} \mu_{B}^{2} }}{{3k_{B} }}\mu_{\text{eff}}^{\exp 2} ,$$
(8)

where NA= 6.023.1023 mol−1 is the Avogadro number; μB= 9.274.10−21 emu is the Bohr magneton and kB= 1.38016.10−16 erg k−1 is the Boltzmann constant.

The positive sign of θcw indicates the existence of FM exchange interaction between the spins (Table 3). The obtained value is greater than TC values, due to the existence of a short-range FM command. This behavior is related to the existence of a magnetic inhomogeneity [50].

On the other hand, the theoretical effective PM moments \(\mu_{\text{eff}}^{\text{Theo}}\) were determined using the relation:

$$\mu_{\text{eff}}^{\text{theo}} = \sqrt {0.67\,\mu_{\text{eff}}^{2} \left( {{\text{Mn}}^{3 + } } \right) + (0.33 - x)\,\mu_{\text{eff}}^{2} \left( {{\text{Mn}}^{4 + } } \right)} ,$$
(9)

where µeff (Mn3+) = 4.9 µB, µeff (Mn4+) = 3.87 µB [51] and µB = 9.27 × 10−24 J T−1.

The obtained values of \(\mu_{\text{eff}}^{ \exp }\), calculated using Eq. (8), and \(\mu_{\text{eff}}^{\text{theo}}\) are grouped in Table 3. The difference between \(\mu_{\text{eff}}^{ \exp }\) and \(\mu_{\text{eff}}^{\text{theo}}\) can be explained by the existence of FM clusters within the PM phase inducing the additional magnetic moments. In addition, it is important to note that the percentage of Mn3+ and Mn4+ ions can be verified quantitatively by the chemical titration. In addition, it is important to note that the percentage of Mn3+ and Mn4+ ions can be verified quantitatively by the chemical titration. In fact, 50 mg of our samples were dissolved in 11.2 ml of concentrated sulfuric acid and 100 mg of oxalic acid dihydrate. The obtained solution is titrated by potassium permanganate. During this titration, the following reactions occur: C2O 2− 4 + 2Mn3+ \(\to\) 2CO2+ 2Mn2+ and C2O 2− 4 + 2Mn3+ \(\to\) 2CO2+ 2Mn2+. Knowing that, nC2O42− reacts = n(C2O42−)initial −n (C2O42−)excess, with n(C2O42−)excess =\(\frac{5}{2}\) (MnO4−). Thus, the number of moles of C2O42− reacting with manganite is 2n(C2O42−)reacts = 2n(Mn4+) + n (Mn3+). Finally, by a simple calculation, the percentages of manganese, at B-site, are (Mn3+ = 67.2%) and (Mn4+ = 32.8%) for La0.67Ba0.25Ca0.08MnO3 and (Mn3+ = 67.1%) and (Mn4+ = 28.1%) for La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3.

Based on the Griffiths theory [47], Griffiths phase is, generally, characterized by a magnetic susceptibility exponent (λ) of less than unity [52]. Usually, the theoretical modeling of Griffiths phase is expressed as follows [53]:

$$\chi^{ - 1} \propto \left( {T - T_{\text{C}}^{\text{R}} } \right)\,^{1 - \lambda } ,$$
(10)

where 0 ≤ λ ≤ 1 is the exponent describing the strength of Griffiths phase and \(T_{\text{C}}^{\text{R}}\) is the critical temperature of the random FM behavior. The choice of \(T_{\text{C}}^{\text{R}}\) was fixed using Jiang et al. method [54]. The corresponding accuracy in the estimate for \(T_{\text{C}}^{\text{R}}\) using this criterion is 1 K [52]. The exponent λ is calculated by fitting the curve presented in the inset of Fig. 5, using Eq. 10, for La0.67Ba0.25Ca0.08MnO3 as an example. Then, in the pure PM region, λ is expected to be zero.

Galitski et al. reported the effect of disorder to Griffiths phase [54]. According to them, \(M(H,T)\) in Griffiths phase follow this relation:

$$M(H,T)\, \propto \,\exp \left( { - \alpha \,\frac{T}{H}} \right)$$
(11)

where α is a constant proportional to the total moment of magnetic cluster. We have fitted M(T) curves in Griffiths phase’s region shown in Fig. 6 based on Eq. 11. This formula justifies the existence of Griffiths phase and exhibits the significant role of disorder in the formation of Griffiths phase. The determined values of λ and \(T_{\text{C}}^{\text{R}}\) for our compounds are given in Table 3. The values of α and λ increase, with increasing x content. Then, the size of the magnetic cluster increases.

To get insight into the magnetic properties of our samples at low temperature, we investigated the hysteresis cycles M (µ0H). Figure 7 shows M (µ0H) at 10 K in the range of µ0H = ± 6 T, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples. From Fig. 7, we can see a similar behavior with a small hysteresis loop. The insets of Fig. 7 display a zoom portion of the low magnetic field region. We can remark that magnetization increased sharply at a low applied magnetic field. We observed a sharp saturation whose MS values are 83.63 and 75.64 emu/g for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively. This indicates the typical FM behavior. Additionally, we remarked that our samples have slight values of the coercive fields (µ0HC) and the remnant magnetizations (Mr). µ0HC values were found to be 24.10−4 and 33.10−4 T, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively. Mr values were found to be 1.91 and 2.77 emu/g, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively. Here, we can conclude that our samples have a soft FM behavior. These results make them good candidates for some technological applications.

Fig. 7
figure 7

Magnetic hysteresis cycles at T = 10 K of La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples. The insets show a zoom of the central portion of the hysteresis at a low field

Full size image

In addition to hysteresis loop, we measured magnetization as a function of the magnetic field [M (µ0H)] around their TC. Figure 8a, a* show [M (µ0H)] around TC, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively. At the low temperature region, we can see a rapid increase in magnetization at the weak magnetic field region up to 1 T. Then, M (µ0H) curves reached saturation as a result of increasing the applied magnetic field. This indicates a typical FM behavior, which is caused by the complete alignment of the spins in our samples. To check the existence of Griffiths type phase in the compounds in the form of FM cluster system within a PM matrix, the curves of the Arrott diagram, are depicted in the inset (b) and (b*) of Fig. 8 at temperatures above and below TC, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively. We notice that the intercepts are negative when T > TC at different temperatures, designating the absence of spontaneous magnetization and the appearance of FM clusters occurring in this temperature region [51]. Generally, the high magnetic field suppresses Griffiths phase effect which, due to the polarization of spins outside the cluster or, in another way, the FM signal, is masked by increasing PM signal as already proposed by Pramanik et al. [55].

Fig. 8
figure 8

(a) and (a*) show the magnetic isotherms measured at different temperatures for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, around their TC. The insets (c) and (c*) shows M2 vs. (μ0H)/M. The insets (b) and (b*) shows parts of (μ0H)/M vs. M2 at different temperatures above and below Tc

Full size image

To determine the nature of the magnetic phase transition (first or second order) for our studied samples, we used the Arrott curves (μ0H/M vs. M2) using M(µ0H) data (Insets (c) and (c*) of Fig. 8 at temperatures, around TC, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively) According to Banerjee’s criterion [56], our samples show a positive slope, which indicates the second order phase transition.

3.3 Magnetocaloric properties

The MCE is very important for cooling technology. MCE is the heating or cooling power of a magnetic material following the application of an external magnetic field. Based on classical thermodynamic theory, the magnetic entropy change (− ∆SM) can be calculated using Maxwell’s equation [57]:

$$\begin{aligned} \Delta \,S_{M} (T,\,\mu_{0} H)\, & = \,S_{M} (T,\,\mu_{0} H) - S_{M} (T,\,0) \\ & = \int\limits_{0}^{{\mu_{0} \,H_{{^{\text{Max}} }} }} {\left( {\frac{{\delta M(T,\mu_{0} )\,}}{\delta T}} \right)}_{{\mu_{0} H}} {\text{d}}(\mu_{0} H). \\ \end{aligned}$$
(12)

In the case of discrete variation of applied fields and temperature intervals, Eq. 11 can be approached as:

$$\left| {\Delta \left. {S_{M} } \right|} \right. = \sum\nolimits_{i} {\frac{{M_{i + 1} - M_{i} }}{{T_{i + 1} - T_{i} }}\,} \Delta H,$$
(13)

where Mi + 1 and Mi are the experimental values of magnetization, obtained at the temperatures Ti + 1 and Ti, respectively.

− ∆SM curves, under different µ0H, are shown in Fig. 9a, a* for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively.

Fig. 9
figure 9

(a) and (a*) show the magnetic entropy change versus temperature for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively, under several magnetic applied field changes

Full size image

The positive sign of − ∆SM means that heat is released when the magnetic field is applied adiabatically. This confirms the FM character of our samples. As expected, all samples exhibited a maximum value \(- \Delta S_{M}^{\hbox{max} }\) near TC. One can observe also that \(- \Delta S_{M}^{\hbox{max} }\) increases with increasing µ0H. For La0.67Ba0.25Ca0.08MnO3 sample, \(- \Delta S_{M}^{\hbox{max} }\) was found to be 3.21 J/kg. K at 5 T.

To quantify the efficiency of MC material, another very important parameter to be determined is the relative cooling power (RCP). It defines how much heat can be transferred between cold and hot sinks in one ideal refrigeration cycle. This parameter related to the maximum value of \(- \Delta S_{M}^{\hbox{max} }\) and the full width at half maximum (δTFWHM) can be calculated using the relation:

$${\text{RCP}} = \left| {\Delta \left. {S_{M}^{\hbox{max} } } \right|} \right. \times \delta T\,_{\text{FWHM}}$$
(14)

The calculated values of RCP were found to be 168 and 187 J/kg at 5 T, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively. To better understand the applicability of our compound in MR effect, the maximum values of (\(\Delta S_{M}^{\hbox{max} }\)) and the RCP values are compared to other samples [58,59,60,61,62,63] (Table 4). We can deduce that our samples can be a good candidate for the magnetic refrigeration.

Table 4 Summary of magnetocaloric properties of La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples compared with other magnetic materials at µ0H = 5T for example
Full size table

Besides, the variation of specific heat (∆CP) can be determined using − ∆SM curves, related to the magnetic field variation from 0 to µ0H. It is expressed by the following formula [64]:

$$\Delta C_{\text{P}} = C_{\text{P}} (T,\mu_{0} H) - C_{\text{P}} (T,0) = T\frac{{\delta \Delta S_{M} }}{\delta T}.$$
(15)

The ΔCP versus temperature under different µ0H is presented in Fig. 10a, a* for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively. We can see that the value of ΔCP changes abruptly from negative to positive in the vicinity of TC. For T > TC, ΔCP is positive. It changed sign with decreasing the temperature. The sum of the two parts is the magnetic contribution to the total ∆CP. This affects the cooling or heating power of a magnetic refrigerator [65], which confirms that ΔCP data of a magnetic material is useful in the design of a refrigerator.

Fig. 10
figure 10

(a) and (a*) show ΔCP as function of temperature under different magnetic fields, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively

Full size image

To improve MCE study of our samples, we can also calculate the adiabatic temperature change (ΔTad). It represents the temperature change of the material when adiabatically magnetized/demagnetized. It is defined as [66]:

$$\Delta T_{\text{ad}} = - \,\Delta S_{M} \,\frac{T}{{C_{{{\text{P}},H}} }}.$$
(16)

∆CP is taken as the sum of the lattice and magnetic contributions [67, 68]:

$$C_{{{\text{P}},H}} = C_{D} + C_{M} \,{\text{with}}\,C_{D} = 9\,{\text{KN}}\left( {\frac{T}{{\theta_{D} }}} \right)^{3} \int\limits_{0}^{{\theta_{D} }} {\frac{{{\text{e}}^{x} x^{4} }}{{({\text{e}}^{x} - 1)^{2} }}} \,{\text{d}}x$$
(17)

and

$$C_{M} = - H_{\text{ext}} \frac{\delta M}{\delta T} - \frac{1}{2}N_{\text{int}} \,\frac{{\delta M^{2} }}{\delta T},$$
(18)

where K is the Boltzmann constant, N is the number of atoms per unit mass, \(\theta_{D}\) is the Debye temperature. \(N{}_{\text{int}} = \frac{{3\,K\,T_{\text{C}} }}{{N_{S} g^{2} \mu_{B}^{2} J(J + 1)}}\) is the mean field constant, \(N_{\text{s}}\) is the number of spins per unit mass, g is the Landé factor and J is the total angular momentum. Figure 11a, a* show ΔTad as a function of temperature, under several magnetic fields, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively. We can observe that ΔTad almost conserves the same behavior of ΔSM [69]. This confirms the FM–PM behavior in our samples.

Fig. 11
figure 11

(a) and (a*) show ΔTad as a function of temperature under different magnetic fields, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively

Full size image

To further study MCE, another method namely Landau’s theory was suggested by Amaral et al. [70]. This theory founded on the − ∆SM data, takes into consideration the electron interaction and magnetoelastic coupling effects.

According to this theory, the variation of the Gibbs’s free energy (G) can be defined as follows [71]:

$$G(T,M) = G_{0} + \frac{1}{2}A(T)M^{2} + \frac{1}{4}B(T)M^{4} + \frac{1}{6}C(T)M^{6} - \mu_{0} HM.$$
(19)

Here A(T), B(T) and C(T) are the Landau parameters.

From the equilibrium condition:\(\frac{\partial G}{\partial M} = 0\), the magnetic equation is evaluated:

$$\frac{{\mu_{0} H}}{M} = \,A(T) + B(T)M^{2} + C(T)M^{4} .$$
(20)

The value of these parameters can be determined using the fit of the isothermal magnetization curve. The insets of Fig. 12a, a* present the temperature dependence of the Landau parameters for our samples.

Fig. 12
figure 12

(a) and (a*) show the variations of experimental (red diamond) and calculated magnetic entropy change versus temperature under 5 T for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively. The insets show the Landau’s coefficients A(T), B(T) and C(T)

Full size image

The insets of Fig. 12a, a* show that A(T) presents a minimum at TC and B(T) is positive, which presents a second-order phase transition. Consequently, this result is uniform with the previous study of the universal curve.

The corresponding − ∆SM(T) is theoretically given by the differentiation of free energy as follows [72]:

$$\begin{aligned} \Delta S_{M} (T,\mu_{0} H) & = - \left( {\frac{\delta G}{\delta T}} \right)\,\mu_{0} H \\ & = - \frac{1}{2}A^{\prime}(T)M^{2} - \frac{1}{4}B^{\prime}(T)M^{4} - \frac{1}{6}C^{\prime}(T)M^{6} , \\ \end{aligned}$$
(21)

where A′(T), B′(T) and C′(T) are the temperature derivatives of Landau’s parameters. Figure 12a, a* present − ∆SM(T) in comparison with the experimental data under µ0H = 5 T, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively. A good agreement is found between these two curves, near TC. These results indicate that magnetoelastic coupling and electronic interaction may explain the MCE properties of these compounds [73].

To understand the influence of the magnetic fields on − ∆SM(T), Oesterreicher et al. [74] proposed the relation between them, which can be expressed as:

$$- \Delta S_{M} = a(\mu_{0} H)^{n} .$$
(22)

Here ‘a’ is a constant and the exponent n depends on the magnetic field and temperature. It can be locally calculated as:

$$n = \frac{{d\,\ln \Delta S_{M} }}{{d\,\ln \mu_{0} H}}.$$
(23)

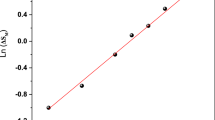
The value of n is determined from the linear plot of ln(−ΔSM) versus ln(μ0H) using Eq. 22 (Fig. 13). One can see that the value of n obtained at TC is equal to 0.690 and 0.677, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively.

Fig. 13
figure 13

Field dependence of \(- \Delta S_{M}^{\hbox{max} }\) (inset represents magnetic field dependence of local exponent n measured at different fields for La0.67Ba0.25Ca0.08MnO3 sample, as an example

Full size image

Based on the mean field approach, the field dependence of −∆SM corresponds to n = 2/3 at TC. This parameter value (n) was estimated to be about 1 and 2 below and above the transition temperature, respectively.

The inset of Fig. 13 presents the temperature dependence of the exponent n, for La0.67Ba0.25Ca0.08MnO3 as an example. n exhibits a moderate decrease with increasing temperature, with a minimum value in the vicinity of TC, sharply increasing above TC. These values are very close to the values of mean field model. This can be due to the existence of local inhomogeneity [75, 76]. The results were comparable to those found by other authors [77, 78].

Moreover, to confirm the nature of the phase transition in our samples, Franco et al. [79] have proposed a phenomenological universal curve. This method was carried out by normalizing

− ∆SM by their respective maximum \(- \Delta S_{M}^{\hbox{max} }\), namely \(\Delta S^{\prime} = {{\Delta S_{M} \left( T \right)} \mathord{\left/ {\vphantom {{\Delta S_{M} \left( T \right)} {\Delta S_{M}^{\hbox{max} } }}} \right. \kern-0pt} {\Delta S_{M}^{\hbox{max} } }}\) and rescaling the temperature axis using two other reference temperatures in a different way below and above TC. The positions of these additional reference temperatures in the curve correspond to: θ = ± 1:

$$\theta = \left\{ \begin{aligned} {{ - \left( {T - T_{\text{C}} } \right)} \mathord{\left/ {\vphantom {{ - \left( {T - T_{\text{C}} } \right)} {\left( {T_{r1} - T_{\text{C}} } \right)}}} \right. \kern-0pt} {\left( {T_{r1} - T_{\text{C}} } \right)}}\,\,\,\,T \le T_{\text{C}} \hfill \\ {{\,\,\,\left( {T - T_{\text{C}} } \right)} \mathord{\left/ {\vphantom {{\,\,\,\left( {T - T_{\text{C}} } \right)} {\left( {T_{r2} - T_{\text{C}} } \right)\,\,\,\,\,T > T_{\text{C}} }}} \right. \kern-0pt} {\left( {T_{r2} - T_{\text{C}} } \right)\,\,\,\,\,T > T_{\text{C}} }} \hfill \\ \end{aligned} \right.,$$
(24)

where Tr1 and Tr2 are two reference temperatures which have been selected as those corresponding to ΔSM(Tr1,2) = \(\Delta S_{M}^{\hbox{max} }\)/2.

According to Tr1and Tr2, the rescaled − ∆SM(T) curves measured with different applied magnetic fields will collapse into a single curve only for second-order phase transition. However, for materials with a first-order phase transition, the rescaled ∆SM(T) curves did not follow a universal behavior.

Figure 14a, a* show the universal curve for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively. It is clear that all curves collapse on a single universal curve. This proves that the transition is of a second order. The obtained results are in good agreement with the analysis of Banerjee’s criterion.

Fig. 14
figure 14

(a) and (a*) show the normalized entropy change versus rescaled temperature (θ) for different applied magnetic fields for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3 samples, respectively

Full size image

4 Conclusion

To sum up, we prepared La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, using the Flux method and then studied its structural, magnetic and magnetocaloric properties. Rietveld refinement of X-ray diffraction patterns demonstrates that our samples crystallize in a rhombohedral structure with \(R\overline{3} c\) space group. These samples exhibit a second-order ferromagnetic–paramagnetic phase transition. In the paramagnetic region, a non-linear behavior, for our samples, is observed in χ−1 vs. T curves. This can be explained by the existence of Griffiths phase. Around room temperature, our samples have an important − ∆SM (3.21 J/kg and 2.76 J/kg at 5 T, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively). The field dependence of − ΔSM is also analyzed, showing the power law dependence, \(- \Delta S_{M} = a(\mu_{0} H)^{n}\), where n = 0.690 and 0.677, for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively at their TC. Additionally, we determined the RCP value. It was found to be 168 and 187 J/kg for La0.67Ba0.25Ca0.08MnO3 and La0.67Ba0.25Ca0.08Mn0.95Ti0.05O3, respectively. According to the universal curve for the temperature dependence of − ΔSM measured for different maximum fields, paramagnetic–ferromagnetic phase transition observed for our samples were of second-order. From the hysteresis cycles, at 10 K for the studied samples, we can note a typical soft ferromagnetic behavior with a low hysteresis loop and coercive field. These confirm that the magnetic domains can rotate easily to the direction of the magnetic field. All results indicate that our samples could be a potential candidate for magnetic refrigeration.