1 Introduction

The acoustic metamaterials (AMs), which have attracted many significant attentions due to their distinctive properties recently, mainly focus on their negative dynamic effective parameters, such as the negative bulk modulus and mass density that are hardly observed in the traditional natural materials [1]. In 2000, a seminal paper was published for conceptually realizing an AM involving the locally resonant structural units [2], which can exhibit the negative mass near the natural frequency of internal resonator. Fang et al. [3] reported a class of ultrasonic metamaterials with the subwavelength Helmholtz resonators that can possess negative dynamic modulus near the resonance frequency. The metamaterial simultaneously owning double negativity was achieved by the independent combination of structures consisting of the negative modulus and mass density unit [4]. Subsequently, various metamaterials with single or double negativity have been presented based on different mechanisms [5–7]. When the wavelength of elastic waves is long compared to the feature size of metamaterials, the homogenization theories can be employed because the metamaterials behave as effective homogeneous media [8] in this situation. The lattice models of metamaterials were constructed with concentrated masses and connected springs to investigate the effective parameters [9]. Currently, a two-step homogenization method (HM) was introduced to obtain the effective parameters of single-resonator metamaterials, which was more convenient for further analysis [10]. Meanwhile, many researchers have also devoted themselves to exploring various significant applications of the AMs, such as the vibration/noise isolation [11–13], cloak [14], waveguiding [15] and sensors applying in measuring liquid properties [16] or nondestructive testing [17].

For locally resonant AMs with single resonator, the frequency region of negative effective parameters is not enough for their practical applications generally [10]; therefore, the optimizing process for the bandgaps of these AMs is very necessary. For example, Lee et al. [18] and Yang et al. [19] presented a type of thin membrane-type structures to construct broadband metamaterials, as well as Ding et al. [6] achieved the negative effective bulk modulus based on the split hollow sphere. Besides traditionally searching novel complex structures, the existing structures with multi-resonators are fine trends for managing the bandgaps. For instance, Huang and Sun [20] demonstrated that there are three bandgaps in mass-in-mass lattice systems with dual resonators that have been found to be available to optimize the negative effective mass density by Tan et al. [21]. In addition, Pai et al. [22] also demonstrated that two stop bands exist around the high-frequency side of the local resonance frequencies of two-mass absorber, respectively, on a metamaterial beam. Here, we present some extensive works from the previous works and clarify the different effects of structure parameters in continuum model.

In this paper, a one-dimensional (1-D) lattice model of the AMs with multi-resonators will be fully considered, and the convenient two-step HM which can accurately match the dispersion relations will be expanded to acquire the effective parameters of AMs in Sect. 2. Then, the effects of relevant parameters on the center frequency and bandwidth of the bandgaps are analytically revealed in Sect. 3. In Sect. 4, the wave propagation in specific continuum models based on mimicking lattice systems [10] is analyzed by the finite element method (FEM), and an application example of the purposed multi-resonators AM in vibration control is presented and discussed.

2 Locally resonant acoustic metamaterials

2.1 Effective mass and bandgaps in lattice model with single resonator

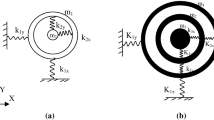
The negativity effective mass in a lattice model of mass-in-mass unit was demonstrated by Huang et al. [9], the unit employed a 1-D monatomic lattice with a single internal resonator, as shown in Fig. 1. For the harmonic input F(t) and the response u i (t), the equation of motion for the unit is derived as Eq. (1).

$$\left[ {\begin{array}{*{20}c} {m_{1} } & 0 \\ 0 & {m_{2} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{u}_{1} } \\ {\ddot{u}_{2} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {k_{2} } & { - k_{2} } \\ { - k_{2} } & {k_{2} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} F \\ 0 \\ \end{array} } \right\}$$
(1)
Fig. 1
figure 1

Mass-in-mass lattice unit with single internal resonator

Full size image

Then, the effective mass m eff is expressed by

$$m_{\text{eff}} = m_{1} + \frac{{m_{2} }}{{1 - \omega^{2} /\omega_{n}^{2} }}$$
(2)

where \(\omega_{n} = \sqrt {k_{2} /m_{2} }\) is the natural frequency of internal resonator, ω is the angular frequency. In the case of θ = m 2/m 1 = 1, the negative effective mass m eff/m st becomes negative within the range of \(1< \omega { /}\omega_{n} < \sqrt {1 + \theta }\), as shown in Fig. 2a.

Fig. 2
figure 2

Comparison of the results, m st = m 1 + m 2, θ = m 2/m 1, δ = k 2/k 1 a effective mass obtained by Eq. (2) with θ = 1, b dispersion curves by Eq. (3) with θ = 1, δ = 2

Full size image

Taking the harmonic wave propagation into account, the dispersion equation of this mass-in-mass chain with single resonator can be derived by below:

$$m_{1} m_{2} \omega^{4} - (m_{1} + m_{2} )k_{2} \omega^{2} - k_{1} (m_{2} \omega^{2} + k_{2} )(2 - {\text{e}}^{ - iqL} - {\text{e}}^{iqL} ) = 0$$
(3)

where q denotes the wave number, L represents the length of each unit cell. There are two obvious bandgaps of the dispersion curves, namely 0.7654 < ω/ω n  < 1.414 and 1.848 < ω/ω n , as shown in Fig. 2b. The negative effective mass region is smaller than the first bandgap, for the reason that the negative effective mass m eff of the mass-in-mass unit results from the inertia force of the internal lumped mass which is unrelated to spring k 1. The upper frequency of the first bandgap is equal to that of the negative effective mass; meanwhile, the starting frequency ω = ω n of the negative effective mass is same with the center frequency of the first bandgap with the maximum attenuation coefficient. In other words, the center frequency of bandgaps mainly depends on the natural frequency of internal resonator, which is generally insensitive to other outer structure, while the bandwidth needs to be future investigated.

2.2 Acoustic metamaterials with multi-resonators

The multi-resonant lattice unit is a n-degree-of-freedom (n-DOF) system, as shown in Fig. 3a, where n = 3, 4, …, which consists of n − 1 coupled lumped masses inside. The corresponding undamped equation of motion is expressed as Eq. (4).

$$\left[ {\begin{array}{*{20}c} {m_{1} } & 0 & 0 & \cdots & 0 \\ 0 & {m_{2} } & 0 & \cdots & 0 \\ 0 & 0 & {m_{3} } & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & {m_{n} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{u}_{1} } \\ {\ddot{u}_{2} } \\ {\ddot{u}_{3} } \\ \vdots \\ {\ddot{u}_{n} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {k_{2} + k_{n + 1} } & { - k_{2} } & 0 & \cdots & { - k_{n + 1} } \\ { - k_{2} } & {k_{2} + k_{3} } & { - k_{3} } & \cdots & 0 \\ 0 & { - k_{3} } & {k_{3} + k_{4} } & \cdots & \vdots \\ \vdots & \vdots & \vdots & \ddots & { - k_{n} } \\ { - k_{n + 1} } & 0 & \cdots & { - k_{n} } & {k_{n} + k_{n + 1} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ {u_{3} } \\ \vdots \\ {u_{n} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} F \\ 0 \\ 0 \\ \vdots \\ 0 \\ \end{array} } \right\}$$
(4)
Fig. 3
figure 3

a Multi-resonant lattice unit, b effective mass in the first-step homogenization, c effective mass in the second-step homogenization

Full size image

For the harmonic input F(t) and the response u i (t)

$$F(t) \equiv F_{0} {\text{e}}^{i\omega t} ,\quad u_{n} \equiv U_{n} {\text{e}}^{i\omega t}$$
(5)

Then, Eq. (4) can be rewritten as follows:

$$\left( { - \omega^{2} [M] + [K]} \right)\left\{ U \right\} = \left\{ F \right\}$$
(6)

where

$$[M] = \left[ {\begin{array}{*{20}c} {m_{1} } & 0 & 0 & \cdots & 0 \\ 0 & {m_{2} } & 0 & \cdots & 0 \\ 0 & 0 & {m_{3} } & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & {m_{n} } \\ \end{array} } \right],\quad [K] = \left[ {\begin{array}{*{20}c} {k_{2} + k_{n + 1} } & { - k_{2} } & 0 & \cdots & { - k_{n + 1} } \\ { - k_{2} } & {k_{2} + k_{3} } & { - k_{3} } & \cdots & 0 \\ 0 & { - k_{3} } & {k_{3} + k_{4} } & \cdots & \vdots \\ \vdots & \vdots & \vdots & \ddots & { - k_{n} } \\ { - k_{n + 1} } & 0 & \cdots & { - k_{n} } & {k_{n} + k_{n + 1} } \\ \end{array} } \right],\quad \{ F\} = \left\{ {\begin{array}{*{20}c} {F_{0} } \\ 0 \\ 0 \\ \vdots \\ 0 \\ \end{array} } \right\}.$$

Therefore, the frequency response function matrix [H] can be expressed as follows:

$$[H] = \left[ { - \omega^{2} [M] + [K]} \right]^{ - 1}$$
(7)

For \(m_{\text{eff}} = \frac{F(t)}{{\ddot{u}_{\text{eff}} }} = \frac{{F_{0} }}{{ - \omega^{2} U_{1} }}\), the effective mass in the first-step homogenization, as shown in Fig. 3b, can be obtained as follows:

$$m_{\text{eff}} = \frac{1}{{ - \omega^{2} H(1,1)}}$$
(8)

For the edges of bandgaps in lattice model with single resonator, a two-step HM has been introduced by Liu et al. [10]. In the first-step homogenization, the effective mass m eff of the mass-in-mass unit above is obtained. Next in the second-step HM, the infinite lattice system of the effective mass m eff connected by the spring k 1 can be regarded as an equivalent homogeneous material with mass M eff and constant elastic coefficient k 1, as shown in Fig. 3c. On the other hand, the equivalent homogeneous material can be treated with the effective mass m eff and effective elastic coefficient k eff, where k eff = F/2A would be obtained by the kinematic equation of the unit cell \(- m_{\text{eff}} \omega^{2} A/2 = F - 2k_{1} A\), where A is the vibration amplitude of mass. By setting \(M_{\text{eff}} /k_{1} = m_{\text{eff}} /k_{\text{eff}}\), the effective mass M eff in the second-step HM is derived to be

$$M_{\text{eff}} = \frac{{m_{\text{eff}} k_{1} }}{{k_{1} - m_{\text{eff}} \omega^{2} /4}}$$
(9)

For example, the effective mass of lattice model with two and three resonators in the two-step HM is illustrated in Fig. 4a, b, respectively, which correspond to n = 3 and n = 4. In contrast, the same referred frequency \(\omega_{0} = \sqrt {k_{2} /m_{2} }\) is adopted here, which is also the nature frequency of single internal resonator in Sect. 2.1. Then, the relevant parameters for the added second and third resonators are set directly here: θ 1 = m 2/m 3 = 2, δ 2 = k 2/k 4 = 1 and θ 2 = m 2/m 4 = 4, δ 3 = k 2/k 5 = 1. There are two negative ranges of the effective mass m eff and three negative ranges of the effective mass M eff with two resonators. When the third internal resonator is added, the effective mass m eff becomes negative in three ranges and the effective mass M eff has four negative ranges. It is obvious that the added coupled resonators gain more stop bands and broader bandwidth beyond the cutoff frequency of the lattice chain, which would be useful in designing AMs structures like bars or beams. However, the more resonators in the confined space of single unit will demand more complex manufacturing techniques.

Fig. 4
figure 4

Comparison of the results, here m st = m 1 + m 2+ ··· + m n a effective mass m eff in the first-step HM; b effective mass M eff in the second-step HM; c the dispersion curves. The solid and dashed lines represent two and three resonators, respectively. The points describe the dispersion curves of the unit cell of continuum model by FEM

Full size image

For comparison, the dispersion equation of this multi-resonant lattice model for harmonic wave propagation is achieved by the Bloch–Floquet theory [23] as follows:

$$\left| {\begin{array}{*{20}c} {k_{2} + k_{n + 1} + 2k_{1} (1 - \cos (qL)) - m_{1} \omega^{2} } & { - k_{2} } & 0 & \cdots & { - k_{n + 1} } \\ { - k_{2} } & {k_{2} + k_{3} - m_{2} \omega^{2} } & { - k_{3} } & \cdots & 0 \\ 0 & { - k_{3} } & {k_{3} + k_{4} - m_{3} \omega^{2} } & \cdots & \vdots \\ \vdots & \vdots & \vdots & \ddots & { - k_{n} } \\ { - k_{n + 1} } & 0 & \cdots & { - k_{n} } & {k_{n} + k_{n + 1} - m_{n} \omega^{2} } \\ \end{array} } \right| = 0$$
(10)

There are three stop bands for double resonators and four stop bands for three resonators as shown in Fig. 4c. The frequency range of negative effective m eff is included in the stop bands, while the negative effective mass M eff can agree well with the bandgaps.

3 Relevant parameters on bandgaps of dual-resonator acoustic metamaterials

3.1 Relevant parameters on the center frequencies of bandgaps

The center frequencies and bandwidth of bandgaps are the primary considerations on designing AMs. The effects of relevant parameters on the center frequencies of dual-resonator AMs are analyzed here. Under the parameters mentioned in the last chapter, Eq. (8) becomes

$$\begin{aligned} m_{\text{eff}} /m_{\text{st}} = & \frac{{(9\theta + 6)\omega_{0}^{4} - (2\theta + 6)\omega^{2} \omega_{0}^{2} + \omega^{4} }}{{(1 + 1.5\theta )(\omega^{2} - \omega_{n1}^{2} )(\omega^{2} - \omega_{n2}^{2} )}} \\ \omega_{n 1}^{2} ,\omega_{n 2}^{2} = & \frac{1}{2}\left[ {\Omega \mp \sqrt {\Omega^{2} - 4\theta_{1} [(1 + 1/\delta_{1} )(1/\delta_{1} + 1/\delta_{2} ) - 1/\delta_{1}^{2} ]} } \right]\omega_{0}^{2} = 3 \mp \sqrt 3 \omega_{0}^{2} \\ \end{aligned}$$
(11)

where Ω = 1+1/δ 1 + θ 1/δ 1 + θ 1/δ 2. Here, ω n1 and ω n2 are the two undamped natural frequencies of internal resonators, which correspond to the two locations of asymptotes as the effective mass m eff tends to infinity and the center frequencies of the first two bandgaps, respectively. The effects of relevant parameters θ 1, δ 1 and δ 2 on the value of ω n1, ω n2 are plotted in Fig. 5. ω n1 is relatively smooth under the change of θ 1, δ 1 and δ 2, while ω n2 become extremely high when the value of δ 1 ≪ 1 (Fig. 5a) or δ 2 ≪ 1 (Fig. 5b). When both δ1 and δ2 tend to 0, the corresponding center frequencies of two bandgaps are increased simultaneously (Fig. 5c). As achieving low-frequency bandgaps is a meaningful topic of AMs, a lower value of θ 1, δ 1 > 1 and δ 2 > 1 is proposed. But it is unable to achieve multi-bandgaps fully below the bandgap of the single-resonator AMs due to the value of ω n2 is always greater than ω 0. Another interesting result is the case of ω n1 = ω 0 (e.g., θ 1 = 1, δ 1 = 5 and δ 2 = 1), where the multi-resonators AMs gain an extra stop band on the basis of the single-resonator AMs approximately.

Fig. 5
figure 5

Values of ω n1, ω n2, namely the center frequencies of the former two bandgaps, a versus θ 1 and δ 1 with δ 2 = 1, b versus θ 1 and δ 2 with δ 1 = 1, c versus δ 1 and δ 2 with θ 1 = 1

Full size image

3.2 Relevant parameters on the boundary frequencies of bandgaps

As shown in Fig. 4b, c, the points L1–L3, Z1, Z2 can agree well with the boundary frequencies of the three bandgaps in the dual-resonator model, where L1–L3 are the locations of the asymptotes as the effective mass M eff tends to infinity and Z1, Z2 are the zero points of the effective mass M eff. The first bandgap locates between L1 and Z1, the second bandgap lies within the L2 and Z2; meanwhile, the third bandgap is the region exceeding L3. When the central frequencies of bandgaps have been determined by the certain values of θ 1, δ 1 and δ 2, the values of five points are still affected by the mass ratio θ and stiffness ratio δ. For the first bandgap, the increasing θ will result in a slightly wider bandwidth as illustrated in Fig. 6a. The bandwidth of the second pass band reaches a maximum value around θ = 1, and the second stop band reaches the minimum value oppositely. Meanwhile, the third pass band is enlarged with the increase of θ monotonically. It is noteworthy that the widths of both the second and third pass band are almost decreased to zero if the value of θ is near zero, which is similar to the monatomic chains.

Fig. 6
figure 6

Values of the points L1–L3, Z1 and Z2, namely the edges of bandgaps a versus θ = m 2/m 1, with δ = k 2/k 1 = 1, b versus δ, with θ = 1

Full size image

Figure 6b shows that the two zero points Z1 and Z2 are invariable with the value of \(\sqrt {(\theta + 3) \mp \sqrt {\theta^{2} - 3\theta + 3} }\), and both the first and second bandgap are broadened relatively with a higher value of δ. If δ is approach to zero just like the metamaterial beam [22], the third bandgap will begin at an extremely high frequency.

4 Continuum model and applications

4.1 Continuum model of multi-resonators acoustic metamaterials

Various continuum models have been put forward with the single negative mass density in last decade [4, 6, 7]; one of these models was presented by Sun et al. [10] based on the mimicking lattice systems, which can agree well with the theoretical result in lattice model. The similar continuum model with dual resonators is illustrated in Fig. 7.

Fig. 7
figure 7

Continuum model of multi-resonant AM by mimicking lattice systems

Full size image

In this paper, the steel (density ρ = 7850 kg/m3, Young’s modulus E = 210 GPa and Poisson’s ratio μ = 0.29) and the foam (density ρ = 115 kg/m3, Young’s modulus E = 8 MPa and Poisson’s ratio μ = 0.33) [24] are selected to be the ‘mass’ and ‘spring’ materials, respectively. The purposed relevant parameters of the continuum models and the corresponding structure dimensions are listed in Table 1. The same referred frequency \(\omega_{0} = \sqrt {k_{2} /m_{2} } = 3336.6\) rad/s is adopted here, which means the dimensions l 1 and l 2 are stable. The parameters of S1 are the same as the lattice model above, while the rest examples have only one relevant parameter different from the S1.

Table 1 Dimensions of the continuum samples for proposed relevant parameters
Full size table

The wave propagation in these continuum models is investigated by FEM. The dispersion properties of the unit cell in S1 are analyzed by means of the Bloch–Floquet periodic boundary conditions. The first three dispersion curves of the unit cell are shown in Fig. 4c as the wave vector varies along the contour of the first Brillouin zone, which has well agreement with dispersion equation Eq. (10). For the steady-state response, a one-dimensional 30 unit cell chain is employed, and a time harmonic displacement is then set as import boundary condition at the left end; meanwhile, the right end is set free. The transmission coefficient is defined as the ratio of the output displacements at the chosen locations to the import displacement. The transmission coefficients of the 15th unit of all the samples are shown in Fig. 8, respectively.

Fig. 8
figure 8

Transmission coefficients of the samples in Table 1. a S1, S2, S3, S4 with varying θ 1, δ 1, δ 2; b S1, S5, S6, S7 with varying θ, δ

Full size image

According to the two-step HM, three forbidden bands of the lattice model are calculated to be (398, 910 Hz), (1068, 1185 Hz) and (1240 Hz, +∞), as shown in Fig. 4, and the center frequencies of the first two bandgaps are 597 and 1155 Hz. From the transmission coefficients of S1 in Fig. 8, the edges of bandgaps are around 360, 920, 1050, 1190, 1220 Hz, and the center frequencies of the first two bandgaps are about 600 and 1150 Hz, which can well coincide with the above predictions. The variable δ 1, δ 2 or θ 1 significantly affects the central frequencies of the first and second bandgaps, as shown in Fig. 8a, and the separate of the two central frequencies can broaden the second bandgap, but these variations have slight influence on the start frequency of the first bandgap. We can observe that two center frequencies of the first two bandgaps are independent of the variable θ and δ in Fig. 8b. A narrower bandwidth of the second pass band can be generated when θ < 1 or θ > 1, but third pass band is broadened concurrently when θ > 1. If the value of δ is increased or θ is approaching to zero, the start frequency of the first bandgap will be reduced.

4.2 An application example

A natural practical application of these AMs is typical vibration control for the existence of bandgaps. Achieving suitable bandgaps which contain the frequency range of pernicious vibration or noise by adopting appropriate parameters is a basic demand. Obviously, the value of \(\omega_{0} \approx \sqrt {E_{k} /\rho_{m} l_{1} l_{2} }\) mainly depends on the density ρ m of ‘mass’ material and Young’s modulus E k of ‘spring’ material under confined space, the center frequencies of bandgaps would be firstly adjusted by θ 1, δ 1 and δ 2; then, the bandwidth would be determined by θ and δ. For the moment, achieving low frequency or broad bandgaps for vibration control is a meaningful topic. A lower start frequency of the first bandgap can be obtained by a value of θ near zero or a larger δ, while the separate of ω n1, ω n2 or suitable values of θ or δ have significant influence on the bandwidth of both pass bands and forbidden bands.

The performances of the AM in vibration control are further studied here. An AM chain consisting of 5 unit cells of S1 is simulated by FEM. An input vibration displacement of U(0, t) = 0.1 (sin 2πft) is generated at one end of the model (1st unit cell) along the chain. At the opposite end (5th unit cell), the vibration output responses at different frequencies are achieved, as shown in Fig. 9. The metamaterial has tiny influence on the vibration transmission in the pass bands at f = 360 Hz (Fig. 9a), f = 1000 Hz (Fig. 9c), f = 1200 Hz (Fig. 9e), and the output displacement become erratically due to the reflection of the vibration waves. While for the frequencies in the forbidden bands at f = 600 Hz (Fig. 9b) and f = 1150 Hz (Fig. 9d), the vibration waves will greatly decay as expected. Moreover, the vibration control with the multi-frequency excitation U(0, t) = 0.1(sin 2πf 1 t + sin 2πf 2 t) is also studied here, where f 1 = 600 Hz, f 2 = 1150 Hz. As shown in Fig. 9f, the structure is able to effectively attenuate the multi-frequency vibration wave. Further development of this model will have wider applications when these AMs are employed in the creation of vibration-less machining environment, as well as in the seismology: protecting buildings against earthquakes.

Fig. 9
figure 9

Displacement response with vibration input excitation at difference frequencies. a 360 Hz, b 600 Hz, c 1000 Hz, d 1150 Hz, e 1200 Hz, f 600 + 1150 Hz

Full size image

5 Conclusions

This paper reveals the effects of relevant parameters on the center frequencies and edges of bandgaps in multi-resonators AMs, and the results indicate the purposed metamaterial can provide a possibility for managing the bandgaps instead of traditionally searching new complex structures or extreme component materials by tweaking the relevant parameters in the model. The two-step HM has been extended to obtain the effective mass of multi-resonators AM in lattice, which is confirmed available for multi-resonators AMs. Then, the dual-resonator continuum models based on the mimicking lattice systems with several special dimensions have been analyzed by the FEM, and the obtained results are in well agreement with the theoretical predictions, which can also demonstrate the validity of conclusions about the effects of the relevant parameters on bandgaps. Finally, the purposed multi-resonator AM has been verified to be feasible in vibration control under both the single-frequency and multi-frequency excitation with only five units. The present studies have further benefit for the design and applications of AMs.