1 Introduction

The experimental studies proved that as the size effect is not considered in classical continuum theories, these theories are incapable of predicting the behavior of nanostructures accurately. Besides, the vast applications of nanocomponents such as nanosensors, micromotors, nanoturbines, nanomotors and NEMS [22, 28–30, 35, 66] demand investigations on size effects and physical properties of nanostructures. Nonclassical elasticity theories have been widely employed to study size effects on the mechanical behavior of nanostructures, and the classical continuum mechanics models offer a useful approach to analyzing the nanobeam. Thus, to include the size effects in a classical continuum model, the model can be extended through the Eringen’s nonlocal elasticity theory [15, 16].

During past few years, researchers have become interested in studying the behavior of nanomachines which are necessary in future goals of nanotechnology. Nonlocal elasticity theory was also employed by Lim et al. [37] to study the buckling of nanostructures in a temperature field. Moreover, Pradhan and Murmu [47] studied the flapwise bending vibration by developing a single nonlocal beam model by applying DQM method. Wang et al. [61] studied the free vibration of micro- and nanobeams based on Eringen’s nonlocal elasticity theory and Timoshenko beam theory. Murmu and Adhikari [41] studied the vibration of double-nanobeam systems based on nonlocal theory. The longitudinal vibration of a cracked nanobeam was examined by Hsu et al. [24] using the nonlocal elasticity theory. Thai [58] and Thai and Vo [59], respectively, presented a nonlocal shear deformation beam theory and a nonlocal sinusoidal shear deformation beam theory for bending, buckling and vibration of nanobeams using the nonlocal differential constitutive relations of Eringen. Ke and Wang [27] studied the thermoelectric–mechanical vibration of the piezoelectric nanobeams based on the nonlocal theory and Timoshenko beam theory. Based on the theory of nonlocal elasticity, Loya et al. [38] studied the flexural vibrations of cracked micro- and nanobeams. Ansari et al. [2] examined the free vibration behavior of piezoelectric Timoshenko nanobeams based on the nonlocal elasticity theory. Bahrami and Teimourian [5] used the wave propagation approach in conjunction with nonlocal elasticity theory to study the buckling and free vibrations of Euler–Bernoulli nanobeams. Rahmani and Jandaghian [48] presented the investigation on buckling of functionally graded nanobeams based on a nonlocal third-order shear deformation theory. Chakraverty and Behera [10] investigated the free vibration of nonuniform Euler–Bernoulli nanobeams based on nonlocal elasticity theory. Jandaghian and Rahmani [25] studied the free vibration analysis of magneto-electro-thermo-elastic (METE) nanobeams resting on a Pasternak foundation based on nonlocal theory. Karličić et al. [26] proposed the nonlocal Euler–Bernoulli beam theory to study the free vibration and stability of a multiple-nanobeam system (MNBS) using the Eringen nonlocal continuum theory.

During past recent years, a few studies have been conducted on the nonlinear vibrational behavior of nanobeams [21, 65]. The nonlinear vibration of nanobeam with the axial initial load was investigated by Wang and Li [64], using the nonlocal continuum theory. Eltaher et al. [14] studied the nonlinear free vibration of material graduations of a nano-Timoshenko beam considering the neutral axis position. The free and forced vibrations of simply supported functionally graded (FG) nanobeams were studied by El-Borgi et al. [13]. Behera and Chakraverty [6] investigated nonlocal nonlinear free vibration of nanobeams using differential quadrature method (DQM). Chang [12] studied nonlinear free vibration of nanobeam subjected to magnetic field by using Eringen’s nonlocal theory. Rezaee and Lotfan [51] investigated the nonlinear vibrations of an axially moving Rayleigh nanobeam. The nonlinear vibration behavior of a single-walled carbon nanotube conveying fluid was investigated by Zhen and Fang [69]. Togun and Bağdatlı [60] studied the nonlinear free and forced vibration of a nanobeam resting on an elastic foundation of the Pasternak type based on the nonlocal Euler–Bernoulli beam theory. The nonlinear vibration of a single-walled carbon nanotube conveying fluid is studied based on nonlocal elastic theory and Euler–Bernoulli beam theory by Zhen and Fang [69]. Most recently, Shafiei et al. [54] studied the nonlinear vibration behavior of axially functionally graded tapered microbeams. Şimşek [56] studied the nonlinear vibration of a nonclassical nanobeam with axially immovable ends based on the Eringen’s nonlocal elasticity theory. Nazemnezhad and Hosseini-Hashemi [44] used the nonlocal elasticity to study the nonlinear free vibration of functionally graded (FG) nanobeams with immovable ends. Fang et al. [17] studied the nonlinear free vibration of double-walled carbon nanotubes based on the nonlocal elasticity theory. Based on Timoshenko beam theory, Askari et al. [3] studied the nonlinear vibration of the nonlocal nanowires. Wang and Li [64] analyzed the nonlinear primary resonance of nanobeam with the axial initial load based on the nonlocal continuum theory. The nonlinear vibration of the nonlocal elastic nanobeams was studied by Kuo [32] using the finite element method. Using the nonlocal beam model, the vibration study of a single-walled carbon nanotube (SWCNT) conveying nanoflow embedded in biological soft tissue is performed by Hosseini et al. [23]. Kuo [33] studied the chaotic behavior of the single-walled carbon nanotubes on elastic medium by the nonlocal elastic theory. Chang and Yeh [11] studied the nonlinear free vibration of Euler–Bernoulli nanobeam subjected to magnetic field based on Eringen’s nonlocal elasticity. The nonlinear finite element analysis was performed on the nonlinear vibration of nonlocal elastic multi-walled carbon nanotubes by Kuo [31]. In another study, Azrar et al. [4] studied the nonlinear free vibration of single-walled carbon nanotubes (CNTs) conveying based on Eringen’s nonlocal elasticity theory.

Rotary effect of nanostructures is of great importance to study, and a lot of researchers have performed analysis on rotating beams [2, 36, 41–43, 46]. Aranda-Ruiz et al. [2] derived the natural frequencies of the flapwise bending vibrations of a nonuniform rotating cantilever nanobeam considering the rotational force. Also recently, Ghadiri and Shafiei [19] investigated free bending linear vibration of rotating nanoplate for various boundary conditions. The nonlocal theory has also been utilized in investigations on rotating nanobeams. Pradhan and Murmu [47] used a single nonlocal beam model to study the flapwise bending vibration of a rotating nanocantilever using Eringen’s nonlocal elasticity theory. Ghadiri and Shafiei [20] investigated the small-scale effect on the flapwise bending vibrations of a rotating nanoplate by nonlocal elasticity theory.

As it is seen, no detailed report has been found in the literature on the nonlinear nonlocal rotary-thermo-mechanical vibration of a nanobeam so far. Motivated by these considerations and in order to improve optimum design of rotary nanosystems, this study aims to investigate the nonlinear thermal vibration of rotating cantilever and propped cantilever nanobeams under temperature changes for different nonlocal parameter. Eringen’s theory in conjunction with Hamilton’s principle is employed to derive the governing equation and nonlinear boundary conditions. The differential quadrature method (DQM) is used in conjunction with direct iterative method to solve the governing equation. Effects of the nonlocality, temperature change, rotational velocity and the nonlinearity of the problem on the normalized vibration properties are investigated. The results of this investigation would be useful to design nanobeams, nanorods, nanoturbine and nanomotors using CNTs, more efficiently.

2 Problem formulation

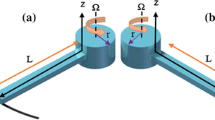
The kinematics of deformation is presented by different theories [49]. As it is shown in Fig. 1, here we consider a nanobeam of length “L” along the axial coordinate, thickness “b” and height “h” which is fixed to a rigid hub at point “O”. The dynamic version of the principle of virtual displacements is used to derive the equations of motion of Euler–Bernoulli beam.

Fig. 1
figure 1

Schematic of rotating nanobeam: a propped cantilever nanobeam and b cantilever nanobeam

Full size image

2.1 Kinematics

The displacement field of a point of the nanobeam is defined as

$$\begin{aligned} & u_{1} = u\left( {x,t} \right) + z\theta ;\quad u_{2} = 0;\quad u_{3} = w\left( {x,t} \right) \\ & \theta \left( {x,t} \right) = - \frac{\partial w}{\partial x} \\ \end{aligned}$$
(1)

where \(u\) and \(w\) are the axial and transverse displacements of point \(\left( {x,t} \right)\) located on the mid-plane (i.e., \(z = 0\)) of the nanobeam and the x-axis is taken along the geometric centroid of the beam. The nonzero nonlinear strain of the Euler–Bernoulli beam theory is the axial strain of a fiber at the distance z from the mid-plane, and it is made up of both bending and stretching of mid-plane, as shown.

$$\varepsilon_{xx} = \frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} - z\frac{{\partial^{2} w}}{{\partial x^{2} }};\quad \varepsilon_{yy} = \varepsilon_{zz} = 0$$
(2)

2.2 Eringen’s nonlocal theory

The classic theory of elasticity is based on the assumption that the material and tensor fields of stress and strain are continuous. The atomic empty spaces are of considerable size with respect to the nanoscales. Thus, using the continuum-based theories for modeling the nanostructures are put into question, and we should instead use the nonclassical theories which consider the small-scale effects and the inherent discontinuities of nanostructures. The nonlocal elasticity theory which was first proposed by Eringen [15] is one of the nonclassical continuum theories which consider the small-scale effects. The classical continuum mechanic theories consider the stress in a point as a function of the strain at that point; however, the nonlocal theory considers the stress at a point as a function of strain at all of the points of the body. In fact, this theory includes the atomic forces in a continuous body into the problem.

Using the classic method, studying the large-scale beams is based on this assumption that the atomic space is negligible compared with the length of the beam and, thus, the characteristic length is not considered in these studies. But, in micro- and nanostructures, the atomic spaces are of considerable length compared with the beam length and, thus, the characteristic length is concluded as an effective parameter in the dynamic and vibration analysis of small-scale structures. In classic elasticity, the stress tensor σ in the point x is defined as a function of strain at that point. On the other hand, the nonlocal elasticity theory relates the stress tensor at point x of mass environment (Ω) to the tensor of the strain (ɛ) of the whole body by a differential equation. Thus, the nonlocal stress tensor at point x can be expressed as:

$$\sigma = \int\limits_{\varOmega } {K\left( {\left| {x^{{\prime }} - x} \right|,\tau } \right)t\left( {x^{{\prime }} } \right){\text{d}}x^{{\prime }} }$$
(3)

where \(K\left( {\left| {x^{{\prime }} - x} \right|} \right)\) is the kernel which is in fact a weight function for the integral equation and \(\left| {x^{{\prime }} - x} \right|\) is the distance of local point x and nonlocal point x′. τ is a parameter which depends on the length of the internal characteristic of the nanostructure (a) and length of the external characteristic (l) and specifies the importance of small scales in the integral equation of the nonlocal elasticity theory. Also, τ can be defined as:

$$\tau = \frac{{e_{0} a}}{l}$$
(4)

where e 0 a is a parameter which can be calculated by comparison of the nonlocal elasticity theory with the experimental results and is called small-scale parameter. The general Hook’s law defines the relation between the strain tensor and macroscopic stress at point x for a Hookean solid as follows:

$$t\left( X \right) = C\left( X \right):\varepsilon \left( X \right)$$
(5)

where C is the fourth-order elasticity tensor and ‘:’ denotes the double-dot product. The general Eqs. (3) and (5) state the nonlocal stress at point x of a Hookean material. Also, Eq. (3) is the weighted average of the portion of strain field in all the body with respect to the stress field at point x. When “τ → 0,” there is no integral and nonlocal effect of stress and strain and Eq. (3) approaches to the classic theory. Thus, the kernel \(K\left( {\left| {x^{{\prime }} - x} \right|} \right)\) should approach to Kronecker delta when “τ → 0,” which means:

$$\mathop {\lim }\limits_{\tau \to 0} K\left( {\left| {x^{{\prime }} - x} \right|,\tau } \right) = \delta \left( {\left| {x^{{\prime }} - x} \right|} \right)$$
(6)

Besides, K has its maximum value at the local point x. By using the kernel, the differential form of the nonlocal elasticity equation can be obtained from the integral form, and by substituting that into Eq. (3), the differential form of the nonlocal elasticity equation can be obtained as follows:

$$\left( {1 - \left( {e_{0} a} \right)^{2} \nabla^{2} } \right)\sigma = C:\varepsilon$$
(7)

The scalar form of Eq. (7) is:

$$\left( {1 - \left( {e_{0} a} \right)^{2} \nabla^{2} } \right)\sigma_{ij} = C_{ijkl} :\varepsilon_{kl}$$
(8)

If the small scales are negligible (τ, μ → 0), Eqs. (7) and (8) will approach to classic theory. Eringen’s nonlocal elasticity theory is vastly utilized in studying the wave propagation, dislocation mechanics, fracture mechanics, surface tension fluids, etc., in past decade. First, Peddieson et al. [45] used this theory to study the size effect in bending behavior of nano- and microstructures. Zhang et al. [68] used the nonlocal elasticity theory to study the small-scale effects on the buckling of the multi-walled carbon nanotubes. Moreover, Wang [62] and Wang and Varadan [63] performed an investigation on the wave propagation in carbon nanotubes. They also examined the small-scale effects on CNTs.

The nonlocal constitutive relation in Eq. (8) for the macroscopic stress yields the following relation for the nonlocal stress component \(\sigma_{xx}\):

$$\sigma_{xx} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} \sigma_{xx} }}{{\partial x^{2} }} = E\varepsilon_{xx}$$
(9)

where E is Young’s modulus. Hence, nonlocal stress resultants over the cross-sectional area can be written as

$$N_{xx} = \int_{A} {\sigma_{xx} {\text{d}}A} ,\quad M_{xx} = \int_{A} {z\sigma_{xx} {\text{d}}A}$$
(10)

Equation (9) together with (10) yields

$$N_{xx} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} N_{xx} }}{{\partial x^{2} }} = EA\left[ {\frac{{{\text{d}}u}}{{{\text{d}}x}} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right]; M_{xx} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} = - EI\frac{{\partial^{2} w}}{{\partial x^{2} }}$$
(11)

where I and A denote the second moment and cross section of area, respectively, and are defined as:

$$I = \int_{A} {z^{2} {\text{d}}A} ;\quad A = \int_{A} {{\text{d}}A}$$
(12)

2.3 Equation of motion and boundary conditions

The governing equation of motion and the associated boundary conditions are derived according to the Hamilton’s principle as

$$\int\limits_{0}^{T} {\left( { - \delta K + \delta\Pi _{U} + \delta\Pi _{E} } \right){\text{d}}t} = 0$$
(13)

where \(\delta K\), \(\delta\Pi _{U}\) and \(\delta\Pi _{E}\), respectively, define the virtual kinetic, virtual strain and potential energies due to the applied loads. The virtual kinetic energy of the nanobeam can be written as:

$$K = \frac{1}{2}\int_{0}^{L} {\int_{A} {\rho \left( {\dot{u}_{1}^{2} + \dot{u}_{3}^{2} } \right)} } {\text{d}}A\;{\text{d}}x$$
(14)
$$\delta K = \int_{0}^{L} {\left[ {m_{0} \left( {\frac{\partial u}{\partial t}\frac{\partial \delta u}{\partial t} + \frac{\partial w}{\partial t}\frac{\partial \delta w}{\partial t}} \right) - m_{1} \left( {\frac{\partial u}{\partial t}\frac{{\partial^{2} \delta w}}{\partial x\partial t} + \frac{\partial \delta u}{\partial t}\frac{{\partial^{2} w}}{\partial x\partial t}} \right) + m_{2} \frac{{\partial^{2} w}}{\partial x\partial t}\frac{{\partial^{2} \delta w}}{\partial x\partial t}} \right]{\text{d}}x}$$
(15)

where over-dot denotes derivative with respect to time and

$$m_{0} = \rho A,\quad m_{2} = \int_{A} {\rho z^{2} {\text{d}}A} = \rho I$$
(16)

the virtual strain energy of the nanobeam then can be defined as:

$$\delta\Pi _{U} = \int_{0}^{L} {\left( {N_{xx} \delta \frac{\partial u}{\partial x} + N_{xx} \frac{\partial w}{\partial x}\delta \left( {\frac{\partial w}{\partial x}} \right) - M_{xx} \delta \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)} {\text{d}}x$$
(17)

\(\Pi _{\text{E}} \left( {x,t} \right)\) which defines the virtual potential energy due to the external stimuli is given by

$$\delta\Pi _{E} = \int_{0}^{L} {\bar{N}\frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial x}{\text{d}}x}$$
(18)

where \(\bar{N}\) is the included axial force in the model as the true spatial variation due to the rotation. Substituting Eqs. (15), (17) and (18) into Eq. (13), the following equation can be obtained as:

$$\int_{0}^{T} {\int_{0}^{L} {\left[ {\begin{array}{*{20}l} { - m_{0} \left( {\frac{\partial u}{\partial t}\frac{\partial \delta u}{\partial t} + \frac{\partial w}{\partial t}\frac{\partial \delta w}{\partial t}} \right) - m_{2} \frac{{\partial^{2} w}}{\partial x\partial t}\frac{{\partial^{2} \delta w}}{\partial x\partial t}} \hfill \\ { + N_{xx} \delta \frac{\partial u}{\partial x} - M_{xx} \delta \frac{{\partial^{2} w}}{{\partial x^{2} }} + N_{xx} \frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial x} + \bar{N}\frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial x}} \hfill \\ \end{array} } \right]} } {\text{d}}x{\text{d}}t = 0$$
(19)

and then, by setting the coefficients of δu, δw and \(\frac{\delta \partial w}{\partial x}\) to be zero, the Euler–Lagrange equation can be obtained as:

$$\frac{\partial N}{\partial x} = m_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }}$$
(20)
$$\frac{{\partial^{2} M_{xx} }}{{\partial x^{2} }} + \frac{\partial }{\partial x}\left[ {\left( {N_{xx} + \bar{N}} \right)\frac{\partial w}{\partial x}} \right] = m_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - m_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}$$
(21)

For “\(0 < x < L\)” and “\(t > 0\),” and boundary conditions at \(x = 0\) and \(x = L\), we have:

$$\begin{aligned} & u = 0\quad {\text{or}}\quad N_{xx} = 0 \\ & w = 0\quad {\text{or}}\quad \frac{{\partial M_{xx} }}{\partial x} + m_{2} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} + \left( {N_{xx} + \bar{N}} \right)\frac{\partial w}{\partial x} = 0 \\ & \frac{\partial w}{\partial x} = 0\quad {\text{or}}\quad M_{xx} = 0 \\ \end{aligned}$$
(22)

In Eq. (18), \(u\) and \(w\) present the nonlocal displacements of the beam. By Eqs. (11) and (20), one arrives at

$$N_{xx} = EA\left[ {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right] + \left( {e_{0} a} \right)^{2} \left( {m_{0} \frac{{\partial^{3} u}}{{\partial x\partial t^{2} }}} \right)$$
(23)

Similarly, from Eqs. (11) and (21) one obtains

$$M_{xx} = - EI\frac{{\partial^{2} w}}{{\partial x^{2} }} + \left( {e_{0} a} \right)^{2} \left\{ {m_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - m_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} - \frac{\partial }{\partial x}\left[ {\left( {N_{xx} + \bar{N}} \right)\left( {\frac{\partial w}{\partial x}} \right)} \right]} \right\}$$
(24)

The equation of motion can be derived in terms of the nonlocal displacement \(w\) by substituting \(N_{xx}\) and \(M_{xx}\) into Eqs. (20) and (21); similarly, the boundary conditions can be derived in terms of the displacements. The axial accumulation of thermal and rotational forces is expressed as

$$\bar{N}_{xx} = N^{\text{thermal}} + N^{\text{rotation}} (x) = \frac{{EA\alpha\Delta {\rm T}}}{1 - 2\nu } + \int\limits_{x}^{L} {\rho A\;\Omega ^{2} \left( {r + \zeta } \right){\text{d}}\zeta }$$
(25)

Substituting Eqs. (25) and (24) into (21) yields

$$\begin{aligned} & \frac{{\partial^{2} }}{{\partial x^{2} }}\left( { - EI\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + \frac{EA}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} \left( {\left( {e_{0} a} \right)^{2} \frac{{\partial^{2} w}}{{\partial x^{4} }} - \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) \\ & \quad \times\left( {e_{0} a} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {\frac{\partial }{\partial x}\left( {\bar{N}_{xx} \frac{\partial w}{\partial x}} \right) + m_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - m_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}} \right] \\ & \quad - \frac{\partial }{\partial x}\left( {\bar{N}_{xx} \frac{\partial w}{\partial x}} \right) = m_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - m_{2} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} \\ \end{aligned}$$
(26)

The nondimensional parameters are derived as follows:

$$\begin{aligned} & \bar{A} = \frac{{AL^{2} }}{2I} \\ & \bar{N} = \frac{{L^{2} }}{EI}\left( {\frac{EA\alpha }{1 - 2\nu }\Delta {\rm T} + \int\limits_{x}^{L} {\rho A\;\Omega ^{2} \left( {r + x} \right)\text{d}x} } \right) \\ &\Phi ^{\text{2}} = \frac{{\rho A\Omega ^{2} L^{4} }}{EI} \\ & w = WL \\ & x = XL \\ & r = \delta L \\ & \mu = \frac{{e_{0} a}}{L} \\ & \bar{m} = \frac{{m_{2} }}{{L^{2} m_{0} }} \\ \end{aligned}$$
(27)

where Φ, δ, μ and ΔΤ are nondimensional angular velocity, hub radius, nonlocal parameter and temperature change, respectively. So nondimensional nonlinear equation of bending flapwise vibration can be written as:

$$\begin{aligned} & - \frac{{\partial^{4} W}}{{\partial X^{4} }} + \bar{A}\left( {\frac{\partial W}{\partial X}} \right)^{2} \left( {\mu^{2} \frac{{\partial^{4} W}}{{\partial X^{4} }} - \frac{{\partial^{2} W}}{{\partial X^{2} }}} \right) - \frac{\partial }{\partial X}\left( {\bar{N}_{xx} } \right)\frac{\partial W}{\partial X} \\ & \quad + \mu^{2} \frac{{\partial^{2} }}{{\partial X^{2} }}\left[ {\frac{\partial }{\partial X}\left( {\bar{N}\frac{\partial W}{\partial X}} \right)} \right] = \frac{{L^{4} m_{0} }}{EI}\frac{{\partial^{2} }}{{\partial t^{2} }}\left\{ {\mu^{2} \left[ {\bar{m}\frac{{\partial^{4} W}}{{\partial X^{4} }} - \frac{{\partial^{2} W}}{{\partial X^{2} }}} \right] - \bar{m}\frac{{\partial^{2} W}}{{\partial X^{2} }} + W} \right\} \\ \end{aligned}$$
(28)

Using \(W\left( {x,t} \right) = a\bar{W}\left( x \right)\cos \omega t\) [18], a nondimensional nonlocal differential equation of nonlinear vibration of nanobeam can be derived to solve the nonlinear equation, where “a” is the nonlinear amplitude. Nondimensional frequency is defined as:

$$\Psi = \left( {\frac{{m_{0} L^{4} }}{EI}\omega^{2} } \right)^{{\frac{1}{4}}}$$
(29)

Furthermore, the exact boundary conditions are defined as clamped (at \(x = 0\)) and free or simply supported (at \(x = L)\) as follows:

clamped at \(X\) = 0:

$$W\left( 0 \right) = 0$$
(30)
$$\frac{\partial W\left( 0 \right)}{\partial X} = 0$$
(31)

free at \(X\) = 1

$$M_{XX} (1) = 0$$
(32)
$$\frac{{\partial M_{XX} (1)}}{\partial X} = 0$$
(33)

simply supported at \(X\) = 1:

$$W\left( 1 \right) = 0$$
(34)
$$M_{XX} (1) = 0$$
(35)

2.4 Solution procedure

Differential quadrature method (DQM) is used for solving the equilibrium equation for the reason that this method is proven to have high accuracy in solving complicated partial differential equations. Simple formulation and low computational cost are the advantages of DQM which was introduced by Bellman et al. [7, 8], while the other numerical methods such as finite difference (FD), dynamic relaxation (DR) and finite element (FE) [50] have not these advantages. The weighting coefficients of DQM depend on the grid spacing. Therefore, using these coefficients every partial differential equation can be simplified to a set of algebraic equations [55]. DQM can be subdivided into several subsets with respect to the applied function and satisfied types of boundary conditions. Thus, the \(r{\text{th}}\)-order derivative of a function \(f\left( x \right)\) is expressed as following linear sum of the function values [55]

$$\left. {\frac{{\partial^{r} f\left( x \right)}}{{\partial x^{r} }}} \right|_{{x = x_{P} }} = \sum\limits_{j = 1}^{n} {C_{ij}^{\left( r \right)} f\left( {x_{i} } \right)}$$
(36)

where the number of grid points along x direction is defined by n. Also, \(C_{ij}\) is obtained as follows:

$$\begin{aligned} C_{ij}^{\left( 1 \right)} & = \frac{{M\left( {x_{i} } \right)}}{{\left( {x_{i} - x_{j} } \right)M\left( {x_{j} } \right)}}\quad i,j = 1,2, \ldots ,n\;{\text{and}}\;i \ne j \\ C_{ii}^{\left( 1 \right)} & = - \sum\limits_{j = 1,i \ne j}^{n} {C_{ij}^{\left( 1 \right)} \quad } i,j = 1,2,, \ldots N \\ \end{aligned}$$
(37)

in which M(x) is defined as:

$$M\left( {x_{i} } \right) = \prod\limits_{j = 1,j \ne i}^{n} {\left( {x_{i} - x_{j} } \right)}$$
(38)

and superscript \(r\) is the order of derivative. Also, \(C^{\left( r \right)}\) is the weighting coefficient along \(x\) directions which is written as:

$$\begin{aligned} C_{ij}^{\left( r \right)} & = r\left[ {C_{ij}^{{\left( {r - 1} \right)}} C_{ij}^{\left( 1 \right)} - \frac{{C_{ij}^{{\left( {r - 1} \right)}} }}{{\left( {x_{i} - x_{j} } \right)}}} \right]\quad i,j = 1,2, \ldots ,n,i \ne j\;{\text{and}}\;2 \le r \le n - 1 \\ C_{ii}^{\left( r \right)} & = - \sum\limits_{j = 1,i \ne j}^{n} {C_{ij}^{\left( r \right)} } \quad i,j = 1,2, \ldots ,n\;{\text{and}}\;1 \le r \le n - 1 \\ \end{aligned}$$
(39)

Chebyshev–Gauss–Lobatto technique has been employed as follows in order to obtain a better mesh point distribution and increased convergence of solutions

$$\zeta_{i} = \frac{1}{2}\left( {1 - \cos \left( {\frac{{\left( {i - 1} \right)}}{{\left( {N - 1} \right)}}\pi } \right)} \right)\quad i = 1,2,3, \ldots ,n$$
(40)

Finally, incorporating boundary conditions Eqs. (30–35) into (28) and using eigenvalue equation in the form of (41) solve the overall problem, and natural frequency will be calculated.

$$\left[ {K^{\text{Linear}} + \frac{3}{4}K^{\text{Non - linear}} \left( w \right)} \right]_{\text{total}} \left\{ w \right\} = \omega^{2} \left\{ w \right\}$$
(41)

An iterative procedure must be employed for solving the resulting system of nonlinear eigenvalue Eq. (41). For this purpose, in the first step, by neglecting the nonlinear terms of the transverse displacement, the eigenvalue problem is solved in each case and the linear eigenvector is then normalized by dividing to the maximum transverse displacement. In the second step, the nonlinear vibration equation can be solved using the eigenvector associated with the eigenvalues of Eq. (41). Finally, the eigenvalue problems are solved again to obtain the new eigenvalues and eigenvectors. This procedure continues until the difference between the nonlinear frequencies of two subsequent iterations ‘e’ and ‘e + 1’ in the iterative procedure is [40],

$$\left| {\omega^{e + 1} + \omega^{e} } \right|/\omega^{e} \le \varepsilon \quad \varepsilon = 10^{ - 4}.$$

3 Numerical results

3.1 Linear vibration

The efficiency of the presented numerical analysis is shown by comparison of the presented linear results with the results presented in Shafiei et al. [52, 53], Lu et al. [39] and Wang et al. [61]. Finally, the parametric study is presented for considering the effects of different parameters such as small-scale, angular velocity, amplitude of nonlinearity and nonlocal effects of the nanobeam. For this purpose, the nanobeam is assumed to be of “\({\text{thickness}} = {\text{height}} = \frac{\text{Length}}{100} = 3.4\;{\text{nm}}\),” the Poisson’s ratio is \(\nu = 0.3\), “Young’s modulus \(E = 971\;{\text{GPa}}\)” and “density \(\rho = 2300\;{\text{kg/m}}^{3}\)” [43]. In the room- or low-temperature (LT) condition, the thermal coefficient is assumed as “\(\alpha_{x} = - 1.6 \times 10^{ - 6} \;{\text{K}}^{ - 1}\)” and for high-temperature (HT) condition it is set to be “\(\alpha_{x} = 1.1 \times 10^{ - 6} \;{\text{K}}^{ - 1}\)” as were used by Yao and Han [67].

Nondimensional frequencies of nonrotating cantilever (Table 1) and propped cantilever (Table 2) nanobeams are compared with the results obtained by Lu et al. [39] and Wang et al. [61], respectively, to validate the present linear results. In addition, nondimensional linear frequency of rotating beam is compared with the results obtained by Shafiei et al. [52, 53], and satisfactory agreement between the results is given in Table 3.

Table 1 Comparison of results for nondimensional linear frequency (\(\Psi\)) of the cantilever nanobeam
Full size table
Table 2 Comparison of results for nondimensional linear frequency (\(\Psi\)) of propped cantilever nanobeam
Full size table
Table 3 Comparison of results for nondimensional angular velocity (Φ) of cantilever non-FG microbeam for δ = μ = 0
Full size table

3.2 Nonlinear vibration

First, to study the nonlinear frequency, the normalized frequency and nondimensional nonlinear amplitude are defined as:

$$\text{Normalized}\;\text{frequency} = \frac{{\text{Nonlinear}\;\text{frequency}\;\text{of}\;\text{nanobeam}\;\left( {a \ne 0} \right)}}{{\text{Linear}\;\text{frequency}\;\text{of}\;\text{nanobeam}\;\left( {a = 0} \right)}}$$
(42)
$$\text{Amp} = a\sqrt {\frac{I}{A}}$$
(43)

Table 4 shows the comparison of the results of the normalized fundamental frequency of the nanobeam in this study and three other studies that used numerical and analytical solutions. It is observed that the results of the DQM and other solution procedures have good agreements.

Table 4 Comparison of results for normalized frequency of nonrotating beam
Full size table

To study the nonlinear vibration of rotating nanobeam, “μ = 0–0.5” as the same range was employed by Aranda-Ruiz et al. [2]. Lu et al. [39] proposed that eigenvalues can be calculated in the range of “μ = 0–0.62.” Besides, the nondimensional angular velocity (Φ), temperature change (ΔT) and nonlinear amplitude of the rotary nanobeam are assumed to be in the range of “0–2,” “0–100” and “0–3,” respectively.

Figures 2 and 3, respectively, show the normalized frequency of cantilever and propped cantilever nanobeams versus amplitude for different nonlocal values in four different rotational velocities when temperature change is set to be zero. It is shown that the normalized frequencies of cantilever and propped cantilever nanobeams increase with the nonlocal value. This behavior is the same for all conditions in this paper. Figure 2 shows that the effect of amplitude and rotational velocity on normalized frequency of cantilever nanobeam varies by the nonlocal values. As the Euler–Bernoulli beam theory is mostly suitable for thin beams, to obtain the best results for the Euler–Bernoulli nanobeam, we should have L/h ≥ 40. Since the nonlocal value is normalized by dividing to the length L, by increasing the nondimensional nonlocal value μ and multiplying it to L, value of e 0 a increases a lot. Thus, it can be said that the dependency of Euler–Bernoulli theory on the nonlocal value is more than the other higher-order theories. This is shown in Fig. 2 where increasing the nonlocal value decreases the effect of nonlinearity (amplitude) and when μ ≥ 0.3 the nonlinearity increases the nondimensional frequency. It should be noted that higher-order theories such as Timoshenko beam theory do not include this effect as the length-to-thickness ratio can be much smaller in these theories. As it is shown in Fig. 2, when μ = 0 increasing the nonlinear effect decreases the nondimensional frequency of cantilever nanobeam. On the other hand, nonlocal value increases the frequency of cantilever nanobeam, and as shown in Fig. 2, when μ ≥ 0.3 the effect of nonlocal parameter is more than the effect of the nonlinearity of the system. Thus, when μ ≥ 0.3 the amplitude increases the normalized frequency, which is not observed in other boundary conditions [9, 40]. Furthermore, variation range of the normalized frequency due to increasing the nonlocal parameter reduces when the rotational velocity increases, and it can be said that this is due to increasing the centrifugal force which reduces the transverse displacement. On the other hand, Fig. 3 shows that when the rotational velocity increases, the normalized frequency of propped cantilever nanobeam decreases. In fact, the effects of nonlocal value and nonlinearity of the system for propped cantilever nanobeam are the same. So, increasing one of them increases the effect of the other one on. This can be observed repeatedly for the propped cantilever nanobeam in the following of this paper. It is also worth to mention that dependency of the normalized frequency on the amplitude increases with nonlocal value and decreases with rotational velocity. The effect of the nonlinearity increases by decreasing the stiffness of the nanobeam. Increasing the rotational velocity induces the eccentricity centrifugal force as the tension load in the nanobeam which increases the stiffness of the nanobeam. Thus, increasing the rotational velocity decreases the effect of the nonlinear amplitude. Also, increasing the nonlocal value decreases the stiffness of the nanobeam, which leads to the decrement of the nonlinearity effect on the nanobeam, which is clearly shown in Fig. 3.

Fig. 2
figure 2

Normalized frequency of cantilever nanobeam versus the amplitude of nonlinearity when \(\Delta T = 0\)

Full size image
Fig. 3
figure 3

Normalized frequency of propped cantilever nanobeam versus the amplitude of nonlinearity when \(\Delta T = 0\)

Full size image

Figures 4 and 5 show the normalized frequency of cantilever nanobeam under LT condition, versus the amplitude and rotational velocity, respectively, and Table 5 shows the normalized frequency of cantilever nanobeam with respect to the temperature change under LT and HT conditions. It can be seen that the normalized frequency decreases when the temperature change increases. Comparing Fig. 4a, c, respectively, with Fig. 4b, d shows that the effect of the amplitude on normalized frequency depends on the nonlocal value which is because of the effect of the stiffness which was previously explained. Figure 5 and comparing Fig. 4a with Fig. 4c and Fig. 4b with Fig. 4d show that the nonlocal value can change the effect of the rotational velocity.

Fig. 4
figure 4

Normalized frequency of cantilever nanobeam versus the amplitude of nonlinearity under LT condition

Full size image
Fig. 5
figure 5

Normalized frequency of cantilever nanobeam versus the rotational velocity under LT condition

Full size image
Table 5 Normalized frequency of cantilever nanobeam versus the temperature change under LT, HT condition, L = 25b = 10h = 50 nm
Full size table

Figures 6 and 7, respectively, show the normalized frequency of cantilever nanobeam under HT condition, versus the amplitude and the rotational velocity. Thus, it can be concluded that the vibrational behavior of cantilever nanobeam is unique. For more explanations, it should be noted that according to Eq. (27), increasing the nonlocal value, when \(L\) is constant, increases \(e_{0} a\), which leads to reduction in stiffness of the nanobeam that normally reduces the frequency, but it increases the frequency. Figure 7 and comparing Fig. 6a with Fig. 6b and Fig. 6c with Fig. 6d show that similar to cantilever nanobeam under LT condition, dependency of the normalized frequency on the amplitude changes with nonlocal value, and this is because the nonlocal value changes the stiffness of the nanobeam and the effect of the nonlinearity depends on the stiffness of the nanobeam.

Fig. 6
figure 6

Normalized frequency of cantilever nanobeam versus the amplitude of nonlinearity under HT condition

Full size image
Fig. 7
figure 7

Normalized frequency of cantilever nanobeam versus the rotational velocity under HT condition

Full size image

Figure 7 shows that the effect of rotational velocity on the normalized frequency of cantilever nanobeam under HT conditions depends on the nonlocal value, which means when \(\mu = 0, 0.1\) or 0.2 the normalized frequency increases with rotational velocity, but when \(\mu = 0.3, 0.4\) or 0.5 the rotational velocity reduces the normalized frequency. Unlike LT condition, the normalized frequency of cantilever nanobeam under HT condition increases with the temperature change.

The normalized frequency of propped cantilever nanobeam under LT condition with amplitude and rotational velocity is represented, respectively, in Figs. 8 and 9. Figure 9 and comparing Fig. 8a with Fig. 8b and Fig. 8c with Fig. 8d show that the normalized frequency increases with nonlocal value.

Fig. 8
figure 8

Normalized frequency of propped cantilever nanobeam versus the amplitude of nonlinearity under LT condition

Full size image
Fig. 9
figure 9

Normalized frequency of propped cantilever nanobeam versus the rotational velocity under LT condition

Full size image

Figure 8 and Table 6 show that the effect of nonlinear parameter on the normalized frequency increases with nonlocal value and also when the rotational velocity decreases.

Table 6 Normalized frequency of propped cantilever nanobeam versus the temperature change under LT, HT condition, L = 25b = 10h = 50 nm
Full size table

Figure 9 shows that the normalized frequency decreases by increasing the rotational velocity. Besides, it can be seen that dependency of the normalized frequency on the rotational velocity increases by increasing the nonlocal value.

Table 6 shows that the effect of the amplitude on normalized frequency of the propped cantilever nanobeam under LT and HT conditions is more than that of the rotational velocity. Besides, it can be seen that the temperature change decreases the normalized frequency and the effect of temperature change on normalized frequency increases with nonlocal value. It can be seen that the normalized frequency increases with amplitude and nonlocal value and decreases with temperature change.

Normalized frequency of propped cantilever nanobeam under HT condition with respect to the amplitude and rotational velocity is investigated in Figs. 10 and 11, respectively. Figures 10 and 11 show that the normalized frequency increases with the temperature change and the nonlocal value and decreases by the increment of the rotational velocity.

Fig. 10
figure 10

Normalized frequency of propped cantilever nanobeam versus the amplitude of nonlinearity under HT condition

Full size image
Fig. 11
figure 11

Normalized frequency of propped cantilever nanobeam versus the rotational velocity under HT condition

Full size image

It is also shown that the dependency of normalized frequency on rotational velocity, temperature change and amplitude increases with nonlocal value.

Comparing Fig. 8 with Fig. 10 shows that unlike LT condition, the temperature change increases the normalized frequency of the propped cantilever nanobeam under HT condition.

Finally, it should be noted that the thermal stress has effects on the vibrational behavior of the nanobeam when the ends of the nanobeam have no vertical or axial movements. Here, the consideration of the thermal stress is to examine the difference of the behavior of these two boundary conditions in the response of the fundamental frequency to the external effect, which is here considered and employed as the thermal effect. Also, the external effect can be in shape of thermal, magnetic, etc., which is shown as the thermal stress in this paper.

4 Conclusion

In the present work, the nonlinear flapwise bending vibration of rotating cantilever and propped cantilever nanobeams under thermal effects was investigated. The equations are solved for the frequencies by using the DQ approach. It was observed that the nonlocal effect increases the normalized frequency of both cantilever and propped cantilever. Unlike propped cantilever, the effect of amplitude and rotational velocity on normalized frequency of cantilever nanobeam depends on nonlocal value. It was shown that when the nonlocal value is μ ≥ 0.3 normalized frequency increases with the amplitude and it decreases when the rotational velocity increases. But, when the nonlocal value is μ ≤ 0.2, increasing the amplitude decreases the normalized frequency and the rotational velocity increases the normalized frequency.

For propped cantilever nanobeam, the normalized frequency always increases with rotational velocity and decreases with temperature change.

The normalized frequency of both cantilever and propped cantilever nanobeams increases with temperature change under HT condition, while increasing the temperature change under LT condition decreases the normalized frequency. Besides, in all cases, increasing the nonlocal value increases the effect of temperature change on normalized frequency. The results can provide useful help for the study and design of the new generation of nanodevice such as nanosensors, micromotors, nanoturbines, nanomotors and NEMS.