1 Introduction

In hot forming processes, the multipass deformation is an effective method to manufacture large and complex forgings [1]. During the multipass deformation, the interpass softening, induced by static recovery (SRV), static recrystallization (SRX) [2, 3], and metadynamic recrystallization (MDRX), may occur [4, 5]. Generally, SRV caused by dislocation climb and slip is prevailing in the alloys with high stacking fault energy. SRX and MDRX behaviors are usually differentiated by the critical strain for initiating dynamic recrystallization (DRX) [6–10]. If the deformation degree exceeds the critical strain, MDRX will take place during the subsequent interpass. Otherwise, SRX may occur. Generally, MDRX can rapidly start without any incubation period during the interpass. In particular, the MDRX softening fraction can be as high as 100 % under relatively high deformation temperature or strain rate, which significantly affects microstructural evolution, as well as the subsequent deformation resistance. Therefore, it is of great significance to investigate the MDRX behaviors of metals or alloys for optimal mechanical properties.

In recent years, some researches have been carried out to study MDRX behaviors of different metals or alloys. Lin et al. [11] proposed a new approach, ‘peak stress method,’ to calculate the MDRX softening fractions and developed the kinetics equations to predict MDRX behaviors in the hot-deformed 2124 aluminum alloy. Zhang et al. [12] studied the metadynamic recrystallization behavior of as-cast 904L superaustenitic stainless steel. Lin and Chen [13] developed an accurate mathematical model to predict the grain size of 42CrMo steel during MDRX. Jung et al. [14] simulated the MDRX behaviors of AISI 4135 steel during hot rolling. Cheng et al. [15] found that the MDRX behavior of TiAl alloy is almost independent on deformation temperature and prestrain, but sensitively affected by strain rate. Cho et al. [16] found that the MDRX rate of Nb-microalloy steel increases with the increased strain rate and deformation temperature, but shows an obvious independency of prestrain. Elwazri et al. [17] found that the MDRX behaviors of microalloyed hypereutectoid steels significantly depend on microalloying elements. Lin et al. [18] established the classical Avrami equation to describe the MDRX behaviors of a low alloy steel. Also, similar Avrami equations were developed to characterize the MDRX behaviors of as-cast 42CrMo steel [19], Q345B alloy steel [20], Nimonic 80A superalloy [21], and vanadium–nitrogen microalloyed steel [22].

Nickel-based superalloy, one of typical precipitation-strengthened alloys, exhibits excellent high-temperature strength, corrosion, and fatigue resistances [23]. Because of their superior performance, nickel-based superalloys are predestined for the critical components of aero-engines, which often subject to complex stress conditions under elevated temperatures. So, the microstructures of final products should be strictly controlled. Up to now, the hot deformation behaviors of nickel-based superalloys have been extensively investigated. Lin et al. [24], Dehghan et al. [25], Zuo et al. [26], and Kumar et al. [27] established accurate constitutive models to predict the flow stresses of nickel-based superalloys during single-pass hot deformation. Wen et al. [28] and Ning et al. [29] established the processing maps of some typical nickel-based superalloys, and the optimum hot deformation domains were obtained for the single-pass hot deformation. Zhang et al. [30] and Lin et al. [31] found that the operating DRX nucleation mechanism is discontinuous dynamic recrystallization (DDRX) in nickel-based superalloys. Also, Chen et al. [32, 33] and Reyes et al. [34] investigated the DRX behaviors of some typical superalloys by experiments, mathematical modeling, or cellular automata (CA) method. Xu et al. [35] found that the long-term stress-rupture life of Nimonic 80A alloy is significantly affected by various duplex grain size distributions. He et al. [36] and You et al. [37] investigated the effects of pretreatments on the microstructures and properties of superalloys and obtained the optimized pretreatment methods. Wen et al. [23], Lin et al. [38], and Ye et al. [39] discussed the effects of δ phase on microstructural evolution, hot tensile deformation behaviors, and fracture characteristics. Antonov et al. [40] elucidated the compositional effects on the formation of δ and η phases and develop relationships to predict the long-term stabilities of δ and η precipitate phases.

Based on the above review, it can be found that previous studies mainly focus on the one-pass hot deformation behaviors of some typical superalloys. However, in practice industrial production, critical components often subject to multipass hot deformation processes. Furthermore, studies show that a combination of DRX and MDRX can provide a new way to optimize grain microstructures and properties. In this study, the MDRX behaviors of a typical nickel-based superalloy are investigated by two-pass hot compression tests. Based on the experimental results, a new approach, ‘maximum stress method,’ is developed to evaluate the MDRX softening fractions. The effects of deformation temperature, strain rate, initial average grain size, and interpass time on the MDRX behaviors are discussed in detail. Moreover, the kinetics equations of MDRX are established and validated.

2 Materials and experiments

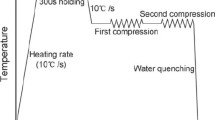
In this study, a commercial nickel-based superalloy with the chemical composition (wt%) of 52.82Ni–18.96Cr–5.23Nb–3.01Mo–1.00Ti–0.59Al–0.01Co–0.03C-(bal.)Fe was used. Cylindrical specimens were machined from a wrought billet, and the diameter and height of specimen were 8 and 12 mm, respectively. All specimens were solution treated at 1040 °C for 45 min and then quickly cooled by water at room temperature. In order to study the MDRX behavior, two-pass hot compression tests were performed using a Gleeble-3500 thermo-mechanical simulator. Tantalum foil between the specimen and dies was used to reduce the friction and avoid the adhesion. Figure 1a shows the experimental procedure of two-pass hot compression tests. Prior to compression, the specimens were heated to the deformation temperature at a heating rate of 10 °C/s and then kept for 300 s to ensure the uniform temperature. Generally, the forming temperatures of nickel-based superalloy can be selected from 940 to 1120 °C. However, previous studies show that the dynamic recrystallized grains easily become coarse when the forming temperature is >1010 °C [32, 33]. Therefore, the deformation temperatures in present study were selected as 950, 980, and 1010 °C. Also, other deformation parameters were chosen according to the industrial forming process of the studied superalloy. Three different strain rates (0.001, 0.01, and 0.1 s−1) were used. Here, the strain of the first-pass deformation was selected as 0.36, which is greatly larger than the critical strain for the onset of DRX [32, 33]. The interpass times were 5, 10, 30, 45, and 60 s. The strain of the second-pass deformation was 0.44. After the second-pass deformation, the specimens were immediately quenched by water. The deformation temperatures and strain rates were the same for the whole two-pass deformation process. Three samples were tested for each deformation condition.

Fig. 1
figure 1

Experimental procedures for: a two-pass hot compression tests; b one-pass hot compression tests

Full size image

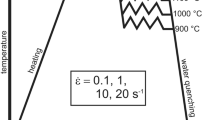
In order to study the effects of initial average grain size on the MDRX behaviors of the studied superalloy, the suitable predeformed treatment Fig. 1b was designed to obtain the initial average grain sizes of 33 and 48 μm, as shown in Fig. 2a, b, respectively. Here, the average grain size was measured by the linear intercept method, according to the standard of ASTM: E112–12. Additionally, Fig. 2c illustrates the optical microstructure of the as-received material after solution heat treatment. It can be found that the initial microstructures are characterized by coarse equiaxed grains, and the average grain size can be evaluated as 75 μm. For the optical microstructure examinations, the specimens were sliced along the compression axis section, mechanically polished, and chemically etched in a cupric chloride solution (5 g CuCl2, 100 ml CH3CH2OH, and 100 ml HCl) for 3–5 min.

Fig. 2
figure 2

Optical microstructures of the studied superalloy with the initial average grain sizes of: a 33 μm; b 48 μm; c 75 μm

Full size image

3 Results and discussion

3.1 Stress–strain curves during two-pass hot deformation

Figure 3 shows the typical true stress–strain curves obtained from two-pass hot compression tests. From Fig. 3a, b, it can be found that the true stress first increases to an obvious peak and then rapidly drops to a relatively lower value at the initial deformation stage, when the deformation temperature is 1010 °C and strain rate is 0.01 s−1. This indicates the occurrence of discontinuous yielding. However, the discontinuous yielding becomes unobvious at the deformation temperatures of 980 and 950 °C (Fig. 3c) or strain rate of 0.001 s−1 (Fig. 3d). This is because the discontinuous yielding usually takes place under relatively high strain rate, which has also been demonstrated by other researchers [41]. There are two kinds of theory to explain the occurrence of discontinuous yielding. One is Cottrell and Bilby theory [42], and the other is dislocation multiplication theory [43]. According to Cottrell and Bilby theory, the occurrence of discontinuous yielding is mainly attributed to the dislocation locking by impurity atoms. The rapid decrease of true stress is related to the disappearance of interaction between impurity atoms and dislocation. Dislocation multiplication theory [43] indicates that the lack of initial mobile dislocation density and a sudden multiplication of mobile dislocation are the prominent reasons for the occurrence of discontinuous yielding. Because there are nearly few interstitial impurity atoms in the studied superalloy, it is obvious that the discontinuous yielding cannot be explained by Cottrell and Bilby theory. Consequently, it is likely that the discontinuous yielding in the studied superalloy is caused by dislocation multiplication. It is well known that the initial mobile dislocation density is extremely insufficient at the beginning of hot deformation. Therefore, a sudden multiplication of mobile dislocation can lead to a relatively large stress (i.e., upper yielding stress). Once the true stress exceeds the upper yielding value, the dislocations become easy to move. Thus, the true stress rapidly decreases to a lower yielding value. Generally, high strain rate enhances the accumulation of dislocation, and dislocation accumulation can be considered as the precondition for the occurrence of discontinuous yielding [44]. So, the discontinuous yielding becomes more and more obvious under relatively high strain rate.

Fig. 3
figure 3

Typical two-pass true stress–strain curves under different: a initial average grain sizes; b interpass times; c deformation temperatures; d strain rates

Full size image

Figure 3a illustrates the true stress–strain curves of the studied superalloy with different initial average grain sizes. From Fig. 3a, it can be found that the true stress is sensitive to the initial average grain size. When the initial average grain size is decreased, the true stresses significantly decrease. Figure 3b shows the effects of interpass time on the true strain–stress curves under 1010 °C and 0.01 s−1. Here, the initial average grain size is 75 μm. From Fig. 3b, it is observed that the yield stresses of the second-pass deformation are remarkably dependent on interpass time. The yield stress of the second-pass deformation decreases with the increase of interpass time, which indicates that the MDRX softening becomes more and more obvious with the increase of interpass time. Figure 3c illustrates the effects of deformation temperature on the true stress–strain curves when the interpass time and initial average grain size are 30 s and 75 μm, respectively. Obviously, the true stresses of the second-pass deformation are significantly affected by deformation temperature. At the deformation temperature of 950 °C, the second-pass true stress only slightly drops, which indicates that the MDRX softening is limited. However, when the deformation temperature is increased to 980 °C, the second-pass true stress first decreases and gradually increases to a peak value. With the further increase of deformation temperature, an obvious drop of true stress can be observed. This mainly attributed to the changed substructures during the interpass and its effects on the DRX behavior of the second-pass deformation. Figure 3d shows the effects of strain rate on true stress–strain curves at 1010 °C. From Fig. 3d, it is observed that the second-pass true stress–strain curves almost coincide with the extrapolated ones in the first-pass deformation at relatively low strain rate (0.001 s−1). It indicates that little softening occurs during the interpass. So, it may be concluded that the MDRX of Inconel 718 superalloy often occurs in the strain rate range 0.01–1.0 s−1. When the strain rate is increased from 0.001 to 0.1 s−1, the softening (reduction of true stress) becomes obvious. Based on the above analysis, it can be concluded that the true stresses of the second-pass deformations are dependent on MDRX behaviors.

3.2 Evaluation of MDRX softening fraction

Generally, there are four conventional stress-based approaches, including offset stress method, back-extrapolation stress method, peak stress method, and mean stress method, to evaluate the MDRX softening fraction during the interpass. In this section, four stress-based approaches are first used to calculate the MDRX softening fraction of the studied superalloy.

In the offset stress method [18], the MDRX softening fraction (\(X_{\text{m}}\)) can be determined by,

$$X_{\text{m}} = \frac{{\sigma_{\text{m}} - \sigma_{2} }}{{\sigma_{\text{m}} - \sigma_{1} }}$$
(1)

where \(\sigma_{\text{m}}\) is the true stress at the interruption, \(\sigma_{1}\) and \(\sigma_{2}\) are the yield stresses of the first and second deformation stages, respectively. Usually, a 0.2 % offset stress is considered as the yield stress, as shown in Fig. 4a. From Fig. 4a, it is difficult to accurately obtain the 0.2 % offset stress due to the occurrence of discontinuous yielding. Moreover, it is reported that the offset method using a strain of 2 % can effectively exclude the SRV effects [45]. So, \(\sigma_{1}\) and \(\sigma_{2}\) are determined as 2 % offset stresses in this study.

Fig. 4
figure 4

Determination of the characteristic stresses used to evaluate MDRX softening fraction by: a offset stress method; b back-extrapolation stress method; c peak stress method; d mean stress method

Full size image

In the back-extrapolation stress method [46], the MDRX softening fraction can be expressed as,

$$X_{\text{m}} = \frac{{\sigma_{\text{m}} - \sigma_{\text{be}} }}{{\sigma_{\text{m}} - \sigma_{1} }}$$
(2)

where \(\sigma_{\text{m}}\) is the true stress at the interruption. \(\sigma_{1}\) is the yield stress of the first-pass deformation. \(\sigma_{\text{be}}\) is the reloading stress, which can be calculated by fitting the reloading curve at high stains and back-extrapolating onto the elastic loading line. The procedure for evaluating the reloading stress is illustrated in Fig. 4b.

In the peak stress method [11], the MDRX softening fraction can be calculated by,

$$X_{\text{m}} = \frac{{\sigma_{\text{m}} - \sigma_{{{\text{p}}_{ 2} }} }}{{\sigma_{{{\text{p}}_{ 1} }} - \sigma_{\text{m}} }}$$
(3)

where \(\sigma_{\text{m}}\) is the true stress at the interruption. \(\sigma_{{{\text{p}}_{ 1} }}\) and \(\sigma_{{{\text{p}}_{ 2} }}\) are the peak stresses of the first and second deformation stages, respectively, as shown in Fig. 4c.

In the mean stress method [47], the MDRX softening fraction (\(X_{\text{m}}\)) can be evaluated by,

$$X_{\text{m}} = \frac{{\bar{\sigma }_{\text{m}} - \bar{\sigma }_{2} }}{{\bar{\sigma }_{\text{m}} - \bar{\sigma }_{1} }}$$
(4)

where \(\bar{\sigma }_{1}\) and \(\bar{\sigma }_{2}\) are the mean stresses of the first- and second-pass deformations, respectively, and can be determined by integrating the area under true stress–strain curve, i.e., \(\bar{\sigma } = (1/\varepsilon_{1} )\int_{0}^{{\varepsilon_{1} }} \sigma d\varepsilon\). \(\bar{\sigma }_{\text{m}}\) is the mean stress for the whole two-pass deformation, as shown is Fig. 4d. The detailed evaluation of mean stress can be found in Ref. [47]. \(\varepsilon_{1}\) and \(\varepsilon_{2}\), two critical parameters to determine \(\bar{\sigma }_{1}\) and \(\bar{\sigma }_{2}\), are generally assumed equal for the first and second deformation stages.

Figure 5 shows the MDRX softening fractions calculated by four conventional stress-based methods. From Fig. 5a, it is observed that the MDRX softening fraction evaluated by the offset stress method is as high as 5.44 at 1010 °C and 0.001 s−1, when the interpass time is 45 s. Similar phenomena can be found in those results evaluated by the back-extrapolation stress and peak stress methods, as shown in Fig. 5b, c. It is well known that the MDRX softening fraction ranges from 0 to 1. Therefore, these evaluated MDRX softening fractions are unreasonable for the studied superalloy. Figure 5d shows that the MDRX softening fractions evaluated by the mean stress method are even smaller than zero, which is meaningless. Therefore, the above conventional stress-based methods are not suitable to evaluate the MDRX softening fractions of the studied superalloy.

Fig. 5
figure 5

Comparisons of the calculated MDRX softening fractions by: a offset stress method; b back-extrapolation stress method; c peak stress method; d mean stress method (with the initial average grain size of 75 μm)

Full size image

Usually, the large MDRX softening fractions are related to the obvious DRX behavior in the first-pass deformation. In particular, for the studied superalloy with low stacking fault energy, DRX is an important softening mechanism [32, 33, 48]. Once the deformation degree exceeds the peak strain, the true stress gradually decreases due to DRX softening. If the DRX degree is relatively large, the interrupted stress (\(\sigma_{\text{m}}\)) will be near the yield stress of the first-pass deformation (\(\sigma_{1}\)). In other words, the differential stress (\(\sigma_{\text{m}} - \sigma_{1}\)) is quite small. Thus, the unreasonable MDRX softening fractions are obtained by the offset stress and back-extrapolation stress methods, as shown in Fig. 5a, b. For the peak stress method, if the interrupted strain is close to the peak strain, the peak stress (\(\sigma_{{{\text{p}}_{ 1} }}\)) of the first-pass deformation will be approximate to the interrupted stress (\(\sigma_{\text{m}}\)). Then, the high MDRX softening fractions appear, as shown in Fig. 5c. Similarly, if the DRX degree of the first-pass deformation is high enough, the value of \(\bar{\sigma }_{\text{m}}\) can be lower than \(\bar{\sigma }_{1}\), which results in the negative MDRX softening fraction, as shown in Fig. 5d. Thus, the conventional stress-based methods are not suitable for evaluating MDRX softening fraction of the studied superalloy. However, due to the unobvious DRX softening in other metals and alloys, such as austenite steel [18], aluminum alloy [11], and microalloyed steel [22], these stress-based methods can accurately evaluate the MDRX softening fraction during the interpass.

In order to obtain the MDRX softening fraction of the studied superalloy, the softening mechanisms are analyzed. Figure 6 shows the schematic map of typical true stress–strain curves. The curves marked with ‘DRV,’ ‘DRX,’ and ‘DRX + MDRX’ are associated with the softening mechanisms of DRV, DRX, and a combination of DRX and MDRX, respectively. Before the second-pass deformation, the differential stress (\(\Delta \sigma\)) between DRV and (DRX + MDRX) types can be considered as the result of the softening induced by DRX and MDRX. Furthermore, the accumulated softening fraction (\(X_{\text{a}}\)) before the second-pass deformation can be evaluated by,

$$X_{\text{a}} = \frac{\Delta \sigma }{{\sigma_{\text{sat}} - \sigma_{ss} }} = \frac{{\sigma_{\text{rec}} - \sigma_{2} }}{{\sigma_{\text{sat}} - \sigma_{ss} }}$$
(5)

where \(\sigma_{\text{rec}}\) is the true stress when DRV is the dominant softening mechanism, and \(\sigma_{\text{sat}}\) is the saturation stress of DRV-type curve. \(\sigma_{\text{ss}}\) is the steady stresses of DRX-type curve. \(\sigma_{2}\) is the yield stress of the second-pass deformation, which can be determined from (DRX + MDRX)-type curve.

Fig. 6
figure 6

Schematic map of true stress–strain curves (symbols ‘DRV’, ‘DRX’, and ‘DRX’ + MDRX’ show the DRV, DRX, and a combination of DRX and MDRX mechanisms, respectively)

Full size image

Due to the low stacking fault energy of the studied superalloy, \(\sigma_{\text{sat}}\) is usually approximate to peak stress (\(\sigma_{\text{p}}\)) of DRX-type curve. Therefore, DRX softening fraction can be expressed as [49],

$$X_{\text{drx}} = \frac{{\sigma_{\text{rec}} - \sigma_{\text{m}}^{{}} }}{{\sigma_{\text{p}} - \sigma_{\text{ss}} }}$$
(6)

Substituting Eq. (6) to Eq. (5) gives,

$$X_{\text{a}} = X_{\text{drx}} + \frac{{\sigma_{\text{m}} - \sigma_{2} }}{{\sigma_{\text{p}} - \sigma_{\text{ss}} }}$$
(7)

Then, it can be easily found that the second term in the right side of Eq. (7) can be considered as the MDRX softening fraction during the interpass. Here, \(\sigma_{\text{ss}}\) is the steady stress of DRX-type curve, which is corresponding to true stress when the complete DRX takes place. However, for two-pass hot deformation, it is difficult to directly obtain \(\sigma_{\text{ss}}\) from (DRX + MDRX)-type curve. Theoretically, if the MDRX degree is extremely low, true stress–strain curve of two-pass hot deformation can be simplified as that of single-pass hot deformation. For example, the MDRX softening fraction is close to zero when the deformation temperature, strain rate, initial average grain size, and interpass time are 1010 °C, 0.01 s−1, 75 μm, and 5 s, respectively, as shown in Fig. 3b. In this case, the value of \(\sigma_{\text{ss}}\) can be determined as 145.3 MPa, which is closely approximate to the yield stress of the first-pass deformation, i.e., \(\sigma_{1}\) = 142.85 MPa. Similar result can also be found in Fig. 3d for the case at the strain rate of 0.001 s−1. So, \(\sigma_{1}\) can be used to substitute \(\sigma_{\text{ss}}\) in Eq. (7) for the studied superalloy. Thus, Eq. (7) can be modified as,

$$X_{\text{a}} = X_{\text{drx}} + \frac{{\sigma_{\text{m}} - \sigma_{2} }}{{\sigma_{\text{p}} - \sigma_{1} }}$$
(8)

It is widely accepted that MDRX takes place when the deformation degree of the first pass is interrupted beyond the critical strain for the onset of DRX. However, if the strain of the first-pass deformation is lower than the peak strain (\(\varepsilon_{\text{p}}\)), \(\sigma_{\text{p}}\) cannot appear. Then, Eq. (8) does not work for this case. So, the maximum stress (\(\sigma_{ \hbox{max} }\)) is used to replace \(\sigma_{\text{p}}\), i.e., Eq. (8) can be revised as Eq. (9).

$$X_{\text{m}} = \frac{{\sigma_{\text{m}}^{{}} - \sigma_{2} }}{{\sigma_{ \hbox{max} } - \sigma_{1} }}$$
(9)

where \(\sigma_{ \hbox{max} }\) is the maximum true stress of the first-pass deformation. \(\sigma_{1}\) and \(\sigma_{2}\) are the yield stresses of the first- and second-pass deformation stages, respectively. From Eq. (9), it can be found that the maximum stress (\(\sigma_{\hbox{max} }\)) is corresponding to the true stress at the interruption (\(\sigma_{\text{m} }\)) when the interrupted strain is lower than the peak strain (\(\varepsilon_{\text{p}}\)). If the interrupted strain exceeds the peak strain, the maximum stress (\(\sigma_{\hbox{max} }\)) is equal to the peak stress (\(\sigma_{\text{p}}\)) of the first-pass deformation. Therefore, Eq. (9) can be named as ‘maximum stress method.’

In order to validate the application of the proposed maximum stress method, the MDRX softening fractions of Nimonic 80A superalloy [21] are estimated at the deformation temperature of 1100 °C, strain rate of 1 s−1, and prestrain of 0.30. The measured MDRX softening fractions of Nimonic 80A superalloy are 0.34, 0.70, 0.79, and 0.92 at the interpass times of 0.5, 1.5, 2, and 5 s, respectively, which are consistent with the MDRX softening fractions estimated by 0.2 % offset stress method [21]. Therefore, it can be concluded that the proposed maximum stress method can also be appropriated to other alloys.

3.3 Effects of deformation parameters on MDRX behaviors

3.3.1 Effects of deformation temperature

Using the proposed ‘maximum stress method,’ the MDRX softening fractions can be evaluated based on the measured true stress–strain curves. Figure 7 shows the changes of MDRX softening fractions with interpass time under 0.01 s−1 and different deformation temperatures. Here, the initial average grain size is 75 μm. It is obvious that the MDRX softening fraction is dependent on deformation temperature. Under the given strain rate and interpass time, the MDRX softening fraction rapidly increases with the increase of deformation temperature. For example, at the interpass time of 30 s, the MDRX softening fraction increases from 0.19 to 0.39 when the deformation temperature is increased from 950 to 980 °C. It is well known that MDRX is mainly characterized by the growth of DRX nuclei, and the MDRX is mainly driven by grain boundary migration during interpass, which is the result of the grain boundary energy reduction. High deformation temperature can increase the grain boundary migration rate and hence accelerates the MDRX. Figure 8 illustrates the effects of deformation temperature on the deformed microstructures at 0.01 s−1. From Fig. 8a, it can be found that only a few small grains appear at the vicinity of initial elongated grain boundaries at 950 °C. When the deformation temperature is increased to 980 °C, the number of small recrystallized grains remarkably increases, as shown in Fig. 8b. With the further increase of deformation temperature, almost all the initial coarse grains are replaced by the fine equiaxed recrystallized grains, which indicates that the metadynamic recrystallization is an effective method to refine grains.

Fig. 7
figure 7

Effects of deformation temperatures on MDRX softening fractions at the strain rate of 0.01 s−1 and the initial average grain size of 75 μm

Full size image
Fig. 8
figure 8

Optical micrographs of the deformed microstructures at the strain rate of 0.01 s−1 and the deformation temperatures of: a 950 °C; b 980 °C; c 1010 °C (under the interpass time of 45 s and the initial average grain size of 75 μm)

Full size image

3.3.2 Effects of strain rate

Figure 9 shows the variations of MDRX softening fractions with interpass time at 1010 °C and different strain rates. Here, the initial average grain size is 75 μm. It is observed that the MDRX behaviors of the studied superalloy are sensitively affected by strain rate. For the given interpass time (60 s), the MDRX softening fraction at relatively high strain rate is obviously larger than that at relatively low strain rate. Figure 10 shows the effects of strain rate on the deformed microstructures. Here, the deformation temperature and interpass time are 1010 °C and 60 s, respectively. As shown in Fig. 10a, bulged original grain boundaries, as well as small recrystallized grains, can be observed, and the whole grain microstructures are heterogeneous when the strain rate is 0.001 s−1. When the strain rate is 0.1 s−1, a large number of recrystallized grains can be observed, and the microstructure becomes homogeneous (Fig. 10b). This indicates that the MDRX degree increases with the increase of strain rate. Furthermore, MDRX can be considered as a continuity of DRX during the cessation of hot deformation. Generally, the nucleation of DRX occurs when the dislocation density in the bulged region exceeds a critical value [32, 50, 51]. A high strain rate can lead to large inhomogeneous dislocation gradients across grain boundaries. Thus, the number of DRX nucleation sites is increased at relatively high strain rate, which promotes the MDRX behavior.

Fig. 9
figure 9

Effects of strain rates on MDRX softening fractions at the deformation temperature of 1010 °C and the initial average grain size of 75 μm

Full size image
Fig. 10
figure 10

Optical micrographs of the deformed microstructures at the deformation temperature of 1010 °C and strain rates of: a 0.001 s−1; b 0.1 s−1 (under the interpass time of 60 s and the initial average grain size of 75 μm)

Full size image

3.3.3 Effects of initial average grain size

Figure 11 shows the effects of initial average grain size on the MDRX softening fraction. Here, the deformation temperature, strain rate, and interpass time are 950 °C, 0.01 s−1, and 45 s, respectively. It is evident that the effects of initial average grain size on the MDRX softening fractions are significant. The MDRX softening fraction increases with the decrease of initial average grain size. Figures 8a and 12 show the effects of initial average grain size on the deformed microstructures at 950 °C and 0.01 s−1. When the initial average grain size is 33 μm, the observed microstructures are characterized by a great number of homogeneously recrystallized grains and only few unrecrystallized initial grains, as shown in Fig. 12a. However, for the superalloy with coarse grains (Figs. 8a, 12b), the initial elongated grains, as well as few small recrystallized grains, are dominant. It indicates that the MDRX degree of the superalloy with initial coarse grains remarkably decreases, compared to that with fine initial grains. Generally, MDRX is mainly characterized by the growth of DRX nuclei. So, it may be concluded that these different MDRX degrees are mainly attributed to the effects of initial average grain size on the number of DRX nuclei. On the one hand, the grain boundary density per unit volume increases with the decrease of initial average grain size. On the other hand, the increased grain boundary density in fine-grain material can enhance the stored deformation energy, which can provide great driven force for DRX nucleation. Consequently, under the fixed deformation conditions, the number of DRX nuclei increases with the decrease of initial average grain size. Thus, the MDRX softening fraction in the studied superalloy with fine grains is higher than that with coarse grains.

Fig. 11
figure 11

Effects of initial average grain size on the MDRX softening fractions (at the interpass time of 45 s)

Full size image
Fig. 12
figure 12

Optical micrographs of the deformed microstructures with the initial average grain sizes of: a 33 μm; b 48 μm (under the interpass time of 45 s)

Full size image

3.3.4 Effects of interpass time

Figures 8b and 13 show the effects of interpass time on the deformed microstructures at 980 °C and 0.01 s−1. From Figs. 8b and 13, it can be observed that the MDRX degree obviously increases with the increase of interpass time. At the interpass time of 0 s, i.e., one-pass hot deformation, the microstructure consists of few small recrystallized grains and a large number of elongated initial grains with serrated boundaries (Fig. 13a). When the interpass time is 10 s, the small recrystallized grains grow up and gradually replace the initial large grains (Fig. 13b). At the interpass time of 45 s (Fig. 8b), the rapid growth of small recrystallized grains can also be observed, and the deformed microstructures are replaced by a large number of recrystallized grains. Such microstructural evolution is closely associated with MDRX mechanism. Generally, the growth of grain during MDRX is a time-consuming process. Long interpass time can ensure enough DRX nuclei to grow up. Thus, the MDRX softening fraction increases with the increase of interpass time. However, the MDRX softening rate becomes slow at relatively long interpass time, as shown in Fig. 9. This is because the grain growth during MDRX is driven by the stored deformation energy. With the increase of interpass time, the stored deformation energy gradually decreases. Thus, the driven force for the further growth of DRX nuclei is reduced. Therefore, the rate of MDRX softening becomes slow with the increase of interpass time.

Fig. 13
figure 13

Optical micrographs of the deformed microstructures at the interpass times of: a 0 s; b 10 s (with the initial average grain size of 75 μm)

Full size image

3.4 Metadynamic recrystallization kinetics models

Based on the above discussion, it can be easily found that the MDRX behaviors of the studied superalloy are sensitive to the deformation temperature, strain rate, initial average grain size, and interpass time. In order to effectively control the microstructures and mechanical properties, it is necessary to establish the kinetic models of MDRX. Usually, the kinetics of MDRX can be described by the following Avrami equation [13, 18, 52],

$$X_{\text{mdrx}} = 1 - \exp \left[ { - 0.693\left( {\frac{t}{{t_{0.5} }}} \right)^{{{\text{k}}_{ 2} }} } \right]$$
(10)

where \(X_{\text{mdrx}}\) is the volume fraction of MDRX. Due to the low stacking fault energy of the studied superalloy, the SRV caused by dislocation climb and slip is extremely weak during the interpass and can be neglected. So, the value of \(X_{\text{mdrx}}\) can be considered as the calculated MDRX softening fraction (\(X_{\text{m}}\)). \(t\) is the interpass time (s), and \(k_{ 2}\) is a material constant. \(t_{0.5}\) is the time for 50 % volume fraction of MDRX. The coupling effects of deformation parameters on \(t_{0.5}\) can be expressed as,

$$t_{0.5} = {\text{a}}_{2} \dot{\varepsilon }^{{{\text{m}}_{ 2} }} d_{0}^{{{\text{p}}_{2} }} \exp \left( {\frac{{Q_{\text{mdrx}} }}{RT}} \right)$$
(11)

where \(\dot{\varepsilon }\) is the strain rate. \(d_{0}\) is the initial average grain size. \(Q_{\text{mdrx}}\) is the activation energy for the MDRX (J/mol). \(R\) is the gas constant (J mol−1 K−1). \(T\) is the absolute deformation temperature (K). \({\text{a}}_{2}\), \({\text{m}}_{ 2}\), and \({\text{p}}_{ 2}\) are material constants.

3.4.1 Determination of Avrami exponent \(k_{2}\)

Taking the logarithm of both sides of Eq. (10) gives,

$$\ln \left( {\ln \left( {\frac{1}{{1 - X_{\text{mdrx}} }}} \right)} \right) = \ln 0.693 + {\text{k}}_{ 2} \ln t - {\text{k}}_{ 2} \ln t_{0.5}$$
(12)

Substituting the values of \(X_{\text{mdrx}}\) and corresponding \(t\) into Eq. (10), \(\ln \{ \ln [1/(1 - X_{\text{mdrx}} )]\} - \ln t\) plots can be illustrated in Fig. 14. By the linear fitting method, it is easy to identify the average value of \(k_{2}\) as 1.0, which is consistent with those results reported by Na et al. [53].

Fig. 14
figure 14

Relationships between \(\ln \{ \ln [1/(1 - X_{\text{mdrx}} )]\}\) and \(\ln t\) under different: a deformation temperatures; b strain rates; c initial average grain sizes (symbols for the experimental results and the solid line for the fitting line)

Full size image

3.4.2 Determination of \(t_{0.5}\)

Taking the logarithm of both sides of Eq. (11) gives,

$$\ln t_{0.5} = \ln a_{2} + m_{ 2} \ln \dot{\varepsilon } + {\text{p}}_{ 2} \ln d_{0} + Q_{\text{mdrx}} /({\text{RT}})$$
(13)

The values of \(t_{ 0. 5}\) can be derived from Eq. (10). Under the fixed deformation temperature and initial average grain size, Eq. (13) can be simplified as,

$$m_{2} = \frac{{d(\ln t_{0.5} )}}{{d(\ln \dot{\varepsilon })}}$$
(14)

Thus, substituting the values of \(t_{0.5}\) and \(\dot{\varepsilon }\) into Eq. (14), the value of \(m_{2}\) can be evaluated as −0.2895 from the slope of the fitting line in \(\ln t_{0.5}\) – \(\ln \dot{\varepsilon }\) plot, as shown in Fig. 15.

Fig. 15
figure 15

Relationship between \(\ln t_{0.5}\) and \(\ln \dot{\varepsilon }\) (symbols for the experimental results and the solid line for the fitting line)

Full size image

Under the fixed strain rate and deformation temperature, differentiating Eq. (13) gives,

$$n_{2} = \frac{{d(\ln t_{0.5} )}}{{d(\ln d_{0} )}}$$
(15)

Then, substituting the values of \(t_{0.5}\) and \(d_{0}\) into Eq. (15), the value of \(p_{ 2}\) can be determined as 0.6367 from the average slopes of the fitting lines of \(\ln t_{0.5} - \ln d\) plot, as shown in Fig. 16.

Fig. 16
figure 16

Relationship between \(\ln t_{0.5}\) and \(\ln d_{0}^{{}}\) (symbols for the experimental results and the solid line for the fitting line)

Full size image

Similarly, the value of \(Q_{\text{mdrx}}^{{}}\) can be calculated by,

$$Q_{\text{mdrx}}^{{}} = R\frac{{d(\ln t_{0.5} )}}{d(1/T)}$$
(16)

The relationships between \(\ln t_{ 0. 5}\) and \(1/T\) are illustrated in Fig. 17. Thus, the value of \(Q_{\text{mdrx}}^{{}}\) can be estimated as 356782.9 J/mol. Additionally, by substituting all the deformation parameters, and material constants into Eq. (11), the material constant \(a_{ 2}\) can be finally derived as \(1.15\;{ \times }\;\text{10}^{{\text{ - }15}}\).

Fig. 17
figure 17

Relationship between \(\ln t_{0.5}\) and 1000/T (symbols for the experimental results and the solid line for the fitting line)

Full size image

Summarily, the kinetics equations of MDRX for the studied superalloy under the two-pass isothermal compression can be expressed as,

$$\left\{ \begin{aligned} &X_{\text{mdrx}} = 1 - \exp \left[ { - 0.693\left( {\frac{t}{{t_{0.5} }}} \right)^{1.0} } \right] \hfill \\ &t_{0.5} = 1.15{ \times 10}^{{\text{ - }15}} \dot{\varepsilon }^{ - 0.2895} d_{0}^{0.6367} \exp \left( {\frac{356782.9}{{{\text{R}}T}}} \right) \hfill \\ \end{aligned} \right.$$
(17)

3.4.3 Verification of the metadynamic recrystallization kinetics model

In order to validate the accuracy of the established kinetics model of MDRX, the comparisons between the experimental and predicted results, including the time for 50 % MDRX volume fraction (\(t_{0.5}\)) and volume fraction of MDRX (\(X_{\text{mdrx}}\)), are carried out, as shown in Figs. 18 and 19. From Figs. 18 and 19, it is found that the predicated \(t_{0.5}\) and \(X_{\text{mdrx}}\) are well consistent with the experimental ones, which indicates that the established MDRX kinetics model can accurately describe the MDRX behaviors of the studied superalloy.

Fig. 18
figure 18

Comparisons between the experimental and predicted t 0.5 (symbols for the experimental results and the solid line for the fitting line)

Full size image
Fig. 19
figure 19

Comparisons of the experimental and predicated \(X_{\text{mdrx}}\) under different: a deformation temperatures; b strain rates; c initial average grain sizes (the solid lines represent the predicted results, and the symbols represent the experimental results)

Full size image

4 Conclusions

The metadynamic recrystallization behaviors of a typical nickel-based superalloy are studied by the two-pass isothermal compression tests. It is found that four conventional stress-based methods, including the offset stress method, back-extrapolation method, peak stress method, and mean stress method, are not suitable to evaluate the MDRX softening fraction of the studied superalloy. Thus, a new approach, ‘maximum stress method,’ is developed. Based on the proposed method, the effects of deformation parameters on the MDRX behaviors are discussed. It is found that the MDRX behaviors of the studied superalloy are sensitively dependent on the deformation temperature, strain rate, initial average grain size, and interpass time. When the deformation temperature, strain rate, and interpass time are increased, the MDRX softening fractions remarkably increase. With the increase of initial average grain size, the MDRX softening fraction obviously decreases. The kinetic equations are established to characterize the MDRX behaviors. The predicted MDRX volume fractions well agree with the experimental ones, which confirm that the established kinetics equations can accurately predict the MDRX behaviors of the studied superalloy.