Evolution of structural, magnetic and magnetocaloric properties in Sn-doped manganites La_0.57Nd_0.1Sr_0.33Mn_1−x Sn _x O₃ (x = 0.05–0.3)

Abstract

Structural and magnetic properties of manganites series La_0.57Nd_0.1Sr_0.33Mn_1−x Sn _x O₃ with (0.05 ≤ x ≤ 0.30) have been investigated, and the critical exponents and magnetocaloric effect are studied around the room temperature, to shed light on Sn substitution influence. A solid-state reaction method was used in the preparation. A structural study using Rietveld refinement of XRD patterns indicates rhombohedral structure with R$\overline{3}$c space group for (0.05 ≤ x ≤ 0.20) and shows the existence of a secondary phase attributed to the neodymium tin oxide (Nd₂Sn₂O₇) pyrochlore for x = 0.3. The variation of the magnetization (M) vs. temperature (T), under an applied magnetic field of 0.05 T, reveals a ferromagnetic–paramagnetic transition at the Curie temperature T _C. In addition, it was discovered that increasing the tin content leads to a reduction in magnetization and a lowering of T _C from 282 K (x = 0.05) to 158 K (x = 0.20) with increasing Sn substitution. The samples exhibit the characteristics of spin/cluster-glass state which is evident from (zero-field-cooled and field-cooled) magnetization vs. temperature curves. Indeed, the thermal evolution of magnetization in the ferromagnetic phase at low temperature varies as T ^3/2, in accordance with Bloch’s law. The spin-stiffness constant D obtained from the Bloch constant was determined. A large magnetocaloric effect has been observed in both samples (x = 0.05 and x = 0.10): the maximum entropy change, $\left| {\varDelta S_{\text{M} }^{\text{peak}} } \right|$, reaches the highest value of 3.22 J/kg K under a magnetic field change of 5 T with a RCP value of 56 J/kg for x = 0.10 composition. This opens an interesting opportunity to this compound to compete with materials which work as magnetic refrigerants near room temperature. Besides, we show that the samples follow the conventional behavior of a second-order ferromagnetic transition. This was possible by investigating the critical behavior at the transition region by adopting the modified Arrott plot method. The values of the critical exponents (β, γ, δ and n) are determined and they are between those predicted by the three-dimensional Heisenberg model.

1 Introduction

Ferromagnetic perovskite manganites with a general formula of $(\text{Ln}_{1 - x}^{3 + } \text{A}_{x}^{2 + } )(\text{Mn}_{1 - x}^{3 + } \text{Mn}_{x}^{4 + } )\text{O}_{3}^{2 - } ,$where Ln³⁺ is a lanthanide cation (La³⁺, Nd³⁺, Y³⁺, Pr³⁺, etc.) and A²⁺ is usually an alkaline earth ion (Ca²⁺, Ba²⁺, Sr²⁺, etc.), have been actively studied considering their interesting physical properties such as competing magnetic orders, metal–insulator transitions and high colossal magnetoresistance [1]. These magnetic materials with large magnetocaloric effect (MCE) have been extensively studied experimentally and theoretically due to their great potential applications for magnetic refrigeration [2]. However, magnetic refrigeration based on MCE is a promising technology because of its higher efficiency, compactness and environmental friendliness [3]. In addition, there are many demands for refrigeration in the temperature range 200–330 K, such as food freezing, air conditioning and gas liquefaction. Most refrigeration employs conventional gas-compression systems based on working gases such as chlorofluorocarbons (CFCs), hydrochlorofluorocarbons (HCFCs) and hydrofluorocarbons (HFCs), which are undesirable ozone-depleting compounds and/or greenhouse effect gases. In fact, the MCE manifests itself as the isothermal magnetic entropy change or the adiabatic temperature change in a magnetic material when it is exposed to a varying magnetic field. There are many factors that can affect the entropy of materials; among them we mention the short-range magnetic order as well as the structural and electronic degrees of freedom. A large value of MCE is considered to be the most important requirement of the application, and therefore it is strongly desirable to find out a new material with large MCE especially at low magnetic fields and near room temperature. Earlier works showed that rare-earth metal gadolinium (Gd) was first considered to be the most conspicuous magnetic refrigeration due to a large effective Bohr magneton and high Curie temperature ($\left| {\varDelta S_{\text{M} }^{\text{peak}} } \right|$= 10.2 J/kg K at μ ₀ H = 5 T, T _C = 294 K) [4]. But the high cost of pure Gd (~4,000 $/kg) prevents it from the actual application. Till now, besides some possible candidates with giant magnetic entropy changes have been observed such as Gd₅Si_4−x Ge _x [5], RCo₂ (R = Er, Ho and Dy) [6], La(Fe_1−x Si _x )₁₃ and its hydration [7], as well as MnFeP _x As_1−x [8], etc.; the hole-substituted manganites should be one of the most promising materials since their Curie temperature and saturation magnetization are strongly composition dependent and the magnetic refrigeration can be realized at various temperature range [9]. Furthermore, taking into account that their higher resistivity is beneficial for reducing eddy current heating, these perovskite manganites have been suggested as a strong candidate for application in magnetic refrigeration technology. A critical exponent analysis in the vicinity of the magnetic phase transition is a powerful tool to investigate the details of the magnetic interaction responsible for the transition [10]. Critical exponents for manganites show wide variation which covers almost all the universality classes even for the similar systems, when different experimental tools are used to determine them. Manganites are intrinsically inhomogeneous, both above and below PM–FM transition temperature (T _C) [11]. So the interactions around the critical point will follow the scaling relations with critical exponents belonging to the conventional universality classes [12]. Critical exponents are found either close to those predicted by the three-dimensional Heisenberg model (3DHM) or close to those predicted by the mean field (MF) theory. This suggests that the nature of the magnetic phase transition in manganites is complex and yet to be understood clearly [13]. The modified Arrott method is employed to explore magnetic behavior in the critical region. In order to establish a relationship between the exponent n and the critical exponents of the material, field dependence of entropy change [follows a power law: ΔS _M = a(μ₀H)ⁿ] and relative cooling power are checked [14].

Indeed, the substitution of the Mn site in the Ln_1−x A _x Mn_1−y B _y O₃ perovskite materials has been studied for different cations (Al³⁺, Ga³⁺, Cr³⁺, Fe³⁺, Ti⁴⁺, In³⁺, Ge⁴⁺, etc.) [15]. This kind of substitution breaks the magnetic path between Mn³⁺ and Mn⁴⁺ with the consequent modifications on the magnetic phase diagram, even at small substitution concentrations [15]. However, only a few studies have been devoted to manganites substituted by Sn atoms [16, 17]. Mössbauer studies have shown that Sn substitutes for Mn and has a valence of 4+ with a very low solubility for samples processed at high temperatures [18].

The present study investigates the substitution effects of a non-magnetic ion, Sn, on the Mn site on the structural, magnetic and magnetocaloric properties of La_0.57Nd_0.1Sr_0.33MnO₃ (LNSMO). The structural and magnetic properties of LNSMO perovskite were reported in our previous work [19]. But the T _C of this compound is about 342 K, which is well above the room temperature. However, for domestic refrigeration purposes, the T _C is required to be near the room temperature with a considerable MCE. With this point of view, the main objective was to tune the T _C from 342 K to near room temperature by Sn substitution.

Several reports are available regarding the critical exponent analysis of both bulk and nano manganites around the paramagnetic–ferromagnetic phase transition through various techniques such as the modified Arrott plot method, Kouvel–Fisher method [20–22]. In the case of conventional methods, an appreciable uncertainty is unavoidable because the starting values of the critical exponents chosen at the beginning of the work may not be accurate. In order to eliminate these problems, the critical exponent analysis related to magnetocaloric effect is described in the Sn-substituted LNSMO.

2 Experimental setup

Polycrystalline samples of La_0.57Nd_0.1Sr_0.33Mn_1−x Sn _x O₃ (LNSMSn _x O) (x = 0.05–0.30) compounds were prepared by a conventional solid-state reaction method in air at high temperature (1,673 K) using stoichiometric amounts of La₂O₃, Nd₂O₃, SrCO₃, MnO₂ and SnO₂ with nominal purities. The steps of this method are cited in our previous work [15]. Phase purity and structure of bulk samples were identified by X-ray diffraction at room temperature using a Siemens D5000 X-ray diffractometer with a graphite monochromatized CuKα radiation (λ _CuKα = 1.544 Å) and 20° ≤ 2θ ≤ 120° with steps of 0.02° and a counting time of 18 s per step. The structure refinement has been carried out by the Rietveld analysis of the X-ray powder diffraction data with FULLPROF software. The profile refinement is started with scale and background parameters followed by the unit cell parameters. Then, the peak asymmetry and preferred orientation corrections are applied. Finally, the positional parameters and the individual isotropic parameters are refined. Magnetizations (M) vs. temperature (T) and vs. magnetic field (μ ₀ H) were measured using BS1 magnetometer developed in Louis Neel Laboratory of Grenoble. To extract the critical exponents of the samples accurately, the magnetic isotherms of all the samples were measured in the range of 0–5 T and with a temperature interval of 2 K in the vicinity of their Curie temperatures (T _C). The magnetocaloric effect was estimated, in terms of isothermal magnetic entropy change (ΔS _M) using the M–H–T data and employing the Maxwell relation [15].

$$ {\varDelta}S_{\rm{M}} {(T,}\,{\mu}_{0} {H) =}\int\limits_{0}^{{{\mu}_0 \,{H}^{\rm{max}}}} {\left({\frac{{{\delta M}\,{(\mu}{}_{0}{H,}\,{T)}}}{\delta T}} \right)}_{{{\mu}_0 {H}}} \,\,\,{{d}\mu}_{0} {H}\,\,\,{,}\, $$

(1)

where S, M, μ ₀ H and T are the magnetic entropy, magnetization of the material, applied magnetic field and the temperature of the system, respectively.

3 Results and discussion

3.1 X-ray diffraction

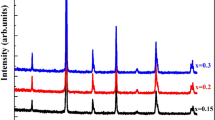
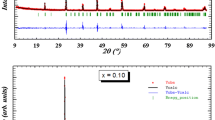
The analysis of the XRD data of the $(0.05\, \le x \le 0.20)$compounds shows single perovskite phase with rhombohedral symmetry. The refinement was carried out using structural parameters of LNSMO as starting values [15]. The observed, calculated and difference patterns for LNSMSn_0.10O are shown in Fig. 1. On the basis of refined crystallographic data, the unit cell and atomic parameters and other fitting parameters of the samples (x = 0.05–0.20) were computed and are given in Table 1. In this table, the residuals for the weighted pattern R _wp, the pattern R _p, the structure factor R _F and the goodness of fit χ² are also reported. The final R _F of refinements was always <9.86 %, which is comparable with those results found in the literature [23]. The unit cell parameters are found to increase almost linearly with increasing B-site cation radius in the case of rhombohedral symmetry samples. According to published data Shannon [24], the ionic radii of manganese and tin are, respectively, $r_{{\text{Mn}^{4 + } }}$ = 0.53 Å and $r_{{\text{Sn}^{4 + } }}$ = 0.69 Å, that is, the difference between the ionic radii of Sn⁴⁺ and Mn⁴⁺ is 23 %. Incidentally, the linear variation might be due to the fact that substituting by a larger ionic radius, the unit cell expands in all the three directions enhancing the volume. However, with an increased Sn content, a minor second phase was observed in the bulks which was determined to be Nd₂Sn₂O₇ from the XRD peaks. The upper limit of entering for Sn⁴⁺ ions was around x = 0.3. The extra peaks which contain the Nd₂Sn₂O₇ are indicated by asterisk (*) in the diffractogram of LNSMSn_0.3O manganite (Fig. 2) and their refinement results are given in Table 2. The insets (a, b) of Fig. 2 present the rhombohedral structure of LNSMSn_0.3O and the cubic structure of impurity Nd₂Sn₂O₇, respectively, obtained from FULLPROF software.

Fig. 1

The observed and calculated XRD patterns obtained by Rietveld refinement for x = 0.10 specimen

Table 1 Refined structure parameters resulting from the Rietveld analysis of LNSMSn _x O (x = 0.05–0.2)

Fig. 2

XRD patterns of LNSMSn_0.30O, the inset a presents the rhombohedral structure of and inset b presents the cubic structure of impurity Nd₂Sn₂O₇ obtained from FULLPROF software

Table 2 Result of refinement of the compounds LNSMSn_0.30O

In order to corroborate the experimental observations, the results have been compared with the Goldschmidt tolerance factor (f _t), given by [25]

$$ f_{\text{t} } = \frac{{\left( {r_{\text{A} } + r_{o} } \right)}}{{\sqrt 2 \left( {r_{\text{B} } + r_{o} } \right)}} $$

(2)

where r _A, r _B and r _O are mean radii of the ions in A, B and oxygen ion positions of ABO₃ perovskite, respectively. Oxide-based manganite compounds have perovskite structure if their tolerance factor lies in the limits of 0.75 < f _t < 1 and in an ideal case the value must be equal to unity. As the calculated values of f _t of all the samples of present investigation are within range, one may conclude that they might be having a stable perovskite structure. It is interesting to note from Table 1 that f _t values decrease continuously with increasing ionic radius of Mn site. The distortion does not only change the lattice symmetry but also modifies the cell deformation which is in agreement with Radaelli et al. [26] that on the synthesis and study of polycrystalline samples of La_0.67−y (Sr, Ba, Ca)_0.33+y Mn_1−x Sn _x O₃, it was concluded that Sn⁴⁺ displaces sites in the manganese sublattice and this substitution resulted in an increase in the volume of the unit cell and a weakening of the ferromagnetic interactions.

3.2 Magnetic properties

The main panel of Fig. 3 displays the zero-field-cooled (ZFC; pink solid circles) and field-cooled (FC; blue open circles) magnetization vs. temperature curves taken at a static low applied magnetic field (μ ₀ H = 0.05 T) with the data recorded while warming up the LNSMSn_0.10O compound. The magnetic moment gradually reduces. Such an irreversibility in the M–T data for the FC and ZFC measurements was observed in several manganite systems and it was suggested that this irreversibility arises possibly due to the canted nature of the spins or due to the random freezing of spins [27]. However, the ZFC curve of LNSMSn_0.1O compound shows a clear cusp at low temperature, which is generally related to a spin-glass or cluster-glass state.

Fig. 3

Plots of ZFC/FC magnetization of LNSMSn_0.10O measured under a magnetic field of 0.05 T. The inset shows the plot of dM/dT vs. temperature

The low-temperature thermal evolution of magnetization was fitted to Bloch’s T^3/2 law. According to this law, the zero-field magnetization M(T) should have temperature dependence:

$$ M\left( {T,H} \right)/M\left( {0,H} \right) = 1 - \text{BT}^{3/2} $$

(3)

where M(0, H) was obtained by extrapolating M(T, H) curves to T = 0 K using a second-order polynomial and M(T, H) is the spontaneous magnetization at finite temperature [21]. The prefactor B is a characteristic constant of the spin waves at low temperature, which can be written as:

$$ B\, = \,2.612\,\,\left( {\frac{{g\mu_{\text{B} } }}{M(0)}} \right)\,\,\left( {\frac{{k_{\text{B} } }}{4\pi D}} \right)^{3/2} $$

(4)

where g ≈ 2 is the gyromagnetic ratio for electrons, μ_B the Bohr magneton, k _B the Boltzmann constant and D is the spin-wave stiffness constant [28]. The stiffness D is defined by spin-wave dispersion relation ε (q) = Δ + Dq ² which is valid for q → 0. Here, ε is the spin-wave energy, q the momentum wave vector and Δ is the gap arising from anisotropy or applied magnetic field μ ₀ H [29]. In our analysis, we assume Δ = 0. Spin-wave excitations have already been studied in manganites [30]. The curve ln(1-M(T, H)/M(0, H)) vs. ln(T ^3/2) in the inset (a) of Fig. 4 is used to show that our compounds obey Bloch’s T ^3/2 law. It is predicted that the slope of the linear fit of this curve must be close to 3/2. We found that slopes are equal to 1.429, 1.406, 2.381 and 2.551 for x = 0.05, 0.1, 0.15 and 0.20, respectively. The main body of Fig. 4 shows the reduced magnetization M(T, H)/M(0, H) as a function of T ^3/2 for μ ₀ H = 0.05 T (T ≤ 80 K) for LNSMSn_0.1O. The slope of the linear fit plot of the data M(T, H)/M(0, H) vs. T ^3/2 provided B values from which the values of the spin-stiffness constant D were determined. The temperature range, considered for fitting, was mentioned above; B and D values are listed in Table 3. This result shows that there is a spin-wave excitation in our samples. The obtained values of D are in an excellent agreement with those reported for other polycrystalline manganites [31, 32] and they are comparable to those found in the ground state of other FM insulating manganites such as La_0.8Ca_0.2MnO₃ [33]. From the inset (b) of Fig. 4, it is concluded that the D values increase with the increase in the average ionic radius <r _B>. The range of the exchange interaction can be quantified by the ratio of D/T _C. This ratio is quite large, as it might be expected for an itinerant electron system [34]. Besides, the variation of D/T _C values listed in Table 3 can be explained by correlated disorder based on the model developed by Bouzerar and Cépas [35]. According to the Heisenberg model, D and the Curie temperature T _C fulfill the following equation:

$$ D\, = \,\frac{{k_{\text{B} } \,r_{ij}^{2} \,T_{\text{C} } }}{{2\,(S_{i} \, + \,1)\,}} $$

(5)

where r _ij is the distance between nearest magnetic atoms (Mn) and S_i is the average spin moment for Mn³⁺, Mn⁴⁺ and Nd³⁺ ions $S_{i} \, = \,\,0.67\, \times \,\,S\,(Mn^{3 + } )\, + \,(0.33 - x)\,\, \times \,\,S(Mn^{4 + } )\, + \,0.1\,\, \times \,\,S\,(Nd^{3 + } )\,$with $\text{S} \,(\text{Mn}^{3 + } )\,\, = \,\,2;\,\,\,\text{S} \,(\text{Mn}^{4 + } )\,\, = \,\,\frac{3}{2}\,\,\text{and} \,\,\text{S} \,(\text{Nd}^{3 + } )\,\, = \,\,\frac{3}{2}\,$. Using Eq. (5), we found that r _ij increases with x content (Table 3). In fact, in our previous work, we found that the parent sample LNSMO exhibits a sharp ferromagnetic–paramagnetic transition [15]. As Sn substitution increases at Mn site, it causes a decrease in the magnetization and in the Curie temperature. This decrease is evidently related to an increase in the degree of magnetic and structural disorder owing to the introduction of non-magnetic Sn⁴⁺ ions, with their rather large ionic radius, into sublattice sites. An additional reason for this effect may be a change in the grain size of the ceramic as the tin content is varied, as observed in Ref. [36]. Here, we have defined the Curie temperature T _C as the temperature at which dM/dT reaches a minimum (inset of Fig. 3). The T _C values are listed in Table 3. In the cubic symmetry field, the triply and quadruply ionized manganese ions have 3d⁴4s⁰ = $(t_{{2\text{g} }}^{3} \,e_{\text{g} }^{1} )\,4\text{s}^{0}$ and 3d³4 s⁰ = $(t_{{2\text{g} }}^{3} \,e_{\text{g} }^{0} )\,4\text{s}^{0}$ electronic configurations, respectively. As opposed to manganese, Sn⁴⁺ has a completely filled d shell. Its electronic configuration is 4d¹⁰5s⁰5p⁰. If Mn⁴⁺ is replaced by Sn⁴⁺, the fraction of quadruply ionized manganese atoms decreases, and the e_g electrons cannot move between Mn³⁺ and Sn⁴⁺ ions. As a result, fewer ions participate in double exchange which is reduced. This reduction can be explained by the decrease in electron-one bandwidth W given by [26]

$$ W\,\alpha\frac{{\cos [\tfrac{1}{2}(\pi - \theta_{{(\text{Mn} /\text{Sn} ) - \text{O} - (\text{Mn} /\text{Sn} )}} )]}}{{(d_{{(\text{Mn} /\text{Sn} ) - \text{O} }} )^{3.5} }} $$

(6)

where d _(Mn/Sn)–O is the bond length and θ _{(Mn/Sn)–O–(Mn/Sn)} is the bond angle. The variations of the bandwidth (W) with x as well as the d _(Mn/Sn)–O and θ _{(Mn/Sn)–O–(Mn/Sn)} are reported in Table 1. In fact, the increase of (Mn/Sn)–O bond length reduces the overlap between the Mn (3d) and O (2p) orbitals and contributes to the decrease in the bandwidth (W), so that both the magnetization and T _C decrease. On the basis of the study of Anderson and Hasegawa [37], we propose a model describing the change of the Curie temperature according to the rate of substitution of manganese for tin. The Curie temperature can be simulated by a polynomial function of degree two and is written in the following form:

$$ T_{\text{C} } = Ax^{2} + Bx + C $$

(7)

where x indicates the rate of tin and A, B and C are constants to be determined. A fit of the curve of variation of T _C with x gives A = 1,800, B = −1,246 and C = 334.2 K (inset c of Fig. 4). The difference between experimental T _C and calculated T _C is small which justifies the parabolic form of the curve.

Fig. 4

Plot of M(T, H)/M (0, H) vs. T ^3/2 of LNSMSn_0.1O at μ ₀ H = 0.05 T. The inset a shows the ln(1 − M(T, H)/M(0, H)) variation with ln(T ^3/2) to determine the slope of the linear curve. The inset b represents the variation of spin-wave stiffness D vs. <r _B>. The inset c shows the variation of the experimental Curie temperature vs. x content

Table 3 Values of the transition temperature T _C, prefactor B, spin-wave stiffness D, D/T _C ratio and the bond length r _ij of LNSMSn _x O (x = 0.05–0.20)

3.3 Magnetocaloric effect

Due to the low Curie temperatures of LNSMSn_0.15O and LNSMSn_0.20O compounds, we have carried out a detailed study only for Sn dilute samples (x = 0.05 and x = 0.1) in which the T _C values are in the vicinity of room temperature. In order to further clarify the nature of the FM–PM phase transition, we measure the isothermal magnetization versus applied field around the Curie temperature, which has been shown in the inset (a) of Fig. 5 for LNSMSn_0.1O. From the slope of the magnetization curves at a higher field of 5 T, we can see that the saturation is not achieved. This indicates a large degree of non-collinearity in the moment of our samples compared to the other La-based manganites [38].

Fig. 5

(μ ₀ H)/M vs. M ² (Arrott plot) for the sample LNSMSn_0.10O. The inset a represents the field dependence of the magnetization measured at different temperatures around T _C. The inset b shows ln (M) vs. ln (μ ₀ H) plot of LNSMSn _x O (x = 0.05 and x = 0.10) at T _C

According to the scaling hypothesis, [39], a second-order magnetic phase transition near Curie point is characterized by a set of critical exponents of β, γ and δ. In order to deduce these parameters, the isothermal magnetization curves (M vs. μ ₀ H) should be changed into the so-called Arrott plot, namely, M ² vs. (μ ₀ H)/M. An inspection of the sign of the slope of these isotherms will give the nature of the phase transition: positive for second order and negative for first order [40]. The main panel of Fig. 5 is an Arrott plot of M ² vs. (μ ₀ H)/M for LNSMSn_0.1O. Clearly, in the present case, the positive slope indicates that the phase transition is a second-order FM–PM phase transition, in agreement with the foregoing discussion. If the system is in line with the Landau mean field theory, [39], the relationship by Arrott plot should be shown as a set of parallel straight lines around T _C. However, one can note that all the curves are nonlinear and show downward curvature even at the high field region, indicating that the critical exponents of β = 0.5 and γ = 1 are not satisfactory. Namely, the mean field theory cannot be used to describe the critical behavior in the present system. In order to obtain the accurate critical exponents, the conventional method is to use some tentative exponents to construct a new Arrott plot and then fit the data of the linear part or directly fit the data of the initial Arrott plot. After that, the obtained intercepts on the x(y)-axis were performed with multistep nonlinear fitting until the final critical exponents reach steady values as shown in Ref. [21]. As mentioned above, because of the drawbacks of this method, we adopted another way to deduce the critical exponents. First, these critical exponents of β, γ and δ satisfy the Widom scaling relation [41]:

$$ \delta = 1 + \gamma /\beta $$

(8)

Meanwhile, the critical exponent of δ is associated with the critical magnetization isotherm at T _C and can be obtained from the following equation [42]:

$$ M_{{\text{T}_{C} }} \, = \,A_{\text{C} } \,(\mu_{0} \,H)^{1/\delta } $$

(9)

(where A _c is the critical amplitude) by determining the slope of high field region of ln (M) vs. ln (μ ₀ H) plot (inset b of Fig. 5). The obtained values of δ are 4.215 and 3.651 for x = 0.05 and x = 0.10, respectively. Notably, we need to establish another equation to solve β and γ. According to Eq. (1), the maximum magnetic entropy change $\left| {\varDelta S_{\text{M} }^{\text{peak}} } \right|$ is obtained at the Curie temperature where the ferromagnetic–paramagnetic phase transition takes place. Then, the magnetic entropy change defined in Eq. (1) can be approximated by

$$ \varDelta S_{\text{M} } \left( {\frac{{T_{1} + T_{2} }}{2}} \right) = \left( {\frac{1}{{T_{2} - T{}_{1}}}} \right)\,\left[ {\int\limits_{0}^{{\mu_{0} H_{\hbox{max} } }} {M(T_{2} } ,\,\mu_{0} H)\,\mu_{0} \,\,dH - \int\limits_{0}^{{\mu_{0} H_{\hbox{max} } }} {M(T_{1} ,\mu_{0} H)\mu_{0} \,dH} } \right] $$

(10)

The ΔS _M values were calculated using Eq. (10) for each sample in the vicinity of its ordering temperature based on the results of magnetization isotherms. Figure 6 shows the temperature dependence of −ΔS _M with a field change of 1 and 5 T of the sample with x = 0.1. There is a peak in the −ΔS _M–T curves near its own T _C for all the samples under various fields. Then, a more abrupt variation of magnetization occurs and results in a large magnetic entropy change. The values of $\left| {\varDelta S_{\text{M} }^{\text{peak}} } \right|$ are found to be about 2.8 J/kg K at 281 K and 3.22 J/kg K at 223 K for x = 0.05 and x = 0.10, respectively, at 5 T. The values of $\left| {\varDelta S_{M}^{peak} } \right|$ are extended over a wide range of temperature around the Curie temperature in both the samples and hence these materials are useful for near room temperature magnetic refrigeration applications. However, compared with Gd [4] or other rare-earth elements [43–45] and their compounds, the manganese oxide materials as well as the present system are the cheapest, the easiest to synthesize and they have a higher chemical stability. These features make the present system as well as some other manganites a competitive material for active magnetic refrigeration application. In a magnetic system with a second-order phase transition, Oesterreicher and Parker [46] previously proposed a universal relation of the field dependence of magnetic entropy change, namely,

$$ \varDelta S_{\text{M} } = a\left( {\mu_{0} H} \right)^{n} $$

(11)

where ‘a’ is a constant and the exponent ‘n’ depends on the magnetic state of the sample. It can be locally calculated as follows:

$$ n\, = \,\frac{{\text{d} \,\ln \,\varDelta S_{\text{M} }^{\text{peak}} }}{{\text{d} \,\ln \,(\mu_{0} \,H)}} $$

(12)

Fig. 6

Temperature dependence of the magnetic entropy change $\left| {\varDelta S_{\text{M} } } \right|$ for different magnetic field intervals for LNSMSn_0.10O sample. The inset shows ln($\left| {\varDelta S_{\text{M} }^{\text{peak}} } \right|$) vs. ln(μ ₀ H) plot of LNSMSn _x O (x = 0.05 and x = 0.10)

It is well known that, in manganites, the exponent is roughly field independent and approaches approximate values of 1 and 2 far below and above transition temperature, respectively [47]. The linear plot of $\ln \,( - \varDelta S_{\text{M} }^{\text{peak}} )\,\text{vs} .\,\ln \,(\mu_{0} H)$ is constructed in the inset of Fig. 6. It can be noted that the values of n obtained from the slope (0.586 for x = 0.05 and 0.522 for x = 0.10) are lower than the mean field predictions (n = 2/3) [47]. These values decrease with increasing temperature and reach the values reported for other manganites, Gd and other magnetic materials containing rare-earth metals [47]. In the case of materials which do not follow mean field model, the field dependence of ΔS _M at T = T _C can be obtained from Arrott–Noakes equation of state [40]. Franco et al. [48] have showed that the Curie point and the temperature where the magnetic entropy change is maximum (T _peak) coincide in the mean field approximation for homogeneous materials. Recently, Fan et al. [49] also have established a method for the determination of critical exponents from the field dependence of the magnetic entropy change using Eq. (11). We have followed the above method for the calculation of critical exponents. Using the values of n, the critical exponents are calculated for each sample with the help of the following relations:

$$ n\,(T_{\text{C} } )\, = \,1 + \,\frac{\beta \, - \,1}{\beta \, + \,\gamma } $$

(13)

which can be transformed using the relation βδ = (β + γ)

$$ n\,(T_{\text{C} } )\, = \,1\, + \,\frac{1}{\delta }\,\left(1 - \frac{1}{\beta }\right) $$

(14)

Thus, if we can know the value of n, the critical exponents of β and γ will be solved. The obtained values are 1.170 and 0.364 for x = 0.05 and 0.943 and 0.356 for x = 0.10, respectively. They are between those predicted for 3D-Heisenberg model.

Universal behavior for the field dependence of ΔS _M, in materials which present a second-order transition, has been recently proposed by Franco et al. [50]. The phenomenological universal curve (that can be calculated from purely magnetic measurements) consists in the collapse of entropy change curves after a scaling process, regardless of the applied magnetic field. Hence, the major assumption is based on the fact that if a universal curve exists, then the equivalent points of the ΔS _M(T) curves measured at different applied fields should collapse onto the same universal curve. The construction of the phenomenological universal curve requires normalizing each iso field ΔS _M to its maximum value $\left| {\varDelta S_{\text{M} }^{\text{peak}} } \right|$ and then rescaling the temperature axis, defining a new variable θ below and above T _C,

$$ \theta = \,\left\{ \begin{gathered} - (T\, - \,T_{\text{C} } )/\,(T_{{\text{r}_{1} }} \, - \,T_{\text{C} } ),\,T \le \,T_{\text{C} } \, \hfill \\ \,\,\,\,(T - \,T_{\text{C} } )\,/\,(T_{{\text{r}_{2} }} \, - T_{\text{C} } ),\,T \succ T_{\text{C} } \hfill \\ \end{gathered} \right. $$

(15)

The two reference temperatures T _r1 et T _r2 satisfy T _r1 < T _C < T _r2. These temperatures are selected for each curve in such a way that for an arbitrary value h < 1, (ΔS _M(T)/$\varDelta S_{\text{M} }^{\text{peak}}$) = h, the reference point in the new curve corresponding to ΔS _M (θ = ±1) = h. The normalized entropy change (ΔS _M(T)/$\varDelta S_{\text{M} }^{\text{peak}}$) as a function of the rescaled temperature (θ) for the magnetic ordering transitions of both compounds with (x = 0.05 and x = 0.1) is shown in Fig. 7. It is also shown that these curves are unique for each universality class [51]. The MCE data of different materials of the same universality class should fall onto the same curve, irrespective of the applied magnetic field. From these results, we can notice that all normalized entropy change curves collapse onto a single curve for each compound. This result implies the validity of our data treatment for compounds with second-order transition. Hence, the recently proposed master curve for the field dependence of ΔS _M to series of alloy compounds also holds for different manganites [50]. Another parameter of importance that is used to evaluate the cooling efficiency of the refrigerant is the relative cooling power (RCP), which corresponds to the amount of heat transferred between cold and hot sinks in the ideal refrigeration cycle defined as [51]:

$$ \text{RCP} = - \varDelta S_{\text{M} }^{\hbox{max} } \, \times \,\delta T_{\text{FWHM}} $$

(16)

where $(\delta \,T_{\text{FWHM}} = \,\,T_{hot} - T_{\text{cold}} )$ is the full width at half maximum of the magnetic entropy change curve. In general, the better the RCP for a given magnetic field, the better the material for magnetic refrigeration. The values of RCP are 51 and 56 J/kg for x = 0.05 and x = 0.10, respectively. They increase simultaneously as the field increases (Fig. 6) and they are comparable to those reported for other manganites [52]. In order to study the origin of MCE, a simple theoretical model based on magnetoelastic couplings and electron interaction was introduced in manganites [53]. Based on the Landau’s theory, near the Curie point of a second-order transition in the presence of an external field, the Gibbs free energy (G) can be expressed in terms of the order parameter M in the following form neglecting the higher order parts [54]:

$$ G(T,M) = \frac{1}{2}A(T)\,M^{2} + \frac{1}{4}\,B(T)M^{4} + \frac{1}{6}\,C(T)M^{6} + .\, \ldots .- \,\mu_{0} M\,H\, $$

(17)

where A, B and C are the Landau coefficients.

Fig. 7

Universal behavior of the scaled entropy change curves of LNSMSn _x O (x = 0.05 and x = 0.10) at different fields

From energy minimization, the magnetic equation of state is derived within this theory:

$$ \mu_{0} H/M = A\left( T \right) + B\left( T \right)M^{2} + C\left( T \right)M^{4} $$

(18)

and the corresponding magnetic entropy is obtained from differentiation of the magnetic part of the free energy with respect to temperature

$$ S_{\rm M} \,(T,\,\mu_{0} H) = - \,\left( {\frac{{\partial G(\mu_{0} H,\,T)}}{\partial T}} \right)_{{\mu_{0} H}} = - \frac{1}{2}\,A^{'} \,(T)\,M^{2} - \frac{1}{4}\,B'(T)\,M^{4} - \frac{1}{6}\,C^{'} (T)\,M^{6} $$

(19)

The notation A′(T), B′(T) and C′(T) denote the first derivation of the Landau coefficients by temperature. In order to apply the above formulation, the temperature dependence of parameters A(T), B(T) and C(T) can be obtained from the nonlinear fitting of the curves (μ ₀ H) vs. (M) using Eq. (18). As an added bonus, the theoretical value of C(T) in Eq. (17) is constant against temperature, and the thermal variation of A(T) and B(T) dominates the entropy change. Using parameters A′(T), B′(T) and C′(T), the temperature dependence of magnetic entropy S (T, μ ₀ H) under the variation of the magnetic field can be calculated through Eq. (19). As shown in Fig. 8, the open circle represents the calculated magnetic entropy change of LNSMSn_0.1O using Eq. (10). The inset of Fig. 8 shows the dependence of the B coefficient on temperature. Obviously, the experimental curves and calculated curves are roughly appropriate considering the fact that the present model does not take into account the influence of the Jahn–Teller effect and exchange interactions on the magnetic properties of manganites. However, the important distinctive feature which is worthy of our attention is that the experimental curve is consistent with the calculated curve in the PM region, whereas an obvious deviation between them occurs in the FM region. Nevertheless, the analysis clearly demonstrates the importance of magnetoelastic coupling and electron interaction in understanding the magnetocaloric properties of lanthanum manganites [55].

Fig. 8

Temperature dependence of the magnetic entropy change (−ΔS _M) measured from magnetic measurements and estimated by the Landau theory for an applied magnetic field of 5 T for the sample LNSMSn_0.10O. The inset represents the temperature dependence of parameter (B)

4 Conclusion

In conclusion, a detailed investigation of structural and magnetic properties of La_0.57Nd_0.1Sr_0.33Mn_1−x Sn _x O₃ (0.05 ≤ x ≤ 0.30) compound and a critical behavior and magnetocaloric effect of both samples with (x = 0.05 and x = 0.1) synthesized by a solid-state reaction technique in air have been carried out. Rietveld refinement of XRD patterns shows that these compounds possess a rhombohedral structure with R$\overline{3}$c space group for (0.05 ≤ x ≤ 0.20). However for x = 0.3, a minor second phase was observed in the bulks, which was determined to be the Nd₂Sn₂O₇ pyrochlore having a cubic structure. Given that the ionic radius of Sn⁴⁺ is greater than that of Mn⁴⁺, this substitution leads to an increase in the volume of a unit cell. The region of homogeneous substitution is quite narrow and does not exceed a small percentage for synthesis by the above method. It was concluded that (Sn) substitution leads to a reduction in the number of ions participating in ferromagnetic double exchange and to an increased magnetic disorder in the samples. This results in lower magnetization of the samples and a reduction in the Curie temperature T _C. The thermal evolution of magnetization in the ferromagnetic phase at low temperature varies as T ^3/2, in accordance with Bloch’s law. Analysis of the spin-wave excitation shows a significant increase in spin-stiffness constant value D with (Sn) content. The magnetic entropy change $\left| {\varDelta S_{\text{M} }^{\text{peak}} } \right|$ of both samples with (x = 0.05 and x = 0.1) showed a maximum around their respective T _C and their magnitude increases from 2.80 J/kg K (x = 0.05) to 3.22 J/kg K (x = 0.10) under a magnetic field change of 5 T. Arrott plots reveal second-order nature of magnetic transition. The values of critical exponents (n = 0.586, δ = 4.215, γ = 1.170 and β = 0.364 for x = 0.05 and n = 0.522, δ = 3.651, γ = 0.943 and β = 0.356 for x = 0.10) are close to theoretical values obtained from the 3D-Heisenberg model. We have analyzed both samples using the Landau theory and concluded that magnetoelastic coupling and electronic interaction define the shape of the magnetic entropy curves, directly affecting the $\left| {\varDelta S_{\text{M} }^{\text{peak}} } \right|$ and RCP values. Relatively large value and broad temperature interval of magnetocaloric effect make the present compounds (especially LNSMSn_0.10O) a promising candidate for magnetic refrigerators near room temperatures.