Influence of Sr substitution on structural, magnetic and magnetocaloric properties in La_0.67Ca_0.33−xSr_xMn_0.98Ni_0.02O₃ manganites

Abstract

A systematic investigation of the effect of Strontium (Sr) doping on the structure, magnetic behavior, and magnetocaloric properties of the manganite perovskites ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$ (LCSMNO) has been performed. The Sr content x takes three values, namely 0.15, 0.2, and 0.3. The sol–gel technique has been employed in the preparation of our compounds. The structural analysis has revealed that our samples exhibit a rhombohedral structure with $R\bar{3}c$ space group symmetry, close to ambient temperature. A second-order paramagnetic (PM) to ferromagnetic (FM) transition has been validated over the Curie temperature range T_C between 319 K (x = 0.15) to 353 K (x = 0.3), based on Arrott's analysis with the behavior of the master curve. According to the calculations made, the maximal values of the magnetic entropy change ${(-\Delta S}_{M}^{max})$ resulting through Landau's theory and the ones obtained by the classic Maxwell relationship are very close. We find the value of ${(-\Delta S}_{M}^{max})$ is equal to 4.386, 4.469, and 4.250 J Kg⁻¹ K⁻¹, respectively, for x = 0.15, 0.2, and 0.3, when an external magnetic field μ0H = 5 T is applied. Based on the results of the study in this work, we find that controlled Sr doping adapts perfectly to the magnetic as well as the magnetocaloric properties of the LCMNO, which plays an important role in the implementation of many potential applications of the material in the field of near-ambient temperature magnetic refrigeration technology.

1 Introduction

Several scientific research teams have extensively investigated perovskite manganese oxides. The general formula of this mineral is Ln_1−xA_xMnO₃. It contains a rare-earth Ln and a monovalent alkali metal or a divalent alkaline earth A [1,2,3,4,5]. These materials have a variety of phases as well as a very important physical property. Since 1993, subsequently to the finding, in thin layers of La_1−xCa_xMnO₃, of the colossal magnetoresistance (CMR) [6, 7], these manganites have been collected. This finding has a very attractive impact on fundamental studies as well as on industrial applications, such as the manufacturing of high storage capacity hard disks and reading heads. The new magnetic refrigeration application has received much attention in recent years. If an external magnetic field is applied or absent, the magnetic solids are heated or cooled. Thanks to its several advantages over conventional gas refrigeration, namely low vibrations and noise, no harmful gas emission and competitive technology, this application is described as an emerging technology. It takes advantage of the magnetocaloric effect.

The Gd presents the best magnetic entropy change − ΔS_M value that equals 10.2 J/K kg [8] and a Curie temperature T_C of 294 K under an applied magnetic field of 5 T. Unfortunately, Gd is very expensive and oxidizable in air. For this reason, research is oriented toward the synthesis of new materials with these magnetocaloric properties near room temperature at reasonable costs.

The current study of perovskite manganites has been stimulated by the possible use of their significant magnetocaloric (MC) properties at ambient temperature and at weak magnetic fields [9, 10]. The MC effect has been studied on a series of massive perovskite manganites LaAgMnO₃ by Tang et al. who discovered a better change in magnetic entropy than that of gadolinium [11, 12]. Therefore, the use of these materials as magnetic refrigerants that work over a very large temperature range is possible. Based on this point of view, this study focuses on the effects of Sr substitution on the magnetic in addition to the magnetocaloric properties in LCSMNO with x = 0.15, 0.2, and 0.3. The compounds were produced using the sol–gel method. Subsequently, we produce a material with very advantageous parameters, for example, no corrosion, easy synthesis, and chemical stability as well as low cost, exhibiting a colossal magnetocaloric effect close to room temperature.

2 Experimental details

The sol–gel method have been used to prepare the ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$ compounds. This technique was described in our previous studies [13]. Three values of the content x are used, namely 0.15, 0.2, and 0.3. In addition, the production of good quality samples has been made by the use of sol–gel method thanks to its various advantages such as easy preparation, excellent homogeneities, low temperature treatment, simplicity of manufacture, a detailed microstructure and chemical control, and fast annealing times [14]. To form various classes of materials such as ceramics, films or thin fibers as well as glasses, this technique has been widely used.

3 Results and discussion

3.1 Structural properties

X-ray diffraction is a widely used method for determining the nature, crystal structure, and lattice parameters of samples. It also allows the identification of the various phases formed and their range of existence as well as to assess the purity of the sample.

A monochromatic and parallel incident X-ray beam penetrates a crystal containing an ordered periodic arrangement of atoms in equidistant, more or less dense three-dimensional reticular planes, which are indicated by their coordinates (h, k, and l). The X-ray crystal interaction causes the diffracted beams to appear in a specific direction. This result is verified only if the diffraction condition is satisfied, that is the radiation wavelength must be the same order of magnitude as the interatomic distances and that this radiation encounters planes at a certain angle θ called the Bragg angle. According to the Bragg’s law [15]:

$$2d_{{{\text{hkl}}}} \sin \theta = n\lambda$$

(1)

where ${d}_{\text{hkl}}$ is the spacing between the planes in the atomic lattice, ${\text{sin}}\,\theta$ is the angle between the incident ray and the scattering planes, n is an integer and $\lambda$ is the wavelength of the incident wave; therefore, the decreasing ${d}_{hkl}$ lead to the increasing h value [16].

From X-ray diffraction patterns obtained at room temperature, it can be seen that all components crystallize in the rhombohedral structure with the space group R ${\bar{3}}$ c.A BS2 magnetometer has been used to perform the magnetic measurements. More precisely, the magnetization has been measured as a function of the applied magnetic field in the vicinity of Curie temperature T_C.

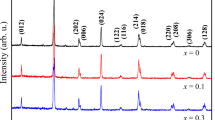
In Fig. 1, we have represented the X-ray powder diffraction patterns of the polycrystalline compounds ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$ (x = 0.15, 0.2, and 0.3). There is no detectable secondary phase in any of the compounds. From diffraction peak indexing, the perovskite structure is rhombohedral with $R\bar{3}c$ space group symmetry. In Table 1, we have grouped the structural parameters. Since the average radius of Sr²⁺ is larger than that related to Ca²⁺ [17], the unit cell volume per formula ranges from 345.922 to 348.768 Å when x increases from 0.15 to 0.3. This results from the optimization of the average A-site radius $\langle {r}_{A}\rangle$ , respectively, from 1.368 to 1.383 Å which leads to the production of MnO₆ octahedron distortion. It should be mentioned that the Mn–O–Mn angle equals 180° in the perfect perovskite structure. In the present work, there is only the doubling of peaks (100) and (104) of rhombohedric symmetry $R\bar{3}c$ for all compounds, as Sr content increases. In the matter of the results available in the literature related to samples with x ranging from 0.055 to 0.110 [18], they have revealed mixed orthorhombic and rhombohedral phases.

Fig. 1

XRD patterns of ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$ with x = 0.15, 0.2, and 0.3 components at ambient temperature

Table 1 Results of Rietveld refinements, determined from XRD patterns measured at room temperature for ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$(x = 0.15, 0.2, and 0.3) compounds

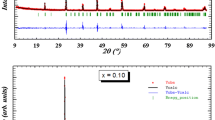
Figure 2 illustrates the Rietveld analysis results related to the three investigated samples. Observed, calculated and differential XRD diagrams are represented. Observed and calculated intensity differences are depicted by the solid green line in the diagram, as well as the positions of the Bragg reflection are expressed by vertical bars. Based on reliability weighting factors R_wp, which are equal to 10.2%, 9.56%, and 9.15%, respectively, for x = 0.15, 0.2, and 0.3 compounds, the results of the adjustment are in good agreement. In Table 1, we have listed in detail the different Rietveld refinement results for all compounds.

Fig. 2

X-ray diffraction pattern and the associated Rietveld refinement of the ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$(x = 0.15, 0.2, and 0.3) compounds

Figure 3a summarizes the cell parameters versus Sr substitution. As Sr dopant content increases, we find that the lattice constants a = b and c increase monotonically with the cell volume V. From the inset of Fig. 3, the increase in cell volume V as a function of Sr doping is expected because the ionic radius Sr²⁺ is greater than that related to Ca²⁺.

Fig. 3

Cell parameters as a function of Sr doping content a lattice constant a = b and c. b The inset shows cell volume V as a function of Sr doping content

Moreover, the average grain size D_sc can be estimated based on XRD patterns according to Scherrer formula [19]:

$$D_{{{\text{sc}}}} = \frac{{0.9 \times \lambda }}{{\beta \times \cos \theta }}$$

(2)

where λ is the X-ray wavelength being used (λ = 0.15406 nm), θ denotes the strongest peak diffraction angle and β shall be defined as follows: β₂ = β_2m–β_2s. In our case, βm can be defined with the experimental full width at half maximum (FWHM) and βs is the FWHM of a standard silicon sample.

Figure 4 illustrates the surface morphology as well as the grain size of ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$ (x = 0.15, 0.2, and 0.3) samples using SEM microscope. Knowing that, the presence of a polycrystalline nature of the compound is revealed by micrography [20]. For this reason, we have shown in Fig. 4, the size distribution of compounds with image J software. As it has already been shown, there is a good modeling of the histogram by Gaussian function. The average crystallite size of the samples was indicated by the Gaussian fitting (see Table 1). From the obtained results, we have observed that the average grain size values obtained through SEM micrographs are significantly higher than the ones estimated by XRD data. This difference can be explained by the constitution of each observed particle in SEM by multiple crystallite domains, caused by defects (vacations, dislocations) or by internal stresses inside the particle [20].

Fig. 4

A statistical analysis of the size distribution of ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$(x = 0.15, 0.2, and 0.3) compounds, the inset displays a typical scanning electron micrography (SEM) of the composites

3.2 Magnetic characterization

The variation of magnetization M versus temperature under an applied magnetic field of 0.05 T for ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$ compounds are shown in Fig. 5. Clearly, we agree that all samples indicate the net paramagnetic to ferromagnetic (PM–FM) transition.

Fig. 5

Temperature dependence of magnetization for ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$(x = 0.15, 0.2, and 0.3) compounds to 0.05 T. The obtained curves are fitted according to the Langevin function

Indeed, Curie temperature can be expressed based on the log-normal weighted Langevin function using the following formula [21, 22]:

$$M\left( T \right) = M_{0} + C \times \left( {\coth \left( {T - T_{{\text{C}}} } \right) - \frac{1}{{\left( {T - T_{{\text{C}}} } \right)}}} \right),$$

(3)

where ${M}_{0}$ is the magnetization at (T = T_C), C is a proportionality term, $(coth\left(T-{T}_{C}\right)-\frac{1}{\left(T-{T}_{C}\right)})$ is a secondary term canceling out at (T = T_C). We have fitted curves to get the T_C values, which are equal to 319, 330, and 350 K for ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$ for x = 0.15, 0.2, and 0.3, respectively (see Fig. 5). In Table 2, we have recorded the Curie temperatures of all samples, which are given using the minimum of the derivative (dM/dT). For the ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$(x = 0.15, 0.2, and 0.3) polycrystalline, the T_C values are equal to 318, 331, and 352 K, in respective way, which is in good agreement with the values given in refs.[23, 24]. In addition, those results are consistent with those obtained from the Langevin function fitting. During the increase of Sr doping from 0.15 to 0.30, this explains that T_C increases briefly from 318 to 352 K. Possible structural factors influencing the increase of T_C are Mn³⁺ /Mn⁴⁺ ratio, the tolerance factor (τ), the bond length (d_Mn–O), the bond angle Mn–O–Mn (Ө_Mn–O–Mn), the size mismatch factor of A-site cations (σ²) that comes out from the doping of Sr²⁺ and Ca²⁺ in the La³⁺ site, and the average ionic radius in A-site $\langle {r}_{A}\rangle$.In the case of ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$, the parameters $\langle {r}_{A}\rangle$ and σ²are determined by the following Eqs. (4) and (5):

$$\left\langle {r_{{\text{A}}} } \right\rangle = 0.67r_{{{\text{La}}}} + \left( {0.33 - x} \right)r_{{{\text{Ca}}}} + xr_{{{\text{Sr}}}}$$

(4)

$$\sigma ^{2} = \sum {y_{{\text{i}}} } r_{{\text{i}}}^{2} - \left\langle {r_{{\text{A}}} } \right\rangle ^{2} = \left[ {0.67r_{{{\text{La}}}}^{2} + \left( {0.33 - x} \right)r_{{{\text{Ca}}}}^{2} + xr_{{{\text{Sr}}}}^{2} } \right] - \left\langle {r_{{\text{A}}} } \right\rangle ^{2}$$

(5)

Table 2 Curie temperature T_C, Curie–Weiss temperature ${}_{cw}$, experimental (${\mu }_{eff}^{exp}$) and calculated (${\mu }_{eff}^{cal}$) effective moments, the average ionic radius in A-site $\langle {r}_{A}\rangle$ and the size mismatch factor of A-site cations (σ²) for ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$(x = 0.15, 0.2, and 0.3) perovskites

Knowing that, the factor ${\sigma }^{2}$ describes the distribution of cations over the A sites as well as their random disorder, on which ${y}_{i}$ expresses the fractional occupancy of the A-site ion and ${r}_{i}$ corresponds to the ionic radius. From Shannon [25], we have derived ionic radii of related cations using twelve coordinate radii for the A-site ions. The obtained values corroborate with those related to a deformed lattice in the manganite perovskites. In Table 2, we have listed all the parameters $\langle {r}_{A}\rangle$ and ${\sigma }^{2}$ of all the samples.

This can be seen quantitatively and more in Fig. 6a–c, where the derivatives of magnetization as a function of temperature (dM/dT) are presented for all compounds. Using a Gaussian function with a Lorentzian function, we have fitted peaks to get the T_C values. Considering that Lorentzian adjustments are always preferable to data and that T_C, determined from the adjustment are shown in Table 2. In Fig. 6d, we have represented the plot of T_C versus $\langle {r}_{A}\rangle$. Thereafter, we see that T_C grows monotonically with increasing $\langle {r}_{A}\rangle$.The most interesting result is shown in Fig. 6e, where T_C rises linearly with the A-size mismatch factor $\langle \sigma \rangle$. It appears clearly that $\langle {\sigma }^{2}\rangle$ stands out as one of the main factors governing the magnetic transition temperature (T_C) of manganite perovskites.

Fig. 6

Derivatives of the magnetization (dM/dT) as well as the fitted Lorentzian function curve (line) of compounds with x = 0.15 (a), x = 0.2 (b) and x = 0.3 (c). d Average cationic radius dependency $<{r}_{A}>$ on temperature T_C. The line is a curve adjusted by a linear equation with R = 0.9939. e Variation of T_C temperature as a function of A-site mismatch $<{\sigma }^{2}>$. The obtained curve is fitted according to the linear equation with R = 0.9872

The growth of T_C is due to the increase of x which leads to an increase of the average A-site ionic radius r_A (see Fig. 6d), resulting in a stronger magnetic exchange interaction between Mn³⁺ and Mn⁴⁺, while favoring the FM order resulting in a shift of Curie temperature toward higher temperatures [26, 27]. We can also relate the variation of T_C to the A-site disorder ${\sigma }^{2}$. Evidently, it can be observed that T_C increases when ${\sigma }^{2}$ increases (see Fig. 6e). Such results were presented in Refs. [27, 28], in which authors demonstrate a linear increment of T_C with ${\sigma }^{2}$ from studies of perovskites having a fixed r_A.

Figure 7 exhibits the inverse of the magnetic susceptibility $1/\chi$ versus the temperature when a magnetic field of 0.05 T is applied for ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$ samples (x = 0.15, 0.2, and 0.3). The inverse of magnetic susceptibility (${\chi }^{-1}$) has a linear trend versus the temperature according to the Curie–Weiss law [29]:

$$\chi^{ - 1} \left( T \right) = \frac{{\left( {T - \theta_{{{\text{cw}}}} } \right)}}{C}$$

(6)

Fig. 7

Inverse susceptibility derived from magnetization measurements at 0.05 T field of the samples. The inset shows Sr content dependence of ${\theta }_{CW}$ and T_C values for ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$(x = 0.15, 0.2, and 0.3) compounds

where C is the Curie constant and ${}_{cw}$ is the Curie–Weiss temperature. These parameters result from adjusting the linear PM range of the data. The Curie constant is given by

$$C = N{{\left( {\mu_{{\text{B}}} \,\mu_{{{\text{eff}}}}^{\exp } } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\mu_{{\text{B}}} \,\mu_{{{\text{eff}}}}^{\exp } } \right)^{2} } {3k_{{\text{B}}} }}} \right. \kern-\nulldelimiterspace} {3k_{{\text{B}}} }}$$

(7)

where N is the Avogadro number, ${\mu }_{B}$ is the Bohr magneton and ${k}_{B}$ is the Boltzmann constant. Subsequently, the experimental effective moment (${\mu }_{eff}^{exp}$) was obtained. In Table 2, we have grouped all the values obtained of ${}_{cw}$ and ${\mu }_{eff}^{exp}$ of all compounds. An FM interaction between spins has been confirmed by the presence of positive ${}_{cw}$ values. The theoretical effective moment (${\mu }_{eff}^{the}$) value can be compared to the experimental value of (${\mu }_{eff}^{exp}$) using the formula below:

$$\mu_{{{\text{eff}}}}^{{{\text{the}}}} = \sqrt {0.63 \times \mu_{{{\text{eff}}}}^{2} \left( {Mn^{3 + } } \right) + 0.35 \times \mu_{{{\text{eff}}}}^{2} \left( {Mn^{4 + } } \right) + 0.02 \times \mu_{{{\text{eff}}}}^{2} \left( {Ni^{2 + } } \right)}$$

(8)

where ${\mu }_{eff}^{the}=5.59 {\mu }_{B}$ for ${Ni}^{2+}$, ${\mu }_{eff}^{the}=4.9 {\mu }_{B}$ for ${Mn}^{3+}and { \mu }_{eff}^{the}=3.87 {\mu }_{B}$ for ${Mn}^{4+}$[9]

In the paramagnetic regime, we have noticed clearly that the measured effective moments (${\mu }_{eff}^{exp}$) are larger than the theoretical moments (${\mu }_{eff}^{the}$) (see Table 2). In general, this result is related to the existence of short-range FM correlation in the PM state [29].

In addition, we have presented in the inset of Fig. 7, the comparative analysis of T_C and θ_cw versus Sr doping concentration. We observe that T_C is almost linearly dependent on Sr content.

We have noticed that the difference between T_C and θ_cw increases progressively with Sr content. This is explained by the progressive destruction of the ferromagnetic long-range order.

For magnetic field strengths up to 5 T, various magnetization curves dependent on the magnetic field (M–H) have been recorded at different temperatures around T_C. Figure 8 depicts the isothermal magnetization M versus ${\mu }_{0}H$ for different temperatures and three compositions (x = 0.15, 0.2, and 0.3). As increasing the applied field, the isothermal magnetization curves of all components showed a saturation tendency with a non-linear behavior resulting in an extremely high increase of the measured magnetization at weak field values. However, we observed a tolerable decrease in magnetization and the non-linear isothermal magnetization curves turned almost linear at temperatures above T_C. The reason for this reduction in magnetization is linked to thermal agitation, which causes damage to the magnetic moment arrangement. Globally, we have noticed that magnetization increases simultaneously with the increasing applied magnetic field, this is due to the rearrangement of the magnetic domains as well as a rise in the magnetic ordering.

Fig. 8

Isothermal magnetization M (${\mu }_{0}H$) curves obtained near T_C at various temperatures (a, c and e). The inset illustrates the Arrott plot M² vs.${\mu }_{0}H/M$ (b, d and f)

Identification of the magnetic phase transition is carried out using the Banerjee criterion [30]. Following this criterion, the slope sign of H/M vs M² curves (Arrott plots) is positive or negative which means a second-order or first-order magnetic phase transition, respectively. In the inset of Fig. 8b, d and f, we have shown the standard Arrott plots for ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$ (x = 0.15, 0.2, and 0.3) samples. We then observed a positive slope close to T_C in all specimens, which indicates the second-order magnetic phase transition.

Magneto-crystalline anisotropy has been described as an intrinsic property of materials playing a very significant part in the coercivity [31]. According to Stoner–Wohlfarth theory, the calculation of the anisotropy constant (Ka) is performed using [32]

$$H_{{\text{C}}} = \left( {0.98 \times K_{{\text{a}}} } \right)/M_{{\text{S}}}$$

(9)

The anisotropy constant decreases from 0.729 J/m3 for x = 0.2 to 0.422 J/m3 for x = 0.3. Knowing that, the saturation magnetization depends on an inverse way to the coercivity and the same behavior has been noted (see Fig. 9). The remanence ratio calculation was performed using [33]

$$R = \frac{{M_{{\text{r}}} }}{{M_{{\text{s}}} }}$$

(10)

Fig. 9

Hysteresis loops of ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$(x = 0.15, 0.2, and 0.3) compounds evaluated at 10 K

From the obtained results, we notice that the remanence ratio increases from 0.032 for x = 0.2 to 0.049 for x = 0.3 (see Fig. 9). The small value of the remanence ratio indicates the isotropic nature of the compounds [33].

3.3 Magnetocaloric study

For measuring the efficiency of a magnetic refrigerator, the isothermal magnetic entropy change ΔS_Mis considered a key parameter [34]. Starting from the M–H curves illustrated in Fig. 8, we have calculated the ΔS_M values from the following Maxwell's relationship:

$$\Delta S_{{\text{M}}} \left( {T,\mu_{0} H} \right) = S_{{\text{M}}} \left( {T,\mu_{0} H} \right) - S_{{\text{M}}} \left( {T,0} \right) = \mathop \smallint \limits_{0}^{{\mu_{0} H}} \frac{{\partial M\left( {T,\mu_{0} H} \right)}}{\partial T}d\left( {\mu_{0} H} \right)$$

(11)

The above integral can be computed using a numerical scheme since the magnetization has been measured over small variations of the adjustable parameters. It is straightforward to obtain the approximate relation:

$$\left| {\Delta S_{{\text{M}}} } \right| = \mathop \sum \limits_{i} \frac{{M_{{\text{i}}} - M_{{{\text{i}} + 1}} }}{{T_{{{\text{i}} + 1}} - T_{{\text{i}}} }}\Delta \mu_{0} H$$

(12)

where M_i represents the magnetization value at temperature T_i.

Figure 10 shows the variations of magnetic entropy exchange (− ΔS_M) with the applied magnetic field (${\mu }_{0}H$) from 0 to 5 T at different temperatures are presented as a three-dimensional (3D) image for ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$ (x = 0.15, 0.2, and 0.3) compounds. It is well known that the values of -ΔS_M increase with the applied field as well as the maximum values (${-\Delta S}_{M}^{max}$) reach up to 4.38, 4.46, and 4.25 J/kg K for x = 0.15, 0.2, and 0.3, respectively, around the Curie temperature (see Table 3).

Fig. 10

Magnetic entropy (–ΔS_M) values of ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$(x = 0.15, 0.2, and 0.3) specimens with a variable applied magnetic field between 0 and 5 T

Table 3 Maximum entropy change and RCP values for ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$(x = 0.15, 0.2, and 0.3) compounds compared to values reported in the literature

It may be noted that (${-\Delta S}_{M}^{max}$) is not the only parameter to determine the applicability of a material. To evaluate the suitability of a material for magnetic refrigeration (MR), Gschneidner and Pecharsky [38] have developed the Relative Cooling Performance (RCP), which is the main index used to assess the cooling efficiency of a magnetic refrigerant. This parameter refers to the product obtained from the maximum values of the magnetic entropy change (${-\Delta S}_{M}^{max}$) and the full width at half the maximum $\delta {T}_{FWHM}$ of the magnetic entropy change curve ($RCP={-\Delta S}_{M}^{max}\times \delta {T}_{FWHM}$) [39]. In this context, this parameter represents the amount of heat exchanged between the cold and hot parts of the refrigerator during an ideal thermodynamic cycle. Table 3 summarizes the results.

The theoretical modeling of the magnetocaloric effect has been studied on the basis of Landau's theory, carried out by Amaral et al. [40, 41]. According to this theory, the free energy (G), related to the order parameter M, versus temperature, can be expressed as follows:

$$G\left( {T,M} \right) = G_{0} + \frac{1}{2}A\left( T \right)M^{2} + \frac{1}{4}B\left( T \right)M^{4} + \frac{1}{6}C\left( T \right)M^{6} - \mu_{0} HM$$

(13)

where A, B and C refer to the Landau parameters. They depend on the temperature. Similarly, that is also shown by the equilibrium condition of the magnetic system that is near the transition state ($\frac{\partial G}{\partial M}=0$). Here, close to the Curie T_C temperature, the following equation is obtained:

$$A\left( T \right)M + B\left( T \right)M^{2} + C\left( T \right)M^{5} = \mu_{0} H$$

(14)

The Landau coefficients have been determined according to Eq. 14 based on the experimental curve of the magnetic field variation versus magnetization M for a specific temperature.

After that, we obtained the magnetic entropy change from Eq. 12, which is given by [42]:

$$- S_{{\text{M}}} \left( {T,M} \right) = \left( {\frac{{\partial G\left( {T,M} \right)}}{\partial T}} \right)_{{\text{M}}} = \frac{1}{2}A^{\prime}\left( T \right)M^{2} + \frac{1}{4}B^{\prime}\left( T \right)M^{4} + \frac{1}{6}C^{\prime}\left( T \right)M^{6}$$

(15)

where ${A}^{^{\prime}}\left(T\right)$,${B}^{^{\prime}}\left(T\right)$ and $C^{\prime}\,({\text{T}})$ are the derivatives of the Landau coefficients.

As shown in Fig. 11, we present both the theoretical and experimental magnetic entropy change curves, which are derived from Landau's theory for x = 0.15, 0.20, and 0.3 compounds at an applied magnetic field of 5 T. We have displayed in the same figure the Landau parameters versus the temperature. For the A (T) curves, a minimum close to the transition temperature T_C is found. Additionally, there was a second-order transition that has been confirmed by B (T) curves, which were shown as positive over T_C and negative under it. Concerning C (T) values, they are very low in the order of 10^–8. Furthermore, we note that both the experimental and theoretical curves indicate appropriate agreement over the T_C with a small deviation below.

Fig. 11

Theoretical and experimental magnetic entropy change (− ΔS) for x = 0.15, 0.2, and 0.3 at ${\mu }_{0}H$ = 5 T and the Landau coefficients A, B, and C that depend on temperature

Some ferromagnetic domains found during the paramagnetic phase are responsible for this. It also ignores the potential effects of exchange interactions as well as the Jahn–Teller distortion. As a basis for determining the transition temperature, we consider the Landau parameter C (T) to be very low. In this case, for Eq. 14, we can ignore term 5, and we have the following equation:

$$A\left( T \right) + B\left( T \right)M^{2} = \mu_{0} H/M$$

(16)

The determination of A (T) has been performed in the linear region using a linear fit of Arrott plots (H/M vs. M2); it is an intercept parameter (insets in Fig. 12). Similarly, A (T) is expressed as A (T) = a₁ (T − T_C) around the Curie temperature [43]. In Fig. 12, we have illustrated the variation of A (T) versus temperature. As shown in the graph, A is negative for T smaller than T_C whereas for T larger than T_C it is positive. Assuming the intersection of A (T) curve and the equation a = 0, we have determined the Curie temperature that is 328 K, 339 K, and 361 K for x = 0.15, 0.2, and 03, correspondingly. It is very similar to the values found in experience.

Fig. 12

Evolution of the A parameter (Landau parameter) versus temperature. Insets shows the Arrott plots (H/M vs. M²)

Thermal magnetization, M (T) under various changes in the applied magnetic field has been shown in Fig. 13 for ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$ (x = 0.15, 0.2, and 0.3) samples, respectively. These curves have been constructed with points that correspond to magnetic fields between 1 and 5 T in the isothermal analyses (Fig. 8).

Fig.13

Temperature dependence of magnetization of LCSMNO composed with the points corresponding to ${\mu }_{0}H$ vary from 1 to 5 T of the isothermal measurements. The inset: dM/dT

When starting from the inset of Fig. 13, it can be seen that as the magnetic field increases, the transition gets wider and the dM/dT versus T-curve minima moves to a higher temperature. Depending on the result published in [44], with the increase of the applied magnetic field, the peak value of T_C curve grows always bigger, for all values of ΔH, the maximum of -ΔSM is always located around the Curie temperature. In fact, explaining this behavior as the applied magnetic field increases, so the maximum of dM/dT moves considerably to higher temperatures, its magnitude disappears fast, resulting in the dominance of the weak field − ΔS_M to T_C.

The nature of the magnetic transition has been investigated using a phenomenological method, referred as the universal master curve in second-order phase transition components, as proposed by Franco et al. [45]. The basis of this method is the plotting of ${\Delta S}_{M}(T)$ curves, which are measured to various maximum applied fields, collapsing on a single master curve. The realization of the universal curve has been carried out using the normalized entropy change ${(\Delta S}_{M}/{\Delta S}_{M}^{max})$, where ${\Delta S}_{M}^{max}$ has been defined in terms of the maximum change occurring in magnetic entropy over various applied fields versus rescaled temperature (θ), this is realized at the transitions of magnetic order that are plotted in Fig. 14. The temperature axis below and above T_Ccan be rescaled in a very different way using the equation given below:

$$\theta = \left\{ {\begin{array}{*{20}c} { - \frac{{T - T_{c} }}{{Tr_{1} - T_{c} }}\quad ~T \le T_{c} } \\ {\frac{{T - T_{c} }}{{Tr_{2} - T_{c} }}~\quad T > T_{c} } \\ \end{array} } \right.$$

(17)

Fig. 14

Universal curve of compounds

Considering that, Tr₁ and Tr₂ have been defined as the two-reference point’s temperatures that have been selected as correspondents to ${\Delta S}_{M}^{max}/2$.

In our case, over a very wide range of temperatures, there is only one universal curve for all the experimental points. This reveals that a second-order phase transition is observed for all the samples investigated in this work.

4 Conclusion

In summary, physical properties involving the structure, the magnetic behavior and some magnetocaloric parameters of ${\text{La}}_{{0.67}} {\text{Ca}}_{{0.33 - x}} {\text{Sr}}_{x} {\text{Mn}}_{{0.98}} {\text{Ni}}_{{0.02}} {\text{O}}_{3}$ (x = 0.15, 0.2, and 0.3) samples have been examined. All samples are processed using the sol–gel method and crystallize in the rhombohedral structure with $R\bar{3}c$ space group. All compounds indicated a ferromagnetic–paramagnetic phase transition. Furthermore, the Curie temperature T_C increases from 319 to 353 K when x increases from 0.15 to 0.3.

Based on Maxwell's thermodynamic relations, the magnetic entropy change (− ΔS_M) has been computed and then determined using Landau's theory. A very good agreement between both analyses confirmed that electron interaction and magnetoelastic coupling of electrons are very important in magnetocaloric properties of manganites. A second-order kind of the magnetic phase transition has been confirmed using the phenomenological universal curve of ΔS_M. Finally, this study has confirmed that all compounds could be regarded as good candidates for use in magnetic refrigeration applications, given the high entropy values that are comparable to those of other manganites.