1 Introduction

Nanoelectromechanical systems (NEMS) are emerging as strong candidates for a host of important applications in semiconductor-based technology and fundamental science [1]. They have been fabricated from graphene sheets (GSs) by mechanically exfoliating thin sheets from graphite over trenches in silicon oxide [2]. GSs are single layers of carbon arranged in a honeycomb lattice and are one of the thinnest materials ever made [3]. They have outstanding mechanical [3, 4], thermal [5, 6] and field-emission properties [7, 8]. Moreover, due to their conductance changing as a function of the extent of surface adsorption, their large specific surface area and low Johnson noise make them a promising candidate for nanosensors or NEMS resonators [9–11]. Dan et al. [9] studied the intrinsic response of graphene vapor sensors and suggested that the contamination layer chemically dopes graphene, enhancing carrier scattering and the sensor response by acting as an absorbent layer that concentrates analyte molecules at the graphene surface. Recently, Sorkin and Zhang [10] constructed a simple atomistic model for circular GS nanosensors that provides useful information for the potential application of GSs in NEMS. Lee et al. [11] assumed a nanomechanical resonator sensor using simply supported rectangular single-layer GSs (SLGSs) and analyzed its vibration properties based on nonlocal elasticity theory.

Double-layer GSs (DLGSs) consist of two layers of GSs connected by van der Waals (vdW) forces, and they are very different from SLGSs. The carrier spectrum of electrons in ideal DLGSs is gapless and approximately parabolic at low energies around two points in the Brillouin zone. The quantum dots created through position-dependent doping break the equivalence between the upper and lower layers [12, 13]. Virojanadara et al. [14] investigated epitaxial growth of graphene on silicon carbide and proposed a new process for preparing large, homogeneous and stable DLGSs on the (0001) SiC surface. Thus, the fundamental properties, such as the vibrational properties of DLGSs, are important for the application of DLGSs as NEMS resonators. From vibrational analysis of DLGSs, the upper and lower layers are found to deflect in either the same or opposite directions, which are defined as the in-phase mode (IPM) and the anti-phase mode (APM) [15–18].

Various models have been proposed to study the vibration modes of GSs [19–26]. Based on the stiffness properties of the reactive empirical bond order potential, Shakouri et al. [19] developed a new atomistic structural model, from which the resonance frequencies of flexural vibration for rectangular SLGSs of different sizes, chiralities and boundary conditions can be calculated. Mianroodi et al. [20] investigated the nonlinear, large-amplitude vibrational properties of SLGSs based on a membrane model, and solved the nonlinear equation by a finite-difference method. Elastic plate theory has been used to study mechanical behavior of GSs by scholars. Wang et al. [21] developed a nonlinear continuum model for the vibrational analysis of multi-layer GSs, in which there are nonlinear vdW interactions between the two adjacent layers. Based on continuum thin plate theory, an agreement with molecular dynamics (MD) simulations has been achieved in predicting the mechanical behavior of SLGSs under a central point load [23, 24]. Nonlocal elasticity theory, which assumes that the stress at a reference point is a function of the strain at every point in the body [27], is superior to the classic continuum model and is widely used in the mechanical analysis of GSs [15, 16, 25, 26]. Arash and Wang [25] investigated free vibration of SLGSs and DLGSs by employing nonlocal continuum theory and MD simulations. The nonlocal plate model can achieve satisfactory vibrational solutions with the calibrated nonlocal parameter, and the results based on the nonlocal model are in good agreement with those obtained by MD simulations. The nonlocal plate model is found to be indispensable in vibration analysis of GSs with a length less than 8 nm on their sides. However, the vibrational analysis of circular GSs has received little attention, especially in circular DLGSs.

In our previous work, vibration analysis of circular DLGSs was carried out using circular plate theory without considering nonlocal effects [17]. In this study, the vibrational properties of NEMS resonators using simply supported circular DLGSs in IPM and APM have been analyzed based on nonlocal elasticity theory. The upper and lower layers of the circular DLGSs are modeled as two thin circular plates that are held together by vdW forces. The resonance frequencies of the circular DLGSs in IPM and APM are simulated by a theoretical approach. Especially, the nonlocal effect on the resonance frequencies is discussed in detail.

2 Governing equations

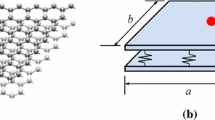
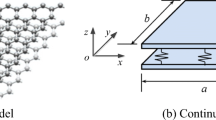
Because the membrane model cannot sustain the compression stress and the bending moments [20], the thin-plate model is used for modeling GSs in this work. Based on the small-deflection theory of thin plates, as shown in Fig. 1, the moment equilibria about the r and θ axes and the equation of shear equilibrium in the z direction are given as [28]

$$\begin{aligned} &{\frac{\partial M_{r}}{\partial r} + \frac{\partial M_{r\theta}}{r\partial \theta} - Q_{r} = 0, } \end{aligned}$$
(1a)
$$\begin{aligned} &{\frac{\partial M_{r\theta}}{\partial r} + \frac{\partial M_{\theta}}{ r\partial \theta} - Q_{\theta} = 0, } \end{aligned}$$
(1b)
$$\begin{aligned} &{\frac{\partial Q_{r}}{\partial r} + \frac{\partial Q_{\theta}}{r\partial \theta} + \frac{Q_{r}}{r} + p - \rho h \frac{\partial^{2}w}{\partial t^{2}} = 0, } \end{aligned}$$
(1c)

where Q r and Q θ are the shear forces in the r and θ directions, p is the distributed transverse pressure, ρ is the mass density, h is the thickness, w is the flexural deflection and t is time. M r , M rθ and M θ are the bending moments and are defined as

$$ \{ M_{r} \quad M_{\theta} \quad M_{r\theta} \} = \int _{ - \pi /2}^{\pi /2} \{ \sigma_{r} \quad \sigma_{\theta} \quad \sigma_{r\theta} \} z \,\mathrm{d}z. $$
(2)
Fig. 1
figure 1

The schematic figure of an infinitesimal element in polar coordinate system

Full size image

According to Eringen [27], in nonlocal elasticity theory, the stress at a reference point in an elastic continuum depends not only on the strain at the point but also on the strains at every point of the body. This is attributed by Eringen to the atomic theory of lattice dynamics and the experimental observations on phonon dispersion. Then, the nonlocal constitutive behavior of a Hookean solid can be defined by the following differential constitutive relationship:

$$ \bigl[1 - (e_{0}a)^{2}\nabla^{2} \bigr]\sigma = S:\varepsilon, $$
(3)

where e 0 a is the nonlocal parameter, in which e 0 is a constant that is dependent on the material and a is the characteristic internal length of a C–C bond (0.142 nm). Note that the value of e 0 must be determined experimentally or by matching the dispersion curves of the plane wave with those of the atomic lattice dynamics, which has not yet been achieved for GSs. σ and ε are the local stress tensor and the related strain tensor, respectively. S is the elasticity tensor. Then, Hooke’s law of stress and strain in thin-plate theory can be written as

$$\begin{aligned} &{ \bigl[1 - (e_{0}a)^{2}\nabla^{2} \bigr] \sigma_{r} = \frac{E}{1 - \nu^{2}}(\varepsilon_{r} + \nu \varepsilon_{\theta} ), } \end{aligned}$$
(4a)
$$\begin{aligned} &{ \bigl[1 - (e_{0}a)^{2}\nabla^{2} \bigr] \sigma_{\theta} = \frac{E}{1 - \nu^{2}}(\varepsilon_{\theta} + \nu \varepsilon_{r}), } \end{aligned}$$
(4b)
$$\begin{aligned} &{ \bigl[1 - (e_{0}a)^{2}\nabla^{2} \bigr] \sigma_{r\theta} = \frac{E}{1 + \nu} \varepsilon_{r\theta}, } \end{aligned}$$
(4c)

where E is the elastic modulus, ν is the Poisson ratio and

$$\begin{aligned} &{\varepsilon_{r} = \frac{\partial u}{\partial r} = - z \frac{\partial^{2}w}{\partial r^{2}}, } \end{aligned}$$
(5a)
$$\begin{aligned} &{\varepsilon_{\theta} = \frac{u}{r} + \frac{\partial v}{r\partial \theta} = - z \biggl(\frac{\partial w}{r\partial r} + \frac{\partial^{2}w}{r^{2}\partial \theta^{2}} \biggr), } \end{aligned}$$
(5b)
$$\begin{aligned} &{\varepsilon_{r\theta} = \frac{\partial u}{r\partial \theta} + \frac{\partial v}{\partial r} - \frac{u}{r} = - 2z\frac{\partial}{\partial r} \biggl(\frac{\partial w}{r\partial \theta} \biggr). } \end{aligned}$$
(5c)

Substituting Eqs. (4a)–(4c) and (5a)–(5c) into Eq. (2) gives

$$\begin{aligned} &{\bigl[1 - (e_{0}a)^{2}\nabla^{2} \bigr]M_{r} = - D\biggl[\frac{\partial^{2}w}{\partial r^{2}} + \nu \biggl( \frac{\partial w}{r\partial r} + \frac{\partial^{2}w}{r^{2}\partial \theta^{2}}\biggr)\biggr],} \end{aligned}$$
(6a)
$$\begin{aligned} &{\bigl[1 - (e_{0}a)^{2}\nabla^{2} \bigr]M_{\theta} = - D\biggl(\frac{\partial w}{r\partial r} + \frac{\partial^{2}w}{r^{2}\partial \theta^{2}} + \nu \frac{\partial^{2}w}{\partial r^{2}}\biggr), } \end{aligned}$$
(6b)
$$\begin{aligned} &{\bigl[1 - (e_{0}a)^{2}\nabla^{2} \bigr]M_{r\theta} = - D(1 - \nu )\frac{\partial}{ \partial r}\biggl(\frac{\partial w}{r\partial \theta} \biggr), } \end{aligned}$$
(6c)

where

$$ D = \frac{Eh^{3}}{12(1 - \nu^{2})}. $$
(7)

From Eqs. (1a)–(6c), the governing equation of nonlocal vibration of a circular plate can be defined as

$$ \nabla^{2}\nabla^{2}w - \bigl[1 - (e_{0}a)^{2} \nabla^{2}\bigr]\biggl(\frac{p}{D} - \frac{\rho h}{D} \frac{\partial^{2}w}{\partial t^{2}}\biggr) = 0. $$
(8)

For the upper and lower layers of circular DLGSs, Eq. (8) can be described by the following two coupled equations:

$$\begin{aligned} &{\nabla^{2}\nabla^{2}w_{1} - \bigl[1 - (e_{0}a)^{2}\nabla^{2}\bigr]\biggl( \frac{p_{1}}{D} - \frac{\rho h}{D}\frac{\partial^{2}w_{1}}{\partial t^{2}}\biggr) = 0, } \end{aligned}$$
(9a)
$$\begin{aligned} &{\nabla^{2}\nabla^{2}w_{2} - \bigl[1 - (e_{0}a)^{2}\nabla^{2}\bigr]\biggl( \frac{p_{2}}{D} - \frac{\rho h}{D}\frac{\partial^{2}w_{2}}{\partial t^{2}}\biggr) = 0, } \end{aligned}$$
(9b)

where the subscripts 1 and 2 denote the quantities associated with the upper and lower layers of the circular DLGSs.

A DLGS is composed of two single layers of GSs that are bound together by vdW forces. Thus, the distributed transverse pressure acting on the upper and lower layers of circular DLGSs is given by

$$\begin{aligned} &{p_{1} = c(w_{1} - w_{2}), } \end{aligned}$$
(10a)
$$\begin{aligned} &{p_{2} = c(w_{2} - w_{1}), } \end{aligned}$$
(10b)

where c is the vdW interaction coefficient between the upper and lower layers, which can be obtained from the Lennard–Jones pair potential [29, 30], and is given as

$$ \begin{aligned}[b] c & = - \biggl( \frac{4\sqrt{3}}{9a} \biggr)^{2}\frac{24\zeta}{ \delta^{2}} \biggl( \frac{\delta}{a} \biggr)^{8}\Biggl[ \frac{3003\pi}{ 256}\sum_{k = 0}^{5} \frac{( - 1)^{k}}{2k + 1}\left ( \begin{array}{c} 5 \\ k \end{array} \right )\biggl( \frac{\delta}{a} \biggr)^{6} \\ &\quad {}\times \frac{1}{(\bar{z}_{1} - \bar{z}_{2})^{12}} - \frac{35\pi}{ 8}\sum_{k = 0}^{2} \frac{( - 1)^{k}}{2k + 1}\frac{1}{(\bar{z}_{1} - \bar{z}_{2})^{6}} \Biggr], \end{aligned} $$
(11)

where a is the characteristic internal length of a C–C bond. ζ=2.968 meV and δ=3.407 Å are parameters chosen to fit the physical properties of GSs. \(\bar{z}_{j} = z_{j}/a\) (j=1,2), where z j is the coordinate of the jth layer in the direction of thickness with the origin at the midplane of the GSs.

To divide the vibration mode into IPM and APM, we assume that

$$\begin{aligned} &{w_{\mathrm{in}} = w_{1} + w_{2}, } \end{aligned}$$
(12a)
$$\begin{aligned} &{w_{\mathrm{an}} = w_{1} - w_{2}. } \end{aligned}$$
(12b)

Substituting Eqs. (10a), (10b) and (12a), (12b) into Eqs. (9a), (9b) gives two simplified equations that correspond to the governing solutions of the IPM and APM of circular DLGSs. The equations are

$$\begin{aligned} &{\nabla^{2}\nabla^{2}w_{\mathrm{in}} + \bigl[1 - (e_{0}a)^{2}\nabla^{2}\bigr]\biggl( \frac{\rho h}{D}\frac{\partial^{2}w_{\mathrm{in}}}{\partial t^{2}}\biggr) = 0, } \end{aligned}$$
(13a)
$$\begin{aligned} &{\nabla^{2}\nabla^{2}w_{\mathrm{an}} - \bigl[1 - (e_{0}a)^{2}\nabla^{2}\bigr]\biggl( \frac{2cw_{\mathrm{an}}}{D} - \frac{\rho h}{D}\frac{\partial^{2}w_{\mathrm{an}}}{\partial t^{2}}\biggr) = 0.} \end{aligned}$$
(13b)

3 Solution of the governing equations

Because the normal vibrations of an elastic linear system are harmonic, the deflection of circular DLGSs for the harmonic vibration can be expressed as

$$ w_{j} = W_{j}(r)\cos (n\theta )\mathrm{e}^{\mathrm{i}\omega t}, \quad j = \mathrm{in}, \mathrm{an}, $$
(14)

where ω is the resonance frequency of circular DLGSs and n is the number of nodal diameters. W j (r) (j=in,an) represents the amplitudes of vibration in the IPM and APM of circular DLGSs.

By substituting Eq. (14) into Eqs. (13a), (13b), we obtain the governing differential equations of the vibrational properties in circular DLGSs for the IPM (j=in) and APM (j=an):

$$ \begin{aligned}[b] &\biggl[ \frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}} + \frac{\mathrm{d}}{r\,\mathrm{d}r} + \biggl( \mu_{j1}^{2} - \frac{n^{2}}{r^{2}} \biggr) \biggr] \\ &\quad {}\times \biggl[ \frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}} + \frac{\mathrm{d}}{r\,\mathrm{d}r} - \biggl( \mu_{j2}^{2} + \frac{n^{2}}{r^{2}} \biggr) \biggr]W_{j}(r) = 0, \\ &\qquad j =\mathrm{in}, \mathrm{an}, \end{aligned} $$
(15)

where

$$\begin{aligned} &{\mu_{\mathrm{in}1}^{2} = \sqrt{(e_{0}a)^{4} \biggl( \frac{\rho h\omega^{2}}{2D} \biggr)^{2} + \frac{\rho h\omega^{2}}{D}} + \frac{(e_{0}a)^{2}\rho h\omega^{2}}{2D}, } \end{aligned}$$
(16a)
$$\begin{aligned} &{\mu_{\mathrm{in}2}^{2} = \sqrt{(e_{0}a)^{4} \biggl( \frac{\rho h\omega^{2}}{2D} \biggr)^{2} + \frac{\rho h\omega^{2}}{D}} - \frac{(e_{0}a)^{2}\rho h\omega^{2}}{2D}, } \end{aligned}$$
(16b)
$$\begin{aligned} &{\begin{aligned}[b] \mu_{\mathrm{an}1}^{2} & = \sqrt{(e_{0}a)^{4} \biggl( \frac{\rho h\omega^{2} + 2c}{2D} \biggr)^{2} + \frac{\rho h\omega^{2} + 2c}{D}} \\ &\quad {}+\frac{(e_{0}a)^{2}\rho h\omega^{2} + 2c}{2D}, \end{aligned} } \end{aligned}$$
(16c)
$$\begin{aligned} &{\begin{aligned}[b] \mu_{\mathrm{an}2}^{2} & = \sqrt{(e_{0}a)^{4} \biggl( \frac{\rho h\omega^{2} + 2c}{2D} \biggr)^{2} + \frac{\rho h\omega^{2} + 2c}{D}} \\ &\quad {}-\frac{(e_{0}a)^{2}\rho h\omega^{2} + 2c}{2D}. \end{aligned} } \end{aligned}$$
(16d)

The general solutions of the above ordinary differential equations can be written as Bessel functions:

$$ \begin{aligned}[b] W_{j}(r) & = C_{1}J_{n}(\mu_{j1}r) + C_{2}Y_{n}(\mu_{j1}r) + C_{3}I_{n}( \mu_{j2}r) \\ &\quad {}+ C_{4}K_{n}(\mu_{j2}r), \quad j = \mathrm{in}, \mathrm{an}, \end{aligned} $$
(17)

where J n and Y n denote the Bessel functions of order n of the first and second types, respectively. I n and K n are the modified Bessel functions of order n of the first and second types, and C k (k=1–4) are arbitrary constants. Since W j (r) (j=in,an) must be finite for all values of r (including r=0), then Y n (μ j r) and K n (μ j r) (j=in,an) have singularities at r=0. Thus, C 2=C 4=0, and Eq. (17) becomes

$$ W_{j}(r) = C_{1}J_{n}(\mu_{j1}r) + C_{3}I_{n}(\mu_{j2}r),\quad j=\mathrm{in},\mathrm{an}. $$
(18)

The boundary conditions for the simply supported edge of r=R are given as

$$\begin{aligned} &{w_{j} \vert _{r = R} = 0,\quad j =\mathrm{in}, \mathrm{an}, } \end{aligned}$$
(19a)
$$\begin{aligned} &{\frac{\partial^{2}w_{j}}{\partial r^{2}} \bigg\vert _{r = R} + \nu \biggl( \frac{\partial w_{j}}{r\partial r} + \frac{\partial^{2}w_{j}}{r^{2}\partial \theta^{2}} \biggr) \bigg\vert _{r = R} = 0, \quad j =\mathrm{in}, \mathrm{an}. } \end{aligned}$$
(19b)

Substituting the deflection functions of the circular DLGSs (w j , j=in,an) into the boundary conditions (Eqs. (19a), (19b)) means that the resonance frequency can be determined by a nontrivial solution of the simultaneous equations

$$ \left \vert \begin{array}{c@{\quad}c} J_{n}(\mu_{j1}r) & I_{n}(\mu_{j2}r) \\ \frac{\mathrm{d}^{2}J_{n}(\mu_{j1}r)}{\mathrm{d}r^{2}} + \frac{\nu\,\mathrm{d}J_{n}(\mu_{j1}r)}{r\,\mathrm{d}r} - \frac{\nu n^{2}J_{n}(\mu_{j1}r)}{r^{2}} & \frac{\mathrm{d}^{2}I_{n}(\mu_{j2}r)}{\mathrm{d}r^{2}} + \frac{\nu\,\mathrm{d}I_{n}(\mu_{j2}r)}{r\,\mathrm{d}r} - \frac{\nu n^{2}I_{n}(\mu_{j2}r)}{r^{2}} \end{array} \right \vert _{r = R} = 0. $$
(20)

4 Results and discussion

Calculation of the vibration characteristics was carried out for a circular DLGS with a simply supported edge. In the simulations, circular DLGSs were modeled as two layers of circular GSs coupled together via vdW interactions. The effective thickness (h) of each layer of the circular DLGS is equal to the diameter of a carbon atom (0.34 nm). The Young’s modulus E and the mass density ρ of circular DLGSs are 1 TPa and 2300 kg/m3, respectively [31]. The vdW interaction coefficient between two adjacent GSs is −108 GPa/nm from Eq. (11). D is the diameter of the circular DLGSs.

The IPM and APM can be derived from Eq. (20) for circular DLGSs with simply supported boundary conditions. Figure 2 shows typical vibration mode shapes of IPM and APM for circular DLGSs obtained using different combinations of low wave numbers (n,m), where n=0 or 1 and m=1 or 2. The vibration amplitude ratio of the upper and lower GSs (W 1/W 2) was found to be 1 for IPM. This means that the two layers of the circular DLGSs have the same vibration amplitudes and always vibrate in the same direction. The vibration amplitude ratio for APM is −1, which means that both sheets are moving with the same amplitude, but in opposite directions.

Fig. 2
figure 2

Shapes of the vibration mode of circular DLGSs with simply supported edge boundary conditions. (a) In-phase mode. (b) Anti-phase mode

Full size image

The nonlocal effect on the resonance frequency of the circular DLGSs with the first five radial mode numbers (m) when n=0 and the aspect ratio D/2h=20 are shown in Fig. 3. Both IPM and APM are sensitive to the nonlocal effects in the higher modes. The resonance frequencies of circular DLGSs with different nonlocal parameters (e 0 a=0, 1 and 2 nm) are almost the same for the first radial mode of IPM and APM in Fig. 3a and b. As the radial mode number increases, the resonance frequencies diverge. The resonance frequencies of circular DLGSs decrease with increasing nonlocal parameter (e 0 a). When the radial mode numbers of the IPM and APM increase, the resonance frequencies of circular DLGSs become more sensitive to the nonlocal parameters. However, the range of variation for IPM is much larger than for APM with the same nonlocal parameter. For example, the resonance frequencies of circular DLGSs in APM with e 0 a=2 nm only increase a little with increasing radial mode number; the resonance frequencies for IPM (0,5) are 2.3, 4.2 and 10.2 THz when e 0 a=0, 1 and 2 nm, whereas they are 16.8, 17.1 and 19.5 THz in APM (0,5) when e 0 a=0, 1 and 2 nm. This is because the resonance frequency is independent of the vdW interaction forces for IPM (neither Eq. (16a) nor (16b) for IPM includes the vdW coefficient c), while it is dependent on the vdW interaction forces for APM (both Eqs. (16c) and (16d) for APM include the vdW coefficient c).

Fig. 3
figure 3figure 3

Nonlocal effect on the resonance frequency of the circular DLGSs with the first five radial mode numbers (m) when n=0 and D/2h=20. (a) In-phase mode. (b) Anti-phase mode

Full size image

Figure 4a and b show the nonlocal effect on the resonance frequency of circular DLGSs with the first five circumferential mode numbers (n) in IPM and APM with m=1 and the aspect ratio D/2h=20. Similar to Fig. 3, the resonance frequencies of the circular DLGSs are almost the same for the first circumferential mode of IPM and APM with different nonlocal parameters (e 0 a=0, 1 and 2 nm) and diverge as the circumferential mode number increases. The higher nonlocal parameters have the smallest resonance frequencies of circular DLGSs in both IPM and APM.

Fig. 4
figure 4figure 4

Nonlocal effect on the resonance frequency of the circular DLGSs with the first five circumferential mode numbers (n) when m=1 and D/2h=20. (a) In-phase mode. (b) Anti-phase mode

Full size image

To make the simulations more applicable for guiding the application of circular DLGSs as NEMS resonators, the nonlocal effect on the resonance frequency in the six lowest vibration modes of circular DLGSs, IPM (0,1), (1,1), (2,1), (0,2), (3,1) and (1,2), are shown in Fig. 5. As the vibration mode increases, the resonance frequencies of circular DLGSs become more sensitive to the nonlocal parameters. In the cases where e 0 could be determined from experiment or by matching dispersion curves of plane waves with those of atomic lattice dynamics, more exact solutions for the vibration analysis were obtained.

Fig. 5
figure 5

Nonlocal effect on the relationship between the resonance frequency and the first six combination modes (m,n) for in-phase mode

Full size image

The nonlocal effects on the relationship between the resonance frequency and the aspect ratio in the first mode (0,1) of IPM and APM are shown in Fig. 6a and b. The aspect ratio D/2h of circular DLGSs is assumed to be greater than 10 since we are using a thin-plate model. The resonance frequencies of the circular DLGSs with different nonlocal parameters all decrease with increasing aspect ratio. For large aspect ratios, the resonance frequency is insensitive to the nonlocal parameters. That is, if the aspect ratio is large enough, for example greater than 50, in the first vibration mode, the local results (e 0 a=0 nm) in this simulation can be used to guide the application of circular DLGSs as nanosensors.

Fig. 6
figure 6figure 6

Nonlocal effect on the relationship between the resonance frequency and the aspect ratio for the first mode (0,1) of (a) in-phase mode and (b) anti-phase mode

Full size image

The nonlocal vibration analysis of a square DLGS based on the finite element model solution was previously reported in the literature [31]. The frequencies of square DLGSs (side length=10 nm) are 0.4215 THz (e 0 a=0 nm) and 0.3853 THz (e 0 a=1 nm) in the mode (1,1) with simply supported boundary conditions. To judge the robustness of the proposed continuum model, we calculated the resonant frequencies of a circular DLGS with diameter of 10 nm that are 0.4277 THz (e 0 a=0 nm) and 0.3854 THz (e 0 a=1 nm) for the same material constants, boundary condition and mode. The resonant frequencies of a circular DLGS are expected to be slightly greater than those of a square DLGS. Therefore, the comparison shows the suitability and reliability of the proposed vibration analysis of circular DLGSs.

5 Conclusions

The nonlocal vibrational properties of circular DLGSs have been investigated using thin-plate theory and an approach has been proposed for analyzing the resonance frequency of circular DLGSs with simply supported boundary conditions. The vibration mode of circular DLGSs can be divided into IPM and APM, which is a unique feature of DLGSs, and the two modes were analyzed in detail. The results showed that the resonance frequencies in APM are less sensitive to the vibration modes than in IPM because of the vdW forces. The nonlocal effect on the resonance frequency of circular DLGSs was also discussed. The nonlocal effect becomes more significant with higher vibration modes and smaller aspect ratios of circular DLGSs. By choosing the exact values of the nonlocal parameters, the proposed method may provide a guide for the application of circular DLGSs as nanomechanical systems resonators.