1 Introduction

Detection systems or sensors at nanoscale are of great significance in a large amount of engineering applications, such as biomedical curing, environmental monitoring, etc [1]. Since the discovery of graphene sheets (GSs) in 2004 [2], GSs have demonstrated a significant potential of application as structural elements in nanoscale devices because of their remarkable physical and mechanical properties, such as high Young’s modulus, low weight, extremely high stiffness and specific surface-to-volume ratio, as well as high sensitivity to the change of environment [3, 4]. Such features of GSs make them ideally suitable for mass, force, and charge sensors.

Recently, GS used as a sensor has been widely investigated by researchers. Sakhaee-Pour et al. [5, 6] discussed the potential of single-layered graphene sheet (SLGS) strain sensor and applied the SLGS to detect the mass of atomistic dust. And then, Arash et al. [7, 8] accomplished research on the potential of a graphene-based resonator sensor in the detection of noble gases. Shen et al. [9, 10] applied nonlocal Kirchhoff plate theory to study the transverse vibration of rectangular and circular graphene sheet-based mass sensors. Jiang et al. [11] investigated the utility of inducing nonlinear oscillations to enhance the mass sensitivity of carbon nanotube (CNT) and GS-based nanomechanical resonators using molecular dynamics simulation. Tsiamaki et al. [12] used an improved spring-mass-based structural mechanics method to study the vibrational behavior of a circular graphene sheet operating as a nanomechanical mass sensor monitoring resonant frequency. Chun [13] proposed a transparent and stretchable all-graphene strain sensor capable of detecting various types of strains induced by stretching, bending, and torsion. By simulation, the results show that the resolution of mass sensor made of a square GS (10 nm) can reach an order of \(10^{-24}\) kg. Moreover, by decreasing the size of graphene sheet, the mass sensitivity can be enhanced [4]. The double-layered graphene sheet (DLGS), treated as two layers of SLGSs connected by van der Waals (vdW) forces, is very different from the SLGS, especially in dynamics. In particular, experimental evidence shows that the DLGS gas sensor exhibits higher response sensitivity to \(\hbox {NO}_{2}\) than monolayer and multilayer graphene [14]. Similarly, Asemi et al. [15] found that the frequency shifts of double nanofilm-based mass sensors were always greater than those of single nanofilm-based ones. Rajabi and Hosseini-Hashemi [1] developed a new nanoscale mass sensor based on the DLGS by considering the effect of interlayer shear using multibeam shear model. The principle of mass detection using the nano-mass sensor is to detect recognizable shifts of its resonant frequency induced by the added mass on the surface of the sensors [3]. Consequently, the study of the vibration characteristics of the nano-mass sensor is the key technique in both design and practical application.

Recently, the continuum elastic model has also become effective in studying the vibrational behavior of GS. He et al. [16] calculated the potential of multilayered GSs using the classical theory of elasticity. Lei et al. [17] analyzed the vibrational properties of an nanomechanical mass sensor with atomic resolution using a fixed-supported circular monolayer GS model with attached nanoparticles, based on the continuum mechanics of elasticity and Rayleigh’s energy method. However, the significant size effect on the mechanical properties of structure was shown in both experiments and simulations in the case of very small dimensions. The size effect cannot be predicted quite well when using the classical continuum mechanics of elasticity. The nonlocal continuum theory presented by Eringen [18, 19] solves scale-dependent problems. The dynamic behavior of GSs can be accurately predicted using the nonlocal continuum models [3]. Using the nonlocal theory of elasticity, many researchers have studied the SLGS nanomechanical resonators [20,21,22,23,24]. In particular, Shi et al. [25] and Chang et al. [26] investigated the vibration of circular DLGSs as nanomechanical resonators using the nonlocal theory. Natsuki et al. [27] analyzed the free vibration of DLGS-based nanomechanical mass sensor using an attached nanoparticle. Rajabi and Hosseini-Hashemi [28] examined the application of viscoelastic orthotropic system of double-nanoplates as nanoscale mass sensors via the nonlocal theory of elasticity.

The strip transfer function method (STFM) [29] can cope with complicated boundaries with much higher efficiency, which is quite suitable for the static and dynamic analyses for plate problems. By using the STFM, the plate is divided by a number of strips. Based on the feedback from each strip, the nodal line displacement is correlated with the longitudinal coordinate of the strip and the time. In the lateral direction of the strip, the transverse displacement of the plate is interpolated by nodal line displacement. Therefore, along the strip longitudinal direction, the closed-form solution of plate displacement can be obtained using the STFM. It also exhibits high computational efficiency along the lateral direction of the strip. However, the conventional STFM is based on the potential functions. To solve this problem, the STFM incorporating the principles of Galerkin method, called the Galerkin STFM (GSTFM), is established. Using the GSTFM, Jiang et al. [30] analyzed the free vibration of a single-layered graphene-sheet-based mass sensor based on the nonlocal Kirchhoff plate theory, showing that the GSTEM is quite accurate and efficient.

In this paper, the GSTFM is used to study the vibration of the DLGS mass sensor. Two Kirchhoff plates with an attached nanoparticle in the upper plate are used to model the DLGS mass sensor based on the nonlocal theory, and the interaction between the two plates is governed by vdW forces. The results obtained from the semi-analytical method are compared with the previous ones, and the differences between the SLGS and DLGS mass sensors are also presented. Parametric studies such as influences of nonlocal parameters, geometry parameters and the location of nanoparticle on the frequency shift are investigated.

2 Governing Equations

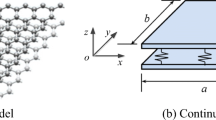
Supposing that in the upper SLGS layer at the location of (\(x_{0}\), \(y_{0})\), there is an attached nanoparticle \(m_{0}\), as shown in Fig. 1. The attached nanoparticle can be treated as a concentrated mass without considering its mass distribution, when its dimension and mass are much smaller than those of the GS- or CNT-based mass sensors [5, 31, 32].

Fig. 1
figure 1

DLGS mass sensor with an attached nanoparticle. a Discrete model, b continuum model

Full size image

In this paper, we use superscripts ‘I’ and ‘II’ to denote the parameters of the upper SLGS layer and the lower SLGS layer, respectively. Van der Waals (vdW) forces exist in a DLGS nanomechanical resonator which is made up of two layers of SLGS. The continuum model and the coordinate system used for the DLGS are, respectively, displayed in Figs. 1 and 2, where the origin is chosen at one corner of the midplane of the nanoplate; the x and y coordinates are taken along the length a and width b of the nanoplate, respectively; and the z coordinate is taken along the thickness 2h of the nanoplate.

Fig. 2
figure 2

Substructures of a rectangle Kirchhoff plate. a Upper layer, b lower layer

Full size image

According to the nonlocal Kirchhoff plate theory, the governing equation of the upper SLGS layer with an attached nanoparticle yields [25, 30]

(1)

And the governing equation of the lower SLGS layer is

(2)

where \(\rho \) is the density, h is the thickness, and \(\delta \) is the Dirac delta function. The moments in Eqs. (1) and (2) can be exactly expressed as

(3)

Here E is Young’s modulus, \(\upsilon \) is Poisson’s ratio, \(D=Eh^{3}/12\left( {1-\upsilon ^{2}} \right) \) is the bending stiffness of thin plate, and \(\mu \) is the nonlocal parameter.

In Eqs. (1) and (2), vdW forces \(f_v =c_v \left( {w^{\mathrm{II}}-w^{{\mathrm{I}}}} \right) \), where \(c_{v}\) is the vdW interaction coefficient between the two layers that can be obtained by [25]

$$\begin{aligned}&c_v =-\left( {\frac{4\sqrt{3}}{9a_{cc} }} \right) ^{2}\frac{24\varepsilon }{\sigma ^{2}}\left( {\frac{\sigma }{a_{cc} }} \right) ^{8}\left[ {\frac{3003\pi }{256}\sum _{k=0}^5 {\frac{\left( {-1} \right) ^{k}}{2k+1}\left( {{\begin{array}{c} 5 \\ k \\ \end{array} }} \right) \left( {\frac{\sigma }{a_{cc} }} \right) ^{6}\frac{1}{h_{{ ij}}^{12} }} } \right. \nonumber \\&\left. {-\frac{35\pi }{8}\sum _{k=0}^2 {\frac{\left( {-1} \right) ^{k}}{2k+1}\left( {{\begin{array}{c} 2 \\ k \\ \end{array} }} \right) \left( {\frac{\sigma }{a_{cc} }} \right) ^{6}\frac{1}{h_{{ ij}}^6 }} } \right] \end{aligned}$$
(4)

in which \(a_{cc}\) is the carbon bond length of C–C equaling 1.42 nm; \(\varepsilon \) and \(\sigma \) are parameters related to the physical properties of the GSs, with \(\varepsilon = 2.968~\hbox { MeV}\) and \(\sigma = 0.34~\hbox { nm}\); and \(h_{{ ij}}\) is the distance between the two layers.

3 Galerkin Strip Transfer Function Method

Usually, the method with the assumed mode is applicable to classical plate problems with simply supported and clamped boundary conditions. However, it is not an ideal way for the Kirchhoff plate with an attached mass owing to the fact that it is difficult to converge at the position of the attached mass. The plate with a concentrated mass can be treated as a special boundary condition, while the STFM is good at dealing with complex boundary conditions. Considering the difficulty of explicitly expressing the potential functions based on Eringen’s nonlocal stress gradient theory, the GSTFM is proposed to solve this problem.

3.1 Formulation of Element Equations

Firstly, along the x direction and from the location of the attached nanoparticle \(x=x_{0, }\) each SLGS layer of the DLGS resonator needs to be divided into two substructures using the GSTFM. As shown in Fig. 2, there are four substructures in total, which are marked with \(\varOmega _1^{\mathrm{I}} \), \(\varOmega _2^{\mathrm{I}} \), \(\varOmega _1^{\mathrm{II}} \) and \(\varOmega _2^{\mathrm{II}} \), respectively. Also, the continuity conditions at \(x=x_{0}\) should be added. Then, the governing equations of the DLGS resonator become

$$\begin{aligned} \begin{array}{ll} \begin{array}{ll} \Omega _i^{\mathrm{I}} \;\;:\;\;\;-\left( {\frac{\partial ^{2}M_{xx,i}^{\mathrm{I}} }{\partial x^{2}}+2\frac{\partial ^{2}M_{xy,i}^{\mathrm{I}} }{\partial x\partial y}+\frac{\partial ^{2}M_{yy,i}^{\mathrm{I}} }{\partial y^{2}}} \right) +\rho h\frac{\partial ^{2}w_{,i}^{\mathrm{I}} }{\partial t^{2}}-c_v \left( {w_{,i}^{\mathrm{II}} -w_{,i}^{\mathrm{I}} } \right) =0 \\ \Omega _i^{\mathrm{II}} \;:\;\;\;-\;\left( {\frac{\partial ^{2}M_{xx,i}^{\mathrm{II}} }{\partial x^{2}}+2\frac{\partial ^{2}M_{xy,i}^{\mathrm{II}} }{\partial x\partial y}+\frac{\partial ^{2}M_{yy,i}^{\mathrm{II}} }{\partial y^{2}}} \right) +\rho h\frac{\partial ^{2}w_{,i}^{\mathrm{II}} }{\partial t^{2}}+c_v \left( {w_{,i}^{\mathrm{II}} -w_{,i}^{\mathrm{I}} } \right) =0 \\ \end{array}\quad ({i=1,2}) \\ \end{array} \end{aligned}$$
(5)

The moments in Eq. (5) can be converted from Eq. (3).

In addition, the continuity conditions at \(x=x_{0}\) for the DLGS are

Fig. 3
figure 3

Strip elements of substructures. a Substructure, b displacements at the strip nodal lines

Full size image
(6)

where \(Q_{xx,i}^{\mathrm{I}} \) and \(Q_{xx,i}^{\mathrm{II}} \) (\(i = 1\), 2) are shear forces of \(\Omega _i^{\mathrm{I}} \) and \(\Omega _i^{\mathrm{II}} \) at \(x=x_{0}\), respectively.

Each divided substructure should be separated into NE strip elements, as shown in Fig. 3.

For the jth element which is in substructure \(\varOmega _i^n\, (n = \hbox {I}, \hbox {II};i = 1, 2)\), we set the unknown displacement vector at the nodal lines

$$\begin{aligned} {\varvec{\phi }} _{j,i}^n \left( {x,t} \right) =\left\{ {{\begin{array}{cccc} {w_{j,i}^n }&{} {\frac{\partial w_{j,i}^n}{\partial y}}&{} {w_{j+1,i}^n }&{} {\frac{\partial w_{j+1,i}^n }{\partial y}} \\ \end{array} }} \right\} ^{\mathrm{T}} \end{aligned}$$
(7)

where n=I, II, and \(i=1\), 2.

\(w_{,i}^n \left( {x,y,t} \right) \) denotes the element’s transverse displacement function, which can be written as

$$\begin{aligned} {w_{,i}^n \left( {x,y,t} \right) ={\varvec{\phi }} _{j,i}^n \left( {x,t} \right) \mathbf{N}\left( y \right) }\quad ({n=\hbox {I,}\;\hbox {II}\;;\;\;i=1,2}) \end{aligned}$$
(8)

where \({{\varvec{N}}}(y)\) is the shape function, and one of the applicable forms can be seen in Ref. [30].

Using Eq. (3), we can get the weak form of Eq. (5) as follows

(9)

where \({\bar{\mathbf{W}}}\) is the trail vector. Substituting Eqs. (8) into (9), we can get

$$\begin{aligned} {\begin{array}{ll} {\begin{array}{l} \Omega _i^{\mathrm{I}} \;\;:\;\;\;\mathbf{k}^{\left( 4 \right) }\frac{\partial ^{4}\phi _{j,i}^{\mathrm{I}} }{\partial x^{4}}+\mathbf{k}^{\left( 2 \right) }\frac{\partial ^{2}\phi _{j,i}^{\mathrm{I}} }{\partial x^{2}}+\mathbf{k}^{\left( 0 \right) }\phi _i^{\left( 1 \right) } + \mathbf{m}^{\left( 2 \right) }\frac{\partial ^{4}\phi _{j,i}^{\mathrm{I}} }{\partial x^{2}\partial t^{2}}+\mathbf{m}^{\left( 0 \right) }\frac{\partial ^{2}\phi _{j,i}^{\mathrm{I}} }{\partial t^{2}} \\ \;\;\;\;\;\;\;\;\;-\,\mathbf{c}^{\left( 2 \right) }\left( {\frac{\partial ^{2}\phi _{j,i}^{\mathrm{II}} }{\partial x^{2}}-\frac{\partial ^{2}\phi _{j,i}^{\mathrm{I}} }{\partial x^{2}}} \right) -\mathbf{c}^{\left( 0 \right) }\left( {\phi _{j,i}^{\mathrm{II}} -\phi _{j,i}^{\mathrm{I}} } \right) =0 \\ \Omega _i^{\mathrm{II}} \;\;:\;\;\;\mathbf{k}^{\left( 4 \right) }\frac{\partial ^{4}\phi _{j,i}^{\mathrm{II}} }{\partial x^{4}}+\mathbf{k}^{\left( 2 \right) }\frac{\partial ^{2}\phi _{j,i}^{\mathrm{II}} }{\partial x^{2}}+\mathbf{k}^{\left( 0 \right) }\phi _{j,i}^{\mathrm{II}}+\,\mathbf{m}^{\left( 2 \right) }\frac{\partial ^{4}\phi _{j,i}^{\mathrm{II}} }{\partial x^{2}\partial t^{2}}+\mathbf{m}^{\left( 0 \right) }\frac{\partial ^{2}\phi _{j,i}^{\mathrm{II}} }{\partial t^{2}} \\ \;\;\;\;\;\;\;\;\;+\,\mathbf{c}^{\left( 2 \right) }\left( {\frac{\partial ^{2}\phi _{j,i}^{\mathrm{II}} }{\partial x^{2}}-\frac{\partial ^{2}\phi _{j,i}^{\mathrm{I}} }{\partial x^{2}}} \right) +\mathbf{c}^{\left( 0 \right) }\left( {\phi _{j,i}^{\mathrm{II}} -\phi _{j,i}^{\mathrm{I}} } \right) =0 \\ \end{array}}&{} ({i=1,2}) \\ \end{array} } \end{aligned}$$
(10)

where \(\mathbf{c}^{\left( 0 \right) } \) and \(\mathbf{c}^{\left( 2 \right) } \) are the vdW force matrices, which can be expressed as

$$\begin{aligned} \mathbf{c}^{\left( 0 \right) }= & {} \int _0^l {c_v \mathbf{N}^{\mathrm{T}}\mathbf{N}\hbox {d}y} -\int _0^l {c_v \mu \mathbf{N}^{\mathrm{T}}\frac{\partial ^{2}{} \mathbf{N}}{\partial y^{2}}\hbox {d}y} \quad \nonumber \\ \mathbf{c}^{\left( 2 \right) }= & {} -\int _0^l {c_v \mu \mathbf{N}^{\mathrm{T}}{} \mathbf{N}\hbox {d}y} \end{aligned}$$
(11)

where \(\mathbf{k}^{\left( 0 \right) } \), \(\mathbf{k}^{\left( 2 \right) } \) and \(\mathbf{k}^{\left( 4 \right) } \) are the strip stiffness matrices, and \(\mathbf{m}^{\left( 0 \right) } \) and \(\mathbf{m}^{\left( 2 \right) } \) the strip mass matrices. Their specific forms can be found in Ref. [30].

The global equations for the substructures can be obtained by assembling the element governing equations, following the same procedure as the finite element method.

Firstly, the unknown global displacement vector should be defined as follows

$$\begin{aligned} {{\varvec{\Phi }} }_{,i}^n \left( {x,t} \right) =\left\{ {{\begin{array}{ccccccc} {w_{{1,}\;i}^n }&{} {\frac{\partial w_{{1,}\;i}^n }{\partial y}}&{} {w_{{2,}\;i}^n }&{} {\frac{\partial w_{{2,}\;i}^n }{\partial y}}&{} \ldots &{} {w_{NE,i}^n }&{} {\frac{\partial w_{NE,i}^n }{\partial y}} \\ \end{array} }} \right\} ^{\mathrm{T}}\quad ({n=\hbox {I,}\;\hbox {II}\;;\;\;i=1,2}) \end{aligned}$$
(12)

After that, the global equations can be achieved as

(13)

where \(\mathbf{K}^{\left( j \right) }\), \(\mathbf{M}^{\left( j \right) }\) and \(\mathbf{C}^{\left( j \right) } \) (\(j=0\), 2 or 4) are the global stiffness matrices, global mass matrices and vdW force matrices, respectively.

Supposing that there are displacement boundary conditions at \(y = 0\) and \(y=b\), or some constraints are imposed on a nodal line, the variation of \({\varvec{\Phi } }_{,i}^n \) in Eq. (13) is not arbitrary. In this case, the dynamic equation is derived by eliminating those known nodal line displacements from \({\varvec{\Phi } }_{,i}^n \). Let \({\varvec{\Phi } }_{,i}^n \) have \(N_{1}\) unknown nodal line displacements, denoted by vector \({\bar{\varvec{\Phi }}}_{,i}^n \), and \(N_{2}\) known nodal line displacements, denoted by vector \({{\bar{\bar{\varvec{\Phi }}}}}_{,i}^n \). Rearranging the elements of \({\bar{\varvec{\Phi }}}_{,i}^n \) and \({{\bar{\bar{\varvec{\Phi }}}}}_{,i}^n \) in \({\varvec{\Phi } }_{,i}^n \), one obtains

$$\begin{aligned} {\varvec{\varPhi } }_{,i}^n ={{{\varvec{T}}}}_1 \bar{\bar{\varvec{\varPhi }}}_{,i}^n +{{{\varvec{T}}}}_2 {{\bar{\bar{\varvec{\varPhi }}}}}_{,i}^n \end{aligned}$$
(14)

where \(T_{1}\) and \(T_{2}\) are row transformation matrices consisting of 0 and 1. Substituting Eqs. (14) into (13), the global governing equations are

$$\begin{aligned} {\begin{array}{ll} {\begin{array}{l} \Omega _i^{\mathrm{I}} \;\;:\;\;\;{\bar{\mathbf{K}}}^{\left( 4 \right) }\frac{\partial ^{4}{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{I}} }{\partial x^{4}}+{\bar{\mathbf{K}}}^{\left( 2 \right) }\frac{\partial ^{2}{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{I}} }{\partial x^{2}}+{\bar{\mathbf{K}}}^{\left( 0 \right) }{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{I}} +\,{\bar{\mathbf{M}}}^{\left( 2 \right) }\frac{\partial ^{4}{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{I}} }{\partial x^{2}\partial t^{2}}+{\bar{\mathbf{M}}}^{\left( 0 \right) }\frac{\partial ^{2}{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{I}} }{\partial t^{2}} \\ \;\;\;\;\;\;\;\;\;-\,\bar{{{{\varvec{C}}}}}^{\left( 2 \right) }\left( {\frac{\partial ^{2}{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{II}} }{\partial x^{2}}-\frac{\partial ^{2}{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{I}} }{\partial x^{2}}} \right) -\,\bar{{{{\varvec{C}}}}}^{\left( 0 \right) }\left( {{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{II}} -{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{I}} } \right) =0 \\ \Omega _i^{\mathrm{II}} \;\;:\;\;\;{\bar{\mathbf{K}}}^{\left( 4 \right) }\frac{\partial ^{4}{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{II}} }{\partial x^{4}}+{\bar{\mathbf{K}}}^{\left( 2 \right) }\frac{\partial ^{2}{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{II}} }{\partial x^{2}}+{\bar{\mathbf{K}}}^{\left( 0 \right) }{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{II}} +\,{\bar{\mathbf{M}}}^{\left( 2 \right) }\frac{\partial ^{4}{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{II}} }{\partial x^{2}\partial t^{2}}+{\bar{\mathbf{M}}}^{\left( 0 \right) }\frac{\partial ^{2}{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{II}} }{\partial t^{2}} \\ \;\;\;\;\;\;\;\;\;+\,\bar{{{{\varvec{C}}}}}^{\left( 2 \right) }\left( {\frac{\partial ^{2}{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{II}} }{\partial x^{2}}-\frac{\partial ^{2}{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{I}} }{\partial x^{2}}} \right) + \bar{{{{\varvec{C}}}}}^{\left( 0 \right) }\left( {{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{II}} -{\bar{\varvec{\Phi }}}_{,i}^{\mathrm{I}} } \right) =0 \\ \end{array}}&\qquad ({i=1,2}) \end{array} } \end{aligned}$$
(15)

where

$$\begin{aligned} {\bar{{\varvec{K}}}}^{\left( 4 \right) }= & {} {\varvec{T}}_1^{\mathrm{T}} {\varvec{K}}^{\left( 4 \right) }{\varvec{T}}_1, \quad {\;\;\;{\bar{{\varvec{K}}}}^{\left( 2 \right) }={\varvec{T}}_1^{\mathrm{T}} {\varvec{K}}^{\left( 2 \right) }{\varvec{T}}_1 },\quad {\bar{{\varvec{K}}}}^{\left( 0 \right) }={\varvec{T}}_1^{\mathrm{T}} {\varvec{K}}^{\left( 0 \right) }{\varvec{T}}_1 \\ {\bar{{\varvec{M}}}}^{\left( 2 \right) }= & {} {\varvec{T}}_1^{\mathrm{T}} {\bar{{\varvec{M}}}}^{\left( 2 \right) }{\varvec{T}}_1, \quad {\;\;{\bar{{\varvec{M}}}}^{\left( 0 \right) }={\varvec{T}}_1^{\mathrm{T}} {\bar{{\varvec{M}}}}^{\left( 0 \right) }{\varvec{T}}_1 } \end{aligned}$$

3.2 Transfer Function Solution Method

After obtaining the global equations, the transfer function method is used in the solution. The Laplace transforms of the global equations are

$$\begin{aligned} {\begin{array}{ll} {\begin{array}{l} \displaystyle \frac{\partial ^{4}}{\partial x^{4}} {\mathop {\varvec{\Phi }}\limits ^{\frown }}_{,i}^{\mathrm{I}} \left( {x,\hbox {s}} \right) =\left( {\mathbf{D}_2 \frac{\partial ^{2}}{\partial x^{2}}+\mathbf{D}_0 } \right) {\mathop {\varvec{\Phi }}\limits ^{\frown }}_{,i}^{\mathrm{I}} \left( {x,\hbox {s}} \right) +\left( {\mathbf{C}_2 \frac{\partial ^{2}}{\partial x^{2}}+\mathbf{C}_0 } \right) {\mathop {\varvec{\Phi }}\limits ^{\frown }}_{,i}^{\mathrm{II}} \left( {x,\hbox {s}} \right) \\ \displaystyle \frac{\partial ^{4}}{\partial x^{4}}{\mathop {\varvec{\Phi }}\limits ^{\frown }}_{,i}^{\mathrm{II}} \left( {x,\hbox {s}} \right) =\left( {\mathbf{D}_2 \frac{\partial ^{2}}{\partial x^{2}}+\mathbf{D}_0 } \right) {\mathop {\varvec{\Phi }}\limits ^{\frown }}_{,i}^{\mathrm{II}} \left( {x,\hbox {s}} \right) +\left( {\mathbf{C}_2 \frac{\partial ^{2}}{\partial x^{2}}+\mathbf{C}_0 } \right) {\mathop {\varvec{\Phi }}\limits ^{\frown }}_{,i}^{\mathrm{I}} \left( {x,\hbox {s}} \right) \\ \end{array} }&{}\quad ({i=1,2}) \\ \end{array} } \end{aligned}$$
(16)

where ‘\(\hat{\,}\)’ denotes the Laplace transformation, s is the Laplace transform parameter, and

$$\begin{aligned} \begin{array}{l} \mathbf{D}_2 =-\mathbf{A}\left( {{\bar{\mathbf{K}}}^{\left( 2 \right) }+s^{2}{\bar{\mathbf{M}}}^{\left( 2 \right) }+{\bar{\mathbf{C}}}^{\left( 2 \right) }} \right) \\ \mathbf{D}_0 =-\mathbf{A}\left( {{\bar{\mathbf{K}}}^{\left( 0 \right) }+s^{2}{\bar{\mathbf{M}}}^{\left( 0 \right) }+{\bar{\mathbf{C}}}^{\left( 0 \right) }} \right) \\ \mathbf{C}_2 =\mathbf{A}{\bar{\mathbf{C}}}^{\left( 2 \right) }\;\;\;\;\mathbf{C}_0 =\mathbf{A}{\bar{\mathbf{C}}}^{\left( 2 \right) }\;\;\;\;\mathbf{A}=\left( {{\bar{\mathbf{K}}}^{\left( 4 \right) }} \right) ^{-1} \\ \end{array} \end{aligned}$$
(17)

By setting the state space vector

$$\begin{aligned} \varvec{ \upeta }\left( {x,s} \right) =\left\{ {{\begin{array}{llll} {\left( {\varvec{ \upeta }_1^{\mathrm{I}} } \right) ^{\mathrm{T}}}&{} {\left( {\varvec{ \upeta }_1^{\mathrm{II}} } \right) ^{\mathrm{T}}} &{} {\left( {\varvec{ \upeta }_2^{\mathrm{I}} } \right) ^{\mathrm{T}}}&{} {\left( {\varvec{ \upeta }_2^{\mathrm{II}} } \right) ^{\mathrm{T}}} \\ \end{array} }} \right\} ^{\mathrm{T}} \end{aligned}$$
(18)

where

(19)

Equation (16) can be rewritten as

$$\begin{aligned} \frac{\partial }{\partial x}\varvec{ \upeta }\left( {x,s} \right) =\mathbf{F}\left( s \right) \varvec{ \upeta }\left( {x,s} \right) \end{aligned}$$
(20)

where

(21)

For the displacement boundary conditions at \(y = 0\) and \(y = \hbox {b}\), the finite element method can be used, similar to Eqs. (15)–(17). For the displacement boundary conditions at \(x = 0\) and \(x =a\), it can be rewritten as

$$\begin{aligned} \mathbf{M}_b \left( s \right) \varvec{ \upeta }\left( {0,s} \right) +\mathbf{N}_b \left( s \right) \varvec{ \upeta }\left( {a,s} \right) =\mathbf{0} \end{aligned}$$
(22)

where

(23)

here \( \left[ {\mathbf{E}_{\mathrm{L}}^{\left( i \right) } \left( s \right) } \right] _{2N_1 \times 2N_1 } \) and \( \left[ {\mathbf{E}_{\mathrm{R}}^{\left( i \right) } \left( s \right) } \right] _{2N_1 \times 2N_1 } \) are coefficient matrices, which are depend on the types of boundary conditions. For simply supported and clamped boundary conditions, the exact forms of \(\mathbf{M}_b \left( s \right) \) and \({{\varvec{N}}}_b \left( s \right) \) are

1. Simply supported

(24)

where

(25)

2. Clamped

(26)

where

(27)

According to Eq. (6), the continuity conditions at \(x=x_{0}\) can also be rewritten as

(28)

Here, \({\mathop {{\varPhi }}\limits ^{\frown }}_{j,1}^{\mathrm{I}} \), the jth component of \({\mathop {\varvec{\Phi }}\limits ^{\frown }}_{,1}^{\mathrm{I}} \), is also the degree of freedom of the nodal lines where the attached nanoparticle locates. Then, Eq. (28) can represented as

$$\begin{aligned} {{\varvec{R}}}_b \left( s \right) \varvec{ \upeta }\left( {x_0 ,s} \right) =\mathbf{0} \end{aligned}$$
(29)

Also, the exact form of \({{\varvec{R}}}_b \left( s \right) \) is

(30)

where

(31)

Also, \({{\varvec{m}}}_{0}\) is an \(N_{1}\times N_{1}\) matrix. The jth diagonal element of \({{\varvec{m}}}_{0}\) is \(m_{0}{\cdot } s^{2}\) and other elements are 0’s.

Fig. 4
figure 4

Different vibration modes of DLGS. a In-phase mode (IPM), b anti-phase mode (APM)

Full size image

Thus, the boundary conditions of Eqs. (22) and (29) can be rewritten as

$$\begin{aligned} \mathbf{M}_b \left( s \right) \varvec{ \upeta }\left( {0,s} \right) +\mathbf{N}_b \left( s \right) \varvec{ \upeta }\left( {a,s} \right) +{{\varvec{R}}}_b \left( s \right) \varvec{ \upeta }\left( {x_0 ,s} \right) =\mathbf{0} \end{aligned}$$
(32)

Then, the characteristic equation of Eqs. (20) and (32) is

$$\begin{aligned} \hbox {det}\left( {\mathbf{M}_b \left( s \right) +\mathbf{N}_b \left( s \right) \hbox {e}^{aF\left( s \right) }+{{\varvec{R}}}_b \left( s \right) \hbox {e}^{x_0 F\left( s \right) }} \right) =\mathbf{0} \end{aligned}$$
(33)

Setting \(s = \mathrm{i}\omega _{k}\) in Eq. (33), the root \(\omega _{k}\) is the kth natural frequency.

4 Results and Discussion

In this study, the vibration of a rectangular DLGS mass sensor is analyzed via a numerical example for simply supported edges and clamped edges, respectively. The DLGS mass sensor is modeled as two layers of nonlocal Kirchhoff plates coupled together via vdW interactions. According to the published literature, the parameters of DLGS adopted are as follows [24]:

Young’s modulus \(E=1.06\) TPa; Poisson’s ratio \(\upsilon = 0.25\); mass density \(\rho = 2.25\hbox { g/cm}^{3}\); the effective thickness of each layer h is 0.34 nm which equals the diameter of a carbon atom; and the vdW interaction coefficient is \(\hbox {c}_{v} = -108\) GPa/nm according to Eq. (2).

The default edge length of the DLGS are \(a=b =10\hbox { nm}\) in Fig. 1; and the initial location of the adding nanoparticle is at \(x_{0} = 0.5a\) and \(y_{0} = 0.5b\).

In response to the mode shape, the vibration mode of DLGS is divided into an in-phase mode (IPM) and an anti-phase mode (APM) [25, 33, 34]. For the IPM, same vibration amplitude and direction are shown for both SLGS layers. By contrast, same amplitude but opposite directions are exhibited for the APM. As shown in Fig. 4, the IPM is always in the lower-order mode, and no relative motions are found between the two layers. On the contrary, the APM appears in the higher-order mode, and the two layers always move in the opposite directions.

4.1 Result Validation

To verify the validity of the method, the results of the present method are compared with those in literature. The comparisons between the fundamental frequencies with a simply supported DLGS of the IPM and the APM are made in Tables 1 and 2, respectively. The results show very good agreement of the results in the present paper with those in Ref. [33]. The error of the IPM trends to be zero, and the maximum error of the APM is only 0.4659%. It means the present method is valid and very effective. Also, the comparison between Tables 1 and 2 shows that the frequencies in the APM are much higher than those in the IPM. That is because vdW forces can increase the rigidity of the system when there is relative motion between the two sheets.

Table 1 Comparison of the IPM fundamental frequencies obtained by the GSTFM with the results in Ref. [33] for nonlocal simply supported DLGS sensor without attached mass (\({\varvec{m}}_{{\varvec{0}}} ={\varvec{0}}\))
Full size table
Table 2 Comparison of the APM fundamental frequencies obtained by the GSTFM with the results in Ref. [33] for nonlocal simply supported DLGS sensor without attached mass (\({\varvec{m}}_{{\varvec{0}}} = {\varvec{0}}\))
Full size table

To compare the differences between the SLGS and DLGS mass sensors, the fundamental frequency results of the SLGS and DLGS (IPM) mass sensors with different attached nanoparticles and nonlocal parameters are listed in Table 3. No differences can be observed between the SLGS and DLGS when \(m_{0} = 0\). The overall trend is that the errors increase with the increase in the mass of attached nanoparticle. The reason is mainly attributed to the nanoparticle. The nanoparticle is only attached to the upper layer of the DLGS, i.e., no nanoparticle is attached to the lower layer. Even so, the maximum error is only 0.5245%. It means the DLGS can be replaced by the SLGS in the IPM. Moreover, it is also found that the increase in the nonlocal parameter can result in the decrease in the error.

Table 3 Comparison of the fundamental frequencies between the SLGS and DLGS nanomechanical resonators
Full size table

4.2 Effect of the Attached Nanoparticle on the DLGS-Based Nanomechanical Sensor

The published results indicated that the responses of resonant frequencies are different for APM and IPM. In general, the APM shows less sensitivity to the vibration modes and a narrower range of resonant frequencies than the IPM because of the existence of vdW forces [25]. Considering that the frequencies in the IPM are much lower than those in the APM, lower energy is required for stimulation. In the following analyses, more attention will be paid to the frequencies in the IPM.

Fig. 5
figure 5

Nonlocal parameter effect on the fundamental frequency shift of a DLGS mass sensor with \(a=b = 10~\hbox { nm}\) and \(x_{0}=y_{0} = 0.5a\). a Simply supported edges, b clamped edges

Full size image
Fig. 6
figure 6

Attached nanoparticle locations effect on the fundamental frequency shift of a DLGS mass sensor with \(a=b = 10~\hbox { nm}\) and \(\mu = 1.0~\hbox {nm}^{2}\). a Simply supported edges, b clamped edges

Full size image

The frequency shift \(\Delta f\) is written as

$$\begin{aligned} \Delta f=\left| {f-f_0 } \right| \end{aligned}$$
(34)

where f and \(f_{0}\) are the frequencies of the DLGS with and without an attached nanoparticle, respectively. The frequency shift \(\Delta f\) is the index to denote the mechanical behavior of the nanomechanical sensor.

The nonlocal effect on the frequency shift \(\Delta f\) of DLGS mass sensor is indicated in Fig. 5. Although increasing the mass of attached nanoparticle results in the decrease in the natural frequency, the overall frequency shift still increases when the mass increases. The frequency shift \(\Delta f\) becomes smaller if the small-scale effect is considered, and it becomes obvious for large nanoparticles. The decrease in \(\Delta f\) can be expected when the nonlocal parameter increases, which is the same as the SLGS mass sensor [30]. In addition, the frequency shift becomes obvious in the case that the attached mass is larger than \(10^{-24}\hbox { kg}\). Therefore, the mass sensitivity of the nanomechanical mass sensor can achieve at least \(10^{-21}\hbox { kg}\). Comparing the data from Fig. 5a with those from Fig. 5b, the clamped DLGS sensors exhibit their sensitivity when comparing the results of frequency shift with those of the simply supported ones.

In addition, the location of nanoparticle also has an influence on the natural frequency variation of the DLGS-based mass sensor. As shown in Fig. 6, the effect of the location of the nanoparticle on \(\Delta f\) is obvious. \(\Delta f\) increases when the nanoparticle approaches the center of the DLGS. Thus, the most sensitive location of the DLGS mass sensor is the center.

Fig. 7
figure 7

Plate side length effect on the fundamental frequency shift of a square DLGS mass sensor with \(\mu = 1.0~\hbox {nm}^{2}\) and \(x_{0} = 0.5a\), \(y_{0} = 0.5b\). a Simply supported edges, b clamped edges

Full size image
Fig. 8
figure 8

Plate side length effect on the fundamental frequency shift of a rectangle DLGS mass sensor with \(b = 10~\hbox { nm}\), \(\mu = 1.0~\hbox {nm}^{2}\) and \(x_{0} = 0.5a\), \(y_{0} = 0.5b\). a Simply supported edges, b clamped edges

Full size image

As discussed in the previous sections, the natural frequency is more sensitive to the plate side length because it is closely correlated to the rigidity and total mass of the nanoplate. Figures 7 and 8 describe the plate side length effect of the DLGS on \(\Delta f\) of the mass sensor. The plate side length effect on \(\Delta f\) is of great significance. The frequency shift can be significant in the case of small side length of the DLGS, especially with large attached mass. Therefore, if the mass sensitivity needs to be increased, smaller-size DLGS resonators are required for the mass sensors. The reason is mainly attributed to the increase in rigidity of the mass sensor when the size reduces. On the other hand, when the side length of a nanoplate gets smaller, the overall mass of the nanoplate will decrease, and the natural frequency will increase consequently. For this case, the ratio of the mass of the added nanoparticle to the total mass of the sensor is relatively high, and hence the portion of the frequency shift will be high as well.

5 Conclusions

In this paper, the GSTFM is applied to solve the governing equations of a DLGS mass sensor carrying an attached nanoparticle based on the nonlocal Kirchhoff plate theory. The results are compared with those in the references. The conclusions are drawn as follows:

  1. 1.

    The IPM results of the DLGS mass sensor are almost the same as those of the SLGS. This means the DLGS can be regarded as the SLGS as a mass sensor at lower modes.

  2. 2.

    Decreasing the nonlocal parameter, moving the attached nanoparticle closer to the DLGS center or making the DLGS smaller can increase the sensitivity of the DLGS mass sensor.

  3. 3.

    The required sensitivity for the DLGS mass sensor has to be at least \(1\times 10^{-24}~\hbox { kg}\).