Flexible estimation of time-varying effects for frequently purchased retail goods: a modeling approach based on household panel data

Abstract

In most previous applications of brand choice models, possible time-varying effects in consumer behavior are ignored by merely imposing constant parameters. However, it is very likely that trends or short-term variations in consumers’ intrinsic brand utilities or sensitivities to marketing instruments occur. For example, preferences for specific brands or price elasticities in product categories such as coffee or chocolate may vary in the run-up to festive occasions like Easter or Christmas. In this paper, we employ flexible multinomial logit models for estimating time-varying effects in brand choice behavior. Time-varying brand intercepts and time-varying effects of covariates are modeled using penalized splines, a flexible, yet parsimonious, nonparametric smoothing technique. The estimation is data driven; the flexible functions, as well as the corresponding degrees of smoothness, are determined simultaneously in a unified approach. Our model further allows for alternative-specific time-varying effects of covariates and can mimic state-space approaches with random walk parameter dynamics. In an empirical application for ground coffee, we compare the performance of the proposed approach to a number of benchmark models regarding in-sample fit, information criteria, and in particular out-of-sample fit. Interestingly, the most complex P-spline model with time-varying brand intercepts and brand-specific time-varying covariate effects outperforms all other specifications both in- and out-of-sample. We further present results from a sensitivity analysis on how the number of knots and other P-spline settings affect the model performance, and we provide guidelines for the model building process about the many options for model specification using P-splines. Finally, the resulting parameter paths provide valuable insights for marketing managers.

1 Introduction

The theory and practice of brand choice plays a crucial role in modern marketing science (Chandukala et al. 2008; Elshiewy et al. 2017). Influenced by the seminal paper of Guadagni and Little (1983), which was the first one to show how to use household scanner panel data for estimating brand choice models, a large number of applications and extensions of discrete choice models directed at explaining consumer brand choice decisions emerged. For example, Gupta (1988) analyzed the impact of sales promotions on brand choice, Winer (1986), Lattin and Bucklin (1989), and Kalyanaram and Little (1994) incorporated reference price effects, Kamakura and Russel (1989) and Jain et al. (1994) unobserved preference heterogeneity into brand choice models, Abe (1998, 1999) and Kneib et al. (2007) used flexible nonlinear function of covariates in semiparametric brand choice models, and Villas-Boas and Winer (1999) and Chintagunta et al. (2005) accounted for price endogeneity in brand choice models. Among discrete choice models, the multinomial logit (MNL) model has been applied most frequently and is considered one of the most important modeling approaches in marketing and related fields nowadays (Chandukala et al. 2008).

In a brand choice context,¹ the deterministic utility function in the MNL model captures the effects of the brands themselves (i.e., intrinsic brand utilities) as well as effects of covariates (like price, promotional activities, and advertising) on a consumer’s utility. Therefore, these models help to understand why consumers choose a specific brand out of several competing alternatives by linking a consumer’s brand choice decision to brand preferences and observable marketing instruments. Furthermore, it has been shown that current decisions of consumers are affected by past decisions due to brand loyalty effects (Guadagni and Little 1983) or by past prices due to psychological reference price effects (Winer 1986).

Even though the latter two constructs (i.e., brand loyalty and reference price effects) induce some inter-temporal effects in brand choice, most applications of choice models in marketing ignore dynamic effects beyond that. In particular, in almost all MNL applications estimated parameters are restricted to be constant over time (i.e., equal across all purchase occasions). This is a strong assumption, and the marketing literature provides rationales why consumer choice behavior may change in the short or long term and consequently why estimated model parameters should be allowed to vary in time.

In the context of retail and consumer goods, it seems plausible to assume that consumers become more price sensitive and more prone to promotions after periods with less intense and less frequent promotional activities (e.g., Foekens et al. 1999; Kopalle et al. 1999). Preferences for certain brands can further be strengthened through advertising investments (Sriram et al. 2007), and advertising may at the same time reduce price elasticities for those brands (e.g., Erdem et al. 2008). Further, situational events like upcoming festive occasions (Christmas, Easter) may lead to a short-term increase in preferences for higher-tier brands in certain product categories like coffee (as considered later in our empirical application). The proposed semiparametric approach can handle all these exemplary situations in an explorative way since it can model evolutions of both brand intercepts and (alternative-specific) covariate effects even if the drivers for those parameter evolutions are not observable or included in the data at hand.

From a managerial point of view, ignoring time-varying effects concerning intrinsic brand utilities may leave competitive trends in a product category undetected with the risk of misjudging the competitive structure between brands. It is further important for retailers to recognize short- or long-term changes in price and promotional sensitivities of their consumers as a basis for adjusting their marketing mix adequately and in due time. All these arguments suggest that dynamics are important in marketing (Leeflang et al. 2009) and should be considered in brand choice models.

Only a few papers have so far considered the possibility of time-varying coefficients in brand choice models. The different model specifications that have been proposed in the literature can be classified into the following three groups:

(1) Reparameterization approaches Parameters that are supposed to be dynamic are reparameterized as functions of time-varying covariates (so-called process functions, see Foekens et al. 1999). For instance, Papatla and Krishnamurti (1996) have modeled price and promotional coefficients as to depend on previous purchases made in the presence of promotional activities. Jedidi et al. (1999) also proposed a varying parameter model allowing consumers’ responses to price and promotional activities to depend on changes in marketing activities over the long term. Heilman et al. (2000) explained the time variation of parameters by changes in the category experience of consumers measured by the number of purchases already made in the respective category. All these models are easy to apply and highly valuable for measuring medium- or long-term effects of marketing activities, but they cannot explain, for example, short-term fluctuations due to situational factors. Another drawback of this modeling approach is that only the temporal variance of the dynamic variables is modeled and not their course in time (van Heerde et al. 2004).

(2) Data splitting/rolling window/before–after analyses In this category, models are fitted only on (successive) subsets of the data. Gordon et al. (2013) split up a rather long period of 6 years into several quarters and estimated models for each quarter separately to investigate the variation over time in price elasticities in multiple product categories. Here, a crucial decision is the selection of the interval length; while a shorter (longer) interval allows for more (less) flexibility and variation over time, it also leads to less (more) stable estimates due to smaller (larger) data subsets for each interval. Furthermore, to circumvent abrupt jumps in the results (due to the piecewise constant approximation of a conceptually continuous process) some researchers opt for a rolling-window approach (Mela et al. 1997). Moreover, parameter estimates in logit models are not comparable in their magnitude across datasets (here across the different subsets) because of differences in scale (Mela et al. 1997). This reduces the usefulness of this kind of approaches to comparable measures, e.g., marginal effects or elasticities. Also, data splitting always lowers the statistical efficiency since it uses the data only in parts.

(3) State-space models and nonparametric methods There is a current trend in marketing to account for specific effects in a more flexible way. State-space models are the most comprehensive method to account for time-varying parameters (Leeflang et al. 2009) because they do neither rely on a parametric function of time-varying covariates nor is data splitting necessary. Here, parameters follow a dynamic process (e.g., random walks, vector autoregressions, or dynamic random effects) and the parameter paths over time are estimated using the Kalman filter. Lachaab et al. (2006) proposed a Bayesian multinomial probit model with time-varying parameters and showed that all model parameters vary over time. Rutz and Sonnier (2011) expanded the model of Lachaab et al. (2006) with a factor analytic structure of random effects, which allows for time-varying effects in the latent space of product properties. Kim et al. (2005) used an MNL model and estimated extremely volatile parameter paths in the detergent category. Closely related to state-space models are nonparametric methods that employ splines. Nonparametric methods share the advantages of state-space models but offer the additional benefit of more control over the degree of smoothness for each estimated parameter path. This is important because it facilitates the interpretation of results. To the best of our knowledge, Baumgartner (2003) was the first to apply nonparametric methods to brand choice models in order to estimate time-varying brand intercepts. A shortcoming of the approach is that one has to fix the reasonable level of smoothness by optimizing some information or cross-validation criterion. Estimating time-varying coefficients for both brand intercepts and covariates would afford extensive search procedures in multidimensional parameter spaces.

All previously proposed approaches in this category (state-space models, nonparametric methods) indeed revealed that parameters can change a lot over time and that the resulting patterns can be highly complex mixtures of short-term fluctuations (e.g., because of situational factors) and long-term trends (e.g., because of advertising). Therefore, reparameterization approaches are most likely not flexible enough and as mentioned do not yield explicit parameter paths, while data splitting or rolling-window approaches suffer from lower statistical efficiency. Flexible nonparametric methods instead borrow strength from neighboring time intervals and allow for more or less smooth parameter paths without imposing too much structure and therefore seem promising for modeling time-varying parameters. Also, state-space models with random walk parameter dynamics are included in our proposed nonparametric approach as a special case, as will be discussed in more detail later.

In the following, we propose flexible MNL models with time-varying parameters to uncover effects in consumer brand choice that change over time. Both time-varying brand intercepts representing intrinsic brand utilities as well as time-varying effects of covariates (generic or alternative specific) are modeled nonparametrically using P(enalized)-splines (Eilers and Marx 1996). Estimation is likelihood based and uses a penalized Fisher scoring procedure. An approximate marginal likelihood procedure is employed to determine the unknown smoothing parameters that control the trade-off between too much flexibility and too much smoothness of each of the nonparametric function estimates in the model. Stated otherwise, both the shape and the degree of smoothness of the nonparametrically estimated time-varying effects—separate for each parameter path of interest (i.e., brand intercepts or covariate effects)—are determined simultaneously within a unified approach. That way, we particularly overcome the limitation of the spline approach of Baumgartner (2003) that requires an extensive search procedure to select the right amount of smoothness for the unknown smooth curve estimates. Our proposed approach is also directly connected to state-space models with random walk dynamics since penalized splines comprise random walks as a special case but allow to introduce differentiability conditions for the estimated time-varying effects leading to potentially smoother effects and enhanced interpretability. The latter is particularly useful when considering smooth temporal variations over a longer period of time, as we would expect to come along with a successful advertising campaign, for instance. On the other hand, the random walk model as proposed in Lachaab et al. (2006) is obtained when considering splines of degree zero (i.e., piecewise constant step functions) which allow the function estimates to evolve rather wiggly.

We structure the remainder of the article as follows: In Sect. 2, we first briefly review the standard MNL model with constant parameters and subsequently introduce more flexible MNL model variants based on the P-spline methodology for the estimation of time-varying effects. We further provide details about the maximum likelihood procedure used for estimation and illustrate how the P-splines approach works. In Sect. 3, we compare the fit and predictive performance of our proposed framework in an empirical study for the ground coffee category to a number of benchmark models. To provide managerial implications, we also focus on market share results on the individual brand level and the evolution of parameter paths of covariates. In Sect. 4, we identify avenues for future research.

2 Methodology

2.1 The multinomial logit model

The MNL model is the most widely used brand choice model to analyze scanner panel data. In such data, we observe purchases of brands in a product category for a sample of households over a certain time horizon. Brand choices are modeled by an unordered categorical response variable Y_nt ∊ C_nt where C_nt = {1, …, J} represents the set of brands available in the product category at the store visited by household $n \left( {n = 1, \ldots , N} \right)$ at purchase occasion $t \left( {t = 1, \ldots , T_{n} } \right)$. Each household’s brand choice depends on her/his latent utilities U_njt, for $j = 1, \ldots , J$, and the household is assumed to choose that brand i which offers maximum utility across all brands, i.e.,

$$ Y_{nt} = i \Leftrightarrow U_{nit} = \mathop {\hbox{max} }\limits_{{j \in C_{nt} }} U_{njt} . $$

(1)

According to random utility theory, the utility of household n for brand j depends on both observable covariates (constituting the deterministic utility V_njt) and unobservable factors (represented by a stochastic error term ɛ_njt) via

$$ U_{njt} = \alpha_{j} + \mathop \sum \limits_{k = 1}^{K} \beta_{k} \cdot x_{knjt} + \varepsilon_{njt} = V_{njt} + \varepsilon_{njt} . $$

(2)

In this linear additive (indirect) utility function, the parameters α_j represent the intrinsic utilities of the J brands also referred to as brand intercepts, whereas the coefficients β_k denote (in a first step generic) effects of K independent variables, like brand prices or promotional instruments.² Note that each covariate $x_{knjt}$ varies in the three dimensions households, brands, and choice occasions, and a setup using brand-specific intercepts and generic effects of covariates (i.e., homogeneous coefficients across brands) is the standard scenario in the brand choice literature (see, e.g., Baltas and Doyle 2001). One potential reason for this is that even in case of a large number of brands the model remains parsimonious. Also, one can argue based on economic theory that the price parameter should be equal across brands because the price effect in the (indirect) utility function comes from the budget constraint of the household, where the values of the brands enter in monetary units (Chandukala et al. 2008). However, the utility function (2) can also account for alternative-specific covariate effects if x is defined as follows (see, e.g., Erdem et al. 2008 for a marketing application of a brand choice model with brand-specific covariate effects): The column vector $\varvec{x}_{knt}$ contains the J stacked values of covariate k from household n at choice occasion t. We then create the J × J diagonal matrix $\varvec{X}_{knt}$ by inserting $\varvec{x}_{knt}$ on the diagonal (i.e., $\varvec{X}_{knt} = {\text{diag}}$($\varvec{x}_{knt}$)). Accordingly, $\varvec{X}_{knt}$ contains J “expanded” covariate vectors as columns, where only the jth entry is nonzero, and thus, the corresponding J parameters for the covariate k are brand-specific. In our empirical application, we examine whether such a model specification leads to additional insights and a better out-of-sample fit (see Sect. 3.4.4).

The random error term ɛ_njt captures unobserved influences not covered by the data. We obtain the MNL model for i.i.d. standard extreme value distributed error terms.³ Accordingly, the choice probability Pr_nit of household n for brand i at purchase occasion t results as (e.g., McFadden 1974; Train 2009):

$$ { \Pr }_{nit} = { \exp }\left( {V_{nit} } \right)/\mathop \sum \limits_{j = 1}^{J} { \exp }(V_{njt} ) . $$

(3)

As the choice probability is invariant to adding a constant value to the deterministic utility, only differences in utilities can be identified. For estimation, we, therefore, set one of the J brand intercepts to zero. Without loss of generality, we choose brand 1 in our empirical application to constitute this reference brand.

Note that our model does not account for endogeneity of covariates (Villas-Boas and Winer 1999; Petrin and Train 2010) and unobserved consumer heterogeneity (Kamakura and Russel 1989; Jain et al. 1994). Both aspects can be relevant in a brand choice context; however, adding household-specific parameters largely increases the computational burden for the proposed nonparametric approach in an application with several thousand households (like ours), and accommodating endogeneity may lead to worse results than ignoring endogeneity if suitable instruments are not available (Rossi 2014). Further note that we incorporate the dynamic constructs brand loyalty and reference price in our empirical application (see Sect. 4 for more details). Both covariates are household specific and hence account for heterogeneity in choice behavior to a certain degree (Guadagni and Little 1983; Kalyanaram and Little 1994).

2.2 MNL models with time-varying parameters

The standard MNL model [Eq. (3)] completely ignores potential time dependencies of a household’s brand choice decisions over successive purchase occasions. Consequently, each household’s observations are treated as independent over time, and coefficients are assumed to be constant over the entire observation period. To allow for time-varying parameters in the MNL model, we introduce time dependency for both brand intercepts and covariate effects.

First, we allow for time-varying brand intercepts by replacing the parametric brand intercepts α_j with (a priori unknown) smooth time-dependent functions f ^α _j (τ), leading to the utility function

$$ U_{njt} = f_{j}^{\alpha } \left( {\tau_{nt} } \right) + \mathop \sum \limits_{k = 1}^{K} \beta_{k} \cdot x_{knjt} + \varepsilon_{njt} . $$

(4)

That way, the brand intercepts can accommodate changes in intrinsic brand utilities across calendar time (τ), which might be caused by long-term trends or short-term fluctuations in brand choice behavior. Notice that for each household n the purchase occasion t takes place at a specific time τ_nt and in our empirical application τ indexes weeks. In most cases, however, the tth purchase occasion takes place at different τ across households. Nevertheless, one household might purchase multiple times within the same τ and, of course, several households can purchase within the same τ. For such observations, the value of f ^α _j (τ) is the same.

Further, we allow for time-varying effects of covariates by replacing the K time-constant effects β_k with (a priori unknown) smooth time-dependent functions f ^β _k (τ), too:

$$ U_{njt} = f_{j}^{\alpha } \left( {\tau_{nt} } \right) + \mathop \sum \limits_{k = 1}^{K} f_{k}^{\beta } \left( {\tau_{nt} } \right) \cdot x_{knjt} + \varepsilon_{njt} . $$

(5)

Accordingly, we will be able to explore if effects of marketing instruments (like price) or if effects of time-varying behavioral covariates (like brand loyalty and reference price) are changing over time. Since the unknown time-varying functions for both brand intercepts and covariate effects will be modeled nonparametrically using P(enalized)-splines while the error term as before follows a parametric distribution (i.i.d. standard extreme value distributed error terms), the utility functions (4) and (5) can be referred to as semiparametric models.

Like in the basic parametric MNL model, brand 1 is treated as the reference brand for identifiability reasons (i.e., setting f ^α₁ (τ) = 0). Therefore, the estimated trajectories of the time-dependent functions f ^α _j (τ) for j ≠ 1 have to be interpreted w.r.t. brand 1. We chose brand 1 as the reference brand in our empirical application because it showed the least variation over time and hence this choice facilitates a straightforward interpretation of the results.

2.3 Penalized splines

P(enalized)-splines originally introduced by Eilers and Marx (1996) have been previously used as a nonparametric technique to flexibly estimate effects of covariates in a retailing context. Most of those applications, however, focused on aggregate retail scanner data and were concerned with price response modeling (e.g., Steiner et al. 2007; Brezger and Steiner 2008; Weber and Steiner 2012; Haupt et al. 2014; Lang et al. 2015; Weber et al. 2017). To the best of our knowledge, only one approach so far applied P-splines in the context of disaggregate scanner panel data in order to estimate nonlinear price–utility effects (Kneib et al. 2007).

The idea of P-splines in the present context is to represent the time-varying functions f(τ) (dropping the indices for simplicity) in terms of a high-dimensional parametric basis and to add an appropriate penalty term to the likelihood for the sake of regularisation. Specifically, we assume that the unknown function f(τ) can be approximated by B-spline basis functions with equally spaced intervals within the considered time horizon, leading to

$$ f\left( \tau \right) = \mathop \sum \limits_{m = 1}^{M} \gamma_{m} \cdot B_{m} \left( {\tau ;\delta } \right), $$

(6)

with B_m(τ; δ) representing the mth B-spline basis functions of degree δ and γ_m denoting the regression coefficient to be estimated for the mth B-spline basis function (see De Boor 2001). As our default choice, we suggest cubic splines (i.e., B-splines with δ = 3), because cubic splines are twice continuously differentiable and therefore visually smooth. The use of cubic splines is also fairly standard for smoothing in generalized additive models, see, for example, Wood (2017). However, in some situations the resulting functions may turn out “too” smooth and more flexibility can be achieved using lower degrees for the spline (see Fahrmeir et al. 2013). Eilers and Marx (1996) have suggested using a “relatively large” number of intervals to ensure enough flexibility for the unknown functions on the one hand, which allows in the context of our problem setting to capture, for example, short-term fluctuations in consumers’ brand choice behavior. We first use M = 40 equidistant intervals in our empirical application (with T = 50) as a default choice and subsequently provide some sensitivity analyses to evaluate the effect of different numbers of M on the results.⁴ On the other hand, the authors recommended adding a penalty term to the likelihood to enforce sufficient smoothness for the estimated curve and to avoid overfitting. A suitable penalty term can be derived from squared rth-order derivatives, and according to B-spline theory (see, e.g., De Boor 2001), we can approximate the derivative penalty with a roughness penalty based on first- or second-order differences on adjacent regression coefficients γ_m leading to the penalty terms $\lambda \sum\nolimits_{m = 2}^{M} {\left( {\gamma_{m} - \gamma_{m - 1} } \right)^{2} }$ or $\lambda \sum\nolimits_{m = 3}^{M} {\left( {\gamma_{m} - 2 \gamma_{m - 1} - \gamma_{m - 2} } \right)^{2} }$, respectively.

The so-called smoothing parameter $\lambda \ge 0$ controls the trade-off between too much flexibility (λ small) and sufficient smoothness (λ large) of the P-spline. For statistical inference, as discussed subsequently, the compact representation of the difference penalties in terms of quadratic forms $\lambda \varvec{\gamma^{\prime}P}_{{\left( \varvec{r} \right)}}\varvec{\gamma}$ will be helpful, where the vector $\varvec{\gamma}$ contains the M regression coefficients γ_m and $\varvec{P}_{{\left( \varvec{r} \right)}} = \varvec{D}_{\left( r \right)}^{'} \varvec{D}_{\left( r \right)}$ corresponds to the penalty matrix constructed from the first- or second-order difference matrix

$$ \varvec{D}_{\left( 1 \right)} = \left( {\begin{array}{*{20}c} { - 1} & { 1} & {} & {} & {} \\ {} & { - 1} & 1 & {} & {} \\ {} & {} & \ddots & \ddots & {} \\ {} & {} & {} & { - 1} & 1 \\ \end{array} } \right)\quad {\text{and}}\quad \varvec{D}_{\left( 2 \right)} = \left( {\begin{array}{*{20}c} 1 & { - 2} & 1 & {} & {} & {} \\ {} & 1 & { - 2} & 1 & {} & {} \\ {} & {} & \ddots & \ddots & \ddots & {} \\ {} & {} & {} & 1 & { - 2} & 1 \\ \end{array} } \right). $$

(7)

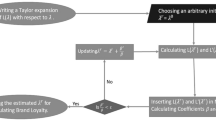
Figure 1 illustrates the fit of a penalized spline along Gaussian response data.⁵ The upper left panel shows some simulated data (gray circles) and the true underlying function (dashed line), i.e., the data-generating mechanism. The upper right panel shows a full set of 40 B-spline basis functions of degree 3 (i.e., cubic splines) superimposed to the data. Estimating the unknown regression coefficients $\gamma_{m} \left( {m = 1, \ldots , 40} \right)$ from the data implies nothing else than weighting each of the B-spline basis functions B_m according to the data, resulting in positive weights (regression coefficients) in areas with positive data and negative weights in areas with negative data (left panel, middle row).

Fig. 1

Working of the P-spline approach (based on Fahrmeir et al. 2013)

Summing up the weighted B-spline basis functions [i.e., computing the linear combination $\sum\nolimits_{m = 1}^{40} {\gamma_{m} } B_{m} \left( {\tau ;3} \right)$ given by Eq. (6)] yields an unpenalized spline fit f(τ) (solid gray line) with much variability due to the variation of the B-spline basis functions (right panel, middle row). When eventually imposing the penalty term and switching from B-splines to P-splines, adjacent B-spline basis functions are coupled to each other in their magnitudes and the estimated regression coefficients vary smoothly over the domain of the covariate (lower left panel). As a consequence, the curve estimate is much smoother and—for an optimized value of 1.122 for the smoothing parameter (using the methodology outlined in Sect. 2.4)—approximately coincides with the true function (lower right panel).

The P-spline framework has several strengths and advantages. First, the approach is “data driven” in the sense that flexible time-varying functions along with their corresponding smoothing parameters are estimated from the data (see next subsection). Hence, the researcher does not need to have prior knowledge about the shape of specific parameter evolutions or how smooth or volatile these functions are. This is in particular beneficial in cases where time-varying parameter trajectories are complex. Second, using a large number of knots enables the researcher to approximate even complex time-varying functions reasonably well, but because of the penalization, the framework is in addition extremely robust, thereby guarding against overfitting. Third, the researcher can still modify certain settings beyond the number of knots (i.e., the degree of the spline and the order of penalization), increasing further the capabilities of the approach. A higher number of knots, as well as a lower degree of the spline or a lower order of penalization, ceteris paribus increase the flexibility for the estimation of time-varying parameters. In particular, using a B-spline with degree zero, a first-order penalty term, and as many knots as time periods enables an approximation of a state-space model with random walk parameter dynamics (Fahrmeir et al. 2013, p. 452). Hence, using such a specification, we can “mimic” state-space brand choice models (Kim et al. 2005; Lachaab et al. 2006) which are typically estimated using the Kalman Filter (or its nonlinear variations).⁶

2.4 Statistical inference

Statistical inference of the flexible time-varying parameter MNL model is based on maximizing the penalized log-likelihood

$$ LL_{\text{pen}} \left( {\varvec{\gamma},\varvec{\lambda}} \right) = LL\left(\varvec{\gamma}\right) - \mathop \sum \limits_{j = 2}^{J} \lambda_{j}^{\alpha }\varvec{\gamma}_{j}^{{\varvec{\alpha '}}} \varvec{P}_{{\left( \varvec{r} \right)}}\varvec{\gamma}_{j}^{\varvec{\alpha}} - \mathop \sum \limits_{k = 1}^{K} \lambda_{k}^{\beta }\varvec{\gamma}_{k}^{\beta '} \varvec{P}_{\left( r \right)}\varvec{\gamma}_{k}^{\beta } , $$

(8)

where j and k index brands and covariates, respectively, the vector $\varvec{\gamma}= \left( {\varvec{\gamma}_{2}^{\varvec{\alpha}} , \ldots ,\varvec{\gamma}_{J}^{\varvec{\alpha}} ,\varvec{\gamma}_{1}^{\beta } , \ldots ,\varvec{\gamma}_{K}^{\beta } } \right)$ captures the regression coefficients related to the time-varying effects $f_{2}^{\alpha } \left( \tau \right), \ldots , f_{J}^{\alpha } \left( \tau \right),f_{1}^{\beta } \left( \tau \right), \ldots ,f_{K}^{\beta } \left( \tau \right)$, and $LL\left(\varvec{\gamma}\right)$ is the log-likelihood of the MNL model

$$ LL\left(\varvec{\gamma}\right) = \mathop \sum \limits_{n = 1}^{N} \mathop \sum \limits_{t = 1}^{{T_{n} }} \mathop \sum \limits_{j = 1}^{J} y_{njt} \ln \left( {Pr_{njt} \left(\varvec{\gamma}\right)} \right). $$

(9)

In Eq. (9), y_njt is a dummy variable indicating whether household n chooses brand j at purchase occasion t. Each time-varying effect is assigned a separate smoothing parameter (stacked in the vector $\varvec{\lambda}$), implying that each of the functions can accommodate a different amount of smoothness. The smoothing parameters are determined based on restricted maximum likelihood (REML) estimation via a mixed model representation of penalized splines [see Kneib et al. (2007) and Guhl et al. (2018) for details]. The basic idea is to recast the P-splines as a mixed model where the smoothing parameter turns into a variance component which can then be estimated from the corresponding marginal (or restricted) likelihood. This restricted maximum likelihood estimation approach is now well established in statistics for determining smoothing parameters (Ruppert et al. 2003; Fahrmeir et al. 2004; Wood 2017). In particular, when re-estimating the model with the same model specifications, one will always end up with exactly the same smoothing parameter estimates. Of course, there are alternatives such as generalized cross-validation that will yield (often only slightly) different results. Given the smoothing parameters, estimation of the penalized MNL can be achieved by a simple modification of the usual Fisher scoring algorithm. A detailed description of the Fisher scoring algorithm for exponential family generalized additive models is provided in Fahrmeir et al. (2004), while the extension to categorical regression settings is described in Kneib and Fahrmeir (2006).

3 Empirical study

3.1 Data

In this section, we present results from an empirical application of our proposed framework to a household panel dataset referring to the product category coffee. The coffee data were provided by the GfK group in Nuremberg, Germany, and we chose this product category because employees of market research companies reported considerable fluctuations in brand shares in the run-up of events like Christmas.⁷ The dataset provides information on the date of the households’ purchase occasions, the brand chosen by a household as well as observed (paid) prices. The raw dataset includes 49,083 purchases of 6407 German households for the five largest national brands of ground coffee over a time span of all 53 weeks in the year 1998. The five national brands account for 75% of all purchases of national coffee brands, and we focus on these five brands since they were available in the assortment of all retailers covered by the data and have as a rule the standard pack size of 500 g.

We use the first three purchases of each household (in sum 12,549 purchases) to initialize the dynamic constructs brand loyalty and reference price that we consider as additional covariates (see the next subsection). Consequently, we discard households with a total of only three or fewer purchases during the whole year 1998 from our analysis (2224 households with 4057 brand purchases). Furthermore, we exclude the first three weeks from the analysis because of the very low number of observations (9 purchases) left after the initialization step. The remaining 4183 households made on average 8 coffee purchases (Q_0.25 = 3 and Q_0.75 = 11; excl. the first three purchases used for initialization of the dynamic covariates), and the median interpurchase time is about 28 days (Q_0.25 = 19 and Q_0.75 = 42). The final dataset contains 32,468 purchases from the 4183 households, and we split these observations randomly into an estimation and validation sample of roughly the same size (16,233 and 16,235). Table 1 shows for each brand the mean price and the standard deviation of prices for 500 g coffee, which is the typical package size in the German market. The table also contains information on the final estimation and validation samples we used to assess the statistical performance of the analyzed brand choice models (with and without time-varying parameters).

Table 1 Summary statistics for the coffee dataset (4183 households; 50 weeks)

Brand 1 has the highest number of purchases, followed by brands 2 and 3. There is no really dominating brand in terms of market share, and shares of the five brands lie between 10 and 30%. Brands 3 and 5 are slightly less expensive (below 8 DM/500 g) as compared to brands 1, 2, and 4. However, the standard deviations of prices indicate that the distribution of prices across brands overlaps to some extent and hence the price positioning of the brands is fairly comparable.⁸ Further, the magnitude of the standard deviations of the price attribute indicates that brand prices vary considerably in the ground coffee category, and a significant part of this variation can be attributed to promotions.⁹

To assess the performance of the MNL models with time-varying parameters, we employ a prediction-oriented approach. In our opinion, a more complex model (like an MNL model with time-varying parameters) should be preferred only if it outperforms a more parsimonious model in validation samples. Because we are interested in the evolution of parameter paths over time, we randomly split our observations in the dataset across all weeks. Each observation of each household has the same probability of 50% of being in the estimation or validation sample, irrespective of its position in the choice sequence and point in time when it occurred. This enables us to evaluate whether estimated parameter dynamics also persist in the validation sample or whether flexible models just pick up random fluctuations in the time dimension (e.g., due to a specific sample composition in a particular week). As given in Table 1, the distribution of the market shares of the brands is very similar in the estimation and validation samples after splitting the dataset randomly into two halves.

3.2 Specification of covariates

Whereas observed prices are readily available from our data, brand loyalties and reference prices have to be computed from each consumer’s purchase history. Previous research has documented the importance of incorporating purchase event feedback effects in brand choice models (Ailawadi et al. 1999), and following Guadagni and Little (1983), we recursively calculated loyalty values by exponentially smoothing past purchases y_nj,t−1 of brand j made by household n at purchase occasion t − 1 using smoothing constant $\theta_{\text{loy}}$ according to:

$$ {\text{loyalty}}_{njt} = \theta_{\text{loy}} \cdot {\text{loyalty}}_{nj,t - 1} + \left( {1 - \theta_{\text{loy}} } \right) \cdot y_{nj,t - 1} , $$

(10)

where y_nj,t−1 = 1, if household n purchased brand j on her/his last store visit (otherwise y_nj,t−1 = 0), $\sum\nolimits_{j = 1}^{J} {{\text{loyalty}}_{njt} } = 1$, and $\theta_{\text{loy}}$ ($0 \le \theta_{\text{loy}} \le 1$) determining the general persistence of brand loyalty. Using a grid search based on the standard MNL model, we obtained a value of $\theta_{\text{loy}} = 0.75$ which is close to estimated values reported in other applications (e.g., Briesch et al. 1997). The exponential smoothing approach of Guadagni and Little has shown its high ability to increase model fit and predictive performance in many applications and has been widely used in the marketing literature to capture brand loyalty (see, e.g., Ailawadi et al. 1999). We initialize the loyalty variable for each brand and household at t = 0, with a value of $0. 2$ (i.e., ${\text{loyalty}}_{nj0} = 1/J$ or equal market shares across brands).

It is also well established to incorporate reference price terms in brand choice models (Kalyanaram and Winer 1995). Reference prices constitute internal prices consumers have in their mind and compare observed prices to when shopping for brands. Consequently, similar to observed prices, lower (higher) reference prices are associated with higher (lower) choice probabilities. Observed prices lower than the reference price are perceived as gains and may additionally stimulate a purchase, whereas observed prices higher than the reference price are perceived as losses and should further decrease choice probabilities. Prospect theory posits asymmetric effects of gains and losses, and that consumers should be more responsive to losses than to gains (Kahneman and Tversky 1979). Accordingly, two additional price terms representing those losses and gains should be considered in brand choice models to allow for different effect sizes of gains and losses. Researchers have provided conflicting empirical results about the existence of (asymmetric) reference price effects. For example, Kalyanaram and Little (1994) and Bell and Lattin (2000) found no empirical support for asymmetric reference price effects, while Abe’s (1998, 1999) estimation results were in accordance with prospect theory.

We follow the widespread framework of adaptive expectations to build a household’s reference prices (refprice) based on the household’s purchase history (e.g., Lattin and Bucklin 1989; Briesch et al. 1997; Abe 1998):

$$ {\text{refprice}}_{njt} = \theta_{\text{ref}} \cdot {\text{refprice}}_{nj,t - 1} + \left( {1 - \theta_{\text{ref}} } \right) \cdot {\text{price}}_{nj,t - 1} , $$

(11)

where $0 \le \theta_{\text{ref}} \le 1$. Once the reference price of household n for brand j and purchase occasion t is determined, gains and losses can be computed as ${\text{gain}}_{njt} = { \hbox{max} }\left( {{\text{refprice}}_{njt} - {\text{price}}_{njt} ,0} \right)$ and ${\text{loss}}_{njt} = { \hbox{max} }\left( {{\text{price}}_{njt} - {\text{refprice}}_{njt} ,0} \right)$, respectively. To determine the smoothing constant $\theta_{\text{ref}}$, we again used a grid search based on the standard MNL model with constant parameters and obtained a value of $\theta_{\text{ref}} = 0.57$. This value is similar to results reported in the relevant literature (e.g., Briesch et al. 1997). Reference prices are initialized for each brand with observed prices at the first purchase occasion of each household.

We follow Kalyanaram and Little (1994) and include refprice, gain, and loss as price covariates. Considering both refprice, gain, loss and observed price would result in perfect collinearity by definition since gain and loss are linear transformations of reference price and price. We chose to incorporate reference prices instead of observed prices because of much lower (absolute) correlations of refprice with gains and losses as compared to price with gains and losses, which in turn improves the statistical efficiency (smaller standard errors).

Altogether, all model specifications considered in our empirical application include brand intercepts, and reference price, gain, loss, as well as loyalty as covariates. Effects on deterministic utilities and brand choice probabilities are expected to be positive for gains and brand loyalties. On the other hand, the effects of reference prices and losses are supposed to be negative. If no additional effect of gain or loss would exist, reference prices should be equal to observed price and, hence, we expect the isolated effect of reference prices (analogously to observed price) to be negative. In addition, according to prospect theory, the effect of gains should be smaller than that of losses (in absolute terms). Also note that all covariates are household specific. Therefore, even though we do not account for unobserved heterogeneity in parameters, these covariates help to explain differences in choice behavior across households w.r.t. brands and prices. Furthermore, all four covariates are dynamic: They vary over time and link purchase occasions. Hence, they help to understand inter-temporal correlations in choice behavior and make sure that if we find time-varying parameters that this variation is not an artifact because of omitted dynamic constructs.

3.3 Statistical measures for model comparison

For model comparison, we employ several statistical performance measures. We use more than one measure because different measures have different properties and multiple measures contribute to the confidence of a model’s performance. In particular, we apply the log-likelihood, Brier score, and spherical score as individual scoring rules to assess model fit and predictive validity. All three measures are strictly proper and well established in the statistical literature (Gneiting and Raftery 2007; Kneib et al. 2007). Moreover, it seems promising to aggregate choice probabilities to market shares to get a more holistic view of the brand choice behavior of the households. Accordingly, we use the average root mean squared error (ARMSE) in market shares as a scoring rule on the aggregate level. The measures are computed as follows:

$$ { \log } {-} {\text{likelihood}} = \mathop \sum \limits_{{{\text{n}} = 1}}^{\text{N}} \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{T}}_{\text{n}} }} { \ln }\left( {\widehat{ \Pr }_{\text{nit}} } \right), $$

(12)

$$ {\text{Brier score}} = - \mathop \sum \limits_{{{\text{n}} = 1}}^{\text{N}} \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{T}}_{\text{n}} }} \mathop \sum \limits_{{{\text{j}} = 1}}^{\text{J}} \left( {{\text{y}}_{\text{njt}} - \widehat{ \Pr }_{\text{njt}} } \right)^{2} , $$

(13)

$$ {\text{Spherical score}} = \mathop \sum \limits_{{{\text{n}} = 1}}^{\text{N}} \mathop \sum \limits_{{{\text{t}} = 1}}^{{{\text{T}}_{\text{n}} }} \frac{{\widehat{ \Pr }_{\text{nit}} }}{{\sqrt {\mathop \sum \nolimits_{{{\text{j}} = 1}}^{\text{J}} \left( {\widehat{ \Pr }_{\text{njt}} } \right)^{2} } }},\,{\text{and}} $$

(14)

$$ {\text{ARMSE}} = \frac{100}{J}\mathop \sum \limits_{j = 1}^{J} \sqrt {\frac{1}{\rm T}\mathop \sum \limits_{\tau = 1}^{\rm T} \left( {{\text{ms}}_{j\tau } - \widehat{\text{ms}}_{j\tau } } \right)^{2} } , $$

(15)

with i denoting the brand household n has chosen on purchase occasion t. Whereas the log-likelihood only considers the logs $\widehat{\Pr }_{nit}$ of brands chosen by households (but not of the brands not chosen by households), Brier and spherical scores utilize the entire predictive distribution of choice probabilities (i.e., $\widehat{\Pr }_{n1t} , \ldots , \widehat{\Pr }_{nJt}$) computed according to the estimated model (see Gneiting and Raftery 2007 for more details). In other words, the log-likelihood does only partly utilize the information contained in the predictive distribution and therefore is rather sensitive w.r.t. extreme observations.

ms_jτ denotes the actual market share of brand j in week τ (computed from observed brand purchases), and predicted market shares $\widehat{\text{ms}}_{j\tau }$ are computed as the average of predicted choice probabilities of households with a purchase act in week τ. We expect the ARMSE to be less sensitive to differences (and errors) on the household level because the predicted household probabilities are aggregated first before calculating the errors. This measure is in particular important for retailers because predicted market shares are relevant for category management, inventory decisions, and marketing mix optimization.¹⁰

Since more complex models are generally expected to perform better in-sample (but not necessarily out-of-sample), we further compute AIC and BIC based on in-sample log-likelihoods to penalize the model complexity and to provide a fair comparison of the different models in the estimation sample. For parametric models, the penalty term is simply based on the number of model parameters, while for the semiparametric models the effective number of parameters has to be determined (see Fahrmeir et al. 2013, p. 474).¹¹ Finally, we also report computational times needed for estimation, as this might be a relevant criterion for practitioners, too.

3.4 Discussion of results

In the following, as the number of compared models is rather large, we discuss our estimation results in several steps. First, we compare models with time-varying parameters (for brand intercepts only, for covariate effects only, for both) with the standard (static) MNL model (Sect. 3.4.1). Next, we compare the results with some dynamic benchmark models that do not use P-splines (e.g., models with deterministic seasonal effects, the nonparametric model of Baumgartner 2003) (subsection 3.4.2). Subsequently, we analyze in a sensitivity analysis the influence of different numbers of knots (i.e., ranging from 10 to 50) in the MNL model with time-varying parameters and continue by assessing the impact of varying degrees of P-splines (i.e., zero degree versus third degree) as well as different orders for the roughness penalty (i.e., first order versus second order) on the model performance (Sect. 3.4.3). Lastly, we analyze models (with and without parameter dynamics) where all covariate effects are allowed to be alternative or brand specific (instead of generic, Sect. 3.4.4).¹² In the following, we concentrate our discussion of results on the estimated time-varying parameters and abstain from the interpretation of results for time-constant parameters which are also part of some of the models. The corresponding results, as well as the estimated smoothing parameters of all P-spline MNL models, can be obtained from the authors upon request.

3.4.1 Time-varying parameter MNL models

Table 2 summarizes the performance measures for the standard MNL model versus the competing flexible models with either time-varying brand intercepts (MNLTVP1_i), or time-varying (generic) covariate effects (MNLTVP1_c), or both (MNLTVP2).

Table 2 Model comparison (MNL, MNLTVP1_i, MNLTVP1_c, and MNLTVP2)

As expected, the more flexible models yield an improved (unpenalized) fit in the estimation sample, with the most flexible MNLTVP2 model (all parameters are time varying) performing best according to all scoring rules (compared to the standard MNL with a relative improvement of about 2% for the log-likelihood and an absolute improvement of 1% in market share prediction, for example). Somewhat surprisingly, the improvement in fit of the MNL model with time-varying brand intercepts (MNLTVP1_i) over the standard MNL model is higher as compared to the improvement in fit of the MNL model with time-varying covariate effects (MNLTVP1_c). This holds for all four scoring rules. One potential reason for this finding might be the fact that the MNLTVP1_c model assumes generic covariate effects (i.e., homogeneous across brands), and in case of brand-specific covariate effects, a different picture might be obtained. We extend our comparison to such models in Sect. 3.4.4.¹³ Based on the ARMSE measure the model with time-varying brand intercepts (MNLTVP1_i) performs de facto as good as the model where all parameters are allowed to vary over time (MNLTVP2).

A real test whether the flexible MNL models actually outperform the standard MNL model consists of a comparison of model performances in holdout (validation) samples. Here, all tendencies observed in the estimation sample are confirmed. In particular, there is an improvement in predictive validity for all time-varying parameter MNL models over the standard MNL model. Furthermore, the fully time-dependent MNLTVP2 model provides the highest predictive validity according to all scoring rules (compared to the standard MNL with a relative improvement of still 1% for the log-likelihood and an absolute improvement of 0.45 in the ARMSE measure, for example). Again, the gain in predictive validity is higher when allowing for time-varying brand intercepts instead of (generic) time-varying covariate effects only.

Using information criteria for assessing the model fit provides somewhat different results. Whereas AIC supports a higher model complexity and favors as before the most complex MNLTVP2 model, the BIC instead tends to the standard MNL model without time-varying parameters. This conflicting finding can be explained by the fact that the BIC penalizes the complexity of a model much more strongly by considering (among others) the sample size for the penalty term, which is very large in our case. Since the out-of-sample performance also improves considerably for all models with time-varying parameters, we conclude that accounting for time-varying parameters pays off in the ground coffee category and that changes in consumer behavior over time are obviously inherent to the data. Stated otherwise, we believe that the penalization via BIC is too strong in our context.

Figure 2 depicts estimated coefficients, with calendar time τ (in weeks) on the horizontal axis and estimated coefficients for brand intercepts or covariate effects on the vertical axis. The solid lines represent point estimates of the most flexible MNLTVP2, whereas the dashed lines refer to the constant coefficients from the estimated standard MNL model. Also shown are the 95% pointwise confidence intervals (shaded intervals) for the time-varying parameters. For the brand intercepts, we use the same range of scale for the y-axis to facilitate comparisons and further plotted the zero line corresponding to the intercept of brand 1 which constitutes the reference brand. Hence, the variation of the reference brand over time is implicitly included in the intercepts of brands 2 to 5.

Fig. 2

Parameter estimates (MNL versus MNLTVP2)

The top four diagrams show the estimated brand intercepts for the coffee brands 2 to 5. Concerning the time-varying intercepts of coffee brands 2 and 4, we obtain rather smooth curves suggesting long-term trends in the development of the intrinsic brand utilities. Specifically, while the brand intercepts of brands 1 and 2 were almost on the same level at the beginning of the year, the intrinsic utility of brand 2 increased during the first half of the year and then stabilized at this higher level toward the end of the year. Also, brand 4 slightly gains in brand utility compared to brand 1 in the second half of the year (after a loss in utility in the first half of the year). If the firm offering brand 1 would be aware of those developments early enough, it could react in due time to strengthen its own position or at least to prevent a further loss in consumer preference. For coffee brands 3 and 5, in contrast, we obtain a completely different pattern regarding the evolution of the brand intercepts. The estimated curves are very wiggly and reveal a lot of short-term fluctuations. Analyzing the local up- and downturns in time, we found that the most distinct local minima of the curves occurred in the run-up to (i.e., one or two weeks before) important festive occasions like Easter (week 14), Pentecost (week 21), or Christmas (week 51). This indicates that coffee brands 3 and 5 are not perceived to be first class brands for festive days. Furthermore, the intrinsic utilities of those brands are lower than that of brand 1 (the reference brand) almost throughout the year. The bottom four diagrams refer to the covariates included in the model. The estimated coefficients for refprice and loss show the expected negative signs and the estimated coefficient for gain the expected positive sign throughout the observation period. The (negative) reference price coefficient decreases over the year indicating an increasing price sensitivity of consumers. This increased price sensitivity comes along with an increasing responsiveness toward gains (at least in the first and last 4 months in the year) and a decreasing responsiveness toward losses. We assign the increased price sensitivity of consumers to an overall decreasing price level for all five coffee brands over the year. We further find asymmetric reference price effects for gains and losses. For example, toward the end of the year, we observe an increasing responsiveness concerning gains but a decreasing responsiveness concerning losses. An explanation for this asymmetry is that decreasing price levels for brands over time involve increased gains for consumers. The result of an increased price sensitivity also coincides with our finding of a decreasing impact of brand loyalty on choice probabilities.

A comparison with the estimated parameters of the standard MNL model reveals that the constant parameters of the MNL model can be considered as average values of the time-varying parameters of the MNLTVP2 model. We conclude that models with time-varying parameters fit and predict the data better compared to models with constant parameters (except for BIC) and that the resulting parameter trajectories are informative and insightful.

3.4.2 Further benchmark MNL models

The discussion of results in the previous subsection has revealed that (a) seasonal effects play a major role in the coffee category (brands 3 and 5) and (b) time-varying brand intercepts have a larger impact on model fit (in- and out-of-sample) than time-varying covariate effects. Therefore, we next compare the results of the previously most flexible MNLTVP2 model with simpler, but still dynamic benchmark models that explicitly account for seasonal effects or exclude time-varying covariate effects. Firstly, we estimate an MNL model with constant parameters but with brand-specific dummy variables for the seasonal effects of Easter, Pentecost, and Christmas (MNLS). This model is readily applicable because the corresponding dates for the festive occasions are known a priori. The MNLS model should be a reasonable benchmark candidate because, as discussed above, seasonal effects seem to differ across brands. Hence, brand-specific dummies are an option to capture seasonal effects per brand. Furthermore, we estimate the model of Baumgartner (2003), referred to as MNLTVPB, which is comparable to our MNLTVP1_i as it also models time-varying brand intercepts nonparametrically. However, it employs a different form of splines (i.e., thin-plate splines instead of P-splines) and uses a different estimation strategy (i.e., a grid search over all possible values for the degrees of freedom, and conditional on a particular value for the degrees of freedom the iterative algorithm of Abe (1999) for estimating the brand choice model as a generalized additive model). Lastly, we calibrate an MNL model with brand–week fixed effects (MNLTVPFE). Hence, brand intercepts are allowed to vary weekly without any restrictions. The latter model represents the most flexible model for the brand intercepts, and we expect this model to suffer from overfitting, which should be reflected by a worse out-of-sample performance. Table 3 summarizes the comparison of these four models.

Table 3 Model comparison (MNLTVP2, MNLS, MNLTVPB, and MNLTVPFE)

First of all, the MNLS model with parametric seasonal effects fits the data clearly better in- and out-of-sample as compared to the static MNL (cf. Table 2, but worse than the MNLTVP2). This indicates that the seasonal effects are indeed important for the choice of coffee brands. On a side note, the estimates for the seasonal effects are − 0.42 (se = 0.16) for brand 2, − 0.85 (se = 0.11) for brand 3, − 0.33 (se = 0.11) for brand 4, and − 1.34 (se = 0.16) for brand 5. Hence, we here also find statistically significant seasonal effects for brands 2 and 4 (compared to the reference brand 1). The seasonal effects are, however, strongest for brands 3 and 5, replicating the results of the flexible models in Sect. 3.4.1. Also, note that the MNLS model has a better AIC and BIC than the standard MNL model without seasonal effects. Second, the MNLTVPB model of Baumgartner (2003) showed the best out-of-sample fit regarding the log-likelihood for 42 degrees of freedom, and hence, we only refer to the results conditional on this df value in Table 3. Most interestingly, this model clearly outperforms the proposed MNLTVP2 model. This finding indicates that the MNLTVP2 model with only 40 knots might not be flexible enough to capture the variation in brand intercepts for the coffee data. Also, it might be the case that the choice of the degree of the splines (i.e., cubic splines) or the order of penalization (i.e., the second-order penalty) limits the flexibility. We will explore both points in the next subsections. Third, the MNLTVPFE model with brand–week fixed effects shows by far the best in-sample fit, as expected. In particular, it has an ARMSE value of 0 because it can perfectly fit the aggregated data (i.e., market shares) on the brand/week level. Out-of-sample it performs, however, marginally worse than the MNLTVPB model of Baumgartner (2003) which shows the best predictive performance across all four models. The results for the information criteria resemble those of Table 2. While the AIC favors the model with the largest number of parameters (MNLTVPFE), the BIC tends to the most parsimonious model (MNLS).

Figure 3 contrasts the estimated time-varying brand intercepts resulting from the MNLTVP2 model with those obtained from the MNLTVPFE model. We abstain from depicting the trajectories of the brand intercepts for the model of Baumgartner (MNLTVPB), since the latter virtually coincide with those of the MNLTVPFE model. As expected, the fixed-effects MNL model has very volatile brand intercepts. This holds not only for brands 3 and 5, where the results are quite similar compared to the estimates of the MNLTVP2 model, but also for brands 2 and 4. While the MNLTVP2 model captures the long-term trends in intrinsic brand utilities, the fixed-effects model now also fits extreme week-to-week variation. However, we cannot find any additional meaningful seasonal patterns for those two brands.

Fig. 3

Parameter estimates (MNLTVPFE versus MNLTVP2)

3.4.3 Sensitivity analysis: number of knots, degree of spline, and order of penalization

The P-spline models used so far (MNLTVP1_i, MNLTVP1_c, MNLTVP2) were based on 40 knots in a dataset with 50 distinct time periods. As described before, we think that this default setting works well in applications of time-varying models using scanner panel datasets of typical dimensions for two reasons: Through the penalization, the risk of overfitting is low, and the rather high number of knots enables the model to be flexible enough to detect reasonable parameter variation over time. However, the number of knots can influence the results, and therefore, we vary the number of knots next to gain more profound insights regarding this sensitivity. In particular, we re-estimate the best-performing model from Sect. 3.4.1 (the MNPTVP2 model) in addition with 10, 20, 30, and 50 knots. In order to save space, we only focus on the most extreme specifications (i.e., 10 and 50 knots) in the following.¹⁴

The estimated paths for the time-varying parameters of both models are depicted in Fig. 4. Interestingly, the main differences between the MNLTVP2 models with 10 and 50 knots almost exclusively apply to the intercepts of brands 3 and 5; all other time-varying effects turn out highly similar. This demonstrates that cubic P-splines are quite robust against too much variation and provide rather conservative estimates (50 knots, brands 2 and 4). On the other hand, specifying too few knots in case of actually volatile parameter paths provides too smooth trajectories that are not able to capture the short-term fluctuations (10 knots, brands 3 and 5). Of course, a higher number of knots involve longer computational times for estimation (cf. Table 4). For this reason, we do not recommend to start with the maximum number of knots (in particular if the number of weeks in the dataset is ≫ 50).

Fig. 4

Parameter estimates (MNLTVP2_10 versus MNLTVP2 _50)

Table 4 Model comparison (MNLTVP2_10, MNLTVP2_50, MNLTVP3_cubic/p1, MNLTVP3_zero/p2, and MNLTVP4)

Table 4 (columns 1 and 2) shows the fit and predictive validity statistics for the models. The numbers in Table 4 indicate that more knots lead to a better performance of the MNLTVP2 model both in- and out-of-sample. Consequently, the model with 50 knots has the best fit (also compared to the version with 40 knots, cf. Table 2), but also the model with only 10 knots slightly outperforms the standard MNL model with time-constant parameters in all four scoring rules (cf. Table 2). Therefore, accounting for time-varying effects seems crucial for the dataset at hand. As before, the AIC supports the most complex model (50 knots), while the BIC tends to the least flexible model (10 knots).

Please note that the performance measures are worse compared to both the model of Baumgartner (MNLTVPB) and the brand–week fixed-effects model (MNLTVPFE) even when using 50 knots (cf. Table 3). This is interesting because these two models only allow for time-varying brand intercepts. Stated otherwise, even though a higher number of knots increase the performance in- and out-of-sample, the MNLTVP2 model with 50 knots still lacks some flexibility that the models above provide. For this reason, we now analyze the impact of two additional settings for P-splines: the degree of the spline and the order of penalization. All subsequent models discussed in this subsection are specified with 50 knots.

Table 4 summarizes in columns 3 to 5 the estimation and validation results of three additional models: the MNLTVP2 model with cubic splines but first (instead of second)-order penalization (MNLTVP3_cubic/p1), a model with zero-degree (instead of cubic) splines and second-order penalization (MNLTVP3_zero/p2), and a model with zero-degree splines and a first-order difference penalty (MNLTVP4). The latter model corresponds to a state-space model with random walk parameter dynamics.¹⁵ Again, we observe that still higher model flexibility pays off: The most flexible MNLTVP4 model clearly outperforms all other model specifications across all performance measures, in particular out-of-sample. As before, the AIC supports the most flexible model (MNLTVP4), while the BIC is conservative and tends to the most parsimonious model (MNLTVP2). A comparison with Table 3 further reveals that the MNLTVP4 model now outperforms both the model of Baumgartner (MNLTVPB) and the brand–week fixed-effects model (MNLTVPFE). Importantly, the MNLTVP4 model provides not only a still better in-sample fit than the MNLTVPFE model (except for ARMSE), but also a somewhat better out-of-sample fit than the model of Baumgartner (MNLTVPB).

Figure 5 contrasts the time-varying parameter estimates obtained for the MNLTVP4 model with those resulting from the MNLTVP2 model with 50 knots. Concerning the brand intercepts (see the top four diagrams), we observe highly similar parameter paths for brands 3 and 5. For brands 2 and 4, the MNLTVP4 model identifies more “wiggly” parameter paths, similar to the MNLTVPFE model (see Fig. 3). However, a closer look reveals that the amplitudes of the parameter evolutions based on the MNLTVP4 model are considerably lower. Hence, even though the very flexible MNLTVP4 model captures weekly variation in the brand intercepts for brands 2 and 4, the model does not overfit due to its excellent out-of-sample performance at the same time (see Table 4).

Fig. 5

Parameter estimates (MNLTVP2 versus MNLTVP4)

The bottom four diagrams show the time-varying parameters of the covariate effects. While the trajectories for the refprice and loyalty effects are very similar for both models, gain and loss effects turn out more volatile for the MNLTVP4 model. Nevertheless, for these two covariates, the parameter paths of the less flexible MNLTVP2 at least capture the general courses of the trajectories (i.e., the long-term trends) obtained by the MNLTVP4 model. Importantly, except for some single weeks for the loss effect, the trajectories of the MNLTVP2 model for both gain and loss effects always lie within the 95% pointwise confidence intervals of the MNLTVP4 model.

3.4.4 Alternative-specific effects of covariates

Finally, we now analyze models with alternative-specific effects of covariates. The motivation for this model extension is based on the observation that accounting for time-varying generic covariate effects so far improved the model performance only marginally as compared to a model with time-varying brand intercepts only (see Table 2).¹⁶ Accommodating brand-specific covariate effects seems reasonable if consumers have different reference price effects for different brands, or if loyalty effects of consumers differ by brand. Note that in nearly all applications of brand choice models in marketing only “generic” parameters for brand-specific covariates (e.g., price or loyalty) have been estimated, and to the best of our knowledge, no brand choice model with flexibly estimated brand-specific time-varying covariate effects has been published yet.

In particular, we compare the following models with alternative-specific covariate effects: the standard MNL model (MNL_b), the MNL model with seasonal dummies (MNLS_b), the flexible time-varying parameter model based on cubic splines, second-order penalization, and 50 knots (MNLTVP2_b), as well as the model with zero-degree P-splines, first-order penalization, and also 50 knots (MNLTVP4_b). Remember that the MNLTVP4 model with generic effects of covariates is so far the best-performing model, as far as the four scoring rules and the AIC are concerned (cf. Table 4). However, the MNLTVP2 model also performed well and provided smoother parameter paths (even with 50 knots) which are easier to interpret and have smaller confidence intervals. In Table 5, we summarize the results.

Table 5 Model comparison (MNL_b, MNLS_b, MNLTVP2_b, and MNLTVP4_b)

Estimating alternative-specific effects for the covariates improves the statistical performance of all model variants as compared to their counterparts with generic covariate effects (except for the ARMSE statistic in some cases). Because this also holds out-of-sample, we conclude that the models with alternative-specific effects of covariates do not suffer from overfitting, too. Further note that the MNLTVP2_b model provides a better in- and out-of-sample performance as compared to the previously best-performing MNLTVP_4 model w.r.t. all individual-level scoring rules and regarding the AIC and BIC. On the other hand, the MNLTVP_4 model shows a better ARMSE performance. A potential reason for this might be that the additional short-term parameter variation enabled by the MNLTVP_4 model works exceptionally well for aggregate predictions, whereas the brand-specific effects in combination with smoother time trends, as provided by the MNLTVP2_b model, work better on the individual level. However, the most flexible model with alternative-specific covariate effects, the MNLTVP4_b, is now the model with the overall best fit and predictive performance. Consistently, the AIC again supports the most flexible model (MNLTVP4_b), while the BIC tends to the much more parsimonious MNLS_b model. Across all model comparisons, the MNLTVP4_b shows the best AIC, whereas the MNLS_b the best BIC. Also, as expected, because of the very large number of parameters to be estimated, models with alternative-specific covariate effects need more time for estimation.

Next, we turn to the estimated parameter paths to get a better understanding of the consequences of modeling brand-specific covariate effects. We proceed in two steps: in Fig. 6, we first compare the parameter paths obtained from the MNLTVP2 and MNLTVP2_b models to illustrate what happens if a model with initially generic covariate effects is extended to account for alternative-specific covariate effects. After that, we compare the MNLTVP2_b and the overall best-performing MNLTVP4_b models in Fig. 7.

Fig. 6

Parameter estimates (MNLTVP2 versus MNLTVP2_b)

Fig. 7

Parameter estimates (MNLTVP2_b versus MNLTVP4_b)

On the one hand, the estimated paths of both models are often quite similar (e.g., refprice of brand 5, gain of brand 3, loss of brand 4, or loyalty of brand 5). In all these cases, the parameter paths obtained from the MNLTVP2_b model are almost identical as compared to the generic covariate effects resulting from the MNLTVP2 model. On the other hand, differences between the two models become evident. The alternative-specific loss effect for brand 5 shows a decreasing trend (it becomes stronger over time), while the generic loss effect has a positive slope. Also, the alternative-specific loss effect for brand 2 now turns out very volatile and nonmonotonic which is harder to interpret. It is further not significantly different from zero for many time periods. Moreover, in some cases, the estimated alternative-specific effects turn out (almost) constant over time (e.g., the loyalty effect for brand 4). Intuitively, the generic covariate effects seem to be a weighted average of the alternative-specific effects, where larger brands seem to dominate the “average” shape (see, e.g., the gain parameters for brands 1 and 3, or the loyalty effects for brands 2 and 3). In addition, also the average magnitude of the effects varies in some cases. For example, the alternative-specific loyalty effect for brand 2 is above average, whereas brands 1 and 3 have lower alternative-specific loyalty effects as compared to the generic loyalty effect. Also, the alternative-specific loss effect for brand 1 is stronger than the average effect predicted by the MNLTVP2 model. The estimated intercepts of both models are very similar for brands 2 and 5. However, the intercept of brand 3 (brand 4) shows considerably less (more) variation over time in the MNLTVP2_b model. Therefore, because now brand-specific covariate effects are added, brand-specific intercepts of the model can adapt, too.

Figure 7 finally contrasts the estimated parameter trajectories of the MNLTVP2_b and MNLTVP4_b models. We observe parallels to Fig. 5; either the shapes virtually coincide (e.g., see the intercepts for brand 4 and 5, the reference price effects for brands 2 and 3, the gain and loss effects for brand 2, or the loyalty effects for brand 1), or in cases where the more flexible model (MNLTVP4_b) provides more volatile parameter paths, the less flexible model (MNLTVP2_b) still captures the general courses of the more wiggly trajectories by more smooth parameter evolutions (e.g., see the intercepts for brands 2, 3, and 4, the reference price effects for brands 1 and 5, the gain effects for brands 1 and 3, the loss effects for brand 1, or the loyalty effects for brand 3). Except for only a few weeks across all intercepts and covariates, all parameters paths of the MNLTVP2_b model lie within the corresponding 95% pointwise confidence intervals of the MNLTVP4 model. Therefore, even though the MNLTVP4_b model outperforms the MNLTVP2_b model both in- and out-of-sample, the substantive insights are quite similar.

3.4.5 Overall comparison

In the preceding sections, we have compared many models and followed a step-by-step model building process (Leeflang et al. 2015). Even though the proposed approach is entirely data driven and explorative in the sense that the user does not have to decide a priori about the shapes of the time-varying parameters or the amount of smoothing, still multiple optional model settings are available (i.e., the number of knots, degree of the spline, order of penalization).

The comparisons have revealed that models with time-varying parameters perform better than the static versions for our coffee data. In particular, brand intercepts vary substantially over time, and for some coffee brands, several models clearly suggested the presence of seasonal effects at (or before) important festive occasions like Easter (week 14), Pentecost (week 21), or Christmas (week 51). This knowledge by augmenting the standard MNL model by dummy variables is used to capture those seasonal patterns, improved fit, and predictive validity. However, because our semiparametric time-varying parameter models revealed additional time variation in all parameters (i.e., for brand intercepts and covariate effects), they outperformed the MNL model with seasonal effects easily. The resulting parameter paths also provide interesting insights for marketing managers because changing brand preferences, varying sensitivities w.r.t. perceived price constructs, or time-varying brand loyalty effects imply different optimal marketing mix strategies for retailers as compared to a situation with constant parameters over time.

Because of the large cross section in our data with more than 4000 households, we next analyzed whether the data support still more complex models, in a first step for time-varying brand intercepts only. Specifically, we estimated the thin-plate spline model of Baumgartner (2003) as well as a parametric MNL model with brand–week fixed effects. Both models turned out to be highly flexible and outperformed our default cubic P-spline model with time-varying brand intercepts and covariate effects. As a consequence, we further increased the flexibility of models within our P-spline framework by using more knots, zero-degree splines, and a first-order penalization. Indeed, the best-performing model so far was now a model that mimics a state-space choice model with random walk parameter dynamics. This model provided parameter paths with a lot of variation over time and did not suffer from overfitting, as indicated by its very good out-of-sample performance. Nevertheless, many of the estimated parameter paths revealed similar shapes across the diverse model specifications, thereby suggesting comparable insights across models. Differences occur mainly w.r.t. the smoothness of the shapes, only seldom w.r.t. the general courses of the parameter evolutions. This underlines not only the robustness of the estimation results but also the robustness of the proposed P-spline approach for estimating time-varying parameters in brand choice models.

Finally, extensions with alternative-specific covariate effects led to a further improvement in fit and predictive performance and provided in some instances interesting additional insights for specific brands, too. The most flexible model specification overall (as many knots as time periods, zero-degree splines, first-order penalization, alternative-specific covariate effects) provided the best in- and out-of-sample performance, although the resulting parameter paths are mostly very similar in their general course (but much wigglier) as compared to the less flexible counterpart model with cubic splines and second-order penalization.

Overall, we conclude that for the analyzed coffee dataset parameter dynamics are indeed present and important for understanding the brand choice behavior of the households (see also the next subsection for specific managerial implications). In our particular case, we find that very flexible specifications worked best. However, the coffee dataset is quite large and given that the simpler semiparametric models yielded comparable parameter paths, we generally recommend to start the modeling process with a medium number of knots (e.g., 40), cubic splines, second-order differences for penalization, and generic effects of covariates (i.e., MNLTVP2). This should lead to a first clear impression whether parameter dynamics are relevant for the dataset at hand. If this model performs well (i.e., providing reasonable parameter paths, and no overfitting), we advise modelers to try even more flexible specifications and to check whether estimation results remain plausible and meaningful and whether in particular the out-of-sample performance can be further improved.

Besides model fit, other criteria can be relevant (e.g., applicability). More complex models need more time for estimation and the range in our application for the coffee data spans from a few seconds to several hours.

3.5 Managerial implications

Instead of overall fit and predictive validity statistics, retailers or brand managers may be more interested in findings at the brand level and improvements from applying a more complex model. Figure 8 displays barplots with in- and out-of-sample RMSE values regarding market shares (based on brand purchases) for each coffee brand and reveals to which extent the brands benefit from the higher flexibility of the MNL models with time-varying parameters. We compare the standard MNL model with the best-performing MNLTVP4_b model.

Fig. 8

RMSE at the individual brand level (MNL versus MNLTVP4_b)

As expected, the more flexible MNLTVP4_b model yields an improved in-sample fit for all individual brands, with errors in estimated market shares not larger than 2.22 market share points across brands and of about only 1 percentage point for brands 2 to 5. The highest improvement of a 3% better RMSE value (in absolute terms) is obtained for coffee brand 3, one of the two brands with the largest fluctuations in the brand intercepts. The plot also indicates a better predictive validity of the MNLTVP4_b model for all brands, with improvements in RMSE over the standard MNL ranging from about 0.5 up to stately 1.75 market share points, with the highest absolute improvements for brands 1 and 3 here. Note that the MNLTVP4_b model not only fits and predicts individual market shares better, but the errors also show less variation across brands. Further, the RMSE values of the MNL model turn out smaller (larger) for brands with low (high) market shares (see Table 1). For a retailer, this is not preferable, because the applied model should work well for a wide variety of brands in the assortment. The dynamic MNLTVP4_b model also works better in this point. The RMSE results at the brand level confirm our aggregate level results on model performance for the coffee data for these two models (cf. Tables 2 and 5).

Figure 9 contrasts actual market shares (solid lines) and market shares predicted from both the MNLTVP4_b model (dashed lines) and the standard MNL model (dotted lines) in the holdout sample. The plot refers to coffee brand 3, which shows a substantial improvement in the predictive validity when allowing for time-varying coefficients. Here, the MNLTVP4_b model often provides more accurate predictions in weeks where fluctuations in market share are particularly large (e.g., weeks 28/29, 32, 39/40, 44, and 46/47). The plot further confirms that the low intrinsic utility of brand 3 in weeks surrounding festive occasions (cf. Fig. 2) coincides with very low market shares of this brand at these times [compare the vertical gray lines for Easter (week 14), Pentecost (week 21), and Christmas (week 51)]. In general, we observe for all coffee brands that especially large variations in market shares are better predicted by the MNLTVP4_b model.

Fig. 9

Actual and predicted market shares (illustrated for coffee brand 3)

Figure 9 also reveals that the standard MNL model seems to be able to predict the general variation in market shares quite well; however, it is not capable of catching the strong amplitudes of the market share fluctuations. Hence, the lack of fit stems from an underestimation of the variability in market shares, which can lead to problems for retailers because of potential out-of-stock situations (underpredicted demand) or wasted shelf space (overpredicted demand).

Besides more accurate demand predictions, which help retailers with inventory management, shelf space allocation planning, and preventing out-of-stock situations, the models with time-varying parameters also provide relevant insights regarding marketing mix strategies. For instance, all models with generic time-varying covariate effects estimated decreasing effects of brand loyalty over time (see Figs. 2, 4, 5, and this also holds for many brands and weeks for the time-varying parameter models with alternative-specific effects, see Figs. 6 and 7). Given that brand loyalty values are more or less stable (which is the case for the present coffee dataset), this implies that it becomes easier for retailers to stimulate households to switch brands which has direct implications for optimal pricing strategies. Dubé et al. (2009) found that as brand loyalty increases optimal prices either rise or fall depending on the relative strengths of the harvesting (i.e., high regular prices) and the investment motives (i.e., deep price promotions) of the retailer’s category manager. Furthermore, changes in gain and loss effects also lead to alternative optimal pricing plans (Kopalle et al. 2012). As gain effects increase (see, e.g., Figs. 2, 5), price promotions become more effective because households react stronger to savings from (temporarily) lower prices. At the same time, when loss effects decrease in absolute terms (again, see Figs. 2, 5), the negative effect of a subsequent increase from the promotion price back to the regular price is also smaller. Note, however, that a change in behavior would also imply a change in reference prices [see Eq. (11)] and hence for specific implications the dynamic pricing problem of the retailer has to be solved.

Overall, our findings suggest the use of time-varying parameter models and should encourage firms and managers to adopt more flexible models to detect such time-varying effects. Nevertheless, it is important to note some limitations of our study which may have an influence on the relative performance of the less complex parametric MNL models versus the more sophisticated flexible time-varying MNL specifications. First, measurement errors are inherent to marketing data and the magnitude of measurement errors might be larger than the improvements achieved by more complex models. This holds in particular when differences in fit or predictive performance between models are not huge, as observed in our empirical study especially for errors in market share predictions in some cases (e.g., compare the rather small differences in RMSE values in the validation sample between the parametric MNL with brand–week fixed effects and the more sophisticated P-spline MNL models). Second, although we accounted for multiple pack purchases of households in a given week and not only for brand choice in a multinomial sense, we still neglect kinds of primary demand effects like choosing different pack sizes. And third, our coffee dataset covers only 75% of all purchases of national coffee brands during the considered time span. Thus, whether it is reasonable to employ a more complex approach depends ultimately on the empirical data at hand, and careful model comparisons are always in order.

4 Future research

We see several avenues for further research: (1) Of course, applications to other product categories are necessary to provide empirical generalizations about time-dependent effects in consumer choice behavior. (2) Further, an important step would be to incorporate unobserved consumer heterogeneity in our approach. Although a few approaches have already considered heterogeneity and dynamics by additively decomposing parameter variation into time variation and cross-sectional heterogeneity (Kim et al. 2005; Lachaab et al. 2006; Guhl et al. 2018), more interesting would be to decouple those two dimensions to accommodate individual household parameter evolutions. (3) Instead of MNL-based time-varying parameter models, it would also be interesting to apply MNP models that relax the IIA assumption. However, the estimation of a flexible probit model using the proposed P-spline framework would require a huge computational effort and might be intractable. (4) It would further be interesting to consider modeling other types of limited dependent variables within our framework, such as including time-varying parameters in purchase incidence and quantity choice (sub)models in order to account for primary demand effects. (5) According to the BIC, simple models with constant parameters should be preferred, even though these models did not perform well in the validation sample. Hence, it seems a fruitful area for future research to study the usefulness of the BIC for model selection in the case of models with time-varying parameters.