The maximin gradual cover location problem

Abstract

In this paper, we consider the multiple facility location problem with gradual cover. Gradual cover means that up to a certain distance from the facility a demand point is fully covered. Beyond another distance the demand point is not covered at all. Between these two distances the demand point is partially covered. When there are $p$ facilities, the cover of each demand point can be calculated by a given formula. One objective in this setting is to find locations for $p$ facilities that maximize the total cover. In this paper we consider another objective of maximizing the minimum cover of every demand point. This guarantees that every demand point is covered as much as possible and there are no demand points with low cover. The model is formulated and heuristic algorithms are proposed for its solution. We solved a real-life problem of locating cell phone towers in northern Orange County, California and demonstrated the solution approach on a set of 40 test problems.

1 Introduction

One of the classic objectives in location modeling is based on the concept of cover. A demand point is covered by a facility within a certain radius and not covered beyond that radius. There may be a different weight associated with each demand point. Church and ReVelle (1974) suggested two cover-based facility location problems: (i) the set covering problem seeks the minimal number of facilities that cover all demand points, and (ii) the maximum cover problem seeks the maximization of the covered weight with a given number of facilities.

Applications to these problems abound including: the location of emergency services (such as fire stations, ambulance stations) where travel distance from the facility to a demand point should not exceed a certain value; covering grassy areas and plants with sprinkler covering discs of a given radius; the location of retail facilities which have “trading areas” extending for some distance around the facility; signal-transmission facilities (cell-phone towers, light posts, warning sirens, TV or radio stations, etc.) where cover is achieved only within a certain distance from the facility. We refer the reader to Kolen and Tamir (1990) and Current et al. (2002) for a discussion of cover models in discrete spaces and to Plastria (1995, 2002) in continuous spaces. Extensions to the classic covering models are summarized in Berman et al. (2010b).

One extension to classic covering models is gradual cover. Classic covering models employ a critical distance such that a demand point is covered within this distance from a facility and not covered as soon as the distance is marginally greater than the critical distance. The cover function is discontinuous because cover drops abruptly. To rectify this discontinuity in the covering measure the gradual cover is suggested. Two critical distances $(r\le R)$, are defined. A demand point is fully covered if the distance to a facility does not exceed $r$, and is not covered at all if the distance to a facility exceeds $R$. For distances between $r$ and $R$ cover declines gradually according to a cover function. The cover function can be linear, step-wise, or general, but should be a non-increasing function of the distance. Most gradual cover models seek the maximization of the total covered weight. When a demand point is partially covered by a calculated proportion, the proportion of the weight is added to the value of the objective function. Church and Roberts (1984) were first to suggest gradual cover. They described a discrete model with a (not necessarily decreasing) step-cover function. Berman and Krass (2002) also discuss the discrete version with the step-cover function and provide efficient formulations and heuristic approaches. The discrete model with a general non-increasing cover function was analyzed in Berman et al. (2003b). The planar version with a linear cover function was analyzed in Drezner et al. (2004) and its stochastic version in Drezner et al. (2010). Karasakal and Karasakal (2004) investigated the gradual cover model and termed it partial cover. Eiselt and Marianov (2009) investigated gradual cover in the context of the set covering problem.

Berman and Krass (2002) suggested that the cover by several facility is determined by the closest facility. Drezner and Wesolowsky (1997) and Drezner and Drezner (2008) suggested that partial cover is interpreted as probability and thus the combined cover, when the probabilities are independent, is calculated based on this assumption.

Maximizing the minimum cover of demand points is irrelevant in classic cover models because a demand point is considered either covered or not, and therefore, the minimum cover proportion is either 0 or 1. In the set covering model (Church and ReVelle 1974), the minimum cover is full cover. However, in the gradual cover setting we wish to provide at least some cover to every demand point and wish the minimum total cover to be as high as possible (Eiselt and Marianov 2009). This is similar to the idea of the $p$-center objective (Kariv and Hakimi 1979; Chen and Chen 2009) where the objective is to provide the farthest customer with the best possible service.

In this paper we investigate the maximization of the minimum cover across demand points in the context of gradual cover in discrete space. A set of demand points and a set of potential locations for the facilities are given. A demand point may be partially covered by several facilities. This means that we would like to provide the least covered demand point with as much cover as possible. A similar objective is discussed in Drezner and Wesolowsky (1997) where the location of signal detectors is sought. The probability of detection depends on the distance and once the location of the detectors is known, the probability of detection of an event occurring at any demand point can be calculated. The objective is to maximize the minimum probability of detection (cover) of events at all demand points. This objective can be classified as an equity objective. For a discussion of equity models, see Mulligan (1991), Erkut (1993), Marsh and Schilling (1994), Eiselt and Laporte (1995), Drezner and Drezner (2007), and Drezner et al. (2009).

2 The maximin gradual cover location model

The maximin gradual cover location model can be either a discrete model when the set of potential locations for the facilities is finite, or continuous meaning that facilities can be located anywhere in the plane. Most of the analysis is pertinent for both cases. We concentrate on the discrete model and design solution algorithms for discrete problems.

2.1 Notation

Let:

$N$ :

be the set of demand points of cardinality $n$

$S$ :

be the set of potential locations

$s$ :

be the cardinality of $S$

$p$ :

be the number of facilities to be located

$d_{ij}$ :

be the distance between demand point $i\in N$ and potential location $j\in S$

$0\le \phi _{ij}\le 1$ :

be the proportion of cover of demand point $i\in N$ by a facility located at potential location $j\in S$ at distance $d_{ij}$

$0\le \phi _i\le 1$ :

be the calculated combined proportion of cover by all $p$ facilities

$r$ :

be the maximum distance for full cover. $\phi _{ij}=1$ when $d_{ij}\le r$

$R$ :

be the minimum distance for no cover. $\phi _{ij}=0$ when $d_{ij}\ge R$

$\theta$ :

be an association factor $0\le \theta \le 1$ depicting the correlation between proportions of cover.

2.2 Background

$\phi _{ij}$ is the proportion of cover of demand point $i\in N$ by a facility located at potential location $j\in S$. $\phi _{ij}=0$ for $d_{ij}\ge R$ and $\phi _{ij}=1$ for $d_{ij}\le r$. $0<\phi _{ij}<1$ is a well defined monotonically non-increasing cover function for $r< d_{ij}< R$. Therefore, when $d_{ij}$ is known, $\phi _{ij}$ is well defined. A reasonable assumption is a linear decline in cover for $r\le d_{ij}\le R$ (Drezner et al. 2004; Berman et al. 2003b) leading to a continuous cover function. Therefore, we no longer use the distances $d_{ij}$ because they can be converted to proportions of cover $\phi _{ij}$. Marianov and Eiselt (2012) considered the location of multiple television transmitters that may be both cooperating and interfering.

As discussed in Berman et al. (2010a), the assumption that the coverage is determined solely by the closest facility may not always be appropriate. In many cases (including light, sound, and microwave signals), the signal emitted by the source dissipates proportionally to the square of the travel distance (distance decay) and the signal received at a demand point is the sum of the signals from all sources. There exists a distance $r$ such that the demand point is “surely” covered within this distance and a distance $R$ for which the signal is so weak that the probability of coverage does not increase.

It is important to note that the model can be applied to a large variety of cover options as long as $\phi _{ij}$ is a well-defined function of the distance $d_{ij}$. For instance, the distances $R$ and $r$ can be different for each demand point, can be different for each potential location, or can be different as $R_{ij}$ and $r_{ij}$ for each pair of demand point $i\in N$ and a potential location $j\in S$. For example, cell phone towers’ cover may well depend on the landscape, hills, valleys, obstruction by buildings, etc. that may lead to different $R$ and $r$ for each pair of a demand point and a potential location.

Suppose that $p$ facilities are located at some potential locations (more than one facility may be located at the same location, which is termed “co-location”). One way to interpret the proportion of cover $\phi _{ij}$ is to view it as probability of cover. By this interpretation, the total cover is $\phi _i=1-\prod _{j=1}^p\left( 1-\phi _{ij}\right)$ if the probabilities of cover are based on independent events (see, for example, Drezner and Wesolowsky 1997; Berman et al. 2003a; Drezner and Drezner 2008). However, assuming independence between events is not always realistic. For example, consider the case where facilities are identical transmission towers and demand is generated by cell phones. The quality of service might well depend on the cell phone used. Cell phones may differ in their model, technology, condition of the battery etc. leading to a positive correlation between cover of demand points.

It can be shown that when the correlation coefficients between events approach 1, then in the limit the total cover is $\max _{1\le j \le p}\left\{ \phi _{ij}\right\}$. It is obvious for two events and it follows for any number of events by mathematical induction. This is equivalent to assuming that cover is achieved by the closest facility, while cover by all other facilities is ignored. It is easy to show that $1-\prod _{j=1}^p\left( 1-\phi _{ij}\right) \ge \max _{1\le j \le p}\left\{ \phi _{ij}\right\} .$ These are the two extreme probabilities and thus a convex combination of these two extreme values can be used to model the whole spectrum of dependency. An association coefficient $0\le \theta \le 1$, that is similar but not identical to a correlation coefficient, is selected. We define the accumulated cover of demand point $i$, $\phi _i$, for a given $\theta$ as:

$$\begin{aligned} \phi _i=\theta \max \limits _{1\le j \le p}\left\{ \phi _{ij}\right\} +(1-\theta )\left[ 1-\prod \limits _{j=1}^p\left( 1-\phi _{ij}\right) \right] . \end{aligned}$$

(1)

Observe that $\theta =0$ leads to the independent events assumption (correlation coefficient of 0) and $\theta =1$ is equivalent to a correlation coefficient of 1. This estimate of the accumulated cover is also applied in Berman et al. (2014).

2.3 The multivariate normal case

It is reasonable to assume that the individual probabilities are generated by a normal distribution. Consider the same example of transmission towers and cell phones. A cell phone requires a signal threshold to be connected. Since there are many factors that determine the signal received by a cell phone (one important factor is the distance), the distribution of the signal can be assumed normal by the central limit theorem, and thus the probability of connection is the probability of exceeding that threshold. Let $d$ be the distance between demand point $i$ and facility $j$. In recent papers on gradual cover (for example Drezner et al. 2004; Berman et al. 2003b), there are two distances $r<R$ such that there is full coverage ($\phi _{ij}=1$) if $d\le r$, no coverage ($\phi _{ij}=0$) if $d\ge R$ and cover declines linearly for $r\le d\le R$. The probability of no coverage ($1-\phi _{ij}$) resembles a cumulative normal probability and can be approximated by it very well by setting $r=\mu -3\sigma$ and $R=\mu +3\sigma$. For $d\le r,~\phi _{ij}\approx 1$ and for $d\ge R,~\phi _{ij}\approx 0$. This leads to $\mu =\frac{r+R}{2}$ and $\sigma =\frac{R-r}{6}$. For $d=\mu ,~\phi _{ij}=\frac{1}{2}$ for both. Note that in Drezner et al. (2010), the coverage function resembles a cumulative normal curve even more because it is assumed that $r$ and $R$ are random variables. See Fig. 1 where the cover curve of Drezner et al. (2010) is compared with the cumulative normal distribution with 2.66$\sigma$ on each side of the mean.

Fig. 1

Stochastic cover compared with cumulative normal cover

If the probabilities are a result of a normal distribution, i.e. $\phi _{ij}=Pr(Z\ge h_j)$, correlated probabilities are a result of a multivariate normal distribution. Suppose that $m\le p$ facilities are partially covering demand point $i$. If there is at least one facility for which $d_{ij}\le r$, the probability of coverage is 1 regardless of the locations of the other facilities. Otherwise, $d_{ij}\ge R$ for $p-m$ facilities and the probability of cover is not affected by these facilities. For a multivariate normal distribution with a correlation matrix $\overline{R}$ (Drezner 1992; Johnson and Kotz 1972):

$$\begin{aligned} Pr\left( Z_1\le h_1, Z_2\le h_2,\ldots ,Z_m\le h_m\right) =\frac{1}{\sqrt{(2\pi )^m|\overline{R}|}}\int \limits _{-\infty }^{h_1}\ldots \int \limits _{-\infty }^{h_m}\mathrm{e}^{-\frac{1}{2}z^T\overline{R}^{-1}z}\mathrm{d}z_m\ldots \mathrm{d}z_1\nonumber \\ \end{aligned}$$

(2)

where $|\overline{R}|$ is the determinant of $\overline{R}$.

We derive the expression for the probability $\phi _i$, when the correlation coefficient between all events is the same, by a multivariate normal distribution based on a correlation matrix $\overline{R}$ with equal off-diagonal values.

2.3.1 Equal off-diagonal correlations

For the multivariate normal distribution, when the correlation matrix $\overline{R}$ has equal off-diagonal correlations $\rho \ge 0$, by Johnson and Kotz (1972), p.48 the $m$-dimensional integral (2) can be reduced to a one-dimensional integral:

$$\begin{aligned} Pr\left( Z_1\le h_1, Z_2\le h_2,\ldots ,Z_m\le h_m\right) =\frac{1}{\sqrt{2\pi }}\int \limits _{-\infty }^{\infty }\prod \limits _{j=1}^m\Phi \left( \frac{h_j-z\sqrt{\rho }}{\sqrt{1-\rho }}\right) \mathrm{e}^{-\frac{z^2}{2}}\mathrm{d}z\nonumber \\ \end{aligned}$$

(3)

where $\Phi (\cdot )$ is the cumulative standardized normal probability. The integral (3) is calculated using Gaussian quadrature formulas based on Hermite polynomials with 20 integration points (Abramowitz and Stegun 1972, Table 25.10 pp. 924).

Consider a particular demand point $i$. The probability that demand point $i$ is covered by facility $j$ is $\phi _{ij}$. We derive the probability $\phi _i$ that demand point $i$ is covered by at least one facility. The probability of non-coverage of demand point $i$ by facility $j$ is $1-\phi _{ij}$. Let

$$\begin{aligned} Pr(Z_j\le h_j)=\Phi (h_j)=1-\phi _{ij}. \end{aligned}$$

(4)

Then, the probability calculated in (3) is the probability of non-coverage of demand point $i$ by all facilities. From (4), we get

$$\begin{aligned} h_j=\Phi ^{-1}\left( 1-\phi _{ij}\right) \end{aligned}$$

(5)

and the probability $\phi _i$ of coverage by at least one facility is:

$$\begin{aligned} \phi _i=1-\frac{1}{\sqrt{2\pi }}\int \limits _{-\infty }^{\infty }\prod \limits _{j=1}^m\Phi \left( \frac{\Phi ^{-1}\left( 1-\phi _{ij}\right) -z\sqrt{\rho }}{\sqrt{1-\rho }}\right) \mathrm{e}^{-\frac{z^2}{2}}\mathrm{d}z. \end{aligned}$$

(6)

2.3.2 Evaluating the relationship between $\rho$ and $\theta$

Suppose we can estimate the value of $\rho$. What value of $\theta$ should be used in (1)? The relationship between $\rho$ and $\theta$ can be explicitly derived in the case of orthant probabilities of the multivariate normal distribution, i.e. $\phi _{i1}=\phi _{i2}=\ldots =\phi _{im}=0.5$ (Steck (1962)). For $m=2$ (Drezner and Wesolowsky 1990) the orthant probability is $\frac{1}{4} +\frac{\arcsin \rho }{2\pi }$ and thus $\phi _i=\frac{3}{4} -\frac{\arcsin \rho }{2\pi }$ leading to $\theta =\frac{2}{\pi }\arcsin \rho$. For $m=3$, by equation (2.8) in Steck (1962), the orthant probability is $\frac{1}{8} +\frac{3\arcsin \rho }{4\pi }$ leading to the same relationship $\theta =\frac{2}{\pi }\arcsin \rho$. For higher dimensions only approximations exist (Steck 1962). We therefore evaluated the relationship between $\rho$ and $\theta$ for a wide range of $\phi _{ij}$ by simulation.

We calculated the value of $\theta$ for multivariate normal distributions with equal off-diagonal correlations $\rho =0.1,\ldots ,0.9$ and $m=2,\ldots ,10$ (81 cases) by randomly generating $0.1\le \phi _{ij}\le 0.9$ 10,000,000 times for each case. The value of $h_j$ for each $\phi _{ij}$ was calculated by (5). The probability $\phi _i$ was then calculated by (6). The value of $\theta$ was then calculated by explicitly solving (1). The average and the standard error of the resulting 10,000,000 values of $\theta$ were calculated for every case. The averages are reported in Table 1 and depicted in Fig. 2. The standard errors of the results are quite small. All 81 standard errors round down to 0.0000. It took about 14 h of computer time to calculate these 810 million $\theta$s which is one million calculations of $\theta$ per minute.

Fig. 2

Values of $\theta$ as a function of $m$ from $\rho =0.1$ (bottom) to $\rho =0.9$

Table 1 Average values of $\theta$

Note that if the location problem is based on $m$ facilities, if for at least one facility $\phi _{ij}=1$ then, $\phi _i=1$ and $\theta$ is undefined (i.e, any value of $\theta$ yields the same $\phi _i=1$). If several $\phi _{ij}=0$, then such facilities can be removed and the actual $m$ is smaller. Therefore, the only “relevant” cases are $0<\phi _{ij}<1$.

Multiple regression, with no intercept, yields

$$\begin{aligned} \theta =\rho [1.392202-0.365589\rho -m(0.140458-0.135549\rho )]. \end{aligned}$$

(7)

For this regression: $R^2=0.9999$ and the significance-$F=5.2\times 10^{-152}$. A value of $\theta$ can be selected by this formula for each demand point once $\rho$ and the number of partially covering facilities $m$ are known.

2.4 The objective function

Let $K\subset S$ of cardinality $p$ be the set of selected locations for the facilities. Each location may be selected more than once. Define $f(K)$ for a given $\theta$:

$$\begin{aligned} f(K)=\min \limits _{i\in N}\left\{ \phi _i=\theta \max \limits _{j\in K}\left\{ \phi _{ij}\right\} +(1-\theta )\left[ 1-\prod \limits _{j\in K}\left( 1-\phi _{ij}\right) \right] \right\} \end{aligned}$$

(8)

Note that the value of $\theta$ may be different for different demand points without altering the analysis or the solution algorithms. However, for simplicity, we assume the same $\theta$ for all demand points.

The objective for a given $p$ is to find the best set $K\subset S$ of cardinality $p$ that maximizes $f(K)$ which is the minimum cover proportion $\phi _i$ (Eq. (1)) for all $i\in N$ for a given $K$:

$$\begin{aligned} F(p)=\max \limits _{K\subset S, |K|=p}\left\{ f(K)\right\} \!. \end{aligned}$$

(9)

2.5 Co-location

In classic cover models there is no advantage in locating more than one facility at the same location. If a demand point is covered by one facility, it will be covered by two facilities located at the same location, and if a demand point is not covered, then it will not be covered if a second facility is located at the same location. However, in gradual cover models, it is possible that locating a second facility at the same location is optimal. For example, consider two facilities, two potential locations, and several demand points. Suppose that cover of every demand point by a facility located at one potential location is zero, and cover by a facility located at the second potential location is 0.5. If we locate a facility at each potential location, the combined cover is 0.5 for each demand point because the other facility does not contribute to the cover. The objective function for this solution is 0.5. When both facilities are located at the second location, then by (1), $\phi _i=0.5\theta +0.75(1-\theta )=0.75-0.25\theta >0.5$ for $\theta <1$. Therefore, co-location of facilities should be allowed. Note that for $\theta =1$ co-location cannot be the only optimal solution. This is similar to the classic cover models. Cover is determined by the closest facility and all other facilities are ignored. Therefore, there is no advantage in locating more than one facility at the same location.

3 Properties

We construct conditions for which the solution to problem (9) is known and thus there is no need to apply a solution algorithm to find it.

Lemma 1

If there exists a subset $K\subset S$ of cardinality $p$ such that for all $i\in N$, there exists $j\in K$ such that $d_{ij}\le r$ (i.e., $\phi _{ij}=1$), then $F(p)=1$ is the optimal solution to (9) and $K$ is an optimal subset.

Proof

For this particular subset $K$, both $\max _{j\in K}\{\phi _{ij}\}=1$ for all $i\in N$ and $1-\prod _{j\in K}\left( 1-\phi _{ij}\right) =1$ for all $i\in N$ and thus $f(K)=1$. Therefore, $F(p)\ge 1$ because $F(p)$ is the maximum value of $f(K)$ for all $K\subset S$. Since $F(p)\le 1$ by definition, $F(p)=1$ is the optimal solution and $K$ is an optimal subset. $\square$

The following Lemma proves that Lemma 1 is both necessary and sufficient.

Lemma 2

If the solution to (9) is $F(p)=1$, then there exists a subset $K\subset S$ of cardinality $p$ such that for all $i\in N$, there exists $j\in K$ such that $d_{ij}\le r$.

Proof

Since $F(p)=\max _{K\subset S}\{f(K)\}$, there exists a subset $K\subset S$ such that $f(K)=1$. For this $K$, $\min _{j\in K}\{d_{ij}\}\le r$ for all $i\in N$ which means that for all $i\in N$ there exists $j\in K$ such that $d_{ij}\le r$. $\square$

Lemma 3

If for every set $K\subset S$ of cardinality $p$, there exists $i\in N$ such that $d_{ij}\ge R$ (i.e. $\phi _{ij}=0$) for all $j\in K$, then $F(p)=0$ is the optimal solution to (9) and any $K\subset S$ serves as a solution.

Proof

Consider any $K\subset S$ of cardinality $p$. For this $K$ there exists $i\in N$ such that $\phi _{ij}=0$ for all $j\in K$. Therefore, for this $i$ both $\max _{j\in K}\{\phi _{ij}\}=0$ and $1-\prod _{j\in K}\left( 1-\phi _{ij}\right) =0$ yielding $\phi _i=0$ and thus $f(K)=0$. Consequently $F(p)=0$ is the optimal solution because $f(K)=0$ for every $K\subset S$. $\square$

The following Lemma proves that Lemma 3 is both necessary and sufficient.

Lemma 4

If $F(p)=0$ is the optimal solution to (9), then for every set $K\subset S$ of cardinality $p$ there exists $i\in N$ such that $d_{ij}\ge R$ for all $j\in K$.

Proof

Since $F(p)=0$, $f(K)=0$ for all $K\subset S$ of cardinality $p$. Therefore, for every $K\subset S$ there exists $i\in N$ such that $\min _{j\in K}\{d_{ij}\}\ge R$ and thus $d_{ij}\ge R$ for all $j\in K$. $\square$

Lemma 5

If $F(\phi _0)=0$ for a given $\phi _0$, then $F(p)=0$ for any $p\le \phi _0$. If $F(\phi _1)=1$ for a given $\phi _1$, then $F(p)=1$ for any $p\ge \phi _1$.

Proof

If $F(\phi _0)=0$, then by Lemma 4 for every set $K\subset S$ of cardinality $\phi _0$ there exists $i\in N$ such that $d_{ij}\ge R$ for all $j\in K$. When $p\le \phi _0$ for every set $K^\prime \subset S$ of cardinality $p$ there exists a subset $K\supset K^\prime$ of cardinality $\phi _0$ that satisfies this property and thus $F(p)=0$ by Lemma 3. If $F(\phi _1)=1$, then by Lemma 2 there exists a subset $K\subset S$ of cardinality $\phi _1$ such that for all $i\in N$, there exists $j\in K$ such that $d_{ij}\le r$. For $p\ge \phi _1$ any subset $K^\prime$ constructed by adding demand points to $K$ satisfies this condition and thus $F(p)=1$ by Lemma 1. $\square$

By Lemma 5 the following are well defined:

$$\begin{aligned} p_{\min }&= \max \{p~|~F(p)=0\}. \\ p_{\max }&= \min \{p~|~F(p)=1\}. \end{aligned}$$

By Lemma 5 when $p\le p_{\min }$ the optimal solution to (9) is $F(p)=0$, and when $p\ge p_{\max }$ then the optimal solution is $F(p)=1$. When $p_{\min }< p< p_{\max }$, $0<F(p)<1$. Consequently, the only “interesting” problems are for $p_{\min }< p< p_{\max }$. We note that it is possible, but not likely, that $p_{\min }+1=p_{\max }$ and there is no $p$ for which $p_{\min }< p< p_{\max }$. In such cases either $F(p)=0$ or $F(p)=1$ for every $p$.

We now show how to establish the values $p_{\min },~p_{\max }$ by either solving a $p$-center problem, or a maximal covering problem, or a set covering problem.

3.1 Finding $p_{\min }$ and $p_{\max }$

In this section we use the definitions in Sect. 2.1. In addition we define:

$R^\prime$ :

be $\max \{d_{ij}~|~d_{ij}<R\}$. Note that by definition if $d_{ij}>R^\prime$, then $d_{ij}\ge R$.

$R(p)$ :

be the optimal solution (radius) to the $p$-center problem with $p$ facilities

$C_p(t)$ :

be the maximum cover (weights equal to 1 and $p$ facilities) with a covering distance $t$

$p(t)$ :

be the minimum number of facilities covering all demand points within a distance $t$

The following Theorem provides a relationship between the maximin gradual cover model and the $p$-center model (Kariv and Hakimi 1979; Chen and Chen 2009).

Theorem 1

If $R(p)\le r$, then the solution to (9) is $F(p)=1$. If $R(p)\ge R$, then the solution to (9) is $F(p)=0$. When solving $p$-center problems: $p_{\min }$ is the largest $p$ such that $R(p)\ge R$ and $p_{\max }$ is the smallest $p$ such that $R(p)\le r$.

Proof

When $R(p)\le r$, at the solution set $K$ to the $p$-center problem, $\max _{i\in N}\min _{j\in K}\{d_{ij}\}\le r$. Therefore, for every $i\in N$ there exists $j\in K$ such that $d_{ij}\le r$ thus $\phi _{ij}=1$ yielding $\phi _i=1$. Consequently, $f(K)=1$ and therefore $F(p)=1$. When $R(p)\ge R$, by the optimality of $R(p)$, for every set $K\subset S$ of cardinality $p$: there exists $i\in N$ such that $\min _{j\in K}\left\{ d_{ij}\right\} \ge R(p)\ge R$. For this $i$, $\phi _{ij}=0$ for all $j\in K$ yielding $\phi _i=0$. By Lemma 3 $F(p)=0$. $\square$

The following Theorem provides a relationship between the maximin gradual cover model and maximal cover problems (Church and ReVelle 1974).

Theorem 2

If $C_p(r)=n$, then the solution to (9) is $F(p)=1$. If $C_p(R^\prime )<n$, then the solution to (9) is $F(p)=0$. When solving the maximum cover problem: $p_{\min }$ is the largest $p$ such that $C_p(R^\prime )<n$ and $p_{\max }$ is the smallest $p$ such that $C_p(r)=n$.

Proof

When $C_p(r)=n$, at the solution set $K$ to the maximal cover problem, all demand points are covered. Therefore, for each $i\in N$ there exists $j\in K$ such that $d_{ij}\le r$ thus $\phi _{ij}=1$. By Lemma 1 $F(p)=1$ is the optimal solution. When $C_p(R^\prime )<n$, for every set $K\subset S$ of cardinality $p$ there exists a demand point $i\in N$ which is not covered. Otherwise, there exists $K\subset S$ for which all demand points are covered and $C_p(R^\prime )=n$. Therefore, there exists $i\in N$ such that $\min _{j\in K}\left\{ d_{ij}\right\} >R^\prime$. For this $i$, for all $j\in K$ $\phi _{ij}=0$. By Lemma 3 $F(p)=0$. $\square$

The following Theorem provides a relationship between the maximin gradual cover model and set covering problems (Church and ReVelle 1974).

Theorem 3

If $p(r)\le p$, then the solution to (9) is $F(p)=1$. If $p(R^\prime )>p$, then the solution to (9) is $F(p)=0$. When solving the set covering problems: $p_{\min }=p(R^\prime )-1$ and $p_{\max }=p(r)$.

Proof

When $p(r)\le p$, at the solution set $K$ all demand points are covered. Therefore, for each $i\in N$ there exists $j\in K$ such that $d_{ij}\le r$ thus $\phi _{ij}=1$. By Lemma 1 $F(p)=1$ is the optimal solution. When $p(R^\prime )>p$, for every set $K\subset S$ of cardinality $p$ there exists a demand point $i\in N$ which is not covered by a distance of $R^\prime$. Otherwise, there exists $K\subset S$ for which all demand points are covered and $p(R^\prime )\le p$. Therefore, there exists $i\in N$ such that $\min _{j\in K}\left\{ d_{ij}\right\} >R^\prime \ge R$. For this $i$, $\phi _{ij}=0$ for all $j\in K$. By Lemma 3 $F(p)=0$. $\square$

4 Solution by heuristic algorithms

We devised an ascent and a tabu search algorithm that performed well. Other metaheuristic algorithms such as simulated annealing (Berman et al. 2009) and genetic algorithms (Alp et al. 2003) that were proposed for the solution of similar problems could be devised as well. We show the effectiveness of metaheuristics for solving this problem by testing these two approaches (ascent and tabu search). In preparation for any of the heuristic search algorithms, the distance matrix $\{d_{ij}\}$ between demand points and potential locations is calculated and the distances are replaced by $\phi _{ij}$.

4.1 The ascent approach

The ascent algorithm is straightforward. Let $K$ be a selected set of $p$ potential locations (with repetition). Since co-location of facilities is allowed, the search neighborhood consists of removing one of the $p$ selected potential locations and entering one of the other $s-1$ potential locations. We show in sect. 4.3 how to execute it in an efficient way.

4.2 Tabu search

Tabu search (Glover 1977, 1986; Glover and Laguna 1997) proceeds from the terminal solution of the ascent algorithm by allowing downward moves hoping to obtain a better solution in subsequent iterations. A tabu list of forbidden moves is maintained. Tabu moves stay in the tabu list for tabu tenure iterations. To avoid cycling, the forbidden moves are the reverse of recent moves. Similar to the ascent algorithm, the changes in the value of the objective function in the neighborhood are evaluated. If there is at least one move leading to a solution better than the best found solution, the best of such moves is executed and the tabu list emptied. If none of the moves leads to a solution better than the best found solution, the best permissible move (disregarding moves in the tabu list), whether improving or not, is executed. The process continues for a pre-specified number of iterations.

Each move involves removing a potential location in $j\in K$ and substituting it with a potential location $k\ne j$. The tabu list consists of potential locations recently removed from $K$ so they are not allowed to re-enter $K$. If a location is present more than once in $K$ it is entered into the tabu list and if the same location is removed again from $K$ because another facility is located at the same location, the tabu list is not increased but the point of entry into the tabu list is the last one. A convenient way to operationalize the tabu list is to record, for every potential location, the last iteration number at which it was removed from $K$. At the beginning all recorded numbers are large negative numbers. A potential location is in the tabu list if the difference between the current iteration number and the recorded number is less than or equal to the tabu tenure. This is especially convenient when the tabu tenure is a random variable that changes every iteration. An exchange between two potential locations is permissible if the potential location entering $K$ is not in the tabu list. The maximum possible number of entries in the tabu list is $s-1$. Following extensive experiments we used for the tabu tenure a randomly generated value between 5 and 95. The tabu tenure is randomly generated each iteration. A wide range for the tabu tenure was shown to yield good results in Drezner and Marcoulides (2009). The tabu search algorithm is summarized as follows:

• 1. A tenure vector consisting of an entry for each potential location is maintained.

• 2. The resulting set $K$ of the ascent algorithm is selected as a starting solution for the tabu search and as the best found solution. The number of iterations for the tabu search is set to $IT=10,000$ and $\mathrm{iter}=0$.

• 3. Every potential location in the tenure vector is assigned a large negative number.

• 4. Set $\mathrm{iter}=\mathrm{iter}+1$. If $\mathrm{iter}=IT$ stop with the best found solution as the tabu solution.

• 5. Otherwise, the tabu tenure, $T$, is randomly selected in the range $[5,95]$.

• 6. All moves (one node to be removed, $i_\mathrm{out}\in K$, and one node to be added, $i_\mathrm{in}\ne i_\mathrm{out}$) are evaluated and the value of the objective function is calculated for each.

• 7. If a move yields a solution better than the best found one, continue to evaluate all the moves and perform the best improving move. Update the best found solution and go to Step 3.

• 8. If no move yields a solution better than the best found solution, select the move which yields the best value of the objective function (whether improving or not) as long as the difference between the current iteration and the entry of $i_\mathrm{in}$ in the tenure vector exceeds $T$.

• 9. The current iteration number is entered into entry $i_\mathrm{out}$ of the selected move in the tenure vector. Go to step 4.

4.3 Efficient calculations

Calculating the value of the objective function for a given set $K$ requires $O(np)$ time. Therefore, calculating the $p(s-1)$ values of the objective function in the neighborhood requires $O(nsp^2)$ time. We can streamline the calculation and reduce the complexity by a factor of $p$. This can be implemented for both the ascent and tabu search approaches. We maintain two vectors $V^\prime$ and $V^{\prime \prime }$ of length $n$ such that for every $i\in N$: $v^\prime _i=\max _{j\in K}\{\phi _{ij}\}$ and $v^{\prime \prime }_i=\prod _{j\in K}(1-\phi _{ij})$. Potential locations $j\in K$ are checked in order for removal. For each such potential location, the two vectors are recalculated and saved in different vectors $\overline{V}^\prime , \overline{V}^{\prime \prime }$ retaining the original $V^\prime , V^{\prime \prime }$. It takes an $O(1)$ effort to recalculate each element in $\overline{V}^\prime$ and $\overline{V}^{\prime \prime }$, for an effort of $O(n)$. When a potential location $k\ne j$ is added to $K$, it takes $O(1)$ to recalculate each element of $\overline{V}^\prime$ and $\overline{V}^{\prime \prime }$ and therefore it takes $O(n)$ to calculate the value of the objective function. The phase of removing potential locations takes a total of $O(np)$ time, and the phase of adding potential locations takes a total of $O(nsp)$ time which is the complexity of one iteration, a saving by a factor of $p$.

4.4 Fine tuning the heuristics

A major problem with these heuristics (especially for a small value of $p$ which is close to $p_{\min }$) is that a large majority of feasible solutions have an objective function of 0 and all neighborhood members of such solutions have an objective function of zero as well. The ascent algorithm will stop at such solutions prematurely and tabu search is not likely to get a positive solution. In order to overcome this difficulty we took the following steps, each improving the performance (especially of tabu search) significantly.

• 1. Since there are many ties for the best improvement, we employed the tie breaker suggested in Drezner (2010). This means that during the scanning of all solutions in the neighborhood, if a solution in the neighborhood ties the best found solution so far during the scan, then it replaces the selected solution with a probability of $\frac{1}{k}$ if it is the $k$th tying solution. The first encountered best solution is always selected. A tying second solution replaces the first one with a probability of 50 %, and so on. The $k$th found tying solution replaces a previously selected solution with a probability of $\frac{1}{k}$. If eventually there are $T$ tying solutions, each solution is selected with a probability of $\frac{1}{T}$. This approach simplifies the selection process because we do not need to save all tying solutions prior to the selection.

• 2. We enter a random component to the probabilities $\phi _{ij}$, when $\phi _{ij}=0$ (i.e. $d_{ij}\ge R$), $\phi _{ij}$ is assigned $-10^{-11}u(d_{ij}-R)$ where $u$ is a random number in [0, 1]. This has three effects: (i) it creates a hierarchy among solutions with zero probability, and (ii) solutions whose excess of $R$ is smaller (i.e. closer to a positive probability) get preference in the selection, and (iii) preference is given to solutions with fewer demand points with $d_{ij}\ge R$.

4.5 A combined approach

Suppose we solve the set covering problem and find $p_{\min }=p(R^\prime )+1$ (Theorem 3) and its associated solution of potential locations. If $p> p_{\min }$ (otherwise we know that the solution is $F(p)=0$), then we can select as a starting solution the set covering solution plus randomly adding $p-p_{\min }$ potential locations. We can then apply the ascent algorithm or the tabu search. In addition, one can find $p_{\max }$ by solving another set covering problem and finding $p(r)$ just in case we can avoid solving this problem heuristically because we know that the optimal solution is $F(p)=1$. Note that the set covering problem needs to be solved only once even when the heuristic approach is repeated many times.

5 Computational experiments

The solution algorithms were programmed in Fortran using double precision arithmetic. The programs were compiled by the Intel 11.1 Fortran Compiler and run, with no parallel processing, on a desktop with the Intel 870/i7 2.93GHz CPU Quad processor, with 8GB memory. Only one thread was used.

5.1 Case study: cell phone towers in North Orange County, California

We investigated covering Northern Orange County, California with cell phone towers. Since cover of a tower depends on the strength of its signal we considered a generic tower with $r=2$ miles and $R=4$ miles with a linear decline in cover for $r\le d_{ij}\le R$. The 2000 census data for Orange County, California are given in Drezner (2004) and were also used in Drezner and Drezner (2007) and Berman et al. (2010a). There are 577 census tracts in the County. We selected the northernmost 131 census tracts, all with a $y$-coordinate of at least 30 miles, to be covered. The objective is to maximize the minimum cover of each census tract with $p$ towers located at the center of the census tract defining it. This means that $n=s=131$. We also investigated the sensitivity of the result to the value of $\theta$ by using $\theta =0.0,0.2,\ldots ,1.0$. Tabu search was replicated 10 times for each instance. Starting solutions were randomly generated and 10,000 iterations were used in the tabu search.

First, we established $p_{\min }$ and $p_{\max }$ by solving the set covering problem for $r$ and $R^\prime$, using Theorem 3. We found that $p_{\min }=4$ and $p_{\max }=13$. We therefore ran the tabu search for $p=5,6,\ldots , 12$. Incidentally, the range for $p$ for all 577 census tracts that cover all of Orange County, was $18\le p\le 52$. We decided not to present the results for all Orange County because it will necessitate a large volume of information. The results for Northern Orange County are depicted in Table 2. As expected, cover decreases with an increase in $\theta$. Run times ranged from 1 to 2.5 s for one run of tabu search.

Table 2 Minimum cover for the case study

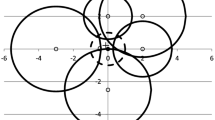
The configurations for locating eight facilities by the two extreme values of $\theta =0,1$ are depicted in Fig. 3. The two configurations are spatially very similar. The $\theta =1$ locations are generally closer to the periphery of the area. When applying $\theta =1$, each demand point is covered only by the closest facility and thus the minimum cover for the demand points on the periphery requires facilities closer to them. Note also that the minimum cover (see Table 2) increases from 70 % for $\theta =1$ to 85 % for $\theta =0$.

Fig. 3

Case study results for locating eight facilities

5.2 Results for test problems

The 40 Beasley (1990) problems designed for testing $p$-median problems were selected as test problems. When a distance between two nodes in the file appears more than once, the last distance is used. We used $\theta =0.2$, $r=10$, and $R=40$ with linear decline between $r$ and $R$. Both demand points and potential locations are nodes of the network. We first calculated $p_{\min }$ and $p_{\max }$ for each network by solving set covering problems and applying Theorem 3. The optimal solution is strictly between 0 and 1 only for problems with $p_{\min }< p< p_{\max }$. These values are given in Table 3. As can be seen from the table, many problems are defined with the number of facilities outside this range. In fact these are artificially constructed networks and we could not determine values of $r$ and $R$ for which the original $p$ for the 40 Beasley (1990) problems is in that range. Therefore, rather than using the original value of $p$ we used $p=p_{\min }+11$.

Table 3 Characteristics of the test problems

In Table 4, we report the results of the combined approach (see Sect. 4.5) followed by Ascent (C-Asc.), followed by tabu (C-Tabu), and running tabu search from a randomly selected starting solution. Both versions of tabu search were run for 10,000 iterations. For each of the three approaches, we report the number of times (out of 30,000 replications for C-Asc. and out of 100 for the two versions of tabu) that the best known solution was found, and total run time in minutes for all runs.

Table 4 Cover results by heuristic algorithms

C-Asc. found the best known solution at least once in only 22 problems out of 40, both versions of Tabu found it at least once for all 40 problems. C-Asc. found the best known solution in 5.3 % of the runs, C-Tabu found it in 75.9 % of the runs, while the regular tabu search found it in 67.9 % of the runs. Run times were comparable. C-Tabu performed best with the regular tabu second best. The ascent algorithm starting at a random solution performed very poorly so we opted not to report its results. The combined approach provided better results for both ascent and tabu.

6 Conclusions

We formulated and solved the multiple facilities gradual cover problem, maximizing the minimum cover across all demand points. We attempt to provide the best possible cover to the least-covered demand point. This is similar to the $p$-center objective where we attempt to minimize the farthest distance to all demand points and thus the least serviced demand point is served in the best possible way. Such an objective can be classified as an equity objective.

We solved the discrete version of the problem, i.e., there exists a finite set of potential locations for the facilities. The best solution approach suggested in this paper is a combination of set covering algorithm and tabu search. As future research we propose to investigate this problem when the potential locations for the facilities are anywhere in the plane.