A robust optimization approach to enhancing reliability in production planning under non-compliance risks

Abstract

Certain regulated industries are monitored by inspections that ensure adherence (compliance) to regulations. These inspections can often be with very short notice and can focus on particular aspects of the business. Failing such inspections can bring great losses to a company; thus, evaluating the risks of failure against various inspection strategies can help it ensure a robust operation. In this paper, we investigate a game-theoretic setup of a production planning problem under uncertainty in which a company is exposed to the risk of failing authoritative inspections due to non-compliance with enforced regulations. In the proposed decision model, the inspection agency is considered an adversary to the company whose production sites are subject to inspections. The outcome of an inspection is uncertain and is modeled as a Bernoulli-distributed random variable whose parameter is the mean of non-compliance probabilities of products produced at the inspected site and, therefore, is a function of production decisions. If a site fails an inspection, then all its products are deemed adulterated and cannot be used, jeopardizing the reliability of the company in satisfying customers’ demand. In the proposed framework, we address two sources of uncertainty facing the company. First, through the adversarial setting, we address the uncertainty arising from the inspection process as the company does not know a priori which sites the agency will choose to inspect. Second, we address data uncertainty via robust optimization. We model products’ non-compliance probabilities as uncertain parameters belonging to polyhedral uncertainty sets and maximize the worst-case expected profit over these sets. We derive tractable and compact formulations in the form of a mixed integer program that can be solved efficiently via readily available standard software. Furthermore, we give theoretical insights into the structure of optimal solutions and worst-case uncertainties. The proposed approach offers the flexibility of matching solutions to the level of conservatism of the decision maker via two intuitive parameters: the anticipated number of sites to be inspected, and the number of products at each site that are anticipated to be at their worst-case non-compliance level. Varying these parameters when solving for the optimal products allocation provides different risk-return tradeoffs and thus selecting them is an essential part of decision makers’ strategy. We believe that the robust approach holds much potential in enhancing reliability in production planning and other similar frameworks in which the probability of random events depends on decision variables and in which the uncertainty of parameters is prevalent and difficult to handle.

1 Introduction

One of the main objectives of production or manufacturing planning (Silver et al. 1998, Graves 2002) is satisfying customer requirements in the most effective, efficient, and reliable way. Typically, the achievement of these objectives, utilizing various modeling and planning techniques, is hindered by the presence of many sources of uncertainty. A recent exhaustive literature survey of models for production planning under uncertainty is given in Mula et al. (2006). This survey reveals that most models focus mainly on tackling demand uncertainty, which shows the need for the development of new models to address additional types of uncertainty.

In recent years, companies from various sectors are perpetually faced with additional sources of uncertainty and risk stemming from the increasing regulations enforced by governmental authorities to protect consumers’ best interest. For instance, current Good Manufacturing Practices (cGMPs) are enforced on pharmaceutical companies by the Food and Drug Administration (FDA) (2013). Another example is the Federal Communications Commission (FCC) rules that must be adhered to by companies in the Information, Technology, and Communication sector. The non-conformance with regulations can potentially cause the loss of revenues, market share, or customers’ trust, or can cause personal or criminal liabilities. Thus, companies try to achieve maximum compliance. Most companies implement a risk management system to deal with most of their risks, including non-compliance (Abrams et al. 2007; Beroggi and Wallace 1994; McNeil et al. 2005; Liebenbergm and Hoyt 2003). In 2008, the use of “governance, risk, and compliance” software, systems, and services (Frigo and Anderson 2009; Bamberger 2010), was estimated at $52.1 billion (Rasmussen 2008).

In this paper, we investigate a production planning adversarial decision model that addresses non-compliance risks. We consider a game-theoretic setup in which an authoritative inspection agency is modeled as an adversary to a company whose production sites are subject to inspections. If a site fails inspection, all products produced at that site are deemed adulterated and cannot be used to satisfy customers’ demand. Typically the agency’s inspection strategy is unknown to the company. The agency has limited inspection budget and full information about the company’s revenues. We take a worst-case perspective and assume that the agency utilizes the information it has in an attempt to minimize the total revenue of the company. Of course, in reality, this is not the case, but from a game-theoretic point of view, it is acceptable to assume an adversary to be prepared for the worst case. Furthermore, the stakes of the company in this game are high; if sites fail inspections, the reliability of the company in satisfying customers’ demand is heavily jeopardized. Thus, the strategy of the company is to choose a production plan that is best in the worst-case. We assume that the agency inspects only a subset of production sites, due to its limited budget, and for the same reason selects only a sample of products to inspect at each site. The outcome of a site inspection is uncertain and depends directly on the products produced. We model it as a Bernoulli-distributed random variable whose parameter, the probability of a site failing an inspection, is taken to be the mean of non-compliance probabilities of products produced at that site. What constitutes non-compliance varies depending on the type of business the company is in. For example, a product may be non-compliant to safety regulations and can cause a site to fail inspection if it exceeds a certain regulated threshold of production safety hazards. Using the mean to model probabilities of failure is based on the premise that the regulatory agency does not have enough information a priori about compliance levels, or the company’s internal operations, so it will take a neutral attitude towards which products to inspect at each site. Information about non-compliance levels of each product is provided by the company based on historical data and is generally uncertain, either because of limited availability of data or the difficulty in estimating their values.

The main contribution of this paper is to provide a general adversarial framework to deal with non-compliance risk in production planning to achieve more robustness in demand satisfaction and revenue generation. We tackle two sources of uncertainty facing the company. The first is the uncertainty arising from the inspection process, as the company does not know a priori which sites the agency will choose to inspect. The second is data uncertainty, which we address via robust optimization techniques. We develop a robust mixed integer program (MIP) that maximizes the worst-case expected revenue of a company and in addition addresses the uncertainty of model parameters, the compliance hazards of the products. With the use of duality theory, we are able to transform the initial bi-level adversarial problem into a single maximization one that can be solved with state-of-the-art commercial solvers. The proposed approach offers the flexibility of matching solutions to the level of conservatism of the decision maker via two intuitive parameters, the anticipated number of sites to be inspected, and the number of products at each site that are anticipated to be at their worst-case non-compliance level. Varying these parameters when solving for the optimal products allocation provides different risk-return tradeoffs and thus selecting them is an essential part of the decision makers strategy. We believe that the robust approach holds much potential in enhancing reliability in production planning and other similar frameworks in which the probability of random events depend on decision variables and in which the uncertainty of parameters is prevalent and difficult to handle.

The rest of the paper is organized as follows: in Sect. 2, we provide a literature review highlighting existing related approaches. In Sect. 3, we formally state the problem under investigation and provide a bi-level adversarial formulation. In Sect. 4, we give an exact compact reformulation of the bi-level problem and analyze the structure of its optimal solution. In Sect. 5, we extend the proposed model to address parameter uncertainty and provide insights into the optimal robust allocation and worst-case deviations of the uncertain parameters. We provide a numerical evaluation of the proposed approach in Sect. 6. We then conclude in Sect. 7.

2 Related literature

A literature review has indicated that there is very little work done in developing models, tools, and techniques to deal with non-compliance risks, and most efforts are recent. Muller and Supatgiat (2007) proposed a quantitative risk-based optimization model that dynamically provides the optimal set of feasible measures for achieving a certain level of compliance. Elisseeff et al. (2010) use causal networks based on a mixture of data and expert-driven modeling to quantify the exposure of a company to non-compliance risk and apply the approach to pharmaceutical manufacturing processes and IT systems availability. Pratsini and Dean (2005) apply statistical approaches to measure non-compliance risks from historical data and feed the resulting risk indices into an optimization model that minimizes the risk exposure and related costs of a company and maximizes its revenues.

The novelty of the approach proposed in this paper is twofold. First, as mentioned above, we develop a new decision model that simultaneously addresses two sources of uncertainty facing companies in regulated industries: one source of uncertainty stems from the random inspections conducted by authoritative agencies and the other source is from data (due to its limited availability or the inherent difficulty in estimating relevant metrics utilizing it). Second, the proposed framework combines the use of game-theory (in particular, an adversarial setup, which as we show is closely related to robust optimization), stochastic programming (using utility expectation and a two-stage formulation based on the game-theoretic setup, which can be cast as a single stage problem by utilizing the adversarial aspect of the game), and robust optimization (to deal with data uncertainty). Combining these different methodologies has proven to be unique and useful in aiding companies optimize their decisions in the face of noncompliance risks. In Takriti and Ahmed (2004), investigate “robust optimization” in the context of two-stage planning systems; however, “robust optimization” in their investigation refers to the model of Mulvey et al. (1995) and not to the methodology in Bental et al. (2009), which is the one we adopt. In McLay et al. (2012), investigate the application of robust optimization to a level-k game theory model for adversarial risk analysis, in which level-k game theory is a practical method for modeling bounded rationality and robust optimization is an alternative way to model the actions of conservative players facing uncertainties that are possible to bound but difficult to represent using probability theory.

Game theory (Nisan et al. 2007) and adversarial modeling are considered as an attractive framework for strategic and stochastic decision making and have been extensively used in a plethora of applications (such as, security Tambe 2011 and resource allocation Sacks and Harel 2006) mainly because games are a simple representation of reality and because adversarial setups are useful for risk analysis. Given the nature of the application studied in this paper (in particular, the inspection process), we have found that the use of a game-theoretic setup with an aggressive adversary (worst-case adversary) is beneficial in terms of enhancing the reliability of a production company in satisfying demand and in terms of providing guarantees on profits. As we will show in the numerical experiments, using a game-theoretic adversarial model outperforms a model that does not consider a game-theoretic setup, +++i.e. it only maximizes the expected profit without taking into consideration the random process of sites inspection.

As mentioned in the previous section, input parameters to the proposed adversarial optimization model are estimated using historical data and are generally uncertain, either due to limited availability of data or due to estimation errors. To deal with data and parameter uncertainties, we apply robust optimization techniques (Bental et al. 2009), which are generally known for their appealing tractability characteristic compared with stochastic programming or stochastic dynamic programming models, which are computationally intensive and suffer from the curse of dimensionality. Sahinidis (2004) provides a short overview and gives a lot of pointers to the existing theory that has been developed to deal with uncertainties in optimization problems; in particular, he references a few papers that utilize both stochastic programming and stochastic dynamic programming in production planning.

Robust optimization, in which one optimizes against worst-case possible realizations of data, dates back to the early 1970s when Soyster (1973) introduced a linear optimization model with solutions that are feasible for all data belonging to a convex set. His model was deemed too conservative and it was not until the 1990s that robust optimization emerged again when El Ghaoui et al. (1997, 1998), and independently Ben-Tal and Nemirovski (1999, 2000), derived robust counterparts for a number of convex optimization problems using ellipsoidal uncertainty sets. In this paper, we use a budgeted polyhedral uncertainty sets, an approach developed by Bertsimas and Sim (2004), in which a single intuitive parameter, referred to as the budget of uncertainty, limits the number of uncertain variables that can jointly reach their worst-case value and thus reflects different levels of risk-averseness or conservatism of the decision maker. In the numerical experiments we will show the benefits of addressing data uncertainty and compare a robust optimization formulation against a stochastic programming formulation. We observe that a deterministic model under-performs against the proposed robust model. We also observe that the robust optimization formulation outperforms the stochastic programming one in terms of CPU time and obtained solutions. However, in the stochastic programming formulation, we are only able to solve, in a reasonable amount of time, an instance that considers up to a 100 scenarios of input parameters.

3 Problem setup

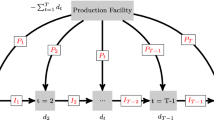
In this section, we describe the problem at hand in details and give a bi-level formulation that captures the adversarial aspect of the problem. The resulting bi-level formulation has a non-convex LP-formulation; therefore, we provide a convex reformulation in Lemma (1).

As mentioned above, we study a production planning problem under uncertainty. In the setup we consider, a production company is perpetually faced with large amounts of uncertainty and risks stemming from regulations enforced by governmental authorities to ensure the quality of products and the protection of consumers. Enforcement of regulations is generally established via regularly conducted inspections of production sites. Failing inspections due to non-compliance can potentially cause the loss of revenues, the loss of market share, or create personal or criminal liabilities. More importantly, it can also jeopardize the reliability of a company to satisfy demand. Therefore, it is important for companies to measure and manage their exposure to non-compliance risks. The model we will treat in this work aims at finding a suitable strategy reflecting a risk-return tradeoff that matches a company’s degree of risk-aversion.

We investigate a game-theoretic setup where the inspection agency is considered an adversary to the company whose production sites are subject to inspections. The decision structure of our problem follows the simple adversarial model proposed in Laumanns et al. (2010). In particular, we also consider a bi-level formulation based on a staged game-theoretic structure in which production decisions are made by the company, followed by the adversary’s actions, and then the outcome of those inspections and their effects on the revenue of inspected sites are reflected. The outcome of an inspection is modeled as a Bernoulli-distributed random variable whose parameter is the mean of non-compliance probabilities. In contrast to Laumanns et al. (2010), which pessimistically assumed that always the highest risk product is inspected, we here let the inspection take a random sample. This is a better match to industry practice and also avoids the low sensitivity of the former model with respect to adding or removing products other than the riskiest one. Based on this new nominal compliance risk model, our goal is to provide theoretical insights and detailed analysis of the benefits gained when adopting such a game-theoretic bi-level formulation. Since (Laumanns et al. 2010) is only an extended abstract, it did not include theoretical analysis. Furthermore, we provide a framework that handles uncertainty in the estimated non-compliance probabilities of the products, which was not addressed in Laumanns et al. (2010) at all.

We start our analysis with the bi-level formulation of our problem. The notation used for the problem data and decision variables is summarized in Table 1. The main objective of the company is to maintain its reliability in demand satisfaction that is jeopardized by the consequences of non-compliance. Each of its products has a site-specific compliance-level and production costs, but generates the same revenue regardless where it is produced. Moreover, each product is only allowed to be produced at a single production site. Given that the inspection agency has limited budget, it will only inspect $K$ sites, where $K \le S$. As mentioned above, the inspection strategy of the agency is unknown, but in the worst case it will pick those sites with highest expected revenues. Thus, the strategy of the company is to allocate products to sites in such a way that will minimize the probability of failing inspections and maximize its expected revenue in the worst-case. The following bi-level formulation achieves this goal:

$$\begin{aligned}&\displaystyle \max _{x,f} \,\,\, \displaystyle \min _{w \in \mathcal W } \displaystyle \sum _{s=1}^S\sum _{p=1}^P (g_{ps}\,x_{ps} - w_s\,r_p\,f_{ps}) \nonumber \\&\hbox {s.t.}\,\,\displaystyle (1-x_{ps}) + f_{ps} \ge \displaystyle \sum _{q=1}^P \frac{\tilde{h}_{qs}\,x_{qs}}{\left( \sum _{l=1}^P x_{ls}\right) }, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\displaystyle \sum _{p=1}^P x_{ps} \ge 1, \,\, \forall \,s \in \mathcal S ,\,\,\,\,\, \sum _{s=1}^S x_{ps} \le 1, \,\, \forall \,p \in \mathcal P ,\nonumber \\&\displaystyle 0 \le f_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\displaystyle x_{ps} \in \{0,1\}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \end{aligned}$$

(1)

In this model, $\mathcal W = \left\{ w_s \in \{0,1\}, \,\, \forall \,s \in \mathcal S \mid \sum _{s=1}^S w_s \le K \right\}$ is the feasible set of the inner minimization problem defined over the binary decision variables $w_s$ that indicate which of the $K \le S$ sites will be inspected. In practice, there are a number of production-related constraints on the decision variables $x_{ps}$, but we neglect them here for ease of notation since they are deterministic and can be added to Problem (1) above without changing the structural results.

Table 1 Problem data and decision variables used throughout the paper.

The objective function in (1) is the company’s total profit minus its expected losses from failing inspections. As mentioned above, the probability of a site $s$ failing an inspection, denoted $f_{ps}$, is given by the arithmetic mean of its products’ non-compliance probabilities and depends on allocation decisions $x_{ps}$ through the constraints

$$\begin{aligned} (1-x_{ps}) + f_{ps} \ge \sum _{q=1}^P \frac{\tilde{h}_{qs}\,x_{qs}}{\left( \sum _{l=1}^P x_{ls}\right) }, \,\, \forall \,p \in \mathcal P , s \in \mathcal S . \end{aligned}$$

(2)

In other words, the inspection works by picking one product at random, and if this product fails to meet the required standard (which for a particular product $p$ at site $s$ happens with probability $h_{ps}$), then the revenue of all products produced at $s$ is lost. The variable $f_{ps}$ will, therefore, represent the probability that a randomly chosen product fails inspection and will be taken as the site failure probability of $s$. The right-hand side of these constraints is guaranteed to be always defined via the constraints $\sum _{l=1}^P x_{ls} \ge 1$ for all $s \in \mathcal S$, which in turn guarantee that all sites are used for production. The constraints $\sum _{l=1}^S x_{ls} \le 1$ for all $p \in \mathcal P$ are used to satisfy the requirement that each product is allocated to only one production site. Note that the objective function in (1) is bi-linear. Also note that the LP-relaxation of the inner minimization problem in $w_s$ has a convex feasible set, but not the LP-relaxation of the outer maximization one, due to the non-convexity of the first set of constraints given in (2). The following lemma provides a convex reformulation of the LP-relaxation of the outer maximization problem:

Lemma 1

(Convex bi-level formulation) Introducing the auxiliary variables $A_{ps}$ and $B_{ps}$ for all $p \in \mathcal P$ and $s \in \mathcal S$, a convex reformulation of the LP-relaxation of (1) is given as follows:

$$\begin{aligned}&\displaystyle \max _{x,f} \,\,\, \displaystyle \min _{w \in \mathcal W } \displaystyle \sum _{s=1}^S\sum _{p=1}^P (g_{ps}\,x_{ps} - w_s\,r_p\,f_{ps}) \nonumber \\&\mathrm s.t. \,\,\displaystyle (1-x_{ps}) + f_{ps} \ge \displaystyle \sum _{q=1}^P \tilde{h}_{qs}\,A_{qs}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\displaystyle (1-x_{ps}) + A_{ps} \ge B_{qs} \,\, \forall \,p,q \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\displaystyle 0 \le A_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\displaystyle \sum _{p=1}^P B_{ps} \ge 1, \,\, \forall \,s \in \mathcal S ,\nonumber \\&\,\,\,\displaystyle 0 \le B_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\displaystyle \sum _{p=1}^P x_{ps} \ge 1, \,\, \forall \,s \in \mathcal S ,\,\,\,\,\, \sum _{s=1}^S x_{ps} \le 1, \,\, \forall \,p \in \mathcal P ,\nonumber \\&\,\,\,\displaystyle 0 \le f_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\displaystyle x_{ps} \in \{0,1\}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S . \end{aligned}$$

(3)

Proof

Let us consider the LP-relaxation of problem (1), i.e. all integer variables are relaxed to be continuous. We first note that for given values of $w_s$ for all $s \in \mathcal S$, the objective function of problem (1) is linear and minimizing in $f_{ps}$. Thus, at optimality, for all products allocated at site $s$ (i.e., $\forall \, p \in \mathcal P : x_{ps}=1$), the constraints $(1-x_{ps}) + f_{ps} \ge \sum _{q=1}^P \frac{\tilde{h}_{qs}\,x_{qs}}{\left( \sum _{l=1}^P x_{ls}\right) }$ will be tight and the corresponding values of $f_{ps}$ will be equal. We introduce the variables $A_{qs} \ge 0 \, \forall \, q \in \mathcal P , s \in \mathcal S$ to replace $\frac{x_{qs}}{\left( \sum _{l=1}^P x_{ls}\right) }$ in the right-hand side and add the constraints

$$\begin{aligned}&\displaystyle 0 \le A_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\displaystyle (1-x_{ps}) + A_{ps} \ge B_s, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\displaystyle B_s \ge \frac{1}{\left( \sum _{p=1}^P x_{ps}\right) }, \,\, \forall \,s \in \mathcal S , \end{aligned}$$

(4)

where $B_s, s \in \mathcal S$, are auxiliary variables utilized in this intermediate step. Again, note that the second and third set of constraints in (4) above will be tight at optimality because the objective function in (1) is linear and minimizing in $f_{ps}, \,\, \forall \,\, p \in \mathcal P , s \in \mathcal S$. We still have the non-convex constraints $B_s \ge \frac{1}{\left( \sum _{p=1}^P x_{ps}\right) }, \,\, \forall \,s \in \mathcal S$. We rewrite them as $\sum _{p=1}^P x_{ps}\,B_s \ge 1, \,\, \forall \,\, s \in \mathcal S$ and introduce the variables $B_{ps} \ge 0, \,\, \forall \,\, p \in \mathcal P , s \in \mathcal S$, along with the following constraints, to replace $x_{ps}\,B_s$:

$$\begin{aligned}&\displaystyle 0 \le B_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\displaystyle \sum _{p=1}^P B_{ps} \ge 1, \,\, \forall \,s \in \mathcal S . \end{aligned}$$

(5)

Finally, we change the right-hand side of the second set of constraints in (4) above and add the corresponding constraints

$$\begin{aligned} \displaystyle (1-x_{ps}) + A_{ps} \ge B_{qs} \,\, \forall \,p,q \in \mathcal P , s \in \mathcal S . \end{aligned}$$

(6)

With this, we have the linear mixed-integer outer maximization problem in (3). Note that for fixed values of $x_{ps},\,\, \forall \,\, p$ it is a linear program whose objective is linear and minimizing in $f_{ps}$ for all $p \in \mathcal P , s \in \mathcal S$ and its optimal solution is one of the extreme points of the polyhedron defining the feasible set. Therefore, for all $p \in \mathcal P$ with $x_{ps}=1$, the second set of constraints in (5) and the constraints in (6) will be tight at optimality, thus setting $A_{ps} = B_{ps} = \frac{1}{\left( \sum _{l=1}^P x_{ls}\right) }$ for all $s \in \mathcal S , p \in \mathcal P$ where $x_{ps}=1$. $\square$

Remark

Another way to convexify problem the LP-relaxation of (1) is to instead use the triple indexed variable $A_{lqs} \ge 0, \,\, \forall \, l,\,q,\, \in \mathcal P , \, s,\, \in \mathcal S$ to replace $\frac{x_{qs}}{\left( \sum _{l=1}^P x_{ls}\right) }$ in the right-hand side of the non-convex constraints $(1-x_{ps}) + f_{ps} \ge \sum _{q=1}^P \frac{\tilde{h}_{qs}\,x_{qs}}{\left( \sum _{l=1}^P x_{ls}\right) }, \,\, \forall \,p \in \mathcal P , s \in \mathcal S$, and add the following set of constraints:

$$\begin{aligned}&\displaystyle (1-x_{ps}) + f_{ps} \ge \sum _{q=1}^P {\tilde{h}_{qs}\,A_{lqs}} , \,\, \forall \,l,\,p \in \mathcal P , s \in \mathcal S \\&\displaystyle (1-x_{qs}) + \sum _{l=1}^P A_{lqs} \ge 1, \,\, \forall \,\, q \in \mathcal P ,\, s \in \mathcal S ,\\&\displaystyle 0 \le A_{lqs} \le x_{qs}, \,\, \forall \,\, l,q \in \mathcal P ,\, s \in \mathcal S ,\\&\displaystyle A_{lqs} \le x_{ls}, \,\, \forall \,\, l,q \in \mathcal P ,\, s \in \mathcal S . \end{aligned}$$

We have found that the reformulation proposed in Lemma 1 has a better performance in terms of computational time, which might be due to it having stronger LP relaxations. Therefore, we focus on it and use it thereafter.

4 Exact tractable formulation

One way to solve the bi-level problem in (3) is to use a naive approach, i.e., to iterate until convergence between solving the inner minimization problem for fixed values of $x_{ps}$ and solving the maximization problem for fixed values of $w_s$. Fixed values are obtained from the solution of the maximization and the minimization, respectively, in the previous iteration step. There are several drawbacks with this approach, the main of which is the lack of tractability. Thus, it can be computationally demanding, especially if a good starting feasible solution, of either the maximization or the minimization problems, was not available.

This section will detail how we derive a compact tractable formulation by transforming (3) into a single maximization problem. We build upon fundamental result linking total unimodularity and integer linear programming to show that the LP relaxation of the adversary’s decision problem in $w \in \mathcal W$ has a binary solution and then use strong duality theory to obtain its dual.

Theorem 2

(Compact Tractable Formulation)

• (i) For fixed values of $f_{ps}$, the solution of the LP-relaxation of the minimization in $w_s, s \in \mathcal S$ is the optimal solution of the original binary minimization problem.

• (ii) Utilizing (i), an exact tractable formulation of (3) is given by

  $$\begin{aligned}&\displaystyle \max _{x,f,\tau ,\theta } \; \displaystyle \sum _{p=1}^P \sum _{s=1}^S \left( g_{ps}\,x_{ps} - \tau _s\right) -K\,\theta \nonumber \\&\mathrm s.t. \; \displaystyle \sum _{p=1}^P r_p\,f_{ps} - \theta - \tau _s \le 0, \,\, \forall \,s \in \mathcal S ,\nonumber \\&\,\,\,\,\displaystyle (1-x_{ps}) + f_{ps} \ge \displaystyle \sum _{q=1}^P \tilde{h}_{qs}\,A_{qs}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle (1-x_{ps}) + A_{ps} \ge B_{qs} \,\, \forall \,p,q \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle 0 \le A_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle \sum _{p=1}^P B_{ps} \ge 1, \,\, \forall \,s \in \mathcal S ,\nonumber \\&\,\,\,\,\displaystyle 0 \le B_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle \sum _{p=1}^P x_{ps} \ge 1, \,\, \forall \,s \in \mathcal S ,\,\,\,\,\, \sum _{s=1}^S x_{ps} \le 1, \,\, \forall \,p \in \mathcal P ,\nonumber \\&\,\,\,\,\displaystyle 0 \le f_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle \tau _s \ge 0, \,\, \forall \,s \in \mathcal S ,\,\, \theta \ge 0,\nonumber \\&\,\,\,\,\displaystyle x_{ps} \in \{0,1\}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S . \end{aligned}$$

  (7)

Proof

(i) The constraints’ coefficient matrix, denoted $C$, of the LP-relaxation of the minimization problem in (3) is totally unimodular. If we partition the set consisting of the rows in $C$ into two disjoint sets, $C_1$ and $C_2$, where $C_1$ is a unity vector (the row of coefficients of the constraint $\sum _{s=1}^S w_s \le K$) and $C_2$ is an identity matrix (its rows are the coefficients of the set of constraints: $w_s \le 1, \,\, \forall \,s \in \mathcal S$), it can be seen that $C$ satisfies the following sufficient conditions for total-unimodularity : (1) every column in $C$ contains at most two non-zero entries (in fact, exactly two), (2) every entry in $C$ is either 0, or 1 and (3) the two non-zero entries of each column of $C$ have the same sign; the row of one is in $C_1$ and the other is in $C_2$. In addition to $C$ being totally unimodular, the right-hand side vector of the LP-relaxation constraints is integral. Thus, based on a fundamental result that links total unimodularity and integer linear programming (Schrijver 1986), each vertex of the polyhedron representing the feasible region of the LP-relaxation is an integer vector. This means that the LP-relaxation of the minimization problem in (3) has a binary optimal solution.

(ii) Utilizing the fact in part (i), we are able to invoke strong duality on the LP-relaxation to reformulate the minimization problem in (3) into a maximization one. We introduce the Lagrangian variables $\tau _s, \rho _s \,\, \forall \,s \in \mathcal S$ and $\theta$ and obtain the Lagrangian function

$$\begin{aligned} \displaystyle L\left( w,\tau ,\rho ,\theta \right) =\!-\!\sum _{s=1}^S\,\sum _{p=1}^P w_s\,r_p\,f_{ps} \!+\! \sum _{s=1}^S \left( \tau _s (w_s \!-\!1) - \rho _s\,w_s\right) \!+\! \theta \left( \sum _{s=1}^S w_s \!-\! K\right) . \end{aligned}$$

From the first-order conditions of the Lagrangian in $w_s$, we have

$$\begin{aligned} \displaystyle \sum _{p=1}^P r_p\,f_{ps} -\theta -\tau _s + \rho _s = 0, \,\, \forall \,s \in \mathcal S , \end{aligned}$$

(8)

and accordingly, the minimization problem in (3) can be replaced by

$$\begin{aligned}&\displaystyle \max _{\theta ,\tau } \displaystyle -\sum _{s=1}^S \tau _s - K\,\theta \nonumber \\&\hbox {s.t.} \displaystyle \sum _{p=1}^P r_p\,f_{ps} -\theta -\tau _s \le 0, \,\, \forall \,s \in \mathcal S ,\nonumber \\&\,\,\,\,\displaystyle \tau _s \ge 0, \,\, \forall \,s \in \mathcal S ,\,\, \theta \ge 0. \end{aligned}$$

(9)

$\square$

Theorem 3

(Structure of the optimal solution)

• (i) Let $F^*_s,\, \tau ^*_s$ and $\theta ^*$ denote the optimal value of $\sum _{p=1}^P r_p\, f_{ps}, \, \tau _s$ and $\theta$, respectively, in (7) above. If the $F^*_s, s \in \mathcal S$ were ranked in decreasing order of their value, i.e., $F^*_1 \ge \dots \ge F^*_S$, then for $\theta ^*\ge 0$ we have the following bounds:

  $$\begin{aligned} \theta ^*&\le F^*_s, \,\, \forall \,s \in \{1, \dots , K\}, \nonumber \\ \theta ^*&\ge F^*_s, \,\, \forall \,s \in \{K+1, \dots , S\}, \end{aligned}$$

  (10)

  where $K$ is the number of inspected sites. Furthermore, $\theta ^*$ can take any value in its range $F^*_K \ge \theta ^* \ge F^*_{K+1}$ rendering an equivalent optimal objective in (7) given by

  $$\begin{aligned} \displaystyle \sum _{s=1}^S g_{ps}\,x^*_{ps} - \sum _{s|F^*_s > F^*_{K+1}} F^*_s \end{aligned}$$

  (11)

  where $x^*_{ps}$ is the optimal value of $x_{ps}$.

• (ii) At optimality, we have $\theta ^*=F_K^*$ and $\tau ^*_K = 0$. Additionally, if all $F^*_s, s \in \mathcal S$, have unique values, i.e., $F^*_1 > \dots > F^*_S$, or sufficiently, $F^*_K$ has a unique value, then there are $K-1$ non-zero $\tau ^*_s$ values.

Proof

(i) To show that $\theta ^*$ has the bounds in (10), we utilize the following complementary slackness conditions:

$$\begin{aligned} \theta \, \left( \displaystyle \sum _{s=1}^S w_s - K \right) = 0, \end{aligned}$$

(12)

$$\begin{aligned} \tau _s\,\left( w_s - 1\right) =0, \,\, \forall \,s \in \mathcal S , \end{aligned}$$

(13)

$$\begin{aligned} \rho _s\,w_s = 0, \,\, \forall \,s \in \mathcal S . \end{aligned}$$

(14)

We also utilize Theorem 2, in which we have shown that, at optimality, $w_s$ will be integer for all $s \in \mathcal S$, either 0 or 1. Let $w_s^*$ and $\rho ^*_s$ denote the optimal values of $w_s$ and $\rho _s$ for all $s \in \mathcal S$. From conditions (13) and (14), we have:

• if $w_s^*=0$ then $\tau ^*_s = 0$ and $\rho ^*_s \ge 0$,

• if $w_s^*=1$ then $\rho ^*_s = 0$ and $\tau ^*_s \ge 0$.

By applying the first-order conditions (8), we have $\theta ^* = F^*_s + \rho _s^*$ and $\rho ^*_s \ge 0$ for all $s \in \mathcal S$ where $w_s^* = 0$, from which we obtain $theta^* \ge F^*_s$ for all $s$ where $w_s^* = 0$. Similarly, we have $\theta ^* = F^*_s - \tau _s^*$ and $\tau _s^* \ge 0$ for all $s$ where $w_s^* = 1$ and thus obtain $\theta ^* \le F^*_s$ for all $s$ where $w_s^* = 1$. If $F_s^*$ have unique values for all $s \in \mathcal S$, only one $\rho ^*_s$ for all $s$ with $w_s^* = 0$ or one $\tau ^*_s$ for all $s$ with $w_s^* = 1$, can be equal to zero, because $\theta ^*$ can only take a single unique value. Now, if $\theta ^* > 0$, then the condition in (12) ensures that $\sum _{s=1}^S w^*_s = K$, and since $w_s^*$ is binary for all $s \in \mathcal S$, it immediately follows that $K$ of the $w_s^*$ values are equal to $1$ and $S - K$ equal to 0. Thus, by assuming that the $F^*_s, s \in \mathcal S$ are ranked in decreasing order of their value, we directly obtain the bounds in (10). Notice that $\theta ^*$ can be equal to any value in the range $F^*_K \ge \theta ^* \ge F^*_{K+1}$, leading to an equivalent optimal objective value in (7):

$$\begin{aligned}&\displaystyle \sum _{s=1}^S g_{ps}\,x^*_{ps} - \sum _{s|F^*_s > F^*_{K+1}}\left( F^*_s - \theta ^* \right) -K\, \theta ^*\\&= \displaystyle \sum _{s=1}^S g_{ps}\,x^*_{ps} - \sum _{s|F^*_s > F^*_{K+1}} F^*_s + K\,\theta ^* -K\, \theta ^*\\&= \displaystyle \sum _{s=1}^S g_{ps}\,x^*_{ps} - \sum _{s|F^*_s > F^*_{K+1}} F^*_s \end{aligned}$$

where $x^*_{ps}$ denotes the optimal value of $x_{ps}$, and $\tau ^*_s = F_s^* - \theta ^* \,\, \forall \,s \, | \, F^*_s > F^*_{K+1}$ (or equivalently $\,\, w_s^* = 1)\,$, and $\tau ^*_s = 0,\,\, \forall \,s \, | F^*_s \le F^*_{K+1}$ $(\text{ or } \text{ equivalently }\,\, w_s^* = 0)\,$.

(ii) We established in (iii) above that $\theta ^*$ can take any value in the range $F^*_K \ge \theta ^* \ge F^*_{K+1}$ leading to the same optimal objective. However, since the objective is minimizing in $\tau _s$, and we have $\tau _s^* = \max \{F^*_s - \theta ^*,\,0\}, \,\, \forall \,s \in \mathcal S$, the optimization model in (7) will set $\theta ^*$ to its upper bound, $F_K^*$. It immediately follows that $\tau _K^*=0$. Now, if $F_s^*, \,\, \forall \,s \in \mathcal S$, have unique values, or sufficiently, $F_K^*$ is unique, then only one $\tau ^*_s,\,\, \forall \,s \, | \, w_s^* = 1$, is equal to zero, $\tau _K^*$, and the rest $(K-1)$ will be non-zero (recall that $\,\,\tau _s^* \ge 0,\,\, \forall \,s \, | \, w_s^* = 1$, and $\tau _s^*= 0,\,\, \forall \,s \, | \, w_s^* = 0$, and that $K$ of $w_s^*, \,\, \forall \,s \in \mathcal S$ are equal to $1$ and $S - K$ equal to 0). $\square$

Remark

Theorem 3 shows that, at optimality, only the $K$ highest $F_s^*$ appear in the objective function [see (11)], where $F_s^*$ is the optimal value of $\sum _{p=1}^P r_p\,f_{ps}$. Let $\mathcal S ^K \subseteq \mathcal S$ denote the set of sites $s \in \mathcal S$ associated with these $K$ highest $F_s^*$. Once this set is identified during the optimization process by the solver, the variables $f_{ps}$ associated with the rest of the sites (i.e. $f_{ps} \,\, \forall \, s \in \mathcal S \backslash \mathcal S ^K$) are not minimized any further but in effect are implicitly subject to the additional constraints:

$$\begin{aligned} \displaystyle \sum _{p=1}^P r_p\,f_{ps} \le F_K^*, \,\, \forall s \in \mathcal S \backslash \mathcal S ^K \end{aligned}$$

(15)

as a result, the focus of the solution algorithm shifts from minimizing $f_{ps} \,\, \forall \, s \in \mathcal S \backslash \mathcal S ^K$ to just satisfying the implicit constraints in (15). As $K$ increases, obtained solutions become more robust against the actions of the adversarial agency; however, they also become more conservative and computationally demanding. Thus, the company has to decide on a reasonable value for $K$ as part of its strategic plan in this game-theoretical setting.

5 Robust production planning model

In this section, we utilize robust optimization techniques, to deal with the uncertainty of parameters in model (7). We start by describing the uncertainty model based on the approach proposed by Bertsimas and Sim (2004). We then provide a robust mixed-integer linear program (MILP) for our production planning model under non-compliance risks, our main result.

5.1 Uncertainty model

We now start describing our uncertainty model to be utilized for the treatment of data uncertainty in our production planning model (7). We focus on uncertainties in non-compliance probabilities $\tilde{h}_{ps}$ , which ultimately affect the probabilities of sites failing inspections $f_{qs}$ through the constraints

$$\begin{aligned} \displaystyle (1-x_{qs}) + f_{qs} \ge \displaystyle \sum _{p=1}^P \tilde{h}_{ps}\,A_{ps}, \,\, \forall \,q \in \mathcal P , s \in \mathcal S . \end{aligned}$$

(16)

If non-compliance probabilities take different values than the nominal ones estimated by the company and used in solving (7), obtained solutions may become sub-optimal, particularly in the lower tail of the revenue distribution. Hence, mistakes in the estimation of the failure hazards would incur a higher risk of losing revenue.

In general, the estimation of failure probabilities is a central task in reliability analysis of engineering systems (Billinton and Allan 1992). Billinton and Allan (1996) point out that reasonable and acceptable data are not always easy to obtain and often subject to a considerable degree of uncertainty. We, therefore, attempt to account for this kind of uncertainty explicitly in our decision model by treating the estimated failure or non-compliance probabilities as intervals instead of point estimates and then adopt a robust optimization approach. We model non-compliance probabilities as uncertain parameters belonging to bounded symmetrical intervals, $\tilde{h}_{ps} \in [\bar{h}_{ps} - \hat{h}_{ps}, \bar{h}_{ps} + \hat{h}_{ps}] ,\,\, \forall \,p \in \mathcal P , s \in \mathcal S$, where $\bar{h}_{ps}$ is the nominal value given by the company with an estimation error of $\pm \hat{h}_{ps}$. Let $\tilde{z}_{ps}$ be a random variable in $[-1,1]$ that obeys an unknown symmetric distribution; the uncertain non-compliance probability $\tilde{h}_{ps}$ can then be represented as

$$\begin{aligned} \displaystyle \tilde{h}_{ps}= \bar{h}_{ps} + \hat{h}_{ps}\,\tilde{z}_{ps} ,\,\, \forall \,p \in \mathcal P , s \in \mathcal S . \end{aligned}$$

(17)

Robust optimization aims at providing solutions that are “reasonably” immune against worst-case possible realizations of data. This aligns with the company’s objective to be protected against downside risk without being overly conservative, because the latter can lead to missing gain opportunities or even incurring additional costs. From a modeling perspective, to achieve a trade-off between risk and return, we introduce a parameter $\Gamma _s$ for each $s \in \mathcal S$, which is referred to in the literature as the budget of uncertainty and limits the number of uncertain parameters allowed to reach their worst-case value through the additional constraints

$$\begin{aligned} \sum _{p=1}^P \left| \tilde{z}_{ps}\right| \le \Gamma _s, \,\, \forall \, s \in \mathcal S . \end{aligned}$$

(18)

Notice that we allow a budget of uncertainty $\Gamma _s$ for each production site $s \in \mathcal S$, as the uncertainty present in products’ non-compliance probabilities might be different at each site.

We now replace the right-hand sides of the constraints in (16) for each $q \in \mathcal P$ and $s \in \mathcal S$ with the maximization problem

$$\begin{aligned}&\displaystyle \max _{\tilde{z}} \displaystyle \sum _{p=1}^P \left( \bar{h}_{ps} + \hat{h}_{ps}\,\tilde{z}_{ps}\right) \,A_{ps}\nonumber \\&\hbox {s.t.}\displaystyle \sum _{p=1}^P \left| \tilde{z}_{ps}\right| \le \Gamma _s, \\&\,\,\,\,\left| \tilde{z}_{ps}\right| \le 1,\,\, \forall \,p \in \mathcal P .\nonumber \end{aligned}$$

(19)

If $\Gamma _s=0$, then all uncertain parameters $\tilde{h}_{ps}$ in (17) reduce to their respective point estimate at their nominal value $\bar{h}_{ps}$. On the other hand, if $\Gamma _s=P$, then $\tilde{z}_{ps}$ can take any value within their bounds $[-1,1]$, and all values $\tilde{h}_{ps}$ can deviate from their nominal value. When $\Gamma _s$ is selected to be between $0$ and $P$, only some of the uncertain parameters are allowed to deviate from their nominal values. This gives the company full control over the degree of conservatism of each of the constraints in (16) by adjusting the value of $\Gamma _s$ to a desired level of robustness against constraint violation.

In the following theorem, we make an observation with regards to the worst-case uncertainty that enables us to transform Problem (19) into a convex linear maximization problem over a polyhedral bounded set. Moreover, for a given site $s \in \mathcal S$, we describe the effect of the choice of $\Gamma _s$ on the size of the uncertainty set in relation to the number of products allocated at that site ($\sum _{p=1}^P x_{ps}$) .

Theorem 4

(Worst-Case Uncertainties and The Effect of $\Gamma _s$)

• (i) In the worst case, non-compliance probabilities are never less than their nominal values, i.e., at optimality, $\tilde{z}_{ps}$ is non-negative for all $p \in \mathcal P$ and $s \in \mathcal S$. Furthermore, for all $s \in \mathcal S$, (19) is equivalent to the following linear maximization problem in $z_{ps}$:

  $$\begin{aligned}&\displaystyle \max _{z} \displaystyle \sum _{p=1}^P \left( \bar{h}_{ps} + \hat{h}_{ps}\,z_{ps}\right) \,A_{ps}\nonumber \\&\mathrm s.t. \displaystyle \sum _{p=1}^P z_{ps}\le \Gamma _s, \\&\,\,\,\,0 \le z_{ps} \le 1,\,\, \forall \,p \in \mathcal P .\nonumber \end{aligned}$$

  (20)

• (ii) Let $J_s = \sum _{p=1}^P x_{ps}$. The optimal solution of the maximization problem (20) is the same for all values of $\Gamma _s \ge J_s$, and the constraint $\sum _{p=1}^P z_{ps} \le \Gamma _s$ will has an effect on the optimal value only if $\Gamma _s < J_s$.

• (iii) Let $H_s =\{ \hat{h}_{ps} \mid p \in \mathcal P \text { and } x_{ps}=1\}$. If the elements in $H_s$ were ranked in decreasing order of their value, i.e., $\hat{h}_{1s} \ge \dots \ge \hat{h}_{{J_s}s}$, then, for $\Gamma _s \le J_s$, the optimization problem (20) will set the uncertain parameters associated with the $\lfloor \Gamma _s\rfloor$ highest $\hat{h}_{.s} \in H_{s}$ to 1, and the one associated with $\left( \lfloor \Gamma _s\rfloor + 1\right)$-th largest $\hat{h}_{.s} \in H_{s}$ to $\left( \Gamma _s - \lfloor \Gamma _s\rfloor \right)$, i.e., $z_{js}=1, \,\, \forall \,\, j | \hat{h}_{js} \in H_{s}, j=1..\lfloor \Gamma _s\rfloor$, and $z_{qs}= \left( \Gamma _s - \lfloor \Gamma _s\rfloor \right) \, |\, \hat{h}_{qs} \in H_{s}, q = \lfloor \Gamma _s\rfloor + 1$.

Proof

• (i) For a given site $s \in \mathcal S$, the coefficients of $\tilde{z}_{ps},\,\, \forall \,p \in \mathcal P ,$ in the objective of (19) are non-negative, i.e., both $\hat{h}_{ps}\,, A_{ps} \ge 0, \,\, \forall \,p \in \mathcal P$. For fixed values of $A_{ps} \ge 0, \,\, \forall \,p \in \mathcal P$, the objective function is linear and maximized for the largest values of its arguments, $\tilde{z}_{ps},\,\, \forall \,p \in \mathcal P$. Therefore, we are able to introduce the variables $z_{ps} \in [0,1]$ to replace the absolute value of $\tilde{z}_{ps}$ in (19). This is intuitive, because in the worst-case, we expect probabilities of non-compliance to be higher than their nominal values, pushing the probability of a site failing an inspection to take on a higher value as well.

• (ii) From Lemma 1, by construction, we have $A_{ps}= \frac{x_{qs}}{\left( \sum _{l=1}^P x_{ls}\right) }, \,\, \forall \,p \in \mathcal P , s \in \mathcal S$. Thus, if $x_{ps}=0$ then $A_{ps}=0$ as well. As mentioned in (i) above, for fixed values of $x_{ps}, \,\, \forall \,p \in \mathcal P$, and accordingly $A_{ps}, \,\, \forall \,p \in \mathcal P$, the maximization problem in (20) is a linear program. Furthermore, the sum in the objective function will have exactly $J_s$ non-zero elements (the number of non-zero $A_{ps}$). Therefore, only $J_s$ of the variables $z_{ps}$ (those that are associated with $A_{ps} > 0$) can have an effect on the optimal solution of (20). Moreover, when $\Gamma _s \ge J_s$, the constraint $\sum _{p=1}^P z_{ps}\le \Gamma _s$ becomes redundant and is not necessarily tight at optimality.

• (iii) It immediately follows from (ii) above and the fact that (20) is a linear optimization problem in $z_{ps}$. In part (ii), we showed that $\Gamma _s$ should to be strictly less than $J_s$ to have an effect on the optimal objective; thus we focus on the range $\Gamma _s \le J_s$. Now, since the objective function in (20) is linear and maximized over a polyhedron, the optimal solution will be achieved at one of the corner points of the feasible set. In particular, if $\Gamma _s$ is integer, then the optimal corner point satisfies that $z_{ps} \in \,\{0,1\},\,\, \forall \,p \in \mathcal P$, because the constraints’ coefficient matrix is totally unimodular and the right-hand side vector is integral (i.e. we have an integral polyhedron) (Schrijver 1986). However, if $\Gamma _s$ is not integer, then the optimal corner point of the feasible set satisfies that $\lfloor \Gamma _s\rfloor$ of $z_{ps}$ are equal to 1, only one $z_{ps}$ is fractional $\in (0,1)$, and the rest of $z_{ps}$ is 0. If we define a set $H_{s} =\{ \hat{h}_{ps} \mid p \in \mathcal P \text { and } x_{ps}=1\}$ and assume that its elements were ranked in decreasing order of their value, then we immediately obtain the statement in (iii).

$\square$

Utilizing Theorem 4, Problem (7) becomes:

$$\begin{aligned}&\displaystyle \max _{x,f,\tau ,\theta } \displaystyle \sum _{p=1}^P \sum _{s=1}^S \left( g_{ps}\,x_{ps} - \tau _s\right) -K\,\theta \nonumber \\&\hbox {s.t.} \displaystyle \sum _{p=1}^P r_p\,f_{ps} - \theta - \tau _s \le 0, \,\, \forall \,s \in \mathcal S ,\nonumber \\&\,\,\,\,\displaystyle (1-x_{ps}) + f_{ps} \ge \displaystyle \max _{z_{\cdot s} \in \mathcal Z _s } \,\,\, \displaystyle \sum _{q=1}^P \left( \bar{h}_{qs} + \hat{h}_{qs}\,z_{qs}\right) \,A_{qs}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle (1-x_{ps}) + A_{ps} \ge B_{qs} \,\, \forall \,p,q \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle 0 \le A_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle \sum _{p=1}^P B_{ps} \ge 1, \,\, \forall \,s \in \mathcal S ,\nonumber \\&\,\,\,\,\displaystyle 0 \le B_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle \sum _{p=1}^P x_{ps} \ge 1, \,\, \forall \,s \in \mathcal S ,\,\,\,\,\, \sum _{s=1}^S x_{ps} \le 1, \,\, \forall \,p \in \mathcal P ,\nonumber \\&\,\,\,\,\displaystyle 0 \le f_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle \tau _s \ge 0, \,\, \forall \,s \in \mathcal S ,\,\, \theta \ge 0,\nonumber \\&\,\,\,\,\displaystyle x_{ps} \in \{0,1\}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S . \end{aligned}$$

(21)

In this model, $z_{\cdot s}$ means the vector $(z_{1s}, z_{2s}, \ldots , z_{Ps})^T$ and $\mathcal Z _s := \{ z_{\cdot s} \in [0,1]^P \mid \sum _{p=1}^P z_{ps}\le \Gamma _s\}$. We note that (21) is a mixed-integer non-linear program due to the nonlinearity of its feasible set. In the following section we invoke strong duality on Problem (20) to obtain a linear reformulation.

5.2 Mixed integer linear formulation for production planning under non-compliance risks

Hereunder, we focus on deriving a linear formulation of the model in (21). We then give some insights into the effects of the choice of $\Gamma _s$ on the structure of the optimal solution.

Theorem 5

(Robust Mixed Integer Linear Program) An equivalent linear formulation of Problem (21) is given by

$$\begin{aligned}&\displaystyle \max _{x,f,\tau ,\theta } \displaystyle \sum _{p=1}^P \sum _{s=1}^S \left( g_{ps}\,x_{ps} - \tau _s\right) -K\,\theta \nonumber \\&\hbox {s.t.} \displaystyle \sum _{p=1}^P r_p\,f_{ps} - \theta - \tau _s \le 0, \,\, \forall \,s \in \mathcal S ,\nonumber \\&\,\,\,\,\displaystyle (1-x_{ps}) + f_{ps} \ge \displaystyle \sum _{q=1}^P \bar{h}_{qs}\,A_{qs} + \Gamma _s\,\alpha _s + \sum _{q=1}^P \xi _{qs}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle \alpha _s + \xi _{ps} - \hat{h}_{ps}\,A_{ps} \ge 0,\,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle (1-x_{ps}) + A_{ps} \ge B_{qs} \,\, \forall \,p,q \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle 0 \le A_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle \sum _{p=1}^P B_{ps} \ge 1, \,\, \forall \,s \in \mathcal S ,\nonumber \\&\,\,\,\,\displaystyle 0 \le B_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle \sum _{p=1}^P x_{ps} \ge 1, \,\, \forall \,s \in \mathcal S ,\,\,\,\,\, \sum _{s=1}^S x_{ps} \le 1, \,\, \forall \,p \in \mathcal P ,\nonumber \\&\,\,\,\,\displaystyle 0 \le f_{ps} \le x_{ps}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle \tau _s \ge 0, \,\, \forall \,s \in \mathcal S ,\,\, \theta \ge 0,\nonumber \\&\,\,\,\,\displaystyle \xi _{ps}\ge 0, \,\, \forall \,p \in \mathcal P , s \in \mathcal S ,\, \alpha _s \ge 0, \,\, \forall \,s \in \mathcal S , \nonumber \\&\,\,\,\,\displaystyle x_{ps} \in \{0,1\}, \,\, \forall \,p \in \mathcal P , s \in \mathcal S . \end{aligned}$$

(22)

Proof

For fixed values of $A_{ps} \ge 0, \,\, \forall \,p \in \mathcal P$, Problem (20) is a linear maximization problem $\,\, \forall \,s \in \mathcal S$, and we thus utilize strong duality to obtain its dual. The Lagrangian function, $\,\forall \,s \in \mathcal S$, is given by

$$\begin{aligned} \displaystyle L_s\left( z, \alpha , \xi , \pi \right)&= \sum _{p=1}^P \left( \bar{h}_{ps} + \hat{h}_{ps}\,z_{ps}\right) \,A_{ps} \nonumber \\&\quad +\, \alpha _s\,\left( \Gamma _s \!-\! \sum _{p=1}^P z_{ps}\right) \!+\! \sum _{p=1}^P \xi _{ps}\left( 1 \!-\! z_{ps}\right) \!+\! \sum _{p=1}^P \pi _{ps}\,z_{ps}.\quad \end{aligned}$$

(23)

We set the gradient of the Lagrangian with respect to $z_{ps}$ to zero and accordingly obtain the following formulation, which is equivalent to (20):

$$\begin{aligned}&\displaystyle \min _{\alpha , \xi } \displaystyle \sum _{p=1}^P \bar{h}_{ps}\,A_{ps} + \Gamma _s\,\alpha _s + \sum _{p=1}^P \xi _{ps}\nonumber \\&\hbox {s.t.} \displaystyle \alpha _s + \xi _{ps} - \hat{h}_{ps}\,A_{ps} \ge 0, \,\, \forall \,p \in \mathcal P ,\nonumber \\&\,\,\,\, \displaystyle \alpha _s \ge 0,\,\, \xi _{ps}\ge 0, \,\, \forall \,p \in \mathcal P . \end{aligned}$$

(24)

Substituting to the optimization model in (21), we obtain the equivalent (22). $\square$

Remark

Note that Problems (9) and (24) are structurally identical and that the parameters $K$ and $\Gamma$ play the same role, known in the literature as budget-of-uncertainty. This shows that the proposed game-theoretic formulation is a robust one and that the feasible region of the adversary’s decisions, $\mathcal W$, is some sort of an uncertainty set. As both $K$ and $\Gamma$ increase, the size of the respective uncertainty sets increase as well, and through these two parameters the decision maker can adjust his level of conservatism (risk aversion), if the decision maker is more conservative, he sets $K$ and $\Gamma$ to a larger value, and vice versa.

The following theorem analyzes the effect of the choice of $\Gamma _s$ on the optimal solution of Problem (22).

Theorem 6

(Effect of $\Gamma _s$ on the Structure of the Optimal Solution)

• (i) Let $\alpha _s^*, \,\, \xi _{ps}^*$, and $A_{ps}^*$ denote the optimal value of $\alpha _s, \,\,\xi _{ps}$, and $A_{ps}$, respectively. If $\Gamma _s = 0, \,\, \forall \,s \in \mathcal S$, then Problem (22) reduces to the nominal problem without uncertainty. In particular, $\xi _{ps}^*=0, \,\, \forall \,p \in \mathcal P , \,s \in \mathcal S$, and $\alpha _s^* \ge \displaystyle \max _{p}\{\hat{h}_{ps}\,A_{ps}^*\},\,\, \forall \,s \in \mathcal S$.

• (ii) Let $J^*_s = \sum _{p=1}^P x^*_{ps}$, where $x^*_{ps}$ is the optimal value of $x_{ps}$. If $\hat{h}_{ps}\,A_{ps}^*,\,\, \forall \,p \in \mathcal P$ were ranked in decreasing order of their value, i.e., $\hat{h}_{1s}\,A_{1s}^* \ge \cdot \ge \hat{h}_{Ps}\,A_{Ps}^*$, then for $\Gamma _s \le J^*_s$, we have the following bounds on $\alpha _s^*$:

  $$\begin{aligned} \alpha _s^*&\le \hat{h}_{ps}\,A_{ps}^*, \,\, \forall \,p \in \{1, \dots , \lfloor \Gamma _s\rfloor \}, \nonumber \\ \alpha _s^*&\ge \hat{h}_{ps}\,A_{ps}^*, \,\, \forall \,p \in \{\left( \lfloor \Gamma _s\rfloor +1\right) , \dots , P\}. \end{aligned}$$

  (25)

  At optimality, if $\Gamma _s$ is integer, then $\alpha ^*_s = \hat{h}_{\lfloor \Gamma _s\rfloor s}\,A_{\lfloor \Gamma _s\rfloor s}^*, \,\, \forall \,s \in \mathcal S$, and accordingly, $\xi ^*_{ps} = \left( \hat{h}_{ps}\,A_{ps}^* - \alpha ^*_s\right) > 0, \,\, \forall \,p \in \{1, \dots , \left( \lfloor \Gamma _s\rfloor -1\right) \}$, and $\xi ^*_{ps} = 0, \,\, \forall \,p \in \{\lfloor \Gamma _s\rfloor , \dots , P\}$. If $\Gamma _s$ is not integer, then $\alpha ^*_s = \hat{h}_{\left( \lfloor \Gamma _s\rfloor +1\right) \, s}\,A_{\left( \lfloor \Gamma _s\rfloor +1\right) \, s}^*, \,\, \forall \,s \in \mathcal S$, $\xi ^*_{ps} =\left( \hat{h}_{ps}\,A_{ps}^* - \alpha ^*_s\right) > 0, \,\, \forall \,p \in \{1, \dots , \lfloor \Gamma _s\rfloor \}$, and $\xi ^*_{ps} = 0, \,\, \forall \,p \in \{\lfloor \Gamma _s\rfloor , \dots , P\}$.

• (iii) If $\Gamma _s > J^*_s$ then $\alpha _s^*=0$ and $\xi _{ps}^*= \hat{h}_{ps}\,A^*_{ps}$.

Proof

• (i) We utilize the following complementary slackness conditions, obtained from invoking strong duality on Problem (20):

  $$\begin{aligned} \alpha _s\,\left( \Gamma _s - \sum _{p=1}^P z_{ps}\right) = 0,\ \,\, \forall \,s \in \mathcal S , \end{aligned}$$

  (26)
  $$\begin{aligned} \xi _{ps}\,\left( 1 - z_{ps}\right) = 0,\ \,\, \forall \,p \in \mathcal P , \,s \in \mathcal S , \end{aligned}$$

  (27)
  $$\begin{aligned} \pi _{ps}\,z_{ps} = 0,\ \,\, \forall \,p \in \mathcal P , \,s \in \mathcal S , \end{aligned}$$

  (28)

  If $\Gamma _s=0,\ \,\, \forall \,s \in \mathcal S$, then $,z_{ps} = 0,\ \,\, \forall \,p \in \mathcal P , \,s \in \mathcal S$. Accordingly, from (27), we have $\xi _{ps}^*=0, \,\, \forall \,p \in \mathcal P , \,s \in \mathcal S$. Thus, at optimality, the objective in (24) reduces to $\sum _{p=1}^P \bar{h}_{ps}\,A^*_{ps}$ and $\alpha _s^* \ge \displaystyle \max _{p}\{\hat{h}_{ps}\,A_{ps}^*\},\ \,\, \forall \,s \in \mathcal S$.

• (ii) From the first-order conditions of the Lagrangian (23), along with (27) and (28) above, we obtain the bounds $\alpha _s^* \le \hat{h}_{ps}\,A_{ps}^*, \,\, \forall \,p \in \mathcal P \,|\, z_{ps}=1$ and $\alpha _s^* \ge \hat{h}_{ps}\,A_{ps}^*, \,\, \forall \,p \in \mathcal P \,|\, z_{ps} < 1$. Moreover, $\xi ^*_{ps} = \hat{h}_{ps}\,A_{ps}^* - \alpha ^*_s, \,\, \forall \,p \in \mathcal P \,|\, z_{ps}=1$ and $\xi ^*_{ps} = 0, \,\, \forall \,p \in \mathcal P \,|\, z_{ps} < 1$. In Theorem 4, we showed that if $\Gamma _s \le J^*_s$, then $\lfloor \Gamma _s \rfloor$ of the variables $z_{ps}, \,\, \forall \,p \in \mathcal P$ is equal to 1 at optimality. Thus, if we rank $\hat{h}_{ps}\,A_{ps}^*,\,\, \forall \,p \in \mathcal P$ in decreasing order of their value, we immediately yield the bounds in (25). Note that, if $\Gamma _s$ is integer, then $\alpha ^*_s$ can take any value in its range rendering an equivalent optimal objective:

  $$\begin{aligned} \displaystyle \sum _{p=1}^P \bar{h}_{ps}\,A^*_{ps} + \left( \Gamma _s - \lfloor \Gamma _s\rfloor \right) \,\alpha ^*_s + \sum _{p \in \{1, \dots , \lfloor \Gamma _s\rfloor \}} \hat{h}_{ps}\,A_{ps}^* \end{aligned}$$

  (29)

  however, when $\Gamma _s$ is integer, $\alpha ^*_s = \hat{h}_{\Gamma _s\,s}\,A_{\Gamma _s\, s}^*, \,\, \forall \,s \in \mathcal S$, because Problem (24), $\,\, \forall \,s \in \mathcal S$, is also minimized with respect to $\xi _{ps}$, which is decreasing in $\alpha _s$. If $\Gamma _s$ is not integer, then $\alpha ^*_s$ is at its lower bound so that (29) is minimized, i.e., $\alpha ^*_s = \hat{h}_{\left( \lfloor \Gamma _s\rfloor +1\right) \, s}\,A_{\left( \lfloor \Gamma _s\rfloor +1\right) \, s}^*, \,\, \forall \,s \in \mathcal S$ . We obtain $\xi _{ps}^*$ accordingly.

• (iii) The objective in (24) is minimizing in $\xi _{ps}$, thus at optimality, $\xi ^*_{ps} = \max \{\hat{h}_{ps}\,A_{ps}^* - \alpha ^*_s, \,0\}$. Now, if the constraint $\sum _{p=1}^P z_{ps} \le \Gamma _s$ in Problem (20) is not tight at optimality, then we are done, because (26) will ensure that $\alpha _s^*=0$, and accordingly, $\xi ^*_{ps}=\hat{h}_{ps}\,A_{ps}^*$. Now, assume that the constraint is tight at optimality, in which case $\alpha ^*_s \ge 0$. Again, if $\alpha ^*_s=0$, then we are done. However, if $\alpha ^*_s$ is strictly greater than $0$, then from the first-order conditions, $\pi _{ps} > 0, \,\, \forall \,p \,|\, A_{ps}^*=0$, because $\xi _{ps} \ge 0$. From (28), if $\pi _{ps} > 0, \,\, \forall \,p \,|\, A_{ps}^*=0$, then $z_{ps}=0, \,\, \forall \,p \,|\, A_{ps}^*=0$. As was shown earlier in the proof of Theorem 4, we have $P - J_s^*$ of the variables $A_{ps}^*, \,\, \forall \,p \in \mathcal P$ equal to $0$, and accordingly, only $J_s^*$ of $z_{ps}, \,\, \forall \,p \in \mathcal P$ can be non-zero at optimality. If $\Gamma _s > J_s^*$, then we have a contradiction, because the constraint cannot be tight as assumed, even if all of $z_{ps}, \,\, \forall \,p$ that can be non-zero are at their upper bound. It immediately follows that $\alpha _s^* = 0$, if $\Gamma _s > J_s^*$. $\square$

Remark

As was mentioned in the remark under Theorem 3, after the set $\mathcal S ^K$ is identified, the focus of the solution algorithm shifts from minimizing the variables $f_{ps} \,\, \forall \, s \in \mathcal S \backslash \mathcal S ^K$ to satisfying the implicit constraints in (15) (i.e. the focus shifts to maintaining feasibility). Note that this may result in suboptimal solutions to the robust problem in (24) and consequently may create a duality gap between it and the original problem (20). However, it will not affect the optimal solution of the overall problem in (22). In effect, this is creating a link between the choice of $K$ and the robust problem (24) (some sort of a switch); as $K$ increases, the computational complexity of the overall model increases, because the robust problems associated with sites $s \in \mathcal S ^K$ must be solved to optimality, rather than just maintaining feasibility.

In the Sect. 6, we provide numerical experiments that show the superior performance of the proposed robust approach to the one that does not take into account parameter uncertainty, the nominal model in (7).

5.3 A stochastic programming formulation

As an alternative to the robust optimization model derived and analyzed above, we now give an alternative stochastic programming model to address the uncertainty of the product hazards. We consider a standard two-stage SP formulation, in which the second stage problem approximates the expected profit by the average over a finite number of $\Omega$ scenarios for the uncertain $\tilde{h}_{sp}$ values, for a given production plan $x$ and the worst-case inspection set.

$$\begin{aligned} \begin{array}{l@{\quad }l} \max \quad \displaystyle \frac{1}{|\Omega |} \sum _{\omega =1}^{|\Omega |} \sum _{p=1}^P \sum _{s=1}^S \left( g_{ps}\,x_{ps} - \tau _s^{(\omega )}\right) -K\,\theta ^{(\omega )} &{}\\ \hbox {s.t.} \quad \displaystyle \sum _{p=1}^P r_p\,f_{ps}^{(\omega )} - \theta ^{(\omega )} - \tau _s^{(\omega )} \le 0, \,\, \forall \,s \in \mathcal S &{} \forall \omega \in \Omega \\ \displaystyle (1-x_{ps}) + f_{ps}^{(\omega )} \ge \displaystyle \sum _{q=1}^P h_{qs}^{(\omega )}\,A_{qs}^{(\omega )} &{} \forall \,p \in \mathcal P , s \in \mathcal S , \forall \omega \in \Omega \\ \displaystyle (1-x_{ps}) + A_{ps}^{(\omega )} \ge B_{qs}^{(\omega )} &{} \forall \,p,q \in \mathcal P , s \in \mathcal S , \forall \omega \in \Omega \\ \displaystyle 0 \le A_{ps}^{(\omega )} \le x_{ps} &{} \forall \,p \in \mathcal P , s \in \mathcal S , \forall \omega \in \Omega \\ \displaystyle \sum _{p=1}^P B_{ps}^{(\omega )} \ge 1 &{} \forall \,s \in \mathcal S , \forall \omega \in \Omega \\ \displaystyle 0 \le B_{ps}^{(\omega )} \le x_{ps} &{} \forall \,p \in \mathcal P , s \in \mathcal S , \forall \omega \in \Omega \\ \displaystyle \sum _{p=1}^P x_{ps} \ge 1 &{} \forall \, s \in \mathcal S \\ \sum _{s=1}^S x_{ps} \le 1 &{} \forall \,p \in \mathcal P \\ \displaystyle 0 \le f_{ps}^{(\omega )} \le x_{ps} &{} \forall \,p \in \mathcal P , s \in \mathcal S , \forall \omega \in \Omega \\ \displaystyle \tau _s^{(\omega )} \ge 0 &{} \forall \,s \in \mathcal S \\ \theta ^{(\omega )} \ge 0 &{} \forall \omega \in \Omega \\ \displaystyle x_{ps} \in \{0,1\} &{}\forall \,p \in \mathcal P , s \in \mathcal S , \end{array} \end{aligned}$$

(30)

The second stage, scenario-dependent decision variables in the model are $x$, $f^{(\omega )}$, $A^{(\omega )}$, $B^{(\omega )}$, $\tau ^{(\omega )}$, $\rho ^{(\omega )}$, and $\theta ^{(\omega )}$. Thus, as typical for a SP formulation, the model size (number of decision variables and constraints) increases linearly with $|\Omega |$ and thus will be practically solvalbe only for relatively small sample sizes. Facing a high dimensionality of the uncertainty set (we have $P \cdot S$ variables $\tilde{h}_{sp}$), it is not clear whether a small number of scenarios will give sufficient information for the model to generate a production plan that performs well across the entire uncertainty range. We will investigate this question in our numerical experiments as well.

6 Numerical experiments

The purpose of this section was to analyze the performance of the proposed model and to show its effectiveness in enhancing the reliability of production decisions. We measure performance in terms of both percentiles and the cumulative distribution function of the expected profit distribution (we use profits as an indicator of demand satisfaction).

The experimental setting is based on a real analysis for the regulatory compliance risk of a pharmaceutical manufacturing company. The data used were synthetically generated based on the relative values of the real case. We consider a company that has to allocate 15 products to 4 production sites; thus $P=15$ and $S=4$. Tables 2 and 3 display the data.

Table 2 Data used for our numerical results: $r$ is a vector of products’ total revenues and $rc$ is a matrix with each element representing the portion of a product’s total revenue realized as profit when produced at a given site; thus when multiplying this fraction by a product’s total revenue, we obtain gross profit $g_{ps}$ ($g_{ps} = rc_{ps}*r_p$)

Table 3 Data used for numerical experiments: $\bar{h}$ is a matrix with each element representing the nominal value of the probability of a product failing an inspection at a given site and $\hat{h}$ is the positive deviation from $\bar{h}$

In our numerical study, we investigate

• 1. the effectiveness of using an adversarial game-theoretic setup for modeling the random process of sites’ inspection. We compare the proposed adversarial model with a model, hereafter referred to as Model-1, that does not consider a game-theoretic setup and only maximizes the expected profit without taking into consideration uncertainties stemming from the inspection process. This model is obtained by setting the parameter $K$ in (22) to zero. Note that the purpose here is to show the need for addressing uncertainties arising from the random inspection process rather than comparing the use of game-theory against other tools to treat these uncertainties.

• 2. the effectiveness of using robust optimization techniques to deal with data uncertainty.

  • We first compare the proposed robust model against a deterministic model, hereafter referred to as Model-2, which considers a game-theoretic setup, but does not address parameters uncertainty; in particular, it does not take into account estimation errors of products’ non-compliance probabilities. This model is obtained by setting the parameter $\Gamma$ in (22) to zero.

  • We then compare the proposed robust model against one, hereafter referred to as Model-3, that addresses data uncertainty via stochastic programming instead of robust optimization. Model-3 is the stochastic program detailed in (30).

• 3. the effect of varying the number of anticipated inspections $K$ and the sizes of uncertainty sets $\Gamma _s, \,\, \forall \, s \in \mathcal S$ on optimal product allocations.

6.1 Numerical experiments setup

We solve the robust optimization problem in (22) for different values of $K$ and $\Gamma _s, \,\, \forall \, s \in \mathcal S$ and obtain the optimal products allocation. We use the same value of $\Gamma _s$ for all sites $\, s \in \mathcal S$; thus, for convenience, we denote it as $\Gamma$ throughout this section. We also solve the stochastic program in (30) for different values of $K$ and $|\Omega |$ (where $|\Omega |$ is the cardinality of the set of scenarios $\Omega$). Using the optimal allocation, we then run simulations with 10,000 scenarios, varying products non-compliance levels $h_{ps}, \,\, \forall \, p, \in \mathcal P , \, s \in \mathcal S$ by sampling them from their respective support $[0,\bar{h}_{ps}+\hat{h}_{ps}]$, and then calculate the total expected profit of the company.

6.2 Comparison against Model-1

Figure 1 exhibits the performance of the adversarial approach against Model-1 ($K=0$) through the corresponding empirical cumulative distribution functions (CDFs) of the expected profit, assuming that the agency inspects half of the sites. The CDFs are obtained for optimal allocations of model (22) with K=0:S (i.e. by varying the number of sites that the company is anticipating will be inspected) and with $\Gamma =2$.

Fig. 1

Empirical CDF showing the performance of our robust model (22) for different values of $K$ and with $\Gamma =2$, when the agency inspects half of the sites

We observe that the game-theoretic setup has the effect of shifting the expected profit distribution to the right, and as a result, albeit indirectly, it provides higher guarantees regarding the reliability of production decisions (product allocation) in the face of the random inspection process. Additionally, the probability of a worst-case realization of expected profit is much lower for the proposed adversarial approach than for Model-1. These observations indicate that (1) addressing uncertainties arising from the random process of inspections is beneficial and (2) using an adversarial game-theoretic setup to do so seems to be an effective tool.

6.3 Comparison against Model-2

Figure 2 shows the percentage difference between our proposed model (22) and Model-2 ($\Gamma =0$) for the 5th, 50th, and 95th percentiles of the expected profit distribution. We note that the results for $\Gamma =5:15$ are identical to those of $\Gamma =4$ and thus are omitted here. We observe that addressing uncertainty in the estimation of failure probability is beneficial. We also observe that the performance of the robust approach proposed here relies on the choice of parameter $\Gamma$. By choosing “reasonable” values for $\Gamma$, the decision maker is protected against risks arising from data uncertainty in the order of the size of uncertainty ranges (i.e. ranges for failure probabilities, which are generally in the order of 1–2 %). A value of $\Gamma =2$ is shown to be a good choice for the results in Fig. 2.

Fig. 2

Percentage difference, between our proposed model (22) for $\Gamma =0:4$ and Model-2 ($\Gamma =0$), of the 5th, 50th, and 95th percentiles of the expected profit distribution, with $K=2$

We can draw similar conclusions from Fig. 3, which shows the percentage difference between our model and Model-2 for the 99 %-VaR and 99 %-CVaR (Value-at-Risk and Conditional Value-at-Risk, respectively), but additionally, we observe that the robust approach (22) generally provides more pronounced gains in the left tail of the expected profit distribution, which shows that the model focuses on improving bad outcomes. Notice that, as mentioned above, in both figures we only show results for up to $\Gamma =4$, because for $\Gamma =5:15$, results are identical to those of $\Gamma =4$. This is in support of Part $(ii)$ of Theorem 4.

Fig. 3

Percentage difference, between our proposed model (22) for $\Gamma =0:4$ and Model-2 ($\Gamma =0$), of the 99 %-VaR and 99 %-CVaR of the expected profit distribution, with $K=2$

In Fig. 4 we show empirical CDFs of expected profits for optimal allocations obtained by varying the value of $\Gamma$ in (22), which again shows that a choice of $\Gamma =2$ provides the highest benefit to the decision maker.

Fig. 4

Empirical CDF showing the performance of our robust model (22) for different values of $\Gamma$ and with $K=2$

Addressing uncertainty in the estimation of failure probabilities via robust optimization techniques has the same effect as that of the adversarial setup, in that it also shifts the expected profit distribution to the right, providing higher guarantees on future profits and on the reliability of production decisions. Notice that the choice of $\Gamma$ critically affects the performance of the proposed approach.

6.4 Comparison against Model-3

We contrast results from our robust model in (22) with that of Model-3 [the stochastic program in (30)]. We obtain optimal allocations from Model-3 using different number of scenarios $|\Omega | \in \{ 10, 25, 50, 75, 100 \}$. For each instance of Model-3, with a fixed number of scenarios, we run the model several times (5 runs) by randomly sampling the scenario set for each run.

In Table 4, we compare the solution time of our approach against that of the stochastic program (Model-3) with different number of scenarios. We see that for Model-3, the solution time grows exponentially with the number of scenarios considered, which is one of the known disadvantages of stochastic programming formulations (the curse of dimensionality).

Table 4 A comparison in solution times between our proposed robust model in (22) and the stochastic programming model in (30) when using 10, 25, 50, 75, and 100 scenarios

In Fig. 5, we show the percentage differences, between our robust model and Model-3 (with different number of scenarios and multiple runs), for the 5th, 50th, and 95th percentiles of the expected profit distribution. We observe that our model outperforms all instances of Model-3. We also observe that the performance of Model-3 is sensitive to the set of scenarios used. For example, we see that for one of the runs of Model-3 with 25 randomly sampled scenarios, Model-3 performs the best (the smallest percentage difference against our model) across all other runs with the same or different number of scenarios.

Fig. 5

Percentage difference, between our proposed model (22) with $\Gamma =2$ and Model-3 [the stochastic program in (30)], of the 5th, 50th, and 95th percentiles of the expected profit distribution, with $K=2$. Note that for Model-3 we use different number of scenarios $|\Omega |$ (the x axis), and for each instance of Model-3 with a fixed number of scenarios, we run the model several times (5 runs) by randomly sampling the scenario set for each run

In Figs. 6 and 7, we again report performance in terms of the 5th, 50th, and 95th percentiles of the expected profit distribution, but now contrast the performance of our model against the mean (in Fig. 6) and median (in Fig. 7) performance of Model-3 across the 5 runs of each instance with different number of scenarios. We observe, from Fig. 7, that the median performance of Model-3 is identical across all instances and, from Fig. 6, that the instance with 25 scenarios has the best mean performance against our model.

Fig. 6

Percentage difference, between our proposed model (22) with $\Gamma =2$ and Model-3 [the stochastic program in (30)], of the 5th, 50th, and 95th percentiles of the expected profit distribution, with $K=2$. Note that for Model-3 we use different number of scenarios $|\Omega |$ (the x axis), and for each instance of Model-3 with a fixed number of scenarios, we compare against the mean performance over 5 runs (where for each run we randomly sample the scenario set)

Fig. 7

Percentage difference, between our proposed model (22) with $\Gamma =2$ and Model-3 [the stochastic program in (30)], of the 5th, 50th, and 95th percentiles of the expected profit distribution, with $K=2$. Note that for Model-3 we use different number of scenarios $|\Omega |$ (the x axis), and for each instance of Model-3 with a fixed number of scenarios, we compare against the median performance over 5 runs (where for each run we randomly sample the scenario set)

From the above, we notice that Model-3 is more sensitive to the choice (quality) of scenarios than to the number of scenarios used. This may suggest that the stochastic programming formulation (30) can be used with a small number of “hand-picked” scenarios that not only reflects the level of risk-aversion of the decision maker but also that leads to product allocations with better performance over the robust model in (22). However, “hand-picking” scenarios is generally not an easy task, and in our model, it is also not obvious how to do so, due to the fact that the probability of a site failing an inspection in a given scenario $\omega$ ($f^\omega _{ps}$ in (30)) is a function of production decisions. Therefore, choosing a scenario for the matrix $h$ will require some consideration of possible product allocation and also some consideration of how multiple scenarios will jointly affect optimal allocation.

6.5 Numerical experiments summary

Results show that the robust adversarial approach shifts the tail distribution, and in some cases the whole distribution, of expected profit to the right, providing higher guarantees for achieving certain amounts of profit and for potentially maintaining the reliability of demand satisfaction. Results also show that it is beneficial to address both sources of uncertainty, the one arising from the random inspection of sites and the other from input data. Moreover, using robust optimization to treat data uncertainty seems to be a more effective than using stochastic programming.

7 Conclusions and managerial implications

The main contribution of this work is providing a general adversarial framework that addresses non-compliance risks in production planning and that enhances the reliability of devised production plans. We give a robust MIP that maximizes the expected worst-case profit of a company and that addresses the uncertainty in model parameters. With the use of duality theory, we are able to transform a proposed bi-level adversarial problem into a robust and compact formulation that can be efficiently solved via readily available standard software. Furthermore, we give theoretical insights into the structure of optimal solutions and worst-case uncertainties. The proposed approach offers the flexibility of matching solutions to the level of conservatism of the decision maker in two intuitive parameters, the anticipated number of sites to be inspected, and the number of products at each site that are anticipated to be at their worst-case non-compliance level. Varying these parameters when solving for the optimal products allocation provides different risk-return tradeoffs and thus choosing them is an essential part of decision makers’ strategy. We give some insights into how to select these parameters. We also provide an empirical evidence that exhibits the superior performance of the devised model. We believe that the robust approach holds much potential in enhancing reliability in production planning and other similar frameworks in which the probability of random events depend on decision variables and in which the uncertainty of parameters is prevalent and difficult to handle.

Managerial implications of our model are twofold. First, the model enables companies in regulated industries to improve their business or manufacturing practices and to align them with imposed regulations which ultimately serves the purpose of these regulations. For example, in the pharmaceutical industry, companies must align their production plans with the FDA’s “current Good Manufacturing Practices”, not only to avoid the large negative impact of non-compliance, but also to continue keeping customer’s trust, safety, and satisfaction. Second, the framework proposed can aid in companies’ strategic planning. Back to the pharmaceutical example above, when companies want to introduce a new product they may need to obtain the FDA’s approval regarding the location or even the circumstances surrounding the introduction of this new product. In this case, our model can serve as a strategic tool in planning ahead to identify the safest locations for producing the new product.