1 Introduction

Over the past several years, population structure has become an integral part of the foundations of evolutionary game theory (Nowak et al. 2009). Among the popular settings for evolutionary processes in finite populations are networks (Lieberman et al. 2005; Ohtsuki et al. 2006; Szabó and Fáth 2007; Taylor et al. 2007; Lehmann et al. 2007), sets (Tarnita et al. 2009a), and demes (Taylor et al. 2001; Wakeley and Takahashi 2004; Rousset 2004; Ohtsuki 2010; Hauert and Imhof 2012). A common way in which to study such a process is to use it to define an ergodic Markov chain and then examine the equilibrium distribution of this chain. One could take a birth–death or imitation process on a network, for example, and incorporate a small strategy mutation rate, \(\mu \), that eliminates the monomorphic absorbing states (Fudenberg and Imhof 2006). This Markov chain will have a unique stationary distribution, \(\lambda \), which is a probability distribution over the set of all strategy configurations on the network. This set of all possible configurations—the state space of the Markov chain—is quite large and difficult to treat directly; one seeks a way in which to use this distribution to determine which strategies are more successful than others.

A prototypical process in evolutionary game theory is the (frequency-dependent) Moran process. Classically, this process takes place in a well-mixed population and proceeds as follows: at each discrete time step, a player is selected for reproduction with probability proportional to fitness. A member of the population is then chosen for death uniformly at random and is replaced by the offspring of the individual chosen for reproduction (Moran 1958). The fitness of a player is calculated from a combination of (i) the outcome of a sequence of two-player games and (ii) the intensity of selection (Nowak et al. 2004; Taylor et al. 2004). For example, in the donation game, each player in the population is either a cooperator (strategy \(C\)) or a defector (strategy \(D\)). A cooperator provides a benefit \(b\) to the opponent at a cost of \(c\), whereas a defector provides no benefit and incurs no cost (Ohtsuki et al. 2006; Sigmund 2010). The payoff matrix for this game is

(1)

A player adds the payoffs from the two-player interactions with his or her neighbors to arrive at a total payoff value, \(\pi \). If \(\beta \geqslant 0\) represents the intensity of selection, then the total payoff value is converted to fitness via \(f:=\exp \left\{ \beta \pi \right\} \) (Traulsen et al. 2008; Maciejewski et al. 2014). For our purposes, we will assume that \(\beta \ll 1\), i.e., that selection is weak. This assumption is necessary here for technical reasons, but it turns out to be quite sensible for many applications of game theory to biology since most organisms possess multiple traits and no single trait (strategy) is expected to have a particularly strong influence on fitness (Tarnita et al. 2011; Wu et al. 2013a). This frequency-dependent Moran process has two absorbing states: all \(C\) and all \(D\). If \(\varepsilon >0\) is a small mutation rate, one may define a modified process by insisting that the offspring inherit the strategy of the parent with probability \(1-\varepsilon \) and take on a novel strategy with probability \(\varepsilon \). The small mutation rate eliminates the monomorphic absorbing states of the process, resulting in a Markov chain with a unique stationary distribution. This setup is readily extended to structured populations and is precisely the type of process we wish to study here.

Rather than looking at the long-run stationary distribution of the Markov chain itself, one may instead consider just the proportion of each strategy in this equilibrium. This approach ignores particular strategy configurations and suggests a natural metric for strategy success: when does selection increase the abundance, on average, of a particular strategy? Such conditions are determined by a multitude of factors: game type, payoff values, update rule, selection strength, mutation rates, population structure, etc. In the limit of weak selection, these conditions are the so-called “\(\sigma \)-rules” or selection conditions, which are given in terms of linear combinations of the payoff values of the game, with coefficients independent of these values (Tarnita et al. 2009b, 2011; Van Cleve and Lehmann 2013). The coefficients appearing in these linear combinations are often referred to as “structure coefficients” to indicate their dependence on the structure of the evolutionary process. What is remarkable about these \(\sigma \)-rules is that they can be stated with very few assumptions on the underlying evolutionary process and do not change when the payoff values are varied.

Tarnita et al. (2011) state a selection condition for games with \(n\) strategies and payoff values that are determined by an \(n\times n\) matrix. This rule is extremely simple and is stated as a sum of pairwise payoff comparisons, weighted by three structure coefficients. Implicit in this setup is the assumption that the aggregate payoff to each player is determined by the individual payoffs from his or her pairwise interactions. In many cases, this assumption is reasonable: The Prisoner’s Dilemma, Snowdrift Game, Hawk–Dove Game, etc. are defined using pairwise interactions, and a focal player’s total payoff is simply defined to be the sum of the pairwise payoffs. This method of accounting for payoffs essentially defines a multiplayer game from smaller games, and this property of the multiplayer game produces a simple selection condition regardless of the number of strategies.

Multiplayer games that are not defined using pairwise interactions have also been studied in evolutionary dynamics (Broom et al. 1997; Broom 2003; Kurokawa and Ihara 2009; Ohtsuki 2014; Peña et al. 2014). One of the most prominent multiplayer games arising in the study of social dilemmas is the public goods game. In the public goods game, each player chooses an amount to contribute to a common pool and incurs a cost for doing so; the pool (“public good”) is then distributed equally among the players. In the linear public goods game, this common pool is enhanced by a factor \(r>1\) and distributed evenly among the players: if players \(1,\ldots ,d\) contribute \(x_{1},\ldots ,x_{d}\in \left[ 0,\infty \right) \), respectively, then the payoff to player \(i\) is

$$\begin{aligned} u_{i}\left( x_{1} , \ldots , x_{d} \right)&= \underbrace{r\left( \frac{x_{1} + \cdots + x_{d}}{d} \right) }_{\mathrm{player} \,{ i}{\hbox {'}}\mathrm{s\, share\, of\, the \,public\, good}} - \underbrace{x_{i}}_{\mathrm{player}\, { i}\hbox {'}\mathrm{s\, contribution}} \end{aligned}$$
(2)

(Archetti and Scheuring 2012). In well-mixed populations, the linear dependence of these distributions on the individual contributions allows one to break down the multiplayer payoff into a sum of payoffs from pairwise interactions, one for each opponent faced by a focal player (Hauert and Szabó 2003). Thus, in this setting, the linear public goods game is equivalent to a two-player matrix game and the study of its dynamics does not require a theory of multiplayer games. We will see that this phenomenon is fortuitous and does not hold for general multiplayer games in structured populations. In particular, a theory of two-player matrix games suffices to describe only a subset of the possible evolutionary games.

Wu et al. (2013b) generalize the rule of Tarnita et al. (2011) and establish a \(\sigma \)-rule for multiplayer games with two strategies. The number of coefficients needed to define this \(\sigma \)-rule grows linearly with the number of players required for each interaction. The strategy space for the linear public goods game could be chosen to be \(\left\{ 0,x\right\} \) for some \(x>0\), indicating that each player has the choice to (i) contribute nothing or (ii) contribute a nonzero amount, \(x\), to the public good. The rule of Wu et al. (2013b) applies to this situation, and the number of coefficients appearing in the selection condition is a linear function of the number of players in the interaction. On the other hand, knowing that the linear public goods game can be reduced to a sequence of pairwise games allows one to apply the rule of Tarnita et al. (2011), giving a selection condition with three structure coefficients regardless of the number of players required for each public goods interaction. Thus, knowing that a game can be reduced in this way can lead to a simpler selection condition.

Assuming that payoff values can be determined by a single payoff function, such as the function defined by a \(2\times 2\) payoff matrix, is somewhat restrictive. Typically, a game is played by a fixed number of players, say \(d\), and there is a function associated to this game that sends each strategy profile of the group to a collection of payoff values, one for each player. For degree-homogeneous population structures, i.e., structures in which every player has \(k\) neighbors for some \(k\geqslant 1\), one can define a \(d\)-player game for \(d\leqslant k+1\) and insist that each player derives a total payoff value by participating in a collection of \(d\)-player interactions with neighbors. On the other hand, if degree-heterogeneous structures are considered instead, then some players may have many neighbors while others have few. Rather than fixing \(d\) first, one can often define a family of payoff functions, parametrized by \(d\). For example, suppose that the number of players involved in an interaction varies, and that each player chooses a strategy from some finite subset \(S\) of \(\left[ 0,\infty \right) \). For a group of size \(d\) and strategy profile \(\left( x_{1},\ldots ,x_{d}\right) \in \left[ 0,\infty \right) ^{\oplus d}\), define the payoff function for player \(i\) to be

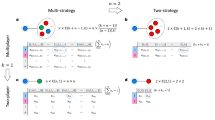
$$\begin{aligned} u_{i}^{d}\left( x_{1} , \ldots , x_{i} , \ldots ,x_{d} \right)&:= r\left( x_{1}\ldots x_{d} \right) ^{\frac{1}{d}} - x_{i} , \end{aligned}$$
(3)

where \(r>1\). This payoff function may be thought of as defining a nonlinear version of the public goods game, but for the moment the interpretation is not important. We will later see that these payoff functions cannot be reduced in the same way that those of the linear public goods game can, regardless of the population structure. This property suggests that each function in this family must be considered separately in the setting of evolutionary game theory. If player \(i\) has \(k_{i}\) neighbors, then each player may initiate a \(\left( k_{i}+1\right) \)-player game with all of his or her neighbors and receive a payoff according to \(u_{i}^{k_{i}+1}\). Thus, a family of payoff functions like this one is relevant for studying evolutionary games in degree-heterogeneous structured populations since one function from this collection is needed for each distinct integer appearing as a degree in the population structure (see Fig. 1). It follows that a general evolutionary game could potentially involve many distinct payoff functions.

Fig. 1
figure 1

Each player initiates an interaction with all of his or her neighbors, and the players in this group receive a payoff according to the family of payoff functions \(\left\{ u^{d}\right\} _{d\geqslant 2}\), where \(u_{i}\left( x_{1},\ldots x_{i},\ldots ,x_{d}\right) =r\left( x_{1}\ldots x_{d} \right) ^{\frac{1}{d}} - x_{i}\). The total payoff value to a particular player is calculated as the sum of the payoffs from each interaction in which he or she is involved. These total payoff values are indicated in the diagram. For this network, the functions \(u^{2}\), \(u^{3}\), and \(u^{4}\) are needed to calculate the total payoffs

Full size image

Even for games in which the payoff values for pairwise interactions are determined by a \(2\,\times \,2\) matrix, the overall payoff values may be calculated in a nonlinear fashion due to synergy and discounting of accumulated benefits in group interactions (Hauert et al. 2006), and this nonlinearity can complicate conditions for one strategy to outperform another (Li et al. 2014). For example, if \(\pi _{1},\ldots ,\pi _{d-1}\) are the payoff values from \(d-1\) pairwise interactions between a focal player and his or her neighbors, then the total payoff to the focal player might be \(\sum _{k=1}^{d-1}\delta ^{k-1}\pi _{k}\), where \(\delta \) is some discounting factor satisfying \(0<\delta <1\). It might also be the case that \(\delta >1\), in which case \(\delta \) is not a discounting factor but rather a synergistic enhancement of the contributions. In each of these situations, the overall payoff is not simply the sum of the payoffs from all pairwise interactions. This observation, combined with the example of the linear public goods game, raises an important question: when is a multiplayer game truly a multiplayer game, and not a game whose payoffs are derived from simpler interactions? To address this question, we introduce the notion of reducibility of payoff functions. Roughly speaking, a payoff function is reducible if it is the sum of payoff functions for games involving fewer players. Our focus is on games that are irreducible, ie. games that cannot be broken down in a manner similar to that of the linear public goods game. We give several examples of irreducible games, including perturbations of the linear public goods game that are irreducible for any number of players. The existence of such perturbations illustrates that one can find irreducible games that are “close” to reducible games, and indeed one can define irreducible games from straightforward modifications of reducible games.

In the absence of reductions to smaller games, new \(\sigma \)-rules are needed in order to determine the success of chosen strategies. For games with many strategies and multiplayer interactions, these rules turn out to be quite complicated. We show how many structure coefficients appear in the selection condition for these games and give several examples of explicit \(\sigma \)-rules. In particular, for \(d\)-player interactions with \(n\) strategies, we show that the number of structure coefficients appearing in these rules grows like a polynomial of degree \(n-1\) in \(d\). If \(d=2\) or \(n=2\), these rules recover the results of Tarnita et al. (2011) and Wu et al. (2013b), respectively. Although the selection conditions are concise for pairwise interactions with many strategies and for multiplayer interactions with two strategies, explicit calculations of structure coefficients can be difficult even for simple population structures (Gokhale and Traulsen 2011; van Veelen and Nowak 2012; Wu et al. 2013b; Du et al. 2014). Here we do not treat the issue of calculating structure coefficients (although we do some calculations for special cases), but instead focus on extending the \(\sigma \)-rules to account for more complicated games. More complicated games generally require more structure coefficients, and we quantify precisely the nature of this relationship.

2 Reducible games

We begin by looking at multiplayer interactions in the simplest type of population.

2.1 Well-mixed populations

In a finite, well-mixed population, each player is a neighbor of every other player. In the language of evolutionary graph theory, the interaction matrix of a well-mixed population is simply a complete graph, and edges between nodes indicate who interacts with whom. Suppose that the population size is \(N=d\), and let \(u_{i}:S^{d}\rightarrow {\mathbb {R}}\) be the payoff function for player \(i\) in a \(d\)-player game, ie. reflecting interactions with all other members of the population. Although the population is well-mixed, it may still be the case that the payoff to player \(i\) depends on \(i\). If this \(d\)-player game can be “reduced,” it should ideally be composed of several games with fewer players, and it should be possible to derive the payoffs from interactions in smaller groups. For example, if payoff values from pairwise interactions are determined by the matrix

(4)

then the payoff to a focal player using \(A\) against \(j\) opponents using \(A\) (and \(d-1-j\) opponents using \(B\)) is

$$\begin{aligned} a_{j}&= ja + \left( d-1-j\right) b . \end{aligned}$$
(5)

In this setting, the payoff to a focal individual depends on only (i) his or her strategy and (ii) the number of opponents playing each strategy, so the function \(u\) defines a \(d\)-player game. By construction, this \(d\)-player payoff function was formed by adding together \(d-1\) payoff values from \(2\times 2\) games, so it can be “reduced” into a sequence of pairwise interactions. Of course, this type of reducibility is stronger than one can hope for in general since it requires all interactions in the smaller games to involve only two players. Starting with an \(d\)-player payoff function, a natural question to consider is whether or not the \(d\)-player interaction can be reduced into a sequence of smaller (but not necessarily two-player) games. The following definition of reducibility in well-mixed populations captures this idea:

Definition 1

(\(k\)-reducibility) \(u\) is \(k\)-reducible if (i) there exists a collection of payoff functions for groups of size \(m\leqslant k\),

$$\begin{aligned} \left\{ \Big \{ v^{\left\{ i_{1},\ldots ,i_{m}\right\} } : S^{m}\rightarrow {\mathbb {R}}^{m} \Big \}_{\left\{ i_{1},\ldots ,i_{m}\right\} \subseteq \left\{ 1,\ldots ,d\right\} } \right\} _{m=2}^{k}, \end{aligned}$$
(6)

such that for each \(i=1,\ldots ,d\) and \(\left( s_{1},\ldots ,s_{d}\right) \in S^{d}\),

$$\begin{aligned} u_{i}\left( s_{1} , \ldots , s_{d} \right)&= \sum _{m=2}^{k}\sum _{\left\{ i_{1},\ldots ,i_{m-1}\right\} \subseteq \left\{ 1,\ldots ,d\right\} -\left\{ i\right\} } v_{i}^{\left\{ i,i_{1},\ldots ,i_{m-1}\right\} }\left( s_{i} , s_{i_{1}} , \ldots ,s_{i_{m-1}} \right) , \end{aligned}$$
(7)

and (ii) \(k\) is the smallest positive integer for which (i) holds.

The reducibility condition of Definition 1 says that the \(d\)-player game may be broken down into a collection of subgames, each with at most \(k\) players, but that it cannot be broken down any further. The sum \(\sum _{\left\{ i_{1},\ldots ,i_{m-1}\right\} \subseteq \left\{ 1,\ldots ,d\right\} -\left\{ i\right\} }\) appearing in this definition simply means that we sample all subsets of size \(m-1\) from the neighbors of the focal player. The order in which these players are sampled is irrelevant; we care only about each subset as a whole. The quantity \(v_{i}^{\left\{ i,i_{1},\ldots ,i_{m-1}\right\} }\left( s_{i} , s_{i_{1}} , \ldots ,s_{i_{m-1}} \right) \) is the payoff to player \(i\) in the \(m\)-player subgame when he or she plays \(s_{i}\) and player \(i_{j}\) plays \(s_{i_{j}}\), where \(i_{j}\) is the \(j\)th interaction partner of player \(i\). These smaller games are well-defined since the population is well-mixed: each player can participate in a multiplayer interaction with any subset of the population. We say that a game is simply reducible if it is \(k\)-reducible for some \(k<d\), and irreducible otherwise.

Although Definition 1 is stated for arbitrary payoff functions, we will mainly work with symmetric payoff functions:

Definition 2

(Symmetric payoff function) A payoff function \(u\) for an \(d\)-player game is symmetric if, for each \(i\in \left\{ 1,\ldots ,d\right\} \),

$$\begin{aligned} u_{i}\left( s_{1} , \ldots , s_{d} \right)&= u_{\pi ^{-1}\left( i\right) }\left( s_{\pi \left( 1\right) } , \ldots , s_{\pi \left( d\right) } \right) . \end{aligned}$$
(8)

whenever \(\left( s_{1},\ldots ,s_{d}\right) \in S^{d}\) and \(\pi \in {\mathfrak {S}}_{d}\), where \({\mathfrak {S}}_{d}\) is the group of permutations on \(d\) letters. \(\pi ^{-1}\) is just the inverse permutation of \(\pi \), and \(\pi ^{-1}\left( i\right) \) is the player using strategy \(s_{i}\) after rearrangement according to \(\pi \).

In other words, a game is symmetric if the payoffs depend on only the strategies being played and not on identities, types, or locations of the players. Intuitively, if a symmetric game is reducible into a sequence of smaller games, then these smaller games should also be symmetric. Indeed, if \(u\) is symmetric and reducible, then the functions \(v^{\left\{ i,i_{1},\ldots ,i_{m-1}\right\} }\) need not themselves be symmetric, but they can be replaced by symmetric functions:

Proposition 1

If \(u\) is reducible and symmetric, then the functions \(v^{\left\{ i_{1},\ldots ,i_{m-1}\right\} }\) may be chosen so that they are symmetric and depend only on \(m\) \((\)as opposed to the particular choice of opponents\()\). That is, the overall \(d\)-player game may be broken down into a sequence of smaller symmetric games, one for each number of opponents.

A proof of Proposition 1 may be found in Appendix A. The basic idea behind the proof is that one may exploit the symmetry of \(u\) to average over the asymmetric functions \(v^{\left\{ i_{1},\ldots ,i_{m-1}\right\} }\) and thus obtain “symmetrized” versions of these functions.

Remark 1

Proposition 1 simplifies the process of showing that a game is reducible. It is often easier to first write down a reduction via smaller asymmetric games rather than directly establishing a reduction via symmetric games. One may simply establish the existence of the asymmetric subgames of Definition 1, and then the reducibility to symmetric subgames follows from the proposition. In the proof of Proposition 1, we give explicit symmetrizations of the payoff functions \(v_{i}^{\left\{ i,i_{1},\ldots ,i_{m-1}\right\} }\), which can be quite complicated in general.

Ohtsuki (2014) defines the notion of degree for symmetric multiplayer games with two strategies: Suppose that \(S=\left\{ a,b\right\} \), and let \(a_{j}\) (resp. \(b_{j}\)) denote the payoff to an \(a\)-player (resp. \(b\)-player) against \(j\) opponents using \(a\) and \(d-1-j\) opponents using \(b\). There are unique polynomials \(p\left( j\right) \) and \(q\left( j\right) \) in \(j\) of degree at most \(d-1\) such that \(a_{j}=p\left( j\right) \) and \(b_{j}=q\left( j\right) \), and the degree of the game is defined to be \(\max \left\{ \deg p, \deg q\right\} \). This concept of degree is closely related to our notion of reducibility:

Proposition 2

If \(n=2\), then a game is \(k\)-reducible if and only if its degree is \(k-1\).

The proof of Proposition 2 may be found in Appendix A.

What is particularly noteworthy about this equivalence is that while degree is defined only for symmetric games with two strategies, \(k\)-reducibility is defined for multiplayer—even asymmetric—games with any number of strategies. Therefore, we can use Proposition 2 to extend the notion of degree to much more general games:

Definition 3

(Degree of game) The degree of a game is the value \(k\) for which the game is \(\left( k+1\right) \)-reducible.

One could easily generalize the definition of reducibility to allow for the aggregate payoff values to be nonlinear functions of the constituent payoffs, but this generalization is somewhat unnatural in evolutionary game theory. Typically, the total payoff to a player who is involved in multiple interactions is calculated by either accumulating or averaging the payoffs from individual interactions. On spatially-homogeneous structures, the evolutionary dynamics of these two methods are the same; the difference amounts to a scaling of the intensity of selection (Maciejewski et al. 2014). Moreover, Maciejewski et al. (2014) show that the method of averaging on a heterogeneous network results in an asymmetry in the games being played: players at locations with different numbers of neighbors are effectively playing different games. This asymmetry is not present if payoff values are accumulated, suggesting that for general population structures the latter method is more natural. Using the method of accumulated payoffs, the total payoff to a player is calculated as the sum of all of the payoffs from the multiplayer games in which he or she is a participant. If these multiplayer games can be reduced, then the total payoff should retain this property of being the sum of the payoffs from smaller games, giving the (linear) notion of reducibility.

In the limit of weak selection, it can also be argued that more general notions of reducibility are equivalent to our definition of reducibility: to simplify notation, suppose that some payoff value \(\varPi \) may be written as a function, \(f\), of a collection of payoff values, \(\pi _{1},\ldots ,\pi _{m}\), from smaller games. In evolutionary dynamics, it is not unreasonable to assume that attenuating (or enhancing) the effect of \(\varPi \) by a factor of \(\beta \geqslant 0\) is the same as multiplying each of \(\pi _{1},\ldots ,\pi _{m}\) by \(\beta \). That is, \(\beta \varPi =\beta f\left( \pi _{1},\ldots ,\pi _{m}\right) =f\left( \beta \pi _{1},\ldots ,\beta \pi _{m}\right) \) for each \(\beta \geqslant 0\). If \(f\) is also assumed to be continuously differentiable at \({\mathbf {0}}\), then \(f\) must necessarily be a linear function of \(\pi _{1},\ldots ,\pi _{m}\). Thus, if \(\beta \) is interpreted as the intensity of selection, then, in the limit of weak selection, any such function \(f\) must be linear, which implies that more general notions of reducibility involving such an \(f\) are captured by Definition 1. We will see in the next section that selection conditions require similar assumptions that make these two requirements on \(f\) necessary in order to derive a \(\sigma \)-rule for the reduced game.

With a definition of reducibility in place, we now focus on specific examples of multiplayer games. Among the simplest multiplayer games is the public goods game. In a public goods game, each player chooses an investment level from the interval \(\left[ 0,\infty \right) \) and contributes this amount to a common pool. (In general, the strategy space for each player in the public goods game is \(S=\left[ 0,K\right] \), where \(K\) is a maximum investment level.) In the linear public goods game, the total contibution to this pool is enhanced by a factor of \(r>1\) and distributed equally among the players. Thus, if \(x_{j}\) denotes player \(j\)’s contribution to the public good, then the payoff function for player \(i\) is given by Eq. 2. The linearity of this payoff function allows the game to be broken down into a sequence of pairwise interactions:

Example 1

(Linear public goods) The function \(v:S^{2}\rightarrow {\mathbb {R}}^{2}\) defined by

$$\begin{aligned} v_{i}\left( x_{i},x_{j}\right)&:= \frac{2r}{d}\left( \frac{\left( \frac{1}{d-1}\right) x_{i}+x_{j}}{2}\right) - \left( \frac{1}{d-1}\right) x_{i} \end{aligned}$$
(9)

satisfies \( u_{i}^{1}\left( x_{1},\ldots ,x_{d}\right) =\sum \nolimits _{j\ne i}v_{i}\left( x_{i},x_{j}\right) \) for each \(i=1,\ldots ,d\) (see Fig. 2). Therefore, this (symmetric) linear public goods game is reducible to a sequence of pairwise (symmetric) games (Hauert and Szabó 2003).

Fig. 2
figure 2

The reducibility of the linear public goods game (for the central player) is illustrated here with four players. The central player (red) invests \(x\), while the players at the periphery (blue) invest \(y\), \(z\), and \(w\), respectively. The payoff to the central player for this interaction is a sum of pairwise payoffs, one for each neighbor. Each of these two-player games is a public goods game with multiplicative factor \(r/2\), and in each of the smaller games the central player contributes one third of his or her total contribution, \(x\) (color figure online)

Full size image

As the next example shows, the introduction of nonlinearity into the payoff functions does not guarantee that the resulting game is irreducible:

Example 2

(Nonlinear public goods) A natural way to introduce nonlinearity into the linear public goods game is to raise the average contribution, \(\left( x_{1}+\cdots +x_{d}\right) /d\), to some power, say \(k\). However, if \(k\) is an integer and \(2\leqslant k\leqslant d-2\), then the payoff function

$$\begin{aligned} u_{i}\left( x_{1},\ldots ,x_{d}\right)&:= r\left( \frac{x_{1}+\cdots +x_{d}}{d} \right) ^{k} - x_{i} \end{aligned}$$
(10)

is reducible (see Appendix A for details).

Another convenient way in which to introduce nonlinearity into the payoff functions of the public goods game is to replace the average, \(\left( x_{1}+\cdots +x_{d}\right) \!/d\), by the Hölder (or “generalized”) average

$$\begin{aligned} \left( \frac{x_{1}^{p}+\cdots +x_{d}^{p}}{d}\right) ^{\frac{1}{p}} \end{aligned}$$
(11)

for some \(p\in \left[ -\infty ,+\infty \right] \). In the limiting cases,

$$\begin{aligned} \lim _{p\rightarrow -\infty }\left( \frac{x_{1}^{p}+\cdots +x_{d}^{p}}{d}\right) ^{\frac{1}{p}}&= \min \left\{ x_{1},\ldots ,x_{d}\right\} ; \end{aligned}$$
(12a)
$$\begin{aligned} \lim _{p\rightarrow 0}\left( \frac{x_{1}^{p}+\cdots +x_{d}^{p}}{d}\right) ^{\frac{1}{p}}&= \left( x_{1}\ldots x_{d}\right) ^{\frac{1}{d}}; \end{aligned}$$
(12b)
$$\begin{aligned} \lim _{p\rightarrow +\infty }\left( \frac{x_{1}^{p}+\cdots +x_{d}^{p}}{d}\right) ^{\frac{1}{p}}&= \max \left\{ x_{1},\ldots ,x_{d}\right\} \end{aligned}$$
(12c)

(see Bullen 2003).

Remark 2

Several special cases of the Hölder public goods game have been previously considered in the literature. For \(p=1\), this game is simply the linear public goods game (see Eq. 2), which has an extensive history in the economics literature. Hirshleifer (1983) refers to the cases \(p=-\infty \) and \(p=+\infty \) as the “weakest-link” and “best-shot” public goods games, respectively. The weakest-link game can be used to describe collaborative dike building, in which the collective benefit is determined by the player who contributes the least to the public good (see Hirshleifer 1983, p. 371). The search for a cure to the disease could be modeled as a “best-shot” game since many institutions may invest in finding this cure, but the public good (the cure) is provided by the first institution to succeed. The Hölder public goods game provides a continuous interpolation between these two extreme scenarios.

The Hölder average gives an alternative way to take the mean of players’ contributions and, for almost every \(p\), leads to a public goods game that is irreducible for any number of players:

Example 3

(Nonlinear public goods) For \(p\in \left[ -\infty ,+\infty \right] \), consider the payoff functions

$$\begin{aligned} u_{i}^{p}\left( x_{1},\ldots ,x_{d}\right)&:= r\underbrace{\left( \frac{x_{1}^{p}+\cdots +x_{d}^{p}}{d}\right) ^{\frac{1}{p}}}_{\mathrm{H}\ddot{\mathrm{o}}\mathrm{lder \,average\, of\,}x_{1},\ldots ,x_{d}} - x_{i} , \end{aligned}$$
(13)

where \(r\) is some positive constant. We refer to the game defined by these payoff functions as the Hölder public goods game. The payoff functions of Example 1 are simply \(u_{i}^{1}\). If \(p,q\in \left[ -\infty ,+\infty \right] \) and \(q<p\), then, by Hölder’s inequality,

$$\begin{aligned} u_{i}^{q}\left( x_{1},\ldots ,x_{d}\right)&\leqslant u_{i}^{p}\left( x_{1},\ldots ,x_{d}\right) \end{aligned}$$
(14)

with equality if and only if \(x_{1}=x_{2}=\cdots =x_{d}\). It is shown in Appendix A that these public goods games are irreducible if and only if \(\frac{1}{p}\not \in \left\{ 1,2,\ldots ,d-2\right\} \). In particular, if \(\frac{1}{p}\not \in \left\{ 1,2,\ldots \right\} \), then \(u_{i}^{p}\) is irreducible for each \(d\). This example exhibits the (reducible) linear public goods game as a limit of irreducible public goods games in the sense that \(\lim _{p\rightarrow 1}u_{i}^{p}=u_{i}^{1}\) (see Fig. 3).

Fig. 3
figure 3

\(u^{p}\left( x,1,1,1\right) \) versus \(x\) for \(r = 1.5\) and seven values of \(p\). In each of these four-player public goods games, the investment levels of the opponents are \(1\) unit. The payoff functions for the nonlinear public goods games \((p\ne 1)\) are slight perturbations of the payoff function for the linear public goods game \((p = 1)\) as long as \(p\) is close to 1

Full size image

Example 4

(Nonlinear public goods) Rather than modifying the average contribution, one could also add a term to the payoff from the linear public goods game to obtain an irreducible game. For example, suppose that in addition to the payoff received from the linear public goods game, each player receives an added bonus if and only if every player contributes a nonzero amount to the public good. If \(\varepsilon >0\), this bonus term could be defined as \(\varepsilon \prod _{j=1}^{d}x_{j}\) so that the payoff function for the game is

$$\begin{aligned} u_{i}\left( x_{1},\ldots ,x_{d}\right)&:= u_{i}^{1}\left( x_{1},\ldots ,x_{d}\right) + \varepsilon \prod _{j=1}^{d}x_{j} . \end{aligned}$$
(15)

In fact, this payoff function is irreducible for all \(\varepsilon \in {\mathbb {R}}-\left\{ 0\right\} \). The details may be found in Appendix A, but the intuition is simple: a function that requires simultaneous information about each player (the cross-term \(x_{1}\ldots x_{d}\)) should not be able to be broken down into a collection of functions that account for only subsets of the population. Letting \(\varepsilon \rightarrow 0\), we view the linear public goods game once again as a limit of irreducible games.

2.2 Structured populations

A fundamental difficulty in extending Definition 1 to structured populations arises from the fact that it may not even be possible to define an \(m\)-player interaction from an \(d\)-player interaction if \(m<d\). The square lattice is a simple example of a structured population that is not well-mixed. The lattice is homogeneous in the sense that it is vertex-transitive, meaning roughly that the network looks the same from every node (Taylor et al. 2007). The square lattice has infinitely many nodes, but this property will not be important for our discussion of reducibility. Suppose that each player in the population chooses an investment level from \(\left[ 0,K\right] \), where \(K>0\) is the maximum amount that can be invested by a single player in the public good. With this investment level as a strategy, every player in the population initiates a public goods game with each of his or her four neighbors. For each game, the five players involved receive a payoff, and a focal player’s total payoff is defined to be the sum of the payoffs from each of the five games in which he or she is a participant: one initiated by the focal player, and four initiated by the neighbors of this player.

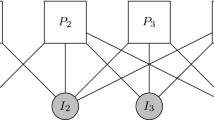
The total payoff to a fixed focal player depends not only on that focal player’s neighbors, but also on the neighbors of the focal player’s neighbors. In other words, the payoff to the focal player is determined by those players who are within two links of the focal player on the lattice. However, for each of the five public goods interactions that contribute to the overall payoff value, the only strategies that matter are those of five players: a central player, who initiates the interaction, and the four neighbors of this central player. These interactions should be examined separately to determine the reducibility of the game; intuitively, this public goods game is “reducible” if each player initiating an interaction can instead initiate a sequence of smaller games that collectively preserve the payoffs to each player involved. For each of these interactions, the interacting group appears to be arranged on a star network, ie. a network with a central node and four leaves connected to the central node, and with no links between the leaves (see Fig. 4). Therefore, although the square lattice is homogeneous, an analysis of the star network—a highly heterogeneous structure—is required in order to consider reducibility in this type of population.

Fig. 4
figure 4

The total payoff to the focal player (purple) depends on his or her immediate neighbors (blue) and the players who are two links away (turquoise). Each of the four-leaf star networks indicates an interaction initiated by the central player. The total payoff to player 0 is then calculated as the sum of the payoffs from these five interactions (color figure online)

Full size image

Example 5

(Linear public goods game on a star network) A star network consists of a central node, \(0\), connected by an undirected link to \(\ell \) leaf nodes \(1,\ldots ,\ell \) (Lieberman et al. 2005; Hadjichrysathou et al. 2011). There are no other links in the network. Suppose that player \(i\) in this network uses strategy \(x_{i}\in S\subseteq \left[ 0,\infty \right) \). Each player initiates a linear public goods game that is played by the initiator and all of his or her neighbors. Thus, the player at the central node is involved in \(d=\ell +1\) interactions, while each player at a leaf node is involved in two interactions. A focal player’s payoff is calculated by adding up the payoffs from each interaction in which he or she is involved. From the perspective of the player at the central node, the interaction he or she initiates is reducible to a sequence of pairwise interactions by Example 1. However, on a star network no two leaf nodes share a link, and thus players at these nodes cannot interact directly with one another; any interaction between two players at leaf nodes must be mediated by the player at the central node.

A natural question one can ask in this context is the following: can the \(d\)-player game initiated by the central player be broken down into a sequence of symmetric \(m\)-player interactions (with \(m<d\)), all involving the central player, in such a way that if player \(i\) adds all of the payoffs from the interactions in which he or she is involved, the result will be \(u_{i}\left( x_{0},x_{1},\ldots , x_{\ell }\right) \)? That is, can the central player initiate a sequence of strictly smaller interactions from which, collectively, each player receives the payoff from the \(d\)-player linear public goods game? The answer, as it turns out, is that this \(d\)-player game can be broken down into a combination of a two-player game and a three-player game, ie. it is 3-reducible: For \(i\in \left\{ 0,1,\ldots ,\ell \right\} \), let

$$\begin{aligned} \alpha _{i}\left( x_{i},x_{j}\right)&:= -\frac{r}{d}\left( d-3\right) \left[ \left( \frac{1}{d-1}\right) x_{i}+x_{j} \right] + \left( \frac{d-3}{d-1}\right) x_{i} ; \end{aligned}$$
(16a)
$$\begin{aligned} \beta _{i}\left( x_{i},x_{j},x_{k}\right)&:= \frac{r}{d}\left[ \left( \frac{2}{d-1}\right) x_{i} + x_{j} + x_{k} \right] - \left( \frac{2}{d-1}\right) x_{i} . \end{aligned}$$
(16b)

\(\alpha _{i}\) is the payoff function for a two-player game, \(\beta _{i}\) is the payoff function for a three-player game, and both of these games are symmetric. If the player at the central node (using strategy \(x_{0}\)) initiates a two-player game with every neighbor according to the function \(\alpha \) and a three-player game with every pair of neighbors according to the function \(\beta \), then the total payoff to the central player for these interactions is

$$\begin{aligned} \sum _{i=1}^{\ell }\alpha _{0}\left( x_{0},x_{i}\right) + \sum _{1\leqslant i<j\leqslant \ell }\beta _{0}\left( x_{0},x_{i},x_{j}\right)&= u_{0}^{1}\left( x_{0},x_{1},\ldots ,x_{\ell }\right) . \end{aligned}$$
(17)

Each leaf player is involved in one of the two-player interactions and \(d-2\) of the three-player interactions initiated by the player at the central node. The payoff to leaf player \(i\in \left\{ 1,\ldots ,\ell \right\} \) for playing strategy \(x_{i}\) in these interactions is

$$\begin{aligned} \alpha _{i}\left( x_{i},x_{0}\right) + \sum _{\begin{array}{c} 1\leqslant j\leqslant \ell \\ j\ne i \end{array}}\beta _{i}\left( x_{i},x_{0},x_{j}\right)&= u_{i}^{1}\left( x_{0},x_{1},\ldots ,x_{\ell }\right) . \end{aligned}$$
(18)

In fact, \(\alpha _{i}\) and \(\beta _{i}\) are the unique symmetric two- and three-player payoff functions satisfying Eqs. (17) and (18). Thus, the \(d\)-player linear public goods interaction initiated by the player at the central node can be reduced to a sequence of symmetric two- and three-player games that preserves the payoffs for each player in the population.

It follows from Example 5 that the reducibility of a game is sensitive to population structure. The star network is a very simple example, but it already illustrates that the way in which a game is reduced can be complicated by removing opportunities for players to interact in smaller groups. The linear public goods game can be reduced to a two-player game in well-mixed populations (it is 2-reducible), but the same reduction does not hold on a star network. The best that can be done for this game on the star is a reduction to a combination of a two-player game and a three-player game. From Fig. 4 and our previous discussion of the lattice, we see that this reduction is also the best that can be done on the square lattice. In particular, it is not possible to reduce the linear public goods game to a two-player game on the square lattice.

What is perhaps more useful in the present context is the fact that a game that is irreducible in a well-mixed population remains irreducible in structured populations. Indeed, as we observed, any player initiating an interaction can choose to interact with any subset of his opponents, so from the perspective of this focal player the population might as well be well-mixed. With Examples 3 and 4 in mind, we now turn our attention to the dynamics of multiplayer games in structured populations.

3 Selection conditions

Let \(S=\left\{ A_{1},\ldots ,A_{n}\right\} \) be the finite strategy set available to each player. Consider an evolutionary process that updates the strategies played by the population based on the total payoff each player receives for playing his or her current strategy, and let \(\beta \geqslant 0\) denote the intensity of selection. Assuming that all payoff values may be calculated using an \(n\times n\) payoff matrix \(\left( a_{ij}\right) \), there is the following selection condition:

Theorem 1

(Tarnita et al. 2011) Consider a population structure and an update rule such that (i) the transition probabilities are infinitely differentiable at \(\beta = 0\) and (ii) the update rule is symmetric for the \(n\) strategies. Let

$$\begin{aligned} \overline{a}_{**}=\frac{1}{n}\sum _{s=1}^{n}a_{ss};\quad \overline{a}_{r*}=\frac{1}{n}\sum _{s=1}^{n}a_{rs};\quad \overline{a}_{*r}=\frac{1}{n}\sum _{s=1}^{n}a_{sr};\quad \overline{a}=\frac{1}{n^{2}}\sum _{s,t=1}^{n}a_{st} . \end{aligned}$$
(19)

\((\overline{a}_{**}\) is the expected payoff to a strategic type against an opponent using the same strategy, \(\overline{a}_{r*}\) is the expected payoff to strategic type \(r\) when paired with a random opponent, \(\overline{a}_{*r}\) is the expected payoff to a random opponent facing strategic type \(r\), and \(\overline{a}\) is the expected payoff to a random player facing a random opponent.) In the limit of weak selection, the condition that strategy \(r\) is selected for is

$$\begin{aligned} \sigma _{1}\left( a_{rr}-\overline{a}_{**} \right) + \sigma _{2}\left( \overline{a}_{r*}-\overline{a}_{*r}\right) + \sigma _{3}\left( \overline{a}_{r*}-\overline{a}\right) > 0 , \end{aligned}$$
(20)

where \(\sigma _{1}\), \(\sigma _{2}\), and \(\sigma _{3}\) depend on the model and the dynamics, but not on the entries of the payoff matrix, \(\left( a_{ij}\right) \). Moreover, the parameters \(\sigma _{1}\), \(\sigma _{2}\), and \(\sigma _{3}\) do not depend on the number of strategies as long as \(n\geqslant 3\).

The statement of this theorem is slightly different from the version appearing in Tarnita et al. (2011), due to the fact that one further simplification may be made by eliminating a nonzero structure coefficient. We do not treat this simplification here since (i) the resulting condition depends on which coefficient is nonzero and (ii) only a single coefficient may be eliminated in this way, which will not be a significant simplification when we consider more general games. This theorem generalizes the main result of Tarnita et al. (2009b) for \(n = 2\) strategies, which is a two-parameter condition (or one-parameter if one coefficient is assumed to be nonzero).

For \(d\)-player games with \(n=2\) strategies, we also have:

Theorem 2

(Wu et al. 2013b) Consider an evolutionary process with the same assumptions on the population structure and update rule as in Theorem 1. For a game with two strategies, \(A\) and \(B\), let \(a_{j}\) and \(b_{j}\) be the payoff values to a focal player using \(A\) (resp. \(B)\) against \(j\) players using \(A\). In the limit of weak selection, the condition that strategy \(A\) is selected for is

$$\begin{aligned} \sum _{j=0}^{d-1}\sigma _{j}\left( a_{j}-b_{d-1-j}\right)&> 0 \end{aligned}$$
(21)

for some structure coefficients \(\sigma _{0},\sigma _{1},\ldots ,\sigma _{d-1}\).

It is clear from these results that for \(n=2\), the extension of the selection conditions from two-player games to multiplayer games comes at the cost of additional structure coefficients. Our goal is to extend the selection conditions to multiplayer games with \(n\geqslant 3\) strategies and quantify the cost of doing so (in terms of the number of structure coefficients required by the \(\sigma \)-rules).

3.1 Symmetric games

Examples 3 and 4 show that a single game in a structured population can require multiple payoff functions, even if the game is symmetric: in a degree-heterogeneous structure, there may be some players with two neighbors, some with three neighbors, etc. If each player is required to play an irreducible Hölder public goods game with all of his or her neighbors, then we need a \(d\)-player payoff function \(u^{p}\) for each \(d\) appearing as the number of neighbors of some player in the population. With this example in mind, suppose that

$$\begin{aligned} \bigcup _{j\in J} \Big \{ u^{j} : S^{d\left( j\right) } \longrightarrow {\mathbb {R}} \Big \} \end{aligned}$$
(22)

is the collection of all distinct, symmetric payoff functions needed to determine the payoff values to the players, where \(J\) is some finite indexing set and \(d\left( j\right) \) is the number of participants in the interaction defined by \(u^{j}\). The main result of this section requires the transition probabilities of the process to be smooth at \(\beta =0\) when viewed as functions of the selection intensity, \(\beta \). This smoothness requirement is explained in Appendix B. We also assume that the update rule is symmetric with respect to the strategies. These requirements are the same as those of Tarnita et al. (2011), and they are satisfied by the most salient evolutionary processes (birth–death, death–birth, imitation, pairwise comparison, Wright–Fisher, etc.).

Theorem 3

In the limit of weak selection, the \(\sigma \)-rule for a chosen strategy involves

$$\begin{aligned} \sum _{j\in J}\left( d\left( j\right) + \sum _{m=1}^{d\left( j\right) -1}\Big (d\left( j\right) -m\Big ) q\left( m,n-2\right) \right) \end{aligned}$$
(23)

structure coefficients, where \(q\left( m,k\right) \) denotes the number of partitions of \(m\) with at most \(k\) parts.

The proof of Theorem 3 is based on a condition that guarantees the average abundance of the chosen strategy increases with \(\beta \) as long as \(\beta \) is small. Several symmetries common to evolutionary processes and symmetric games are then used to simplify this condition. The details may be found in Appendix B.

As a special case of this general setup, suppose the population is finite, structured, and that each player initiates an interaction with every \(\left( d-1\right) \)-player subset of his or her neighbors. That is, there is only one payoff function and every interaction requires \(d\) players. (Implicitly, it is assumed that the population is structured in such a way that each player has at least \(d-1\) neighbors.) A player may be involved in more games than he or she initiates; for example, a focal player’s neighbor may initiate a \(d\)-player interaction, and the focal player will receive a payoff from this interaction despite the possibility of not being neighbors with each participant. The payoffs from each of these games are added together to form this player’s total payoff. In this case, we have the following result:

Corollary 1

If only a single payoff function is required, \(u:S^{d}\rightarrow {\mathbb {R}}\), then the selection condition involves

$$\begin{aligned} d + \sum _{m=1}^{d-1} \left( d-m\right) q\left( m,n-2\right) \end{aligned}$$
(24)

structure coefficients.

Since the notation is somewhat cumbersome, we relegate the explicit description of the rule of Theorem 3 to Appendix B (Eq. 96). Here, we give examples illustrating some special cases of this rule:

Example 6

For a symmetric game with pairwise interactions and two strategies,

$$\begin{aligned} 2 + \sum _{m=1}^{2-1}\left( 2-m\right) q\left( m,2-2\right)&= 2 + 0 = 2 \end{aligned}$$
(25)

structure coefficients are needed, recovering the main result of Tarnita et al. (2009b).

Example 7

For a symmetric game with pairwise interactions and \(n\geqslant 3\) strategies,

$$\begin{aligned} 2 + \sum _{m=1}^{2-1}\left( 2-m\right) q\left( m,n-2\right)&= 2 + \sum _{m=1}^{2-1}\left( 2-m\right) q\left( m,1\right) = 2 + 1 = 3 \end{aligned}$$
(26)

structure coefficients are needed, which is the result of Tarnita et al. (2011).

Example 8

For a symmetric game with \(d\)-player interactions and two strategies,

$$\begin{aligned} d + \sum _{m=1}^{d-1}\left( d-m\right) q\left( m,2-2\right)&= d + 0 =d \end{aligned}$$
(27)

structure coefficients are needed, which gives Theorem 2 of Wu et al. (2013b).

Strictly speaking, the number of structure coefficients we obtain in each of these specializations is one greater than the known result. This discrepancy is due only to an assumption that one of the coefficients is nonzero, which allows a coefficient to be eliminated by division (Tarnita et al. 2009b; Wu et al. 2013b).

Example 9

Suppose that each player is involved in a series of two-player interactions with payoff values \(\left( a_{ij}\right) \) and a series of three-player interactions with payoff values \(\left( b_{ijk}\right) \). Let \(\overline{a}_{**}\), \(\overline{a}_{r*}\), \(\overline{a}_{*r}\), and \(\overline{a}\) be as they were in the statement of Theorem 1. Similarly, we let

$$\begin{aligned} \overline{b}_{***}&:= \frac{1}{n}\sum _{s=1}^{n}b_{sss} ;\quad \overline{b}_{r*\bullet } := \frac{1}{n^{2}}\sum _{s,t=1}^{n}b_{rst} ;\quad \overline{b} := \frac{1}{n^{3}}\sum _{s,t,u=1}^{n}b_{stu} , \end{aligned}$$
(28)

and so on. (\(\overline{b}_{***}\) is the expected payoff to a strategic type against opponents of the same strategic type, \(\overline{b}_{r*\bullet }\) is the expected payoff to strategic type \(r\) when paired with a random pair of opponents, \(\overline{b}\) is the expected payoff to a random player facing a random pair of opponents, etc.) The selection condition for strategy \(r\) is then

$$\begin{aligned}&\sigma _{1} \left( a_{rr}-\overline{a}_{**}\right) + \sigma _{2}\left( \overline{a}_{r*}-\overline{a}_{*r}\right) + \sigma _{3}\left( \overline{a}_{r*}-\overline{a}\right) \nonumber \\&\quad + \sigma _{4}\left( b_{rrr}-\overline{b}_{***}\right) + \sigma _{5}\left( \overline{b}_{rr*}-\overline{b}_{**r}\right) + \sigma _{6}\left( \overline{b}_{r**}-\overline{b}_{*rr}\right) + \sigma _{7}\left( \overline{b}_{rr*}-\overline{b}_{**\bullet }\right) \nonumber \\&\quad + \sigma _{8}\left( \overline{b}_{r*\bullet }-\overline{b}_{*r\bullet }\right) + \sigma _{9}\left( \overline{b}_{r**}-\overline{b}_{*\bullet \bullet }\right) + \sigma _{10}\left( \overline{b}_{r*\bullet }-\overline{b}\right) >0 , \end{aligned}$$
(29)

where \(\left\{ \sigma _{i}\right\} _{i=1}^{10}\) is the set of structure coefficients for the process.

We may also extend the result of Wu et al. (2013b) to games with more than two strategies:

Example 10

For a symmetric game with \(d\)-player interactions and three strategies,

$$\begin{aligned} d + \sum _{m=1}^{d-1}\left( d-m\right) q\left( m,3-2\right)&= \frac{d\left( d+1\right) }{2} \end{aligned}$$
(30)

structure coefficients appear in the selection condition. In fact, we can write down this condition explicitly without much work: Suppose that \(S=\left\{ a,b,c\right\} \) and let \(a_{i,j}\), \(b_{i,j}\), and \(c_{i,j}\) be the payoff to a focal playing \(a\), \(b\), and \(c\), respectively, when \(i\) opponents are playing \(a\), \(j\) opponents are playing \(b\), and \(d-1-i-j\) opponents are playing \(c\). Strategy \(a\) is favored in the limit of weak selection if and only if

$$\begin{aligned}&\sum _{0\leqslant i+j\leqslant d-1} \sigma \left( i,j\right) \left( \left( a_{d-1-i,i}-b_{i,d-1-i}\right) + \left( a_{j,d-1-j}-b_{d-1-j,j}\right) \right. \nonumber \\&\left. \quad + \left( a_{j,i}-b_{i,j}\right) + \left( a_{d-1-i,0}-c_{d-1-j,0}\right) \right. \nonumber \\&\quad \left. + \left( a_{j,d-1-i-j}-c_{i,d-1-i-j}\right) + \left( a_{j,0}-c_{i,0}\right) \right) > 0 \end{aligned}$$
(31)

for some collection of \(d\left( d+1\right) /2\) structure coefficients, \(\left\{ \sigma \left( i,j\right) \right\} _{0\leqslant i+j\leqslant d-1}\).

Let \(\varphi _{n}\left( d\right) \) be the number of structure coefficients needed for the condition in Corollary 1. The following result generalizes what was observed in Example 10 and by Wu et al. (2013b):

Proposition 3

For fixed \(n\geqslant 2\), \(\varphi _{n}\left( d\right) \) grows in \(d\) like \(d^{n-1}\). That is, there exist constants \(c_{1},c_{2}>0\) such that

$$\begin{aligned} c_{1} \leqslant \lim _{d\rightarrow \infty } \frac{\varphi _{n}\left( d\right) }{d^{n-1}} \leqslant c_{2} . \end{aligned}$$
(32)

Proof

We establish the result by induction on \(n\). We know that the result holds for \(n=2\) (Wu et al. 2013b). Suppose that \(n\geqslant 3\) and that the result holds for \(n-1\). As a result of the recursion \(q\left( m,k\right) =q\left( m,k-1\right) +q\left( m-k,k\right) \) for \(q\), we see that \(\varphi _{n}\left( d\right) =\varphi _{n-1}\left( d\right) +\varphi _{n}\left( d-\left( n-2\right) \right) -d\). Thus,

$$\begin{aligned} \varphi _{n}\left( d\right)&= \sum _{k=0}^{\left\lfloor \frac{d}{n-2}\right\rfloor -1}\varphi _{n-1}\left( d-k\left( n-2\right) \right) + \varphi _{n}\left( d-\left\lfloor \frac{d}{n-2}\right\rfloor \left( n-2\right) \right) \!-\! \left\lfloor \frac{d}{n-2}\right\rfloor d , \end{aligned}$$
(33)

and it follows from the inductive hypothesis that the result also holds for \(n\). \(\square \)

Wu et al. (2013b) give examples of selection conditions illustrating the linear growth predicted for \(n=2\). For \(n=3\) and \(n=4\), we give in Fig. 5 the number of distinct structure coefficients for an irreducible \(d\)-player game in a population of size \(d\) for the pairwise comparison process (see Szabó and Tőke 1998; Traulsen et al. 2007). Although the number of distinct coefficients is slightly less than the number predicted by Corollary 1 in these examples, their growth (in the number of players) coincides with Proposition 3. That is, growth in the number of structure coefficients is quadratic for three-strategy games and cubic for four-strategy games. Even for these small population sizes, one can already see that the selection conditions become quite complicated. The details of these calculations may be found in Appendix C.

Fig. 5
figure 5

The number of distinct structure coefficients vs. the number of players, \(d\), in an irreducible \(d\)-player interaction in a population of size \(N=d\). By Proposition 3, the blue circles grow like \(d^{2}\) and \(d^{3}\) in a (\(n=3\)) and b (\(n=4\)), respectively. In both of these figures, the process under consideration is a pairwise comparison process. The actual results, whose calculations are described in Appendix C, closely resemble the predicted results, suggesting that in general, one cannot expect fewer than \(\approx \!\!d^{n-1}\) distinct structure coefficients in a \(d\)-player game with \(n\) strategies (color figure online)

Full size image

3.2 Asymmetric games

As a final step in increasing the complexity of multiplayer interactions, we consider payoff functions that do not necessarily satisfy the symmetry condition of Definition 2. One way to introduce such an asymmetry into evolutionary game theory is to insist that payoffs depend not only on the strategic types of the players, but also on the spatial locations of the participants in an interaction. For example, in a two-strategy game, the payoff matrix for a row player at location \(i\) against a column player at location \(j\) is

(34)

This payoff matrix defines two payoff functions: one for the player at location \(i\), and one for the player at location \(j\). More generally, for each fixed group of size \(d\) involved in an interaction, there are \(d\) different payoff functions required to describe the payoffs resulting from this \(d\)-player interaction. For example, if players at locations \(i_{1},\ldots ,i_{d}\) are involved in a \(d\)-player game, then it is not necessarily the case that \(u_{i_{j}}=u_{i_{k}}\) if \(j\ne k\); for general asymmetric games, each of the payoff functions \(u_{i_{1}},\ldots ,u_{i_{d}}\) is required. Suppose that \(J\) is a finite set that indexes the distinct groups involved in interactions. For each \(j\in J\), this interaction involves \(d\left( j\right) \) players, which requires \(d\left( j\right) \) distinct payoff functions. Thus, there is a collection of functions

$$\begin{aligned} \bigcup _{j\in J} \Big \{ u_{i}^{j} : S^{d\left( j\right) } \longrightarrow {\mathbb {R}} \Big \}_{i=1}^{d\left( j\right) } \end{aligned}$$
(35)

that describes all possible payoff values in the population, where \(u_{i}^{j}\) denotes the payoff function for the \(i\)th player of the \(j\)th group involved in an interaction.

Let \(S\left( - ,-\right) \) denote the Stirling number of the second kind, i.e.,

$$\begin{aligned} S\left( m,k\right)&= {\left\{ \begin{array}{ll}\displaystyle \frac{1}{k!}\sum _{j=0}^{k}\left( -1\right) ^{k-j}\left( {\begin{array}{c}k\\ j\end{array}}\right) j^{m} &{} 0\leqslant k\leqslant m, \\ 0 &{} k>m .\end{array}\right. } \end{aligned}$$
(36)

In words, \(S\left( m,k\right) \) is the number of ways in which to partition a set of size \(m\) into exactly \(k\) parts. Therefore, the sum \(\sum _{k=0}^{m}S\left( m,k\right) \) is the total number of partitions of a set of size \(m\), which is denoted by \(B_{m}\) and referred to as the \(m\)th Bell number (see Stanley 2009).

Theorem 4

Assuming the transition probabilities are smooth at \(\beta =0\) and that the update rule is symmetric with respect to the strategies, the number of structure coefficients in the selection condition for a chosen strategy is

$$\begin{aligned} \sum _{j\in J}d\left( j\right) \sum _{k=0}^{n}\Big ( S\left( 1+d\left( j\right) ,k\right) - S\left( d\left( j\right) ,k\right) \Big ) . \end{aligned}$$
(37)

The proof of Theorem 4 may be found in Appendix B, along with an explicit description of the condition (Eq. 91). Note that if the number of strategies, \(n\), satisfies \(n\geqslant 1+\max _{j\in J}d\left( j\right) \), then

$$\begin{aligned} \sum _{k=0}^{n} S\left( 1+d\left( j\right) ,k\right)&= B_{1+d\left( j\right) } ; \end{aligned}$$
(38a)
$$\begin{aligned} \sum _{k=0}^{n} S\left( d\left( j\right) ,k\right)&= B_{d\left( j\right) } . \end{aligned}$$
(38b)

From these equations, (37) reduces to

$$\begin{aligned} \sum _{j\in J}d\left( j\right) \Big ( B_{1+d\left( j\right) } - B_{d\left( j\right) } \Big ) . \end{aligned}$$
(39)

Therefore, for a fixed set of interaction sizes \(\left\{ d\left( j\right) \right\} _{j\in J}\), the number of structure coefficients grows with the number of strategies, \(n\), until \(n=1+\max _{j\in J}d\left( j\right) \); after this point, the number of structure coefficients is independent of the number of strategies.

Interestingly, the selection condition for asymmetric games gives some insight into the nature of the structure coefficients for symmetric games:

Example 11

Suppose that the population structure is an undirected network without self-loops (Ohtsuki et al. 2006), and let \(\left( w_{ij}\right) \) be the adjacency matrix of this network. If the interactions are pairwise and the payoffs depend on the vertices occupied by the players, then for \(n\geqslant 3\) strategies there are

$$\begin{aligned} B_{2+1}-B_{1+1}&= 5 - 2 = 3 \end{aligned}$$
(40)

structure coefficients needed for each ordered pair of neighbors in the network. Suppose that

(41)

is the payoff matrix for a player at vertex \(i\) against a player at vertex \(j\). If

$$\begin{aligned} \overline{a}_{**}^{ij}=\frac{1}{n}\sum _{s=1}^{n}a_{ss}^{ij};\quad \overline{a}_{r*}^{ij}=\frac{1}{n}\sum _{s=1}^{n}a_{rs}^{ij};\quad \overline{a}_{*r}^{ij}=\frac{1}{n}\sum _{s=1}^{n}a_{sr}^{ij};\quad \overline{a}^{ij}=\frac{1}{n^{2}}\sum _{s,t=1}^{n}a_{st}^{ij} \end{aligned}$$
(42)

are the “localized” versions of the strategy averages given in display (19), then strategy \(r\) is favored in the limit of weak selection if and only if

$$\begin{aligned} \sum _{i=1}^{N}\sum _{\left\{ j\ :\ w_{ij}=1 \right\} }\left( \sigma _{1}^{ij}\left( a_{rr}^{ij}-\overline{a}_{**}^{ij} \right) + \sigma _{2}^{ij}\left( \overline{a}_{r*}^{ij}-\overline{a}_{*r}^{ij}\right) + \sigma _{3}^{ij}\left( \overline{a}_{r*}^{ij}-\overline{a}^{ij}\right) \right)&> 0. \end{aligned}$$
(43)

Whereas there are three structure coefficients in this model if there is no payoff-asymmetry, there are

$$\begin{aligned} 3\sum _{i,j=1}^{N}w_{ij}&= 6\times \Big (\#\text { of links in the network}\Big ) \end{aligned}$$
(44)

structure coefficients when the payoff matrices depend on the locations of the players. Of course, if we remove the asymmetry from this result and take \({\mathbf {M}}^{ij}\) to be independent of \(i\) and \(j\) (so that \(a_{st}^{ij}=a_{st}\) for each \(s,t,i,j\)), then the selection condition (43) takes the form

$$\begin{aligned} \sigma _{1}\left( a_{rr}-\overline{a}_{**} \right) + \sigma _{2}\left( \overline{a}_{r*}-\overline{a}_{*r}\right) + \sigma _{3}\left( \overline{a}_{r*}-\overline{a}\right)&> 0, \end{aligned}$$
(45)

where

$$\begin{aligned} \sigma _{1}&= \sum _{i=1}^{N}\sum _{\left\{ j\ :\ w_{ij}=1 \right\} }\sigma _{1}^{ij} ; \end{aligned}$$
(46a)
$$\begin{aligned} \sigma _{2}&= \sum _{i=1}^{N}\sum _{\left\{ j\ :\ w_{ij}=1 \right\} }\sigma _{2}^{ij} ; \end{aligned}$$
(46b)
$$\begin{aligned} \sigma _{3}&= \sum _{i=1}^{N}\sum _{\left\{ j\ :\ w_{ij}=1 \right\} }\sigma _{3}^{ij} . \end{aligned}$$
(46c)

In this way, the structure coefficients of Tarnita et al. (2011) are a sum of “local” structure coefficients.

4 Discussion

We have introduced a notion of reducibility in well-mixed populations that captures the typical way in which multiplayer games defined using a \(2\,\times \,2\) payoff matrix “break down” into a sequence of pairwise games. Based on the usual methods of calculating total payoff values (through accumulation or averaging), a game should be irreducible if it cannot be broken down linearly into a sequence of smaller games. An irreducible game in a well-mixed population will remain irreducible in a structured population because population structure effectively restricts possibilities for interactions among the players. Although reducible games in well-mixed populations need not remain reducible when played in structured populations, the existence of irreducible games shows that, in general, one need not assume that a game may be broken down into a sequence of simpler interactions, regardless of the population structure. This observation is not unexpected, but many of the classical games studied in evolutionary game theory are of the reducible variety.

As we observed with the linear public goods game, there are reducible games that may be perturbed slightly into irreducible games. For example, the “Hölder public goods” games demonstrate that it is possible to obtain irreducible games quite readily from reducible games. However, one must use caution: In the Hölder public goods game, the irreducibility of \(u^{p}\) depends on the number of players if \(\frac{1}{p}\in \left\{ 1,2,\ldots \right\} \). For such a value of \(p\), interactions with sufficiently many participants may be simplified if the population is well-mixed. Therefore, perturbing a linear public goods game to obtain a nonlinear public goods game does not necessarily guarantee that the result will be irreducible for every type of population. The deformations we introduced turn out to be irreducible for almost every \(p\), however, so one need not look hard for multiplayer public goods games that cannot be broken down.

Ohtsuki (2014) defines the notion of degree of a multiplayer games with two strategies. For this type of game, reducibility and degree are closely related in the sense that a game is \(k\)-reducible if and only if its degree is \(k-1\). Degree has been defined only for symmetric multiplayer games with two strategies. On the other hand, reducibility makes sense for any multiplayer game, even asymmetric games with many strategies. As a result, we have extended the concept of degree to much more general games: the degree of a game is defined to be the value \(k\) for which the game is \(\left( k+1\right) \)-reducible. Thus, the \(d\)-player irreducible games are precisely those whose degree is \(d-1\); those built from pairwise interactions only are the games of degree \(1\).

We derived selection conditions, also known as \(\sigma \)-rules, for multiplayer games with any number of strategies. In the limit of weak selection, the coefficients of these conditions are independent of payoff values. However, they are sensitive to the types of interactions needed to determine these payoff values. By fixing a \(d\)-player game and insisting that each player plays this game with every \(\left( d-1\right) \)-player subset of his or her neighbors, we arrive at a straightforward generalization of the known selection conditions of Tarnita et al. (2011) and Wu et al. (2013b). Of particular significance is the fact that the number of structure coefficients in a game with \(n\) strategies grows in \(d\) like \(d^{n-1}\). Implicit in this setup is the assumption that each player has at least \(d-1\) neighbors, which may or may not be the case. To account for a more general case in which each player simply plays a game with all of his or her neighbors, it is useful to know that one may define games that are always irreducible, independent of the number of players. There are corresponding selection conditions in this setting formed as a sum of selection conditions, one for each distinct group size of interacting players in the population. For each of these cases, we give a formula for the number of structure coefficients required by the selection condition; this number grows quickly with the number of players required for each game.

The payoff functions of the game are not always independent of the population structure. If \(\frac{1}{p}\not \in \left\{ 1,2,\ldots \right\} \), then the public goods game with payoff functions \(u_{i}^{p}\) is irreducible for any number of players. If the population structure is a degree-heterogeneous network, and if each player initiates this public goods game with all of his or her neighbors, then there is an irreducible \(k\)-player game for each \(k\) appearing as a degree of a node in the network. We established that the number of \(\sigma \)-coefficients depends on the number of players in each game, so in this example the number of coefficients depends on the structure of the population as well. This result contrasts the known result for two-player games in which the values of the structure coefficients may depend on the network, but the number of structure coefficients is independent of the network structure.

Our focus has been on the rules for evolutionary success for a general game and not on the explicit calculation of the structure coefficients (although calculations for small populations are manageable—see Appendix C). We extended these rules to account for more complicated types of interactions in evolutionary game theory. These selection conditions are determined by the signs of linear combinations of the payoff values, weighted by structure coefficients that are independent of these payoff values. Our general rules quantify precisely the price that is paid—in terms of additional structure coefficients—for relaxing the assumptions on the types of games played within a population. Based on the number of structure conditions required for the selection conditions, Theorems 3 and 4 seem to be in contravention of the tenet that these rules should be simple. Indeed, the simplicity of the selection condition of Tarnita et al. (2011) appears to be something of an anomaly in evolutionary game theory given the vast expanse of evolutionary games one could consider. This observation was made by Wu et al. (2013b) using a special case of the setup considered here, but our results show that \(\sigma \)-rules can be even more complicated in general. The simplicity of the rule of Tarnita et al. (2011), however, is due to the number of structure coefficients required, not necessarily the structure coefficients themselves. In theory, these structure coefficients can be calculated by looking at any particular game. In practice, even for pairwise interactions, these parameters have proven themselves difficult to calculate explicitly. Due to the difficulties in determining structure coefficients, the fact that there are more of them for multiplayer games may not actually be much of a disadvantage. With an efficient method for calculating these values, the general \(\sigma \)-rules derived here allow one to explicitly relate strategy success to payoff values in the limit of weak selection for a wide variety of evolutionary games.