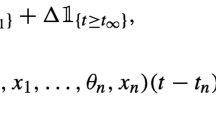1 Introduction

Risk control is an important issue in practical applications and thus there have been many risk measures developed for reflecting risk features of systems [3, 4, 12, 14, 16, 22]. As is known, one of the common and popular risk measures is the variance, which is often used to characterize the stability of random rewards/costs. The typical applications of the variance are the well-known mean-variance problems arising in finance and economics, which can be roughly classified into three groups according to the goals: (i) minimizing the variance subject to a constraint that its expected reward be equal to or at least some level [1, 8, 11, 25, 31, 32], (ii) maximizing the expected reward subject to a constraint that its variance not exceed some level [21, p. 408], and (iii) maximizing the variance penalized reward where the variance is incorporated as a penalty in the objective function [5, 6, 26, 28, 29, 30]. The earlier works on mean-variance problems were due to Markowitz’s portfolio allocation analysis [17, 18], where an investor seeks the lowest risk level that is quantified by the variance of the return after specifying his/her acceptable return level. Nowadays, the mean-variance problems have received increasing attentions and have been widely studied for various dynamic systems described by stochastic differential equations [1, 15, 29, 30, 31], Markov decision processes (MDPs) [7, 9, 10, 16, 20], and so on.

This paper is devoted to a mean-variance problem in semi-Markov decision processes (SMDPs). In the literature on MDPs, there are three kinds of variances, namely, the finite horizon reward variance [5, 24, 27], the infinite horizon discounted reward variance [6, 9, 24], and the limiting average variance [6, 7, 8, 10, 11, 16, 20, 21, 25, 28, 32]. Collins [5] considers finite horizon variance penalized discrete-time MDPs (DTMDPs) with finite states and actions, where it is assumed that there are no accumulated rewards and only a terminal reward. They formulate the variance penalized reward as a convex function of the distribution of the state at terminal time, and solve the problem by a convex analysis technique. Sobel [24] studies the finite horizon and infinite horizon discounted reward variances for DTMDPs as well as the infinite horizon discounted reward variance for SMDPs. They derive formulas for these variances via a formula of the distribution function of the discounted reward. However, the optimality results such as the existence of mean-variance optimal policies have not been given therein. Van Dijk and Sladký [27] treat the finite horizon reward variance for continuous-time Markov reward chains, where explicit expressions for the mean and variance are provided, but the presentation is restricted to the uncontrolled case and, as pointed out by the authors, it will be challenging to extend the results to the controlled case. Filar et al. [6] investigate the variance penalized problems for discounted finite DTMDPs, in which the variance measures are the “stage-wise variance” and the “discount normalized variance” rather than the precise variance of the total discounted reward. Guo et al. [9] discuss the discounted reward variance for finite continuous-time MDPs (CTMDPs), where they minimize the variance over a set of all deterministic stationary policies with a given expected reward. They show that the mean-variance problem can be transformed to an equivalent discounted optimization problem, and further prove that a mean-variance optimal policy and the efficient frontier can be obtained by policy iteration methods with a finite number of iterations. For the limiting average variance, there are a lot of works related to this issue; see, for instance, [6, 25, 28] for finite DTMDPs; [10, 11, 16, 32] for DTMDPs with general state space and unbounded rewards/costs; [8] for finite multi-chain CTMDPs; [7, 20] for CTMDPs with denumerable state spaces, Borel action spaces and unbounded rewards/costs; and [23] for uncontrolled semi-Markov processes with finite states. The methods used to deal with the limiting average variance problems are the dynamic programming and nonlinear programming approaches. In the dynamic programming approach [7, 8, 10, 11, 16, 20, 32], the limiting average variance is converted to a mean by the central limit theorem for Markov processes [10, p.175] and the martingale technique. However, in the nonlinear programming approach [5, 6, 25, 28], the problems are formulated as appropriate nonlinear programs in the space of state-action frequencies (or called occupancy measures).

As indicated above, most of the current works are concentrated on limiting average variance, while only a few address finite or infinite horizon discounted reward variance, especially finite horizon ones in continuous-time. This paper selects a finite horizon mean-variance problem in SMDPs, for which the state and action spaces are assumed to be Borel spaces, and the reward rate function may be unbounded. We aim at minimizing the variance of the finite horizon total reward in all deterministic Markov policies with a given mean. Our motivation is threefold. First, finite horizon optimization problems are a class of basic problems since, as we know, the lifetime of most systems in the real world is finite. Second, SMDPs are a sort of more general stochastic control models than DTMDPs and CTMDPs, in which the sojourn times are allowed to follow an arbitrary probability distribution, while the ones in DTMDPs are a fixed constant and the ones in CTMDPs are exponentially distributed. Third, although finite horizon variance penalized problems have been studied for DTMDPs in Collins [5], the associated arguments and techniques in [5] for the case of only terminal rewards are not suitable to the case of continuously accumulated rewards, due to which the finite horizon total reward mean-variance in SMDPs is an unsolved and novel problem.

In this paper, we adopt the dynamic programming approach to solve our mean-variance problem. That is, we shall convert the variance to a mean with a new reward/cost function and then apply the existing results of MDPs with a mean. However, in contrast to infinite horizon discount or limiting average mean-variance problems, finite horizon reward mean-variance problems appear more complicated because the time horizon should be now considered. In order to conduct the conversion of the finite horizon reward variance to a mean, we therefore first show that the mean of the finite horizon total reward generated by SMDPs coincides with the mean of an infinite horizon total reward of a DTMDP with a two dimension state space of time-state pairs and a one-step reward function derived from the reward rate for SMDPs (see Theorem 3.1(a)). Then, using the theory of \(N\)-step contraction, we succeed in characterizing policies with a given mean and converting the second order moment of the finite horizon reward to a mean of an infinite horizon reward/cost of a DTMDP with a new one-step reward/cost under suitable conditions (see Theorems 3.1(b) and 3.2). Based on the treatments above, we formulate our mean-variance problem to an equivalent infinite horizon DTMDP with a two dimension state space, new admissible action sets and a new transition law, and further establish the optimality equation and the existence of a mean-variance optimal policy by using the existing theory of DTMDPs. We also provide the value iteration and the Howard’s policy improvement algorithms for computing the value function and mean-variance optimal policies, respectively (see Theorem 3.3). Moreover, we develop a linear program (LP) and the dual program (DP) for solving our mean-variance problem. It is worthwhile to remark that the key point of obtaining the LP and DP lies in that the finite horizon total reward variance have been transformed as an equivalent expected infinite horizon reward of a DTMDP.

This paper proceeds as follows. Section 2 introduces the control model and the optimality problem. After giving technical preliminaries in Sect. 3, we state our main results on the existence and computation of mean-variance optimal policies in Sect. 4. A linear program and the dual program for solving the mean-variance problem are developed in Sect. 5. Finally, concluding remarks are made in Sect. 6.

2 Problem Formulation

We consider an SMDP model with a set of data as below

$$\begin{aligned} \Big \{E, A, \{ A(x), x \in E \}, Q(\cdot ,\cdot \mid x,a), r(x,a) \Big \}, \end{aligned}$$
(2.1)

consisting of

  1. (a)

    a Borel space \(E\), called the state space and endowed with the Borel \(\sigma \)-algebra \(\mathcal{{B}}(E)\);

  2. (b)

    a Borel space \(A\), called the action set and endowed with the Borel \(\sigma \)-algebra \(\mathcal{{B}}(A)\);

  3. (c)

    a family \(\{ A(x), x \in E \}\) of nonempty measurable subsets \(A(x)\) of \(A\), where each \(A(x)\) denotes the set of admissible actions at state \(x\in E\);

  4. (d)

    a semi-Markov kernel \(Q(\cdot ,\cdot |x,a)\), a stochastic kernel on \(R_+ \times E\) given \(K\), where \(R_+=[0,+\infty )\), and \(K=\{(x,a)\mid x \in E, a \in A(x) \} \) denotes the set of feasible state-action pairs and is assumed to be in \(\mathcal{{B}}(E \times A)\);

  5. (e)

    a real-value measurable function \(r(x,a)\) on \(K\), called the reward rate.

Remark 2.1

According to the Radon-Nikodym theorem, the semi-Markov kernel \(Q\) can be partitioned as shown below:

$$\begin{aligned} Q(t, D | x,a) = \int _D F(t |x,a,y) p(dy |x,a) \ \ \forall t \in R_+, D \in \mathcal{{B}}(E), (x,a) \in K,\nonumber \\ \end{aligned}$$
(2.2)

where \(F( \cdot |x,a,y)\) denotes the sojourn time distribution in state \(x\) when action \(a\) is chosen and the next state is to be \(y\), and \(p(\cdot |x,a)\) is the transition law of the system states.

To better understand the meaning of the data above, we describe how an SMDP evolves. In an SMDP, a controller observes the system states continuously in time. If the system jumps to \(x \in E\) at time \(t\), an action \(a \in A(x)\) is chosen according to some policy. As a consequence of this action choice, two things occur: first, the system jumps to \(y\) after a sojourn time \(s\) in \(x\) with the probability \(Q(ds, dy \mid x,a)\); second, rewards are continuously accumulated at rate \(r(x,a)\) until next jump. Since the time horizon is finite, we have to consider also the jump times besides the post-jump states when making decisions in a finite horizon SMDP. So, a (deterministic Markov) policy \(f\) is a measurable function from \(R_+ \times E\) to \(A\) such that \(f(t,x) \in A(x)\) for every \((t,x) \in R_+ \times E\), where \((t,x)\) represents the current jump time and the current state. The set of all policies is denoted by \(F\). Of course, we assume that \(F\) is nonempty.

For each \(n\ge 0\), we denote by \(T_n\) the \(n\)th jump time point of the SMDP, and by \(X_n\) the post jump state of the SMDP on \([T_n,T_{n+1})\). Then, \(\Theta _{n+1}:=T_{n+1}-T_n\) plays the role of sojourn time at state \(X_n\). Given a semi-Markov kernel \(Q\), an initial time-state pair \((t, x)\in R_+ \times E\) and a policy \(f \in F\), by the Ionescu Tulcea theorem, we can construct a probability space (\(\Omega , {\mathcal {F}}, P^f_{(t,x)} \)), on which the stochastic process \(\{T_n, X_n, n\ge 0\}\) is defined, such that

$$\begin{aligned}&P^f_{(t,x)}(T_0=t, X_0=x) = 1, \end{aligned}$$
(2.3)
$$\begin{aligned}&P^f_{(t,x)}(\Theta _{n+1} \le s, X_{n+1} \in B \mid T_0, X_0, \ldots , T_n, X_n) = Q(s, B \mid X_n, f(T_n,X_n)),\nonumber \\ \end{aligned}$$
(2.4)

for each \(s \in R_+, B \in \mathcal{{B}}(E)\) and \(n\ge 0 \).

Let \(T_{\infty }:=\lim _{k\rightarrow \infty }T_{k}\) be the explosive time of the SMDP. Note that \(T_{\infty }\) may be finite. We do not intend to consider the controlled process after the moment \(T_\infty \). For each \(t < T_\infty \) and \(f \in F\), let

$$\begin{aligned} Z(t)= \sum _{n\ge 0} I_{\{T_n\le t <T_{n+1}\}} X_n, \ W(t)= \sum _{n\ge 0} I_{\{T_n\le t <T_{n+1}\}} f(T_n, X_n) \end{aligned}$$

denote the underlying continuous-time state and action processes, respectively, where \(I_D\) stands for the indicator function on the set \(D\). In the sequel, we consider a \(T\)-horizon SMDP (with a fixed \(T \in R_+\)). To make the \(T\)-horizon SMDP sensible, we need to avoid the possibility of an infinite number of jumps during the interval \([0,T]\).

Assumption 2.1

For all \(( t, x) \in [0,T] \times E\) and \(f \in F\), \( P^f_{(t, x)}(\{T_{\infty } > T\})=1\).

Assumption 2.1 above is trivially fulfilled in DTMDPs with that \(T_{\infty } =\infty \). We suppose that Assumption 2.1 holds throughout the paper. Now, for each \(f \in F\), we define the mean of the finite horizon total reward under \(f\) by

$$\begin{aligned} V(f, t,x):=E^f_{(t,x)} \Big [ \int ^T_t r(Z(s),W(s))d s \Big ], (t,x) \in [0,T] \times E, \end{aligned}$$
(2.5)

and the variance of the finite horizon total reward under \(f\) by

$$\begin{aligned} \sigma ^2(f, t,x):= E^f_{(t,x)} \Big [ \int ^T_t r(Z(s),W(s))d s - V(f,t,x) \Big ]^2, (t,x) \in [0,T] \times E.\nonumber \\ \end{aligned}$$
(2.6)

Moreover, for a given function \(g\) on \( [0,T] \times E\), let \(F_g\) denote the set of all policies with a mean \(g\), i.e., \( F_g:=\{ f \in F | V(f,t,x)= g(t,x), \ \text{ for } \text{ all } \ (t,x) \in [0,T] \times E\}\). We always assume that \(F_g\ne \emptyset \) in the paper. Then, our mean-variance optimization problem is as follows:

$$\begin{aligned} (MV): \text{ minimize } \ \ \sigma ^2(f) \ \ \ \text{ over } \ f \in F_g. \end{aligned}$$
(2.7)

That is, our aim is at finding a policy \(f^* \in F_g\) such that

$$\begin{aligned} \sigma ^2(f^*, t,x) = \inf _{f \in F_g} \sigma ^2(f, t,x) \ \forall (t,x) \in [0,T] \times E. \end{aligned}$$

Such a policy \(f^*\), when it exists, is called mean-variance optimal.

Remark 2.2

  1. (a)

    The criteria functions \(V(f,t,x)\) and \(\sigma ^2(f,t,x)\) can be interpreted as the mean and variance when we start at some jump time \(t\) in state \(x\), respectively. In general, the criteria functions should have been of the from \(V(f,0,x)\) and \(\sigma ^2(f,0,x)\). Therefore, our criteria functions here generalize the usual ones in the existing studies.

  2. (b)

    Note that, when taking \(g(t,x)= \sup _{f \in F} V(f, t,x)\), the problem (\(MV\)) in (2.7) becomes seeking an optimal policy with maximal mean and minimal variance. This type of mean-variance problems have been widely studied for limiting average variance [7, 8, 10, 11, 16, 20, 32].

In next sections, we devote ourselves to exploring conditions for the existence of mean-variance optimal policies, and developing methods for computing a mean-variance optimal policy.

3 Technical Preliminaries

To investigate the problem (\(MV\)) in (2.7), we need a framework. First, let \(w(\cdot )\) be a measurable function on \(E\) satisfying \(w\ge 1\). For every real-valued function \(u\) on \(E\), we define its \(w\)-norm by

$$\begin{aligned} \Vert u \Vert _w :=\sup _{x \in E}|u(x)|/w(x). \end{aligned}$$

The function \(w\) is usually referred to as a weight function. Let \( \mathbb {B}_w(E):=\{u:\Vert u \Vert _w < \infty \} \) be the Banach space of \(w\)-bounded Borel-measurable functions on \(E\). Similarly, we define the Banach spaces \(\mathbb {B}_w([0,T] \times E)\) and \(\mathbb {B}_w([0,T] \times K)\) likewise, where \(w\) is viewed as weight functions defined on the spaces \([0,T] \times E\) and \([0,T] \times K\), respectively, i.e., \(w(t,x):=w(x)\) or \(w(t,x,a):=w(x)\) for all \((t,x,a) \in [0,T] \times K\). Furthermore, let

$$\begin{aligned}&\mathbb {B}_w^0([0,T] \times E):=\{l\in \mathbb {B}_w([0,T] \times E) | l(T,x) =0 \ \forall x \in E \}, \\&\mathbb {B}_w^0([0,T] \times K):=\{l\in \mathbb {B}_w([0,T] \times K) | l(T,x,a) =0 \ \forall (x,a) \in K \}. \end{aligned}$$

Then, for \(l \in \mathbb {B}_w^0([0,T] \times K)\) and \(f \in F\), define an operator \(H^f_l\) on \(\mathbb {B}^0_w([0,T] \times E)\) as follows:

$$\begin{aligned} H^f_l u(t,x) := l(t,x,f) + \int _ E \int ^{T-t}_0 u(t+s, y) Q(ds, dy \mid x,f(t,x)), \end{aligned}$$

for \(u \in \mathbb {B}^0_w([0,T] \times E)\), \((t,x) \in [0,T] \times E\), where \( l(t,x,f):= l(t,x,f(t,x))\).

Our works rely on the theory of \(N\)-step contraction. To this end, we shall impose some assumptions on the data of our model.

Assumption 3.1

There exist constants \(\delta >0\) and \(\epsilon >0\) such that

$$\begin{aligned} F(\delta |x,a,y)\le 1-\epsilon \ \ \forall \ (x,a) \in K, y \in E, \end{aligned}$$

with \( F(\cdot |x,a,y)\) as in (2.2).

Assumption 3.2

There exist a weight function \(w\ge 1\) on \(E\), constants \(M >0\) and \(b_1>0\) such that, for each \((x,a) \in K\),

  1. (a)

    \( |r(x,a)| \le M w(x)\);

  2. (b)

    \( \int _E w(y) p(dy | x,a) \le w(x)+ b_1\), with \(p(\cdot | x,a)\) as in (2.2).

Remark 3.1

  1. (a)

    Assumption 3.1 implies Assumption 2.1 in view of Proposition 2.1 in [13], due to which Assumption 2.1 will be omitted whenever Assumption 3.1 is satisfied. Moreover, note that the constant \(\delta \) in Assumption 3.1 above may be smaller than the time horizon \(T\) (which is arbitrarily fixed), and thus Assumption 3.1 can be widely verified; for example, it is obviously satisfied in the model of DTMDPs.

  2. (b)

    In fact, Assumption 3.1 has been frequently used in SMDPs so as to avoid the possibility of infinitely many transitions within any (rather than a fixed) finite time; see, for instance, [12] for a probability criterion, [19] for expected finite horizon reward criteria, and [21] for discounted and average reward criteria.

The following lemma is fundamental to our main results.

Lemma 3.1

Suppose Assumption 3.1 and 3.2(b) hold. Let \(f \in F\) be an arbitrary policy, \(l \in \mathbb {B}_w^0([0,T] \times K)\) be a reward/cost function, and

$$\begin{aligned} J_l(f,t,x):= E_{(t,x)} ^f \left[ \sum _{k=0}^\infty l(T_k \wedge T, X_k, f) \right] , (t,x) \in [0,T] \times E. \end{aligned}$$

Then, the following assertions are true.

  1. (a)

    \(H^f_l\) is an \(N\)-step contraction from \(\mathbb {B}^0_w([0,T] \times E)\) to itself for some \(N\ge 1\).

  2. (b)

    \( J_l(f)\) is the unique solution in \(\mathbb {B}^0_w([0,T] \times E)\) to the equation \(u=H^f_l u\).

Proof

(a) First, we verify that \(H^f_l\) maps \(\mathbb {B}^0_w([0,T] \times E)\) to itself under Assumption 3.2(b). To see this, pick \(u \in \mathbb {B}^0_w([0,T] \times E)\) and observe that

$$\begin{aligned} |H^f_l u(t,x)|&\le \Vert l \Vert _w w(x) + \int _{ E}\int ^{T-t}_0 Q(ds, dy \mid x,f(t,x)) \Vert u \Vert _w w(y) \\&\le \Vert l \Vert _w w(x) + \Vert u \Vert _w \int _{E } w(y) F(T-t \mid x, f(t,x), y) p(dy | x,f(t,x)) \\&\le \Vert l \Vert _w w(x) + \Vert u \Vert _w (w(x)+b_1) \\&\le \Big [ \Vert l \Vert _w + \Vert u \Vert _w (1+b_1) \Big ]w(x). \end{aligned}$$

Moreover, since \(H^f_l u(T,x)=0\) for each \(x \in E\), it follows that \(H^f_l u \in \mathbb {B}^0_w([0,T] \times E)\).

We now show that \(H^f_l\) is an \(N\)-step contraction from \(\mathbb {B}^0_w([0,T] \times E)\) to itself for some \(N\ge 1\). To do so, define

$$\begin{aligned} F_\delta (t)= \left\{ \begin{array}{l@{\quad }l} 0, &{} t< 0,\\ 1-\epsilon , &{} 0 \le t < \delta ,\\ 1, &{} {t\ge \delta }. \end{array} \right. \end{aligned}$$

Then, for any \(u,v \in \mathbb {B}^0_w([0,T] \times E)\), under Assumption 3.2(b), we have

$$\begin{aligned}&|H^f_l u(t,x)- H^f_l v(t,x)| \\&\quad \le \Vert u -v\Vert _w \int _{ E}\int ^{T-t}_0 w(y) Q(ds, dy \mid x,f(t,x)) \\&\quad \le \Vert u -v\Vert _w \int _{E } w(y) F(T-t \mid x, f(t,x), y) p(dy | x,f(t,x)) \\&\quad \le F_\delta (T-t) \Vert u-v \Vert _w (w(x)+b_1), \ \ \ (t,x) \in [0,T] \times E. \end{aligned}$$

Furthermore, for each \((t,x) \in [0,T] \times E\), we get

$$\begin{aligned}&|(H^f_l)^2 u(t,x)- (H^f_l)^2 v(t,x)| \\&\quad \le \Vert u -v\Vert _w \int _{ E}\int ^{T-t}_0 F_\delta (T-t-s) (w(x)+b_1) Q(d s, dy \mid x,f(t,x)) \\&\quad \le \Vert u -v\Vert _w \int _{ E}\int ^{T-t}_0 F_\delta (T-t-s) (w(x)+b_1)\\&\qquad F(d y|x,f(t,x),y) p(dy \mid x,f(t,x)). \end{aligned}$$

We next verify

$$\begin{aligned}&\int ^{T-t}_0 F_\delta (T-t-s) F(d y|x,f(t,x),y) \le F_\delta ^{(2)}(T-t)\nonumber \\&\quad := \int _0^{T-t} F_\delta (T-t-s) d F_\delta (s), \forall \ y \in E. \end{aligned}$$

Indeed, if \((T-t)< \delta \), it is clear that

$$\begin{aligned} \int ^{T-t}_0 F_\delta (T-t-s) F(d y|x,f(t,x),y) \le (1-\epsilon )^2= F_\delta ^{(2)}(T-t), \forall \ y \in E; \end{aligned}$$

if \((T-t) \ge \delta \), a straightforward calculation shows that

$$\begin{aligned} \int ^{T-t}_0 F_\delta (T-t-s) F(d y|x,f(t,x),y)&\le (1-\epsilon )+ \epsilon F_\delta (T-t-\delta )\\&= F_\delta ^{(2)}(T-t), \forall \ y \in E. \end{aligned}$$

Hence, we obtain

$$\begin{aligned} \left| (H^f_l)^2 u(t,x)- (H^f_l)^2 v(t,x)\right|&\le F_\delta ^{(2)}(T-t) \Vert u-v \Vert _w (w(x)+ 2 b_1), \\&(t,x) \in [0,T] \times E. \end{aligned}$$

Similarly, an induction argument yields that, for any \(n\ge 2\),

$$\begin{aligned}&\left| (H^f_l)^n u(t,x)- (H^f_l)^n v(t,x)\right| \\&\quad \le F_\delta ^{(n)}(T-t) \Vert u-v \Vert _w (w(x)+ nb_1), \ \ \ (t,x) \in [0,T] \times E, \end{aligned}$$

where \(F_\delta ^{(n)}\) is the \(n\)-fold convolution of \(F_\delta \), defined by

$$\begin{aligned} F_\delta ^{(n)}(t)=\int _0^t F_\delta ^{(n-1)}(t-s) d F_\delta (s), \ \ \ t \in R_+. \end{aligned}$$

On the other hand, it follows from Assumption 3.1 and the argument of the proof of Theorem 1 in Mamer [19] that for any \(n>k\) and \(s>0\),

$$\begin{aligned} F_\delta ^{(n)}(s) \le (1-\epsilon ^k)^{\lfloor n/k \rfloor }, \end{aligned}$$

where \(k\) is a nonnegative integer satisfying \(k> s/\delta \), and \({\lfloor n/k \rfloor }\) denotes the largest integer not larger than \( n/k\). Hence, noting that \(F_\delta ^{(n)}(T-t)\le F_\delta ^{(n)}(T)\) for every \(t \in [0,T]\), we obtain

$$\begin{aligned}&\Vert (H^f_l)^n u- (H^f_l)^n v \Vert _w \le (1-\epsilon ^{k^*})^{\lfloor n/{k^*} \rfloor } (1+ nb_1) \Vert u-v \Vert _w, \end{aligned}$$

for a nonnegative integer \(k^*\) satisfying \(k^* > T/\delta \), and every \(n >k^*\). Choosing \(N\) large enough so that \((1-\epsilon ^{k^*})^{\lfloor N/{k^*} \rfloor } (1+ Nb_1) <1\) establishes that \(H^f_l\) is an \(N\)-step contraction with respect to the metric generated by \( \Vert \cdot \Vert _w\).

(b) First, given the semi-Markov kernel \(Q\), an initial time-state pair \((t, x)\in [0,T] \times E\) and a policy \(f \in F\), we observe that \(\{T_n \wedge T, X_n, n\ge 0 \}\) is in fact a Markov chain defined on the probability space (\(\Omega , {\mathcal {F}}, P^f_{(t,x)} \)), which has a two-dimension state space \([0,T] \times E\) and a transition law

$$\begin{aligned} \mathbb {Q}(B \times C \mid t,x, f):= \int _0^{T-t} I_B(t+s) Q(ds, C |x, f(t,x)), \end{aligned}$$
(3.1)

for \( B \times C \in \mathcal {B}([0,T]\times E), (t,x) \in [0,T] \times E\). Then, under Assumptions 3.1 and 3.2(b), by induction we can show that

$$\begin{aligned}&\int _{[0,T] \times E} w(y) \mathbb {Q}^{(n)}(d s,dy \mid t,x, f(t,x))\\&\quad = \int _{E } \int _0^{T-t} w(y) Q^{(n)}(ds, dy \mid x, f(t,x)) \\&\quad \le F_\delta ^{(n)}(T-t) (w(x)+n b_1) \\&\quad \le (1-\epsilon ^{k^*})^{\lfloor n/{k^*} \rfloor } (1+nb_1)w(x), \end{aligned}$$

for every \(n >k^*\), where \(k^*\) is as in the proof of part (a). Applying this result yields

$$\begin{aligned} \Big |J_l(f,t,x) \Big |&= \left| \sum _{n=0}^\infty \int _{[0,T] \times E} l(s,y, f(s,y)) P_{(t,x)} ^f( (T_n \wedge T) \in ds, X_n \in dy) \right| \\&\le \sum _{n=0}^\infty \int _{[0,T] \times E} \Vert l \Vert _w w(y) \mathbb {Q}^{(n)}(ds, dy \mid t,x, f) \\&\le \Vert l \Vert _w \sum _{n=0}^\infty F_\delta ^{(n)}(T-t) (1+n b_1) w(x)\\&\le \Vert l \Vert _w w(x) \sum _{n=0}^\infty (1-\epsilon ^{k^*})^{\lfloor n/{k^*} \rfloor } (1+n b_1). \end{aligned}$$

Since \(0<(1-\epsilon ^{k^*})<1\), by the properties of the infinite series and the D’alembert test, it is clear that the series \( \sum _{n=0}^\infty (1-\epsilon ^{k^*})^{\lfloor n/{k^*} \rfloor } (1+n b_1) \) converge to some constant \(L\). Thus, we obtain that

$$\begin{aligned} |J_l(f,t,x)| \le L \Vert l \Vert _w w(x) \ \ \forall (t,x) \in [0,T] \times E, \end{aligned}$$

which together with \(J_l(f,T,x)=0\) immediately leads to that \(J_l(f) \in \mathbb {B}^0_w([0,T] \times E)\).

Furthermore, it follows from the properties (2.3– 2.4) and the fact \(l(T,x,a)=0\) that

$$\begin{aligned} J_l(f,t,x)&= E_{(t,x)} ^f [ l(T_0 \wedge T,X_0, f)]+ E_{(t,x)} ^f \left[ E_{(t,x)} ^f \left[ \sum _{k=1}^\infty l(T_n \wedge T, X_k, f) |T_1, X_1 \right] \right] \\&= l(t,x, f)+ \int _{[0,T] \times E} \mathbb {Q}(d (t+s), dy \mid t,x, f)\\&\times \, E_{(t,x)} ^f \left[ \sum _{k=1}^\infty l(T_n \wedge T, X_k, f) |T_1=t+s, X_1=y \right] \\&= l(t,x, f)+ \int _E \int ^{T-t}_0 Q(d s, dy \mid x, f(t,x)) E_{(t+s,y)} ^f \left[ \sum _{k=0}^\infty l(T_n \wedge T, X_k, f)\right] \\&= l(t,x, f)+ \int _E \int ^{T-t}_0 Q(d s, dy \mid x, f(t,x)) J_l(f, t+s, y), \end{aligned}$$

which indicates that \(J_l(f)=H_l^f J_l(f)\). This fact together with part (a) achieves the proof. \(\square \)

Now, as the usual treatments for the mean-variance problems [7, 8, 9, 10, 11, 16, 20], we shall characterize policies in \(F_g\) and transform the finite horizon reward variance to a mean. These will be done in the rest of this section. First, we demonstrate how to distinguish a policy in \(F_g\).

Theorem 3.1

Suppose Assumptions 3.1 and 3.2 hold.

  1. (a)

    For each \((t,x) \in [0,T] \times E\) and \(f \in F\), we have

    $$\begin{aligned} V(f,t,x) = J_{\tilde{r}}(f,t,x):= E^f_{(t,x)} \left[ \sum _{m=0}^{\infty } \tilde{r}(T_m \wedge T, X_m, f) \right] , \end{aligned}$$
    (3.2)

    with the function \(\tilde{r}(t,x, a)\) defined by

    $$\begin{aligned} \tilde{r}(t,x, a):= r(x, a) \int _0^{T-t} \Big ( 1- Q(s, E| x, a ) \Big ) d s \ \ \ \forall (t,x,a) \in [0,T] \times K. \end{aligned}$$

    Furthermore, \( V( f)\) is the unique solution in \(\mathbb {B}^0_w([0,T] \times E)\) to the equation \(V( f)=H^f_{\tilde{r}} V( f)\).

  2. (b)

    A policy \(f \in F\) is in \(F_g\) if and only if \(f(t,x) \in A_g(t,x)\) for all \((t,x) \in [0,T] \times E\), where

    $$\begin{aligned} A_g(t,x):= \left\{ a \in A(x) | g(t,x) = \tilde{r}(t,x, a) + \int _{ E}\int ^{T-t}_0 Q(ds, dy \mid x,a)g(t+s,y) \right\} . \nonumber \\ \end{aligned}$$
    (3.3)

Proof

(a) We first prove \(V(f) \in \mathbb {B}_w^0([0,T] \times E)\). It is obvious that \(V(f,T,x)=0\). Moreover, we have

$$\begin{aligned}&|V(f,t,x)| \nonumber \\&\quad \le E^f_{(t,x)} \left[ \int ^T_t \Big |r(Z(s),W(s)) \Big | ds \right] \nonumber \\&\quad = E^f_{(t,x)} \left[ \sum _{m=0}^{\infty } \int ^{T \wedge T_{m+1}}_{T \wedge T_m} \Big |r(Z(s),W(s))\Big | ds \right] \nonumber \\&\quad = \sum _{m=0}^{\infty } E^f_{(t,x)} \Big [ | r(X_m, f(T_m \wedge T, X_m))| (T-T_m)^+ \wedge (T_{m+1}-T_m) \Big ] \nonumber \\&\quad = \sum _{m=0}^{\infty } E^f_{(t,x)} \Big [ | r(X_m, f(T_m \wedge T, X_m))| E^f_{(t,x)} \Big [ (T-T_m)^+ \wedge (T_{m+1}-T_m) | T_m, X_m \Big ] \Big ] \nonumber \\&\quad = \sum _{m=0}^{\infty } E^f_{(t,x)} \Big [ |r(X_m, f(T_m \wedge T,X_m))| \int _0^{(T-T_m)^+} \Big ( 1- Q(s, E| X_m, f(T_m \wedge T,X_m) \Big ) ds \Big ] \nonumber \\&\quad = \sum _{m=0}^{\infty } E^f_{(t,x)} \Big [ |r(X_m, f(T_m \wedge T, X_m))| \int _0^{T-T_m\wedge T} \Big ( 1- Q(s, E| X_m, f(T_m \wedge T,X_m) \Big ) ds \Big ] \nonumber \\&\quad = \sum _{m=0}^{\infty } E^f_{(t,x)} \Big [ | \tilde{r}(T_m\wedge T, X_m, f(T_m \wedge T,X_m))| \Big ]= J_{|\tilde{r}|}(f,t,x), \end{aligned}$$
(3.4)

where the first equality follows from the property (2.3) and Assumption 2.1, the second equality is due to the monotone convergence theorem, and the fourth equality is by the property (2.4). Now, taking \(l(t,x, a)=|\tilde{r}(t,x, a)|\), noting that \(|\tilde{r}| \in \mathbb {B}_w^0([0,T] \times K)\) under Assumption 3.2(a), and using a manner as in the proof of Lemma 3.1(b) above, we can show that \(J_{|\tilde{r}|}(f)\) is in \(\mathbb {B}_w^0([0,T] \times E)\) and so is \(V(f)\). Moreover, since the right hand side of (3.4) is finite, using the argument similar to (3.4) above and the dominated convergence theorem gives that

$$\begin{aligned} V(f,t,x) = E^f_{(t,x)} \left[ \sum _{m=0}^{\infty } \tilde{r}(T_m \wedge T, X_m, f) \right] =J_{\tilde{r}}(f,t,x). \end{aligned}$$

The rest statement of part (a) immediately follows from Lemma 3.1(b).

\((b)\) It is a straightforward result of part (a). \(\square \)

Next, we give an example to show how to determine a policy in \(F_g\) with the help of Theorem 3.1(b), in which \(F_g\) may have more than one element.

Example 3.1

Consider a \(T\)-horizon SMDP with some \(T>0\). The state space \(E=\{1,2 \}\), the action set \(A(1)=\{1,2,3\}, A(2)=\{4,5\}\), the sojourn time distribution \(F(s | x,a,y)=1-e^{-m(x)s}\), and the transition law \(p(y |x,a)= \dfrac{a}{m(x)}+ \delta _{\{x\}}(y)\) for \(x,y \in E\), \(a \in A(x)\) and some function \(m(x)\) satisfying \(m(1)\ge 3, m(2)\ge 5\). We consider a bit more general reward rates - nonhomogeneous reward rates \(r(t,x,a)\), for which Theorem 3.1 still holds with appropriate adjustments. More specifically, for every \(t \in [0,T]\), the reward rates are given by \(r(t,1,1)=2\),

$$\begin{aligned} \ r(t,1,2)=\left\{ \begin{array}{l@{\quad }l@{\quad }l} 1+e^{-6(T-t)}, &{} 0\le t\le \dfrac{T}{2},\\ 3, &{} \dfrac{T}{2} < t\le T, \end{array} \right. r(t,1,3)= \left\{ \begin{array}{l@{\quad }l@{\quad }l} 10, &{} 0\le t\le \dfrac{T}{2},\\ 2 e^{-6(T-t)}, &{} \dfrac{T}{2} < t\le T, \end{array} \right. \end{aligned}$$

and \(r(t,2,4)= 7+e^{-6(T-t)}, r(t,2,5)=8\). Then, for \((t,x) \in [0,T] \times E\), we have

which is equivalent to

$$\begin{aligned} A_g(t,x)= \Big \{ a \in A(x) | g_t(t,x) + r(t,x, a) +a g(t,y) - a g(t,x)= 0 \Big \}, \end{aligned}$$

where \(g_t(t,x)\) denotes the derivative of \(g(t,x)\) with respect to time \(t\).

Now, take the mean reward function \(g(t,x)\) as follows:

$$\begin{aligned}&g(t,1)=3(T-t)-\frac{1}{6} \left( 1- e^{-6(T-t)}\right) , \\&g(t,2)=3(T-t) + \frac{5}{6} \left( 1- e^{-6(T-t)}\right) , \ \forall \ t \in [0,T]. \end{aligned}$$

Then, one can verify \(f^1(t,x)\) and \(f^2(t,x)\) are both in \(A_g(t,x)\) for every \((t,x) \in [0,T] \times E\), where the two policies \(f^1, f^2\) are defined by

$$\begin{aligned} f^1(t,1)=1, f^1(t,2)=5, \ \forall \ t \in [0,T]; \end{aligned}$$

and

$$\begin{aligned} f^2(t,1)=2, t \in \left[ 0, \dfrac{T}{2}\right] ; \ \ f^2(t,1)=3, t \in \left( \dfrac{T}{2}, T\right] ; \ \ f^2(t,2)=4 , \ t \in [0,T], \end{aligned}$$

respectively. Hence, by Theorem 3.1(b), we have \(f^1, f^2 \in F_g\).

To transform the finite horizon reward variance to a mean, we require an additional condition below.

Assumption 3.3

There exists a constant \(b_2>0\) such that

$$\begin{aligned} \int _E w^2(y) p(dy | x,a) \le w^2(x)+ b_2 \ \ \forall \ (x,a) \in K, \end{aligned}$$
(3.5)

where the weight function \(w(\cdot )\) is as in Assumption 3.2.

Remark 3.2

By taking the square root of both sides of (3.5) and using Jensen’s inequality, we have

$$\begin{aligned} \int _E w(y) p(dy | x,a) \le w(x)+ \sqrt{b_2} \ \ \forall \ (x,a) \in K. \end{aligned}$$

Thus, Assumption 3.3 implies Assumption 3.2(b).

It should be remarked here that, under Assumptions 3.1 and 3.3, a similar argument to the proof of Lemma 3.1(a) indicates that the operator \(H^f_l\) is an \(N\)-step contraction from \(\mathbb {B}^0_{w^2}([0,T] \times E)\) to \(\mathbb {B}^0_{w^2}([0,T] \times E)\) for some \(N\ge 1\) and \(l \in \mathbb {B}^0_{w^2}([0,T] \times K)\). To conduct the transformation of the variance to a mean, we will also use the following notation. Let

$$\begin{aligned} c_g(t,x, a)&:= 2r^2(x,a)\int ^{T-t}_0 s (1-Q(s,E \mid x,a))ds \nonumber \\&\quad + \ 2r(x,a) \int _E \int ^{T-t}_0 s g(t+s,y) Q(ds,dy \mid x,a) \end{aligned}$$
(3.6)

for all \((t,x,a) \in \mathcal {K}_g:=\{(t,x, a) \mid t \in [0,T], x \in E, a \in A_g(t,x)\}\), and let \(S(f)\) denote the second order moment of the finite horizon total reward, that is,

$$\begin{aligned} S(f,t,x):= E_{(t,x)} ^f \Big [\int _t^T r(Z(s),W(s))ds \Big ]^2, \ (t,x) \in [0,T] \times E. \end{aligned}$$

Obviously, \(S(f,t,x) =\sigma ^2(f, t,x) +g^2(t,x)\) for each \( f \in F_g\) and \((t,x) \in [0,T] \times E\). Therefore, the problem (\(MV\)) in (2.7) is equivalent to minimizing \(S(f)\) over \(F_g\). This fact implies that we can convert the second order moment \(S(f)\) to a mean instead of the variance \(\sigma ^2(f)\) to a mean, which, however, will bring some convenience and simplicity for our presentation.

Theorem 3.2

Under Assumptions 3.1–3.3, the following assertions hold for each \( f \in F_g\).

  1. (a)

    \(S(f)\) is the unique solution in \(\mathbb {B}^0_{w^2}([0,T] \times E)\) to the equation \(u=H^f_{c_g}u\).

  2. (b)

    \(S(f,t,x)=J_{c_g}(f, t,x) := E_{(t,x)} ^f \Big [\sum \limits _{k=0}^\infty c_g(T_k \wedge T, X_k, f) \Big ]\), \((t,x)\in [0,T] \times E\).

Proof

(a) For each \(f\in F\) and \(x \in E\), it is obvious that \(S(f,T,x)=0\). To complete the proof of \(S(f) \in \mathbb {B}^0_{w^2}([0,T] \times E)\), we let

$$\begin{aligned} R(t,x, a) := r^2(x,a) \int ^{T-t}_0 2 s (1-Q(s,E \mid x, a))d s, \ \ (t,x,a) \in [0,T]\times K. \end{aligned}$$

Indeed, using the properties of the product of two infinite series, Cauchy-Schwartz inequality, the properties (2.3–2.4), and Assumptions 3.1–3.3, we have

$$\begin{aligned}&S(f,t,x) \\&\quad = E_{(t,x)} ^f \left[ \int _t^T r(Z(s),W(s))d s \right] ^2 \\&\quad = E_{(t,x)} ^f \left[ \sum _{n=0}^\infty \int _{T \wedge T_n}^{T \wedge T_{n+1}} r(Z(s),W(s))ds \right] ^2 \\&\quad = E_{(t,x)} ^f \left[ \sum _{n=0}^\infty r(X_n,f(T_n \wedge T,X_n)) [(T-T_n)^+ \wedge (T_{n+1}-T_n) ] \right] ^2\\&\quad \le E_{(t,x)} ^f \left[ \sum _{n=0}^\infty \Big | r(X_n,f(T_n \wedge T,X_n))\Big | [(T-T_n)^+ \wedge \Theta _{n+1} ] \right] ^2\\&\quad = E_{(t,x)} ^f \left[ \sum _{n=0}^\infty \sum _{k+l=n} \Big |r(X_k,f(T_k \wedge T,X_k)) \Big | \Big [(T-T_k)^+ \wedge \Theta _{k+1}\Big ]\right. \\&\quad \quad \left. \times \Big | r(X_l, f(T_l \wedge T,X_l))\Big | \Big [(T-T_l)^+ \wedge \Theta _{l+1} \Big ] \right] \\&\quad = \sum _{n=0}^\infty \sum _{k+l=n} E_{(t,x)} ^f \Big [ \Big |r(X_k, f(T_k \wedge T,X_k)) \Big | \Big [(T-T_k)^+ \wedge \Theta _{k+1} \Big ] \\&\quad \quad \times \Big | r(X_l, f(T_l \wedge T,X_l)) \Big | \Big [(T-T_l)^+ \wedge \Theta _{l+1} \Big ] \Big ] \\&\quad \le \sum _{n=0}^\infty \sum _{k+l=n} \sqrt{E_{(t,x)} ^f \Big [ |r(X_k,f(T_k \wedge T,X_k))| [(T-T_k)^+ \wedge \Theta _{k+1} ] \Big ]^2} \\&\quad \quad \times \sqrt{E_{(t,x)} ^f \Big [ | r(X_l,f(T_l \wedge T,X_l))| [(T-T_l)^+ \wedge \Theta _{l+1} ] \Big ]^2 } \\ \end{aligned}$$
$$\begin{aligned}&\quad \le \sum _{n=0}^\infty \sum _{k+l=n} \sqrt{E_{(t,x)} ^f \Big [ r^2(X_k,f(T_k \wedge T,X_k)) \int ^{(T-T_k)^+ }_0 2 s (1-Q(s,E \mid X_k,f(T_k \wedge T,X_k)))ds \Big ]}\\&\quad \quad \times \sqrt{E_{(t,x)} ^f \Big [ r^2(X_l,f(T_l \wedge T,X_l)) \int ^{(T-T_l)^+ }_0 2 s (1-Q(s,E \mid X_l,f(T_l \wedge T,X_l)))ds \Big ]} \\&\quad \le \sum _{n=0}^\infty \sum _{k+l=n} \sqrt{E_{(t,x)} ^f \Big [ r^2(X_k,f(T_k \wedge T,X_k)) \int ^{T-T_k \wedge T}_0 2 s (1-Q(s,E \mid X_k,f(T_k \wedge T,X_k)))ds \Big ]}\\&\quad \quad \times \sqrt{E_{(t,x)} ^f \Big [ r^2(X_l,f(T_l \wedge T,X_l)) \int ^{T-T_l\wedge T }_0 2 s (1-Q(s,E \mid X_l,f(T_l \wedge T,X_l)))ds \Big ]} \\&\quad = \sum _{n=0}^\infty \sum _{k+l=n} \sqrt{E_{(t,x)} ^f \Big [ R(T_k \wedge T, X_k, f(T_k \wedge T,X_k)) \Big ]} \sqrt{E_{(t,x)} ^f \Big [ R(T_l \wedge T, X_l, f(T_l \wedge T,X_l)) \Big ] }\\&\quad = \sum _{n=0}^\infty \sum _{k+l=n} \sqrt{ \int _{[0,T] \times E} R(s,y,f) \mathbb {Q}^{(k)}(ds, dy \mid t,x, f)} \\&\quad \quad \times \sqrt{\int _{[0,T] \times E} R(s, y, f) \mathbb {Q}^{(l)}(d s, dy \mid t,x, f) } \\&\quad \le M^2 T^2 \sum _{n=0}^\infty \sum _{k+l=n} \sqrt{ F_\delta ^{(k)}(t) (w^2(x)+k b_2) } \sqrt{ F_\delta ^{(l)}(t) (w^2(x)+l b_2) } \\&\quad \le M^2 T^2 \sum _{n=0}^\infty (w^2(x)+nb_2) \sum _{k+l=n} \sqrt{ F_\delta ^{(k)}(t) } \sqrt{ F_\delta ^{(l)}(t)} \\&\quad \le M^2 T^2 w^2(x) \sum _{n=0}^\infty (1 +n b_2) \sum _{k+l=n} \sqrt{ (1-\epsilon ^{k^*})^{\lfloor k/k^* \rfloor + \lfloor l/k^* \rfloor }} \\&\quad \le M^2 T^2 w^2(x) \sum _{n=0}^\infty (1 +n b_2) \sum _{k+l=n} \sqrt{(1-\epsilon ^{k^*})^{\lfloor n/k^* \rfloor -2} } \\&\quad \le M^2 T^2 w^2(x) \sqrt{ (1-\epsilon ^{k^*})^{-2} } \Big [ 1+ \sum _{n=1}^\infty n (1 +n b_2) \sqrt{ (1-\epsilon ^{k^*})^{\lfloor n/k^* \rfloor } } \Big ] \\&\quad \le M^2 T^2 (1-\epsilon ^{k^*})^{-1} \Big [ 1+ \sum _{n=1}^\infty n (1 +n b_2) (1-\epsilon ^{k^*})^{\frac{\lfloor n/k^* \rfloor }{2}} \Big ] w^2(x), \end{aligned}$$

where \(\mathbb {Q}(\cdot , \cdot \mid t,x, f)\) and \(k^*\) are as in the proof of Lemma 3.1(b). Since \(0<(1-\epsilon ^{k^*})<1\), by the properties of the infinite series and the D’alembert test, it is clear that the series \( \sum _{n=1}^\infty n (1 +n b_2) (1-\epsilon ^{k^*})^{\frac{\lfloor n/k^* \rfloor }{2}} \) converge to some constant \(L\). Thus, we obtain

$$\begin{aligned} S(f,t,x) \le M^2 T^2 (1-\epsilon ^{k^*})^{-1} (1+L) w^2(x) \ \ \forall (t,x) \in [0,T] \times E, \end{aligned}$$

which implies that \(S(f) \in \mathbb {B}^0_{w^2}([0,T] \times E)\) for each \(f \in F\).

We now show that \(S(f)\) satisfies \(S(f)=H^f_{c_g}S(f)\) for each \(f \in F_g\). To this end, fix any \((t,x) \in [0,T] \times E\) and \(f \in F_g\). Then, we see that

$$\begin{aligned} S(f,t,x)&= E_{(t,x)} ^f \left[ \int _t^T r(Z(s),W(s))ds \right] ^2 \\&= E_{(t,x)} ^f \left[ \int _t^{T \wedge T_1} r(Z(s),W(s))ds + \int _{T \wedge T_1}^T r(Z(s),W(s))ds \right] ^2 \\&= E_{(t,x)} ^f \left[ \int _t^{T \wedge T_1} r(Z(s),W(s))ds \right] ^2 + E_{(t,x)} ^f \left[ \int _{T \wedge T_1}^T r(Z(s),W(s))ds \right] ^2 \\&\quad +2 E_{(t,x)} ^f \left[ \left( \int _t^{T \wedge T_1} r(Z(s),W(s))ds \right) \left( \int _{T \wedge T_1}^T r(Z(s),W(s))ds \right) \right] . \end{aligned}$$

For simplicity, let

$$\begin{aligned}&L_1 = E_{(t,x)} ^f \left[ \int _t^{T \wedge T_1} r(Z(s),W(s))ds \right] ^2, \\&L_2 = 2 E_{(t,x)} ^f \left[ \left( \int _t^{T \wedge T_1} r(Z(s),W(s))ds \right) \left( \int _{T \wedge T_1}^T r(Z(s),W(s))ds \right) \right] ,\\&L_3 = E_{(t,x)} ^f \left[ \int _{T \wedge T_1}^T r(Z(s),W(s))ds \right] ^2. \end{aligned}$$

We next compute \(L_1\), \(L_2\) and \(L_3\), respectively. First, noting that \(Z(t)=X_0=x\) for all \(t < T_1\), we obtain

$$\begin{aligned} L_1&= r^2(x,f(t,x)) E_{(t,x)} ^f \Big [T \wedge T_1-t \Big ]^2 \\&= r^2(x,f(t,x)) \int _0^\infty 2s P_{(t,x)} ^f \Big (T \wedge T_1-t >s \Big ) d s \\&= 2 r^2(x,f(t,x)) \int _0^\infty s P_{(t,x)} ^f \Big (T > t+ s, T_1 > t+ s \Big ) d s \\&= 2r^2(x, f(t,x))\int ^{T-t}_0 s (1-Q(s,E \mid x,f(t,x)))ds. \end{aligned}$$

Using the properties (2.3–2.4) as well as the fact \(f \in F_g\) yields

$$\begin{aligned} L_2&= 2 r(x,f(t,x)) E_{(t,x)} ^f \left[ ( T \wedge T_1-t ) \left( \int _{T \wedge T_1}^T r(Z(s),W(s))ds \right) \right] \\ \!&= \! 2 r(x,f(t,x)) E_{(t,x)} ^f \left[ E_{(t,x)} ^f \left[ ( T \wedge T_1\!-\!t ) \left( \int _{T \wedge T_1}^T r(Z(s),W(s))ds \right) | T_1, X_1\right] \right] \\ \!&= \! 2 r(x,f(t,x)) E_{(t,x)} ^f \left[ ( T \wedge T_1\!-\!t ) E_{(t,x)} ^f \left[ \left( \int _{T \wedge T_1}^T r(Z(s),W(s))ds \right) | T_1, X_1 \right] \right] \\&= 2 r(x,f(t,x)) \int _{ E}\int ^{T-t}_0 Q(du, dy \mid x,f(t,x)) ( T \wedge (t+u)-t ) \\&\times E_{(t,x)} ^f \left[ \left( \int _{t+u}^T r(Z(s),W(s))ds \right) | T_1=t+u, X_1=y \right] \\&= 2 r(x,f(t,x)) \int _{ E}\int ^{T-t}_0 u E_{(t+u,y)} ^f \left[ \left( \int _{t+u}^T r(Z(s),W(s))ds \right) \right] \\&\quad Q(du, dy \mid x,f(t,x)) \\&= 2 r(x,f(t,x)) \int _{ E}\int ^{T-t}_0 u V(f,t+u,y) Q(du, dy \mid x,f(t,x)) \\&= 2 r(x,f(t,x)) \int _{ E}\int ^{T-t}_0 s g(t+s,y) Q(d s, dy \mid x,f(t,x)). \end{aligned}$$

Moreover, it follows from the properties (2.3–2.4) again that

$$\begin{aligned} L_3&= E_{(t,x)} ^f \left[ \int _{T \wedge T_1}^T r(Z(s),W(s))ds \right] ^2 \\&= E_{(t,x)} ^f \left[ E_{(t,x)} ^f \left[ \left( \int _{T \wedge T_1}^T r(Z(s),W(s))ds \right) ^2 | T_1, X_1 \right] \right] \\&= \int _{ E}\int ^{T-t}_0 Q(du, dy \mid x,f(t,x)) E_{(t,x)} ^f \left[ \left( \int _{T \wedge T_1}^T r(Z(s),W(s))d s \right) ^2\right. \\&\quad \left. | T_1=t+u, X_1 =y \right] \\&= \int _{ E}\int ^{T-t}_0 Q(du, dy \mid x,f(t,x)) E_{(t+u,y)} ^f \left[ \left( \int _{t+u}^T r(Z(s),W(s))d s \right) ^2 \right] \\&= \int _{E}\int ^{T-t}_0 Q(d s, dy \mid x,f(t,x)) S(f, t+s, y). \end{aligned}$$

Thus, we have

$$\begin{aligned} S(f,t,x)&= c_g(t,x, f)\\&\quad + \int _{E}\int ^{T-t}_0 S(f, t+s, y) Q(d s, dy \mid x,f(t,x)), \ (t,x) \in [0,T] \times E, \end{aligned}$$

i.e., \(S(f)=H^f_{c_g}S(f)\) for \(f \in F_g\).

By Theorem 3.1(a), we see that for all \(f \in F_g\), \(g=V(f) \in \mathbb {B}_{w}^0([0,T] \times E)\), which together with Assumption 3.2 implies that \(c_g(\cdot ,\cdot ,f) \in \mathbb {B}_{w^2}^0([0,T] \times E)\). Therefore, under Assumptions 3.1 and 3.3, applying Lemma 3.1(a) with replacing \(w^2(\cdot )\) by \(w(\cdot )\) reveals that \(H^f_{c_g}\) is an \(N\)-step contraction from \(\mathbb {B}^0_{w^2}([0,T] \times E)\) to itself for some \(N \ge 1\). Hence, by the Banach’s Fixed Point Theorem, \(H^f_{c_g}\) has a unique fixed point in \(\mathbb {B}^0_{w^2}([0,T] \times E)\), and so the proof is complete.

\((b)\) Since \(c_g(\cdot ,\cdot ,f)\) is in \(\mathbb {B}^0_{w^2}([0,T] \times E)\) for all \(f \in F_g\), using the analog of the proof of Lemma 3.1 yields that \(J_{c_g}(f, t,x) := E_{(t,x)} ^f \Big [\sum _{k=0}^\infty c_g(T_k \wedge T, X_k, f) \Big ]\) is in \(\mathbb {B}^0_{w^2}([0,T] \times E)\) and also satisfies the equation \(u=H^f_{c_g}u\). Hence, by part \((a)\), \(J_{c_g}(f, t,x)=S(f,t,x)\). \(\square \)

Remark 3.3

  1. (a)

    Since we shall minimize \(S(f)\), it is appropriate to interpret \(c_g\) in Theorem 3.2 (b) as a cost function rather than a reward function.

  2. (b)

    Note that the constraint of “\(f \in F_g\)” (rather than “\(f \in F\)”) is essential in converting the variance to a mean here. The success of such a conversion indicates the potential of developing a LP to solve our mean-variance problem; see Sect. 5 for details. Moreover, it is natural to consider the constraint of “\(f \in F_{\ge g}:=\{ f \in F | V(f,t,x) \ge g(t,x), \text{ for } \text{ all } \ (t,x) \in [0,T] \times E\}\)”, for which case the conversion technique in the proof of Theorem 3.2 possibly fails because it is unknown how to obtain the one-step cost function “\(c_g\)”.

  3. (c)

    It seems difficult to express the variance (or the second order moment) of finite horizon total rewards as a convex function of occupancy measures. Hence, the nonlinear programming approach [5, 6, 25, 28] cannot work in our setup. However, if we consider the “stage-wise variance” as in Filar et al. [6], i.e.,

    $$\begin{aligned} \hat{\sigma }^2(f, t,x)&:= \int ^T_t E^f_{(t,x)} \Big [ r(Z(s),W(s)) - E^f_{(t,x)} \big [ r(Z(s),W(s)) \big ] \Big ]^2 d s \\&\quad \forall \ (t,x) \in [0,T] \times E, \end{aligned}$$

    the nonlinear programming approach may be performable, but it is still difficult to deal with since the time horizon introduces a special dimension with additional complexity, which is very different from the infinite horizon cases [6].

4 Existence and Computation of Mean-Variance Optimal Policies

As mentioned above, the problem (\(MV\)) in (2.7) is equivalent to minimizing \(S(f)\) over \(F_g\). Thus, in view of Theorem 3.2(b), we can solve the problem \((MV)\) via the following DTMDP

$$\begin{aligned} \Big \{[0,T]\times E, \{ A_g(t,x), (t,x) \in [0,T] \times E \}, \mathbb {Q}(\cdot ,\cdot \mid t,x, a), c_g(t,x,a) \Big \}, \end{aligned}$$
(4.1)

with \(A_g(t,x)\) as in (3.3), \(\mathbb {Q}\) as in (3.1), and \(c_g\) as in (3.6). The set of feasible state-action pairs now is \(\mathcal {K}_g =\{(t,x, a) \mid t \in [0,T], x \in E, a \in A_g(t,x)\}\). In general, we shall assume \(\mathcal {K}_g\) contains the graph of a measurable function. However, this is implied by the fact that \(F_g \ne \emptyset \). In the following, we employ the current works on infinite horizon DTMDPs to solve such a DTMDP. For this purpose, we define dynamic programming operators \(\mathcal{H}^f\) and \(\mathcal{H}^*\) on \(\mathbb {B}^0_{w^2}([0,T] \times E)\) as follows: for \(f \in F_g\), \(u \in \mathbb {B}^0_{w^2}([0,T] \times E)\), \((t,x) \in [0,T] \times E\),

$$\begin{aligned} \mathcal{H}^f u(t,x)&:= c_g(t,x,f(t,x)) + \int _ E \int ^{T-t}_0 u(t+s,y) Q(d s, dy \mid x, f(t,x)), \\ \mathcal{H}^* u(t,x)&:= \inf _{a \in A_g(t,x)} \left[ c_g(t,x,a) + \int _ E \int ^{T-t}_0 u(t+s,y) Q(d s, dy \mid x,a) \right] . \end{aligned}$$

Moreover, for all \((t,x) \in [0,T] \times E\), let

$$\begin{aligned} \sigma _g^2(t,x):= \inf _{f \in F_g} \sigma ^2(f, t,x), \ \ \ S_g(t,x):= \inf _{f \in F_g}S(f, t,x) \end{aligned}$$

be the value functions (depending on \(g\)). Obviously, \(S_g(t,x) =\sigma ^2_g( t,x) +g^2(t,x)\). In the meantime, to ensure the existence of a mean-variance optimal policy, we need some more assumptions, which are similar to Assumption 8.3.1 and Assumption 8.3.3 in [10] for infinite horizon discounted DTMDPs.

Assumption 4.1

For each \((t,x) \in [0,T] \times E\),

  1. (a)

    \(A(x)\) is compact;

  2. (b)

    The reward rate \(r(x, a)\) is continuous in \(a \in A(x)\);

  3. (c)

    The function \(u'(t,x,a):= \int _ E \int ^{T-t}_0 Q(d s, dy \mid x,a)u(t+s,y)\) is continuous in \(a \in A(x)\) for every function \(u\) in \(\mathbb {B}^0([0,T] \times E)\), where \(\mathbb {B}^0([0,T] \times E)\) denotes the Banach space of real-valued bounded measurable functions \(u\) on \([0,T] \times E\), with \(u(T,x)=0\).

  4. (d)

    The function \(w'(t,x,a):= \int _ E w^2(y) Q(T-t, dy \mid x,a) \) is continuous in \(a \in A(x)\), with \(w\) as in Assumption 3.2.

Remark 4.1

Assumption 4.1 is a set of compact-continuity conditions important for the existence of mean-variance optimal policies, and in particular, it is satisfied when \(A(x)\) is finite for each \(x \in E\).

Lemma 4.1

Under Assumption 4.1, for each \((t,x) \in [0,T] \times E\), we have the following statements.

  1. (a)

    \(u'(t,x,a):= \int _ E \int ^{T-t}_0 Q(d s, dy \mid x,a)u(t+s,y)\) is continuous in \(a \in A(x)\) for every function \(u\) in \(\mathbb {B}^0_{w^2}([0,T] \times E)\).

  2. (b)

    \(A_g(t,x)\) is compact.

  3. (c)

    The cost function \(c_g(t,x, a)\) is continuous in \(a \in A_g(t,x)\).

Proof

  1. (a)

    Using a similar argument to the proof of Lemma 8.3.7 in [10], part (a) follows from Assumption 4.1(c–d).

  2. (b)

    Fix \((t,x) \in [0,T] \times E\). To show \(A_g(t,x)\) is compact, it suffices to prove \(A_g(t,x)\) is closed because \(A_g(t,x) \subset A(x)\) and \(A(x)\) is compact. Indeed, let \(\{a_n\} \subset A_g(t,x)\) such that \(a_n \rightarrow a \in A(x)\). Then, for each \(n\), we have

    $$\begin{aligned} g(t,x)&= r(x, a_n) \int _0^{T-t} \Big ( 1- Q(s, E| x, a_n ) \Big ) d s\\&\quad +\int _{ E}\int ^{T-t}_0 Q(d s, dy \mid x,a_n)g(t+s,y). \end{aligned}$$

    Note that, by the dominated convergence theorem and the continuity of \(Q(s, E| x, \cdot )\) (implied by Assumption 4.1(c)), \(\int _0^{T-t} \Big ( 1- Q(s, E| x, a ) \Big ) d s\) is continuous \(a \in A(x)\). Moreover, since \(g \in \mathbb {B}^0_w([0,T] \times E) \subset \mathbb {B}^0_{w^2}([0,T] \times E)\), by part \((a)\), \(\int _{ E}\int ^{T-t}_0 Q(d s, dy \mid x,a)g(t+s,y)\) is continuous in \(a \in A(x)\). Thus, let \(n \rightarrow \infty \) in the above equality, under Assumption 4.1, we obtain

    $$\begin{aligned} g(t,x)&= r(x, a) \int _0^{T-t} \Big ( 1- Q(s, E| x, a ) \Big ) d s\\&\quad + \int _{ E}\int ^{T-t}_0 Q(d s, dy \mid x,a)g(t+s,y), \end{aligned}$$

    which shows that \(a \in A_g(t,x)\).

  3. (c)

    Recall that

    $$\begin{aligned} c_g(t,x, a)&= 2r^2(x,a)\int ^{T-t}_0 s (1-Q(s,E \mid x,a))ds \nonumber \\&+ \, 2r(x,a) \int _E \int ^{T-t}_0 s g(t+s,y) Q(ds,dy \mid x,a), \ \ \ (t,x,a) \in \mathcal {K}_g. \end{aligned}$$

    First, by the dominated convergence theorem and the continuity of \(Q(s, E| x, \cdot )\), \(\int _0^{T-t} s \Big ( 1- Q(s, E| x, a ) \Big ) d s\) is continuous \(a \in A(x)\). Second, noting that \(v(t,x) = t g(t,x) \in \mathbb {B}^0_w([0,T] \times E) \subset \mathbb {B}^0_{w^2}([0,T] \times E)\), by part \((a)\), \(\int _{ E}\int ^{T-t}_0 s g(t+s,y)Q(d s, dy \mid x,a)\) is continuous in \(a \in A(x)\). Thus, using these facts together with Assumption 4.1(b), we conclude that \(c_g(t,x, a)\) is continuous in \(a \in A_g(t,x)\).

\(\square \)

Remark 4.2

  1. (a)

    Lemma 4.1 in fact provides a set of compact-continuity results on the new data of the converted DTMDP model (4.1), while Assumption 4.1 is a set of compact-continuity hypotheses on the primitive data of the original SMDP model (2.1), which are more easily verified in practice.

  2. (b)

    From the proof of Lemma 4.1(b), we see that, to ensure \(A_g(t,x)\) to be compact-valued, the reward rate \(r(x,\cdot )\) should be continuous rather than be lower semi-continuous, and the continuity of \(u'(t,x,\cdot )\) and \(w'(t,x,\cdot )\) in Assumption 4.1(c–d) on \(A(x)\) cannot be weaken to that on \(A_g(t, x)\).

We now state our main results.

Theorem 4.1

Under Assumptions 3.1–4.1, the following assertions hold.

  1. (a)

    \((\sigma ^2_g+g^2)\) is the unique solution in \(\mathbb {B}^0_{w^2}([0,T] \times E)\) to the optimality equation:

    $$\begin{aligned} (\sigma ^2_g+g^2)(t,x) = \mathcal{H}^* (\sigma ^2_g+g^2) (t,x), \ \ (t,x) \in [0,T] \times E. \end{aligned}$$
    (4.2)
  2. (b)

    A policy \(f \in F_g\) is mean-variance optimal if and only if it attains the minimum of the right-side of (4.2), i.e., \( (\sigma ^2_g+g^2) = \mathcal{H}^f (\sigma ^2_g+g^2) \).

  3. (c)

    A mean-variance optimal policy \(f^* \in F_g\) exists.

  4. (d)

    The value function \(\sigma _g^2\) can be obtained by the value iteration algorithm:

    $$\begin{aligned} \sigma _g^2 = \lim _{n\rightarrow \infty } S_n -g^2, \text{ with } \ S_{n+1}: =\mathcal{H}^* S_n, S_0:=0. \end{aligned}$$
  5. (e)

    A mean-variance optimal policy \(f^* \in F_g\) can be calculated by the Howard’s policy improvement algorithm below:

Howard’s policy improvement algorithm

  1. 1.

    For a given \(g\), compute \(A_g(t,x)\), and then get \(F_g\) by Theorem 3.1(b).

  2. 2.

    Choose \(f_0 \in F_g\) arbitrarily and set \(k=0\).

  3. 3.

    Compute \(S(f_k)=\sigma ^2(f_k) +g^2\) as the unique solution to the equation \(u = \mathcal{H}^{f_k} u\) in \(\mathbb {B}^0_{w^2}([0,T] \times E)\).

  4. 4.

    Obtain \(f_{k+1}\) as a minimizer of \(S(f_k) = \mathcal{H}^*S(f_k)\) such that \(\mathcal{H}^{f_{k+1}}_{c_g}S(f_k) = \mathcal{H}^*S(f_k)\) (where we set \(f_{k+1}(t,x)=f_k(t,x)\) for some \((t,x)\) if possible).

  5. 5.

    If \(f_{k+1}=f_k\), then stop since \(f_{k+1}\) is mean-variance optimal by Theorem 4.1(b). Else set \(k=k+1\) and go to step 3.

Proof

  1. (a)

    Under Assumptions 3.1–4.1, using Lemma 4.1, the measurable selection theorem, and a similar argument to the proof of Lemma 3.1(a) yield that \(\mathcal{H}^*\) is an \(N\)-step contraction from \(\mathbb {B}^0_{w^2}([0,T] \times E)\) to itself for some \(N \ge 1\). Hence, by Banach’s Fixed Point Theorem, \(\mathcal{H}^*\) has a unique fixed point \(u^*\) in \(\mathbb {B}^0_{w^2}([0,T] \times E)\), i.e., \(u^*=\mathcal{H}^*_{c_g}u^*\). To prove part (a) we need to show that: \((a_1)\) \(S_g \in \mathbb {B}^0_{w^2}([0,T] \times E)\), and \((a_2)\) \(S_g = u^*\). However, \((a_1)\) is an immediate result of Theorem 3.2(a). Thus, it remains to prove \((a_2)\), which can be verified in a similar way as in the proof of [10, Theorem 8.3.6].

  2. (b)

    Observe that \(\mathcal{H}^f=H^f_{c_g}\), and thus, by Theorem 3.2(a), \(S(f)\) or \((\sigma ^2(f)+g^2)\) is the unique solution in \(\mathbb {B}^0_{w^2}([0,T] \times E)\) to the equation \(u=\mathcal{H}^f u\) for \(f \in F_g\). If a policy \(f \in F_g\) satisfies \((\sigma ^2_g+g^2) = \mathcal{H}^f (\sigma ^2_g+g^2)\), we then have \(\sigma ^2(f)=\sigma ^2_g\), which shows that \(f \in F_g\) is mean-variance optimal. The converse is obvious.

  3. (c)

    It follows from \(S_g = \mathcal{H}^*S_g \), Lemma 4.1 and the measurable selection theorem that there exists an \(f^* \in F_g\) such that \(S_g = \mathcal{H}^{f^*}S_g \). This fact together with part (b) implies that \(S(f^*,t,x)=S_g(t,x)\). Obviously, such an \(f^* \in F_g\) is mean-variance optimal.

  4. (d)

    By Banach’s Fixed Point Theorem, there exists a function \(u \in \mathbb {B}^0_{w^2}([0,T] \times E)\) with \(u =\mathcal{H}^* u\) and \(u=\lim _{n\rightarrow \infty } (\mathcal{H}^*)^n 0\). However, by part (a), we obtain \(\sigma ^2_g+g^2=\lim _{n\rightarrow \infty } (\mathcal{H}^*)^n 0\), which proposes the value iteration algorithm.

  5. (e)

    It is from Theorem 7.5.1 in [2].

\(\square \)

Remark 4.3

(The weakly continuous case.) In view of Assumption 4.1(c), our discussions above in fact work in the “strongly continuous” context. In some applications, however, one wishes to work in the “weakly continuous” context, in which case Assumption 4.1(c) is replaced by that the function \(u'(t,x,a)\) is continuous on \([0,T] \times K\) for every continuous function \(u \in \mathbb {B}^0([0,T] \times E)\). In this situation, to obtain the related results in Theorem 4.1, we have to strengthen other parts of Assumption 4.1 as follows: (a) \(A(x)\) is compact, and \(x \mapsto A(x)\) is continuous; (b) The reward rate \(r(x, a)\) is continuous on \(K\); (d) The function \(w'(t,x,a):= \int _ E w^2(y) Q(T-t, dy \mid x,a) \) is continuous on \(K\), and \(w(\cdot )\) is continuous. Moreover, to ensure \((t,x) \mapsto A_g(t,x)\) is continuous, we should further require that \(g(t,x)\) are continuous in \((t,x)\). Under the new set of hypotheses, Theorem 4.1 remains valid, and in addition, we get that \(S_g(t,x)\) and \(\sigma _g^2(t,x)\) are continuous functions in \(\mathbb {B}^0_{w^2}([0,T] \times E)\). For more details on the “weakly continuous” case, refer to [2, Section 7.3] or [10, Section 8.5].

5 Linear Programming for the Mean-Variance Problem

In this section, we further develop a linear program and the dual program for solving the problem (\(MV\)) from computational aspects. The key idea is to use the characterization of the function \(S_g\) as the largest solution in \(\mathbb {B}^0_{w^2}([0,T] \times E)\) to the inequality \(u \le \mathcal{H}^* u\). We are now interested in computing a so-called mean-variance \(\gamma \)-optimal policy by linear programming, where \(\gamma (\cdot ,\cdot )\) is an initial distribution for the jump time and state such that \(\int _{[0,T]\times E} w^2(x) \gamma (dt, d x) < \infty \).

A policy \(f \in F_g\) is called mean-variance \(\gamma \)-optimal if \(\sigma ^2(f^*, \gamma ) = \inf _{f \in F_g} \sigma ^2(f,\gamma )\), where \(\sigma ^2(f, \gamma ) := \int _{[0,T] \times E} \sigma ^2(f, t,x) \gamma (dt,d x)\). Clearly, the variance \(\sigma ^2(f, \gamma )\) is well-defined and finite for each \(f \in F_g\). Since minimizing the variance \(\sigma ^2(f, \gamma )\) is equivalent to minimizing the second order moment \(S(f, \gamma ):= \int _{[0,T] \times E} S(f, t,x) \gamma (dt,d x)\) over \(F_g\), our mean-variance optimization problem can be formulated as:

$$\begin{aligned} (MV_\gamma ): \text{ minimize } \ \ S(f,\gamma ) \ \ \ \text{ over } \ f \in F_g, \end{aligned}$$
(5.1)

which is equivalent to the following formulation:

$$\begin{aligned} (P) \left\{ \!\!\!\!\!\begin{array}{l@{\quad }l@{\quad }l} &{} \text{ maximize } \ \int _{[0,T] \times E} u(t,x) \gamma (dt,d x), \\ &{} \text{ subject } \text{ to: } \\ &{} u(t,x)-\int _ E \int ^{T-t}_0 u(t+s,y) Q(d s, dy \mid x,a) \le c_g(t,x, a) \ \forall (t,x, a) \in \mathcal {K}_g, \\ &{} u \in \mathbb {B}^0_{w^2}([0,T] \times E). \end{array}\right. \nonumber \\ \end{aligned}$$
(5.2)

In general, we prefer to solve the problem using its dual formulation. However, it is difficult to directly derive the dual program from the primal LP \((P)\) above. To tackle the difficulty, we rewrite the constraint

$$\begin{aligned} u(t,x)- \int _ E \int ^{T-t}_0 u(t+s,y) Q(d s, dy \mid x,a) \le c_g(t,x, a) \ \forall (t,x, a) \in \mathcal {K}_g \end{aligned}$$

in (5.2) as

$$\begin{aligned} u(t,x)- \int _{[0,T] \times E} u(s,y) \mathbb {Q}(d s, d y \mid t,x, a) \le c_g(t,x, a) \ \forall (t,x, a) \in \mathcal {K}_g \end{aligned}$$
(5.3)

in the “discrete-time” version, which leads to the dual program:

$$\begin{aligned} (D) \ \ \left\{ \begin{array}{l@{\quad }l@{\quad }l} &{} \text{ minimize } \ \int _{\mathcal {K}_g} c_g(t,x, a) \eta (dt,d x, da), \\ &{} \text{ subject } \text{ to: } \\ &{} \ \ \hat{\eta }(B \times C) - \int _{\mathcal {K}_g} \mathbb {Q}(B \times C \mid t,x, a) \eta (dt,d x, da) =\gamma (B \times C),\\ &{}\ B \times C \in \mathcal {B}([0,T] \times E), \ \ \eta \in \mathbb {M}_{w^2}(\mathcal {K}_g), \end{array} \right. \end{aligned}$$

where \(\hat{\eta }\) is the projection of \(\eta \) on \([0,T] \times E\), \(\mathcal{{B}}([0,T] \times E)\) denotes the Borel \(\sigma \)–algebra on the product space \([0,T] \times E\), and \(\mathbb {M}_{w^2}(\mathcal {K}_g)\) represents the set of nonnegative finite measures \(\eta \) on \([0,T] \times E \times A\) concentrated on \(\mathcal {K}_g\) satisfying \(\int _{[0,T]\times E} w^2(x) \hat{\eta }(dt, d x) < \infty \).

The dual program \((D)\) is feasible. In fact, for a policy \(f \in F_g\), we define the occupancy measure \(\hat{\eta }^{f}_{\gamma }\) on \([0,T] \times E\) by

$$\begin{aligned} \hat{\eta }^{f}_{\gamma }(\Gamma ):= E^{f}_\gamma \bigg [\sum \limits _{m=0}^{\infty } I_\Gamma (T_m\wedge T, X_m) \bigg ]=\sum \limits _{m=0}^{\infty } P^{f}_\gamma \bigg ((T_m\wedge T, X_m) \in \Gamma \bigg ) \end{aligned}$$
(5.4)

for each \(\Gamma \in \mathcal {B}([0,T] \times E)\). Let

$$\begin{aligned} \eta ^{f}_{\gamma }(dt,d x, da) := \hat{\eta }^{f}_{\gamma }(dt,dx)\delta _{\{f(t,x)\}}(da) \end{aligned}$$
(5.5)

be a measure on \(\mathcal {K}_g\). Then, using a similar manner as in the proof of Lemma 3.1, we can show that such a measure \(\eta ^{f}_{\gamma }\) is in \(\mathbb {M}_{w^2}(\mathcal {K}_g)\) under Assumptions 3.1–3.3. Moreover, \(\eta ^{f}_{\gamma }\) is feasible for \((D)\). Indeed, for every \(B \times C \in \mathcal {B}([0,T] \times E)\), we have

$$\begin{aligned}&\hat{\eta }^{f}_{\gamma }(B \times C) \\&\quad = P^{f}_\gamma ((T_0\wedge T, X_0) \in B \times C) \\&\quad \quad + \sum \limits _{m=1}^{\infty } E^{f}_\gamma \bigg [ P^{f}_\gamma \bigg ((T_m\wedge T, X_m) \in B \times C | T_{m-1}\wedge T, X_{m-1} \bigg ) \bigg ] \\&\quad = \gamma (B \times C) + \sum \limits _{m=1}^{\infty } \int _{[0,T] \times E} P^{f}_\gamma \bigg (( T_{m-1}\wedge T, X_{m-1}) \in (dt,dx) \bigg ) \\&\quad \quad \times \ \ P^{f}_\gamma \bigg ((T_m\wedge T, X_m) \in B \times C | T_{m-1}\wedge T=t, X_{m-1}=x \bigg ) \\&\quad = \gamma (B \times C) + \int _{[0,T] \times E} \mathbb {Q}(B \times C \mid t,x, f(t,x)) \\&\qquad \sum \limits _{m=1}^{\infty } P^{f}_\gamma \bigg (( T_{m-1}\wedge T, X_{m-1}) \in (dt,dx) \bigg ) \\&\quad = \gamma (B \times C) + \int _{[0,T] \times E} \mathbb {Q}(B \times C \mid t,x, f(t,x)) \hat{\eta }^{f}_{\gamma }(dt,d x) \\&\quad = \gamma (B \times C) + \int _{\mathcal {K}_g} \mathbb {Q}(B \times C \mid t,x, a) \eta ^{f}_{\gamma }(dt,d x, da). \end{aligned}$$

The next theorem shows that the linear programs \((P)\) and \((D)\) actually help to find an optimal solution of the problem (\(MV_\gamma \)). More precisely, the value of both linear programs coincide and yield the optimal value of the problem (\(MV_\gamma \)). We denote by \( val(P)\) and \( val(D)\) the maximal and minimal values of \((P)\) and \((D)\), respectively.

Theorem 5.1

Suppose Assumptions 3.1–4.1 hold. Then:

  1. (a)

    \((P)\) has an optimal solution \(u^* \in \mathbb {B}^0_{w^2}([0,T] \times E)\), and \(u^*=S_g\), and

    $$\begin{aligned} val(P) = \int _{[0,T] \times E}S_g(t,x) \gamma (dt,d x) = val(D). \end{aligned}$$
  2. (b)

    \((D)\) has an optimal solution \(\eta ^* \in \mathcal {M}_{w^2}(\mathcal {K}_g)\), and there exists a policy \(f^* \in F_g\) such that

    $$\begin{aligned} val(D) = \int _{\mathcal {K}_g} c_g(t,x, a) \eta ^*(dt,d x, da) = \int _{[0,T] \times E}S(f^*, t,x) \gamma (dt,d x). \end{aligned}$$

    In particular, the policy \(f^*\) is mean-variance \(\gamma \)-optimal.

Proof

  1. (a)

    Note that the constraints in (5.2) are equivalent to \(u\le \mathcal{H}^*u\). By Theorem 4.1(a), \(S_g\) is the unique solution in \(\mathbb {B}^0_{w^2}([0,T] \times E)\) to the equation \(u=\mathcal{H}^*u\), which shows that \(S_g\) is feasible for \((P)\). Moreover, let \(u \in \mathbb {B}^0_{w^2}([0,T] \times E)\) be any feasible solution for \((P)\). Then \(u\le \mathcal{H}^*u\) and by iterating the operator \(\mathcal{H}^*\) we obtain

    $$\begin{aligned} u\le (\mathcal{H}^*)^n u \rightarrow S_g, \ \mathrm{as} \ n \rightarrow \infty , \end{aligned}$$

    i.e., \(u\le S_g\), and so \(\int u d\gamma \le \int S_g d\gamma \). Hence, \(S_g\) is an optimal solution to \((P)\).

  2. (b)

    By Theorem 4.1, there exists a mean-variance optimal policy \(f^* \in F_g\). Let \(\eta ^*:=\eta ^{f^*}_{\gamma }\) as in (5.5). Then, as shown above, \(\eta ^*\) is in \(\mathcal {M}_{w^2}(\mathcal {K}_g)\) and is feasible for \((D)\). Since \(f^* \in F_g\) is optimal, by weak duality we get

    $$\begin{aligned} val(P) \le val(D) \le \int _{\mathcal {K}_g} c_g d \eta ^*=\int S(f^*) d\gamma =\int S_g d\gamma =val(P), \end{aligned}$$

    which implies that

    $$\begin{aligned} val(D) = \int _{\mathcal {K}_g} c_g d \eta ^*=\int S(f^*) d\gamma . \end{aligned}$$

    The proof is achieved.

\(\square \)

6 Concluding Remarks

In previous sections, we have studied a finite horizon reward mean-variance problem for SMDPs by the dynamic programming approach. The optimality is over the class of all deterministic Markov policies. After characterizing policies with a given mean and transforming the finite horizon reward variance to a mean, we establish the existence and computation of mean-variance optimal policies under reasonable conditions. A linear program and the dual program have also been developed for solving the mean-variance problem. It is worth mentioning that our results can be reduced to those for DTMDPs and CTMDPs with control only at jumps when the semi-Markov kernel \(Q\) has some special structures. Moreover, our technique and treatments are suitable to the case of infinite horizon or first passage reward mean-variance for SMDPs. However, it seems challenging to deal with finite horizon reward mean-variance problems for CTMDPs with control continuously in time.

In our dynamic programming approach, there are two basic steps: one is to characterize policies with a given mean, another is to transform the finite horizon reward variance to a mean. One can observe that the consideration of deterministic Markov policies and the constraint on policies with a given mean are essential in the two steps, respectively. Thus, a natural question arises: can we drop the two restrictions? More clearly, does our technique framework fit the case of randomized history-dependent policies or the case with a constraint that the mean be at least (rather than equal to) some level? Unfortunately, the answer may be no. In our point of view, the nonlinear programming approaches proposed in [5, 6, 25, 28] might be an alternative appropriate direction to this question. However, in contrast to the infinite horizon cases [6, 25, 28], a special dimension of time horizons has to be introduced that will bring additional complexity. In addition, finite horizon variance penalized problems for SMDPs as well as CTMDPs with control continuously in time are also a new topic. Furthermore, it would be interesting to consider finite horizon mean-variance problems for piecewise deterministic Markov controlled processes that are a more general and important class of stochastic control problems. All of these issues deserve careful thought and further research.